材料力学-拉压静不定问题
合集下载
材料力学拉压静不定问题
§1-8 温度应力和装配应力
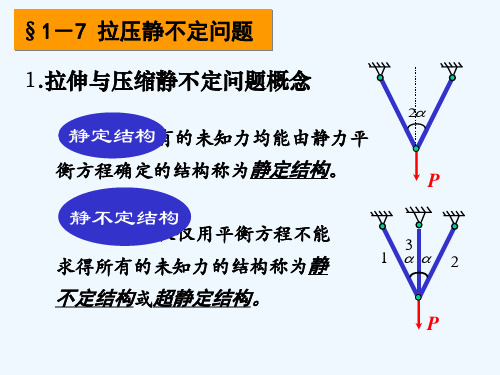
一、温度应力
在超静定结构中,由于各个杆件的变形受到相互的 制约,当温度改变时,必然要在杆内引起附加应力,由 于温度改变而在杆内引起的应力称为温度应力。
对于无约束的杆件,当温度变化为 t t2t1时,杆 件的变形为:
lt tl
式中: ——为材料的线膨胀系数。
例 图示结构,杆①、杆② EA均相同,当杆①温
P
0.72P
求结构的许可载荷
N 1 0 .0P 7 A 1 1
角钢面积由型钢表查得: A1=3.086 cm2
P 1 A 1 1 / 0 . 0 7 3 0 8 . 6 1 6 0 / 0 . 0 7 7 0 5 . 4 k N
N 2 0 .7P 2 A 2 2
P 2 A 2 2 / 0 . 7 2 2 5 0 2 1 2 / 0 . 7 2 1 0 4 2 k N
变形内力关系(物理方程)
方程
P
N3
N1
N2
A
P
例2 求图示两端固定等直杆的约束反力
解:解除约束,以已知方向约束反力代替
EA
EA
平衡方程: PRARB0
A
a
P B 为得到变形协调方程,解除多余约束,分别
b
考虑外力和多余约束反力产生的位移叠加
设B为多余约束,此处的实际位移必须为0
RA
P
R B 几何方程: lP lRB
PP
PP
解:平衡方程:
yy
Y 4 N 1 N 2 P 0
44NN1 1
N2
几何方程
N2
L1 L2
物理方程及补充方程:
L1N E11A L1 1 N E22A L2 2 L2
04-2.7 拉压静不定问题

A l1
F
研究变形
内力假设受拉
变形假设伸长
内力假设与变形假设一致 !
注意事项2:几何方程的求法
B
CD
1
2 3
l3 A l2
A 方法1
l1 F
B
CD
1
2 3
l2Al3
A l1
F
方法2
新节点向原杆作垂线 原节点向新位置作垂线
Statically indeterminate problem 特点:未知力的数目多于静力平衡方程的数目
未知力的数目 pk. 静力平衡方程的数目
例子
B
C
1 2
A
F
y
FN1
FN2
A
x
F
未知力数目: 2 ( FN1 , FN2 ) 静力平衡方程数目: 2 ( ∑Fx = 0, ∑Fy = 0 ) 判断: 静定结构——静定问题
仅用静立平衡方程 便能求解全部未知量
例子
FN2 FN3
FN1
FN4
F
F
未知力数目:4个 静力平衡方程数目:2个 判断:静不定结构,静不定问题
需要补充 2 个方程
3. 静不定次数
Degree of statical indeterminancy
未知力数目与平衡方程数目之差
也是需要补充的方程数目
FN2 FN3
5.25°
2°
5°
4° 2.75°
5.25° 2.75°
4°X5=20° 4° 5° 4°X3=12°
6° 5°
Ⅲ 5°
4°X4=16° 4°
Ⅰ
纵向对接桁 Ⅳ
16
内力按刚度比分配实例2
初始设计
材料力学2-2拉压静不定

1
ቤተ መጻሕፍቲ ባይዱ
7)组合体伸长: 6)应力: (压) (拉)
作业: P73
P81
2.43
2.47
P81
2.48
九、应力集中的概念
P
P 0 A
P
max
P
P
P
P
理论应力集中系数:k
max 0
习 题 课
例题1:图示构架,两杆的材料相同,其横截面面积之 比为A1:A2=2:3,承受载荷为P,试求: 1)为使两杆内的应力相等,夹角应为多大? 2)若P=10kN,A1=100mm2,则杆内的应力为多大?
0.06 10 3 L1 0 .1 L2 0 .3
作业:
P82 2.51
P84 2.53
soc
1
L
1L 3L soc , 3L
)2 ( 0 soc 1 N 2 3 N,0 Y )1(
2
已知三杆的EA相同,3杆制造短了长度, 若将三杆用铰A装配,试求装配后各杆的受力。
解: 1)平衡方程
2)装配后的变形几何关系(变形图)
3
L N L 1N soc 3 A 3E soc 1A 1E
3
L N 3L 3 N , 1 1 1L 3L A A 3E 1 1E
3
soc 3L 2L 1L
2)变形几何关系、变形图:
3)物理关系:
5)联立求解:
4)补充方程:
3. 静不定问题特征: 1)各杆的受力与刚度有关; 2)静不定问题可能产生初应力或温度应力。
tAE R tE B t A A
例1: D1=45mm,t = 3mm,d2=30mm,E1=210GPa, 1=1210 -61/oC, E2=110GPa, 2=16 10 - 61/oC, t从30o升高至180o(30o为装配时温度),求钢管和铜 杆内的应力以及组合体的伸长。 解:1)
ቤተ መጻሕፍቲ ባይዱ
7)组合体伸长: 6)应力: (压) (拉)
作业: P73
P81
2.43
2.47
P81
2.48
九、应力集中的概念
P
P 0 A
P
max
P
P
P
P
理论应力集中系数:k
max 0
习 题 课
例题1:图示构架,两杆的材料相同,其横截面面积之 比为A1:A2=2:3,承受载荷为P,试求: 1)为使两杆内的应力相等,夹角应为多大? 2)若P=10kN,A1=100mm2,则杆内的应力为多大?
0.06 10 3 L1 0 .1 L2 0 .3
作业:
P82 2.51
P84 2.53
soc
1
L
1L 3L soc , 3L
)2 ( 0 soc 1 N 2 3 N,0 Y )1(
2
已知三杆的EA相同,3杆制造短了长度, 若将三杆用铰A装配,试求装配后各杆的受力。
解: 1)平衡方程
2)装配后的变形几何关系(变形图)
3
L N L 1N soc 3 A 3E soc 1A 1E
3
L N 3L 3 N , 1 1 1L 3L A A 3E 1 1E
3
soc 3L 2L 1L
2)变形几何关系、变形图:
3)物理关系:
5)联立求解:
4)补充方程:
3. 静不定问题特征: 1)各杆的受力与刚度有关; 2)静不定问题可能产生初应力或温度应力。
tAE R tE B t A A
例1: D1=45mm,t = 3mm,d2=30mm,E1=210GPa, 1=1210 -61/oC, E2=110GPa, 2=16 10 - 61/oC, t从30o升高至180o(30o为装配时温度),求钢管和铜 杆内的应力以及组合体的伸长。 解:1)
拉压强度变形变形能静不定课件

料等。
数据采集与处理
实验过程记录
详细记录实验过程,包括实验条件、操作步骤、 实验数据等。
数据处理方法
介绍数据的处理方法,如平均值、标准差、回归 分析等,并说明其适用范围和优缺点。
数据图表展示
用图表展示实验数据,如柱状图、折线图、散点 图等,以便直观地观察和分析数据。
强度评价与优化建议
强度评价标准
1. 在研究拉压强度变形和变形能时,只考虑了材料在单向拉伸和压缩下 的性能,而实际工程中材料往往承受多向载荷,因此需要进一步研究多
向载荷下的拉压强度变形和变形能。
2. 在研究静不定问题时,只考虑了简单的几何形状和边界条件,而实际 工程中的结构往往更为复杂,因此需要进一步研究复杂结构的静不定问题。
研究不足与展望
• 在数值模拟方面,虽然采用了一些常用的有限元软件进行模拟 分析,但这些软件的精度和可靠性仍需进一步验证和完善。
研究不足与展望
未来研究方向包括
2. 对复杂结构的静不定问题进行深入研究,开发更为高 效和准确的数值计算方法。
1. 对多向载荷下的拉压强度变形和变形能进行深入研究, 建立更为完善的理论模型和数值模拟方法。
拉形形能静不定件
目 录
• 拉压强度概述 • 弹性变形 • 塑性变形 • 静不定结构分析 • 拉压强度实验及数据分析 • 总结与展望
contents
01
拉述
定义与意义
拉压强度是指材料在承受拉伸或 压缩载荷时,抵抗破坏的能力。
拉压强度是材料的重要力学性能 指标之一,对于工程结构和机械
零件的正常运行至关重要。
介绍拉压强度的评价标准,包括屈服强度、抗拉强度等,并说明 其物理意义和计算方法。
强度评价结果
根据实验数据进行评价,比较试样的拉压强度与理论值的差异,并 分析原因。
数据采集与处理
实验过程记录
详细记录实验过程,包括实验条件、操作步骤、 实验数据等。
数据处理方法
介绍数据的处理方法,如平均值、标准差、回归 分析等,并说明其适用范围和优缺点。
数据图表展示
用图表展示实验数据,如柱状图、折线图、散点 图等,以便直观地观察和分析数据。
强度评价与优化建议
强度评价标准
1. 在研究拉压强度变形和变形能时,只考虑了材料在单向拉伸和压缩下 的性能,而实际工程中材料往往承受多向载荷,因此需要进一步研究多
向载荷下的拉压强度变形和变形能。
2. 在研究静不定问题时,只考虑了简单的几何形状和边界条件,而实际 工程中的结构往往更为复杂,因此需要进一步研究复杂结构的静不定问题。
研究不足与展望
• 在数值模拟方面,虽然采用了一些常用的有限元软件进行模拟 分析,但这些软件的精度和可靠性仍需进一步验证和完善。
研究不足与展望
未来研究方向包括
2. 对复杂结构的静不定问题进行深入研究,开发更为高 效和准确的数值计算方法。
1. 对多向载荷下的拉压强度变形和变形能进行深入研究, 建立更为完善的理论模型和数值模拟方法。
拉形形能静不定件
目 录
• 拉压强度概述 • 弹性变形 • 塑性变形 • 静不定结构分析 • 拉压强度实验及数据分析 • 总结与展望
contents
01
拉述
定义与意义
拉压强度是指材料在承受拉伸或 压缩载荷时,抵抗破坏的能力。
拉压强度是材料的重要力学性能 指标之一,对于工程结构和机械
零件的正常运行至关重要。
介绍拉压强度的评价标准,包括屈服强度、抗拉强度等,并说明 其物理意义和计算方法。
强度评价结果
根据实验数据进行评价,比较试样的拉压强度与理论值的差异,并 分析原因。
材料力学:ch14静不定问题分析
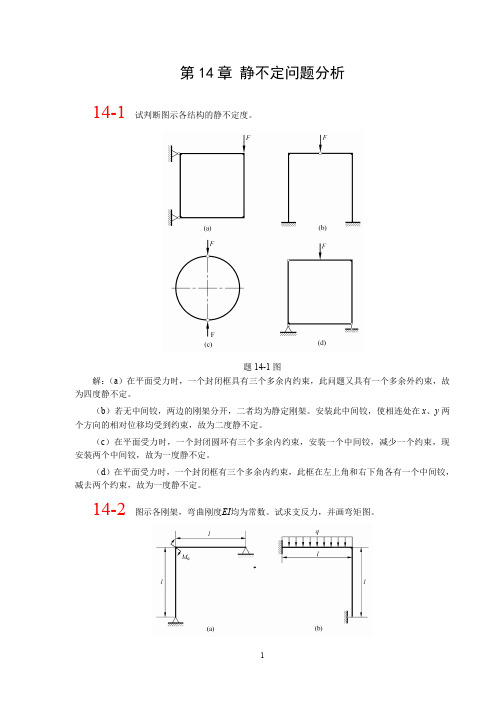
弯矩方程为
图 14-2(b)
M x1 FBx x1 ,
M
x 2
F Bx l
q 2
x
2 2
将其代入 积分后,得 代入协调条件
M x1 x1 , M x2 l
ΔBx
1 EI
lM
0
x1
M
x1
dx1
1 EI
lM
0
x2
M
x2
dx2
ΔBx
1 EI
4 3
FBxl 3
ql 4 6
ΔBx 0
(←
→)
设C与D处的水平反力为Fx,根据题 14-6 所得的ΔA/B,这里有Fx引起的 C/ D ,
代入协调条件
ΔC/ D
π2 8 4π
Fx R3 EI
(→
←)
最后得 B 处支反力为
ΔC / D Δ'C / D Δ''C / D 0
Fx
8 π
2π 2 8
F
(→
←)
FBy F (↑)
16
π
π
Me
()
求 ΔAx 的载荷状态及单位状态示如图(3)和(4)。
弯矩方程为
M
M
e
4M π
e
sin
M R1 cos
将其代入 积分后,得到
Δ Ax
1 EI
π/2 M M Rd
0
ΔAx
π2 2π 4 2π
MeR2 EI
0.0658
MeR EI
2
(←)
14-4图a所示圆弧形小曲率杆,轴线半径为R,承受集度为q的均布剪切载荷作用。设弯曲
图 14-9(a) 根据对称条件,截面 C 的水平位移 ΔCx 为零,即
材料力学第六章静不定

FN2
FN3
(c) F
材料力学
中南大学土木工程学院
13
静不定结构的特点(1)
内力按刚度比分配。 思考:静定结构是否也是这样?
B
C
D
B
刚度较大 内力较大
A
F
材料力学
中南大学土木工程学院
C
刚度增加 内力不变
A
F
14
静不定结构的特点(2) 配应力
——装
B
C
B
D
C
A
静定结构 ——无装配应力
A
中南大学土木工程学院
8
OAB为刚性梁,①、②两杆材料相同,
EA2=2EA1。求②杆与①杆的应力之比。
解:变形协调关系
O
l2 sin 450
2l1
即 l2 2l1
450
①
②
a
A l1
a
l2
B
F
由物理关系建立补充方程,考虑对O取矩得平衡方程,联
立求出两杆轴力,再求应力后得结果。
小技巧
l1
FN1
2 3
EA
l ,l2
1F.5NE2lA,l3
FN3
2 3
2EA
l
代入变形协调方程得补充方程
2FN2 2FN1 FN3
联立平衡方程求得
14 2 3 FN1 23 F 0.76F
FN2 3
3 2 F 0.14F 23
求拉压静 不定结构 注意事项
32 2 3 FN3 23 F 1.24F ()
材料力学
未知力:4个 平衡方程:2个 静不定次数 = 4-2 = 2 需要补充2个方程 此结构可称为2次静不定结构
高等教育大学本科课件 材料力学 第14章 静不定问题分析

M
l
A
B
HA RA HC
相当系统
x1 l
A
l x2 C RC B
l x2 1C
单位载荷状态
真实载荷状态(相当系统):
HA HC
RA
M l
HC
M ( x1 )
(
M l
HC
) x1
M ( x2 ) HC x2
C 0
单位载荷状态:
M( x1 ) x1 M( x2 ) x2
C
1 EI
[
l
0 M( x1 ) M( x1 )dx1
§14-2 用力法分析静不定问题
➢ 几个概念: 基本系统: 解除多余约束后的静定结构(静定基)
相当系统: 作用有载荷和多余反力的基本系统。
Page11
BUAA
MECHANICS OF MATERIALS
➢ 第一类静不定问题:存在多余的外部约束
解除多余的外部约束,代之以支反力
相当系统
在解除约束处,建立变形协调条件
Page3
BUAA
➢ 内力静不定
MECHANICS OF MATERIALS
存在多余内部约束 平面桁架:
内力静不定度 = m - 2n + 3 m: 杆数 n: 节点数
外力静定 内力静不定(一度)
几何可变
4 - 24 + 3 = -1
5 - 24 + 3 = 0
6 - 24 + 3 = 1
Page4
例1:已知EI为常数,求A
A
M l
B
解: 解静不定,求解多余未知力
l
存在1个多余外部约束:
一度外力静不定
C
简单拉压的静不定问题

图示对称桁架,已知 :E1A1= E2A2=EA, l1=l2=l,试求节点 A 的铅垂位移fA
f A AB (l l )cos b l cos a
l aa A F
b
l
cos b cos(a ) cos a sin a ( )2 cos a
4. 建立补充方程
l AC lCB 0 FAx l1 FBx l2 0 F FAx FBx 0 (b) (a)
5. 支反力计算 联立求解平衡方程(a)与补充方程(b),得
FAx Fl2 l1 l2 FBx Fl1 l1 l2
例 4-2 已知:F = 50 kN,[1] = 160 MPa,[2 ] = 120 MPa ,A1= A2。试问:A1=? A2=?
轴力分段(阶梯形杆)
l
i 1
nபைடு நூலகம்
FNi li Ei Ai
FNi-杆段 i 轴力(设正) n-总段数,l—伸长为正
变截面变轴力杆 取微段dx, 微段变形
FN ( x )dx EA(x )
FN ( x ) l dx l EA( x )
若nB,如何求变形?
横向变形与泊松比
拉压杆的横向变形
E
0.39
'
E
叠加原理
算例
试分析杆 AC 的轴向变形 l
1.分段解法
FN1 F2 F1
( l )分段
FN2 F2
FN1l1 FN2l2 ( F2 F1 )l1 F2 l2 EA EA EA EA F2 ( l1 l2 ) F1l1 EA EA
处的向心加速度:
f A AB (l l )cos b l cos a
l aa A F
b
l
cos b cos(a ) cos a sin a ( )2 cos a
4. 建立补充方程
l AC lCB 0 FAx l1 FBx l2 0 F FAx FBx 0 (b) (a)
5. 支反力计算 联立求解平衡方程(a)与补充方程(b),得
FAx Fl2 l1 l2 FBx Fl1 l1 l2
例 4-2 已知:F = 50 kN,[1] = 160 MPa,[2 ] = 120 MPa ,A1= A2。试问:A1=? A2=?
轴力分段(阶梯形杆)
l
i 1
nபைடு நூலகம்
FNi li Ei Ai
FNi-杆段 i 轴力(设正) n-总段数,l—伸长为正
变截面变轴力杆 取微段dx, 微段变形
FN ( x )dx EA(x )
FN ( x ) l dx l EA( x )
若nB,如何求变形?
横向变形与泊松比
拉压杆的横向变形
E
0.39
'
E
叠加原理
算例
试分析杆 AC 的轴向变形 l
1.分段解法
FN1 F2 F1
( l )分段
FN2 F2
FN1l1 FN2l2 ( F2 F1 )l1 F2 l2 EA EA EA EA F2 ( l1 l2 ) F1l1 EA EA
处的向心加速度:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例6:等截面刚杆,已知:横截面积A=200 mm2,P=20 kN。 许用应力 =160 MPa,弹性模量E=200 GPa。
试校核杆的强度。
平衡方程
几何方程 物理方程
Y 0,
1.先解静不定
RA 3P RD 0
RA A a B 2P C P D a C a D
LP LRD
A P B 为得到变形协调方程,解除多余约束,分别
a
b
P
考虑外力和多余约束反力产生的位移叠加 设B为多余约束,此处的实际位移必须为0
RA
B
A P B A
RB 几何方程:
ΔlP 物理方程:
lP lRB
Pa lP , EA
RB Pb ab RA
lRB
RB (a b) EA
解:(一)绘受力图,列平衡方程,根据实际情况,杆 ②在 C 点安装后,杆②受拉,杆①受压,受力图如图示。
受力图一 根据平衡条件得:
M A 0, N1 a N 2 2a 0, N1 2 N 2 a
(二)绘变形几何关系图如图示
变形几何关系图一 根据图可得变形几何关系方程为
N2 E2 A2 P 0.72 P 4 E1 A1 E2 A2
求结构的许可载荷
N1 0.07P A1 1
角钢面积由型钢表查得: A1=3.086 cm2
P A1 1 / 0.07 308.6 160 / 0.07 705.4 kN 1
N 2 0.72P A2 2
§1-7 拉压静不定问题
1.拉伸与压缩静不定问题概念
2
静定结构
所有的未知力均能由静
力平衡方程确定的结构称为静定结构。
P
3
静不定结构
而仅仅用平衡方
程不能求得所有的未知力的结构
称为静不定结构或超静定结构。
1
2
P
2、超静定问题的解法 (1)静力平衡方程——力学——原有基础 (2)变形协调方程——几何——灵活思考
补充方程与平衡方程联立解得: N1 A N2
B
P
C
P 2P N1 ;N 2 5 5
例5:图示结构,三根杆的材料及横截 面积为 E1 E2 E3, A1 A2 A3
l1 l2 l cos , l3 l
1
3
2
试求三杆的轴力。 解:列平衡方程
P
N1
F 0: N N F 0: ( N N ) cos N
解得:
RB
ΔlR
代入平衡方程解得:
Pa ab
设杆的B段有初始间隙δ,求约束反力
解:设外力在B处的位移大于初始间隙δ
EA
EA
B处的实际位移为初始间隙δ
B
A
P
a
b
B
δ
ΔlP
B
几何方程:
物理方程:
lP lRB
lRB RB (a b) EA
A
P
Pa lP , EA
P
P
max
max
理论应力集中系数
P
P
P
P
max k 0
max
弹性力学计算 实验测试(光弹性实验)
圣文南(Saint-Venant)原理: 对弹性体某一局部区域的外 力系,若用静力等效的力系来代 替;则力的作用点附近区域的应 力分布将有显著改变,而对略远 处其影响可忽略不计。 如右图所示,根据现代力学 分析方法(有限元计算方法或光 弹性测试方法)的研究结果显示: 由于在杆端外力作用的方式不同, 将会对杆端附近处各截面的应力 分布产生影响(应力非均匀分 布),而对远离杆端的各个截面, 影响甚小或根本没有影响。
(二)绘变形几何关系图如图示
由图可列出变形几何关系方程
2 l N 2
2 lt l N 1 l N 2
即
化简后得
2 N 1a N 2a 2ta 2 EA EA
(三)求解内力和应力
N 1 2 N 2 1 2 N 1a N 2 a 2 2ta EA EA
解:平衡方程:
y y
Y 4N
1
N2 P 0
几何方程
L1 L2
物理方程及补充方程:
N1L1 N 2 L2 L1 L2 E1 A1 E2 A2
P P
解平衡方程和补充方程,得: E1 A1 N1 P 0.07 P 4 E1 A1 E2 A2
求解静不定问题的一般方法
1.画受力图,列平衡方程,判断静不定次数; 2.根据结构的约束条件画变形图,找变形 协调关系,列几何方程; 3.由力与变形(或温度与变形)的物理关系, 列物理方程; 4.联立几何方程与物理方程建立补充方程; 5.补充方程与平衡方程联立解全部未知力.
平衡方程 几何方程
物理方程
补充方程
相对误差:
6.7
B 2P
C P
a a
166.5 160 % 160 4% 5%
N(kN) D26.7
D
RD
结论:杆安全!
RA 33.3 kN, RD 26.7 kN
§1-8 温度应力和装配应力
一、温度应力
在超静定结构中,由于各个杆件的变形受到相互的 制约,当温度改变时,必然要在杆内引起附加应力,由 于温度改变而在杆内引起的应力称为温度应力。 对于无约束的杆件,当温度变化为 t t2 t1 时,杆 件的变形为:
P A2 2 / 0.72 2502 12 / 0.72 1042 kN 2
P P
E1 A1 N1 P 4 E1 A1 E2 A2 E2 A2 N2 P 4 E1 A1 E2 A2
超静定结构的特点:
超静定结构中杆件的内力按照杆件的刚度占总刚度的比例 分配。即:杆的刚度越大,杆件承受的内力越大。 而静定结构杆件内力仅与外力相关。
解得:…
A
RB
ΔlR
需根据间隙大小进行分类讨论
例3 木制短柱的四角用四个40404的等边角钢加固,角钢和木
材的许用应力分别为[]1=160 MPa和[]2=12 MPa,弹性模量
分别为E1=200 GPa 和 E2 =10 GPa;求许可载荷P。 P P P P 4N1 N2 N2
4N 1
两个概念 温度变形; 再次变形
LT
RA RB EA T
5.温度应力
RB
LR
RA EA T T E T A A
二、装配应力 在加工构件时,由于尺寸上的一些微小误差,对超静 定结构则会在构件内产生应力,这种应力称为装配应力。 例 两杆 EA 相同,水平杆为刚性杆。杆②比设计长度 l 短了 ,求安装后两杆的内力和应力。
联立(a)、(b)可得:
2 EA 2E N1 I 5l 5l N EA E 2 5l II 5l
§1-9 应力集中概念
应力集中:
由于结构或功能上的需要,使 构件截面尺寸或形状发生突变 引起的应力急剧增加的现象。
x 1 2
y 1 2
3
P
2
未知力3个;平衡方程只有2个。 这个问题就是一次静不定问题。
变形几何关系(变形协调方程) 补充 变形内力关系(物理方程) 方程
P
N1
P
N3 N2
A
P
例2 求图示两端固定等直杆的约束反力
解:解除约束,以已知方向约束反力代替 平衡方程: P RA RB 0 EA EA
P a 3P a LP EA EA RD 3a LRD EA
联立以上4式得:
A
a B 2P P a a
RA 33.3 kN, RD 26.7 kN RD
2.校核杆的强度
画杆的轴力图
最大轴力 N max 33.3 kN
y 33.3 RA A a
N max 33.3 103 max A 200 106 166.5 MPa
例4: 图示悬吊结构ABC梁刚性,各杆EA相同,求各杆内力 a 1
B
C A
a P l
解:1.平衡方程
M
A
0, N1 a N 2 2a P 2a 0 N1 2N2 2P 0
2.几何方程(以直代曲) 2l1 l2
l1
l2
2 l
3.物理方程
N1l N 2l l1 , l2 EA EA
A
RA
L
B
RB
解:1.平衡方程 (共线力系)
X 0, R
2一次静不定) LT RB LR
得:RA RB
LT (温度变形)=LR (再次变形)
2.几何方程
LT (温度变形)=LR (再次变形)
3.物理方程 RB L LR , LT T L EA RB L 4.补充方程 T L EA 补充方程与平衡方程联立解得:
lt t l
式中: ——为材料的线膨胀系数。
例 图示结构,杆①、杆② EA 均相同,当杆①温 度升高 t 度时,两杆的内力和应力为多少?
解(一)绘受力图如图示(设二杆均受压)
受力图
列平衡方程
M A 0, N1 a N 2 2a , N1 2 N 2 1
2l1 l2
即:
2N 1l N 2l b EA EA
(三)求解内力和应力
M A 0, N 1 a N 2 2a 0, N 1 2 N 2 a 2 N 1l N 2l b EA EA
