高考数学必备公式总结
高考数学公式总结

高考数学公式总结一、平面几何公式1.两点之间的距离公式:设平面上的两点A(x₁,y₁)和B(x₂,y₂),则两点之间的距离d为:d=√[(x₂-x₁)²+(y₂-y₁)²]2.直线的斜率公式:设直线L过平面上的两点A(x₁,y₁)和B(x₂,y₂),则直线L的斜率k为:k=(y₂-y₁)/(x₂-x₁);若L与x轴平行,则斜率k不存在。
3.直线的一般式方程:设直线L的方程为Ax+By+C=0,则L的斜率k 为:k=-A/B4.直线的点斜式方程:设直线L过平面上的一点P(x₁,y₁),且L的斜率为k,则L的斜率方程为:y=k(x-x₁)+y₁5.直线的两点式方程:设直线L过平面上的两点A(x₁,y₁)和B(x₂,y₂),则L的两点式方程为:(y-y₁)/(x-x₁)=(y₂-y₁)/(x₂-x₁)6.直线的截距式方程:设直线L与x轴和y轴分别交于点A(a,0)和B(0,b),则L的方程为:x/a+y/b=17.两直线互相垂直的判定:设直线L₁的斜率为k₁,直线L₂的斜率为k₂,则L₁与L₂互相垂直的充要条件是:k₁*k₂=-18.两直线互相平行的判定:设直线L₁的斜率为k₁,直线L₂的斜率为k₂,则L₁与L₂互相平行的充要条件是:k₁=k₂9.直线与坐标轴的交点:设直线L的方程为Ax+By+C=0,则与x轴交点的纵坐标为0,横坐标为-x₁=-C/A;与y轴交点的横坐标为0,纵坐标为-y₁=-C/B10.平面图形的面积公式:-矩形的面积公式:设矩形的长为a,宽为b,则面积S=a*b-正方形的面积公式:设正方形的边长为a,则面积S=a²-三角形的面积公式:设三角形的底为b,高为h,则面积S=(1/2)*b*h-梯形的面积公式:设梯形的上底长为a,下底长为b,高为h,则面积S=(1/2)*(a+b)*h-圆的面积公式:设圆的半径为r,则面积S=π*r²二、立体几何公式1.三角形的周长公式:设三角形的边长分别为a、b和c,则周长P=a+b+c2.三角形的面积公式:设三角形的底为b,高为h,则面积S=(1/2)*b*h3.等腰三角形的面积公式:设等腰三角形的底为b,高为h,则面积S=(1/2)*b*h4.等边三角形的面积公式:设等边三角形的边长为a,则面积S=(√3/4)*a²5.直角三角形的勾股定理:设直角三角形的直角边长分别为a和b,斜边长为c,则a²+b²=c²6.立体图形的体积公式:-立方体的体积公式:设立方体的边长为a-正方体的体积公式:设正方体的边长为a,则体积V=a³-圆柱体的体积公式:设圆柱的底面半径为r,高为h,则体积V=π*r²*h-圆锥体的体积公式:设圆锥的底面半径为r,高为h,则体积V=(1/3)*π*r²*h-球体的体积公式:设球的半径为r,则体积V=(4/3)*π*r³三、数列与数学推理公式1.等差数列的通项公式:设等差数列的首项为a₁,公差为d,第n项为aₙ,则通项公式为:aₙ=a₁+(n-1)*d2.等差数列求和公式:设等差数列的首项为a₁,公差为d,共有n项,则前n项和Sₙ的公式为:Sₙ=(n/2)*(a₁+aₙ)3.等比数列的通项公式:设等比数列的首项为a₁,公比为r,第n项为aₙ,则通项公式为:aₙ=a₁*r^(n-1)4.等差数列求和公式:设等差数列的首项为a₁,公比为r,共有n项,则前n项和Sₙ的公式为:Sₙ=a₁*(1-rⁿ)/(1-r)5.数学推理中常用的公式:-二项式定理:设实数a和b,正整数n,则(a+b)ⁿ=C(n,0)*aⁿ*b⁰+C(n,1)*aⁿ⁻¹*b¹+…+C(n,n)*a⁰*bⁿ,其中C(n,k)表示从n个不同元素中取k个的组合数。
高考数学必考公式归纳

高考数学必考公式归纳高考数学必考公式归纳如下:1. 三角函数公式:sin30°=1/2,sin45°=√2/2,sin60°=√3/2cos30°=√3/2,cos45°=√2/2,cos60°=1/2tan30°=√3/3,tan45°=1,tan60°=√3cot30°=√3,cot45°=1,cot60°=√3/3sin15°=(√6-√2)/4,sin75°=(√6+√2)/4cos15°=(√6+√2)/4,cos75°=(√6-√2)/4sin18°=(√5-1)/4(这个值在高中竞赛和自招中会比较有用,即黄金分割的一半)2. 正弦定理:在△abc中,a/sina=b/sinb=c/sinc=2r(其中,r为△abc的外接圆的半径。
)3. 直线过焦点公式:必有ecosA=(x-1)/(x+1),其中A为直线与焦点所在轴夹角,是锐角。
x为分离比,必须大于1。
注:上述公式适合一切圆锥曲线。
如果焦点内分(指的是焦点在所截线段上),用该公式;如果外分(焦点在所截线段延长线上),右边为(x+1)/(x-1),其他不变。
4. 函数的周期性问题:若f(x)=-f(x+k),则T=2k;若f(x)=m/(x+k)(m不为0),则T=2k;若f(x)=f(x+k)+f(x-k),则T=6k。
5. 周期函数加周期函数未必是周期函数,如:y=sinx与y=sinπx相加不是周期函数。
以上信息仅供参考,具体考试内容以实际为准。
高考数学必备公式整理

高考数学必备公式整理一、函数与图像1. 二次函数的标准式:y = ax² + bx + c二次函数的顶点坐标:(h,k)二次函数的轴对称线方程:x=h二次函数的对称轴与x轴交点坐标:(h,0)2. 一次函数的标准式:y = kx + b一次函数的斜率:k一次函数的截距:b一次函数的与x轴的交点坐标:(0,b)3. 一元二次方程的求根公式:x = (-b ± √(b² - 4ac)) / 2a一元二次方程的判别式:∆= b² - 4ac当判别式大于0时,方程有两个不相等实根;当判别式等于0时,方程有两个相等实根;当判别式小于0时,方程没有实根。
二、平面几何1.正方形的周长公式:P=4s(s为边长)正方形的面积公式:A=s²2.长方形的周长公式:P=2a+2b(a为长,b为宽)长方形的面积公式:A = ab3.圆的周长公式:C=2πr(r为半径)圆的面积公式:A=πr²4.直角三角形勾股定理:c²=a²+b²(c为斜边,a、b为两直角边)等边三角形边长公式:a=b=c(a、b、c为三边的边长)三、立体几何1.球的表面积公式:A=4πr²(r为半径)球的体积公式:V=(4/3)πr³2. 圆锥的侧面积公式:S = πrl (r为底圆半径,l为斜高)圆锥的侧面积公式:S=πr(r+l)3. 圆柱的侧面积公式:S = 2πrh (r为底圆半径,h为高)圆柱的体积公式:V=πr²h4.体积的加法原理:若两个几何体没有相交,则它们的体积相加。
四、三角函数1. 正弦定理:a/sinA = b/sinB = c/sinC (a、b、c为三角形的边长,A、B、C为对应的角)2. 余弦定理:c² = a² + b² - 2abcosC (c为三角形的边长,a、b 为对应的边,C为对应的角)3. 正切函数:tanθ = sinθ/cosθ5.三角函数的性质:(1)sin(-θ) = -sinθ(2)cos(-θ) = cosθ(3)tan(-θ) = -tanθ(4)sin(π±θ) = ±sinθ(5)cos(π±θ) = -cosθ(6)tan(π±θ) = ±tanθ五、概率与统计1.事件的概率公式:P(A)=n(A)/n(S)(P(A)代表事件A发生的概率,n(A)代表事件A的可能结果数,n(S)代表样本空间的大小)2.加法原理:若事件A、B互斥(即事件A发生时事件B不发生),则P(AUB)=P(A)+P(B)3.互斥事件的概率和:P(AUB)=P(A)+P(B)以上是高考数学必备的一些公式整理,希望能对大家复习备考有所帮助。
高考数学必背必记公式
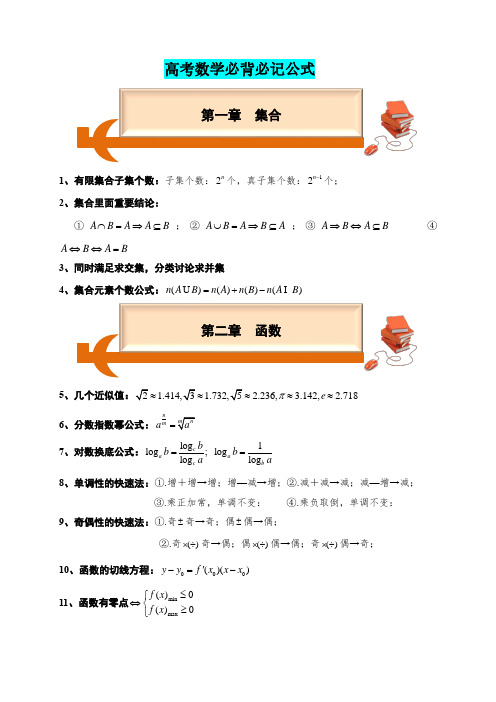
高考数学必背必记公式1、有限集合子集个数:子集个数:2n 个,真子集个数:12n −个;2、集合里面重要结论:①A B A A B ⋂=⇒⊆;②A B A B A ⋃=⇒⊆;③A B A B ⇒⇔⊆ ④A B A B ⇔⇔=3、同时满足求交集,分类讨论求并集4、集合元素个数公式:()()()()n A B n A n B n A B =+−U I5、几个近似值:2 1.414,3 1.732,5 2.236, 3.142, 2.718e π≈≈≈≈≈6、分数指数幂公式:n m n ma a = 7、对数换底公式:log 1log ;log log log c a a c b b b b a a ==8、单调性的快速法:①.增+增→增;增—减→增;②.减+减→减;减—增→减;③.乘正加常,单调不变: ④.乘负取倒,单调不变:9、奇偶性的快速法:①.奇±奇→奇;偶±偶→偶;②.奇()⨯÷奇→偶;偶()⨯÷偶→偶;奇()⨯÷偶→奇;10、函数的切线方程:000()()y y f x x x '−=−11、函数有零点min max ()0()0f x f x ≤⎧⇔⎨≥⎩第一章 集合第二章 函数12、函数无零点max min ()0()0f x f x ⇔≤≥或13、函数周期性:()()f a x f b x +=+的周期Tb a =−; 14、函数对称性:()()f a x f b x +=−的对称轴2a bx +=; 15、抽象函数对数型:若()()()f xy f x f y =+,则()log a f x x =; 16、抽象函数指数型:若()()()f x y f x f y +=,则()x f x a =; 17、抽象函数正比型:若()()()f x y f x f y +=+,则()f x kx =; 18、抽象函数一次型:若()f x c '=,则()f x cx b =+; 19、抽象函数导数型:若()()f x f x '=,则()x f x ke =或()0f x =;20、两个重要不等式:1ln(1)1(0)ln 1x x e x x x e x x x ⎧≥+⇒+≤≤−==⎨≤−⎩当且仅当时“”成立21、洛必达法则:()()()()limlim x ax a f x f x g x g x →→'='(当()0()0f x g x ∞→∞或时使用) 22、恒成立问题:max min(1)()()(2)()()a f x a f x a f x a f x ≥⇔≥<⇔<23、证明()()f x g x >思路:思路1:(1)()()()()0h x f x g x h x =−⇔>(常规首选方法)思路2:min max ()()f x g x >(思路1无法完成)24、等差数列通项公式:1(1)n a a n d =+− 25、等差数列通项公式:11()(1)22n n n a a n n S na d +−==+ 26、等比数列通项公式:11n n a a q −=27、等比数列通项公式:11(1)11n n n a a qa q S q q+−==−−第三章 数列28、等差数列的性质:若m n p q +=+,则m n p q a a a a +=+ 29、等比数列的性质:若m n p q +=+,则m n p q a a a a = 30、等差中项:若,,a A b 成等差数列,则2A a b =+ 31、等比中项:若,,a G b 成等比数列,则2G ab = 32、裂项相消法1:若111(1)1n n nn −++=,则有1111n n T n n =−=++ 33、裂项相消法2:若1111(2)22n n n n −++⎛⎫= ⎪⎝⎭,则有1111(1)2212n T n n =+−−++ 34、裂项相消法3:若111111n nnn a a d a a ++=−⎛⎫⎪⎝⎭,则有11111()nn T d a a +=− 35、裂项相消法4:若1111(21)(21)22121n n n n −+−−+⎛⎫= ⎪⎝⎭,则有11(1)221n T n =−+ 36、错位相减法求和通式:1112()1(1)1n n n n dq b b a b q a b T q q q −=+−−−−37、三角函数的定义:正弦:sin y r α=;余弦:cos x r α=;正切:tan yxα=;其中:22r x y =+38、诱导公式:π倍加减名不变,符号只需看象限;半π加减名要变,符号还是看象限。
高考数学必背公式整理

高考数学必背公式整理一、平面几何公式1. 直线的一般方程:Ax + By + C = 02. 两点间的距离公式:AB = √[(x2 - x1)² + (y2 - y1)²]3. 点到直线的距离公式:d = |Ax0 + By0 + C| / √(A² + B²)4. 两直线夹角的余弦公式:cosθ = (A₁A₂ + B₁B₂) / (√(A₁² + B₁²) √(A₂² + B₂²))5. 两直线平行的条件:A₁ / A₂ = B₁ / B₂ ≠ C₁ / C₂6. 两直线垂直的条件:A₁A₂ + B₁B₂ = 07. 两直线交点的坐标:x = (B₁C₂ - B₂C₁) / (A₁B₂ - A₂B₁),y = (A₂C₁ - A₁C₂) / (A₁B₂ - A₂B₁)二、立体几何公式1. 体积公式:长方体的体积 V = lwh,正方体的体积V = a³,圆柱的体积V = πr²h,圆锥的体积V = (1/3)πr²h,球体的体积 V = (4/3)πr³2. 表面积公式:长方体的表面积 S = 2lw + 2lh + 2wh,正方体的表面积 S = 6a²,圆柱的表面积S = 2πrh + 2πr²,圆锥的表面积S = πrl + πr²,球体的表面积S = 4πr²三、三角函数公式1. 余弦定理:c² = a² + b² - 2abcosC2. 正弦定理:a / sinA = b / sinB = c / sinC3. 三角恒等式:sin²θ + cos²θ = 1,1 + tan²θ = sec²θ,1 + cot²θ = csc²θ四、导数公式1. 基本导数:(xⁿ)' = nxⁿ⁻¹,(sinx)' = cosx,(cosx)' = -sinx,(tanx)' = sec²x,(cotx)' = -csc²x,(lnx)' = 1/x,(ex)' = ex2. 乘法法则:(uv)' = u'v + uv'3. 除法法则:(u/v)' = (u'v - uv') / v²4. 链式法则:(f(g(x)))' = f'(g(x)) * g'(x)五、积分公式1. 基本积分:∫xⁿdx = (xⁿ⁺¹) / (n⁺¹),∫sinxdx = -cosx,∫cosxdx = sinx,∫sec²xdx = tanx,∫csc²xdx = -cotx,∫1/xdx = ln|x|,∫exdx = ex2. 乘法法则:∫uvdx = ∫u'vdx + ∫uv'dx3. 替换法则:∫f(g(x))g'(x)dx = ∫f(u)du六、概率统计公式1. 排列公式:Aₙₙ = n! / (n - m)!2. 组合公式:Cₙₙ = n! / (m!(n - m)!)3. 二项式定理:(a + b)ⁿ = Cⁿ₀aⁿb⁰ + Cⁿ₁aⁿ⁻¹b¹ + ... + Cⁿₙa⁰bⁿ4. 期望公式:E(X) = Σ(xP(x))5. 方差公式:Var(X) = Σ(x²P(x)) - [E(X)]²以上是高考数学中常用的必背公式。
高考数学万能公式口诀大全

高考数学万能公式口诀大全高考数学,一直是众多学子心中的难题。
要在高考数学中取得优异成绩,掌握各种公式和口诀是必不可少的。
下面就为大家整理一份高考数学万能公式口诀大全,希望能对大家有所帮助。
一、函数部分1、函数性质口诀函数奇偶看对称,奇函数关于原点,偶函数关于 y 轴;单调递增与递减,导数正负来判断;周期函数看规律,最小正周期要牢记。
2、反函数口诀反函数,要互换,原函数的定义域,是反函数的值域;原函数的值域,是反函数的定义域,两者关系要理清。
3、幂函数口诀幂指函数最常见,性质众多要分辨;指数大于零,图象过原点,在第一象限内,函数为增函;指数小于零,图象不过点,在第一象限内,函数为减函。
4、指数函数口诀指数函数底数分,大于一为增函数,小于一为减函数;底数若是大于零,图象经过一、二象限,且在 y 轴右侧;底数若是小于零,图象经过二、三象限,且在 y 轴左侧。
5、对数函数口诀对数函数真数大,底数大于一为增,底数小于一为减;对数函数真数小,底数大于一为减,底数小于一为增。
二、三角函数部分1、诱导公式口诀奇变偶不变,符号看象限。
解释:对于形如kπ/2 ± α 的角,当 k 为奇数时,函数名要改变(正弦变余弦,余弦变正弦);当 k 为偶数时,函数名不变。
然后根据角所在的象限确定符号。
2、两角和与差公式口诀正余同余正,余余反正正;和差化积与积化和差,同名相乘用余弦,异名相乘用正弦。
解释:正弦和余弦的两角和与差公式中,“正余同余正”指的是正弦加正弦、余弦加余弦都用余弦公式,“余余反正正”指的是余弦减余弦、正弦减正弦都用正弦公式。
3、倍角公式口诀二倍角公式很重要,正弦余弦要记牢;正弦二倍角,一减余弦二倍半;余弦二倍角,余弦平方减正弦平方。
4、辅助角公式口诀辅助角公式要记清,提出根号二化同形;正余弦前面系数平,和为一才能行。
解释:对于形如 asinx + bcosx 的式子,可以化为√(a²+ b²)sin(x+φ) 的形式,其中φ 的值由tanφ = b/a 确定。
高考必记数学公式汇总

高考必记数学公式汇总1. 一元一次方程:ax + b = 0-解的公式:x=-b/a2. 一元二次方程:ax^2 + bx + c = 0- 解的公式:x = (-b ± √(b^2 - 4ac)) / (2a)3.三角函数:- 正弦定理:a/sinA = b/sinB = c/sinC- 余弦定理:c^2 = a^2 + b^2 - 2abcosC- 正切定理:tanA = a/b4.平面几何:-点到直线的距离:d=,Ax+By+C,/√(A^2+B^2)-平行线的性质:两条直线的斜率相等-垂直线的性质:两条直线的斜率的乘积等于-15.统计与概率:-高斯分布:P(x)=(1/(√(2π)σ))*e^(-((x-μ)^2/(2σ^2))) - 期望值计算:E(x) = ∑(xi * P(xi))- 方差计算:Var(x) = ∑((xi - E(x))^2 * P(xi))6.矩阵:-矩阵乘法:若A是一个mxn的矩阵,B是一个nxp的矩阵,那么它们的乘积C是一个mxp的矩阵,其中C的第i行第j列元素为A的第i行与B的第j列的乘积之和。
7.三角函数补充:- 反正弦函数:sin^(-1)(x)- 反余弦函数:cos^(-1)(x)- 反正切函数:tan^(-1)(x)8.指数与对数函数:-指数函数的性质:a^m*a^n=a^(m+n)- 对数函数的性质:log(a) * log(b) = log(a*b)9.数列与数学归纳法:-等差数列通项公式:an = a1 + (n-1)d-等差数列求和公式:Sn = (n/2)(a1 + an)-等比数列通项公式:an = a1 * r^(n-1)-等比数列求和公式:Sn=a1*(1-r^n)/(1-r)10.导数与微分:- 基本导数公式:(常数)' = 0,(x^n)' = nx^(n-1),(e^x)' = e^x,(sinx)' = cosx,(cosx)' = -sinx-链式法则:(f(g(x)))'=f'(g(x))*g'(x)11.不等式与绝对值:-绝对值不等式性质:,a*b,=,a,*,b,a+b,≤,a,+,b- 一次不等式:ax + b > 0 (a ≠ 0)- 二次不等式:ax^2 + bx + c > 0 (a ≠ 0)这些是高考中常见的一些数学公式,掌握并熟练运用它们可以帮助你在数学考试中提高得分。
高考数学必修公式大全

数学必修1-5常用公式及结论必修1: 一、集合1、含义与表示:(1)集合中元素的特征:确定性,互异性,无序性 (2)集合的分类;有限集,无限集(3)集合的表示法:列举法,描述法,图示法2、集合间的关系:子集:对任意x A ∈,都有 x B ∈,则称A 是B 的子集。
记作A B ⊆ 真子集:若A 是B 的子集,且在B 中至少存在一个元素不属于A ,则A 是B 的真子集, 记作A ≠⊂B 集合相等:若:,A B B A ⊆⊆,则A B =3. 元素与集合的关系:属于∈ 不属于:∉ 空集:φ4、集合的运算:并集:由属于集合A 或属于集合B 的元素组成的集合叫并集,记为 A B U交集:由集合A 和集合B 中的公共元素组成的集合叫交集,记为A B I补集:在全集U 中,由所有不属于集合A 的元素组成的集合叫补集,记为U C A 5.集合12{,,,}n a a a L 的子集个数共有2n 个;真子集有2n –1个;非空子集有2n –1个; 6.常用数集:自然数集:N 正整数集:*N 整数集:Z 有理数集:Q 实数集:R 二、函数的奇偶性1、定义: 奇函数 <=>f (– x ) = – f ( x ),偶函数 <=>f (–x ) = f ( x )(注意定义域)2、性质:(1)奇函数的图象关于原点成中心对称图形; (2)偶函数的图象关于y 轴成轴对称图形;(3)如果一个函数的图象关于原点对称,那么这个函数是奇函数; (4)如果一个函数的图象关于y 轴对称,那么这个函数是偶函数. 二、函数的单调性1、定义:对于定义域为D 的函数f (x ),若任意的x 1, x 2∈D ,且x 1< x 2① f ( x 1) < f ( x 2) <=> f ( x 1) – f ( x 2) < 0<=>f (x )是增函数 ② f ( x 1) > f ( x 2) <=> f ( x 1) – f ( x 2) > 0<=>f (x )是减函数 2、复合函数的单调性:同增异减三、二次函数y =ax 2 +bx +c (0a ≠)的性质1、顶点坐标公式:⎪⎪⎭⎫ ⎝⎛−−a b ac a b 44,22, 对称轴:a bx 2−=,最大(小)值:a b ac 442−2.二次函数的解析式的三种形式(1)一般式2()(0)f x ax bx c a =++≠; (2)顶点式2()()(0)f x a x h k a =−+≠; (3)两根式12()()()(0)f x a x x x x a =−−≠. 四、指数与指数函数 1、幂的运算法则:(1)a m • a n =a m + n ,(2)n m n m a a a −=÷,(3)(a m )n =a m n (4)(ab )n = a n • b n(5) n n nb a b a =⎪⎭⎫⎝⎛(6)a 0 = 1 ( a ≠0)(7)n n a a 1=− (8)m n m n a a =(9)m n m naa 1=−2、根式的性质(2)当na =; 当n ,0||,0a a a a a ≥⎧==⎨−<⎩.4、指数函数y = a x (a > 0且a ≠1)的性质:(1)定义域:R ; 值域:( 0 , +∞) (2)图象过定点(0,1)5.指数式与对数式的互化: log b a N b a N =⇔=(0,1,0)a a N >≠>. 五、对数与对数函数 1对数的运算法则:(1)a b = N <=> b = log a N (2)log a 1 = 0(3)log a a = 1(4)log a a b = b (5)a log a N = N(6)log a (MN) = log a M + log a N (7)log a (N M) = log a M -- log a N(8)log a N b = b log a N (9)换底公式:log a N =aNb b log log (10)推论 log log m n a a nb b m=(0a >,且1a >,,0m n >,且1m ≠,1n ≠, 0N >). (11)log a N =aN log 1(12)常用对数:lg N = log 10 N (13)自然对数:ln A = log e A (其中 e = 2.71828…) 2、对数函数y = log a x (a > 0且a ≠1)的性质:(1)定义域:( 0 , +∞) ; 值域:R (2)图象过定点(1,0)六、幂函数y = x a 的图象:(1) 根据 a例如:y = x 221x x y == 11−==x xy七.图象平移:若将函数)(x f y =的图象右移a 、上移b 个单位, 得到函数b a x f y +−=)(的图象; 规律:左加右减,上加下减 八. 平均增长率的问题如果原来产值的基础数为N ,平均增长率为p ,则对于时间x 的总产值y ,有(1)x y N p =+. 九、函数的零点:1.定义:对于()y f x =,把使()0f x =的X 叫()y f x =的零点。
