动网格相关知识--1
动网格
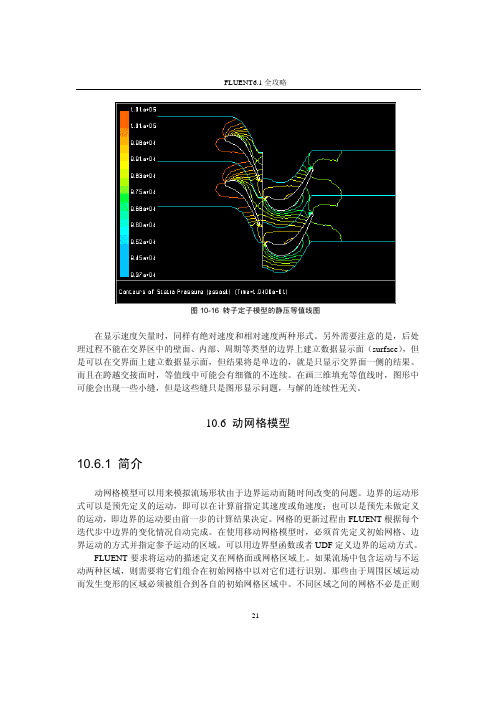
FLUENT6.1全攻略图10-16 转子定子模型的静压等值线图在显示速度矢量时,同样有绝对速度和相对速度两种形式。
另外需要注意的是,后处理过程不能在交界区中的壁面、内部、周期等类型的边界上建立数据显示面(surface),但是可以在交界面上建立数据显示面,但结果将是单边的,就是只显示交界面一侧的结果。
而且在跨越交接面时,等值线中可能会有细微的不连续。
在画三维填充等值线时,图形中可能会出现一些小缝,但是这些缝只是图形显示问题,与解的连续性无关。
10.6 动网格模型10.6.1 简介动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。
边界的运动形式可以是预先定义的运动,即可以在计算前指定其速度或角速度;也可以是预先未做定义的运动,即边界的运动要由前一步的计算结果决定。
网格的更新过程由FLUENT根据每个迭代步中边界的变化情况自动完成。
在使用移动网格模型时,必须首先定义初始网格、边界运动的方式并指定参予运动的区域。
可以用边界型函数或者UDF定义边界的运动方式。
FLUENT要求将运动的描述定义在网格面或网格区域上。
如果流场中包含运动与不运动两种区域,则需要将它们组合在初始网格中以对它们进行识别。
那些由于周围区域运动而发生变形的区域必须被组合到各自的初始网格区域中。
不同区域之间的网格不必是正则21FLUENT6.1全攻略22的,可以在模型设置中用FLUENT 软件提供的非正则或者滑动界面功能将各区域连接起来。
10.6.2 动网格守恒方程在任意一个控制体中,广义标量Φ的积分守恒方程为:()∫∫∫∫∂∂+⋅∇=⋅−+V V Φg V VdV S A d ΦΓA d u u ρΦV ρΦd dt d G G G G (10-7) 式中ρ为流体密度,u G 为速度向量,g u G 移动网格的网格速度,Γ为扩散系数,ΦS 为源项,V ∂代表控制体V 的边界。
方程(10-7)中的时间导数项,可以用一阶后向差分格式写成:()()t V V dV dt d nn V ΔΦ−Φ=Φ+∫ρρρ1 (10-8) 式中n 和n+1代表不同的时间层。
Fluent中的动网格

Fluent中的动网格动网格是目前求解计算域变化问题的常用方法。
参考Fluent帮助,可以知道动网格技术与一般流动计算设置的主要区别在于网格更新方法和更新域设置。
这里就这两方面问题的一点体会作一简单记录。
一、网格更新方法弹簧近似光滑法将任意两网格节点之间的连线理想地看成一条弹簧,并通过近似弹簧的压缩或拉伸实现网格和计算域的改变。
该方法网格拓扑不变,无需网格的插值处理,对结构化(四边形、六面体)和非结构化(三角形、四面体)网格同样适用。
但不适合于大变形情况,当计算区域变形较大时,变形后的网格质量变差,严重影响计算精度。
动态分层法在运动边界相邻处根据运动规律动态增加或减少网格层数,以此来更新变形区域的网格。
该方法适用于结构化网格,通过设置适当的分层和缩减系数,更新后的网格依然为较为均匀的结构化网格,对计算精度影响较小。
对于运动域具有多自由度和任意变形情况,该方法处理起来非常困难。
网格重生方法在整个网格更新区域内依据设定的最大和最小网格尺寸判断需要进行网格重生的网格,并依据设置的更新频率进行网格重生处理。
该方法适用于非结构化网格,能够较好的应用于任意变形的计算区域处理。
二、更新域设置更新域设置是动网格设置中的一项重要工作,最常用的设置是刚体运动域和变形域,这里针对这两种域的设置注意事项和技巧作一简单介绍。
1、域动网格一般来讲,设置为刚体运动域的区域一般为壁面类边界,通过设置固壁的运动,模拟计算域内物体的运动。
由于固壁边界有时形状较为复杂,壁面附近网格尺度与周围网格尺度存在较大差别,网格更新时变形较大。
在这种情况下,可以设置一个包含固壁运动边界的计算域,通过该计算域的整体运动模拟域内物体的运动,在有的地方将这种方法称为域动网格法。
在域动网格法中,需要设置包含运动物体的内部计算域、内部计算域界面均为刚体运动域。
如下图所示。
2、动态分层法中的分界面在应用动态分层网格更新方法时,当分层界面在计算域内部时,需要采用Split interface(这里称分界面)将运动域运动范围与固定计算域区分开来,以保证动态分层网格处理(如果运动域网格与固定域网格没有分界面,动态分层无法执行)。
滑移网格与动网格
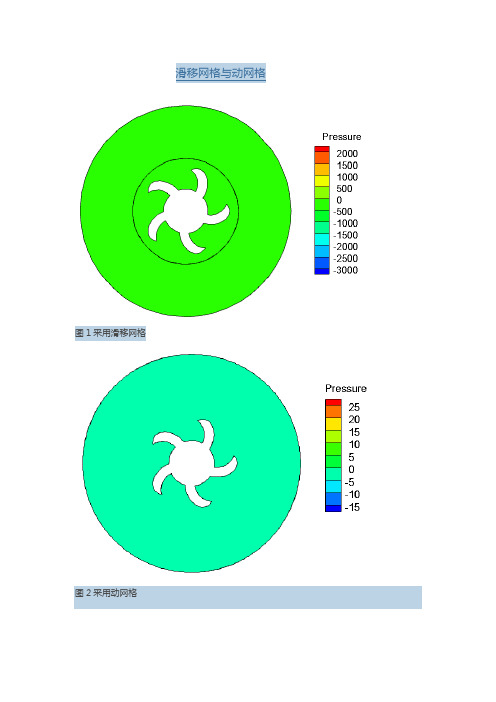
图1采用滑移网格
图2采用动网格
滑移网格与动网格都可以计算瞬态运动问题。
但是存在以下区别:
(1)滑移网格需要建立多个域,实际上还是计算区域运动,是一个独立区域内所有网格一起运动,而动网格则是真正意义上的网格运动。
(2)滑移网格不会涉及到网格的变形与重生,但是要设计到交界面设置
(3)滑移网格不会造成负体积,而动网格极易形成负网格
(4)滑移网格是一种简化了的模型,最大计算误差出现在交界面位置
(5)动网格误差常出现在运动壁面位置,因此实际应用中往往将边界层与壁面合在一起运动。
(6)SRF,MRF与MP只能计算稳态,在新版本的FLUENT中应用的是坐标系变换,和滑移网格的设置有所区别。
动网格归纳

• 动网格模型可以用来模拟流场形状由于边 界运动而随时间改变的问题。
• 边界的运动形式可以是预先定义的运动, 即可以在计算前指定其速度或角速度;也 可以是预先未做定义的运动,即边界的运 动要由前一步的计算结果决定。
• 网格的更新过程由FLUENT根据每个迭代步 中边界的变化情况自动完成。在使用移动 网格模型时,必须首先定义初始网格、边 界运动的形式并指定参予运动的区域。可
动网格模型
• 要求将运动的描述定义在网格面或网格区 域上。如果流场中包含运动与不运动两种 区域,则需要将它们组合在初始网格中以 对它们进行识别。那些由于周围区域运动 而发生变形的区域必须被组合到各自的初 始网格区域中。
• 不同区域之间的网格不必是正则的,可以 在模型设置中用FLUENT提供的非正则或者 滑动界面功能将各区域连接起来。
设置步骤
• (1)选择unsteady • (2)设定边界条件 • (3)激活动网格模型并设定相应参数
Define->Dynamic Mesh ->Parameters • (4)指定移动网格区域的运动参数
Define->Dynamic Mesh->Zones • (5)Save • (6)预览
Solve->Mesh Motion
• 网格畸变率 • 网格尺寸
在定义了动边界面以后如果在其附近同
• (1)需要进行局部调整的表面网格是三角 形(直线)。
• (2)将被重新划分的面网格单元必须紧邻 动网格节点。
• (3)表面网格单元必须处于同一个面上并 构成一个循环。
• (4)被调整单元不能是对称面(线)或正
动态层模型
• 适用于:棱柱形网格区域(六面体或楔形) • 限制: • (1)与运动边界相邻的网格必须为楔形或
多相流-动网格

弹簧式 弹簧式适用于小范围的边界变 形,单元的连接和数量不变, 弹簧式适用于小范围变形的三
角形/四面体网格
A Pera Global Company © PERA China
动网格模型
FLUENT引入动网格模型来移动边界,并调整网格 例子:
– 内燃机汽缸内的活塞运动 – 容积泵 – 机翼摆动 – 阀门开关过程 – 动脉扩张和收缩
A Pera Global Company © PERA China
动网格方法
层铺法 随着边界的移动,单元层生 成或消失。单元层可以是四 边形/六面体/四面体类型, 适合边界在小范围或大范围
内的线性或旋转运动
局部重划法 随着边界移动,网格扭曲大 的区域网格重新划分。适用 于三角形/四面体网格类型,
– 所有的流体域在运动坐标系下定义 – 旋转坐标系引入了附件加速度
为什么要使用运动坐标系?
– 在静止坐标系下流场是瞬态的,使 用旋转坐标系后流场可以看做稳态 的
– 优势 • 用稳态方法求解*
• 边界条件更简单 • 调试更快捷 • 更容易的后处理的分析
Centrifugal Compressor (single blade passage)
均值,随每步迭代更新
• 分布可以是径向或轴向
– 求解收敛后,混合平面将调整 为一般流动条件
Mixing plane (Pressure outlet linked with
a mass flow inlet)
MPM的优势:只需要一个流道,和叶片数量无关
A Pera Global Company © PERA China
A Pera Global Company © PERA China
fluent 动网格

Remeshing方法中的一些参数设定:Remeshing中的参数Minimum length scale和Maximum Length Scale,这两个参数你可以参考mesh scale info中的值,仅是参考,因为mesh scale info中的值是整个网格的评价值,设置的时候看一下动网格附近的网格和整个网格区域的大小比较,然后确定这两个参数,一般来讲,动网格附近的网格较密,这些值都比整体的小,所以在设置时通常设置为比mesh scale info中的Minimum length scale大一点,比Maximum Length Scale小一点。
以上是一般来讲的设置思路。
下面是我在NACA0012翼型动网格例子中的设置:Remeshing中的参数设定:为了得到较好的网格更新,本例在使用局部网格重新划分方法时,使用尺寸函数,也就是Remeshing+Must Improve Skewness+Size Function的策略。
将Minimum Length Scale及Maximum Length Scale均设置为0,为了使所有的区域都被标记重新划分;Maximum Cell Skewness(最大单元畸变),参考Mesh Scale Info…中的参考值0.51,将其设定为0。
4,以保证更新后的单元质量;Size Remesh Interval(依照尺寸标准重新划分的间隔),将这个值设定为1,在FLUENT,不满足最大网格畸变的网格在每个时间步都会被标记,而后重新划分,而不满足最小,最大及尺寸函数的网格,只有在Current Time=(Size Remesh Interval)*delta t的时候,才根据这些尺寸的标准标记不合格的单元进行重新划分,为了保证每步的更新质量,将其修改为1,就是每个时间都根据尺寸的标准标记及更新网格.Size Function Resolution(尺寸函数分辨率),保持默认的3;Size Function Variation(尺寸函数变量):建议使用一个小值,在0.1到0。
Fluent_动网格总结

0.3
Maximum Length Scale
1.4
Maximum Cell Skewness
0.7
Size Remeshing Interval
5
结论:(2)(3)中 Minimum Length Scale 和 Maximum Length Scale 差距过大,导致新生成 网格的长细比大,看上去质量应不高。(4)(5)(6)中的网格同差,但比(2)(3)强一点。 由于尺度差距较大,很难设置的好,除非全局网格都画小。否则 Max/Min 大了后,网格质 量不会好的哪里去。sizing function 应该可以解决这个问题。以(4)的参数作为基本参数,进 行 sizing function 参数设置的分析。
Value 0.3 1.4 0.7 5 3 1 0.3
网格质量明显变好,但无关网格也发生了变化,物体周围的局部网格也令人满意。
江之上制作
7
(8)
Parameter Minimum Length Scale Maximum Length Scale Maximum Cell Skewness Size Remeshing Interval
Resolution Variation(a) Rate(beta)
Value 0.3 1.4 0.7 5 10 1 0.3
不知道怎么回事,远处的网格不变了。附近的网格(全局图中)密了一些。
(9)
Parameter
Value
Minimum Length Scale
0.3
Maximum Length Scale
江之上制作
8
Parameter Minimum Length Scale Maximum Length Scale Maximum Cell Skewness Size Remeshing Interval
0630滑移网格法

滑移网格法滑移网格法作为众多网格方法中的一种,在CFD 计算方面应用十分广泛,特别是在处理有旋转域的相关问题上。
但是“滑移”在中文的传统意义上是属于“动”的一种,使得很多人将滑移网格法错误的认为是动网格方法的一种。
以下将具体介绍动网格的三种实现-方法,以及滑移网格和滑移网格方法的具体实现步骤。
1 动网格方法动网格可以用来模拟流场形状由于边界运动而随时间改变的问题。
其在商用软件中的应用十分广泛。
-动网格可以分为以下三种:弹簧近似光顺法、动态分层法、局部网格分层法。
1.1 弹簧近似光顺法弹簧近似光顺法近似将网格节点间通过弹簧相连,任意一个网格节点的位移均会打破网格系统的力的平衡,通过反复迭代,得到一个新的网格系统,变化过程中网格总量不变。
但在处理计算域较大变形问题时,误差较大。
1.2 动态分层法动态分层法是根据移动边界的运动规律,在变形区域实时增加或减少网格。
局部网格发生增减。
相对弹簧近似光顺法,可以处理计算域变形较大的问题。
1.3 局部网格分层法局部网格分层法是在弹性光顺法的基础上发展得到的。
在弹性光顺法得到新的网格系统的基础上,删除部分网格并从新生成。
该方法有一个网格拉伸度尺寸标准,弹性光顺法得到的网格满足标准则继续使用原网格,不满足则从新生成。
由上可见,动网格方法在数值模拟计算域形状发生变化的相关问题上具有较好的效果。
但在处理计算域旋转但形状不变的问题上有所不足。
而滑移网格方法可以很好的弥补这一不足。
2 滑移网格法滑移网方法是在计算过程中,移动单元区域沿网格分界面滑动,移动网格区域内部网格保持不变。
这一特点使得其在数值模拟带有旋转区域相关问题时,具有较大的优势。
2.1 滑移网格法实现步骤(1)读取各计算计算域网格,识别转/静交接面;(2)对转/静交界面上的网格节点进行外延,构造滑移边界;(3)找到每个滑移点的宿主单元,并计算对应的插值型函数;(4)进行流场的定常数值计算,达到收敛标准;(5)开始非定常计算,第一个物理时刻t=0;(6)对旋转域进行相应旋转,重新构造滑移边界、宿主单元搜索和插值函数计算;(7)进行第t 个物理时刻计算,直到满足内迭代收敛标准;判断非定常计算是否完成,完成则终止计算;否则开始下一物理时刻t=t+1时刻的计算,返回(6)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/dvbbs/dispbbs.asp?boardid=61&Id=1396题记:在学习使用Fluent的时候,有不少朋友需要使用动网格模型(Dynamic Mesh M odel),因此,本版推出这个专题,进行大讨论,使大家在使用动网格时尽量少走弯路,更快更好地掌握;也欢迎使用过的版友积极参与讨论指导,谢谢!该专题主要包括以下的主要内容:§一、动网格的相关知识介绍;§二、以NACA0012翼型俯仰振荡实例进行讲解动网格的应用过程;§三、与动网格应用有关的参考文献;§四、使用动网格进行计算的一些例子。
§一、动网格的相关知识介绍有关动网格基础方面的东西,请具体参考FLUENT User’s Guide或FLUENT全攻略的相关章节,这里只给出一些提要性的知识要点。
1、简介动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。
边界的运动形式可以是预先定义的运动,即可以在计算前指定其速度或角速度;也可以是预先未做定义的运动,即边界的运动要由前一步的计算结果决定。
网格的更新过程由FLUENT 根据每个迭代步中边界的变化情况自动完成。
在使用动网格模型时,必须首先定义初始网格、边界运动的方式并指定参予运动的区域。
可以用边界型函数或者UDF 定义边界的运动方式。
FLUENT 要求将运动的描述定义在网格面或网格区域上。
如果流场中包含运动与不运动两种区域,则需要将它们组合在初始网格中以对它们进行识别。
那些由于周围区域运动而发生变形的区域必须被组合到各自的初始网格区域中。
不同区域之间的网格不必是正则的,可以在模型设置中用FLUENT软件提供的非正则或者滑动界面功能将各区域连接起来。
注:一般来讲,在Fluent中使用动网格,基本上都要使用到UDF,所以你最好具备一定的C语言编程基础。
2、动网格更新方法动网格计算中网格的动态变化过程可以用三种模型进行计算,即弹簧近似光滑模型(spr ing-based smoothing)、动态分层模型(dynamic layering)和局部重划模型(local reme shing)。
弹簧近似光滑模型原则上弹簧光顺模型可以用于任何一种网格体系,但是在非四面体网格区域(二维非三角形),最好在满足下列条件时使用弹簧光顺方法:(1)移动为单方向。
(2)移动方向垂直于边界。
如果两个条件不满足,可能使网格畸变率增大。
另外,在系统缺省设置中,只有四面体网格(三维)和三角形网格(二维)可以使用弹簧光顺法,如果想在其他网格类型中激活该模型,需要在dynamic-mesh-menu 下使用文字命令spring-on-all-shapes?,然后激活该选项即可。
动态分层模型动态分层模型的应用有如下限制:(1)与运动边界相邻的网格必须为楔形或者六面体(二维四边形)网格。
(2)在滑动网格交界面以外的区域,网格必须被单面网格区域包围。
(3)如果网格周围区域中有双侧壁面区域,则必须首先将壁面和阴影区分割开,再用滑动交界面将二者耦合起来。
(4)如果动态网格附近包含周期性区域,则只能用FLUENT 的串行版求解,但是如果周期性区域被设置为周期性非正则交界面,则可以用FLUENT 的并行版求解。
如果移动边界为内部边界,则边界两侧的网格都将作为动态层参与计算。
如果在壁面上只有一部分是运动边界,其他部分保持静止,则只需在运动边界上应用动网格技术,但是动网格区与静止网格区之间应该用滑动网格交界面进行连接。
局部网格重划模型需要注意的是,局部网格重划模型仅能用于四面体网格和三角形网格。
在定义了动边界面以后,如果在动边界面附近同时定义了局部重划模型,则动边界上的表面网格必须满足下列条件:(1)需要进行局部调整的表面网格是三角形(三维)或直线(二维)。
(2)将被重新划分的面网格单元必须紧邻动网格节点。
(3)表面网格单元必须处于同一个面上并构成一个循环。
(4)被调整单元不能是对称面(线)或正则周期性边界的一部分。
动网格的实现在FLUENT 中是由系统自动完成的。
如果在计算中设置了动边界,则F LUENT 会根据动边界附近的网格类型,自动选择动网格计算模型。
如果动边界附近采用的是四面体网格(三维)或三角形网格(二维),则FLUENT 会自动选择弹簧光顺模型和局部重划模型对网格进行调整。
如果是棱柱型网格,则会自动选择动态层模型进行网格调整。
在静止网格区域则不进行网格调整。
动网格问题中对于固体运动的描述,是以固体相对于重心的线速度和角速度为基本参数加以定义的。
既可以用型函数定义固体的线速度和角速度,也可以用UDF 来定义这两个参数。
同时需要定义的是固体在初始时刻的位置。
注:这一小节主要讲述了动网格的更新方法,最好能掌握,尤其是各种方法的适用范围,通常来讲,在一个case中,我们使用的更新方法都是根据网格类型以及和要实现的运动来选择的,很多时候都是几种更新方法搭配起来使用的。
总结一下:使用弹簧近似光滑法网格拓扑始终不变,无需插值,保证了计算精度。
但弹簧近似光滑法不适用于大变形情况,当计算区域变形较大时,变形后的网格会产生较大的倾斜变形,从而使网格质量变差,严重影响计算精度。
动态分层法在生成网格方面具有快速的优势,同时它的应用也受到了一些限制。
它要求运动边界附近的网格为六面体或楔形,这对于复杂外形的流场区域是不适合的。
使用局部网格重划法要求网格为三角形(二维)或四面体(三维),这对于适应复杂外形是有好处的,局部网格重划法只会对运动边界附近区域的网格起作用。
3、动网格问题的建立设置动网格问题的步骤中需要注意的如下:在Solver(求解器)面板中选择非定常流(unsteady)计算;设定边界条件,即设定壁面运动速度;激活动网格模型,并设定相应参数;指定移动网格区域的运动参数;保存算例文件和数据文件;预览动网格设置,菜单操作为:Solve -> Mesh Motion...;应用自动保存功能保存计算结果,在动网格计算中,因为每个计算步中网格信息都会改变,而网格信息是储存在算例文件中的,所以必须同时保存算例文件和数据文件;如果想建立网格运动的动画过程,可以在Solution Animation(计算结果动画)面板中进行相关设置。
注:在这一步中,需要提醒一下,使用动网格进行正式计算之前,最好养成预览动网格更新的习惯;就是在正式计算前,浏览一下动网格的更新情况,这样可以避免在计算过程中出现动网格更新本身的问题。
在预览更新时,很多人都说会出现负体积的警告,更新不成功,出现这样的问题时,最好先把时间步长改的更小点儿试试,一般来讲,排除UDF本身的原因,出现更新出错的原因都与时间步长有关,这需要结合所使用的更新方法多琢磨。
4、设定动网格参数为了使用动网格模型,需要在dynamic mesh(动网格)面板中激活Dynamic Mesh(动网格)选项。
如果计算的是活塞运动,则同时激活In-Cylinder(活塞)选项。
然后选择动网格模型,并设置相关参数。
1)选择网格更新模型在Mesh Methods(网格划分方法)下面选择Smothing(弹簧光顺模型),Layering(动态层模型)和(或)Remshing(局部网格重划模型)。
2)设置弹簧光顺参数激活弹簧光顺模型,相关参数设置位于Smoothing(光顺)标签下,可以设置的参数包括Spring Constant Factor(弹簧弹性系数)、Boundary Node Relaxation(边界点松弛因子)、Convergence Tolerance(收敛判据)和Number of Iterations(迭代次数)。
弹簧弹性系数应该在0 到1 之间变化,弹性系数等于0 时,弹簧系统没有耗散过程,在图中算例中,靠近壁面的网格没有被改变,而是保持了原来的网格形状和密度;在弹性系数等于 1 时,弹簧系统的耗散过程与缺省设置相同,从图中可以发现壁面发生变形,壁面附近网格因为过度加密而质量下降。
因此在实际计算中应该在0 到1 之间选择一个适当的值。
边界点松弛因子用于控制动边界上网格点的移动。
当这个值为零时,边界节点不发生移动;在这个值为1 时,则边界节点的移动计算中不采用松弛格式。
在大多数情况下,这个值应该取为0到1 之间的一个值,以保证边界节点以合适的移动量发生移动。
收敛判据就是网格节点移动计算中,迭代计算的判据。
迭代次数是指网格节点移动计算的最大迭代次数。
3)动态分层在Layering(动态分层)标签下,可以设置与动态层模型相关的参数。
通过设定Const ant Height(常值高度)与Constant Ratio(常值比例)可以确定分解网格的两种方法。
S plit Factor(分割因子)和Collapse Factor(合并因子)则分别为上面介绍的alpha_s和a lpha_c。
4)局部网格重新划分网格在Remeshing(重划网格)标签下,设置与局部重划模型相关的参数。
可以设置的参数包括Maximum Cell Skewness(最大畸变率)、Maximum Cell Volume(最大网格体积)和Minimum Cell Volume(最大网格体积),其含义如前所述,主要用于确定哪些网格需要被重新划分。
在缺省设置中,如果重新划分的网格优于原网格,则用新网格代替旧网格;否则,将保持原网格划分不变。
如果无论如何都要采用新网格的话,则可以在Options(选项)下面选择Must Improve Skewness(必须改善畸变率)选项。
如果Options(选项)下面的Size Function(尺寸函数)被激活,则还可以用网格尺寸分布函数标志需要重新划分的网格。
假设在某点附近的理想网格尺寸为L ,而某个网格的尺寸为L' ,如果:L’不属于[0.8*gamma*L,1.25*gamma*L]则网格被标志为需要重新划分的网格,并在随后的计算中被重新划分。
式中的gamma 用下面的公式计算:当alpha>0时,gamma=1+alpha*d_b^(1+2*beta)当alpha<0时,gamm a=1+alpha*d_b^[(1-beta)^-1]式中d_b为网格到壁面边界的最小距离,alpha和beta就是需要设置的Size Function Variation(尺寸函数增量)和Size Function Rate(尺寸函数变化率)。
以上两式中,alpha以边界网格尺寸为基准控制内部网格的大小,alpha等于0.5表示内部网格的尺寸至少是边界网格的1.5倍,alpha等于-0.5表示内部网格的尺寸等于边界网格的0.5倍,如果alpha等于0则表示内部网格与边界网格大小相同;bata的取值在-1到1之间,用于控制网格从边界到内部区域的变化速率。
