高中物理 6.4相对论的速度变换公式 质能关系课件 教科版选修3-4
高中物理教科版选修(3-4)6.3 教学课件 《相对论的速度变换公式 质能关系》(教科版)

变
换
伽利略速度变换公式是相对论速度变换公式在低速时的特殊表现。
教育科学出版社 高二| 选修3-4
相对论的质量变换
当物体以速率v运动时的质量m与它静止时的质量m0之间有下面的关系:
动质量
静质量
m m0
1
v c
2 2
物体运动的速率
教育科学出版社 高二| 选修3-4
相对论的质量变换
m m0
1
v2 c2
1 2
m0v2
教育科学出版社 高二| 选修3-4
Ek
1 2
m0v
2
这就是我们过去熟悉的动能表达式,这也能让我们看出,牛顿 力学是相对论力学在低速情况下的特例。
教育科学出版社 高二| 选修3-4
人类利用核能的时代正是从 爱因斯坦质能方程的发现开启的!
小结:
狭义相对论的三个重要公式: 1、速度变换公式:
ac cb
v v'u 0.5c 0.9c 1.4c
可能吗?
教育科学出版社 高二| 选修3-4
0
1
u2 c2
l l0
1 u2 c2
若u≧c,根号内的数值将≦0,没有物理意义。
实际物体的速度只能接近光速,却不可能达到,更不可能超过c。
教育科学出版社 高二| 选修3-4
E0 m0c2
m m0
1
v2 c2
Ek
m0 c 2
1
v2 c2
m0c2
教育科学出版社 高二| 选修3-4
思考与讨论
Ek
当v 1时 c
m0 c 2
1
v c
高二物理教科版选修3-4课件:6.4-6.5 相对论的速度变换公式质能关系 广义相对论点滴(选学)

答案
不能.
三、广义相对论点滴
1.广义相对论的基本原理
返回
(1)广义相对性原理:在 任何参考系 中物理规律都是一样的.
(2) 等效原理:一个不受引力作用的加速度系统跟一个受引力
作用的 惯性系统 是等效的.
2.广义相对论的几个结论
(1)光线在引力场中 弯曲 .
(2)引力场的存在使得空间不同位置的 时间进程 出现差别(引力 红移).
第六章 相对论
6.4-6.5 相对论的速度变换公式 质能关系 广义相对论点滴(选学)
学习目标定位
1.知道相对论速度变换公式、相对论质量和质能方程.
2.了解广义相对论的基本原理. 3.初步了解广义相对论的几个主要观点以及主要观测证据.
学习探究区
一、相对论的速度变换
二、相对论质量和能量
三、广义相对论点滴
二、相对论质量和能量
延伸思考
返回
有人根据 E=mc2得出结论:质量可以转化为能量,能量可以转 化为质量,这种说法对吗? 答案 不对.E=mc2表明质量与能量之间存在一一对应的关系,
物体吸收或放出能量,则对应的质量会增加或减少,质量与能
量并没有相互转化 .对于一个封闭的系统,质量是守恒的,能量
也是守恒的.
二、相对论质量和能量
答案 不可以超过光速.
返回
因为回旋加速器的理论基础是粒子在磁场中做圆周运动的
周期 (T = ) 等于交变电场的周期;速度较小时粒子的质量 m
可以认为不变,周期T不变,电场变化与粒子圆周运动同步,
但速度较大时,质量增大明显,粒子做圆周运动的周期T变
大,无法做到圆周运动的周期与高频电压的周期同步.
例3 这说明星体发出的光( C ) A.经太阳时发生了衍射 B.可以穿透太阳及其他障碍物
教科版选修3-4 第6章 第4节 相对论的速度变换公式 质能关系
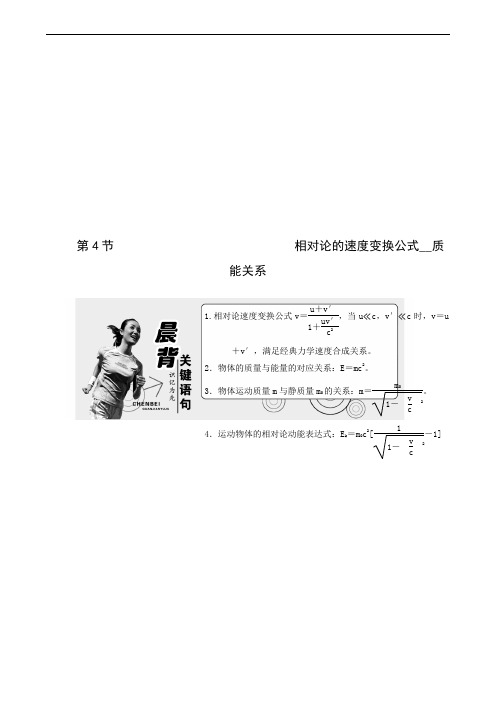
第4节相对论的速度变换公式__质能关系1.相对论速度变换公式v =u +v′1+uv′c2,当u ≪c ,v′≪c 时,v =u+v′,满足经典力学速度合成关系。
2.物体的质量与能量的对应关系:E =mc 2。
3.物体运动质量m 与静质量m 0的关系:m =m 01-v c 2。
4.运动物体的相对论动能表达式:E k =m 0c 2[11-v c2-1]v′沿着火车前进的方向相对火车运动,那么这个人相对地面的速度v 为v =u +v′1+uv′c2。
理解这个公式时请注意:(1)如果车上的人的运动方向与火车的运动方向相反,则v′取负值。
(2)如果u ≪c ,v′≪c ,这时v′uc 2可忽略不计,这时相对论的速度合成公式可近似变为v =v′+u 。
(3)如果v′与u 的方向垂直或成其他角度时,情况比较复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)在高速运动的火车上,设车对地面的速度为v ,车上的人以速度u′沿着火车前进的方向相对火车运动,那么他相对地面的速度u 与u′+v 的关系是( )A .u =u′+vB .u <u′+vC .u >u′+vD .以上均不正确解析:选B 按照经典的时空观,u =u′+v ,而实际上人对地面的速度按照相对论速度公式计算,u =u′+v1+u′v c2,因此u 比u′与v 之和要小,但只有在u′和v 的大小接近光速时才能观察此差别。
相对论质量和能量[自读教材·抓基础]1.质能关系式E =mc 2。
式中m 是物体的质量,E 是它具有的能量。
由此可见,物体质量越大,其蕴含的能量越大。
能量与质量成正比。
2.相对论质量 m =m 01-v 2c2(m 0指静质量); 与静质量对应的静能量为E 0=m 0c 2。
[跟随名师·解疑难]1.对质速关系m =m 01-v c2的理解(1)式中m 0是物体静止时的质量(也称为静质量),m 是物体以速度v 运动时的质量。
教科版高中物理选修3-4课件 6 相对论的速度变换定律 质量和能量的关系课件2

课堂互动讲练
长度的相对性问题 例1 如图6-3-2所示,假设一根10 m长的梭镖 以光速穿过一根10 m长的管子,它们的长度都是 在静止状态下测量的.以下叙述中哪项最好的描 述了梭镖穿过管子的情况( )
图6-3-2
A.梭镖收缩变短,因此在某些位置上,管子能完全 遮住它 B.管子收缩变短,因此在某些位置上,梭镖从管子 的两端伸出来 C.两者都收缩,且收缩量相等,因此在某个位置, 管子恰好遮住梭镖 D.所有这些都与观察者的运动情况有关
(4)由质能关系式可知 ΔE=Δmc2.
即时应用 (即时突破,小试牛刀)
3.一观察者测出电子质量为2m0,求电子速率是多 少?(m0为电子静止时的质量)
解析:m=2m0,代入质量公式 m=
m0 ,可得 1-vc2
2m0=m=
m0 ,解得 1-vc2
v=
23c=0.866c.
答案:0.866c
(2)质能方程
物体质量 m 与其蕴含的能量 E 之间的关系是:E =_m__c_2 _.
核心要点突破
一、对狭义相对论几个主要结论的理解 1.几个主要结论
在相对事件发生地或 物体静止的参考系中
观察
在相对事件发生地或物体运动的参考 系中观察
同时的 事件同时但不同地点
相对性
发生
事件不同时发生
时间间 隔的相
为 u=u′+v,与经典物理学的速度合成公式相同.
2.根据此式若u′=c,则u=c,那么c在惯性系中 都是相同的. 3.如果u′与v的方向不在一条直线上,(相互垂直 或成其他角度)时,情况比较复杂,上式不适用.
即时应用 (即时突破,小试牛刀) 2.地球上一观察者,看见一飞船A以速度2.5×108 m/s 从他身边飞过,另一飞船B以速度2.0×108 m/s跟随A 飞行.求: (1)A上的乘客看到B的速度是多少? (2)B上的乘客看到A的速度是多少? 解析:(1)A上的乘客看到地面的速度为u′=- 2.5×108 m/s,B相对于地面的速度为v=2.0×108 m/s,
高中物理 6.4 相对论的速度变换公式 质能关系堂基础巩固 教科版选修3-4(1)

【三维设计】2021-2021学年高中物理 相对论的速度变换公式 质能关系堂基础巩固 教科版选修3-41.依照相对论判定以下说法正确的选项是( )A .狭义相对论全面否定了经典力学理论B .若是物体在地面上静止不动,任何人在任何参考系里面测出该物体的长度都是一样的C .由E =mc 2可知,质量可转变成能量D .物体速度越大,质量也越大解析:相对论并无否定经典力学理论,而是使经典力学理论的利用范围加倍清楚了,A 错;在不同参考系里测量同一物体的长度,测量值是不同的,B 错;E =mc 2指明了物质能量与质量的对应关系,物体质量与能量不能转化,C 错;由m =m 01-(v c )2可知D 对。
答案:D2.关于物体的质量,以下说法正确的选项是( )A .在牛顿力学中,物体的质量是维持不变的B .在牛顿力学中,物体的质量随物体的速度转变而转变C .在相对论力学中,物体静止时的质量最小D .在相对论力学中,物体的质量随物体速度的增大而增大解析:在牛顿力学中,物体的质量是维持不变的,应选项A 正确,B 错误;在相对论力学中,由于物体的速度v 不可能达到光速c ,因此v <c ,1-(vc )2<1,依照m =m 01-(v c )2,可判定选项C 、D 均正确。
答案:ACD3.假想有一艘飞船以v =0.8c 的速度在地球上空飞行,若是这时从飞船上沿其运动方向抛出一物体,该物体相关于飞船的速度为0.9c ,从地面上的人看来,物体的速度为( )A .1.7cB .0.1cC .0.99cD .无法确信 解析:依照相对论速度变换公式:v =u +v ′1+uv ′c 2,得v =错误!=0.99c ,应选项C 正确。
答案:C 4.设宇宙射线粒子的能量是其静止能量的k 倍。
那么粒子运动时的质量等于其静止质量的________倍,粒子运动速度是光速的________倍。
解析:宇宙射线粒子在静止时的能量为E 0=m 0c 2,运动时的能量为E =mc 2因此k =E E 0=mm 0m =km 0①而相对论中的质量m =m 01-(v c )2② 由①②两式解得vc =k 2-1k 。
高中物理 第六章 相对论 第4节 相对论的速度变换公式 质能关系课件 教科版选修3-4.ppt

7
活动三 相对论质量 物体的能量和质量之间存在
密切的联系,他们的关系是:
Emc2
这就是著名的爱因斯坦质能方程
8
具体推导过程如下:
Ek EE0 Emc2
E0 m0c2
v 1 c
Ek
m0c2 1 v 2
m0c2
c
1v2 11v2
判天地之美,析万物之理
物理学家费尔德曾指出: 当你领悟一个出色的公式时,你会得到
如同听巴哈的乐曲一样的感受。
1
4
相对论的速度变换公式 质能关系
2
活动一 相对论的速度变换
u
v
车对地的速度为v,人对车的速度为v′
地面上的人看到车上人相对 地面的速度为:
v
u v
1
uv c2
3
v
u v
1
uv c2
c
2c
Ek
m0c2
m0c2
1 2
m0c2
v
2
c
1
1
v
2
2c
1 2
m0v 2
9
Ek
1 2
m0v2
这就是我们过去熟悉的动能表达式,这也能让 我们看出,牛顿力学是相对论力学在低速情况下的 特例.
10
如果车上人运动方向与火车运动方向相反,则v′取负 值
4
活动二 相对论质量
物体的运动速度不能无限增加,那么物体的质量是否随 着速度而变化?
严格的论证表明,物体高速(与光速相比)运动时的质 量与它静止时的质量之间有下面的关系:
m
Hale Waihona Puke m01v2
高中物理教科版高二选修3-4课件:第6章_4_相对论的速度变换公式_质能关系、5_广义相对论点滴(选学)
应用广义相对论的原理解决时空变化问题的方法 1.应该首先分析研究的问题或物体做怎样的运动,是处于怎样的参考系 中.无论是匀加速运动的参考系,还是均匀的引力场中,其规律是相同的. 2.然后根据“引力使时间变慢,空间变短”的理论分析其所在位置或运动 情况会产生怎样的变化.
学业分层测评(二十二) 点击图标进入…
量的粒子(如光子),它却可以有动质量 m.
(2)质能方程 ①爱因斯坦质能关系式 E=mc2. ②理解这个公式请注意 a.质能方程表达了物体的质量和它所包含的能量的关系;一定的质量总是 和一定的能量相对应. b.静止物体的能量为 E0=m0c2,这种能量叫做物体的静能量.每个有静质 量的物体都具有静能量.
【答案】 ACE
4.在适当的时候,通过仪器可以观察到太阳后面的恒星,这说明星体发出 的光在________引力场作用下发生了________.
【解析】 根据爱因斯坦的广义相对论可知,光线在太阳引力场作用下发 生了弯曲,所以可以在适当的时候(如日全食时)通过仪器观察到太阳后面的恒 星.
【答案】 太阳 弯曲
2.电子的静止质量 m0=9.11×10-31kg. (1)试用焦和电子伏为单位来表示电子的静质能; (2)静止电子经过 106 V 电压加速后,其质量和速率各是多少?
【解析】 (1)由质能方程得:
E = m0c2 = 9.11×10 - 31×(3×108)2
J = 8.2×10 - 14
J
=
【提示】 一定变化.由质能方程 ΔE=Δmc2 可知,质量变化时,一定对应 能量的变化.
1.相对论速度变换公式的理解 假设高速火车对地面的速度为 v,车上的一高速粒子以速度 u′沿火车前进 的方向相对火车运动,那么此粒子相对于地面的速度为 u=1u+′u+′c2vv. (1)若粒子运动方向与火车运动方向相反,则 u′取负值.
高中物理第六章3时间、长度的相对性4相对论的速度变换公式质能关系5广义相对论点滴(选学课件教科版选修3_4
1234
21905年,爱因斯坦创立了“相对论”,提出了著名的质能方程.下面涉 及对质能方程理解的几种说法中正确的是 ( ) A.若物体能量增大,则它的质量增大 B.若物体能量增大,则它的质量减小 C.若核反应过程质量减小,则需吸收能量 D.若核反应过程质量增大,则会放出能量 解析:由E=mc2,若E增大,则m增大;若E减小,则m减小,故选项A正确, 选项B错误.若m减小,则E减小;若m增大,则E增大,��0
1-
������
2
.
������
(4)相对论时空观.
空间和时间的量度都与物体的运动有关,是相对的.运动棒的长
度的测量建立在必须同时进行观测的基础上,说明空间和时间的量
度又是紧密联系的.
2.相对论的速度变换定律 质量和能量的关系
(1)相对论的速度变换定律.
根据时空相对性,狭义相对论给出:以速率u相对于参考系S运动
(2)时间间隔的相对性(时间延缓).
①定性描述:
同样的两件事,在它们发生于同一地点的参考系内所经历的时间 最短,在其他参考系内观测,这段时间要长些.这一现象称为相对论 时间延缓.
②定量计算:
设与事件发生者相对静止的观察者测出两事件发生的时间间隔
为τ0,与事件发生者相对运动的观察者测得两事件发生的时间间隔
探究一 探究二
(2)对时间、空间与物质的联系性认识不同.
①经典时空观认为时间均匀流逝,与物质无关;空间是物质运动
的场所,空间本身不受物质运动状态的影响;同时空间与时间也是 没有联系的.总之一句话,时间、空间都是绝对的,不同参考系中观 察同一物理过程时间是相同的,观察同一物体长度是相同的.
②相对论时空观认为物理过程的快慢与物体的运动状态有关,运
相对论之时间、长度的相对性相对论的速度变换公式 质能关系6.(3、4)-高中物理课件
0
件的时间间隔,则它们的关系是τ=
. 1
u2 c2
【判一判】 (1)“动钟变慢”是时钟的精度因运动而发生了变化.( ) (2)“动钟变慢”是两个不同的惯性系进行时间比较的一种效 应.( ) (3)小王乘坐宇宙飞船以接近光速的速度离开地球去遨游太空, 经过一段时间返回地球,小王惊奇地发现弟弟比自己要苍老许 多,该现象的科学解释是小王的弟弟思念小王而加速生长 了.( )
一、同时的相对性 1.经典的时空观:在同一个惯性系中不同地点同时发生的两个 事件,在另一个惯性系中观察也是_同__时__的. 2.相对论的时空观:“同时”具有_相__对__性,即在同一个惯性 系中不同地点同时发生的两个事件,在另一个惯性系中观察 _可__能__不__是__同__时__而是一先一后发生的.
二、运动时钟变慢
1.经典的时空观:某两个事件,在不同的惯性系中观察,它们
的时间间隔总是_相__同__的.
2.相对论的时空观:某两个事件,在不同的惯性参考系中观
察,它们的时间间隔是_不__同__的.
设τ0表示相对事件发生地静止的惯性系中观测的时间间隔,
τ表示相对事件发生地以u高速运动的参考系中观察同样两事
提示:(1)根据狭义相对论假设,又根据大量实验事实证明, 光速不能被超越,(1)对. (2)不能把质量和能量混为一谈,不能认为质量消灭了,只剩 下能量在转化,更不能认为质量和能量可以相互转变.在一切 过程中,质量和能量是分别守恒的,只有在微观粒子的裂变和 聚变过程中有质量亏损的情况下才会有质能方程的应用,即 ΔE=Δmc2,(2)错. (3)牛顿第一定律告诉我们质量是物体的固有属性,不会随地 理位置和状态而改变,(3)对.
四、相对论的速度变换、相对论质量和能量
《相对论的速度变换定律 质量和能量的关系》课件1
相对论质量m=
m0 1-vc 2
所以ρ′=a′m b= ab
m0 1-1-vcvc2 2=1-ρvc 2.
答案
ρ 1-vc 2
自主学习
名师解疑
分类例析
对质能方程的理解和应用
【典例3】 一个运动物体的总能量为E,E中是否考虑了物体的
动能?
解析 总能量E=E0+Ek,E0为静质能,实际上包括分子的
名师解疑
分类例析
【变式2】
一匀质矩形薄板,在它静止时测得其长为a,宽为b,质量为
m0,由此可算得其面积密度为ρ=
m0 ab
.假定该薄板沿长度方向
以接近光速的速度v做匀速直线运动,此时再测算该矩形薄
板的面积密度为多少?
自主学习
名师解疑
分类例析
解析 由相对论长度公式得a′=a
1-vc 2
自主学习
名师解疑
分类例析
【变式1】 若一宇宙飞船对地以速度v运动,宇航员在飞船内沿同方向 测得光速为c,问在地上的观察者看来,光速应为v+c吗? 解析 由相对论速度变换公式u=1u+′u+′c2vv,式中u′、v分别 为v和c.代入公式求得光对地速度u=1v++vcc2c=cvv+ +cc=c. 答案 在地面的观察者看来,光速是c不是v+c.
自主学习
名师解疑
分类例析
解析 已知v=0.05c,ux′=0.8c. 由相对论速度叠加公式得ux=1u+x′ux+c′2vv=cu2x+′u+x′vvc2 =c20+.8c0+.8c0×.050c.05c2c=0.817c. 答案 0.817c 借题发挥 高速运动的物体,其速度的叠加不再按照宏观运动规 律伽利略速度变换,而是遵守相对论速度变换定律.
自主学习
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【方法总结】
在两个惯性系中,虽然观察
到的结果并不相同,一个10 m/s,另一个30
m/s,但我们却应用了同样的运动定律和速
度合成法则.
第二节
狭义相对论的两个基本假设
狭义相对论提出的历史背景
19世纪后半叶,关于电磁场的研究不断深入, 人们认识到了光的电磁本质.我们已经知道,电 磁波是以巨大且有限的速度传播的,因此在电磁 场的研究中不断遇到一些矛盾,这些矛盾导致了 相对论的Βιβλιοθήκη 现.狭义相对论的两个基本假设
光速不变原理
在任何惯性系中,光在真空中的速度恒为c, 与光源的运动和观测者的运动无关
光速不变原理与伽利略速度叠加原理是针锋 相对的,具有观念上的革命性.
例.下列几种说法: ①所有惯性系统对物理基本规律都是等价的. ②在真空中,光的速度与光的频率、光源的运动状态无关.
③在任何惯性系中,光在真空中沿任何方向的传播速度都相
如果在车厢运动的速度远小于光速时, 在光到达车壁时间内,车厢运动的距 离观察不出来,所以经典时空观中的 同时的绝对性是在参考系低速运动的 情况下得出的结论。
例:如图所示,沿铁道排列的A、B两电杆正中央安装 一闪光装置C,光信号到达A电杆称为事件1,到达B电 杆称为事件2.则( D ) A.在地面观察者看来,事件1比事件2先发生;从车厢 中观察者看来,事件1、2同时发生 B.在地面观察者看来,事件1比事件2后发生;从车厢 中观察者看来,事件1、2同时发生 C.在地面观察者看来,事件1、2同时发生;从车厢中 观察者看来,事件2比事件1后发生 D.在地面观察者看来,事件1、2同时发生;从车厢中 观察者看来,事件2比事件1先发生
科学的旗手—爱因斯坦
1909—1914 进入大学工作
(苏黎世、布拉格等地)
1914—1933 柏林大学教授、 德国物理研究所所长、院士 1916 提出广义相对论
1933—1955 美国普林斯顿大学 高级研究所研究员 1955.4.18 逝世
1879-1955
相对论是关于时空和引力的基本理论, 主要由爱因斯坦创立,分为狭义相对论 (特殊相对论)和广义相对论(一般相对论)。 相对论的基本假设是光速不变原理,相 对性原理和等效原理。相对论和量子力 学是现代物理学的两大基本支柱。相对 论极大的改变了人类对宇宙和自然的 “常识性”观念,提出了“同时的相对 性”,“四维时空”“弯曲空间”等全 新的概念。
(1)同时的绝对性:在一个参考系中同时发生的事件, 在其他参考系中观察也是同时的.
(2)时间间隔的绝对性:任何事件经历的时间在不同的 参考系中测量都是相同的. (3)长度的绝对性:无论选用什么参考系,对空间两 点距离的测量结果是相同的. (4)物体的质量不随物体的运动而改变.
因此,在经典时空观下,长度、时间、质量这三个基 本物理量都与参考系的选择无关.
出的光,对地速度都为 c
第三节
时间、长度的相对性
同时的相对性
在一个参考系中观察同时发生的两件事,在 另一参考系中观察不同时发生
在车厢内观察
在站台上观察
狭义相对论简介
同时的相对性 我看到闪光到达车厢的 前壁和后壁是“同时” 的
v
光源
到底是 谁错了?
我看到闪光先到达后 壁,后到达前壁
根据光速不变假设,二人说法都是对的。因此, 对不同的观察者来说,“同时”是相对的
第一节 牛顿力学中运动的相对性
惯性系:
牛顿运动定律能够成立的参考系.
在参考系中的物体F合=0时,物体保 持静止或匀速运动,这样的参考系 就叫惯性系。 相对于这个惯性系做匀速直线运动的 另一个参考系也是惯性系
思考:什么是非惯性系?
伽利略相对性原理:
力学规律在任何惯性系中都是相同的。 这个论述叫做伽利略相对性原理
例:哥哥乘坐宇宙飞船以接近光的速度离开地 球去遨游太空,经过一段时间返回地球,哥哥 惊奇地发现弟弟比自己要苍老许多.则该现象 的科学解释是( C ) A.哥哥在太空中发生了基因突变,停止生长了 B.弟弟思念哥哥而加速生长了 C.由相对论可知,物体速度越大,在其上时间 进程就越慢,生理过程也越慢 D.这是神话,科学无法解释
(又叫经典相对性原理)
伽利略相对性原理的三种表述
(1)表述一:力学规律在任何惯性系中都是相同的.
(2)表述二:通过任何力学实验,都不可能发现 惯性系是处于绝对静止状态还是在做匀速直线运动. (3)表述三:任何惯性参考系都是平权的.
经典时空观:(绝对时空观)
时间和空间彼此独立、互不关联,且不受 物质运动的影响.
同. 关于上述说法( D )
A.只有①②是正确的 B.只有①③是正确的 C.只有②③是正确的 D.三种说法都是正确的
例. 判断下列说法是否正确 ( CD ) 1 A.在以 1000c 竖直方向升空的火箭上向前发出的光, 对地速度一定比 c 大 1 B.在以 1000c 竖直方向升空的火箭上向后发出的光, 对箭速度一定比 c 大 1 C.在以 c 1000 竖直方向升空的火箭上沿水平方向发 出的光,对地速度为 c 1 D. 在以 c 竖直方向升空的火箭上向任一方向发 1000
伽利略速度变换
在绝对时空观下: 在相对地面以速率u开行的车厢内,某人相对于车厢 以速率v′向前急跑时相对地面的速率
v
v=u+v′
如果他向后跑时,相对于地面的速率v
v=u-v′
例:如图所示,在列车车厢的光滑水平面上有一个 质量为m=5 kg的小球,正随车厢一起以20 m/s的速 度匀速前进,现在给小球一个水平向前的F=5 N的 拉力作用,求经10 s时,车厢里的观察者和地面的观 察者看到小球的速度分别是多少?
矛盾之一:光速问题
为什么 呢???
对惯性系S,光源发出的光速是c 若惯性系S’相对于S以速度v 运动 对惯性系S’,光源发出的光速是c-v
为什么电磁规律 对两个惯性系不 一样了呢?
狭义相对论的两个基本假设
狭义相对性原理
物理规律(力学、电磁学、光学等)对于 所有惯性系都具有相同的形式
爱因斯坦把伽利略的力学相对性原理推广到了 电磁物理规律和一切其他物理规律,成为第一 个假设.
运动时钟的变慢
u
固有时为 0
在站台上观测
时间间隔为
由狭义相对论导出时间变换公式:
注意:
0
u 1 2 c
2
0
(1)时钟延缓效应并不是钟由于相对运动而发生了物理结 构上的变化,而是由相对运动的不同观测者对时间进行量 度时引起的一种观测效应。
(2)当u远小于光速时,时间间隔相差很小,这就是人 们能够接受经典时空观的原因。
