完整版挡土墙结构算例
【挡土墙】完整版计算

上墙体积V1 下墙体积
(立方米) V2(立方
2.51
11.35
基础体积 上墙重量W1 下墙重量
V3(立方
(t)
W2(t)
0.37
5.77
26.10
基础重量 W3(t) 0.84
上墙力臂 Z1(m) 1.99
四:上墙破裂面计算
填料内摩擦 计算内摩擦 第一破裂角 第二破裂角 与平台夹 第一破裂 第二破裂面 角(φ) 角(δ) (θ1) (αi) 角(α) 面位置(m) 位置(m)
(t)
H(m) 土高ah(m)
1.80
7.52
0.00
砌体容重 r2(t) 2.30
基础容重 r3(t) 2.30
三:挡土墙截面数据
挡土墙全高 (H) 7.52
上墙高 (H1) 2.64
上墙宽 (B1) 0.70
挡土墙面坡 上墙背坡
(n)
(n1)
0.05
0.14
上墙底宽 (B11)
1.20
平台宽 (B2) 1.70
1:抗滑稳定性验算
摩阻系数 (f) 0.40
容许系数 [Kc] 1.30
计算系数K 3.53
判断 满足
2:抗倾覆稳定性验算
ΣMy
ΣM0
ΣN
容许系数 [K0]
计算系数K
判断
92.34
26.33
46.74
1.50
3.51
满足
3:基底应力验算
偏心距e
C
计算应力σ
B/6/COS(a
σ1(t) σ2(t)
0)
地基承载力 σ(t)
25.00
平台宽 (B2)
1.70
下墙背坡 (n2)
砌体挡土墙计算实例

砌体挡土墙计算实例在土木工程中,砌体挡土墙是一种常见的结构,用于支撑土体,防止其坍塌或滑移。
为了确保挡土墙的稳定性和安全性,需要进行精确的计算。
下面,我们将通过一个具体的实例来详细介绍砌体挡土墙的计算过程。
假设我们要设计一个高度为 5 米的砌体挡土墙,墙背填土为砂土,填土表面水平,墙后地下水位在墙底以下 1 米处。
挡土墙采用 MU30 毛石、M75 水泥砂浆砌筑,墙身重度为 22kN/m³。
一、土压力计算首先,我们需要计算作用在挡土墙上的土压力。
根据库仑土压力理论,主动土压力系数可以通过以下公式计算:Ka =tan²(45° φ/2)其中,φ 为填土的内摩擦角。
假设填土的内摩擦角为 30°,则主动土压力系数 Ka 为:Ka = tan²(45° 30°/2) = 033土压力的分布呈三角形,顶部为零,底部最大。
土压力强度可以通过以下公式计算:σa =γhKa其中,γ 为填土的重度,h 为计算点距离填土表面的高度。
假设填土重度为 18kN/m³,则墙顶处土压力强度为零,墙底处土压力强度为:σa = 18×5×033 = 297kN/m²土压力的合力可以通过三角形面积计算:Ea = 05×297×5 = 7425kN/m合力作用点距离墙底的高度为:h = 5/3 = 167m二、抗滑移稳定性验算为了保证挡土墙不会沿基底滑移,需要进行抗滑移稳定性验算。
抗滑移稳定系数 Ks 可以通过以下公式计算:Ks =(μ∑Gn + Ep) / Ea其中,μ 为基底摩擦系数,∑Gn 为垂直于基底的重力之和,Ep 为墙前被动土压力。
由于本例中不考虑墙前被动土压力,Ep 为零。
假设基底摩擦系数为 04,重力之和为:∑Gn = G + Ey其中,G 为挡土墙自重,Ey 为墙后土压力的水平分力。
挡土墙自重 G 可以通过墙身体积乘以重度计算:G = 05×5×22 = 55kN/m墙后土压力的水平分力 Ey 为:Ey =Ea×cos(δ)其中,δ 为墙背与填土之间的摩擦角,假设为 15°。
挡土墙例题原版

挡土墙例题原版在土木工程领域,挡土墙是一种常见且重要的结构,用于支撑土体或岩石,防止其坍塌或滑移,以保证边坡的稳定性和周边建筑物的安全。
接下来,让我们通过一个具体的挡土墙例题,深入了解其设计和计算的过程。
假设有一个高度为5 米的挡土墙,墙后填土为砂土,填土表面水平,填土的重度为 18kN/m³,内摩擦角为 30°。
挡土墙的墙背竖直、光滑,墙底与地基的摩擦系数为 04。
首先,我们来计算土压力。
由于墙背竖直、光滑,我们可以使用朗肯土压力理论。
根据朗肯土压力理论,主动土压力系数 Ka = tan²(45°30°/2) = 0333。
主动土压力的强度分布为:pa =γzKa,其中 z 为计算点距离填土表面的深度。
在墙顶处(z = 0),主动土压力强度为 0。
在墙底处(z = 5m),主动土压力强度为 pa = 18×5×0333 =2997kN/m²。
接下来,计算主动土压力的合力。
主动土压力的合力 Ea 可以通过对主动土压力强度分布进行积分得到。
Ea =05×γ×H²×Ka = 05×18×5²×0333 = 125kN/m。
合力作用点距离墙底的距离为 H/3 = 5/3 = 167m。
然后,我们需要考虑挡土墙的稳定性。
抗滑移稳定性验算:挡土墙受到的水平土压力会产生滑移的趋势,需要验算其抗滑移稳定性。
抗滑移安全系数 Ks =(W + Ep)μ / Ea ,其中 W 为挡土墙的自重,Ep 为墙底的被动土压力(此处由于墙底条件,被动土压力可忽略不计),μ 为墙底与地基的摩擦系数。
假设挡土墙自重为 150kN/m,那么 Ks =(150 + 0)×04 / 125 =048 < 13 (规范要求的抗滑移安全系数),不满足抗滑移要求。
抗倾覆稳定性验算:土压力对挡土墙还会产生倾覆的力矩,需要验算其抗倾覆稳定性。
挡土墙设计计算案例
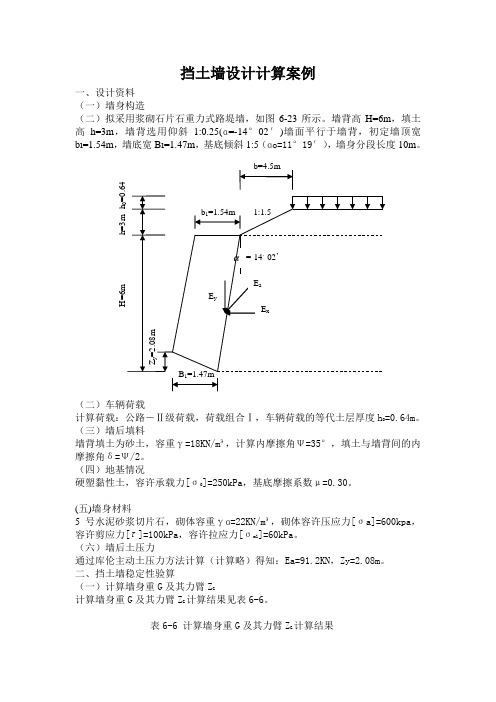
挡土墙设计计算案例一、设计资料(一)墙身构造(二)拟采用浆砌石片石重力式路堤墙,如图6-23所示。
墙背高H=6m,填土高h=3m,墙背选用仰斜1:0.25(ɑ=-14°02′)墙面平行于墙背,初定墙顶宽bı=1.54m,墙底宽Bı=1.47m,基底倾斜1:5(ɑo=11°19′),墙身分段长度10m。
(二)车辆荷载计算荷载:公路-Ⅱ级荷载,荷载组合Ⅰ,车辆荷载的等代土层厚度h=0.64m。
(三)墙后填料墙背填土为砂土,容重γ=18KN/m³,计算内摩擦角Ψ=35°,填土与墙背间的内摩擦角δ=Ψ/2。
(四)地基情况硬塑黏性土,容许承载力[σ]=250kPa,基底摩擦系数μ=0.30。
(五)墙身材料5号水泥砂浆切片石,砌体容重γɑ=22KN/m³,砌体容许压应力[σa]=600kpa,容许剪应力[τ]=100kPa,容许拉应力[σml]=60kPa。
(六)墙后土压力通过库伦主动土压力方法计算(计算略)得知:Ea=91.2KN,Zy=2.08m。
二、挡土墙稳定性验算(一)计算墙身重G及其力臂ZG计算墙身重G及其力臂ZG计算结果见表6-6。
表6-6 计算墙身重G及其力臂ZG 计算结果体积V (m³) 自重G (KN )力臂Z G (m )V1=(6×0.25+1.47)×6 =17.82 Gı=γVı =392.04ZGı=1/2(6×0.25+1.47-1/3×6×0.25)=2.47 V2=1/2×(6×0.25)×6 =4.50 G2=γV2 =99.00ZG2=(6×0.25+1.47-1/3×6×0.25) =2.47 V3=1/2×(6×0.25+1.47-1.54)²/0.25=4.09 G3=γV3 =89.98 ZG3=1/3(6×0.25+1.47-1.54)=0.48 V4=1/2×1.47²/5=0.22 G4=γV4 =4.84ZG4=1/3×1.47=0.49 V=V1-V2-V3-V4=9.01G=γV =198.22ZG=(GıZGı-G2ZG2-G3ZG3-G4ZG4)/G=1.48(二)抗滑稳定性验算 由式(6-3)得:3.132.1'1911sin 22.198)'1911'3017'0214cos(2.913.0)]'1911'3017'0214sin(2.91'1911cos 22.198[sin )cos()]sin(cos [)(0000>=︒-︒+︒+︒-⨯︒+︒+︒-+︒=-+++++=-+=ααδαμαδααμααG E E G G E E G Kc T T N N该初拟的挡土墙抗滑稳定性满足要求。
挡土墙算例

挡土墙设计与验算说明1.1 设计资料1.1.1 墙身构造本设计任务段为K1+300~K1+360的横断面,为了减少填方量,收缩边坡,增强路基的稳定性,拟在本段设置一段重力式路堤挡土墙,其尺寸见挡土墙设计图。
拟采用浆砌片石仰斜式路堤挡土墙,墙高H=8m ,墙顶填土高度为m a 2=,顶宽m 2,底宽m 25.2,墙背仰斜,坡度为-0.25:1,(α=-14.04°),基底倾斜,坡度为5:1,(0α=11.18°),墙身分段长度为10m 。
1.1.2 车辆荷载根据《路基设计规范(JTG 2004)》,车辆荷载为计算的方便,可简化换算为路基填土的均布土层,并采用全断面布载。
换算土层厚694.0185.120===γqh 其中: 根据规范和查表m KN q /5.12102101020)810(=+--⨯-= γ为墙后填土容重318m KN =γ1.1.3 土壤地质情况填土为砂性土土,内摩擦角︒34=φ,墙背与填土间的摩擦角︒==172/φδ,容重为318m KN=γ砂性土地基,容许承载力为[σ]=500KPa 。
1.1.4 墙身材料采用7.5号砂浆,25号片石,砌体容重为323mKN=γ3;按规范:砌体容许压应力为[]Kpa a 900=σ,容许剪应力为[]Kpa 180=τ,容许拉应力为[]Kpa l 90=ωσ。
1.2 墙背土压力计算对于墙趾前土体的被动土压力,在挡土墙基础一般埋深的情况下,考虑到各种自然力和人畜活动的作用,以偏于安全,一般均不计被动土压力,只计算主动土压力。
其计算如下:1.2.1 主动土压力计算KNa E E KNa E E KN B tg E a y a X a 88.7)02.1417sin(67.151)sin(36.151)02.1417cos(67.151)cos(∴67.1510)'3038'3638sin()34'3638cos()93.18799.094.56(18)sin()cos()(00=︒-︒⨯=+==︒-︒⨯=+==︒+︒︒+︒-⨯⨯=++-A =δδφθφθθγ 1.2.2 土压力作用点位置确定mtg B mh h ah aH H h h h H h H a H my x y 785.225.014.225.214.2)08.4694.0256.228228(308.4694.03)36.1856.238(28)22(33)3(08.436.156.2836.125.07986.075.056.225.07986.07986.020.322223301223022123=⨯+=Z -=Z =⨯⨯-⨯-⨯⨯+⨯⨯⨯++⨯⨯-⨯+=--+⨯++-+=Z =--=--==-=+==-⨯-=+-=αm h h H h tga tg θd h tg αtg θatg θb h 213211.3 墙身截面性质计算1.3.1截面面积 A 1 =2×8=16m 2 A 2 =2.295×0.55=1.26m 2 A 3 =2.295×0.45/2=0.516 m 2 ΣA=A1+A2+A3 =17.776m 23.3.2 各截面重心到墙趾的水平距离: X1=2.255+9×0.25-2 /2-8×0.25/2=2.5 mX2=(2.25+2.25/5×0.25)/2+0.55/2×0.25=1.25m X3=(0.0+2.25+(2.25+2.25/5×0.25))/3=1.5m∴ 墙身重心到墙趾的水平距离i igi A X Z A=∑∑= (10.8×2.28+0.72×0.77+1.81×1.59)/17.776=2.382墙身重力:G=γk ΣAi=23×17.776=408.848kN1.4 墙身稳定性验算1.4.1 抗滑稳定性验算验算采用“极限状态分项系数法”。
典型浆砌石挡土墙结构计算书

附件2:挡土墙计算书1、 断面尺寸墙高H=8m ,上墙身高2.6m ,墙顶水平宽度0.6m ,墙底宽3.21m ,墙面坡率1:0.1,上墙背坡率1:0.5,下墙背坡率1:0.25。
见图:2、破裂角,破裂面及土压力(1)上墙破裂角计算,判断是否出现第二破裂面,上墙土压力计算 1)、计算第一破裂面倾角:11111111tan 0.526.619.713581.3181.310.56829.58A tg tg tg=26.6a a y a d j q y q =-=-=++=++==-+=-+==2)、顶破裂面距离墙顶:11tan 1tan 2.60.51 2.60.568 3.78m11 H H 交于荷载内侧。
a q ++=?+?挡土墙截面图3)、判断是否出现第二破裂面由于破裂面交于荷载内侧,判断是否出现第二破裂面 作假想墙背,其倾角为111,tan 0.45,24.23αααⅱ == ,第二破裂面倾角:135,4527.524.232i i ααα¢=-=>=所以不会出现第二个破裂面 4)、计算上墙土压力22tan (45)tan (4517.5)20.587cos(4517.5)cos(45)2KK --===++a.主动土压力系数jj 12211111111011111185 2.60.587136.70522cos()36.705cos(26.635)17.46sin()36.705sin(26.635)32.292.600.87333x y y E H KK KNE E KN E E KNh H Z m K 01=y b 主动土压力E 2h K 1+H .土压力作用点位置Z g a j a j ×===创创==+=?==+=?==+=+= (1)下墙破裂角计算,判断是否出现第二破裂面,下墙土压力计算22221)t 0.2514.3614.3619.713540.3540.350.7436.5A g tg tg tg2计算第二破裂面倾角 a a y a d j q y q =-==-=++=-++==-+=-+==12212)tan 1tan tan tan 2.60.51 5.60.25 5.60.74 2.60.568 6.521m1221破裂面距墙顶边缘:H H H Ha a q q +-++=?-???3)、判断是不否出现第二破裂面 由于破裂面交于荷载中部:墙背倾角为222222,tan tan 0.25,14.04ααααααⅱⅱ==-=- = ,第二破裂面倾角:135,4527.524.232i i ααα¢=-=>=所以不会出现第二个破裂面 4)、计算下墙土压力()()2222cos()tan tan sin()cos(36.535)tan 36.50.250.164sin(36.555.64)K K a.主动土压力系数 q j q a q y +=+++=-=+114104222222222222205.4220.53 5.41 2.115.61118.5 5.60.164 2.11100.3822cos()100.38cos(1435)93.71sin()100.38sin(1435)x y h h h m h h H E H KK KN E E KN E E 211=2b 主动土压力E =H 2H 2 2.6K 1+H 5.6g a j a j ×=-=创 +=++===创创==+=?+==+=?+()()()4240222121222235.97233330.53 5.410.816.25.40.53 1.96833 2.113 5.4 2.11tan 3.21 1.9680.25 3.702y x y KN h h H h h H Z K H K m Z B Z m y 3).土压力作用点位置Z =a =-=+-=创-+-=创 =-=-?=3、墙身截面计算:通过试算后,取墙顶宽度10.6,b m =则上墙底宽度:()21121tan tan 0.6 2.60.50.1 2.16,b H b H m =++=+?=γα 下墙底宽度: 3.21,B m = 墙身重:2322.49517.27k G A KN ==?γ1)、上墙墙身自重1G ,及其对墙趾的力力臂1i G Z1112131111111212131323 3.5681.88223 1.023, 1.20.8 1.733123 1.5635.88, 2.00.6 2.32123 1.023, 2.20.8 2.473k k G k G k G G A KNG A KN Z m G A KN Z mG A KN Z m==?==?=+?==?=+?==?=+?γγγγ 2)、下墙墙身自重2G ,及其对墙趾的力力臂2i G Z212223222121222223232318.93435.39230.49.2,0.332317.4400.2, 2.55230.920.7, 4.3k k G k G k G G A KNG A KN Z m G A KN Z m G A KN Z m==?==?===?===?=γγγγ4、挡土的抗滑移稳定性验算12517.2735.9732.29585.53c Xy y u N K E N G E E KN其中N 作用于基底竖向力的代数和(KN)即=®=++=++=ååå1212()0.4(517.2735.9732.29)2.11 1.317.4693.71y y c x xu G E E K E E 满足要求++?+===>++å5、挡土墙的抗倾覆稳定性验算上墙土压力作用点距墙趾223.702, 1.33 5.6 6.93x y Z m Z m ==+=,11121321222311121321222311222.323 2.479.20.33400.2 2.5520.7 4.332.29 3.6335.97 3.7021542.05.y G G G G G G y x y xM G Z G Z G Z G Z G Z G Z E Z E Z KN m=23 1.73+35.88 =++++++? 创+??? +? =å1542.05 2.63 1.6585.53yl M K N满足要求===>åå6、基底偏心距与基底应力计算:01122017.460.8793.71 1.968199.6121542.05199.611.151171.063.21/2 1.150.4550.803()24x y x y yn n M E Z E Z MM Z NmB Be Z m 满足要求=+=??-=-===-=-=<=å邋å1212337.546585.5360.455(1)(1)360()27.283.21 3.21y yN M A W G E E e KPa BB满足要求s s =++´=??<邋7、墙身截面验算 法向应力及偏心距e 验算 上挡土墙截面;11121311111112131110111101181.8832.29114.1723 1.7335.88 2.323 2.4732.290.87207.21.17.460.8715.19.207.2115.190.82228.34y y G G G y xx x yn N G E KN M G Z G Z G Z E Z KN mM E Z kN MM M Z N ¢=+=+=¢=+++ =????¢==?ⅱ--¢===¢ååå邋å11111121142.050.840.1850.803226114.1760.185(1)(1)2.05 2.0585.85360()25.54n mB e Z m m N e B B KPa 满足要求 满足要求s s ⅱ=-=-=<¢¢´=? =<å下挡土墙截面;2122232222212223222222222435.3935.97471.369.20.33400.2 2.5520.7 4.335.97 3.70293.71 3.702346.91.1245.723462y y G G G y xOx x y o n N G E KN M G Z G Z G Z E Z M E Z kN MM M Z N 1245.72KN¢=+=+=¢=++++=??? =¢==?ⅱ--==¢ååå邋å22221222.910.95942.723.21950.655/40.803226471.3660.655(1)(1)3.21 3.21326.62360()32.94n mB e Z m B m N e B B KPa 满足要求 满足要求=ⅱ=-=-=<=¢¢´=? =<åσσ8、剪应力力验算:1)、水平剪应力验算(取上挡土墙截面): 11117.468.521602.05x E Kpa B ===<åτ 2)、斜截面剪应力验算21222222122222221212318.93435.391118.5 5.40.164 2.1193.3422cos()93.34cos(1435)87.14sin()93.34sin(1435)33.455.5223126.96, 1.34k x y k G G A KNE H KK KNE E KN E E KN G A kN Z m G ¢==?¢==创创=ⅱ=+=?+=ⅱ=+=?+=ⅱ==?=¢γγαδαδγ222324222223232424 1.62336.8, 2.171.62336.8, 2.7110.2123234.83, 2.29k G k G k G A kN Z m G A kN Z m G A kN Z m¢==?=ⅱ==?=ⅱ==?=γγγ()()121102201121017.468.522.0532.2981.8855.692.05123.58223.588.5255.69tan 26.6tan 0.089tan 31.470.51600.915tan 1.093cos 1tan tan tan x x y r k r x x x E b E G b b A i A i i i oi=23.8 ====++=====----===-?=-?--+τττγτττατατττατ()()()2221tan tan tan cos 23.88.5210.50.91555.690.91510.50.91523.580.915r i i = =43.53 < 160 Kpa 满足要求轾-+犏臌轾创-?创-? 犏臌ατ。
挡土墙计算
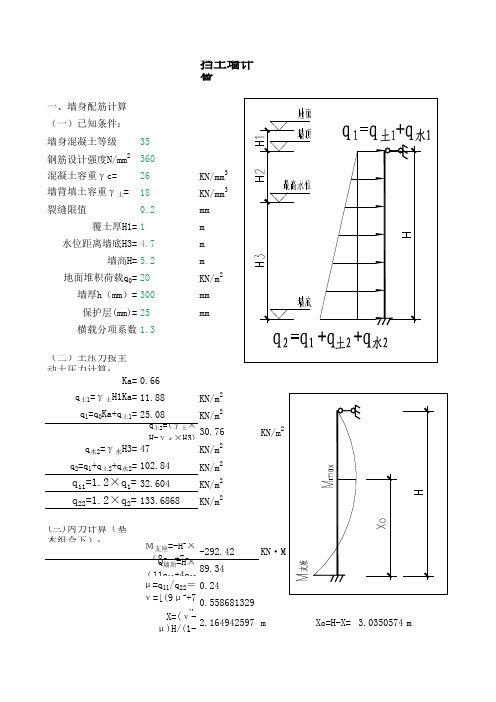
挡土墙计算一、墙身配筋计算(一)已知条件:墙身混凝土等级35钢筋设计强度N/mm 2360混凝土容重γc=26KN/mm 3墙背填土容重γ土=18KN/mm 3裂缝限值0.2mm 覆土厚H1=1m 水位距离墙底H3=4.7m 墙高H=5.2m 地面堆积荷载q 0=20KN/m 2墙厚h(mm)=300mm 保护层(mm)=25mm 横载分项系数1.3(二)土压力按主动土压力计算:Ka=0.66q土1=γ土H1Ka=11.88KN/m 2q 1=q 0Ka+q 土1=25.08KN/m 2q 土2=(γ土×H-γ水×H3)30.76KN/m 2q 水2=γ水H3=47KN/m 2q 2=q 1+q 土2+q 水2=102.84KN/m 2q 11=1.2×q 1=32.604KN/m 2q 22=1.2×q 2=133.6868KN/m 2(三)内力计算(基本组合下):M支座=-H 2×(8q 22+7q 11-292.42KN·M Q 墙顶=H×(11q 11+4q 2289.34μ=q 11/q 22=0.24ν=[(9μ2+7μ0.558681329X=(ν-μ)H/(1-2.164942597m Xo=H-X= 3.0350574mMmax =Q 墙顶X-q 11X 2/2+84.13227KN·M (四)配筋计算混凝土抗压强度fcd=16.7N/mm 2ho=265mm 钢筋设计强度fy=360N/mm 2计算宽度b=1000mm M支座 =f cd bx(h 0-x/2)292420114.00 =16700x(265-x/2)x =77.371 m ≤ξb h 0 =0.53×265.00 =140.5mm 解得A s = M支座/(ho-3691mm 2Mmax =f cd bx(h 0-x/2)84000000.00 =16700x(265-x/2)x =19.714 mm ≤ξb h 0 =0.53×265.00 =140.5mm 解得跨中A s = Mmax/(ho-940mm 2(五)裂缝计算钢筋直径d=22mm 钢筋间距75mm 每延米实配钢筋A s =5068.44mm 2标准组合下Mk 支座=-H 2×-224.94KN·M σsk=Mk支座192.4974N/mm2αcr=2.1ρte=0.033789574ftk=2.2ψ=0.880148956< 1 且>0.2所以ψ取0.880148956Es=200000c=25deq=22裂缝宽度W fk =0.177163082mm 裂缝满足要求。
(完整版)挡土墙结构算例

4.4.3计算及步骤
4.4.3.1土压力计算
图4.3主动土压力计算图(其中 , 型和计算荷载
墙踵板可视为支承于扶肋上的连续板,不计墙面板对它的约束,而视其为铰支。内力计算时,可将墙踵板顺墙长方向划分为若干单位宽度的水平板条,根据作用于墙踵板上的荷载,对每一个连续板条进行弯矩,剪力计算,并假定竖向荷载在每一连续板条上的最大值均匀作用在板条上。
图4.5墙面板的水平内力计算
墙面板承受的最大水平正弯矩及最大水平负弯矩在竖直方向上分别发生在扶肋跨中的1/2H1处和扶肋固支处的第三个H1/4处,如图4.6所示。
设计采用的弯矩值和实际弯矩值相比是安全的,如图4.5-c)所示。例如,对于固端梁而言,当它承受均布荷载时,其跨中弯矩应为 ,但是,考虑到墙面板虽然按连续梁计算,然而它们的固支程度并不充分,为安全起见,故设计值按式确定。
4基底应力验算:
其中
其中
5截面应力计算:
截面最大应力出现在接近基底处,由基底应力验算可知偏心距及基底应力均满足要求,故墙身截面应力也能满足要求,故不做验算。
通过上述计算及验算,所拟截面满足各项要求,故决定采用该截面。
4.4扶臂式挡土墙设计
扶壁式挡土墙的设计内容主要包括墙身构造设计、墙身截面尺寸的拟定,墙身稳定性和基底应力及合力偏心距验算、墙身配筋设计和裂缝开展宽度等。
4.3.3计算方法及步骤
1)按墙高确定的附加荷载强度进行换算:
,q插求得q=15KPa
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3 重力式挡土墙适用条件及设计原则为防范土体坍滑,路线沿线应设置挡土墙,本例形式为重力式仰斜路肩墙,详尽尺寸以下:拟采用浆砌片石重力式路肩墙,如上图所示,墙高H=6m( 未计倾斜基底)。
墙后填土容重为19KN / m3,内摩擦角45 ,砌体容重k23KN / m3 4.3.2 构造设计重力式挡土墙拟订计算图示以下:图重力式挡土墙拟订计算表示图θ计算方法及步骤1)按墙高确定的附加荷载强度进行换算:qh0,q插求得q=15KPa因此 h02)土压力计算:10 , 3523 ,45E a1H 2 K a1 H2 cos 2 222 cos 2 cos1sinsincoscosEaxE a cos( ) cos 10 23 142.504 KNEayE a sin( ) sin 10 23E p 1 H 2K p1 H 2cos 2 222 cos 2 cos1sinsincoscosEpxE p cos( ) cos 23 10EpyE p sin()sin 23 103) 挡土墙截面验算如设计图,墙顶宽。
① 计算墙身重及其力臂 Z G ,计算结果以下:S1 1 6 1 1 61 622G S 20 1 203.6 KN倾斜基底,土压力对墙趾 O 的力臂为:Z yZ x② 抗滑牢固性Q1 E yE x tan 0 Q 2 E p tan 0Q1Eytan 0 Q1E xQ 2Ep因此抗滑牢固性满足要求③抗推翻牢固性验算:0.8GZ G Q1 (E y Z x E x Z y )Q 2 E p Z p162.980 KNm0因此抗推翻牢固性亦满足要求。
④基底应力验算:e BZ N2eB6Pmax N1 1 6eA BPminN1 1 6eA B其中N 1G G Q 1E y1.1 cos0Q1 E x sin0P max N1 1 6e 400.421 1 150.512 KPaA B1.2 f 319.62 KPaPmin N1 1 6e 400.421 1 6A B其中2⑤截面应力计算:截面最大应力出现在凑近基底处,由基底应力验算可知独爱距及基底应力均满足要求,故墙身截面应力也能满足要求,故不做验算。
经过上述计算及验算,所拟截面满足各项要求,故决定采用该截面。
4.4 扶臂式挡土墙设计扶壁式挡土墙的设计内容主要包括墙身构造设计、墙身截面尺寸的拟订,墙身牢固性和基底应力及合力独爱距验算、墙身配筋设计和裂缝睁开宽度等。
适用条件及设计原则扶壁式挡土墙墙高不宜高出15m,一般在9— 10m 左右,段长度不宜大于20m,扶肋间距应依照经济性要求确定,一般为1/4— 1/2 墙高,每段中宜设置三个或三个以上的扶肋,扶肋厚度一般为扶肋间距的1/10—1/4,但不应当小于。
采用随高度逐渐向后加厚的变截面,也可以采用等厚式,以便于施工。
墙面板宽度和墙底板的厚度与扶肋间距成正比,墙面板顶宽不得小于,可采用等厚的垂直面板。
墙踵板宽一般为墙高的 1/4—1/2,且不小于。
墙趾板宽宜为墙高的 1/20—1/5,墙底板板端厚度不小于。
如图 4.2 所示。
≧202000B1=(1/20-1/5)HB3=(1/4-1/2)HH1H≧30 (1/10-1/4)L B1 B2B3o.41L La) 平面图;b)横断面图图 4.2 扶壁式挡土墙构造(单位cm)构造设计依照《建筑边坡工程技术规范》及工程地质条件,此扶壁式挡土墙墙高拟订为H=10m,分段长度为 20m,扶肋间距 L=4m,扶肋宽度。
墙面板顶宽 b=0.30m,为了利于施工,采用等厚垂直面板,墙底板板端厚度0.4m,墙踵板宽度 B1=1m。
计算及步骤土压力计算图主动土压力计算图(其中23 ,45 ,)如图 4.3 所示,扶壁式挡土墙墙背垂直, BC 为开挖后的土坡坡面,作为第一破裂面, BC 与垂直方向的夹角为 25 度, ADBC 即为破裂棱体。
这个棱体作用着三个力,即破裂棱体的自重 W,主动土压力的反力 Ea,破裂面的反力 R。
其中Ea 的方向与墙背成角,由工程地质条件所给得23 ,且偏于阻拦棱体下滑的方向。
R 的方向与破裂面法线成角,同样偏于阻拦棱体下滑的方向。
由于棱体处于平衡状态,因此力的三角形闭合。
从力的三角形中可得:式中Ea cos( )Wsin()45 2368依照前面计算得的牢固坡角,此处的挡墙后填土坡度拟订为25 度,填土的重度为 19 kN / m3,则:S ADBC a b h AE ACcos252 2其中 a 3m, b 3 9.6 tg 25o7.48m, h9.6m 。
因此,算得 S ADBC67.7 。
主动土压力:cos(25 45 )E a W 440.544 kNsin( 25 68 )墙面板设计计算1)计算模型与计算荷载墙面板计算平时取扶肋中到扶肋中或跨中到跨中的一段为计算单元( 如图4.4 所示 ),视为固支于扶肋及墙踵板上的三向固支板,属于超静定构造,一般作简化近似计算。
计算时,将其沿墙高或墙长划分为若干单位宽度的水平板条与竖向板条,假设每一个单位条上作用均布荷载,其大小为该条单位地址处的平均值,近似按支承于扶肋的连续板来计算水平板条的弯矩和剪力,按固支于墙底板上的刚架梁来计算竖向板条的弯矩。
墙面板的荷载仅考虑墙后主动土压力的水均分力,而墙自重、土压力竖向分力及被动土压力等均不考虑。
其中土压应力为:e Ea / H1440.544 / 9.6 45.890kN / m3hk图 4.4 墙面板简化土应压力求pi hk4h i / H 1i ( 0 h i H / 4)pihk 22.945 ( H / 4 h i 3H / 4)pihk4 9.6 h i / H 1h i (3H 1 / 4 h i H 1 )2)水平内力依照墙面板计算模型,水平内力计算简图如图 4.5 所示。
各内力分别为:支点负弯矩: M 1 1/ 12 pi l 2 2支点剪力: Q pi l / 2跨中正弯矩: M2 1/ 20 pil 2 2 kNm边跨自由端弯矩:m30kNm 其中, l 为扶肋间净距。
ihlb)1/121/121/121/201/20a)c)a)计算模型; b) 荷载的作用图; c) 设计弯矩图图墙面板的水平内力计算墙面板承受的最大水公正弯矩及最大水平负弯矩在竖直方向上分别发生在扶肋跨中的 1/2H1处和扶肋固支处的第三个 H1/4 处,如图 4.6 所示。
设计采用的弯矩值和本质弯矩值对照是安全的,如图 4.5-c)所示。
比方,对于固端梁而言,当它承受均布荷载时,其跨中弯矩应为pi l 2 / 24 ,但是,考虑到墙面板诚然按连续梁计算,但是它们的固支程度其实不充分,为安全起见,故设计值按式确定。
3)竖直弯矩墙面板在土压力的作用下,除了上述的水平弯矩外,将同时产生沿墙高方向的竖直弯矩。
其扶肋跨中的竖直弯矩沿墙高的分布如图 4.7 所示。
负弯矩出现在墙杯一侧底部 H1/4 范围内,正弯矩出现在墙面一侧,最大值在第三个H1/4 段内,其最大值可近似按以下公式计算:竖直负弯矩:M D hk H 1l4e4/1Hdc cbba a)b) aa)跨中弯矩b)扶肋处弯矩图 4.6 墙面板跨中及扶肋处的弯矩图竖直正弯矩:M hk H 1l / 4沿墙长方向(纵向),竖直弯矩的分布如图 4.6 所示,呈抛物线形分布。
设计时,可采用中部2l/3 范围内的竖直弯矩不变,两端各l/6 范围内的竖直弯矩较跨中减少一半的阶梯形分布。
4 l/6 2l/3 l/6/1H2D/2 D M1 M/H 1+H4 l/1-HMDMD/4a)b)a)竖直弯矩沿墙高分布;b) 竖直弯矩沿墙纵向分布图 4.7 墙面板竖直弯矩图4) 扶肋外悬臂长度 l ’的确定扶肋外外悬臂节长 l ’,可按悬臂梁的固端弯矩与设计用弯矩相等求得,即:M 1/12pi l 21/ 2pi l'2 l '墙踵板设计计算1) 计算模型和计算荷载墙踵板可视为支承于扶肋上的连续板, 不计墙面板对它的拘束, 而视其为铰支。
内力计算时, 可将墙踵板顺墙长方向划分为若干单位宽度的水平板条,依照作用于墙踵板上的荷载, 对每一个连续板条进行弯矩, 剪力计算, 并假设竖向荷载在每一连续板条上的最大值平均作用在板条上。
作用在墙踵板上的力有:计算墙背间与本质墙背的土重 W1 ;墙踵板自重W2;作用在墙踵板顶面上的土压力竖向分力 W3;作用在墙踵板端部的土压力竖向分力 W4 ;由墙趾板固端弯矩 M1 的作用在墙踵板上引起的等代荷载 W5;以及地基反力等,以下列图。
为了简化计算, 假设 W3 为中心荷载, W4 是悬臂端荷载 E ty 所引起的,本质 应力呈虚线表示二次抛物线分布,简化为实线表示的三角形分布; M1 引起的等代荷载的竖向应力近似地假设成图4.7 所示的抛物线形,其重心位于距固支端5/8B3 处 , 以 其 对 固 支 端 的 力 矩 与 M1 相 平衡 , 可 得墙 踵 处 的 应力w52.4M 1/ B 32 。
将上述荷载在墙踵板上的引起的竖向应力叠加,即可获取墙踵板的计算荷载。
由于墙面板对墙踵板的支撑拘束作用, 在墙踵板与墙面板的连结处, 墙踵板沿墙长方向板条的弯矩为零, 并向墙踵方向变形逐渐增大。
故可近似假设沿墙踵板的计算荷载为三角形分布,最大值在踵点处。
如图 4.8 所示。
各部分应力计算:W 1( H 1 B 3 tan ) 19 3W 2h t320 8kNcos cos 2 cos 2 K a coscos 2coscos 2EB 3 1 H 2 K a 1 19 10 .650 2 0.270 290 .454 kN / m2 2W 3 E B 3 sin 290.454 sin 35B32E t sinW 4B3因此,2E t sin 2 350.567 sin 35W 4B3墙踵板固端处的计算弯矩M1:M 1 B12[3i( h )(t1 2t pj ) ( 12 )B1]6 Bmax N M其中:minA WN 802.537 kNA 1 (1 3) 2W 1 ab2 1 2 26 6M Ne03 2 2因此max min N MA WkPa即1356.003kPa;2求得M 1 B12 3 1 h t1 2t pj 1 2 B16 B1213 24 19 26M 1 43.744 kPaW 5B32 32因此W W 1W 2W 3W 4W 5 2EB3yA235 5°WW σσEtyW1EB3B3B3b)c)HB EB35/8B3W3M1W2EtEtyCM1W5σWσB3 DBB3B321σe)d)σa) 墙踵板受力求; b)E B3 y 对墙踵板的作用; c) E ty 对墙踵板的作用;d)M1 对墙踵板的作用;e) 墙踵板法向应力总和图 4.8 墙踵板计算荷载图式上述中:E B3 ——作用在 BC 面上的土压力( kN );E t ——作用在 CD 面上的土压力( kN ); M1 ——墙趾板固端处的计算弯矩( kNm );, h ——墙后填土和钢筋混凝土的容重( Kn/m ); t 3 ——墙踵板厚度( m );2 ——墙踵板端处的地基反力 (kPa)。
