信号与线性系统通信08A卷
(NEW)吴大正《信号与线性系统分析》(第4版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】上册

二、判断题
任何系统的全响应必为零状态响应与零输入响应之和。( )[北京 邮电大学2012研]
【答案】×
【解析】零输入响应为仅由起始状态所产生的响应。零状态响应是系统 的初始状态为零时,仅由输入信号引起的响应。由此可知仅当系统满足 线性时,其全响应必为零状态响应与零输入响应之和。
三、分析计算题
1.已知某系统的转移函数 ,求系统的零状态响应
【答案】
【解析】设f1(t)=ε(t)由LTI系统的线性和时不变性得(由于该题 没有给出系统的初始状态,所以这里不考虑)
f(t)=ε(t-1)-ε(t-2)=f1(t-1)-f1(t-2)
3.已知某LTI系统,当t>0时有: 当输入f(t)=(e-t+2e-2t)ε(t)时,输出响应为(e-t+5e-2t) ε(t); 当输入f(t)=(2e-t+e-2t)ε(t)时,输出响应为(5e-t+e-2t) ε(t); 当输入f(t)=(e-t+e-2t)ε(t)时,输出响应为(e-t+e-2t) ε(t); 则当输入为f(t)=(e-t-e-2t)ε(t)时,系统的输出响应为 ______。[长沙理工大学2006研]
整理得:
则
关) 取其逆变换得:
(仅与输入有关) (仅与系统的初始状态有
第3章 离散系统的时域分析 一、选择题
1.有限长序列 的长度为4,欲使 与 的圆卷积和线卷积相同, 则长度L的最小值为( )。[中国科学院研究生院2012研] A.5 B.6 C.7 D.8 【答案】C
【解析】 的长度为4,则其线卷积的长度为4+4-1=7。当 与 的圆卷积 时, 与 的圆卷积和线卷积相同,可知L的最小
【答案】
;
;稳定
【解析】由
可知,该系统任意两个相邻的输出值之差就是该
信号与系统( A卷答案 )

淮南师范学院201 -201学年第 学期《信号与系统》A 卷参考答案及评分标准一、填空题(每题2分,共10分) 1.离散信号2.()f t 3.冲激信号或()t δ 4.可加性 5.()t δ 二、选择题(每题2分,共10分) 1. (B) 2. (C) 3. (C) 4. (A) 5. (C)三、判断题(每题2分,共10分) 1. × 2. √ 3. √ 4. √ 5. √四、简答题(每题5分,共10分)1. 简述根据数学模型的不同,列出系统常用的几种分类。
(本题5分)答:根据数学模型的不同,系统可分为4种类型. -----------------------(1分) (1) 即时系统与动态系统 -----------------------(1分) (2) 连续系统与离散系统 -----------------------(1分)(3) 线性系统与非线性系统 -----------------------(1分) (4) 时变系统与时不变系统 -----------------------(1分)2. 简述稳定系统的概念及连续时间系统时域稳定的充分必要条件。
(本题5分)答:(1)一个系统(连续的或离散的)如果对任意的有界输入,其零状态响应也是有界的则称该系统是有界输入有界输出稳定系统。
-----------------------(2分)(2)连续时间系统时域稳定的充分必要条件是()h t dt M ∞-∞≤⎰-----------------------(3分)五、计算题(每题10分,共60分) 1、如有两个序列11,0,1,2()0,k k f k +=⎧=⎨⎩ 其余 21,0,1,2()0,k f k =⎧=⎨⎩ 其余试求卷积和12()()()f k f k f k =*(本题10分)解: 1 1 1⨯ 1 2 3-------------------------- 3 3 3 2 2 21 1 1---------------------------------1 3 6 5 3 -----------------------(5分){}12()()()0,1,3,6,5,3,00f k f k f k k =*=↑= -----------------------(5分)2、求象函数2()(2)(4)sF s s s =++的拉普拉斯逆变换()f t (本题10分)解:12()24k k F S s s =+++2424s s =-+++ -----------------------(5分) 24()(24)()tt f t ee t ε--∴=-+ -----------------------(5分)3. 已知某LTI 离散系统的差分方程为()(1)2(2)2()y k y k y k f k +---=, 求单位序列响应()h k (本题10分)解:12()()2()2()Y Z Z Y Z Z Y Z F Z --+-= -----------------------(2分)()()()Y Z H Z F Z =12212z Z --=+-2222Z Z Z =+- -----------------------(2分) ()2(2)(1)H Z ZZ Z Z =+-21413132Z Z =⋅+⋅-+ -----------------------(2分) 24()3132Z ZH Z Z Z =⋅+⋅-+ -----------------------(2分)24()[(2)]()33k h k k ε=+⋅- -----------------------(2分)4. 已知02,()0,F jw ωωωω⎧<⎪=⎨>⎪⎩ ,求()F jw 的傅里叶逆变换(本题10分)解:1()()2j t f t F j e d ωωωπ+∞=-∞⎰ 0011j te d ωωωωπ=⋅-⎰ -----------------------(5分) 0011j t ejtωωωπ=⋅⋅- 02sin()t t ωπ= -----------------------(5分) 5. 已知某系统框图其中()()f t t ε= (1) 求该系统的冲激响应()h t (2) 求该系统的零状态响应()zs y t (本题10分)解:''()3'()2()4'()()y t y t y t f t f t ++=+2(32)()(41)()S S Y S S F S ++=+ -----------------------(2分)2()(41)()()(32)Y S S H S F S S S +==++ 113712S S =-⋅+⋅++ -----------------------(2分) (1) 冲激响应 2()[(3)7]()tth t e e t ε--=-⋅+ -----------------------(2分)(2) 41()()()(1)(2)zs S Y S H S F S S S S +=⋅=++ -----------------------(1分)1117132122S S S =⋅+⋅-⋅++ -----------------------(1分) 零状态响应217()(3)()22tt zs y t e e t ε--=+- -----------------------(2分)6. 如图所示的电路,写出以)(t u s 为输入,以)(t u c 为响应的微分方程。
信号与系统第四版习题解答精选全文完整版

可编辑修改精选全文完整版《信号与系统》(第四版)习题解析高等教育2007年8月目录第1章习题解析1第2章习题解析5第3章习题解析14第4章习题解析21第5章习题解析29第6章习题解析39第7章习题解析47第8章习题解析52第1章习题解析1-1题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解(a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2给定题1-2图示信号f( t ),试画出下列信号的波形。
[提示:f( 2t )表示将f( t )波形压缩,f (2t)表示将f ( t )波形展宽。
](a) 2 f (t - 2 ) (b) f ( 2t )(c)f (2t )(d)f (-t +1 )题1-2图解以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
S RS LS C题1-3图解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i C t u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
题1-4图解系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) +f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
08硕士信号与系统A卷
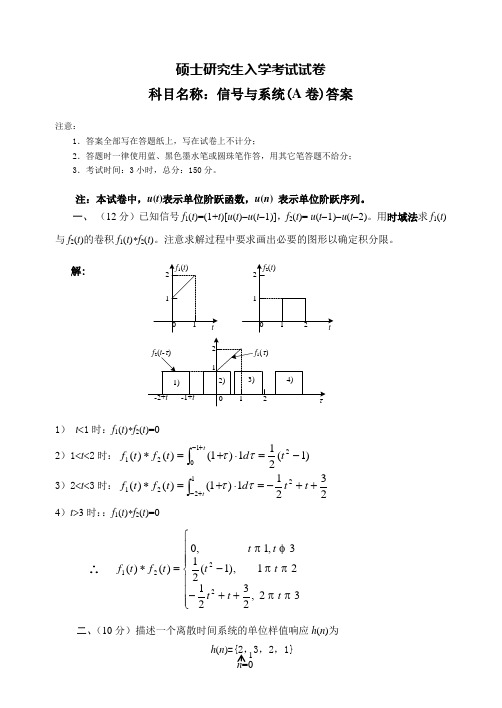
硕士研究生入学考试试卷 科目名称:信号与系统(A 卷)答案注意:1.答案全部写在答题纸上,写在试卷上不计分;2.答题时一律使用蓝、黑色墨水笔或圆珠笔作答,用其它笔答题不给分; 3.考试时间:3小时,总分:150分。
注:本试卷中,u (t )表示单位阶跃函数,u (n ) 表示单位阶跃序列。
一、 (12分)已知信号f 1(t )=(1+t )[u (t )-u (t -1)],f 2(t )= u (t -1)-u (t -2)。
用时域法求f 1(t )与f 2(t )的卷积f 1(t )*f 2(t )。
注意求解过程中要求画出必要的图形以确定积分限。
1) t <1时:f 1(t )*f 2(t )=02)1<t <2时:)1(211)1()()(21021-=⋅+=*⎰+-t d t f t f tt t 3)2<t <3时:23211)1()()(21221++-=⋅+=*⎰+-t t d t f t f t t t4)t >3时::f 1(t )*f 2(t )=0∴ ⎪⎪⎪⎩⎪⎪⎪⎨⎧++--=*32 ,232121),1(213 ,1 ,0)()(2221ππππφπt t t t t t t t f t f 二、(10分)描述一个离散时间系统的单位样值响应h (n )为解:求该系统的系统函数H (z ),写出描述该系统的差分方程,画出系统的仿真框图。
解: ∑=----+++==3321232)()(n nz z z zn h z H差分方程为:y (n )=2x (n )+3x (n -1)+2x (n -2)+x (n -3)x (n -3)三、(12分)已知某LTI 系统的微分方程为)(3d )(d )(2d )(d 3d )(d 22t e t t e t r t t r tt r +=++ 其中e (t )、r (t )分别为激励和响应。
当激励e (t )=e -4t u (t )时,系统的全响应为)()e 61e 27e 314()(42t u t r t t t -----=求系统的单位冲激响应h (t )、零状态响应r zs (t )、自由响应r h (t )、强迫响应r p (t )、暂态响应r t (t )及稳态响应r s (t )。
四川大学信号与系统考研真题+答案08

´ 1,设 x(t) = d (2t -1) ,在下面正确的结果用 ,错误的结果用 标出。
ò① ¥ x(t)dt = 1
-¥
2
´ ③ x(t) = 0.5d (t -1)
② x(t) = 0.5d (t - 0.5)
´ ④ x(t) = 2d (t - 0.5)
´ 2,下面是因果系统用 ,不是因果系统用 标出
川大 08 硕题解 一,填空题(每小题 3 分,共 21 分)
ò ò 1,信号 x(t) = sin 3p t 的总能量 E=
¥
siin3p t
2
dt
=
1
¥
w Re ct(
2
) dw = 3 焦。
pt
-¥ p t
2p -¥
6p
x(t)
=
3sin c(3p t)
«
Re ct( w 6p
)( A
=
3;t p
f (n) = 3n
-2 -1 0 1 2
n
笫-种情况 x(n) 是持续有限长的能量型信号,但能量型信号的 ROC 是 0 £ z £ ¥ ,
即除去 0及¥ 外没有(限值处的)极点,而题给有一个极点 1,故此情
况不会发生。
笫二种情况:① x(n) 在 n ³ 0 的范围里,一定有一因子 a-n , a > 3 ;使 x(n) · 3n 为
的反变换
Re s[(s + 6) (s
+
7s 6)(s
- 1)
est ]s=-6
=
6e-6
tu(t)
Re
s[( s
- 1)
(s
+
7s 6)(s
- 1)
安徽大学2009-A卷-王发牛
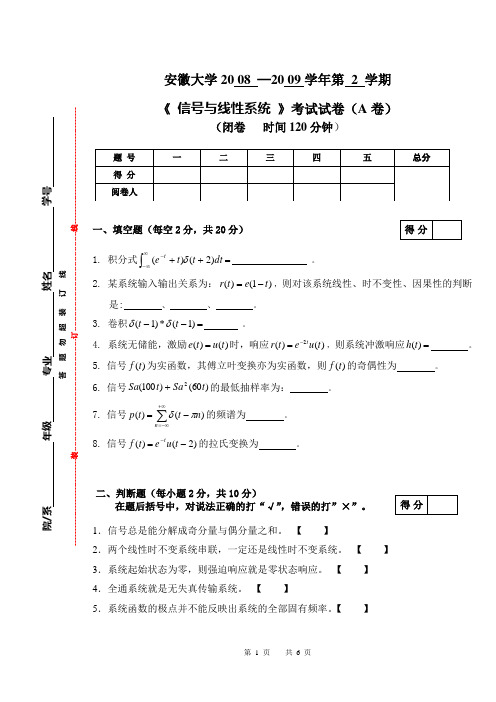
安徽大学20 08 —20 09学年第 2 学期《 信号与线性系统 》考试试卷(A 卷)(闭卷 时间120分钟)一、填空题(每空2分,共20分)1. 积分式=++⎰∞∞--dt t t e t )2()(δ 。
2. 某系统输入输出关系为:)1()(t e t r -=,则对该系统线性、时不变性、因果性的判断是: 、 、 。
3. 卷积=--)1(*)1(t t δδ 。
4. 系统无储能,激励)()(t u t e =时,响应)()(2t u e t r t -=,则系统冲激响应=)(t h 。
5. 信号)(t f 为实函数,其傅立叶变换亦为实函数,则)(t f 的奇偶性为 。
6. 信号)60()100(2t Sa t Sa +的最低抽样率为: 。
7. 信号∑+∞-∞=-=n n t t p )()(πδ的频谱为 。
8. 信号)2()(-=-t u e t f t 的拉氏变换为 。
二、判断题(每小题2分,共10分)在题后括号中,对说法正确的打“√”,错误的打”×”。
1.信号总是能分解成奇分量与偶分量之和。
【 】2.两个线性时不变系统串联,一定还是线性时不变系统。
【 】 3.系统起始状态为零,则强迫响应就是零状态响应。
【 】 4.全通系统就是无失真传输系统。
【 】5.系统函数的极点并不能反映出系统的全部固有频率。
【 】院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------三、画图题(每小题5分,共20分)1.绘出函数)1()]1()([)(-+--=t u t u t u t t f 的波形。
信号与线性系统管致中第8章通信系统

PPT文档演模板
信号与线性系统管致中第8章通信系 统
• 已调信号的最大峰值等于载波峰值的 2倍。 这就要求发射机的峰值功率容限是载波功率的 4 倍,发射机的效率是很低的。
• 从功率利用的角度, 越大越好;从包络检波
的效果来看, 越小越好。因此,在包络解调中,
通常折衷地取
。
PPT文档演模板
信号与线性系统管致中第8章通信系 统
• 对正弦载波的情况,若调制信号是脉冲信号,
•则称为:
• ASK------幅度键控(Amplitude Shift Keying)
• FSK------频率键控(Frequency Shift Keying)
• PSK------相位键控(Phase Shift Keying)
PPT文档演模板
信号与线性系统管致中第8章通信系 统
• 如果 然。
,定义
为调制指数 , 显
•特例
• 当调制信号是单音正弦时,在 的情况下,
已调信号的频谱如下:
PPT文档演模板
信号与线性系统管致中第8章通信系 统
• 此时,已调信号的平均功率是载波功率的1.5 倍, 而这些功率中真正用于传输有用信息的边带功率 只是载波功率的1/2,只占整个已调信号总功率的 1/3。
•二. 脉冲载波的情况:
• 根据被控制的参量可分为:脉冲幅度调制、脉
冲宽度调制、脉冲周期(位置)调制。
•PAM------Pulse Amplitude Modulation
•PWM-----Pulse Width Modulation
•PPM------Pulse Periodic(Position) Modulation
PPT文档演模板
【北京工业大学】【信号与系统】【2008年试题及答案】

822
科目名称:
Hale Waihona Puke 信号与系统北京工业大学 2008 年硕士研究生入学考试试题
★ 所有答案必须做在答题纸上,做在试题纸上无效!
一、 选择题(每小题 2 分,共 20 分):
从下列各小题的四个备选答案中, 选出正确的答案编号写在答题纸上 (如选择: a 或者 abc)
则使 x( n) = x1 ( n) + x2 ( n) 的 1. 设 x1 ( n) 和 x2 ( n) 分别是基本周期为 N1 和 N 2 的周期序列。 周期为 N 的条件是 a) c) 。 b) d)
K 使系统稳定,且在 x(t ) = δ (t ) 时,有 e(t ) → 0 。
4. 设 x(t ) 的 Fourier 变换为 X (ω ) , h(t ) 的 Fourier 变换为 H (ω ) ,且
y (t ) = x(t ) ∗ h(t ) , z (t ) = x(3t ) ∗ h(3t )
可以证明 z (t ) = Ay ( Bt ) ,这里 。
a) c)
1 1 A= ,B = 3 3 A = 3, B = 3
N1 = N 2 = N k1 N1 + k2 N 2 = (k1 + k 2 ) N
k1 N1 = k2 N 2 = N k1 N1 ≠ k 2 N 2 ≠ N
。
2. 自相关运算 rxx ( n) 是一个在 n = 0 时有最大值的偶对称函数,满足 a) c)
rxx (n) ≤ rxx (0) rxx (n) ≤ rxx (0)
9. Hilbert 变换是将 x (t ) 的相位移动 −
π 的运算。它的许多特性都是基于相位移动和卷 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.某 LTI 连续时间系统的信号流图如图⑥所示,
2
s 1 4 s 1 s 1 k
学号
F (s )
1
Y (s )
5
图⑥
试写出该系统的系统函数 H (s ) 。 分) (8
学生所在学院
专业、班级
f (t )
sin 2 t , s(t ) cos(1000t ) 2 t
试求: ⑴ f (t ) 的频谱 F ( j ) ; 分) (4 ⑵系统的冲激激响应 h(t ) ; 分) (4 ⑶该系统输出零状态响应的频谱 Yzs ( j ) ; 分) (4 ⑷该系统输出零状态响应的时间表示式 yzs (t ) 。 分) (4
f(t)
H ( j )
y (t)
s(t) 图③
4.已知某 LTI 连续时间系统,当输入 f (t ) e (t ) 时,其零状态响应
t
yzs (t ) (et 2e2t 3e3t ) (t ) ,求该系统的阶跃响应 g (t ) 。 分) (8
5.已知某二阶 LTI 离散时间系统的系统函数 H (z ) 的零点在 1 ,极点在 j ,且 H (0) 1 ⑴求该系统的系统函数 H (z ) ; 分) (4 ⑵试用信号流图模拟该系统; 分) (4 二、计算题(共 60 分) 1.已知 LTI 连续时间系统的单位冲激响应 h(t ) 初始状态为 y (0 ) y '(0 ) 1 。 ⑴写出描述该系统的微分方程; 分) (4 ⑵求系统的零输入响应 y (t ) ; 分) (4
(a) 图②
(b)
江
苏
大
学 试
题
第2页
3.已知系统如图③所示, f (t ) 8 cos100t cos500t , s(t ) cos500 t ,理想低通滤波器的 频率响应函数 H ( j ) ( 120) ( 120) ,试求其输出信号 y (t ) 。 分) (8
zi
1 2
(e t e3t ) (t ) ,输入激励信号 f (t ) ห้องสมุดไป่ตู้t ) ,
⑶零状态响应 y (t ) ; 分) (4
zs
⑷全响应 y (t ) ; 分) (2 ⑸指出全响应中的自由响应分量、强迫响应分量;瞬态响应分量、稳态响应分量; 分) (2 2.如图④(a)所示的系统,带通滤波器的频率响应如图(b)所示,其相频特性 ( ) 0 ,若输入为
学号
y(t) x(t)
1 2 1
t
-2 -1 0 1 2 -2 -1 -1 0 1 2 3
t
(a) 专业、班级 图①
(b)
2.已知某离散 LTI 时间系统的输入 f (k ) 和单位序列响应 h( k ) 如图②(a)和(b)所示,求该系 统的零状态响应 yzs (k ) 。 分) (8
学生所在学院
S i (t )
+
uc (0 )
C1
C2
R
-
图⑤ 4 . 某 LTI 离 散 时 间 系 统 , 已 知 当 输 入 f (k ) (k ) 时 , 其 零 状 态 响 应
姓名
yzs (k ) [4(4) k (1) k ] (k ) ⑴求该系统的系统函数 H (z ) ; 分) (4 ⑵求该系统的单位序列响应 h(k ) ; 分) (4
命题教师:
王洪金
江 苏 大 学 试 题
(2009-2010 学年第二学期) 课程名称 使用班级 题 得
姓名
共4页 第1页
信号与线性系统 通信 081/2 一 二 三 四 五
开课学院 考试日期 六 七
计算机学院 2010 年 6 月 24 日 八 九 十 总分 核查人
号 分
阅卷教师
一、简单计算题(共 40 分) 1.已知连续时间信号 x(t ) 和 y (t ) 分别如图①(a)和(b)所示,若 z (t ) x(2t ) y(t ) (t ) ⑴试画出信号 z(t ) 的波形; 分) (4 ⑵写出 z(t ) 的时域函数表示式; 分) (4
H ( j ) ( ) 0
f (t )
f (t ) s (t )
H ( j )
1
1001 999 0
999 1001
s (t )
(a)
图④
(b)
江
苏 大
学
试
题
第 3 页
3.如图⑤所示电路,已知 C1 1F , C2 2 F , R 1 ,若 C1 上的初始电压 uc (0 ) U 0 , C2 上的初始电压为零。当 t 0 时,开关 S 闭合,求开关闭合后的回路电流 i(t ) 。 分) (8
