随机过程matlab程序
随机过程matlab程序
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
-6
-4
-2
0
2
4
6
44798133900177/281474976710656 exp(-5/2 x 2+3 x y-y 2 )
0.2
0.15
0.1
0.05
0
5 0
5 0
y
-5
-5
x
% % The daily log returns on the stock have a mean of 0.05/year and a standard deviation of 0.23/year. These can be converted to rates per trading day by deviding by 253 and sqrt(253), respectively.
% A=normrnd(mu,sigma,1,N)
capmu=mean(x)
tao=1 x1=A.*cos(w*(t+tao)+theta); capgamma=mean((x-capmu).*(x1-capmu))
% m time simulation clear; w=2; N=1000; mu=2; sigma=3; m=500;capmu1=[];capgamma1=[]; for i=1:m
rho=(1+s*t)/(sigma1*sigma2); f=1/(2*pi*sigma1*sigma2*sqrt(1-rho^2))*exp(-1/(2*(1-rho^2))*((x-mu1)^2/sigma1^ 2-2*rho*(x-mu1)*(y-mu2)/(sigma1*sigma2)+(y-mu2)^2/sigma2^2)); ezsurf(f)
Matlab中的随机过程建模技巧

Matlab中的随机过程建模技巧随机过程是描述随机现象随时间变化的数学模型。
它在工程、金融、生物医学等许多领域都有广泛的应用。
在Matlab中,我们可以利用其强大的数学工具箱来进行随机过程的建模和分析。
本文将介绍一些在Matlab中常用的随机过程建模技巧。
一、随机过程的基本概念在进行随机过程建模之前,我们先来回顾一下一些基本概念。
1. 马尔可夫性质马尔可夫性质是指一个随机过程在给定过去的条件下,未来与过去和未来的时间无关。
在Matlab中,可以使用markovchain对象来表示马尔可夫链,并利用其属性和方法进行分析。
2. 随机过程的平稳性如果一个随机过程的统计性质在时间平移的情况下不发生变化,那么该随机过程就是平稳的。
在Matlab中,可以使用stationary函数来判断一个随机过程是否是平稳的。
3. 随机过程的自相关函数与功率谱密度自相关函数描述了一个随机过程在不同时间点的取值之间的相关性。
功率谱密度则描述了一个随机过程在不同频率下的能量分布。
在Matlab中,可以使用xcorr 和pwelch函数分别计算随机过程的自相关函数和功率谱密度。
二、随机过程的模拟模拟随机过程是随机过程建模的重要步骤之一。
在Matlab中,可以使用rand、randn等函数生成服从特定分布的随机数序列,并利用for循环和if语句等控制结构模拟出具有特定统计性质的随机过程。
例如,我们可以使用randn函数生成服从正态分布的随机数序列,然后利用for 循环和格朗日方程生成具有平稳性的随机过程。
具体实现代码如下:```MatlabN = 1000; % 随机数序列长度X = zeros(1, N); % 存储随机过程的数组X(1) = randn; % 初始化随机过程的初始值for n = 2:NX(n) = 0.9*X(n-1) + sqrt(1 - 0.9^2)*randn;endplot(X);```通过运行上述代码,我们可以得到一个服从AR(1)过程的随机数序列,并通过绘图函数plot将其可视化。
利用MATLAB进行随机过程建模

利用MATLAB进行随机过程建模简介随机过程是一个随机变量随时间的变化过程,具有概率性质。
在许多领域,如金融、通信、生物医学等,随机过程的建模和分析是十分重要的。
MATLAB是一种功能强大、易于使用的数值计算软件,它提供了丰富的工具和函数,方便进行随机过程的建模和仿真。
本文将介绍如何利用MATLAB进行随机过程建模。
一、MATLAB中的随机变量生成在进行随机过程建模之前,首先需要生成相应的随机变量。
MATLAB提供了多种方法来生成不同分布的随机变量。
常用的包括均匀分布、正态分布、指数分布等。
例如,要生成一个均匀分布的随机变量,可以使用rand函数。
以下代码生成一个长度为1000的均匀分布的随机变量序列:```matlabrng(0); % 设置随机数种子,保证结果可复现X = rand(1, 1000); % 生成均匀分布的随机变量```同样地,通过normrnd函数可以生成正态分布的随机变量,通过exprnd函数可以生成指数分布的随机变量。
二、随机过程的建模在随机过程建模中,常用的模型包括马尔可夫过程、随机游走、泊松过程等。
利用MATLAB可以方便地进行这些模型的建模和仿真。
1. 马尔可夫过程马尔可夫过程是一种具有马尔可夫性质的随机过程,其下一个状态只依赖于当前状态。
MATLAB提供了markovchain函数用于创建马尔可夫链模型。
以下代码创建一个状态空间为{'A', 'B', 'C'}的马尔可夫链:```matlabstates = {'A', 'B', 'C'}; % 状态空间transitionMatrix = [0.5 0.2 0.3; 0.3 0.5 0.2; 0.2 0.3 0.5]; % 状态转移矩阵mc = markovchain('StateNames', states, 'TransitionMatrix', transitionMatrix); % 创建马尔可夫链模型```可以通过simulate函数模拟马尔可夫过程的状态序列。
MATLAB中的随机过程建模与求解技巧

MATLAB中的随机过程建模与求解技巧随机过程是描述随机事件在一定时间范围内的演化规律的数学模型。
在现实生活和工程实践中,随机过程的分析和建模扮演着重要的角色。
而MATLAB作为一种功能强大的数值计算和科学工程计算软件,提供了丰富的工具和函数来进行随机过程的建模与求解。
本文将介绍一些MATLAB中常用的随机过程建模与求解技巧,帮助读者更好地应用MATLAB进行相关工作。
一、概述随机过程建模随机过程建模是指根据已有的数据或者经验,通过数学模型描述随机过程的统计特性。
在MATLAB中,常用的随机过程建模方法包括:1. 随机过程的数学描述:通过定义随机过程的概率密度函数、累积分布函数、自相关函数等统计特性,来描述随机过程的数学特征。
MATLAB提供了丰富的统计函数如normpdf、normcdf、autocorr等,可以帮助用户进行随机过程的数学描述。
2. 随机过程的参数估计:对于给定的随机过程数据,通过参数估计的方法来确定随机过程的参数。
MATLAB提供了统计工具箱中的函数如gamfit、exponentialfit等,可以帮助用户进行随机过程参数的估计。
3. 随机过程的模型选择:在建模随机过程时,需要选择合适的数学模型来描述随机过程的统计特性。
MATLAB提供了丰富的概率分布和随机过程模型如正态分布、泊松分布、布朗运动等,可以帮助用户根据数据选择合适的模型进行建模。
二、随机过程建模实例为了更好地理解随机过程建模的过程和技巧,下面将通过一个具体的例子来说明。
假设某电信公司每天收到的短信数量服从泊松分布,并且每天的短信数量之间相互独立。
现有一周的短信数量数据如下:data = [10, 8, 12, 9, 11, 13, 7];我们希望通过这些数据来建立一个泊松分布的模型,以便对未来的短信数量进行预测。
首先,我们可以使用MATLAB的统计工具箱中的函数poissfit来估计泊松分布的参数。
代码如下:lambda = poissfit(data);根据估计得到的参数lambda,我们可以生成符合泊松分布的随机过程数据,代码如下:simulated_data = poissrnd(lambda, 1, 100);其中,参数lambda表示单位时间内的事件平均发生率,这里我们假设为已知的估计值。
MATLAB中的随机过程模拟与分析技巧

MATLAB中的随机过程模拟与分析技巧随机过程是描述一系列随机事件演变的数学模型,在实际问题中有广泛的应用。
MATLAB作为一款功能强大的数值计算软件,提供了丰富的工具和函数来模拟和分析随机过程。
本文将介绍在MATLAB中进行随机过程模拟与分析的一些常用技巧。
一、随机变量的生成在随机过程分析中,随机变量是基本的概念,它描述了随机事件的取值情况。
在MATLAB中,可以通过随机数生成函数来生成服从各种分布的随机变量,如均匀分布、正态分布等。
例如,可以使用rand函数生成0到1之间的均匀分布随机变量,使用randn函数生成符合标准正态分布的随机变量。
二、随机过程的模拟通过生成随机变量,可以进一步模拟随机过程。
随机过程的模拟可以通过生成一系列随机变量来实现。
例如,可以使用rand函数生成一组服从均匀分布的随机变量,并通过随机过程模型来描述这组随机变量的演变过程。
在MATLAB中,可以使用循环语句和数组来实现随机过程的模拟。
三、随机过程的统计分析在对随机过程进行模拟后,通常需要对其进行进一步的统计分析。
MATLAB提供了一系列用于随机过程统计分析的函数,如均值、方差、自相关函数、功率谱密度等。
这些函数可以帮助我们从时间域和频率域两个角度来分析随机过程的特性。
通过统计分析,我们可以得到随机过程的均值、方差、平稳性等重要信息。
四、随机过程的仿真实验MATLAB还提供了强大的仿真实验工具,可以通过模拟大量的随机过程样本来研究其统计规律。
仿真实验通常涉及到随机过程的多次模拟和统计分析。
在MATLAB中,可以使用循环语句和向量化操作来进行高效的仿真实验。
通过对仿真实验结果的分析,可以验证理论模型的正确性,评估系统的性能,以及优化系统参数等。
五、随机过程的滤波与预测在实际应用中,随机过程通常具有噪声干扰,对其进行滤波与预测是很重要的任务。
MATLAB提供了多种滤波与预测方法的函数,如卡尔曼滤波、递归最小二乘法等。
这些方法可以帮助我们提取有用信息,消除噪声干扰,并对未来的随机过程变量进行预测。
matlab 二维相关随机过程

matlab 二维相关随机过程一、简介MATLAB是一种强大的科学计算工具,常用于数据分析、仿真和可视化。
二维相关随机过程是一种随时间和空间变化的随机过程,通常用来研究信号处理、图像处理、数据压缩等领域。
本文将介绍如何使用MATLAB进行二维相关随机过程的分析与模拟。
二、MATLAB中的二维相关函数MATLAB提供了丰富的二维相关函数,用于计算二维数据的相关性。
其中最常用的函数是"corrcoef"和"xcorr2"。
1. "corrcoef"函数用于计算两个二维数据的Pearson相关系数。
它返回一个2x2的矩阵,矩阵的对角线上是两个数据的自相关系数,而矩阵的非对角线上是两个数据的互相关系数。
2. "xcorr2"函数用于计算两个二维数据的二维互相关。
它返回一个与输入数据大小相同的矩阵,矩阵中的每个元素表示对应位置的互相关值。
三、二维相关随机过程的模拟在MATLAB中,我们可以使用随机函数和相关函数来模拟二维相关随机过程。
1. 生成随机数据:可以使用MATLAB的随机函数,如"randn"函数生成服从正态分布的随机数据。
通过设定合适的均值和方差,可以生成满足实际需求的随机数据。
2. 计算相关系数:利用之前介绍的"corrcoef"函数,可以计算生成的随机数据的相关系数矩阵。
相关系数可以描述数据之间的相关性程度,从而帮助我们理解二维相关随机过程。
3. 生成二维相关随机过程:通过将随机数据传入"corrcoef"函数,然后再利用"xcorr2"函数计算互相关矩阵,我们可以生成满足相关性要求的二维相关随机过程。
可以通过调整相关系数和相关程度,来控制生成的二维数据的特性。
四、案例分析为了进一步说明如何使用MATLAB进行二维相关随机过程的分析与模拟,我们将以图像处理为例进行讲解。
使用Matlab进行随机过程建模方法

使用Matlab进行随机过程建模方法随机过程建模是现代科学研究中一项重要的技术手段,它不仅在工程领域有广泛的应用,而且在金融、生物学和医学等领域也有着不可忽视的作用。
Matlab是一个强大的数值计算和科学工程计算软件,它提供了丰富的工具箱和函数,使得使用Matlab进行随机过程建模成为一项相对容易的任务。
本文将介绍使用Matlab进行随机过程建模的方法和技巧,并通过实例进行演示。
一、概述随机过程是描述随机现象随时间演化的数学模型。
它是一组随机变量的集合,这些随机变量的取值与时间相关。
随机过程的建模过程可以分为三个步骤:确定随机变量的类型、选择合适的分布函数以及确定各个随机变量之间的关系。
在Matlab中,可以利用统计工具箱中的函数来进行这些步骤的操作。
二、确定随机变量的类型在随机过程建模中,首先需要确定随机变量的类型。
常见的随机变量类型包括离散型和连续型。
离散型随机变量的取值有限或可列举,例如投掷硬币的结果;连续型随机变量的取值属于某个实数区间,例如温度的变化。
在Matlab中,可以利用符号计算工具箱中的函数来定义离散型和连续型随机变量,并进行相应的计算和操作。
三、选择合适的分布函数确定随机变量的类型后,下一步是选择合适的分布函数来描述随机变量的分布规律。
常见的分布函数包括正态分布、均匀分布和指数分布等。
在Matlab中,可以使用统计工具箱中的函数来生成符合特定分布的随机变量,并进行概率计算和仿真实验。
四、确定随机变量之间的关系随机过程中的随机变量之间通常存在某种关系,例如自相关性和互相关性等。
在Matlab中,可以利用信号处理工具箱中的函数来计算随机过程之间的相关性,并进行模拟实验。
五、案例演示为了更好地说明使用Matlab进行随机过程建模的方法和技巧,下面以船舶运行的随机过程为例进行演示。
假设船舶的速度服从正态分布,航向角度服从均匀分布,航行距离服从指数分布。
首先,利用Matlab的统计工具箱中的函数生成符合这些分布的随机变量;然后,根据随机变量之间的关系,利用信号处理工具箱中的函数计算船舶速度和位置的相关性;最后,使用Matlab的数据可视化工具进行结果展示和分析。
Matlab仿真窄带随机过程

随机过程数学建模分析任何通信系统都有发送机和接收机,为了提高系统的可靠性,即输出信噪比,通常在接收机的输入端接有一个带通滤波器,信道内的噪声构成了一个随机过程,经过该带通滤波器之后,则变成了窄带随机过程,因此,讨论窄带随机过程的规律是重要的。
一、窄带随机过程。
一个实平稳随机过程X(t),若它的功率谱密度具有下述性质:中心频率为ωc,带宽为△ω=2ω0,当△ω<<ωc时,就可认为满足窄带条件。
若随机过程的功率谱满足该条件则称为窄带随机过程。
若带通滤波器的传输函数满足该条件则称为窄带滤波器。
随机过程通过窄带滤波器传输之后变成窄带随机过程。
图1 为典型窄带随机过程的功率谱密度图。
若用一示波器来观测次波形,则可看到,它接近于一个正弦波,但此正弦波的幅度和相位都在缓慢地随机变化,图2所示为窄带随机过程的一个样本函数。
图1 典型窄带随机过程的功率谱密度图图2 窄带随机过程的一个样本函数二、窄带随机过程的数学表示1、用包络和相位的变化表示由窄带条件可知,窄带过程是功率谱限制在ωc附近的很窄范围内的一个随机过程,从示波器观察(或由理论上可以推知):这个过程中的一个样本函数(一个实现)的波形是一个频率为ƒc且幅度和相位都做缓慢变化的余弦波。
写成包络函数和随机相位函数的形式:X(t)=A(t)*cos[ωc t+ Φ(t)]其中:A(t)称作X(t)的包络函数; Φ(t)称作X(t)的随机相位函数。
包络随时间做缓慢变化,看起来比较直观,相位的变化,则看不出来。
2、莱斯(Rice)表示式任何一个实平稳随机过程X(t)都可以表示为:X(t)=A c(t) cosωc t-A S(t) sinωc t其中同相分量:A c(t)= X(t) cosφt= X(t) cosωc t+sinωc t=LP[X(t) *2cosωc t]正交分量:A S(t) = X(t)sinφt=cosωc t— X(t) sinωc t= LP[-X(t) *2sinωc t](LP[A]表示取A的低频部分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精心整理基本操作-5/(4.8+5.32)^2area=pi*2.5^2x1=1+1/2+1/3+1/4+1/5+1/6exp(acos(0.3))arr2(:,1:2:3)arr3=[12345678]arr3(5:end)arr3(end)绘图x=[0:1:10];y=x.^2-10*x+15;plot(x,y)x=0:pi/20:2*piy1=sin(x);y2=cos(x);plot(x,y1,'b-');holdon;plot(x,y2,‘k--’);legend(‘sinx’,‘cosx’);x=0:pi/20:2*pi;y=sin(x);figure(1)plot(x,y,'r-')gridon平面的ya=xa;建立Mfunctionifdisp(elseif grade>86.0disp('ThegradeisB.');elseif grade>76.0disp('ThegradeisC.');elseif grade>66.0disp('ThegradeisD.');elsedisp('ThegradeisF.');endendendendendfunction y=func(x)if abs(x)<1y=sqrt(1-x^2);else y=x^2-1;endfunction summ(n)i=1;sum=0;whilei=i+1;endstr=[endsymsxdiff(f)diff((x^2+y^2+z^2)^(1/2),x,2)重积分int(int(x*y,y,2*x,x^2+1),x,0,1)级数symsn;symsum(1/2^n,1,inf)Taylor展开式求y=exp(x)在x=0处的5阶Taylor展开式taylor(exp(x),0,6)矩阵求逆A=[0-6-1;62-16;-520-10]det(A)inv(A)特征值、特征向量和特征多项式A=[0-6-1;62-16;-520-10];lambda=eig(A)[v,d]=eig(A)poly(A)多项式的根与计算p=[10-2-5];r=roots(p)p2=poly(r)y1=polyval(p,4)例子:例子设设Ex=symsum(k*p*(1-p)^(k-1),k,1,inf)symsxy;f=x+y;Ex=int(int(x*y*f,y,0,1),0,1)参数估计例:对某型号的20辆汽车记录其5L汽油的行驶里程(公里),观测数据如下:29.827.628.327.930.128.729.928.027.928.728.427.229.528.528.030.029.129.829.626.9设行驶里程服从正态分布,试用最大似然估计法求总体的均值和方差。
x1=[29.827.628.327.930.128.729.928.027.928.7];x2=[28.427.229.528.528.030.029.129.829.626.9];x=[x1x2]';p=mle('norm',x);muhatmle=p(1),sigma2hatmle=p(2)^2[m,s,mci,sci]=normfit(x,0.5)假设检验例:下面列出的是某工厂随机选取的20只零部件的装配时间(分):9.810.410.69.69.79.910.911.19.610.210.39.69.911.210.69.810.510.110.59.7设装配时间总体服从正态分布,标准差为0.4,是否认定装配时间的均值在0.05的水平下不小于10。
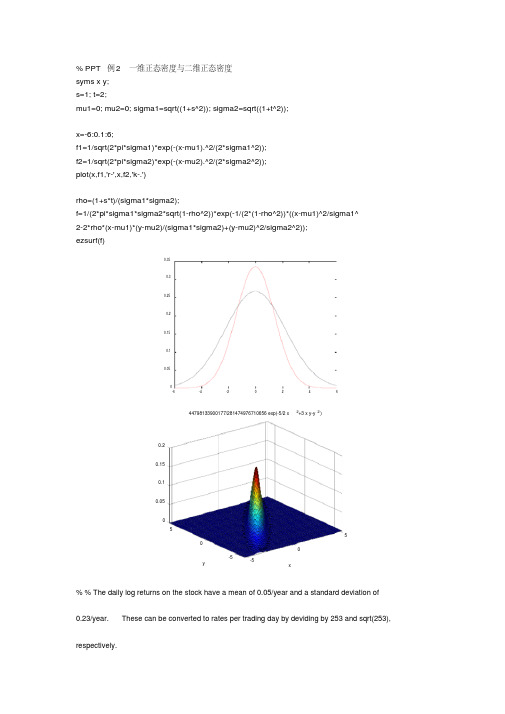
解::%PPT例2symsxy;s=1;t=2;%P34例[p1,p2]%输出ans=0.06710.0000%P40例3.2.1p3=poisspdf(9,12)%输出p3=0.0874%P40例3.2.2p4=poisspdf(0,12)%输出p4=6.1442e-006%P35-37(Th3.1.1)解微分方程%输入:symsp0p1p2;S=dsolve('Dp0=-lamda*p0','Dp1=-lamda*p1+lamda*p0','Dp2=-lamda*p2+lamda*p1', 'p0(0)=1','p1(0)=0','p2(0)=0');[S.p0,S.p1,S.p2]%输出:ans=[exp(-lamda*t),exp(-lamda*t)*t*lamda,1/2*exp(-lamda*t)*t^2*lamda^2]%P40泊松过程仿真%simulate10timesclear;m=10;lamda=1;x=[];fori=1:m%seedend[x',t1']%输出:ans=%输入:N=[];N=[N,0];N=[N,1];elseift<t1(3)N=[N,2];elseift<t1(4)N=[N,3];elseift<t1(5)N=[N,4];elseift<t1(6)N=[N,5];elseift<t1(7)N=[N,6];elseift<t1(8)N=[N,7];elseift<t1(9)N=[N,8];elseift<t1(10)N=[N,9];elseN=[N,10];endendplot(0:0.1:(t1(m)+1),N,'r-')%输出:clear;fori=1:ms=rand(end[x',t1']N=[];N=[N,0];endN=[N,i];endendN=[N,m];endend%输出:%P48非齐次泊松过程仿真%simulate10timesclear;m=10;lamda=1;x=[];for i=1:ms=rand('seed');%exprnd(lamda,'seed',1);setseeds x=[x,exprnd(lamda)];t1=cumsum(x);end[x',t1']N=[];T=[];for t=0:0.1:(t1(m)+1)T=[T,t.^3];%timeisadjusted,cumulativeintensityfunctionist^3.if t<t1(1)N=[N,0];endfor i=1:(m-1)if t>=t1(i)&t<t1(i+1)N=[N,i];endendif t>t1(m)N=[N,m];endendplot(T,N,%outputans=%P50clear;lamda=1;t=input(forrand('state',sum(clock));x=exprnd(lamda);%intervaltimet1=x;while t1<tx=[x,exprnd(lamda)];t1=sum(x);%arrivingtimeendt1=cumsum(x);y=trnd(4,1,length(t1));%rand(1,length(t1));gamrnd(1,1/2,1,length(t1)));frnd(2,10,1,le ngth(t1)));t2=cumsum(y);end[x',t1',y',t2']X=[];m=length(t1);for t=0:0.1:(t1(m)+1)if t<t1(1)X=[X,0];endfor i=1:(m-1)if t>=t1(i)&t<t1(i+1)X=[X,t2(i)];endendifendendclear;rand(n=1;whilex<tifx>=tendendz=binornd(200,0.5,1,n);%generatensalesy=sum(z);above(i)=sum(y>432000);endpro=mean(above)Output:pro=0.3192%%Simulatethelosspro.ForaCompoundPoissonprocess clear;niter=1.0E3;%numberofiterationslamda=1;%arrivingratet=input('Inputatime:','s')below=repmat(0,1,niter);%setupstoragefori=1:niterrand('state',sum(clock));x=exprnd(lamda);%intervaltimen=1;whilex<tx=x+exprnd(lamda);%arrivingtimeifx>=tn=n;elseendendend%计算1到;n=10fork=1:njueduivec(k,1:6)=jueduiveckend%比较相邻的两行n=70;jueduivecn=chushivec0*(P^n)n=71;jueduivecn=chushivec0*(P^n)%Replacethefirstdistribution,Comparingtwoneighbourabsolute-vectorsoncemorechushivec0=[1/61/61/61/61/61/6];P=[0,1/2,1/2,0,0,0;1/2,0,1/2,0,0,0;1/4,1/4,0,1/4,1/4,0;0,0,1,0,0,0,;0,0,1/2,0,0,1/2;0,0,0,0,1,0] ;n=70;jueduivecn=chushivec0*(P^n)n=71;jueduivecn=chushivec0*(P^n)%赌博问题模拟(带吸收壁的随机游走:结束1次游走所花的时间及终止状态)a=5;p=1/2;m=0;while m<100m=m+1;r=2*binornd(1,p)-1;if r==-1a=a-1;elsea=a+1;endifbreak;endend[ma]%%p=q=1/2p=1/2;form=0;a=5;whilem=m+1;if r==-1a=a-1;elsea=a+1;endendif a==0t1=t1+m;m1=m1+1;elset2=t2+m;m2=m2+1;endendfprintf('Theaveragetimesofarriving0and10respectivelyare%d,%d.\n',[t1/m1,t2/m2]);fprintf('Thefrequenciesofarriving0and10respectivelyare%d,%d.\n',[m1/N,m2/N]);%verify:fprintf('Theprobabilityofarriving0anditsapproximaterespectivelyare%d,%d.\n',[5/10,m1/N]);fprintf('Theexpectationofarriving0or10anditsapproximaterespectivelyare%d,%d.\n',[5*(10-5)/(2*p), (t1+t2)/N]);p=1/4;m1=0;m2=0;N=1000;t1=zeros(1,N);t2=zeros(1,N);for n=1:1:Nm=0;a=5;while a>0&a<15m=m+1;r=2*binornd(1,p)-1;if r==-1a=a-1;elsea=a+1;endendif a==0elseendendfprintf(fprintf(%verify:fprintf(fprintf(%输入:clear;P*Q输出:ans=[-p00*lamda+p01*mu,p00*lamda-p01*mu][-p10*lamda+p11*mu,p10*lamda-p11*mu]输入:[p00,p01,p10,p11]=dsolve('Dp00=-p00*lamda+p01*mu','Dp01=p00*lamda-p01*mu','Dp10=-p10*lamda+p11*m u','Dp11=p10*lamda-p11*mu','p00(0)=1,p01(0)=0,p10(0)=0,p11(0)=1')输出:p00=mu/(mu+lamda)+exp(-t*mu-t*lamda)*lamda/(mu+lamda)p01=(lamda*mu/(mu+lamda)-exp(-t*mu-t*lamda)*lamda/(mu+lamda)*mu)/mumu/(mu+lamda)-exp(-t*mu-t*lamda)*mu/(mu+lamda)p11=(lamda*mu/(mu+lamda)+exp(-t*mu-t*lamda)*mu^2/(mu+lamda))/mu%BPATH1Brownianpathsimulation:for…endrandn('state',100)%setthestateofrandnT=1;N=500;dt=T/N;dW=zeros(1,N);%preallocatearrays...W=zeros(1,N);%forefficiencydW(1)=sqrt(dt)*randn;%firstapproximationoutsidetheloop...W(1)=dW(1);%sinceW(0)=0isnotallowedfor j=2:Nendxlabel(ylabel(randn(xlabel(ylabel(randn(M=1000;plot([0,t],[ones(5,1),U(1:5,:)],'r--'),hold off%plot5individualpaths xlabel('t','FontSize',16)ylabel('U(t)','FontSize',16,'Rotation',0,'HorizontalAlignment','right') legend('meanof1000paths','5individualpaths',2)aveerr=norm((Umean-exp(9*t/8)),'inf')%sampleerror%输出:aveerr=0.0504。
