随机过程课程作业(附MATLAB源码)
系统辨识:随机过程的特征估计

实验3 随机过程的特征估计实验报告1、产生一组均值为1,方差为4 的正态分布的随机序列(1000 个样本),估计该序列的均值与方差。
解:MATLAB代码:R=NORMRND(1,2,1,1000) %产生均值为1方差为4的正态分布的1000个随机序列mean(R) %返回序列R的均值V AR(R) %返回序列R的方差figure(1);subplot(2,1,1)stem(R); %绘制离散R序列title('序列R')subplot(2,1,2)hist(R,15); %绘制R序列的分布title('序列R的分布')输出结果:均值:ans = 1.0911方差:ans =4.2540从输出结果中可以看到,输出的均值和方差接近所给值,R序列的分布图可接近正态分布。
2、按如下模型产生一组随机序列:x(n)=0.8x(n-1)+w(n)其中w(n)为均值为1,方差为4 的正态分布白噪声序列。
估计过程的自相关函数与功率谱。
解:MATLAB代码:Fs=1; %采样频率n=0:1/Fs:1000;%生成均值为1方差为4的正态分布白噪声序列w=randn(1,1000);w=w/std(w);w=w-mean(w);a=1; %均值为1b=4; %方差为4w=a+sqrt(b)*w;x=zeros(1,1000);x(1)=w(1);for n=2:1000x(n)=0.8*x(n-1)+w(n);endnfft=1000;cxn=xcorr(x,'unbiased'); %计算x(n)的自相关函数figure(1);subplot(3,1,1);plot(cxn); %绘制自相关函数图title('信号x的自相关函数')%自相关法功率谱估计CXk=fft(cxn,1000);Pxx=abs(CXk);index=0:round(nfft/2-1);k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));subplot(3,1,2)plot(k,plot_Pxx);title('信号x的功率谱');%周期图法功率谱估计window=boxcar(length(x));%矩形窗[Pxx,f]=periodogram(x,window,nfft,Fs);%直接法Subplot(3,1,3)plot(f,10*log10(Pxx))title('周期图法得到的功率谱')3、设信号为x(n)=sin(2πf1n)+2cos(2πf2n)+w(n),n=1,2,....,N,其中f1=0.05,f2=0.12,w(n)为正态白噪声,试在N=356 和1024 点时,分别产生随机序列x(n)、画出x(n)的波形并估计x(n)的相关函数和功率谱。
随机过程课程作业(附MATLAB源码)

绘制样本曲线的MATLAB命令:t=1:50:100000;xt1=0.5*cos(0.5.*t+pi/3);subplot(2,2,1)plot(t,xt);axis([1 100000 -1 1]);title('样本曲线一,sita=pi/3');xt2=0.5*cos(0.5.*t+pi/2);subplot(2,2,2);plot(t,xt);axis([1 100000 -1 1]);title('样本曲线二,sita=pi/2');xt3=0.5*cos(0.5.*t+3*pi/4);subplot(2,2,3);plot(t,xt);axis([1 100000 -1 1]);title('样本曲线三,sita=3*pi/4');xt3=0.5*cos(0.5.*t+3*pi/2);subplot(2,2,4);plot(t,xt);axis([1 100000 -1 1]);title('样本曲线四,sita=3*pi/2');四条样本曲线图:选取第一条样本曲线对时间求均值:MATLAB 命令为:avX=sum(xt1)/length(t)avX =0.0018泊松过程的模拟:a 采用增量迭加法产生泊松过程根据泊松过程是一个平稳增量随机过程,那么可知1100()()()()()()()()n n n N t N t N t N t N t N t N t N t -=-+-+⋅⋅⋅+-+其中1()()()n n N t N t P λτ--=假设某泊松过程的参数λ=3,时间最大为30,τ=1那么MTALAB 参数的样本曲线命令为lamda=2;Tmax=30;hao=1;for j=1:4i=1;N(1)= 0;while(i<Tmax)N(i+1)=N(i)+poissrnd(lamda*hao);i=i+1;endsubplot(2,2,j);stairs(N);enda 采用点间间距迭加法产生泊松过程根据定理1.13可知,如果某计数过程任意相机出现的链各个质点的点间间距是独立过程,且每一个Tn 都服从参数为λ的指数分布,那么N(t)是强度为λ的泊松过程1100()()()()()()()()n n n N t N t N t N t N t N t N t N t -=-+-+⋅⋅⋅+-+其中1()()()n n N t N t P λτ--=假设某泊松过程的参数λ=3,时间最大为30,τ=1那么MTALAB 参数的样本曲线命令为lamda=2;Tmax=50;i=1;T(1)=random('exponential',lamda);while(T(i)<Tmax)T(i+1)=T(i)+random('exponential',lamda);i=i+1;endT(i)=Tmax;x=0:1:i;w(1)=0;for p=1:iw(p+1)=T(p);end%length(w)%length(x)stairs(w,x);。
随机过程习题课

3
(2)求[0,2]内收到3次且[0,3]内收到5次呼唤的概率 P ( N ( 2) 3, N ( 3) 5) P ( N (2) N (0) 3, N ( 3) N ( 2) 2) ( 2 2)3 ( 22 ) ( 2 1)2 ( 21) 64 6 e e e 3! 2! 3 (3)已知[0,3]内收到5次呼唤,求[0,2]内收到3次呼唤的概率.
E ( 2 ) E ( )( t1 t 2 ) E ( 2 )( t1t 2 ) C X (t1 , t 2 ) RX (t1 , t 2 ) X (t1 ) X (t 2 )
[ E ( 2 ) E ( )2 ] [ E () E ( ) E ( )]( t1 t 2 ) [ E ( 2 ) E ( )2 ]( t1t 2 )
37 19 19 , , 75 75 75
p(2)
1 p(0) P (2) 3
即两年后所占市场份额分别是 20
(2)试问至第2年底,A公司转移多少客户给B公司。 p12 (2)
p12 (2) 0.24
即第2年底,A公司转移24%客户给B公司。 (3)若某顾客第一年底是A公司的客户,第三年是B公司 的客户,第四年仍然是A公司的客户,求该事件的概率
0 1 3 F ( x; ) 4 2 3 1 x 2 2
(1) t
4
X 4 P
2 X( ) A 4 2
2 2 1 3 2 1 3 3 2 1 3 2
2 x 2 2 2 x x 3 2 2 3 2 2
( 2) t
P ( N ( 2) 3 N ( 3)
64 6 e P ( N ( 2) 3, N ( 3) 5) 35 5) 6 6 P ( N ( 3) 5) e 5!
随机过程-实验报告

P2 = 0.4167 0.3889 0.3889 0.3611 0.3889 0.3611 0.2222 0.2222 0.2500
7
(1) 2 步转移概率 P2 = 0.4167 0.3889 0.3889 0.3611 0.3889 0.3611 0.2222 0.2222 0.2500
(2) X 2 的分布律 S2 = 0.1667 (3) 平稳分布 T= 0.4000 0.3714 0.2286 2、为适应日益扩大的旅游事业的需要,某城市的 A,B,C 三个照相馆组成一个联 营部,联合经营出租相机的业务,旅游者可由 A,B,C 三处任何一处租出相机,用完 后还到 A,B,C 三处的任何一处即可.估计转移概率如表所示,今欲选择 A,B,C 之一 附设租机维修点,问该点设在何处为好? (程序与结果) 还相机处 A B C 租相机处 A 0.2 0.8 0 B 0.8 0 0.2 C 0.1 0.3 0.6
1 / 2 P 1/3 1/ 3 1/3 1/3 1/ 2 1/ 6 1/3 1/ 6
(1) 计算 2 步转移概率;(2) 已知初始分布为 P 2 / 5, 2 / 5,1 / 5 ,求 X 2 的分布律 (3) 求平稳分布,要求给出程序与结果。 程序:
9
程序: p=[0.2 0.8 0;0.8 0 0.2; 0.1 0.3 0.6]; P2=p^2 a=[p'-eye(3);ones(1,3)];b=[0 0 0 1]';T=a\b 结果:
0.1389
0.0611
解:由题意可知,该问题的转移概率矩阵 P 为:
8
0 .2 P 0 .8 0 .1
实验内容 判定一个 Markov 链是否是遍历的,若是遍历的,求其极限分布。并能从实际问 题中抽象出 Markov 链,并求出其极限分布,并理解其实际意义。 实验习题 1、已知齐次马氏链 X n , n 0,1, 2, 的状态空间 E 1, 2, 3 ,状态转移矩阵为
随机过程实验

实验名称:随机变量的仿真与实验实验内容:用MATLAB 分别产生服从(二项分布、泊松分布、正态分布、均匀分布、指数分布、瑞利分布)的随机变量,并分析他们的:1、分布函数或概率密度函数2、均值、方差1、服从二项分布的随机变量理论分析如果随机变量X 的分布律为k n k k n k q p C k X P p -===}{0<p<1, q=1-p, k=0,1,2,…n,则称X 服从参数为n ,p 的二项分布,记为X~B(n ,p)。
其期望和方差分别为E(X) = np ,D(X)=npq 。
随机变量X~B(20,0.4),可以通过matla b 计算其期望和方差,绘制分布律和分布函数。
程序如下:n = 20;p = 0.4;[E,D] = binostat(n ,p); %计算期望和方差f = binopdf(1:21, n, p); %计算分布律F = binocdf(1:21, n, p); %计算分布函数subplot(2,2,1); stem(f); %绘制分布律title('二项分布理论分布律 n=20 p=0.4');xlabel('x');ylabel('p');subplot(2,2,3); stem(F); %绘制分布函数title('二项分布理论分布函数 n=20 p=0.4');xlabel('x');ylabel('f');计算得结果E(X) = 8,D(X) = 4.800,分布律和分布函数如图1。
图1 X~B(20,0.4)的分布律和分布函数样本分析利用matlab中binornd函数产生一个X~B(20,0.4)的样本,样本点总数为20000。
计算其均值和方差,计算分布律和分布函数,并与理论结果进行比较。
程序如下:n = 20;p = 0.4;R = binornd(n,p,1,20000);e = mean(R); %期望d = var(R); %方差f = zeros (1,21);F = zeros (1,21);for j = 1:21 %计算统计分布律for i=1:20000if j == R(i)f(1,j) = f(1,j) + 1;endendf(1,j) = f(1,j) / 20000;endsubplot(2,2,1);stem(f);title('二项分布样本分布律 n=20 p=0.4');xlabel('x');ylabel('p');for j = 1:21 %计算分布函数for i = 1:jF(1, j) = F(1, j) + f(1,i);endendsubplot(2,2,3);stem(F);title('二项分布样本分布函数 n=20 p=0.4');xlabel('x');ylabel('f');计算结果为e=8.0218,d=4.7760,与理论值(E(X)=8,D(X)=4.8)基本接近。
随机信号大作业

随机信号大作业随机信号大作业第一章上机题:设有随机初相信号X(t)=5cos(t+),其中相位是在区间(0,2)上均匀分布的随机变量。
(1)试用Matlab编程产生其三个样本函数。
(2)产生t=0时的10000个样本,并画出直方图估计P(x)画出图形。
解:(1)由Matlab产生的三个样本函数如下图所示:程序源代码:clcclearm=unifrnd(0,2*pi,1,10);fork=1:3t=1:0.1:10;X=5*cos(t+m(k));plo t(t,X);holdonendxlabel('t');ylabel('X(t)');gridon;axistight;(2)产生t=0时的10000个样本,并画出直方图估计P(x)的概率密度并画出图形。
源程序代码:clear;clc;=2*pi*rand(10000,1);x=5*cos();figure(2),hist(x,20);holdon;第二章上机题:利用Matlab程序设计一正弦型信号加高斯白噪声的复合信号。
(1)分析复合信号的功率谱密度,幅度分布的特性;(2)分析复合信号通过RC积分电路后的功率谱密度和相应的幅度分布特性;(3)分析复合信号通过理想低通系统后的功率谱密度和相应的幅度分布特性。
解:设正弦信号的频率为10HZ,抽样频率为100HZx=sin(2*pi*fc*t)正弦曲线图:程序块代码:clearall;fs=100;fc=10;n=201;t=0:1/fs:2;x=sin(2*pi*fc*t);y=awgn(x,10);m=50;i=-0.49:1/fs:0.49;forj=1:mR(j)=sum(y(1:n-j-1).*y(j:199),2)/(n-j);Ry(49+j)=R(j);Ry(51-j)=R(j);endsubplot(5,2,1);plot(t,x,'r');title('正弦信号曲线');ylabel('x');xlabel('t/20pi');grid;(1)正弦信号加上高斯白噪声产生复合信号y:y=awgn(x,10)对复合信号进行傅里叶变换得到傅里叶变换:Y(jw)=fft(y)复合信号的功率谱密度函数为:G(w)=Y(jw).*conj(Y(jw)/length(Y(jw)))复合信号的曲线图,频谱图和功率谱图:程序块代码:plot(t,y,'r');title('复合信号曲线');ylabel('y');xlabel('t/20pi');grid;程序块代码:FY=fft(y);FY1=fftshift(FY);f=(0:200)*fs/n-fs/2;plot(f,abs(FY1),'r');title('复合信号频谱图');ylabel('F(jw)');xlabel('w');grid;程序块代码:P=FY1.*conj(FY1)/length(FY1);plot(f,P,'r');title('复合信号功率谱密度图');ylabel('G(w)');xlabel('w');grid;(2)正弦曲线的复合信号通过RC积分电路后得到信号为:通过卷积计算可以得到y2即:y2=conv2(y,b*pi^-b*t)y2的幅度分布特性可以通过傅里叶变换得到Y2(jw)=fft(y2)y2的功率谱密度G2(w)=Y2(jw).*conj(Y2(jw)/length(Y2(jw)))复合信号通过RC积分电路后的曲线频谱图和功率谱图:程序块代码:b=10;y2=conv2(y,b*pi^-b*t);Fy2=fftshift(fft(y2));f=(0:400)*fs/n-fs/2;plot(f,abs(Fy2),'r');title('复合信号通过RC系统后频谱图');ylabel('Fy2(jw)');xlabel('w');grid;程序代码:P2=Fy2.*conj(Fy2)/length(Fy2);plot(f,P2,'r');title('复合信号通过RC系统后功率密度图');ylabel('Gy2(w)');xlabel('w');grid;(3)复合信号y通过理想滤波器电路后得到信号y3通过卷积计算可以得到y3即:y3=conv2(y,sin(10*t)/(pi*t))y3的幅度分布特性可以通过傅里叶变换得到Y3(jw)=fft(y3),y3的功率谱密度G3(w)=Y3(jw).*conj(Y3(jw)/length(Y3(jw)))复合信号通过理想滤波器后的频谱图和功率密度图:程序块代码:y3=conv2(y,sin(10*t)/(pi*t));Fy3=fftshift(fft(y3));f3=(0:200)*fs/n-fs/2;plot(f3,abs(Fy3),'r');title('复合信号通过理想滤波器频谱图');ylabel('Fy3(jw)');xlabel('w');grid;程序块代码:P3=Fy3.*conj(Fy3)/length(Fy3);plot(f3,P3,'r');title('理想信号通过理想滤波器功率密度图');ylabel('Gy3(w)');xlabel('w');grid;。
随机过程实验
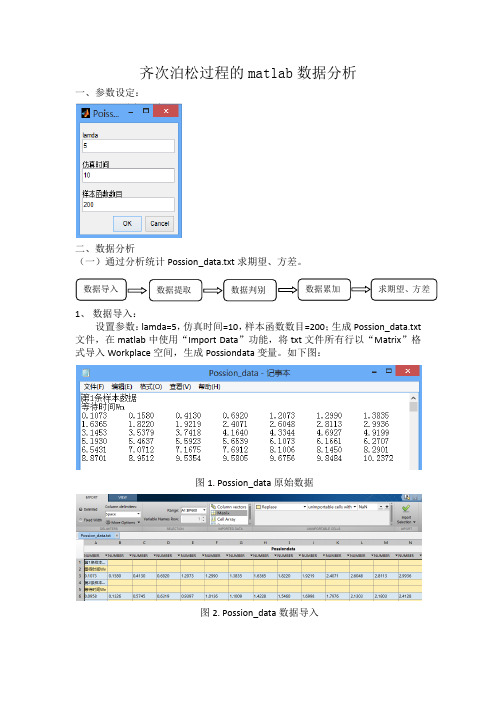
齐次泊松过程的matlab数据分析一、参数设定:二、数据分析(一)通过分析统计Possion_data.txt求期望、方差。
1、数据导入:设置参数:lamda=5,仿真时间=10,样本函数数目=200;生成Possion_data.txt 文件,在matlab中使用“Import Data”功能,将txt文件所有行以“Matrix”格式导入Workplace空间,生成Possiondata变量。
如下图:图1. Possion_data原始数据图2. Possion_data数据导入图3. 生成Possiondata2、数据提取编程将Possiondata数组中的第3,6,9…300行提取出来形成一个新的数值poiss。
图4. 提取有效数据3、数据判别(1)、按照试验指导大纲,将时间间隔设成0.1,将每一条样本函数按照0.1的时间间隔进行统计,将在同一个0.1间隔内的数据归为一类。
得到“t1”图5. 数据判别归类(2)、采用“length”函数将上表中的数据进行计数得到以下参数:图6. 统计类中数量(3)、将“t2”进行累加,并同样的方法计算所有样本函数得到“s”:图7. 得到样本计数样本图8. 第一条样本计数过程图9. SJGC生成的第一条样本函数4、计算期望、方差使用“mean”函数计算期望值,使用“var”函数计算方差得到下图:图10. 均值_方差图从图中可以看出,泊松过程的均值与方差具有一致性。
图11. SJGC生成的均值函数图(二)求泊松过程的速率方法1根据所得到的的均值函数,使用“polyfit”函数采用一次函数模拟得到斜率4.9138,即为泊松速率。
方法2考虑到泊松事件的时间间隔是指数分布,且均值为泊松过程速率的倒数。
对样本函数进行处理,将两次到达时间相减得到每相邻两次事件发生的时间间隔,使用“expfit”函数得到估计的均值,对其求倒得到泊松速率。
使用循环语句得到每一条样本函数的速率,最后求平均得到要求的泊松速率。
随机作业最终版-荀涛

自动化学院随机过程基础及应用课程设计学号:S307040123专业:精密仪器及机械学生姓名:荀涛任课教师:赵希人 (教授)随机作业学号:S307040123 姓名:荀涛本次作业是由MATLAB 6.5环境下写出。
第一题:一、用PC机产生[0,1]均匀分布的白序列{X(k),k=1,2, (2000)(1)打印出前50个数X(i),i=1,2,…,50(2)分布检验(3)均值检验(4)方差检验(5)相关检验源程序:x=rand(1,2000)%EX=mean(x)%均值检验DX=var(x)%方差检验subplot(2,1,1),hist(x,10)y=linspace(-10,10,21)for m= -10 :10mAbs=abs(m)s=0for n=1:2000-mAbss=s+(x(n+mAbs)-EX)*(x(n)-EX)endy(m+11)=(1/(2000-mAbs))*sendx2=[-15:30/20:15]subplot(2,1,2),plot(x2,y)1.前50个数:0.98625 0.8853 0.40484 0.62714 0.38546 0.84786 0.52685 0.8074 0.3935 0.96173 0.0301210.95373 0.71438 0.64655 0.44665 0.17463 0.83525 0.97009 0.13497 0.25099 0.91001 0.676470.62316 0.51222 0.0034827 0.22689 0.97846 0.86125 0.014385 0.48578 0.4164 0.77290.48815 0.52256 0.78205 0.59123 0.12639 0.10972 0.66291 0.99709 0.34618 0.17605 0.0678890.3094 0.33476 0.37617 0.95221 0.71932 0.77934 0.617662.分布检验见图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绘制样本曲线的MATLAB命令:
t=1:50:100000;
xt1=0.5*cos(0.5.*t+pi/3);
subplot(2,2,1)
plot(t,xt);
axis([1 100000 -1 1]);
title('样本曲线一,sita=pi/3');
xt2=0.5*cos(0.5.*t+pi/2);
subplot(2,2,2);
plot(t,xt);
axis([1 100000 -1 1]);
title('样本曲线二,sita=pi/2');
xt3=0.5*cos(0.5.*t+3*pi/4);
subplot(2,2,3);
plot(t,xt);
axis([1 100000 -1 1]);
title('样本曲线三,sita=3*pi/4');
xt3=0.5*cos(0.5.*t+3*pi/2);
subplot(2,2,4);
plot(t,xt);
axis([1 100000 -1 1]);
title('样本曲线四,sita=3*pi/2');
四条样本曲线图:
选取第一条样本曲线对时间求均值:
MATLAB 命令为:
avX=sum(xt1)/length(t)
avX =
0.0018
泊松过程的模拟:
a 采用增量迭加法产生泊松过程
根据泊松过程是一个平稳增量随机过程,那么可知
1100()()()()()()()()n n n N t N t N t N t N t N t N t N t -=-+-+⋅⋅⋅+-+
其中1()()()n n N t N t P λτ--=
假设某泊松过程的参数λ=3,时间最大为30,τ=1那么MTALAB 参数的样本曲线命令为
lamda=2;Tmax=30;hao=1;
for j=1:4
i=1;N(1)= 0;
while(i<Tmax)
N(i+1)=N(i)+poissrnd(lamda*hao);
i=i+1;
end
subplot(2,2,j);
stairs(N);
end
a 采用点间间距迭加法产生泊松过程
根据定理1.13可知,如果某计数过程任意相机出现的链各个质点的点间间距是独立过程,且每一个Tn 都服从参数为λ的指数分布,那么N(t)是强度为λ的泊松过程
1100()()()()()()()()n n n N t N t N t N t N t N t N t N t -=-+-+⋅⋅⋅+-+
其中1()()()n n N t N t P λτ--=
假设某泊松过程的参数λ=3,时间最大为30,τ=1那么MTALAB 参数的样本曲线命令为
lamda=2;Tmax=50;
i=1;T(1)=random('exponential',lamda);
while(T(i)<Tmax)
T(i+1)=T(i)+random('exponential',lamda);
i=i+1;
end
T(i)=Tmax;x=0:1:i;w(1)=0;
for p=1:i
w(p+1)=T(p);
end
%length(w)
%length(x)
stairs(w,x);。
