第二章 极限与连续习题解答
第二章_极限与连续_习题解答

1习题2-11. 观察下列数列的变化趋势,讨论有界性和单调性。
如果有极限请写出极限值:(1)13nn x ⎛⎫=- ⎪⎝⎭;解:{}n x 的前五项为:11111,,,,392781243⎧⎫---⎨⎬⎩⎭,从趋势可知,{}n x 不单调;11()33n -≤ ,故{}n x 有界。
{}n x 有极限值0。
(2)1n nx n =+; 解: {}01nx <<,所以有界。
111021(1)(2)n n n n xx n n n n ++-=-=>++++,所以单调递增, {}n x 有极限值1 (3)()10.1nn x =-; 解:{}01nx <<,所以有界。
()0.1n随着n 值的增大而减小,所以相应的n x 的值增大,所以为单调递增。
{}n x 的极限值为1 (4)cos2n n x n π=; 解:分别取)(2+∈=N k k n 和)(12+∈+=N k k n ,显然cos2n n x n π=是无界不单调的,故没有极限值。
(5)1n x n =-。
解:是无界的,且单调递减。
不存在极限2. 用极限定义证明::对于任意的正数2,即(3)3limn +3. 对下面情况进行讨论,对得到的结论作出论证:(1) 数列{}n x 和{}n y 都发散,{}n n x y ±和{}n n x y 的收敛性如何?解:{}n n x y ±,{}n n x y 可能收敛,可能发散。
如sin ,n n x n y n ==,n n n n x y n n x y n n ±±⋅⋅=s i n 、=s i n 均发散的。
又如1,n n x n y n ==,1n n x y n n±±=是发散的,n n x y ⋅=1是收敛的。
({}n n x y ±收敛需要再举个例子) (2) 数列{}n x 、{}n y 中有一个收敛,另一个发散,{}n n x y ±、{}n n x y 的收敛性如何? 解:{}n n x y ±一定发散,而{}n n x y 可能收敛可能发散。
第二章-极限与连续--基础练习题(含解答)

第二章 极限与连续 基础练习题(作业)§2.1 数列的极限一、观察并写出下列数列的极限:1.4682,,,357极限为1 2.11111,,,,,2345--极限为03.212212⎧-⎪⎪=⎨+⎪⎪⎩n nn nnn a n 为奇数为偶数极限为1§2.2 函数的极限一、画出函数图形,并根据函数图形写出下列函数极限: 1.lim →-∞xx e极限为零 2.2lim tan x x π→无极限3.lim arctan →-∞x x极限为2π-4.0lim ln x x +→ 无极限,趋于-∞二、设2221,1()3,121,2x x f x x x x x x +⎧⎪=-+<⎨⎪->⎩,问当1x →,2x →时,()f x 的极限是否存在?211lim ()lim(3)3x x f x x x ++→→=-+=;11lim ()lim(21)3x x f x x --→→=+= 1lim () 3.x f x →∴=222lim ()lim(1)3x x f x x ++→→=-=;222lim ()lim(3)53x x f x x x --→→=-+=≠ 2lim ()x f x →∴不存在。
三、设()111xf x e=+,求 0x →时的左、右极限,并说明0x →时极限是否存在.()101lim lim 01x x xf x e ++→→==+()11lim lim 11x x x f x e--→→==+lim ()x f x →∴不存在。
四、试讨论下列函数在0x →时极限是否存在. 1.绝对值函数()||=f x x ,存在极限为零 2.取整函数()[]=f x x 不存在 3.符号函数()sgn =f x x 不存在§2.3 无穷小量与无穷大量一、判断对错并说明理由: 1.1sinx x是无穷小量. 错,无穷小量需相对极限过程而言,在某个极限过程中的无穷小量在其它极限过程中可能不再是无穷小量。
第二章 极限与连续习题

习题二1.写出下列数列的前五项:(1)nn y 211-= (2)nn n y ⎪⎭⎫⎝⎛-=11(3)n n y n πsin 1= (4)4)12(32+++=n n n n y n(5)!n n m m m y n )1()1(+--=2、用数列极限的定义证明下列极限: (1)11lim=+∞→n n n (2)1211lim =⎪⎪⎭⎫⎝⎛-∞→n n (3)01lim=∞→n n3.用观察的方法判断下列数列是否收剑。
(1)y n :-31,53,-75,97 ,-119,… (2)y n :1,23,31,45,51 ,67,…(3)y n :0,21,041,0,61 ,0,81,…4、用极限的定义证明下列极限: (1)8)13(lim 3=-→x x (2)232lim=+∞→x x x (3)424lim 22-=+--→x x x (4)02lim =-∞→x x5.设⎩⎨⎧≥-<=3133)(x x x xx f 作f (x )的图形,并讨论当x →3时,f (x )的左右极限(利用第4题(1)的结果)。
6.证明x xx 0lim →不存在。
7.函数2)1(1-=x y 在什么变化过程中是无穷大量?又在什么变化过程中是无穷小量?8.以下数列在n →∞时是否为无穷小量?(1)nn n y 21)1(1+-= (2)ny nn)1(1-+=(3)21ny n =9.当x →0时,下列变量中哪些是无穷小量? 100x 2,3x ,x 2,01.0x ,2x x ,xx 2,x 2+0.1x 221x x - 10.求下列各极限:(1))253(lim 22+--→x x x (2)13lim 2423++-→x x x x(3)⎪⎭⎫ ⎝⎛--→321lim 0x x (4)23lim22--→x x x (5)121lim221---→x x x x (6)xx x x x x 2324lim2220+--→(7)221123limx x x x -+-→ (8)h x h x h 330)(lim -+→(9)11lim 1--→x x n x (n 为正整数)(10)1632lim-+∞→x x x (11)211000lim xxx +∞→(12)u u u ++∞→11lim 43 (13)1)1(lim 2+-∞→n n n(14)502030)12()23()12(lim+--+∞→x x x x(15)22011limx x x +-→ (16)3231lim xx x +---∞→(17)22312lim 4---+→x x x(18)⎪⎪⎭⎫⎝⎛---→x x x 1113lim 31 (19))11(lim 22+--+++∞→x x x x x(20))))(((lim x q x p x x -+++∞→(21)⎪⎪⎭⎫⎝⎛+-+++∞→2222111lim n n n n n n n (22))cos 3(1lim 32x x x x x +++∞→11.设f (x )=x ,求h x f h x f h )()(lim 0-+→12.设⎪⎩⎪⎨⎧<≤<+≤+=x x x x x x f x1101023)(22分别讨论x →0及x →1时f (x )的极限是否存在? 13.设⎪⎪⎩⎪⎪⎨⎧<-≤<-=<=x x x xx x x x f x 263202000)(212 讨论x →0及x →2时f (x )的极限是否存在,并且求)(lim x f x -∞→及)(lim x f x +∞→。
极限与连续复习题答案

极限与连续复习题答案1. 极限的定义是什么?答:极限是数学分析中的一个基本概念,它描述了一个函数在某一点附近的行为。
如果函数f(x)在点x=a的极限存在,那么当x趋近于a 时,f(x)的值会无限接近某个确定的数值L。
用数学符号表示为:lim(x→a) f(x) = L。
2. 连续函数的定义是什么?答:连续函数是指在定义域内,函数值与自变量之间没有跳跃的函数。
如果函数f(x)在点x=a处连续,那么当x趋近于a时,f(x)的极限值等于函数在该点的函数值,即lim(x→a) f(x) = f(a)。
3. 极限存在的必要条件是什么?答:极限存在的必要条件是函数在该点的左极限和右极限都存在且相等。
即lim(x→a-) f(x) = lim(x→a+) f(x)。
4. 连续函数与极限的关系是什么?答:连续函数与极限的关系是,如果函数在某点连续,那么该点的函数极限值等于函数值。
反之,如果函数在某点的极限存在且等于函数值,那么该函数在该点连续。
5. 极限的运算法则有哪些?答:极限的运算法则包括:- 和差法则:lim(x→a) [f(x) ± g(x)] = lim(x→a) f(x) ±li m(x→a) g(x);- 乘法法则:lim(x→a) [f(x) * g(x)] = lim(x→a) f(x) *lim(x→a) g(x);- 商法则:如果lim(x→a) g(x) ≠ 0,则lim(x→a) [f(x) / g(x)]= lim(x→a) f(x) / lim(x→a) g(x);- 幂法则:lim(x→a) [f(x)]^n = [lim(x→a) f(x)]^n;- 指数法则:lim(x→a) e^[f(x)] = e^lim(x→a) f(x);- 对数法则:如果f(x) > 0,则lim(x→a) log[f(x)] = loglim(x→a) f(x)。
6. 无穷小量和无穷大量在极限中的作用是什么?答:无穷小量是指当x趋近于某个值时,函数值趋近于0的量。
高等数学作业集第2章极限与连续及答案

x+ x �
(4) 1 + x − 1 − x � x , 1 阶,等价 x = x1/8 ,1/8 阶,
12.求下列极限 (1) lim
x →+∞
x sin x 2x + 3
x sin x 2x + 3 1 sin x lim = � 0 (无穷小与有界量的乘积) x →+∞ x (2 + 3 / x)
(1/ 2) n 4 4n +1 + 2n 4 + (1/ 2) n 4 + nlim →+∞ 解: = lim lim = = n →+∞ 3 ⋅ 4 n − 3n n →+∞ 3 − (3 / 4) n 3 − lim(3 / 4) n 3
n →∞
(3) lim ( n + 1 − n − n )
2 1/2
− 1 (3) cos( x 2 ) − 1 ,(4) tan( x3 )
x�
3 3 (4) tan( x ) � x [3 阶]; (3) x [1/2 阶]; (2) (1 + x 2 )1/2 − 1 � x 2 / 2 [2 阶];
cos( x 2 ) − 1 � − x 4 / 2 [4 阶]
2 3 − x x2 2 3 − =1 + 0 − 0 =1 x x2
(5) lim
4 x3 + 3x 2 x →∞ 5 x 4 + 2 x
4 x3 + 3x 2 1 4 + 3(1/ x) 1 4 + 3(1/ x) 4 解: lim =lim =lim �lim =0 × =0 x →∞ 5 x 4 + 2 x x →∞ x 5 + 2(1/ x 3 ) x →∞ x x →∞ 5 + 2(1/ x 3 ) 5
高等数学习题详解-第2章 极限与连续(精品范文).doc

【最新整理,下载后即可编辑】习题2-11. 观察下列数列的变化趋势,写出其极限: (1) 1n n x n =+ ; (2)2(1)n n x =--;(3)13(1)nn x n=+-; (4)211n x n=-. 解:(1) 此数列为12341234,,,,,,23451n n x x x x x n =====+ 所以lim 1n n x →∞=。
(2) 12343,1,3,1,,2(1),n n x x x x x =====-- 所以原数列极限不存在。
(3)1234111131,3,3,3,,3(1),234n n x x x x x n=-=+=-=+=+-所以lim 3n n x →∞=。
(4)12342111111,1,1,1,,1,4916n x x x x x n =-=-=-=-=- 所以lim 1n n x →∞=-2.下列说法是否正确:(1)收敛数列一定有界 ; (2)有界数列一定收敛; (3)无界数列一定发散;(4)极限大于0的数列的通项也一定大于0. 解:(1) 正确。
(2) 错误 例如数列{}(-1)n 有界,但它不收敛。
(3) 正确。
(4) 错误 例如数列21(1)nn x n ⎧⎫=+-⎨⎬⎩⎭极限为1,极限大于零,但是11x =-小于零。
*3.用数列极限的精确定义证明下列极限:(1) 1(1)lim1n n n n-→∞+-=;(2) 222lim 11n n n n →∞-=++; (3)323125lim -=-+∞→n n n证:(1) 对于任给的正数ε,要使1(1)111n n n x n n ε-+--=-=<,只要1n ε>即可,所以可取正整数1N ε≥.因此,0ε∀>,1N ε⎡⎤∃=⎢⎥⎣⎦,当n N >时,总有1(1)1n n n ε-+--<,所以1(1)lim 1n n n n-→∞+-=. (2) 对于任给的正数ε,当3n >时,要使222222332211111n n n n n x n n n n n n n n nε---+-=-==<<<+++++++,只要2n ε>即可,所以可取正整数2max ,3N ε⎧⎫=⎨⎬⎩⎭.因此,0ε∀>,2max ,3N ε⎧⎫∃=⎨⎬⎩⎭,当n N >时,总有22211n n n ε--<++,所以222lim 11n n n n →∞-=++. (3)对于任给的正数ε,要使25221762()()131333(31)313n n x n n n n ε+--=--=<=<----,只要123n ε->即可,所以可取正整数213N ε≥+.因此,0ε∀>,213N ε⎡⎤∃=+⎢⎥⎣⎦,当n N >时,总有522()133n n ε+--<-,所以323125lim-=-+∞→n n n . 习题2-21. 利用函数图像,观察变化趋势,写出下列极限: (1)21lim x x →∞ ; (2) -lim x x e →∞; (3) +lim x x e -→∞; (4) +lim cot x arc x →∞; (5) lim2x →∞;(6) 2-2lim(1)x x →+; (7) 1lim(ln 1)x x →+; (8) lim(cos 1)x x π→- 解:(1)21lim 0x x →∞= ;(2) -lim0x x e →∞=;(3) +lim 0x x e -→∞=; (4) +lim cot 0x arc x →∞=; (5) lim 22x →∞= ;(6) 2-2lim(1)5x x →+=; (7) 1lim(ln 1)1x x →+=; (8) lim(cos 1)2x x π→-=- 2. 函数()f x 在点x 0处有定义,是当0x x →时()f x 有极限的( D )(A ) 必要条件 (B ) 充分条件 (C ) 充要条件 (D ) 无关条件解:由函数极限的定义可知,研究()f x 当0x x →的极限时,我们关心的是x 无限趋近x 0时()f x 的变化趋势,而不关心()f x 在0x x =处有无定义,大小如何。
高等数学函数的极限与连续习题精选和答案

1、函数()12++=x x x f 与函数()113--=x x x g 相同.错误 ∵当两个函数的定义域和函数关系相同时,则这两个函数是相同的。
∴()12++=x x x f 与()113--=x x x g 函数关系相同,但定义域不同,所以()x f 与()x g 是不同的函数。
2、如果()M x f >(M 为一个常数),则()x f 为无穷大. 错误 根据无穷大的定义,此题是错误的。
3、如果数列有界,则极限存在.错误 如:数列()nn x 1-=是有界数列,但极限不存在4、a a n n =∞→lim ,a a n n =∞→lim .错误 如:数列()nn a 1-=,1)1(lim =-∞→nn ,但n n )1(lim -∞→不存在。
5、如果()A x f x =∞→lim ,则()α+=A x f (当∞→x 时,α为无穷小). 正确 根据函数、极限值、无穷小量的关系,此题是正确的。
6、如果α~β,则()α=β-αo .正确 ∵1lim=αβ,是 ∴01lim lim =⎪⎭⎫⎝⎛-=-αβαβα,即βα-是α的高阶无穷小量。
7、当0→x 时,x cos 1-与2x 是同阶无穷小.正确 ∵2122sin 412lim 2sin 2lim cos 1lim2022020=⎪⎪⎪⎪⎭⎫ ⎝⎛⋅⋅==-→→→x x x x x x x x x 8、 01sin lim lim 1sin lim 000=⋅=→→→xx x x x x x .错误 ∵xx 1sin lim 0→不存在,∴不可利用两个函数乘积求极限的法则计算。
9、 e x xx =⎪⎭⎫⎝⎛+→11lim 0.错误 ∵e x xx =⎪⎭⎫⎝⎛+∞→11lim10、点0=x 是函数xxy =的无穷间断点.错误 =-→x x x 00lim 1lim 00-=--→x x x ,=+→x x x 00lim 1lim 00=+→xx x ∴点0=x 是函数xxy =的第一类间断点.11、函数()x f x1=必在闭区间[]b a ,取得最大值、最小值.错误 ∵根据连续函数在闭区间上的性质,()x f x1=在0=x 处不连续 ∴函数()x f x1=在闭区间[]b a ,不一定取得最大值、最小值 二、填空题:1、设()x f y =的定义域是()1,0,则 (1)()xef 的定义域是( (,0)-∞ );(2)()x f 2sin 1-的定义域是( ,()2x x k x k k Z πππ⎧⎫≠≠+∈⎨⎬⎩⎭);(3)()x f lg 的定义域是( (1,10) ). 答案:(1)∵10<<xe (2)∵1sin 102<-<x (3)∵1lg 0<<x2、函数()⎪⎩⎪⎨⎧≤<-=<<-+=403000222x x x x x x f 的定义域是( (]4,2- ).3、设()2sin x x f =,()12+=ϕx x ,则()[]=ϕx f ( ()221sin +x ).4、nxn n sinlim ∞→=( x ).∵x x n x n x n n x n x n n n n =⋅==∞→∞→∞→sinlim 1sin limsin lim 5、设()11cos 11211xx x f x x x x π-<-⎧⎪⎪=-≤≤⎨⎪->⎪⎩,则()10lim x f x →--=( 2 ),()=+→x f x 01lim ( 0 ). ∵()1010lim lim (1)2x x f x x →--→--=-=,()()01lim lim 0101=-=+→+→x x f x x6、设()⎪⎩⎪⎨⎧=≠-=00cos 12x ax x x x f ,如果()x f 在0=x 处连续,则=a ( 21 ).∵21cos 1lim 20=-→x x x ,如果()x f 在0=x 处连续,则()a f xx x ===-→021cos 1lim 20 7、设0x 是初等函数()x f 定义区间的点,则()=→x f x x 0lim ( ()0x f ).∵初等函数()x f 在定义区间连续,∴()=→x f x x 0lim ()0x f8、函数()211-=x y 当x →( 1 )时为无穷大,当x →( ∞ )时为无穷小.∵()∞=-→2111limx x ,()011lim2=-∞→x x9、若()01lim2=--+-+∞→b ax x x x ,则=a ( 1 ),=b ( 21-). ∵()b ax x xx --+-+∞→1lim2()()()bax x x bax x x b ax x x x +++-+++---+-=+∞→111lim 222()()b ax x x b ax x x x +++-+-+-=+∞→11lim 222()()()b ax x x b x ab x a x +++--++--=+∞→11211lim 2222欲使上式成立,令012=-a ,∴1a =±,上式化简为()()()2211212112lim lim lim1x x x bab ab x b ab a →+∞→+∞→+∞--++-++--+==+∴1a =,021=+ab ,12b =-10、函数()x x f 111+=的间断点是( 1,0-==x x ). 11、()34222+--+=x x x x x f 的连续区间是( ()()()+∞∞-,3,3,1,1, ).12、若2sin 2lim =+∞→x xax x ,则=a ( 2 ). ()200lim sin 2lim sin 2lim =+=+=⎪⎭⎫ ⎝⎛+=+∞→∞→∞→a a x x a x x ax x x x ∴2=a13、=∞→x x x sin lim( 0 ),=∞→xx x 1sin lim ( 1 ), ()=-→xx x 11lim ( 1-e ),=⎪⎭⎫ ⎝⎛+∞→kxx x 11lim ( ke ). ∵0sin 1lim sin lim=⋅=∞→∞→x x xx x x 111sin lim1sin lim ==∞→∞→xx x x x x()[]1)1(110)(1lim 1lim --⋅-→→=-+=-e x x xx x x k kx x kxx e x x =⎥⎦⎤⎢⎣⎡+=⎪⎭⎫ ⎝⎛+∞→∞→)11(lim 11lim14、limsin(arctan )x x →∞=( 不存在 ),lim sin(arccot )x x →+∞=( 0 )三、选择填空:1、如果a x n n =∞→lim ,则数列n x 是( b )a.单调递增数列 b .有界数列 c .发散数列2、函数()()1log 2++=x x x f a 是( a )a .奇函数b .偶函数c .非奇非偶函数 ∵()()11log 1)(log 22++=+-+-=-x x x x x f aa()()x f x x a -=++-=1log 23、当0→x 时,1-xe 是x 的( c )a .高阶无穷小b .低阶无穷小c .等价无穷小4、如果函数()x f 在0x 点的某个邻域恒有()M x f ≤(M 是正数),则函数()x f 在该邻域( c )a .极限存在b .连续c .有界5、函数()x f x-=11在( c )条件下趋于∞+. a .1→x b .01+→x c .01-→x6、设函数()x f xxsin =,则()=→x f x 0lim ( c )a .1b .-1c .不存在 ∵1sin lim sin limsin lim000000-=-=-=-→-→-→xx x x x xx x x1sin lim sin lim 0000==-→+→xx x x x x 根据极限存在定理知:()x f x 0lim →不存在。
第二章 极限与连续(五)
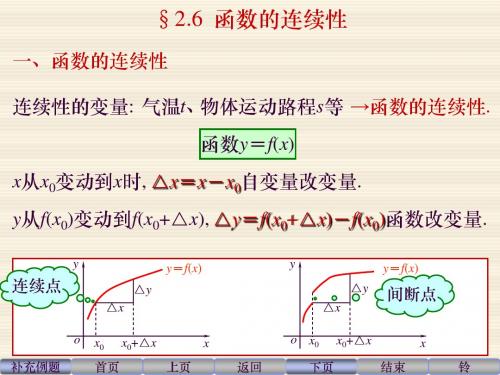
f ( x) f(x)+g(x),差f(x)-g(x),积f(x)·g(x),商 ,在点x0处也连续. g( x)
定理: 定理:连续增(减)函数的反函数x=f -1(y) 是连续增(减)函数. 定理: 定理:一切初等函数在其定义区间内都是连续的.
y
y=f(x)
f (ξ1)≥f(x)
f (ξ2)≤f(x)
o a 上页
(a≤x≤b)
补充例题 首页
ξ1
返回
ξ2
b 下页
x
(a≤x≤b)
结束 铃
§2.6 函数的连续性
四、在闭区间上连续函数的性质 定理(介值定理) 定理(介值定理):设函数f(x)在闭区间[a,b]上连续,且在这 区间的端点取不同的函数值f (a)=A与f (b)=B,那么不 论C是A与B之间怎样一个数,在开区间(a,b)内至少有一 个点,使得f(ξ)=C.
定理: 定理:连续增(减)函数的反函数x=f -1(y) 是连续增(减)函数. 定理: 定理:一切初等函数在其定义区间内都是连续的. 计算初等函数极限的方法: 如果f(x)是初等函数,且x0是其定义域内的一点,则有
x→x0
lim f ( x) = f ( x0 )
返回
补充例题
首页
上页
下页Βιβλιοθήκη 结束铃§2.6 函数的连续性
∆ → x 0
y lim ∆ = 0
x→x0
lim f ( x) = f ( x0 )
例: 证明线性函数y=ax+b在(-∞,+∞)内连续,并求x0点的极限.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(1) lim n→∞
( −2 )n ( −2 )n+1
+ 3n + 3n+1
=
lim
n→∞
⎛ ⎜⎝
−
2 3
⎞n ⎟⎠
+1
( −2 )
⋅
⎛ ⎜⎝
−2 3
⎞n ⎟⎠
+
3
=
1 3
;
(2)
lim
n→∞
⎛⎜⎝1 −
1 22
⎞ ⎟⎠
⎛⎜⎝1 −
1 32
⎞⎟⎠ "⎛⎜⎝1 −
1 n2
⎞ ⎟⎠
x⋅ 1 x2 2 x3
=
1 2
;
(2)
lim
x→2
sin ( x − 2)
x2 − 4
=
lim
x→2
sin ( x − 2) (x − 2)
⋅
x
1 +
2
=
1 4
;
(3)
lim
x→∞
⎛ ⎜⎝
x − 2 ⎞x x ⎟⎠
=
lim
x→∞
⎛⎜⎝1
−
2
⎞
−
x 2
⋅(
−2)
x ⎟⎠
=
e−2 ;
(4)
lim
x→∞
1
( ) 3.(1) lim f x→0−
x
=
lim
x→0−
1+
ex
1
= 1;
1− ex
−1
( ) (2) lim f x→0+
x
=
lim
x→0+
ex
−1
+1
=
−1 ;
e x −1
(3) lim f ( x) ≠ lim f ( x) ,故 lim f ( x) 不存在.
x→0−
x→0+
x→0
1.(1) lim x→0
x→0
x
x→0
x
x→0
x
6. 令 F ( x) = f ( x) − f ( x + π ) ,则 F ( x) ∈C [0,π ]
F (0) = f (0) − f (π ) , F (π ) = f (π ) − f (2π ) = f (π ) − f (0) 若 f (0) = f (π ) ,则ξ = 0 或ξ = π ,结论显然成立; 若 f (0) ≠ f (π ) , 则 F (0) ⋅ F (π ) < 0 , 由 零 点 定 理 , 至 少 存 在 ξ ∈(0,π ) , 使 F (ξ ) = 0 .
1+ x −1
2⋅1 x = lim 2 = 1
x→0+
x→0+
x
x x→0+
f (0− ) = lim f ( x) = lim sin x = 1
x→0−
x x→0−
f (0+ ) = f (0− ) = f (0) ,则 f ( x) 在 x = 0 连续
所以 f ( x) 在 (−∞, +∞) 内连续.
tan (2x) ⋅ ln (1+ x) sin (3x) ⋅arctan (2x)
=
lim
x→0
2x⋅ x 3x ⋅2x
=
1 3
;
( ) (2) lim 2 − 1+ cos x = lim
1− cos x
= 1⋅ 1 = 2 ;
x→0
sin2 x
x x→0 2 2 + 1+ cos x 2 2 2 8
(3)
lim
x→0
1
−
cos (sin
x2
x)
=
lim
x→0
1 2
sin 2 x2
x
=
1 2
.
2. f (0+ ) = lim f ( x) = lim ln (1+ 2x) = 2
x→0+
x→0+
x
( ) f 0− = lim f ( x) = lim a + x − a − x = lim
2
=1
+1
=
lim
x→−1
2−x x2 − x +1
=
1.
( ) 2. 由 lim ax + b − 2 = 1,得 lim ax + b − 2 = 0 ,即 b − 2 = 0 ⇒ b = 4 ,
x→0
x
x→0
又由 lim ax + 4 − 2 = lim
a
= a =1⇒ a = 4.
x→0
x
x→0 ax + 4 + 2 4
x→0−
x→0−
由 f ( x) 在 x = 0 连续,则有,即 a = 0时
f
( x) = sin x ,当 x > 0 时
f
2
(x) =
1+ x −1
均为初等函数,故
x
x
连续,
x = 0 f (0) =1
( ) ( ) 2
f 0+ = lim f ( x) = lim
n→∞ 1− r 1− r
( ) (4) lim x x +1 − x = lim
x = lim 1 = 1 ;
x→+∞
x→+∞ x +1 + x x→+∞ 1+ 1 +1 2
x
( ) (5)
lim
x→−1
⎛ ⎜⎝
3 x3 +1
−
1⎞ x +1 ⎟⎠
=
lim
x→−1
(x
2+
+ 1)
x − x2 x2 − x
x→1+
x→1+
x→1−
x→1−
f (−1+ ) = 1, f (−1− ) = −1
故 x = ±1 为第一类跳跃间断点.
( ) 3. f 0+ = lim f ( x) = lim x cos 1 = 0
x→0+
x→0+
x
f (0− ) = lim f ( x) = lim (a + x2 ) = a
lim f ( x) = 1 , lim f ( x) = 0 ,则 x = 1 为第一类跳跃间断点.
x→1+
x→1−
⎧x
2.
f
(
x
)
=
⎪ ⎨
0
⎪⎩− x
x < 1, x = 1, x > 1,
f (1+ ) = lim f ( x) = lim (−x) = −1, f (1− ) = lim f ( x) = lim x = 1
又因为 0
<
xn
≤ 10
,
{
xn
}
为有界数列,故
lim
n→∞
xn
存在且 lim n→∞
xn
≥
0
;
设 lim n→∞
xn
=
a
,则有
a=
6 + a ,即 a2 − a − 6 = 0 ,
解得
a
=
3或a
=
−2
(舍去),所以 lim n→∞
xn
=
3.
1. x = 0,1 无定义,即为间断点,
又 lim f ( x) = ∞ ,则 x = 0 为第二类无穷间断点; x→0
⎛ ⎜ ⎝
x2 x2
+ 1 ⎞x2
−
1
⎟ ⎠
=
lim
x→∞
⎛⎜⎝1
+
2 ⎞ x2 −1⋅2+1 2
x2 −1 ⎟⎠
= e2 .
2. x1 = 10 , x2 = 6 + x1 = 4 ,则 x2 < x1
设 n = k −1 时, xk < xk−1
则n = k 是
{ } xk+1 = 6 + xk < 6 + xk−1 = xk ,所以 xn 是单调递减的数列;
5. lim ln (1+α x) = α ;
x→0
x
(2) lim sin
x − sin a
=
lim
2 cos
x + a sin 2
x−a 2
=
cos a ;
x→a x − a
x→a
x−a
( ) (3) lim eαx − eβx
eβ x = lim
e(α −β )x −1
= lim eβx (α − β ) x = α − β .
x→0−
x→0−
x
x→0− a + x + a − x a
( ) ( ) 由 lim f ( x) 存在,即 f 0+ = f 0− ⇒ 1 = 2 ,得 a = 1 .
x→0
a
4
1.(1) lim x→0
tan x − sin x3
x
=
sin lim
x→0
x (1− cos x)
x3 cos x
= lim x→0
= lim 1 ⋅ 3 ⋅ 2 ⋅ 4 ⋅ 3 ⋅ 5 " n −1 ⋅ n +1 n→∞ 2 2 3 3 4 4 n n
=
lim
n→∞
1 2
⎛⎜⎝1 +
