第二章极限习题及答案：函数的连续性
高等数学函数极限与连续习题及答案
1、函数
()12
++=x x
x f 与函数()11
3--=x x x g 相同．
错误 ∵当两个函数的定义域和函数关系相同时，则这两个函数是相同的。
∴()12
++=x x x f 与()11
3--=x x x g 函数关系相同，但定义域不同，所以()x f 与
()x g 是不同的函数。
2、如果()M x f >（M 为一个常数），则()x f 为无穷大．
错误 根据无穷大的定义，此题是错误的。 3、如果数列有界，则极限存在．
错误 如：数列()n n x 1-=是有界数列，但极限不存在 4、a a n n =∞
→lim ，a a n n =∞
→lim ．
错误 如：数列()n n a 1-=，1)1(lim =-∞
→n n ，但n n )1(lim -∞
→不存在。
5、如果()A x f x =∞
→lim ，则()α+=A x f （当∞→x 时，α为无穷小）．
正确 根据函数、极限值、无穷小量的关系，此题是正确的。 6、如果α～β，则()α=β-αo ．
正确 ∵1lim =α
β
，是
∴01lim lim =⎪⎭
⎫
⎝⎛-=-αβαβα，即βα-是α的高阶无穷小量。 7、当0→x 时，x cos 1-与2x 是同阶无穷小．
正确 ∵2122sin 412lim 2sin 2lim cos 1lim
2
02
2020=⎪⎪⎪⎪⎭
⎫ ⎝⎛⋅⋅==-→→→x x x x x x x x x 8、 01
sin lim lim 1sin lim 000=⋅=→→→x
x x x x x x ．
错误 ∵x
x 1
sin lim 0→不存在，∴不可利用两个函数乘积求极限的法则计算。
高数极限习题及答案
练习题
1. 极限
x
x x x x x x x x
x x x x x x 1lim
)4(1
1lim
)3(15
86
5lim )2(31lim )1(2
3
1
2
2
32
---+-+-+++-∞
→→→∞→
(5) 已知011lim 2
=⎪⎪⎭
⎫
⎝⎛--++∞→b ax x x x , 求常数a , b .
(6) x x x x sin 1sin lim 20→ (7) 211lim 22x x x x ⎪⎪⎭⎫
⎝⎛+-∞
→
(8) x
x x
21lim 0
-→ (9)
x x x sin )
31ln(lim 0-→
(10)
⎪⎪⎭⎫
⎝⎛-∞→1lim 1
x
x e x
2. 函数的连续性
(1) 确定b 的值, 使函数
⎩
⎨⎧<≥+==-00
2)(1
x e x b x x f y x 在x =0点连续.
(2) 确定a , b 的值, 使函数
1
lim
)(22
1
2+-+==-∞
→n
n n x bx
ax x
x f y 在整个实数轴上连续.
(3) 讨论下列函数的连续性, 并判断其间断点的类型.
①
x x x f s i n )(=
② ⎪⎪⎩⎪⎪⎨⎧
=≠+-=00
01212)(1
1x x x f x
x
3. 连续函数的性质 (1) 设
1)(1
-+++=-x x
x x f n n ,
证明：
)(x f 有一个不大于1的正根.
(2) 若),()(∞+-∞∈C x f , 且A x f x =∞
→)(lim , 证明: ),()(∞+-∞在x f 内有界.
提高
1º),()(∞+-∞在x f 内至少有一个最值存在. 2º 对于最值与A 间的任意值C , 存在21,ξξ, 使得
函数极限与连续习题(含答案)
基本初等函数是实变量或复变量的指数函数、对数函数、幂函数、三角函数和反三角函数经过有限次四则运算及有限次复合后所构成的函数类。
函数的极限与连续训练题
1、 已知四个命题：（1）若)(x f 在0x 点连续，则)(x f 在0x x →点必有极限
（2）若)(x f 在0x x →点有极限，则)(x f 在0x 点必连续
（3）若)(x f 在0x x →点无极限，则)(x f 在0x x =点一定不连续
（4）若)(x f 在0x x =点不连续，则)(x f 在0x x →点一定无极限。
其中正确的命题个数是（ B ） A 、1 B 、2 C 、3 D 、4
2、若a x f x x =→)(lim 0
，则下列说法正确的是（ C ） A 、)(x f 在0x x =处有意义 B 、a x f =)(0
C 、)(x f 在0x x =处可以无意义
D 、x 可以只从一侧无限趋近于0x
3、下列命题错误的是（ D ）
A 、函数在点0x 处连续的充要条件是在点0x 左、右连续
B 、函数)(x f 在点0x 处连续，则)lim ()(lim 0
0x f x f x x x x →→= C 、初等函数在其定义区间上是连续的 D 、对于函数)(x f 有)()(lim 00
x f x f x x =→ 4、已知x x f 1)(=，则x
x f x x f x ∆-∆+→∆)()(lim 0的值是（ C ） A 、21x B 、x C 、21x - D 、x - 5、下列式子中，正确的是（ B ）
A 、1lim 0=→x x
函数极限与连续习题(含答案)
基本初等函数是实变量或复变量的指数函数、对数函数、幂函数、三角函数和反三角函数经过有限次四则运算及有限次复合后所构成的函数类。
函数的极限与连续训练题
1、 已知四个命题：（1）若)(x f 在0x 点连续，则)(x f 在0x x →点必有极限
（2）若)(x f 在0x x →点有极限，则)(x f 在0x 点必连续
（3）若)(x f 在0x x →点无极限，则)(x f 在0x x =点一定不连续
（4）若)(x f 在0x x =点不连续，则)(x f 在0x x →点一定无极限。
其中正确的命题个数是（ B ） A 、1 B 、2 C 、3 D 、4
2、若a x f x x =→)(lim 0
，则下列说法正确的是（ C ） A 、)(x f 在0x x =处有意义 B 、a x f =)(0
C 、)(x f 在0x x =处可以无意义
D 、x 可以只从一侧无限趋近于0x
3、下列命题错误的是（ D ）
A 、函数在点0x 处连续的充要条件是在点0x 左、右连续
B 、函数)(x f 在点0x 处连续，则)lim ()(lim 0
0x f x f x x x x →→= C 、初等函数在其定义区间上是连续的 D 、对于函数)(x f 有)()(lim 00
x f x f x x =→ 4、已知x x f 1)(=，则x
x f x x f x ∆-∆+→∆)()(lim 0的值是（ C ） A 、21x B 、x C 、21x - D 、x - 5、下列式子中，正确的是（ B ）
A 、1lim 0=→x x
函数的连续性的例题与习题
函数的连续性的例题与习题
函数连续性这个内容所涉及到的练习与考试题目，大致有3大类。第一类是计算或证明连续性；第二类是对间断点（或区间）的判断，包括间断点的类型；第三类是利用闭区间上的连续函数的几个性质（最值性质，零点存在性质），进行理论分析。
下面就这三大类问题，提供若干例题和习题。还是那句老话：看到题目不要看解答，而是先思考先试着做！这是与看文学小说的最大区别。
要提醒的是，例题里有不少是《函数连续性（一）（二）》中没有给出解答的例题，你事先独立做了吗？如果没有做，是不会做好是根本不想做，还是没有时间？
一．函数的连续
例（例（一），这个序号值的是《函数连续性（一）中的例题号，请对照）
设()f x 满足()()()f x y f x f y +=+，且()f x 在0x =连续。证明：()f x 在任意点x 处连续。 分析：证明题是我们很多同学的软肋，不知道从何下手。其实，如果你的基本概念比较清晰，证明题要比计算题号做，因为它有明确的方向，不像计算题，不知道正确的答案是什么
在本题里，要证的是“()f x 在任意点x 处连续”，那么我们就先固定一个点x ，用函数连续的定义来证明在x 处连续。你可能要问：函数连续的定义有好几个，用哪一个? 这要看已知条件，哪个容易用，就用那一个。在本题中，提供了条件()()()f x y f x f y +=+，也就是()()()f x y f x f y +-=，你的脑海里就要想到，如果设y x =∆，那么就有 ()()()y f x x f x f x ∆=+∆-=∆；这个时候，你应该立即“闪过”，要用题目给的第二个条件了：()f x 在0x =连续！它意味着：0
第二章极限习题及答案：函数的连续性
分段函数的极限和连续性
例 设⎪⎪⎩⎪⎪⎨⎧<<=<<=)
21( 1)1( 21
)10( )(x x x x x f
（1）求）x f (在点1=x 处的左、右极限，函数）x f (在点1=x 处是否有极限？ （2）函数）x f (在点1=x 处是否连续？ （3）确定函数）x f (的连续区间．
分析：对于函数）x f (在给定点0x 处的连续性，关键是判断函数当0x x →时的极限是否等于)(0x f ；函数在某一区间上任一点处都连续，则在该区间上连续．
解：（1）1lim )(lim 1
1
==-
-
→→x x f x x
11lim )(lim 1
1
==++→→x x x f
∴1)(lim 1
=→x f x
函数）x f (在点1=x 处有极限． （2）)(lim 2
1)1(1
x f f x →≠=
函数）x f (在点1=x 处不连续．
（3）函数）x f (的连续区间是（0，1），（1，2）．
说明：不能错误地认为)1(f 存在，则）x f (在1=x 处就连续．求分段函数在分界点0
x 的左右极限，一定要注意在分界点左、右的解析式的不同．只有
)(l i m ),(lim )(lim 0
x f x f x f x x x x x x →→→+-=才存在．
函数的图象及连续性
例 已知函数2
4)(2
+-=
x x x f ，
（1）求）x f (的定义域，并作出函数的图象； （2）求）x f (的不连续点0x ；
（3）对）x f (补充定义，使其是R 上的连续函数．
分析：函数）x f (是一个分式函数，它的定义域是使分母不为零的自变量x 的取值范围，给函数）x f (补充定义，使其在R 上是连续函数，一般是先求)(lim 0
第二章 极限与连续(五)
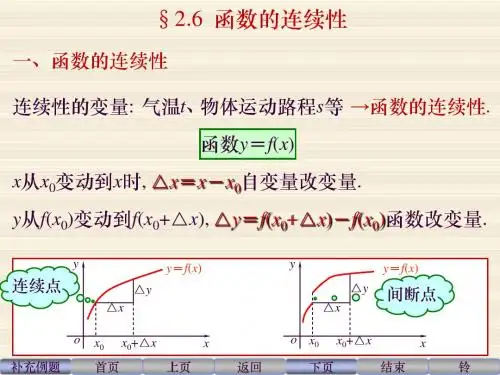
f ( x) f(x)+g(x),差f(x)－g(x),积f(x)·g(x),商 ,在点x0处也连续. g( x)
外,在其它点都连续.
例: 考察y＝tan x及y＝cot x的连续性.
例:
lim ln(sin x) π = lnsin = 0 2
结束 铃
x→ 2
求 lim ln(sin x)
x→ 2
π
ln(sinx)在(0,π)内 有定义且连续, π/2∈ (0,π).
上页 返回 下页
π
补充例题
首页
§2.6 函数的连续性
四、在闭区间上连续函数的性质 定理: 定理 : 如果函数y＝f(x)在闭区间[a,b]上连续,则f(x)在这 个闭区间上有界. 定理(最大值与最小值定理): 定理(最大值与最小值定理):在闭区间[a,b]上的连续函数 f(x)一定有最大值和最小值.
间断点
x 结束 铃
x0+△x 上页
§2.6 函数的连续性
一、函数的连续性 函数连续的定义2: 函数连续的定义2:设函数y＝f(x)在点x0的某个邻域内有定 义.如果函数f(x)当x→x0时的极限存在,且等于它在点x0处 的函数值f(x0),即
第二章 极限与连续 习题及答案
第二章 极限与连续
一、填空 1、⎪⎭
⎫
⎝
⎛+→x x x x x sin 11sin
lim 0
= 。 2、)arcsin(lim 2
x x x x -++∞
→= 。
3、n
n n n 1sin
)1()
12(531lim
3
+-+++∞→ = 。
4、[]x
x x 20
)1ln(1lim ++→= 。
5、设()x f x 1
lim →存在，且()()x f x x x f x 12
lim 2→+=，则()x f x 1
lim →= 。
6、设x
x x k x 2)(
lim -∞
←-=x
x x 2sin lim ∞→ ，则k= .
7、设3)
1sin(lim 221=-++→x b
ax x x ，则a = ,b = .
8、当0→x 时，x x sin 1tan 1--+∽
k
x 4
1，则k = 。 9、如果函数()⎪⎩⎪⎨⎧=<<+-=0
10)11(1x a
x x
x x f x
在其定义域上连续，则a = 。 10、函数2
31
22+--=x x x y 的间断点为 ，其中可去间断点为 ，
补充定义 使其连续。 二、选择
1、下列命题正确的是（ ）
A 、无限多个无穷小之和仍是无穷小。
B 、两个无穷大的和仍是无穷大
C 、无穷大与有界变量（但不是无穷小）的乘积一定是无穷大。
D 、两个无穷大的积仍是无穷大。
2、已知x
e x
f 1)(=，则x =0是函数的（ ）
A 、无穷型间断点
B 、跳跃间断点
C 、可去间断点
D 、其它类型间断点
3、x x ln arctan sin lim 0
+
→=（ ） A 、1 B 、-1 C 、0 D 、不存在
第二章7函数的连续性
f (0 0) f (0) a
内容小结
在点 连续的等价形式
在点
左连续 间断的类型
可去间断点 跳跃间断点 无穷间断点 振荡间断点
右连续
第一类间断点 第二类间断点
左右极限都存在
左右极限至少有一 个不存在
连续函数的运算与 初等函数的连续性
一、连续函数的运算法则
二、初等函数的连续性
第二章
一、连续函数的运算法则
定理3可修改为下面求复合函数极限的定理 定理4 （复合函数求极限） lim ( x) a, 但 若函数 在点 x0 有极限，即 x x
x x0
a ( x0 ), 或者
在点 x0 无定义(即 x0 是可去间断点)
0
又函数 f (x)点 a 连续，则复合函数 f [ ( x)] 在点 x0 的极限存在，且为 lim f [ ( x)] f [ lim ( x)] f (a ) 若函数 f (x) 连续，则∣f (x) ∣一定连续. 反之，若∣f (x) ∣连续，函数 f (x)不一定连续. x 为有理数 x 为无理数 是由连续函数链 例如,
§2.8 函数的连续性
一、 函数连续性的定义 二、 函数的间断点
第二章
现实世界中很多变量是连续不断的.如气温、时间、 物体的运动等等，都是连续变化的. 这种现象反映在数学上就是连续性， 函数的连续性是微积分的又一重要概念！
函数极限与连续习题(含答案)
基本初等函数是实变量或复变量的指数函数、对数函数、幂函数、三角函数和反三角函数经过有限次四则运算及有限次复合后所构成的函数类。
函数的极限与连续训练题
1、 已知四个命题：（1）若)(x f 在0x 点连续，则)(x f 在0x x →点必有极限
（2）若)(x f 在0x x →点有极限，则)(x f 在0x 点必连续
（3）若)(x f 在0x x →点无极限，则)(x f 在0x x =点一定不连续
（4）若)(x f 在0x x =点不连续，则)(x f 在0x x →点一定无极限。
其中正确的命题个数是（ B ） A 、1 B 、2 C 、3 D 、4
2、若a x f x x =→)(lim 0
，则下列说法正确的是（ C ） A 、)(x f 在0x x =处有意义 B 、a x f =)(0
C 、)(x f 在0x x =处可以无意义
D 、x 可以只从一侧无限趋近于0x
3、下列命题错误的是（ D ）
A 、函数在点0x 处连续的充要条件是在点0x 左、右连续
B 、函数)(x f 在点0x 处连续，则)lim ()(lim 0
0x f x f x x x x →→= C 、初等函数在其定义区间上是连续的 D 、对于函数)(x f 有)()(lim 00
x f x f x x =→ 4、已知x x f 1)(=，则x
x f x x f x ∆-∆+→∆)()(lim 0的值是（ C ） A 、21x B 、x C 、21x - D 、x - 5、下列式子中，正确的是（ B ）
A 、1lim 0=→x x
高等数学函数的极限与连续习题精选及答案
1、函数
()12
++=x x x f 与函数()11
3--=x x x g 相同．
错误 ∵当两个函数的定义域和函数关系相同时，则这两个函数是相同的。 ∴
()12
++=x x x f 与()113--=
x x x g 函数关系相同，但定义域不同，所以()x f 与()
x g 是不同的函数。
2、如果()M x f >（M 为一个常数），则()x f 为无穷大． 错误 根据无穷大的定义，此题是错误的。
3、如果数列有界，则极限存在．
错误 如：数列()n
n x 1-=是有界数列，但极限不存在
4、a a n n =∞
→lim ，a a n n =∞
→lim ．
错误 如：数列()n
n a 1-=，1)
1(lim =-∞
→n
n ，但n n )1(lim -∞
→不存在。
5、如果()A x f x =∞
→lim ，则()α+=A x f （当∞→x 时，α为无穷小）． 正确 根据函数、极限值、无穷小量的关系，此题是正确的。 6、如果α～β，则()α=β-αo ．
正确 ∵1lim
=α
β
，是 ∴01lim lim =⎪⎭
⎫
⎝⎛-=-αβαβα，即βα-是α的高阶无穷小量。 7、当0→x 时，x cos 1-与2
x 是同阶无穷小．
正确 ∵2122sin 412lim 2sin 2lim cos 1lim
2
02
2020=⎪⎪⎪⎪⎭
⎫ ⎝⎛⋅⋅==-→→→x x x x x x x x x 8、 01
sin lim lim 1sin lim 000=⋅=→→→x
x x x x x x ．
错误 ∵x
x 1
sin lim 0→不存在，∴不可利用两个函数乘积求极限的法则计算。
函数极限与连续习题(含答案)
基本初等函数是实变量或复变量的指数函数、对数函数、幂函数、三角函数和反三角函数经过有限次四则运算及有限次复合后所构成的函数类。
函数的极限与连续训练题
1、 已知四个命题：（1）若)(x f 在0x 点连续，则)(x f 在0x x →点必有极限
（2）若)(x f 在0x x →点有极限，则)(x f 在0x 点必连续
（3）若)(x f 在0x x →点无极限，则)(x f 在0x x =点一定不连续
（4）若)(x f 在0x x =点不连续，则)(x f 在0x x →点一定无极限。
其中正确的命题个数是（ B ） A 、1 B 、2 C 、3 D 、4
2、若a x f x x =→)(lim 0
，则下列说法正确的是（ C ） A 、)(x f 在0x x =处有意义 B 、a x f =)(0
C 、)(x f 在0x x =处可以无意义
D 、x 可以只从一侧无限趋近于0x
3、下列命题错误的是（ D ）
A 、函数在点0x 处连续的充要条件是在点0x 左、右连续
B 、函数)(x f 在点0x 处连续，则)lim ()(lim 0
0x f x f x x x x →→= C 、初等函数在其定义区间上是连续的 D 、对于函数)(x f 有)()(lim 00
x f x f x x =→ 4、已知x x f 1)(=，则x
x f x x f x ∆-∆+→∆)()(lim 0的值是（ C ） A 、21x B 、x C 、21x - D 、x - 5、下列式子中，正确的是（ B ）
A 、1lim 0=→x x
《高等数学一》第二章 极限与连续 历年试题模拟试题课后习题(汇总)(含答案解析)
第二章极限与连续
[单选题]
1、
若x0时，函数f(x)为x2的高阶无穷小量，则=（）
A、0
B、
C、1
D、∞
【从题库收藏夹删除】
【正确答案】 A
【您的答案】您未答题
【答案解析】
本题考察高阶无穷小.
根据高阶无穷小的定义，有.
[单选题]
2、
与都存在是函数在点处有极限的（）.
A、必要条件
B、充分条件
C、充要条件
D、无关条件
【从题库收藏夹删除】
【正确答案】 A
【您的答案】您未答题
【答案解析】
时，极限存在的充分必要条件为左、右极限都存在并且相等，所以若函数在点处有极限，则必有与都存在.但二者都存在，不一定相等，所以不一定有极限.
[单选题]
3、
（）.
A、
B、1
C、
D、0
【从题库收藏夹删除】
【正确答案】 A
【您的答案】您未答题
【答案解析】
[单选题]
4、
如果则（）.
A、0
B、1
C、2
D、5
【从题库收藏夹删除】
【正确答案】 D
【您的答案】您未答题
【答案解析】
根据重要极限,
[单选题]
5、
（）.
A、0
B、∞
C、2
D、-2
【从题库收藏夹删除】
【正确答案】 C
【您的答案】您未答题
【答案解析】
分子分母同除以，即
[单选题]
6、
（）.
A、0
B、∞
C、2
D、-2
【从题库收藏夹删除】
【您的答案】您未答题
【答案解析】
[单选题]
7、
设，则（）.
A、
B、2
C、
D、0
【从题库收藏夹删除】
【正确答案】 B
【您的答案】您未答题
【答案解析】
[单选题]
8、
当时，与等价的无穷小量是（）.
A、
B、
C、
D、
【从题库收藏夹删除】
【正确答案】 B
【您的答案】您未答题
由于故与等价,
推广，当时，
[单选题]
9、
时，与等价的无穷小量是（）. A、
B、
C、
高等数学 第二章 极限与连续 2.8 函数的连续性
则称函数 f (x)在 x0 连续. 否则，间断.
注意：函数 在点 x0 连续，必须同时具备下列条件：
(1)
在点 有定义，即
存在；
(2) 极限
存在；
(3)
定义2.14 若 在区间[a, b]上每一点都连续，则称 f (x)在[a, b]上连续，或称它是该区间上的连续函数.
注意：若 若
则称 f (x)在 x a处左连续； 则称 f (x)在 x b处右连续。
y y1 y x x2 x2 2x x x2.
注意：函数的改变量可以为正，也可以为负。
二、连续函数的概念
定义2.12 设函数y=f (x)在 U(x0 , ) 有定义。若当x在 x0
处取得该变量 x (x 0) 时，有
lim y lim
x0
x0
f (x0 x) f (x0 )
等价定义：设函数 y= f (x) U (x0, ) 有定义，若自变量x 从 x0 改变到在x0 x (x 0)，则函数 y 的改变量为
y f (x0 x) f (x).
函数的增量
y
y f (x)
y
y
y f (x)
y
x
x
0 x0 x0 x x 0 x0 x0 x x
例1 设正方形边长为x，求边长改变量为Δx 时， 面积的增量。
很显然，
高数极限习题测验及答案
练习题
1. 极限
x
x x x x x x x x
x x x x x x 1lim
)4(1
1lim
)3(15
86
5lim )2(31lim )1(2
3
1
2
2
32
---+-+-+++-∞
→→→∞→
(5) 已知011lim 2
=⎪⎪⎭
⎫
⎝⎛--++∞→b ax x x x , 求常数a , b .
(6) x x x x sin 1sin lim 20→ (7) 211lim 22x x x x ⎪⎪⎭⎫
⎝⎛+-∞
→
(8) x
x x
21lim 0
-→ (9)
x x x sin )
31ln(lim 0-→
(10)
⎪⎪⎭⎫
⎝⎛-∞→1lim 1
x
x e x
2. 函数的连续性
(1) 确定b 的值, 使函数
⎩
⎨⎧<≥+==-00
2)(1
x e x b x x f y x 在x =0点连续.
(2) 确定a , b 的值, 使函数
1
lim
)(22
1
2+-+==-∞
→n
n n x bx
ax x
x f y 在整个实数轴上连续.
(3) 讨论下列函数的连续性, 并判断其间断点的类型.
①
x x
x f sin )(=
② ⎪⎪⎩⎪⎪⎨⎧
=≠+-=00
01212)(1
1
x x x f x
x
3. 连续函数的性质 (1) 设
1)(1
-+++=-x x
x x f n n ,
证明：
)(x f 有一个不大于1的正根.
(2) 若),()(∞+-∞∈C x f , 且A x f x =∞
→)(lim , 证明: ),()(∞+-∞在x f 内有界.
提高
1º),()(∞+-∞在x f 内至少有一个最值存在. 2º 对于最值与A 间的任意值C , 存在21,ξξ, 使得
经济数学(极限与连续习题及答案)——习题集资料文档
第二章 函数的极限与连续
习题 2－1
1.写出下面数列的前5项，并观察当n —>∞时，哪些数列有极限，极限为多少? 哪些数列没有极限.
{}{}{}{}{}
{}{}211(1) 1 (2) 21(3) (4) (1)11(1)(5) sin (6) 2n n n n
n n n n n n x x n n x x n
n x x n π⎧⎫-⎪⎪⎧
⎫=-=⎨⎬⎨⎬
⎩⎭⎪⎪⎩⎭
-⎧⎫==-⎨⎬+⎩⎭
⎧⎫+-⎪⎪⎧⎫
==⎨⎬⎨⎬
⎩⎭⎪⎪⎩⎭
解 （1）3231
,1615 ,87 ,43 ,21 有极限 , 极限为 1.
(2)
524
,415 ,38 ,23 ,0 没有极限. (3)
64
,53 ,42 ,31 0, 有极限 , 极限为 1. (4) －1, 2, －3, 4, －5 没有极限.
(5)
5sin
,4sin ,3sin ,2sin ,sin π
ππππ, 有极限 , 极限为 0 . (6) 0, 1, 0 , 1, 0 没有极限 . 2. 用极限的定义证明：
(1) 若k >0，则 1lim
0k
n n →∞=
n 212
(2) lim
313n n →∞+=+
解 (1) 因为对任给的ε> 0，要使不等式
110(0)k k
k n n ε-=<>
11
().
k n ε>即便可
所以对任给的ε> 0, 取正整数 N =
1
1
[()]1
k
ε
+ , 则当n >N 时, 就
恒有 1
0k n ε-<
故由数列极限的定义知, 1
lim
0k
n n →∞=.
(2) 因为对任给的ε > 0, 不妨设
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
函数的连续性
分段函数的极限和连续性
例 设⎪⎪⎩⎪⎪⎨⎧<<=<<=)
21( 1)1( 21
)10( )(x x x x x f
（1）求）x f (在点1=x 处的左、右极限，函数）x f (在点1=x 处是否有极限？ （2）函数）x f (在点1=x 处是否连续？ （3）确定函数）x f (的连续区间．
分析：对于函数）x f (在给定点0x 处的连续性，关键是判断函数当0x x →时的极限是否等于)(0x f ；函数在某一区间上任一点处都连续，则在该区间上连续．
解：（1）1lim )(lim 1
1
==-
-
→→x x f x x
11lim )(lim 1
1
==++→→x x x f
∴1)(lim 1
=→x f x
函数）x f (在点1=x 处有极限． （2）)(lim 2
1)1(1
x f f x →≠=
函数）x f (在点1=x 处不连续．
（3）函数）x f (的连续区间是（0，1），（1，2）．
说明：不能错误地认为)1(f 存在，则）x f (在1=x 处就连续．求分段函数在分界点0x 的左右极限，一定要注意在分界点左、右的解析式的不同．只有)(lim ),(lim )(lim 0
x f x f x f x x x x x x →→→+
-
=才存在．
函数的图象及连续性
例 已知函数2
4)(2
+-=
x x x f ，
（1）求）x f (的定义域，并作出函数的图象；
（2）求）x f (的不连续点0x ；
（3）对）x f (补充定义，使其是R 上的连续函数．
分析：函数）x f (是一个分式函数，它的定义域是使分母不为零的自变量x 的取值范围，给函数）x f (补充定义，使其在R 上是连续函数，一般是先求)(lim 0
x f x x →，再让)(lim )(0
0x f x f x x →=即可．
解：（1）当02≠+x 时，有2-≠x ． 因此，函数的定义域是()()+∞--∞-,22,
当2≠x 时，.22
4)(2
-=+-=x x x x f
其图象如下图．
（2）由定义域知，函数）x f (的不连续点是20-=x ． （3）因为当2≠x 时，2)(-=x x f 所以4)2(lim )(lim 2
2
-=-=-→-→x x f x x
因此，将）x f (的表达式改写为
⎪⎩
⎪
⎨⎧-=--≠+-=)2(4)2(2
4
)(2x x x x x f 则函数）x f (在R 上是连续函数．
说明：要作分式函数的图象，首先应对函数式进行化简，再作函数的图象，特别要注意化简后的函数与原来的函数定义域是否一致．
利用函数图象判定方程是否存在实数根
例 利用连续函数的图象特征，判定方程01523
=+-x x 是否存在实数根．
分析：要判定方程0)(=x f 是否有实根，即判定对应的连续函数)(x f y =的图象是否与x 轴有交点，因此只要找到图象上的两点，满足一点在x 轴上方，另一点在x 轴下方即可． 解：设152)(3+-=x x x f ，则）x f (是R 上的连续函数．
又038)3(,1)0(<-=-=f f ，因此在[]0,3-内必存在一点0x ，使0)(0=x f ，所以0x 是方程
01523
=+-x x 的一个实根．
所以方程01523=+-x x 有实数根．
说明：作出函数)(x f y =的图象，看图象是否与x 轴有交点是判别方程0)(=x f 是否有实数根的常用方法，由于函数152)(3+-=x x x f 是三次函数，图象较难作出，因此这种方法对本题不太适用．
函数在区间上的连续性
例 函数2
4)(2
--=
x x x f 在区间（0，2）内是否连续，在区间[]2,0上呢？
分析：开区间内连续是指内部每一点处均连续，闭区间上连续指的是内部点连续，左点处右连续，右端点处左连续．
解：22
4)(2
+=--=
x x x x f （R ∈x 且2≠x ）
任取200< 0x f x x x f x x x x =+=+=→→ ∴ )(x f 在（0，2）内连续． 但)(x f 在2=x 处无定义，∴ )(x f 在2=x 处不连续． 从而)(x f 在[]2,0上不连线 说明：区间上的连续函数其图象是连续而不出现间断曲线． 函数在某一点处的连续性 例 讨论函数)0()11lim ()(+∞<≤⋅+-=∞ →x x x x x f n n n 在1=x 与2 1=x 点处的连续性 分析：分类讨论不仅是解决问题的一种逻辑方法，也是一种重要的数学思想． 明确讨论对象，确立分类标准，正确进行分类，以获得阶段性的结论，最后归纳综合得出结果，是分类讨论的实施方法．本题极限式中，若不能对x 以1为标准，分三种情况分别讨论，则无法获得)(x f 的表达式，使解 答搁浅． 讨论)(x f 在1=x 与2 1=x 点处的连续性，若作出)(x f 的图像，则可由图像的直观信息中得出结论，再据 定义进行解析论证． 由于)(x f 的表达式并非显式，所以须先求出)(x f 的解析式，再讨论其连续性，其中极限式中含n x ，故须分类讨论． 解：（1）求)(x f 的表达式： ①当1 x x f n n n n =⋅+-= ⋅+-= ∞ →∞ →0 101lim 1lim 1)( ②当1>x 时，x x x x x x f n n x -=⋅+-=⋅+-=∞→1 01 01)1(1 )1(lim )( ③当1=x 时，01 111lim )(=⋅+-=∞ →x x f n n x ∴⎪⎩ ⎪ ⎨⎧+∞<<-=<≤=x x x x x f 1,1,010,0)( （2）讨论)(x f 在1=x 点处的连续性： 1)(lim )(lim ,1lim )(lim 1 1 1 1 -=-===++→→-→-→x x f x x f x x x x ∴)(lim 1 x f x + →不存在，)(x f 在1=x 点处不连续 （3）讨论)(x f 在2 1=x 点处的连续性： 2 1lim )(lim ,2 1lim )(lim 2 12 12 12 1= == =-+--→ → → → x x f x x f x x x x 2 1lim )(lim ,2 1lim )(lim 2 12 12 12 1= == =-+--→ → → → x x f x x f x x x x ∴)2 1 (21 )(lim 2 1f x f x == → ，)(x f 在21=x 点处连续． 根据函数的连续性确定参数的值