数据融合报告_基于交互多模算法的机动目标跟踪
基于交互多模型的高机动群目标跟踪技术

( )群 航迹 的更 新 3
利 用 互 联 成 功 的量 测 和 目标 量 测 估 算 出群 的
中心和速度,从而完成群的航迹更新过程 。
单个量 测 的跟 踪 门
行外推,并以外推中心建立跟踪 门,与下个时刻落
入群 中的各量 测进 行互 联 ,从而 实现对 单 目标航 迹 的维持 。编 队群 目标 跟踪 算法 具有很 多优 点 ,如 节 省 了雷 达和计 算机 资源 ;可 以提 供单个 目标的估 计 位 置 ;减 小 了由量测丢 失和 虚假 量测所 造 成的 不 良 影 响 ;群跟 踪与 单个 目标跟 踪使 用 同一 跟踪 逻辑 。 考 虑 一组 由 m 个 目标 组成 的飞行 编 队的跟 踪
e e t es l t nt a e v r gg o p t c i g f c i ou i m n u e i r u a k n . v o o n r
Ke wo ds F r t n y r : omai Gr u T a kn Alo tm; Ma e v r g o o p rc ig grh i n u e n Gr u T res Itrcig i o p ag t; nea t Mut l Mo e; n lpe i dl
B r hlm 在 广 义 伪 贝 叶 斯算 法 的基 础 上提 出的 a a S o 种 具 有 Mak v 转 移 概 率 的 结构 自适 应 算 法 。 ro I MM 算法具 有一 阶广义 伪 贝叶斯 ( P )计算 上 G B1 的优 势 和二 阶广 义伪 贝叶 斯 ( P 2 G B )的 良好性 能 ,
骤如 下 :
2 基于交互 式多模型 的群 目标跟踪
基于 交 互式 多模 型 的编 队群 目标 跟踪 算 法
模型目标算法实验报告总结(3篇)

第1篇YOLOv11目标检测模型1. 模型介绍:YOLOv11是由Ultralytics公司开发的新一代目标检测算法,其在COCO数据集上实现了较高的平均精度(mAP)得分,同时参数数量比YOLOv8m少22%,计算效率更高。
2. 实验目的:本实验旨在实现一个目标检测方案,使用YOLOv11算法适配不同分辨率(超高、高、节能)的输入,并将其预处理为统一的640x640分辨率,以识别图片中的数字区域。
3. 实验方法:- 网络结构:对比YOLOv8和YOLOv11模型组成,分析核心模块和注意力模块的区别。
- 数据预处理:将不同分辨率的输入预处理为统一的640x640分辨率。
- 实验设置:设置实验参数,如迭代次数、采样间隔等。
- 实验效果:分析准确率、内存占用、功耗和推理时间等指标。
4. 实验结果:- 准确率:YOLOv11在COCO数据集上实现了较高的mAP得分。
- 内存占用:YOLOv11参数数量较少,计算效率高,内存占用较低。
- 功耗:由于计算效率高,YOLOv11的功耗较低。
- 推理时间:YOLOv11的推理时间较短。
基于EKF的目标跟踪实例1. 模型介绍:该实例实现了基于IMM算法的目标跟踪,使用三种不同的运动模型(匀速直线运动、左转弯和右转弯)来预测目标的位置,并通过卡尔曼滤波进行状态估计。
2. 代码介绍:- 使用MATLAB编写代码,实现基于IMM算法的目标跟踪。
- 代码包含仿真参数设置、模型量测矩阵、模型过程噪声加权矩阵等。
3. 实验结果:- 通过仿真验证了IMM算法在目标跟踪中的有效性。
总结YOLOv11和基于EKF的目标跟踪实例都是计算机视觉领域中的重要技术。
YOLOv11在目标检测方面具有较高的准确率和计算效率,而基于EKF的目标跟踪实例在目标跟踪方面具有较高的精度。
这些技术在实际应用中具有广泛的应用前景。
第2篇一、实验背景随着人工智能技术的快速发展,模型目标算法在计算机视觉、机器人控制等领域得到了广泛应用。
基于神经网络的多机动目标跟踪算法

神 经 网络 数 据 关 联 算 法 ( NDA) J DA 的 基 在 P 础上 , 过对似 然矩 阵 的处理 , 够得 到有 效 的量测 通 能
与 目标 的对应 关 系 即最 佳 关联 假 设 , 时还 具 备 了 同 跟 踪起始 和 终结 的 作 用 , 大减 少 了 计算 量 。基 于 大 N DA算 法得 到的最 佳关 联假 设 , 将简 化信 息融合 并 行 自适 应滤波 算法 与该 关联 算法 结合 进行 多机 动 目 标 的状 态滤波 与 预 测 , 保证 了对 多 机 动 目标 的 跟踪
维普资讯
2 0 年 1 月 06 0
西 北 工 业 大 学 学 报
J u n lo rh se nPoy e h ia iest o r a fNo twe tr l tc nc lUnv riy
OC . t
20 06
第 2 卷第 5 4 期
算 法
在 多 目标 跟 踪 问题 中 , 定所 获 得 的量 测与 对 确
收 稿 日期 :0 50 —9基 金 项 目 : 空 基 础 科 学 基 金 (5 3 2 ) 2 0 —90 航 0D5 O 1 和西 北 工 业 大 学 电子 信 息 学 院 研 究 生 创 新 实 验 室 资 助 作者简介 : 李 辉 (9 8 )西 北 工 业 大 学 副教 授 , 要从 事 通 信 信 号 及 雷 达 数 据 处 理 的 研 究 。 16 一 , 主
方法 基础 上引 入神 经 网络 。 主要 思想 是 , 正时 刻 其 在
找 出一 个关 联 概率 最 大 的量 测 去更新 对应 目标 的状
态 , 他 目标状 态 的更 新 与该 量 测和 目标 无关 。显 其 然 , 有 2个 或多 个量 测 与给定 目标 关联 概率相 同 , 若
基于IMM-MHT算法的杂波环境多机动目标跟踪

基于IMM-MHT算法的杂波环境多机动目标跟踪邵俊伟;同伟;单奇【摘要】针对杂波环境下多机动目标的跟踪问题,提出将交互多模型(IMM)算法与多假设跟踪(MHT)算法结合,并运用Murty算法和假设树修剪方法进行假设生成和假设管理,提高IMM-MHT算法的实用性.仿真结果表明,IMM-MHT算法具有较高的正确关联率和较好的跟踪稳定性,且与只使用单模型的MHT算法相比,具有更好的跟踪精度.【期刊名称】《舰船电子对抗》【年(卷),期】2014(037)002【总页数】5页(P87-90,93)【关键词】数据关联;多假设跟踪;交互多模型【作者】邵俊伟;同伟;单奇【作者单位】中国电子科技集团公司第38研究所,合肥230088;陆军驻中电集团38所军事代表室,合肥230088;中国电子科技集团公司第38研究所,合肥230088【正文语种】中文【中图分类】TP957.510 引言随着战场环境的日趋复杂以及目标机动性能的日益提升,如何在杂波环境下跟踪机动目标正成为雷达数据处理系统要应对的关键问题之一。
传统数据关联算法,如最近邻[1](NN)、概率数据关联[2](PDA)、联合概率数据关联[3](JPDA)等,以当前扫描周期内的量测为基础进行数据关联,若某一扫描周期内的关联结果与真实情况有较大差别,则之后的跟踪过程常会发生错误,甚至丢失目标。
多假设跟踪[4](MHT)的关联结果不仅取决于当前扫描周期内的量测数据,而且还与历史量测信息有关。
对不能确定的关联,会形成多种逻辑假设,并用后续的量测数据来解决这种不确定性。
在理想条件下,MHT是最优的数据关联算法,可以有效地解决杂波环境下的数据关联问题。
但是,MHT算法所需的计算和存储资源会随着量测数和跟踪步数的增长呈指数增加,若要实际应用,还需要有效的假设管理技术。
对机动目标,以单一的运动模型来刻画其运动过程,往往和实际情况有偏差,最终会由于模型失配导致跟踪误差增大甚至跟踪失败。
基于SRCDKF的交互式多模型算法

meh d u h a F b sdI to ssc sEK ae MM g r h ,a d as v isc mp t gcmpiae a o imar .N me u nec r i l- l i a o tm n oa od o ui o l td Jc b tx u r smo t al smua l n c i o o
矩阵在传播过程 中的半正定性, 从而具有 良好的数值 稳定 性 。 本文结合上述方法 的优势, 针对非线性机动 目标 跟踪问题 , 提出了基于平方根 中心差分卡尔曼滤波器
计算 , 比 P 也 F方法 节约 了大量 运算 。根据 Sg a点选 im 取 的不 同 ,SK P F方法 主要 分 为 U setd卡尔 曼 滤波 ncne ( K ) 中心 差 分 卡 尔 曼 滤 波 ( D F) 而 C K U F和 CK , D F具
来代表系统所有可能的行为方式 , 基于每个模 型的滤 波器并行的工作 , 系统的整体估计则是各模型滤波器 所作估计的数据融合。 实 际跟踪 问题 中 , 测量 值多在 极坐 标系 下获得 , 而
多好 的方 法来解 决 此 问题 , 互 式多 模 型 方法 (MM) 交 I 综合了这些方法的优点 , 目前工程 中广泛应用 的方 是 法 之一 | J l 。该 方法 的主 要思想 是设 计一 系列 的模 型
的相关统计参量 , 从而避免了 E F K 方法 中 J oi a b 矩阵 c
XI Zh ng t A o —i WANG h n 。i W U ng ng, S e g l, Ya
( aj gR sac ntueo l t nc eh o g , N nig2 0 3 , hn ) N ni eer Istt f e r is c n l y n h i E co T o aj 10 9 C i n a
【国家自然科学基金】_交互式多模型_基金支持热词逐年推荐_【万方软件创新助手】_20140731
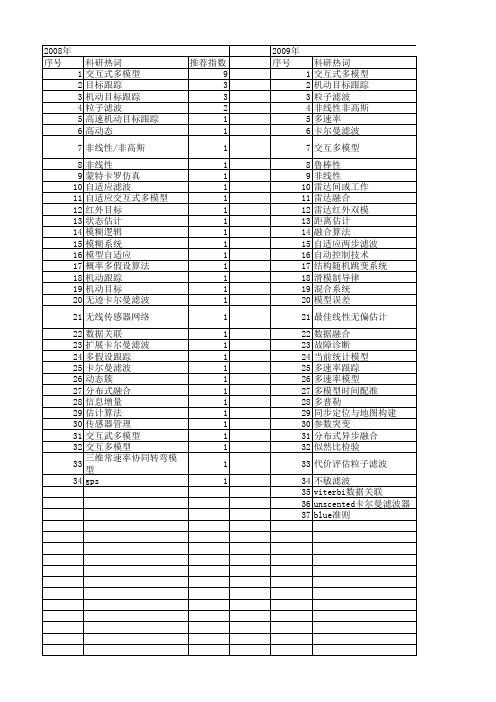
推荐指数 10 4 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
2011年 科研热词 机动目标跟踪 交互式多模型 粒子滤波 目标跟踪 多模型算法 高脉冲重复频率 马尔可夫参数 量测不确定 运动学分析 跟踪算法 距离模糊 融合算法 蒙特卡罗 自适应交互式多模型 脉冲间隔数 统计距离 累加弦长 算法 电子 混合滤波 有向图切换 无迹卡尔曼滤波 当前统计模型 弹道识别 平方根无迹卡尔曼滤波 导航 多模型交互 多传感器融合 多传感器组合导航 多传感器信息融合 声网络 场面监视雷达 噪声分布 后验信息 变结构多模型 双波段 农田地形 信息学 交互式多模型算法 交互式多模型滤波器 推荐指数 5 5 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
基于IMM多传感器顺序粒子滤波跟踪机动目标算法

, 衍生 出 I 并 MM
特点, 提出一种基于 I 的顺 序粒子 滤波算 法 , MM 进一 步提
取 和利用多量测 的冗余 和互补 信息 , 提高系统 状态估计 精
度
卡 尔 曼 一 子 滤 波 器 等 改 进 算 法 , 善 强 非 线 性 对 跟 踪 粒 改 精 度 的影 响 。
收 稿 日期 :0 1o _ 9 2 1_ 9 2
() 8 ( 9 )
上 即标准 I MM算 法 的基本 实现过程 。I 中各 个子 滤波 MM 器匹配粒子滤波算法就构成 I F滤波 器 , 滤波器可 以 MMP 此 有效处 理 系统 非线 性 和非 高斯 问 题。与 I MM算 法 相 比, I MMP F算法是通过粒子来逼 近状态 的后验分 布 , 反映各 为 模 型对粒 子的影 响 , 初始 化时 每个粒子 都需 要与其 他模 型 的状 态估计值进 行交互 运算 , 同样 I MMP F的其他 步骤 , 也 需要 细化到单个粒 子 的运算 , 详 细 的过程 参考 文献 [ , 更 9 1 ] O。
的子 滤波 器, 出 I 提 MM 粒 子 滤 波 (neat g m lpe it cn ut l r i i
估 计问题 , 而对多模 式运动的 目标 , 估计精度不能保证 。基 于以上分析 , 本文在 I MMP F基 础上 , 结合 多传感 器量 测的
m dl a i eft n ,MMP )算 法 o e p rc lr g I t lie i F
M a u e i a g tt a k n l o ih s d o ne v rng t r e r c i g a g rt m ba e n I M u t-e s r s q e ta a tc e fle i g M m lis n o e u n i lp ri l t rn i
基于深度学习的多模态数据融合和分析算法研究

基于深度学习的多模态数据融合和分析算法研究标题:基于深度学习的多模态数据融合和分析算法研究摘要:多模态数据融合和分析在许多领域中都起着重要的作用。
随着深度学习技术的迅猛发展,研究人员对于如何利用深度学习算法来处理多模态数据的兴趣逐渐增加。
本论文主要研究了基于深度学习的多模态数据融合和分析算法。
首先,介绍了多模态数据融合和分析的背景和意义。
然后,详细阐述了深度学习的基本原理和常用算法。
接着,提出了一种基于深度学习的多模态数据融合和分析算法,并进行了实验验证。
最后,总结了研究结果,并对未来的研究方向进行了展望。
关键词:深度学习,多模态数据,融合和分析,算法1. 引言多模态数据是指来自不同传感器或不同源头的数据,如图像、文本、语音等。
这些数据在包含了丰富的信息的同时也带来了挑战。
传统的数据融合和分析方法往往需要手动设计特征或规则,效果受限且鲁棒性较差。
而深度学习技术通过自动学习数据表征,具有强大的表达能力和适应性,因此被广泛应用于多模态数据融合和分析领域。
2. 深度学习的基本原理和算法深度学习是一种模仿人脑神经网络结构进行学习的机器学习方法,通过多层次的非线性变换从数据中学习表征,并通过迭代优化算法提高模型的性能。
常用的深度学习算法有神经网络、卷积神经网络(CNN)、循环神经网络(RNN)等。
3. 多模态数据融合和分析算法研究基于深度学习的多模态数据融合和分析算法可分为两个阶段:特征提取和融合,以及模型训练和分析。
3.1 特征提取和融合针对多模态数据,可以使用不同的深度学习模型进行特征提取,如使用CNN提取图像特征,使用RNN提取文本特征等。
在特征提取的基础上,利用深度学习模型进行特征融合,最常见的方式是使用多层感知器(MLP)进行融合,将不同模态的特征进行拼接或加权求和。
3.2 模型训练和分析在特征融合后,利用深度学习模型进行模型训练和分析。
可以使用监督学习方法进行分类、回归等任务,也可以使用无监督学习方法进行聚类、降维等任务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名:学号:院系:电子与信息工程学院课程名称:数据融合技术及应用实验题目:基于交互多模算法的机动目标跟踪同组人:实验成绩:总成绩:教师评语教师签字:年月日基于交互多模算法的机动目标跟踪摘要目标跟踪在国防和民用领域均有着广泛的应用。
随着飞行器机动性的提高,目标运动轨迹呈现出一定的复杂性、随机性和多样性。
因此,研究机动目标跟踪是一个在理论与应用中均具有挑战性的课题。
设计目标跟踪系统的主要目的是可靠而精确地跟踪目标,因此,对机动目标跟踪问题进行理论和应用方面的研究,具有重大理论意义及工程应用价值。
在二维空间内在建立目标运动模型和观测模型的基础上采用基于交互多模算法(IMM)的卡尔曼滤波器对机动目标进行跟踪。
IMM算法可以很好的完成对机动目标的跟踪。
关键词目标跟踪;机动;交互多模算法1、引言机动是指目标作改变原来规律的运动,比如为执行某种战术意图,作转向、俯冲、爬升、下滑、蛇形、增速、降速等都属于目标机动。
在四五十年代,目标速度和机动性不高,可以假设其运动规律在一定的时间内为匀速直线运动。
但是,随着目标性能及各种控制和制导技术的发展,目标在某些时刻,比如发现自身被跟踪或者要进攻时,目标也可以进行闪避机动或采取某些特殊的攻击姿态,这时目标的机动性就十分强。
[1]由于机动的复杂性、随机性、多样性以及各种飞行器的机动性能越来越高。
在此背景下,提高对机动目标的跟踪性能便成为越来越重要的问题,迫切需要研究更合理的机动目标模型以及性能更为优越的跟踪滤波方法。
实现机动目标精确跟踪,首要解决的问题就是使所建立的目标运动模型与实际的目标运动模型匹配。
目前常用的有多模型(MM),交互式多模型(IMM),切换模型等。
多模型方法就是对一组具有不同机动模型分别进行Kalman滤波,最终的参数估计是各滤波器估计值的加权和;在多模型基础上,Shalom提出了交互式多模型方法,这一方法对无序目标的机动检测,显示了更好的鲁棒性和跟踪的稳定性;切换模型则是分别建立机动和非机动运动模型,利用机动检测实现在这两个模型之间的切换。
一般来说,交互式多模型的跟踪性能较好。
本文对作匀速运动的二维空中机动目标进行研究,利用交互式多模型方法对雷达目标进行跟踪,达到了比较好的效果。
2、运动模型在二维平面内当目标在空中作匀速运动时,通常包括匀速直线运动和匀速转向运动或P=,且无虚警存在,在笛卡尔坐标系下作两者交替,设采样间隔为T,目标检测概率1D匀速运动的目标离散运动模型和观测模型[2](假定在采样时刻k)为:()()()XΦX(2-1)+=+k k GV k1()()()()k H k k W kZ X(2-2)=+2.1 匀速直线运动模型当目标作匀速直线运动时,有:()()()()()()()22100/2001000,0010/200010Tx y x k xk y k y k T T T G T T T u k V k u k =⎡⎤⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦X Φ (2-3) 其中()x u k 和()y u k 分别为相互独立的零均值方差为2xu σ和2yu σ的高斯白噪声。
()()()v 1000,v 0010x y k H W k k ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦(2-4)其中x y v (k),v (k)是相互独立的高斯白噪声,均值为零,方差为2σ。
2.2 匀速转向运动模型当目标作匀速转向运动时,有:()()()()()()()()()2222100/20/4001000/200010/20/4,000100/200001010000101Tx y x k xk y k y k x k y k TT T T T T T T G T T u k V k u k =⎡⎤⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦X Φ (2-5)其中()x u k 、()y u k 分别为相互独立的零均值方差为2x u σ、2yu σ和的高斯白噪声。
100000001000H ⎡⎤=⎢⎥⎣⎦()()()v v x y k W k k ⎡⎤=⎢⎥⎣⎦(2-6)其中x y v (k),v (k)是相互独立的高斯白噪声,均值为零,方差为2σ。
3、卡尔曼滤波器在带有噪声(加性的背景噪声)的观测数据中进行随机信号本身取值的估计称为波形估计。
波形估计所采用的基本方法是线性最小均方估计,实现这一估计的典型滤波器是卡尔曼滤波器[2]。
3.1 状态方程卡尔曼滤波器基本的信号模型如下: ()()()()()()()()11,k k k k G k V k k H k k +=++=X ΦX Y X (3-1)观测模型如下:()()()k k W k =+Z Y (3-2) 其中()k V ,()k W 为零均值高斯白噪声且有:()()(){}()()()(){}()()(){}(){}()()(){}(){}()()(){}()()(){}()()()()()0000000000cov cov cov 000,00var 00,00,ˆ/,/T kj T kj T xTX X X X Xk E k j k k E k j k k j E E j E j E k k VAR k k k k k k k k δδ===========⎡⎤⎣⎦==W W W R V V V Q W V X m X W X P X V X μX P X μP P (3-3)3.2 卡尔曼滤波基本步骤①、根据前一次滤波值()ˆ1/1k k --X(或初值()ˆ0/0X )经计算预测值 ()()()ˆˆ/1,11/1k k k k k k -=---X ΦX (3-4)②、根据前次得到的滤波误差方差阵()1/1X k k --P (或初值()0/0X P )计算预测误差方差阵()()()()()()()/1,11/1,1111T X X T k k k k k k k k G k k G k -=----+---P ΦP ΦQ (3-5)③、计算卡尔曼增益:()()()()()()()1/1/1TTX X k k k H k H k k k H k k -⎡⎤=--+⎣⎦K P P R (3-6)④、计算滤波估计()()()()()()ˆˆˆ//1/1k k k k k k H k k k ⎡⎤=-+--⎣⎦X X K Z X (3-7)⑤、计算滤波误差方差阵()()()()//1X X k k k H k k k =--⎡⎤⎣⎦P I K P (3-8) 下面是计算滤波估计以及Kalman 滤波增益和误差方差阵计算的流程图:(k K 1k k →+1k k →+图3.1滤波估计计算流程图(左)、滤波增益和误差方差阵计算流程图(右)3.3 起始条件的确定在应用Kalman 滤波算法时,需要指定滤波的初始条件,根据目标的初始状态来建立滤波器的起始估计,即()()()()ˆ0/00,0/00x X==X m P P 。
然而在实际情况中,通常目标的初始状态是无法得知的,可以利用前几个观测值建立状态的起始估计。
对于只考虑目标位置和速度的状态估计的非机动模型,则可用两点起始法来确定初始条件,即用前两个观测值建立起始初值。
起始估计值为:()()()()()()()221/ˆ2/2221/x x x y y y z z z T z z z T ⎡⎤⎢⎥-⎡⎤⎣⎦⎢⎥=⎢⎥⎢⎥⎢⎥⎡⎤-⎣⎦⎣⎦X(3-9) 起始估计的估计误差为(2)(1)(2)(1)2(2/2)(2)(1)(2)(1)2x x x x y y yy v v v T u T v v v T u T -⎡⎤⎢⎥-⎢⎥⋅+⎢⎥=⎢⎥-⎢⎥-⎢⎥⋅+⎢⎥⎣⎦X (3-10)起始估计的估计误差协方差矩阵为22222222222222/002/004(2/2)00/200/4xy ux xu y TT TT T T TT ⎡⎤σσ⎢⎥σσ⎢⎥σ+⎢⎥=⎢⎥σσ⎢⎥⎢⎥σσ⎢⎥σ+⎢⎥⎣⎦P (3-11)4、交互多模算法假定有r 个模型:()()()1,1,,j j j k k G V k j r +=+=X ΦX (4-1) 其中,()j k W 是均值为零、协方差矩阵为j Q 的白噪声序列。
用一个马尔可夫链来控制这些模型之间的转换[3],马尔可夫链的转移概率矩阵为:1111r r rr p p p p ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P(4-2) 测量模型为:()()()()j j j k H k k W k =+Z X (4-3) IMM 算法步骤可归纳如下[4]: ①、输入交互()()()()()()(){()()()}()()(){}()111ˆˆ1/11/11/11/1ˆ1/11/11/1ˆˆˆ1/11/11/11/11/,1/roj i iji oj riiij i Toj i oj k ij i i ij i jk k k k k k k k k k k k k k k k k k k k k k P M k M k p k c μμμμ==---=------⎡=----+--⎣⎤⎡⎤--------⎦⎣⎦--=-=-∑∑X X P P X X X X Z (4-4)其中1,,j r = ,ij p 是模型i 转到模型j 的转移概率,j c 为规一化常数,()11rj ij i i c p k μ==-∑。
②、对应于模型()j M k ,以()ˆ1/1oj k k --X,()1/1ojk k --P 及()k Z 作为输入进行Kalman 滤波。
1)预测()()()0ˆˆ/1,11/1j j jk k k k k k -=---X ΦX (4-5) 2)预测误差方差阵 ()()()()()()()0/1,11/1,1111j j T j j X X Tj jk k k k k k k k G k k Gk -=----+---P ΦP ΦQ (4-6)3)卡尔曼增益 ()()()()()()()1/1/1jTjTj XXk k k H k H k k k Hk k -⎡⎤=--+⎣⎦K P P R (4-7)4)滤波()()()()()()ˆˆˆ//1/1j j j jk k k k k k H k k k ⎡⎤=-+--⎣⎦X X K Z X (4-8) 5)滤波误差方差阵()()()()//1j jj X Xk k k H k k k ⎡⎤=--⎣⎦P I K P (4-9) ③、模型概率更新()(){}()(){}(){}()()()111//,/11/k k k j j j j rj ij i j j i k P M k P k M k P M k k p k k c c c μμ--====Λ-=Λ∑Z Z Z Z (4-10)其中,c 为归一化常数,且()1rjjj c k c==Λ∑,而()j k Λ为观测()k Z 的似然函数,()()(){}()()()111/2/211/,exp 22k T j j j j j n j k P k M k k k π--⎧⎫Λ==-⎨⎬⎩⎭Z Z υS υS ,()()()()()()()()()ˆ/1/1j j T j j Xk k H k k k k H k k k H k k =--=-+υZ X S P R ,。
