§7.4散度与高斯公式
合集下载
高斯定理表达式

高斯定理表达式
高斯定理表达式是:∮F·dS=∫(▽·F)dV。
高斯定理也称为高斯通量理论,或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式(通常情况的高斯定理都是指该定理,也有其它同名定理)。
在静电学中,表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。
散度与高斯公式
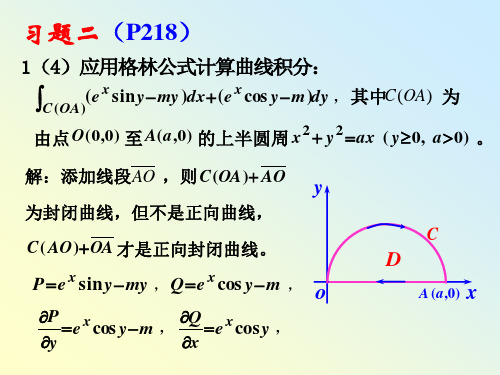
D
CuvdxuvdyC ydx ydy(01)dxdy. D
错解:由题意得
F(
x,
y){
y,
1}
,
G(
x,
y){0,
1}
,
F ( x, y)G( x, y)1 ,故 F Gdxdydxdy 。
D
D
§10.5 高斯公式
10.5.1 高斯(Gauss)公式 一、高斯定理
设空间闭区域 由分片光滑的闭曲面Σ围成,
x
,
y){
u
u,
v
v
}
,又已知在圆周x
2
y
2
1
x y x y
上, u(x, y) 1 ,v( x, y) y ,求F Gdxdy 。
D
解:
F Gdxdy
v(
u x
u ) u( y
v x
v y
)dxdy
D
D
u v u v
[(v
x
u x
)(v
y
u y
)]dxdy [ 间的部分的下侧,
cos,cos,cos
是Σ在( x, y, z)处
o
y
的外法向量的方向余弦. x
解 曲面不是封闭曲面, 为利用
z
高斯公式
补充 1 : z h ( x2 y2 h2 ) 1 h
1取上侧, 1构成封闭曲面, 1围成空间区域 . 在上使用高斯公式 ,
o Dxy
y
x
( x2 cos y2 cos z2 cos )dS
C( AO)OA 才是正向封闭曲线。
P e x sinymy ,Qe x cos ym , o
P e x cos ym , Q e x cos y ,
高斯公式

高斯公式 仍成立. 好抵消,因而
例1 利用高斯公式计算曲面积分:
( x y )dxdy ( y z ) xdydz
其中 为柱面x 2 y 2 1及平面z 0, z 3所围成的空间 闭区域Ω的整个边界曲面的外侧 .
解:因由已知: P ( y-z ) x , Q 0,
2 2 2
xy
而 (简写)
1 1
π , cos 0, cos 0, cos 1 2
( x cos y cos z cos )ds
2 2 2
1
z ds h dxdy πh
或
P Q R x y z dv ( P cos Q cos R cos )dS
此时, 是Ω的整个边界曲面的外侧, 、 、 cos cos cos 是 上点( x,y,z )处的法向量的方向余弦,以上 二式称为 高斯公式 .
D xy
对于(1)与(2)式,同样可得:
如果穿过Ω内部,且平行于x轴的直线与Ω的边界曲 面 的 交点恰好为两个,
P 有: x dv P( x, y, z )dydz 成立. Ω
如果穿过Ω内部,且平行于y轴的直线与Ω的边界 曲面的 交点恰好为两个,
Q 有: dv Q( x, y, z )dzdx 成立. y
z z 2 ( x, y )
z1 ( x, y ) z 2 ( x, y )
(4) 1取下侧, 2 取上侧, 3是以Dxy的边界 曲线为准 线, 母线平行于z轴的柱面上的一 部分,取外侧.
则(3)式左边:
z2 ( x , y ) R R z dv z dz dxdy Ω Dxy z1 ( x , y ) Rx, y, z 2 ( x, y ) Rx, y, z1 ( x, y )dxdy
高等数学 第六节 高斯公式 通量与散度

Φ Pdydz Qdzdx Rdxdy
n
Σ
当 > 0, 说明流入 的流体质量少于
流出的, 表明 内有泉;
n
当 < 0, 说明流入 的流体质量多于流出的,
表明 内有洞 ; 当 = 0, 说明流入与流出 的流体质量相等 。
根据高斯公式, 流量也可表为
P x
Q y
R z
dxdydz
2、是否满足高斯公式的条件;
3、Σ 是取闭曲面的外侧。
第2xzdydz yzdzdx z2dxdy ,
其中 是由曲面 z x2 y2 与
z 2 x2 y2 所围立体的表面外侧。
z
Dxy
2y
x
第十一章 第六节
7
例2 计算 ( x y)dxdy ( y z)xdydz ,其中 Σ 是
cos
n
0
r
0
n
0
r
0
则
x cos y cos z cos
r
r
r
1 3
r
cos
dS
1
3dv V
3 第十一章 第六节
23
内容小结
1 高斯公式及其应用
公式
P Q R
Ω
(
x
y
z
)dv
Σ
Pdydz
Qdzdx
Rdxdy
应用 (1) 计算曲面积分
(非闭曲面时注意添加辅助面的技巧)
(2) 闭曲面积分为零的充要条件:
Gauss
I 2 (x y z)dv
1 1
1
对称性
2 zdv h2dS
1方 程
1
1 2
h4
9(7)散度和高斯公式

柱面
z
n
的直即线边至界多面相由交于1,两 2点,. 3
三部分组成:
n
1 : z z1( x, y) (取下侧) 2 : z z2( x, y) (取上侧)
O
x Dxy
y n
3 :母线平行于z轴的柱面. (取外侧)
13
散度和高斯(Gauss)公式
R z
dv
R(
x,
y,
z)dxdy
由三重积分的计算法
缩成P点时, 极限
F dS
lim
lim
存在,
V 0 V V 0 V
则该极限值就称为向量场
A
在P点处的
散度.
记为 div F, 即
F dS
div F
lim V 0
V
lim V 0 V
4
散度和高斯(Gauss)公式
若 F 表示流速,则散度表示在某一点处, 单位时间内通过单位体积Rzd)vdv
2(
xdv
ydv
zdv
)
先
二
后
一
法
2
(zPdcvos
Q cos Rcos0)dS
{( x, y, z) x2 y2
0
z2 ,0
z
h}
h
2 zdz dxdy
0
Dz
2 h z z2dz 2 h z3dz h4
0
0
2
Dxy
于是 R( x, y, z)dxdy
{R[x, y, z2( x, y)] R[x, y, z1( x, y)]}dxdy
Dxy
R z
dv
R(
x
,
y,
z
微积分高斯公式

3
(r
sin
z)
dz
9
0
00
2
思考: 若 改为内侧, 结果有何变化?
若 为圆柱侧面(取外侧) , 如何计算?
例2. 利用Gauss 公式计算积分
z
其中 为锥面 x2 y2 z2 介于 z = 0 及
z = h 之间部分的下侧. 解: 作辅助面
1 hh
o
y
x
1: z h, (x, y) Dxy : x2 y2 h2, 取上侧
z
2 z d x d ydz h4
2
h
z
z2
dz
h4
0
1 h4
2
1 hh
o
y
x
例3. 设 为曲面 z 2 x2 y2, 1 z 2 取上侧, 求
I (x3z x) d y d z x2 yz d z d x x2z2 d x d y.
解: 作取下侧的辅助面
z 2
1 : z 1 (x, y) Dxy : x2 y2 1
I 用柱坐标
用极坐标 1 1
1 1
o
d
x
d
ydz
(1)
( Dxy
x
2
)
d
x
d
y
x
1y
2
d
0
1
dr
0
2 cos2 d 0
13
12
例4. 设函数
在闭区域 上具有一阶和
二阶连续偏导数, 证明格林( Green )第一公式 P u v
u
2v x2
2v y2
2v z2
d
x
d
y
d
z
高斯公式 通量及散度

o 1 x
y
例2. 利用Gauss 公式计算积分
z
其中 ∑ 为锥面 x2 + y2 = z2 介于 z = 0 及 z = h 之间部分的下侧.
∑1 h h
∑
o y 解: 作辅助面 2 2 2 x ∑1: z = h, (x, y) ∈Dxy : x + y ≤ h , 取上侧
记∑,∑1所围区域为, 则
n n
当Φ = 0 时, 说明流入与流出∑ 的流体质量相等 .
③
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
为了揭示场内任意点M 处的特性, 设∑ 是包含点 M 且 方向向外的任一闭曲面 , 记∑ 所围域为, 在③式两边同除以 的体积 V, 并令 以 任意方式缩小至点 M 则有 Φ lim →M V
r2 3x2 r 2 3y2 r 2 3z2 = q + + 5 5 5 r r r ( r ≠ 0) =0
计算结果与仅原点有点电荷的事实相符.
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
内容小结
1. 高斯公式及其应用 公式:
∫∫∑ Pd y d z + Qd z d x + Rd xd y P Q R )d xd y d z = ∫∫∫ ( + + x y z
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
2. 闭曲面积分为零的充要条件 定理2. 设P(x, y, z), Q(x, y, z), R(x, y, z) 在空间二 维 定理 间二 单连通域G内具有连续一阶偏导数, ∑为G内任一闭曲面, 则
∫∫∑ Pd y d z + Qd z d x + Rd xd y = 0
高斯公式流量与散度

(10-15) 这里Σ是Ω的整个边界曲面的外侧,公式(10 15)称为高斯 公式.
一、高斯公式
证明
先证明 设闭区域Ω在xOy面上的投影区域为Dxy.假设穿过Ω内部 且平行于z轴的直线与Ω的边界曲面Σ的交点恰好是两个,即其 边界曲面Σ由曲面
及以垂直于Dxy边界的柱面Σ3组成(见图10-18),其中Σ1取下
高斯公式可写成 上述公式表明,向量场A通过闭曲面Σ流向外侧的流量等于 向量场A的散度在闭曲面Σ所围闭区域Ω上的积分.
二、向量场的流量与散度
【例4】
求向量场
穿过曲面
流向外侧的流量.
解设
为Σ上任何一点的切平面的法向量,则由高斯公式知所求的
流量为
谢谢聆听
二、向量场的流量与散度
设区域的体积为V,则
表示单位时间内区域Ω内单位体积流体的平均发散量,即平均散度. 令Ω收缩到一点M( x,y,z ),若极限
存在,则称此极限值为向量场A在点M的散度,记为di有向量场
其中函数P,Q,R均具有一阶连续偏导数,Σ是场内的一片有向 曲面,n是Σ在点x,y,z处的单位法向量,则积分
称为向量场A通过曲面Σ向着指定侧的流量(或通量).如果A是定 常流体(假定密度为1)的速度,则|Q|表示单位时间内穿过Σ流 体的质量.如果Σ是闭曲面,则表示单位时间内通过闭曲面Σ的流体 的质量,它是从Σ流出的流体的质量与流入Σ的流体的质量之差, 表示单位时间内流体从Σ包围的区域Ω内部向外发出的总质量.
一、高斯公式
注意
对于一般的空间有界闭区域高斯公式均成立.若曲面 Σ与平行于坐标轴的直线的交点多于两个,则用有限个 光滑的曲面将Ω分为有限个满足条件的小闭区域来讨论.
一、高斯公式
【例1】
求 及半球面
一、高斯公式
证明
先证明 设闭区域Ω在xOy面上的投影区域为Dxy.假设穿过Ω内部 且平行于z轴的直线与Ω的边界曲面Σ的交点恰好是两个,即其 边界曲面Σ由曲面
及以垂直于Dxy边界的柱面Σ3组成(见图10-18),其中Σ1取下
高斯公式可写成 上述公式表明,向量场A通过闭曲面Σ流向外侧的流量等于 向量场A的散度在闭曲面Σ所围闭区域Ω上的积分.
二、向量场的流量与散度
【例4】
求向量场
穿过曲面
流向外侧的流量.
解设
为Σ上任何一点的切平面的法向量,则由高斯公式知所求的
流量为
谢谢聆听
二、向量场的流量与散度
设区域的体积为V,则
表示单位时间内区域Ω内单位体积流体的平均发散量,即平均散度. 令Ω收缩到一点M( x,y,z ),若极限
存在,则称此极限值为向量场A在点M的散度,记为di有向量场
其中函数P,Q,R均具有一阶连续偏导数,Σ是场内的一片有向 曲面,n是Σ在点x,y,z处的单位法向量,则积分
称为向量场A通过曲面Σ向着指定侧的流量(或通量).如果A是定 常流体(假定密度为1)的速度,则|Q|表示单位时间内穿过Σ流 体的质量.如果Σ是闭曲面,则表示单位时间内通过闭曲面Σ的流体 的质量,它是从Σ流出的流体的质量与流入Σ的流体的质量之差, 表示单位时间内流体从Σ包围的区域Ω内部向外发出的总质量.
一、高斯公式
注意
对于一般的空间有界闭区域高斯公式均成立.若曲面 Σ与平行于坐标轴的直线的交点多于两个,则用有限个 光滑的曲面将Ω分为有限个满足条件的小闭区域来讨论.
一、高斯公式
【例1】
求 及半球面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x y z 连续条件。
例1.求 Ò xdy dz+ydz dx zdx dy, 其中 是正方体 0 x a,0 y a,0 z a, 的表面,取外侧。
注:当 P x, Q y, R z 时,由 Gauss 公式得
Ò xdy dz ydz dx zdx dy 3 dV 3V .
一闭曲面,设 所围的空间域的体积为V , 直径为d , 外侧的单位法向量为n。 若当d 0时,
比式
1 V
A
ndS
的极限存在,则称此极限为
A 在点
M
处的散度,记为 divA M (简记为 divA ),即
Ò r
divA lim
1
r A
nvdS
d0 V
比式 1 V
vndS 表示小区域
内有“源”与
7.3.4 散度与高斯( Gauss )公式
一、高斯定理
设 是以分片光滑曲面 为界面的空间闭区域,向量场
A(x, y, z) {P(x, y, z),Q(x, y, z), R(x, y, z)} 在上具有一阶 连续偏导数,则有
乙 Ar nvdS Pdy dz Qdz dx Rdx dy
例 5.设有数量场 u ln x2 y2 z 2 ,求 div(gradu) 。
解: gradu {u , x
u , y
u} z
x2
1 y2
z
2
{x,
y,
z}
,
(
x
)
1
2x2
,
x x2 y 2 z 2 x2 y 2 z 2 (x2 y 2 z 2 )2
(
y
)
1
2y2
,
y x2 y 2 z 2 x2 y 2 z 2 (x2 y 2 z 2 )2
z
(
x
2
z y2
z2
)
1 x2 y2
z2
2z2
(x2 y2 z2)2
,
div(gradu)
x2
3 y2
z
2
2(x2 (x2 y
y2 z 2 z2
2) )2
x
2
1 y2
z
2
.
有向封闭曲面 外侧的流量 vndS ,其中n为 外
侧的单位法向量 , 所围成的区域为 。 总流量 流出的流量—流入的流量。
(1) 0 ,流出大于流入,表明 内 有“源”; (2) 0 ,流出小于流入,表明 内 有“洞”;
(3)0 ,流出等于流入。
二、散度
定义 2 设有向量场 A(x, y, z) ,在场中取包含点 M 的任
)dV
积分中值定理
P Q R
( x
y
z
)
M
V ,
(M )
Ò
r divA
M
lim
d 0
r A
nvdS
V
P lim ( MM x
Q y
R ) z
M
( P x
Q y
R ) z
M
∵M
是场中任一点,
r divA
P
Q
R .
x y z
∴
divA
P
Q
R
x y z
—散度的计算公式
故
AndS
divAdV
曲面,其法向量与y 轴正向夹角大于 .
2
z
o x
1 y
7.3.5 散度
一、通量
定义 1 设 A(x, y, z) 为一向量场, 为场中一有向
曲面,称
A
ndS
为向量场
A穿过曲面
的通量
。
当 A 是电场强度E
时,
EndS
即为电通量;
当 A 是磁场强度H
时,
HndS
即为磁通量。
设一稳定的不可压缩的流体速度场为v(x, y, z) ,流过
。
Hale Waihona Puke Gauss 公式是一个极其重要的公式,它建立了曲 面积分与三重积分之间的联系,有着明确的物理意义, 即一区域中总散度等于通过边界的通量。
四、散度的性质
rr
r
r
(1) div(aA bB) adivA bdivB,其中a,b是常数。
(2) 若u( x, y, z)的梯度存在,则
r
rr
div(uA) udivA A gradu
故 V dV 13 xdydz ydzdx zdxdy 。
Ò 例2. 计算I
x3dy dz y3dz dx z3dx dy, x2 y2 z2
其中是球面x2 y2 z2 a2的内侧。
例3. 计算
I
2(
x 2
x2 )dy
dz
8 xydz
dx
4 x( x
z)dx
dy,
其中是旋转抛物面z x2 y2介于z 0和z 4两平面
(
P x
Q y
R z
)dV
其中 取外侧。此公式称为高斯公式。
注:
(1)Gauss 公式的条件是:封闭、外侧、偏导数连续, 三者缺一不可。
若积分曲面 不 封闭,则添加辅助曲面使之封闭; 当封闭曲面取内侧时,Gauss 公式中的符号应为负号; 应用Gauss 公式前首先要检验 P, Q, R, P , Q , R 的
设向量场 A {P(x, y, z),Q(x, y, z), R(x, y, z)} ,其中 P、Q、R 具有一阶连续偏导数,在场中取包含点
M (x, y,z) 的任一闭曲面 ,其所围区域 的体积 为 V ,d 为 的直径, n为 外侧的单位法向量, 由高斯公式得
r
Ò A
nvdS
P (
x
Q y
R z
有“洞”的平均状态,而 divv M 则表示在点 M 处
有“源”与有“洞”的状态。
向量场 A(x, y, z) 的散度是数量。若divA M 0 ,则表示
该点处有“源”;若 divA M 0 ,则表示该点处有“洞”;
若 divA M 0 ,则表示该点处既无“源”也无“洞”。
三、散度的计算
间的部分,取上侧。
解:积添分补曲平面面不1是:封闭z 曲4,面(x,2不 y能2 直4接) ,利取用下Ga侧us;s 公式计算。
zz
4 1
Dxyoo
2
xx
2 yy
例4. 计算
I x(8 y 1)dy dz 2(1 y2 )dz dx 4 yzdx dy
其中是由曲线z y 1 (1 y 3)绕 y 轴旋转所得的 x 0
例1.求 Ò xdy dz+ydz dx zdx dy, 其中 是正方体 0 x a,0 y a,0 z a, 的表面,取外侧。
注:当 P x, Q y, R z 时,由 Gauss 公式得
Ò xdy dz ydz dx zdx dy 3 dV 3V .
一闭曲面,设 所围的空间域的体积为V , 直径为d , 外侧的单位法向量为n。 若当d 0时,
比式
1 V
A
ndS
的极限存在,则称此极限为
A 在点
M
处的散度,记为 divA M (简记为 divA ),即
Ò r
divA lim
1
r A
nvdS
d0 V
比式 1 V
vndS 表示小区域
内有“源”与
7.3.4 散度与高斯( Gauss )公式
一、高斯定理
设 是以分片光滑曲面 为界面的空间闭区域,向量场
A(x, y, z) {P(x, y, z),Q(x, y, z), R(x, y, z)} 在上具有一阶 连续偏导数,则有
乙 Ar nvdS Pdy dz Qdz dx Rdx dy
例 5.设有数量场 u ln x2 y2 z 2 ,求 div(gradu) 。
解: gradu {u , x
u , y
u} z
x2
1 y2
z
2
{x,
y,
z}
,
(
x
)
1
2x2
,
x x2 y 2 z 2 x2 y 2 z 2 (x2 y 2 z 2 )2
(
y
)
1
2y2
,
y x2 y 2 z 2 x2 y 2 z 2 (x2 y 2 z 2 )2
z
(
x
2
z y2
z2
)
1 x2 y2
z2
2z2
(x2 y2 z2)2
,
div(gradu)
x2
3 y2
z
2
2(x2 (x2 y
y2 z 2 z2
2) )2
x
2
1 y2
z
2
.
有向封闭曲面 外侧的流量 vndS ,其中n为 外
侧的单位法向量 , 所围成的区域为 。 总流量 流出的流量—流入的流量。
(1) 0 ,流出大于流入,表明 内 有“源”; (2) 0 ,流出小于流入,表明 内 有“洞”;
(3)0 ,流出等于流入。
二、散度
定义 2 设有向量场 A(x, y, z) ,在场中取包含点 M 的任
)dV
积分中值定理
P Q R
( x
y
z
)
M
V ,
(M )
Ò
r divA
M
lim
d 0
r A
nvdS
V
P lim ( MM x
Q y
R ) z
M
( P x
Q y
R ) z
M
∵M
是场中任一点,
r divA
P
Q
R .
x y z
∴
divA
P
Q
R
x y z
—散度的计算公式
故
AndS
divAdV
曲面,其法向量与y 轴正向夹角大于 .
2
z
o x
1 y
7.3.5 散度
一、通量
定义 1 设 A(x, y, z) 为一向量场, 为场中一有向
曲面,称
A
ndS
为向量场
A穿过曲面
的通量
。
当 A 是电场强度E
时,
EndS
即为电通量;
当 A 是磁场强度H
时,
HndS
即为磁通量。
设一稳定的不可压缩的流体速度场为v(x, y, z) ,流过
。
Hale Waihona Puke Gauss 公式是一个极其重要的公式,它建立了曲 面积分与三重积分之间的联系,有着明确的物理意义, 即一区域中总散度等于通过边界的通量。
四、散度的性质
rr
r
r
(1) div(aA bB) adivA bdivB,其中a,b是常数。
(2) 若u( x, y, z)的梯度存在,则
r
rr
div(uA) udivA A gradu
故 V dV 13 xdydz ydzdx zdxdy 。
Ò 例2. 计算I
x3dy dz y3dz dx z3dx dy, x2 y2 z2
其中是球面x2 y2 z2 a2的内侧。
例3. 计算
I
2(
x 2
x2 )dy
dz
8 xydz
dx
4 x( x
z)dx
dy,
其中是旋转抛物面z x2 y2介于z 0和z 4两平面
(
P x
Q y
R z
)dV
其中 取外侧。此公式称为高斯公式。
注:
(1)Gauss 公式的条件是:封闭、外侧、偏导数连续, 三者缺一不可。
若积分曲面 不 封闭,则添加辅助曲面使之封闭; 当封闭曲面取内侧时,Gauss 公式中的符号应为负号; 应用Gauss 公式前首先要检验 P, Q, R, P , Q , R 的
设向量场 A {P(x, y, z),Q(x, y, z), R(x, y, z)} ,其中 P、Q、R 具有一阶连续偏导数,在场中取包含点
M (x, y,z) 的任一闭曲面 ,其所围区域 的体积 为 V ,d 为 的直径, n为 外侧的单位法向量, 由高斯公式得
r
Ò A
nvdS
P (
x
Q y
R z
有“洞”的平均状态,而 divv M 则表示在点 M 处
有“源”与有“洞”的状态。
向量场 A(x, y, z) 的散度是数量。若divA M 0 ,则表示
该点处有“源”;若 divA M 0 ,则表示该点处有“洞”;
若 divA M 0 ,则表示该点处既无“源”也无“洞”。
三、散度的计算
间的部分,取上侧。
解:积添分补曲平面面不1是:封闭z 曲4,面(x,2不 y能2 直4接) ,利取用下Ga侧us;s 公式计算。
zz
4 1
Dxyoo
2
xx
2 yy
例4. 计算
I x(8 y 1)dy dz 2(1 y2 )dz dx 4 yzdx dy
其中是由曲线z y 1 (1 y 3)绕 y 轴旋转所得的 x 0
