基本算法语句
计算机的基本算法语句类型和讲解

计算机从上而下按照语
句排列的顺序执行这些语句.
语句n
输入语句和输出语句分 别用来实现算法的输入信息, 输出结果的功能.
语句n+1
例1.用描点法作函数 yx33x2 的24 图x 象3时0,
需要求出自变量和函数的一组对应值,编写程序, 分别计算当x=-5,-4,-3,-2,-1,0,1,2,3,4,5时的函数值。
注意: INPUT语句不但可以给单个变量赋值,还可以
给多个变量赋值,其格式为:
INPUT “提示内容1,提示内容2,提示内容3,…”;变量1,变量2,变量 3,…
例如,输入一个学生数学,语文,英语三门课的成绩, 可以写成:
INPUT “数学,语文,英语”;a,b,c
二.输出语句 输出语句的一般格式
框图: 开始
输入x
yx33x224x30
程序: INPUT “x=”;x y=x^3+*3 x^2-2*4 x+30 PRINT x PRINT y END
输出x,y 结束
程序:
INPUT “x=”;x -----------------输入语句
y=x^3+3*x^2-24*x+30 ---------赋值语句
PRINT “S=”; S
三.赋值语句 (1)赋值语句的一般格式: 变量=表达式
(2)赋值语句的作用是:先计算出赋值号右边表达 式的值,然后把这个值赋给左边的变量,使该变量的 值等于表达式的值。 (3)赋值语句中的“=”称作赋值号,与数学中的等 号的意义是不同的.赋值号的左右两边不能对换. (4)赋值语句左边只能是变量名字而不是表达式, 如:2=x是错误的
〖例4〗交换两个变量A和B的值,并输出交换前后 的值。
基本算法语句复习课

D.998
考点题型6 While语句,先判断条件, 再执行循环体(循环次数不确定)
6设计一个计算1×3×5×7×9的算法.下面给出 了程序的一部分,则在横线①上填入—— S=1 I=3 While I< = ① S=S×I I=I+2 Wend Print S End
考点题型2 赋值语句 将表达式的值转给变量
2编写一个程序,要求输入两个正数a和b的
值,输出ab与ba的值
考点题型3 If---Then---Else语句, 条件满足或不满足均有可执行的操 作内容
3编写程序,输入两点的坐标,输出这两点
连线的斜率.
考点题型4 If---Then语句,条件不满 足时无可执行的操作内容
4.条件语句的格式是: (2) If 条件 Then 语句l E1se 语句2 End If
(1)为了便于阅读和醒目,语句1和语句2
及Else一般缩进书写. (2)“条件”可以是复合条件,此时用and 加以连结.
5、循环语句 (1) “While”语句(循环次数不定时). 一般形式为: WHILE 条件 循环体 WEND
4编写程序,输入两个实数,由小到大输出
这两个数.
考点题型5 Until语句,先执行循环 体,后判断条件(循环次数确定)
5算法:S=0 I=1 Do S=S+I I=I+1 Loop Until I>1000 中,执行循环的次数是( ) A.1 000 B.999 C.1001
i=0
i = i+1 : t=i^2
PRINT t
否 i变量如果原来没有值,则执 行赋值语句后,获得一个值,如果已有值, 则执行该语句,以赋值号右边表达式的值 代替该变量的原值,即将原值“冲掉”。
基本算法语句

输入、输出语句常见形式 输入语句 INPUT 的常用方法: INPUT “提示内容”;变量 INPUT 变量 INPUT “提示内容”;变量1,变量2,变量3, … INPUT 变量1,变量2,变量3, … 输出语句 PRINT 的常用方法: PRINT “提示内容”;表达式 PRINT 表达式 PRINT “提示内容”;表达式1,表达式2,表达式3, … PRINT 表达式1,表达式2,表达式3, … PRINT “提示内容”
当型循环结构
DO 循环体 LOOP UNTIL 条件
WHILE 条件 循环体 WEND
例3 根据下面的程序框图写出相应的QBASIC程序
开始 i=1 i=1,Sum=0
循环结构
sum = 0 DO
循环语句
S=s+i i=i+1 否 i>100? 是 输出S 结束
sum = sum + i i=i+1 LOOP UNTIL i>100 PRINT s END
变式:编写程序,计算一个学生数学、语文、英语三门课的平均成绩 框图: 算法: 第一步:分别输入三科的成绩a,b,c; 第二步:计算average=(a+b+c)/3; 第三步:输出三科平均分。 程序: INPUT “Maths=”;a INPUT “Chinese=”;b INPUT “English=”;c average=(a+b+c)/3 PRINT “The average=”;average END
答: 2
程序2: A=10 A=A+15 PRINT A END 程序3: a=1 b=3 PRINT “a+b=”;a+b END
答: 25
基本算法语句(输入输出赋值)

算 法
程 序 框 图
程 序 设 计 语 言
文字语言
图形语言
程序设计语言的基本算法语句有哪些?
输入语句、输出语句、赋值语句 条件语句、循环语句
例1、任意给定一个正实数,设计一个程序, 求以这个数为半径的圆的面积. 第一步:输入一个正实数r; 第二步:计算S=π r2; 第三步:输出圆的面积S. 输入语句
其中 p
abc 2 开始
,
设计一个求三角形面积的程序。
程序: 程序框图:
输入a,b,c 计算p
计算S 输出,b,c p=(a+b+c)/2 S=SQR(p*(p-a)*(p-b)*(p-c)) PRINT “三角形面积S=”;S END
例4、设计程序交换两个变量A和B的值,并 输出交换前后的值。
程序:
INPUT INPUT PRINT X=A A=B B=X PRINT END “A”;A “B”;B A,B
A,B
小结
作业 P24 练习题 T2 T4
基本算法语句
输入、输出、赋值语句
瑞四中 林光明
回顾
1. 什么是算法?什么是程序框图? 算法通常指按照一定的规则解决的某一类 问题的明确和有限的步骤。 程序框图是一种用程序框、流程线及文字 说明来准确、直观的表示算法的图形。
2. 算法的基本逻辑结构有哪些? 算法的基本结构有三种:顺序结构、条件 结构、循环结构(循环结构又分为当型和直 到型)。
程序框图:
开始
输入数学a
输入语文b 输入英语c 总分s=a+b+c 平均分p=s/3
程序: INPUT “Maths=”;a INPUT “Chinese=”;b INPUT “Enghlish=”;c s=a+b+c p=s/3 PRINT “zongfen=”;s PRINT “The average=”;p END
算法、程序框图与基本语句知识点及联系—精品文档
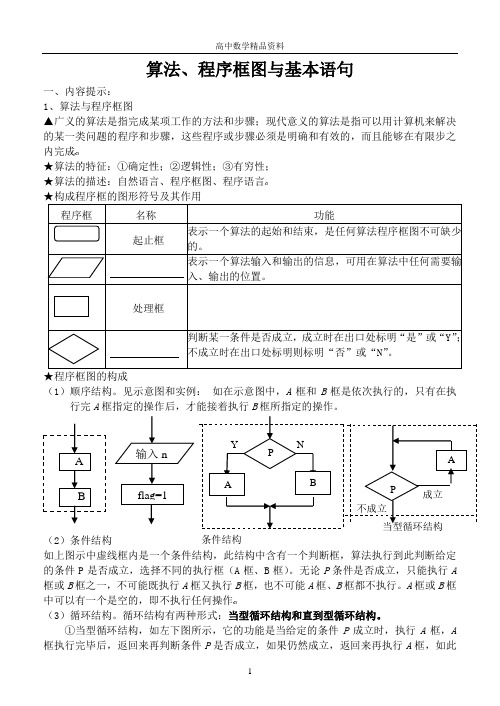
算法、程序框图与基本语句一、内容提示: 1、算法与程序框图▲广义的算法是指完成某项工作的方法和步骤;现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成★算法的特征:①确定性;②逻辑性;③有穷性; ★算法的描述:自然语言、程序框图、程序语言 ★构成程序框的图形符号及其作用程序框名称功能起止框表示一个算法的起始和结束,是任何算法程序框图不可缺少的。
表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。
处理框判断某一条件是否成立,成立时在出口处标明“是”或“Y ”;不成立时在出口处标明则标明“否”或“N ”。
★程序框图的构成(1)顺序结构。
见示意图和实例: 如在示意图中,A 框和B 框是依次执行的,只有在执行完A 框指定的操作后,才能接着执行B 框所指定的操作。
(2)条件结构如上图示中虚线框内是一个条件结构,此结构中含有一个判断框,算法执行到此判断给定的条件P 是否成立,选择不同的执行框(A 框、B 框)。
无论P 条件是否成立,只能执行A 框或B 框之一,不可能既执行A 框又执行B 框,也不可能A 框、B 框都不执行。
A 框或B 框中可以有一个是空的,即不执行任何操作(3)循环结构。
循环结构有两种形式:当型循环结构和直到型循环结构。
①当型循环结构,如左下图所示,它的功能是当给定的条件P 成立时,执行A 框,A 框执行完毕后,返回来再判断条件P 是否成立,如果仍然成立,返回来再执行A 框,如此A B输入n flag=1 P A B YN A 成立 不成立 P 当型循环结构条件结构反复执行A 框,直到某一次返回来判断条件P 不成立时为止,此时不再执行A 框,离开循环结构。
继续执行下面的框图。
②直到型循环结构,如右下图所示,它的功能是先执行重复执行的A 框,然后判断给定的条件P 是否成立,如果P 仍然不成立,则返回来继续执行A 框,再判断条件P 是否成立。
知识讲解_高考总复习:算法与程序框图
高考总复习:算法与程序框图【考纲要求】1.算法的含义、程序框图(1)了解算法的含义,了解算法的思想;(2)理解程序框图的三种基本逻辑结构:顺序、条件、循环。
2.基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义。
【知识网络】【考点梳理】考点一、算法1.算法的概念(1)古代定义:指的是用阿拉伯数字进行算术运算的过程。
(2)现代定义:算法通常是指按照一定规则解决某一类问题的明确和有限的步骤。
(3)应用:算法通常可以编成计算机程序,让计算机执行并解决问题。
2.算法的特征:①指向性:能解决某一个或某一类问题;②精确性:每一步操作的内容和顺序必须是明确的;算法的每一步都应当做到准确无误,从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确.“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.③有限性:必须在有限步内结束并返回一个结果;算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制的持续进行.④构造性:一个问题可以构造多个算法,算法有优劣之分。
3.算法的表示方法:(1) 用自然语言表示算法: 优点是使用日常用语, 通俗易懂;缺点是文字冗长, 容易出现歧义;(2) 用程序框图表示算法:用图框表示各种操作,优点是直观形象, 易于理解。
要点诠释:泛泛地谈算法是没有意义的,算法一定以问题为载体。
考点二:程序框图1. 程序框图的概念:程序框图又称流程图,是最常用的一种表示法,它是描述计算机一步一步完成任务的图表,直观地描述程序执行的控制流程,最便于初学者掌握。
2.程序框图常用符号:连接点用于连接另一页或另一部分的框图注释框框中内容是对某部分流程图做的解释说明3.画程序框图的规则:(1)使用标准的框图的符号;(2)框图一般按从上到下、从左到右的方向画;(3)除判断框图外,大多数框图符号只有一个进入点和一个退出点。
6基本算法语句

同样6105与2146的公约数也必是8251的约数,所以 8251与6105的最大公约数也是6105与2146的最大 公约数
继续下去,我们得到:
6105=2146×2+1813 2146=1813×1+333 1813=333×5+148 333=148×2+37 148=37×4+0 则37为8251与6105的最大公约数
1、一般格式:
WHILE 条件 循环体 WEND
循环体
2、说明:先判断条件,再执行循环体
满足条件?
否
是
四、直到型循环语句( until 语句)
1、一般格式:
DO 循环体 LOOP UNTIL 条件
2、说明:先执行循环体一次,再判断。
循环体
不是
满足条件?
是
我们这节课就利用基本的算法程序来解决一 些实际问题,进一步体会算法的程序思想。
案例1.辗转相除法与更相减损术
在初中,我们已经学过求最大公约数的知识, 你能求出18与30的最大公约数吗?
2 3 18 9 3 30 15 5
互质
所以,18和30的最大公约数是:2×3=6 但是,当我们处理较大数(如:8251与6105)的最大公因 数时,如果利用这种方法可能计算量比较大,步骤比较多。 下面我们介绍一种古老而有效的算法——辗转相除法
在某些情况下,也可以这样来表示IF-THEN语句: 二、条件语句二
一般格式:
满足条件? 是 否 语句 1
IF 条件 THEN 语句 END IF
说明:“条件”表示判断的条件,“语句”表示满足条件时执行 的操作内容;条件不满足时,结束程序,END IF表示条件语 句的结束。
算法的循环结构是由循环语句来实现的,对应 的两种循环结构分别用下列语句表示: 三、当型循环语句(WHILE 语句)
1[1].2.3基本算法语句_循环语句
![1[1].2.3基本算法语句_循环语句](https://img.taocdn.com/s3/m/827a13d626fff705cc170a5a.png)
——循环语句
循环结构有两种-----当型与直到型. 直到型循环结构 当型循环结构
循环体 循环体
满足条件? 否
是
满足条件?
否
是
即WHILE语句和UNTIL语句。
(1)WHILE语句的一般格式是: WHILE 条件 循环体 WEND WHILE——当…… 时候
WEND——朝……方向 行走
循环体
条件
满足条件?
否
是
(2)UNTIL语句的一般格式是:
直到型循环结构 DO 循环体 LOOP UNTIL
循环体
条件
满足条件?
否
是
WHILE语句的一般格式 WHILE 条件 循环体 WEND
UNTIL语句的一般格式
DO 循环体 LOOP UNTIL
条件
区别:在WHILE语句中,是当条件满足时执行循环 体,而在UNTIL语句中,是当条件不满足时执行循环 体。
结束
结构
变式训练(2): 编写程序求:1×3×5×7×……×101的值. 直到型 开始 如何修改? UNITL语句
i=1 S=0 S=1 S=S+i S=S*i
i=i+2 i=i+1
i>100? i>101? 否
是
输出S 结束
i=1 S=0 S=1 DO S=S+i S=S*i i=i+1 i=i+2 LOOP UNTIL i>100 101 PRINT S END
是
S=S+i
结束
直到型
开始
UNTIL语句 i=1 S=0 DO S=S+i i=i+1 LOOP UNTIL i>100 PRINT S END
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.两种条件语句的执行过程 计算机在执行条件语句时,首先对 If 后的条件进行判断, 如果条件符合,就执行 Then 后的语句 1,若条件不符合, 对于 If—Then—Else 语句就执行 Else 后的语句 2,然后 结束这一条件语句.对于 If—Then 语句,则直接结束该 条件语句.
3.两种循环语句的区别 在当型语句中,是当条件满足时执行循环体,而在直到型 语句中是当条件不满足时执行循环体,二者是有区别的, 在解决问题时用两种循环语句编写应注意条件的不同.
则输出的结果是________.
伪代码所示的算法是一个求和运算:
1×1 3+3×1 5+5×1 7+…+99×1101 =[1-13+13-15+15-17+…+919-1101]×12 =1-1011×12=15001.
答案
50 101
对应的流程图为
要点梳理
说明:上面“For”和“End For”之间缩进的步骤称为循环体, 如果省略“Step 步长”,那么重复循环时,I 每次增加 1. (2)不论循环次数是否确定都可以用下面循环语句来实现循环结 构当型和直到型两种语句结构.
当型语句的一般格式是
,
对应的流程图为
要点梳理
直到型语句的一般格式是
输入、输出和赋值语句
例 1 要求输入两个正数 a 和 b 的值,输出 ab 与 ba 的值,画 出流程图,写出伪代码.
解 流程图:
伪代码如下
变式训练 1
编写伪代码,求用长度为 l 的细铁丝分别围成一个正方形和 一个圆时的面积.要求输入 l 的值,输出正方形和圆的面积.(π 取 3.14)
解 伪代码如下:
要点梳理
3.算法的选择结构由 条件语句来表达,条件语句有两种,一
种是 If—Then—Else 语句,其格式是
.
对应的流程图为
要点梳理 另一种是 If—Then 语句,其格式是 程图为
对应的流
要点梳理
4.算法中的循环结构,可以运用循环语句来实现. (1)当循环的次数已经确定,可用“For”语句表示 “For”语句的一般形式为
.
对应的流程图为
[难点正本 疑点清源] 1.关于赋值语句,有以下几点需要注意:
(1)赋值号左边只能是变量名字,而不是表达式,例如 3←m 是错误的. (2)赋值号左右不能对换,赋值语句是将赋值号右边的表 达式的值赋给赋值号左边的变量,例如 Y←x,表示用 x 的值替代变量 Y 的原先的取值,不能改写为 x←Y.因为 后者表示用 Y 的值替代变量 x 的值. (3)在一个赋值语句中只能给一个变量赋值,不能出现多 个“←”.
伪代码如下:
变式训练 2
已知分段函数
y=-0,x+1,
x<0, x=0,
x+1, x>0,
编写伪代码,输入自
变量 x 的值,输出其相应的函数值,并画出流程图.
解 伪代码如下:
流程图
循环语句
例 3 编写伪代码,求 1+12+13+…+n1>1 000 的最小自然数 n 的值.
解 伪代码如下:
变式训练 3 某算法的伪代码如下:
基本算法语句
要点梳理
1.基本算法语句 五种基本算法语句分别是 赋值语句、输入语句、输出语 句、条件语句 、 循环语句.
2.赋值语句、输入语句、输出语句 赋值语句用符号“←”表示,其一般格式是变量←表 达式(或变量),其作用是对程序中的变量赋值;输入语句 “Read a,b”表示输入的数据依次递给a,b,输出语 句“Print x”表示输出运算结果x .
条件语句
例2
已知函lt;0,
设计一个算法并用
伪代码实现每输入一个 x 的值,都得到相应的函数值.
解 用 x,y 分别表示自变量和函数值,则相应的算法如下: S1 输入 x 的值; S2 判断 x 的取值范围,如果 x≥0,则 y←x2-1,求函数值, 否则 y←2x2-5; S3 输出函数值 y.
