用于一般函数优化的蚁群算法

合集下载

蚁群算法

蚁群算法目录1 蚁群算法基本思想 (1)1.1蚁群算法简介 (1)1.2蚁群行为分析 (1)1.3蚁群算法解决优化问题的基本思想 (2)1.4蚁群算法的特点 (2)2 蚁群算法解决TSP问题 (3)2.1关于TSP (3)2.2蚁群算法解决TSP问题基本原理 (3)2.3蚁群算法解决TSP问题基本步骤 (5)3 案例 (6)3.1问题描述 (6)3.2解题思路及步骤 (6)3.3MATLB程序实现 (7)3.1.1 清空环境 (7)3.2.2 导入数据 (7)3.3.3 计算城市间相互距离 (7)3.3.4 初始化参数 (7)3.3.5 迭代寻找最佳路径 (7)3.3.6 结果显示 (7)3.3.7 绘图 (7)1 蚁群算法基本思想1.1 蚁群算法简介蚁群算法（ant colony algrothrim ，ACA ）是由意大利学者多里戈（Dorigo M ）、马聂佐（ Maniezzo V ）等人于20世纪90初从生物进化的机制中受到启发，通过模拟自然界蚂蚁搜索路径的行为，提出来的一种新型的模拟进化算法。

该算法用蚁群在搜索食物源的过程中所体现出来的寻优能力来解决一些系统优化中的困难问题，其算法的基本思想是模仿蚂蚁依赖信息素，通过蚂蚁间正反馈的方法来引导每个蚂蚁的行动。

蚁群算法能够被用于解决大多数优化问题或者能够转化为优化求解的问题，现在其应用领域已扩展到多目标优化、数据分类、数据聚类、模式识别、电信QoS 管理、生物系统建模、流程规划、信号处理、机器人控制、决策支持以及仿真和系统辩识等方面。

蚁群算法是群智能理论研究领域的一种主要算法。

1.2 蚁群行为分析EABCDF d=3d=2 m=20 t=0AB C Dd=3d=2 m=10 m=10t=11.3 蚁群算法解决优化问题的基本思想用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。

路径较短的蚂蚁释放的信息量较多，随着时间的推进，较短路径上积累的信息浓度逐渐增高，选择该路径的蚂蚁个数愈来愈多。

蚁群算法及案例分析精选全文

问过的节点;另外,人工蚁
群在选择下一条路径的时
候并不是完全盲目的,而是
按一定的算法规律有意识
地寻找最短路径
自然界蚁群不具有记忆的
能力，它们的选路凭借外
激素，或者道路的残留信
息来选择，更多地体现正
反馈的过程
人工蚁群和自然界蚁群的相似之处在于,两者优先选择的都
是含“外激素”浓度较大的路径; 两者的工作单元(蚂蚁)都
正反馈、较强的鲁棒性、全
局性、普遍性
局部搜索能力较弱，易出现
停滞和局部收敛、收敛速度
慢等问题
优良的分布式并行计算机制
长时间花费在解的构造上，
导致搜索时间过长
Hale Waihona Puke 易于与其他方法相结合算法最先基于离散问题，不
能直接解决连续优化问题
蚁群算法的
特点
蚁群算法的特点及应用领域
由于蚁群算法对图的对称性以
及目标函数无特殊要求，因此
L_ave=zeros(NC_max,1);
%各代路线的平均长度
while NC<=NC_max
%停止条件之一：达到最大迭代次数
% 第二步：将m只蚂蚁放到n个城市上
Randpos=[];
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))';
scatter(C(:,1),C(:,2));
L(i)=L(i)+D(R(1),R(n));
hold on
end
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)])

蚁群算法

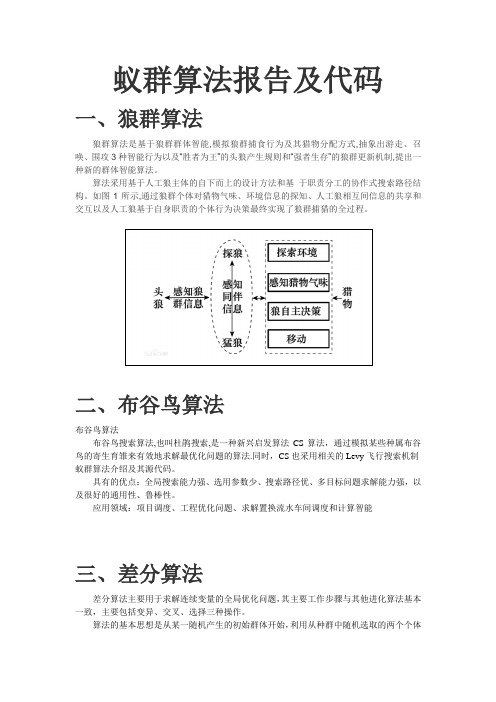
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。

算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。

如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。

二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法，通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时，CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。

具有的优点：全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强，以及很好的通用性、鲁棒性。

应用领域：项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题，其主要工作步骤与其他进化算法基本一致，主要包括变异、交叉、选择三种操作。

算法的基本思想是从某一随机产生的初始群体开始，利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源，将差向量加权后按照一定的规则与第三个个体求和而产生变异个体，该操作称为变异。

然后，变异个体与某个预先决定的目标个体进行参数混合，生成试验个体，这一过程称之为交叉。

如果试验个体的适应度值优于目标个体的适应度值，则在下一代中试验个体取代目标个体，否则目标个体仍保存下来，该操作称为选择。

在每一代的进化过程中，每一个体矢量作为目标个体一次，算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，引导搜索过程向全局最优解逼近。

四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。

从理论上分析，迭代过程中，在保留上一代最佳个体的前提下，遗传算法是全局收敛的。

五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法，是集群智能思想的一个具体应用，它的主要特点是不需要了解问题的特殊信息，只需要对问题进行优劣的比较，通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优值突现出来，有着较快的收敛速度。

一种求解函数优化的自适应蚁群算法

ｔｐｃｆｓｌｔｎｉｏｓｂｏｉｓａｄｄｎｍｃｌｄｕｔｇｔｅｓａｇｅｅｔｎｏｈａｈｎｈｔｔｆｔｅｈｓａｅｏｏｉｎｕｄｍａｎｙａｉｌａｊｓｎｈｔｔｙｏｓｌｃｏｆｔｅｐｔｓａｄｔｅｓａｇｏｈｅｕｏｔｎａｙｉｒｅｆｉｒｅｙ
ａｄＡｐ￣ａｏｓ２０４４）４ —ｌ．ｎｐｃｆｎ，０７，３（：０３ｌ
ＡｂｔａｔＡｎａａｔｅａｔｃｌｎｌｏｔｍｓｐｅｅｔｄｆｒｔｅｐｉｚｔｎｏｌ－ｎｍｕｓｒｃ：ｄｐｖｎｏｏｙａｇｒｈｉｒｓｎｅｏｈｏｔａｉｆｍｕｔｍｉｉｍｃｎｉｕｕｕｃｉｎＢｄｖｄｎｉｉｍｉｏｉｏｔｏｓｆｎｔ．ｙｉｉｉｇｎｏ
ｔｉｉｆｒａｉｎｕｄｔｇｂｓｄｏｅｄｓｉｕｉｎｏｈｏｕｉｎ，ｈａｇｒｔｍａｎｈｕｄｍａｎｉｉｈｔｅｓｌｔｎｉｒｌｎｍｔｐａｉａｅｎｔｉｒｂｔｆｔｅｓｌｔｓｔｅｌｏｈｃｎｆｄｔｅｓｂｏｉｎｗｈｃｈｏｕｉｓａｏｏｎｈｔｏｏｉｉｏｌｃｔｄａｄｔｅｅｅｍｉｅｔｅｓｅｉｃｖｌｅｆｅｏｕｉｎｗｉｉｅｕｄｍａｎＴｅｉｌｔｎｒｓｌｓｏｔａｅｌｏｏａｅ，ｎｎｄｔｒｎｓｈｐｃｆａｕｏｔｓｌｔｔｎｔｓｂｏｉ．ｈｓｍｕａｉｅｕｔｈｗｈｔｔａｇ — ｈｉｈｏｈｈｏｓｈｒｈｈｓｍａｙｇｏｅｏｍａｃｓｓｃｓａｏｄｎｏａｐｉｍ，ｉｈｐｅｉｏｏｕｉｎ，ｕｃｏｖｒｅｃｎｏｄｒｌｂｌｉｍａｎｏｄｐｒｒｎｅｕｈａｖｉｉｇｌｃｌｏｔｔｆｍｕｈｇｒｃｓｎｓｌｔｉｏｑｉｋｃｎｅｇｎｅａｄｇｏｅｉｉ— ａｉｔ，ｉｈａｅｂｔｒｔａｈｓｆｓｌｅｅｉｌｏｔｍｎｌｎｌｓｌｃｉｎａｇｒｔｍ．ｙｗｈｃｒｅｔｈｎｔｏｅｏｉｅｇｎｔａｇｒｈａｄｃｏａｅｅｔｌｏｈｅｍｐｃｉｏｉＫｅｒｓａｔｃｌｎｌｏｔｍ；ｕｃｏｐｉｚｔｎ；ｉｐｒｅｅｒｅ；ｅｅｉａｇｒｈｙｗｏｄ：ｎｏｏｙａｇｒｈｆｎｔｎｏｔｉｉｍｉａｉｄｓｅｄｄｇｅｇｎｔｌｏｔｍｏｓｃｉ

用于求解函数优化的蚁群算法设计

０引言
蚁群算法（ｎＣｌｙＡｇｒｈ是通过对自然界Ａｔｏｎｌｉｍ）ｏｏｔ
化算法一样，过候选解组成的群体在进化过程中通来寻求最优解。蚁群算法具有如下优点：（）强的鲁棒性。对基本蚁群算法模型稍加１较
Ａ￣ｒｅ：ｏｓｌｅｆｎｔｎｏｔｚｔｎｐｏｌｍ，ｈｒｍｎｐａｅｓａｅｉｄｒｅａｅｎａｔｏｏｙａｇｒｈｂ — ｌｔａｔＴｏｖｃｉｐｉａｉｒｂｅｐｅｏｏｅｕｄｔｔｔ￣ｓｅｖｄｂｓｄｏｎｌｎｏｔｍｙｉｕｏｍｉｏｒｉｃｌｉｎｄｃｇｂｎｒｏｉｇｏｅｅｃａｏｔｍ．ｈｒｖｄａｇｒｈａｅｎｔｓｄｆｒｖｒｔｓｏｌｓａｔｓｆｎｔｎ．ｕｉｉａｙｃｄｎｆｎｔｌｒｈＴｅｉｏｅｏｔｈｓｂｅｅｔａｉｉｆｃａｉｌｅｔｕｃｏｓｎｇｉｇｉｍｐｌｉｍｅｏｅｅｓｃｉ
用于求解函数优化的蚁群算法设计
Ａｎａｔｃｌｎｌｏｔｄｓｇｏｈｕｃｉｎｏｔｚｔｎｎｏｏｙａｇｒｈｍｅｉｎｆｒｔｅｆｎｔｐｉａｉｉｏｍｉｏ
吴华芹
ＷＵａｑｎＨｕ — ｉ
（南省化学工业学校信息工程系，河河南郑州
摘
要：了求解一般的函数优化，为在标准蚁群算法的基础上，引入了遗传算法的编码方式，对蚁群算法的信

蚁群算法（ACO）解决TSP问题

蚁群算法（ACO）解决TSP问题⼀、蚁群算法1.基本原理蚁群算法（Ant Colony Optimization，ACO）是⼀种基于种群寻优的启发式搜索算法，有意⼤利学者M.Dorigo等⼈于1991年⾸先提出。

该算法受到⾃然界真实蚁群集体在觅⾷过程中⾏为的启发，利⽤真实蚁群通过个体间的信息传递、搜索从蚁⽳到⾷物间的最短路径等集体寻优特征，来解决⼀些离散系统优化中的困难问题。

经过观察发现，蚂蚁在寻找⾷物的过程中，会在它所经过的路径上留下⼀种被称为信息素的化学物质，信息素能够沉积在路径上，并且随着时间逐步挥发。

在蚂蚁的觅⾷过程中，同⼀蚁群中的其他蚂蚁能够感知到这种物质的存在及其强度，后续的蚂蚁会根据信息素浓度的⾼低来选择⾃⼰的⾏动⽅向，蚂蚁总会倾向于向信息素浓度⾼的⽅向⾏进，⽽蚂蚁在⾏进过程中留下的信息素⼜会对原有的信息素浓度予以加强，因此，经过蚂蚁越多的路径上的信息素浓度会越强，⽽后续的蚂蚁选择该路径的可能性就越⼤。

通常在单位时间内，越短的路径会被越多的蚂蚁所访问，该路径上的信息素强度也越来越强，因此，后续的蚂蚁选择该短路径的概率也就越⼤。

经过⼀段时间的搜索后，所有的蚂蚁都将选择这条最短的路径，也就是说，当蚁巢与⾷物之间存在多条路径时，整个蚁群能够通过搜索蚂蚁个体留下的信息素痕迹，寻找到蚁巢和⾷物之间的最短路径。

蚁群算法中，蚂蚁个体作为每⼀个优化问题的可⾏解。

⾸先随机⽣成初始种群，包括确定解的个数、信息素挥发系数、构造解的结构等。

然后构造蚁群算法所特有的信息素矩阵每只妈蚁执⾏蚂蚊移动算⼦后，对整个群体的蚂蚁做⼀评价，记录最优的蚂蚁。

之后算法根据信息素更新算⼦更新信息素矩阵，⾄此种群的⼀次选代过程完成。

整个蚂蚁群体执⾏⼀定次数的选代后退出循环、输出最优解。

2.术语介绍（1）蚂蚁个体。

每只蚂蚁称为⼀个单独的个体，在算法中作为⼀个问题的解。

（2）蚂蚁群体。

⼀定数量的蚂蚁个体组合在⼀起构成⼀个群体，蚂蚁是群体的基本单位。

蚁群算法求函数最大值的程序

蚁群算法求函数最大值的程序蚁群算法是一种模拟蚂蚁觅食行为的启发式算法，常用于求解函数最大值问题。

本文将详细介绍蚁群算法的原理和实现步骤，以及一个示例程序。

1.蚁群算法原理蚁群算法基于蚁群觅食行为中的信息素交流和随机跳跃，通过多个智能体（模拟蚂蚁）在解空间中的和信息传递，逐步寻找到函数的最大值。

具体而言，蚁群算法包含以下关键要素：-蚂蚁：代表着算法解空间的个体，通过在解空间中的移动来探索新的解。

-信息素：用于模拟蚂蚁之间的信息传递和集体合作，蚂蚁在移动过程中会根据信息素浓度进行选择。

-目标函数：蚁群算法通过目标函数来评估到的解的优劣，从而引导蚂蚁进行。

-路径选择规则：蚂蚁在移动过程中根据一定的规则选择下一步的移动路径。

信息素浓度、目标函数值等因素都可以作为路径选择规则的参考。

-信息素更新规则：当蚂蚁选择了条路径后，会根据该路径的质量（目标函数值等）来更新路径上的信息素浓度。

2.蚁群算法步骤蚁群算法的一般步骤如下：1.初始化蚂蚁群和信息素矩阵。

2.对每只蚂蚁，计算其适应度并选择下一步的移动方向。

3.更新每只蚂蚁的位置，并根据移动结果更新信息素矩阵。

4.检查是否满足停止条件，如果满足则输出最优解，否则返回步骤23.蚁群算法示例程序下面是一个求解函数f(x)=x^2在[-10,10]范围内的最大值的蚁群算法示例程序。

```pythonimport randomimport math#目标函数def target_function(x):return x ** 2#初始化蚂蚁群ant_count = 100ants = [random.uniform(-10, 10) for _ in range(ant_count)] #初始化信息素矩阵pheromones = [1 for _ in range(ant_count)]#蚁群算法参数max_iter = 100 # 最大迭代次数alpha = 1 # 信息素重要程度因子beta = 1 # 启发因子rho = 0.1 # 信息素挥发因子Q=1#信息素强度best_solution = None#迭代优化过程for iter in range(max_iter):#计算每只蚂蚁的适应度并选择下一步移动方向for i in range(ant_count):ant = ants[i]fitness = target_function(ant)#选择下一步移动方向if random.random( < pheromones[i]:ant += random.uniform(-1, 1) # 信息素浓度高的蚂蚁随机选择一个方向else:ant += random.uniform(-0.1, 0.1) # 信息素浓度低的蚂蚁随机选择一个方向ants[i] = ant#更新最优解if best_solution is None or target_function(ant) >target_function(best_solution):best_solution = ant#更新信息素矩阵for i in range(ant_count):#蚂蚁越接近最优解，释放的信息素越多pheromones[i] = (1 - rho) * pheromones[i] + Q *(target_function(ants[i]) / target_function(best_solution)) #输出最优解print("最大值点坐标为：", best_solution)print("最大值为：", target_function(best_solution))```4.程序解释该示例程序使用Python编写，实现了蚁群算法来求解函数f(x)=x^2在[-10, 10]范围内的最大值。

蚁群算法求解函数优化的算法设计

一
蚁群算法（ｎｏｎｌｏｔｍ）受到人们ＡｔｌｙＡｇｒｈ是Ｃｏｉ对自然界中真实的蚁群集体行为的研究成果的启发而提出的一种基于种群的模拟进化算法，于属随机搜索算法。由意大利学者Ｍ．ｏｉＤｒｏ等人首ｇ先提出，分利用了蚁群搜索食物的过程与著名充的旅行商问题（Ｓ）间的相似性，过人工模ＴＰ之通
Ｊｎ２０ｕ．０７
蚁群算法求解函数优化的算法设计
尚峰，华芹吴ຫໍສະໝຸດ （．１洛阳市质量技术监督局检验测试中心，河南洛阳４１０；．７０３２河南省化学工业学校信息工程系，河南郑州４０４）５０２
摘要：为了求解一般的函数优化，文章在对标准蚁群算法的基础上，引入遗传算法的编码方式，
息量决定转移方向，时刻蚂蚁ｋｔ从城市ｉ向城市ｊ转移的概率Ｐｉｔ计算如下：ｉ）（
进化算法一样，通过候选解组成的群体在进化过
程来寻求最优解。蚁群算法具有如下优点：（）强的鲁棒性：基本蚁群算法模型稍１较对
有发展前景的方法，种带有构造性特征的新的这
度，可根据某种启发式算法具体确定，ＴＰ问在Ｓ
题中一般取－ｉ／Ｉｑ：１ｄｉｉｏ
蚂蚁ｋｋ：， … ，根据各条路径上的信（ｌ２，ｍ）
搜索方法已产生并被广泛应用。蚁群算法是一种随机搜索算法，其它模拟与

用于求解函数优化的蚁群算法设计

ＥｇｎｅｉｇａｄＡｐｉａｉｎ，０７４（５：７５．ｎｉｅｒｎｎｐｌｔｓ２０，３２）５－９ｃｏ
ＡｂｔａｔＴｓｌｅｆｎｔｎｐｉｚｔｎｐｏｌｍ，ｈｖｅｃｂｄａｔｃｌｎｌｏｔｍｄｉｇｂｎｒｏｉｇｏｅｅｉｌｏｓｒｃ：ｏｏｖｕｃｉｏｔｏｍｉｉｒｂｅｗｅａｅｄｓｒｅｎｏｏｙａｇｒｈａｄｎｉａｙｃｄｎｆｇｎｔａｇ — ａｏｉｉｃｒｔｍｎｅｅｏｅｈｒｍｏｅｐａｅｓｒｔｇ．ｈｘｅｍｅｔｗａｅｕｅｅｓｒｃｕｅｏｅｒｈｎｔｘＢｅａｓｈｉｈａｄｄｖｌｐｄｐｅｏｎｕｄｔｔｅｙＩｔｅｅｐｒｎ，ｅｈｖｓｄａｎｗｔｔｒｆｓａｃｉｇｍａｒ．ｃｕｅｔｅａｎｉｕｉ
但是在该方案中只需要为每个执行的协议设置唯一标识符发送者严格按照各个接收者提供的hm和其所对应的可信中心公布的信息执行协议由文章中安全性分析可知攻击者和冒名者都是不可能获得任何消Байду номын сангаас的这就保证了多个协议并发执行的安全使得提出的协议更加符合实际应用情况
维普资讯
ＣｍｕｅｎｉｅｒｇａｄＡｐｉｔｎ计算机工程与应用ｏｐｔｒＥｇｎｅｉｎｐｌａｉｓｎｃｏ
１引言
生物学研究表明在自然界中一群互相协作的蚂蚁能够找到食物源和巢之间的最短路径，而单只蚂蚁则不能。蚂蚁问相互协作的方法是它们在所经过的路上留下一定数量的信息素（）该迹能被其它蚂蚁检测出来，迹，一条路上的迹越多，其它蚂蚁将以越高的概率跟随此路径，从而该路径上的迹会被加强。蚁群算法（ｎＣｌｙＡｇｒｈ是受到人们对蚁群集体行为Ａｔｏｏｌｉｍ）ｎｏｔ的研究成果的启发而提出的一种基于种群的模拟进化算法，属于随机搜索算法。该算法思想由意大利学者Ｍ．ｏｉＤｒｏ等人首ｇ先提出ｌ，１充分利用了蚁群搜索食物的过程与著名的旅行商问．

蚁群算法matlab代码

蚁群算法matlab代码蚁群算法，英文名为Ant Colony Algorithm，缩写为ACO，是一种启发式算法，是一种模拟蚂蚁寻找食物路径的算法。

在实际生活中，蚂蚁找到食物并返回巢穴后，将其找到食物的路径上的信息素留下，其他蚂蚁通过检测信息素来指导寻路，成为了一种集体智慧行为。

ACO也是通过模拟蚂蚁寻找食物路径的方式来寻找优化问题的最优解。

在ACO算法中，信息素是一个重要的概念，代表了走过某一路径的“好概率”，用这个“好概率”更新一些路径上的信息素，使得其他蚂蚁更可能选择经过这条路径，从而实现路径优化的目的。

在本文中，我们将讨论如何使用Matlab实现蚁群算法来优化问题。

1. 设定问题首先，我们要选取一个优化问题，并将其转换为需要在优化过程中进行选择的决策变量。

例如，我们想要优化旅行商问题（TSP）。

在TSP中，我们需要让旅行商以最短的距离经过所有城市，每个城市仅经过一次，最终回到出发的城市。

我们可以将每个城市编号，然后将TSP转化为一个最短路径选择的问题，即最短路径从编号为1的城市开始，经过所有城市，最终回到编号为1的城市。

2. 设定ACO参数在使用ACO优化问题时，需要设定一些参数，这些参数会影响算法的表现。

ACO算法需要设定的参数有：1.信息素含量：初始信息素的大小，即每个路径上的信息素浓度。

2.信息素挥发速度：信息素的随时间“减弱”程度。

3.信息素加成强度：蚂蚁经过路径后增加的信息素量。

4.启发式权重：用于计算启发式因子，即节点距离的贡献值。

5.蚂蚁数量：模拟蚂蚁数量，即同时寻找路径的蚂蚁个数。

6.迭代次数：模拟的迭代次数，即ACO算法运行的次数。

7.初始节点：ACO算法开始的节点。

3. 创建ACO优化函数我们可以使用Matlab来创建一个函数来实现ACO算法。

我们称其为“ACOoptimization.m”。

function best_path =ACOoptimization(city_location,iter_num,ant_num,init ial_path,alpha,beta,rho,update_flag) %ACO优化函数 %输入： %city_location: 城市坐标矩阵，格式为[x1,y1;x2,y2;...;xn,yn] %iter_num: 迭代次数 %ant_num: 蚂蚁数量 %initial_path: 起始路径，即初始解 %alpha,beta,rho: 超参数，用于调节蚂蚁选择路径的概率 %update_flag: 是否更新信息素的标志（1表示更新，0表示否） %输出： %best_path: 最优解，即最短路径%初始化信息素 pheromone = 0.01 *ones(length(city_location),length(city_location)); %初始化路径权重 path_weight =zeros(ant_num,1); %城市数量 n_cities =length(city_location);%主循环 for iter = 1:iter_num %一个迭代里所有蚂蚁都寻找一遍路径 for ant =1:ant_num %初始化蚂蚁位置current_city = initial_path; %标记是否经过了某个城市 visit_flag =zeros(1,n_cities);visit_flag(current_city) = 1; %用来存储当前路径 current_path = [current_city];%蚂蚁找东西 for i =1:n_cities-1 %计算路径概率p =calculate_probability(current_city,visit_flag,phero mone,city_location,alpha,beta); %蚂蚁选择路径 [next_city,next_index] = select_path(p);%路径更新current_path = [current_path;next_city];visit_flag(next_city) = 1;current_city = next_city;%更新路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end-1),:),city_location(current_path(end),:));end%加入回到起点的路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end),:),city_location(current_path(1),:));%判断是否为最优解 ifant == 1 best_path = current_path; else if path_weight(ant) <path_weight(ant-1) best_path =current_path; end end%更新信息素 ifupdate_flag == 1 pheromone =update_pheromone(pheromone,path_weight,initial_path,current_path,rho); end end end end在函数中，我们首先定义了ACOalg函数的参数，包括城市坐标矩阵，迭代次数，蚂蚁数量，初始路径，超参数alpha，beta，rho，以及是否需要更新信息素。

蚁群算法（C语言实现）

蚁群算法（C语⾔实现）蚁群算法(ant colony optimization, ACO)，⼜称蚂蚁算法，是⼀种⽤来在图中寻找优化路径的机率型算法。

它由Marco Dorigo于1992年在他的中提出，其灵感来源于蚂蚁在寻找⾷物过程中发现路径的⾏为。

蚁群算法是⼀种模拟进化算法,初步的研究表明该算法具有许多优良的性质.针对参数优化设计问题,将蚁群算法设计的结果与遗传算法设计的结果进⾏了⽐较,数值仿真结果表明,蚁群算法具有⼀种新的模拟进化优化⽅法的有效性和应⽤价值。

预期的结果：各个蚂蚁在没有事先告诉他们⾷物在什么地⽅的前提下开始寻找⾷物。

当⼀只找到⾷物以后，它会向⼀种信息素，吸引其他的蚂蚁过来，这样越来越多的蚂蚁会找到⾷物！有些蚂蚁并没有象其它蚂蚁⼀样总重复同样的路，他们会另辟蹊径，如果令开辟的道路⽐原来的其他道路更短，那么，渐渐，更多的蚂蚁被吸引到这条较短的路上来。

最后，经过⼀段时间运⾏，可能会出现⼀条最短的路径被⼤多数蚂蚁重复着。

原理：为什么⼩⼩的蚂蚁能够找到⾷物？他们具有智能么？设想，如果我们要为蚂蚁设计⼀个⼈⼯智能的程序，那么这个程序要多么复杂呢？⾸先，你要让蚂蚁能够避开障碍物，就必须根据适当的地形给它编进指令让他们能够巧妙的避开障碍物，其次，要让蚂蚁找到⾷物，就需要让他们遍历空间上的所有点；再次，如果要让蚂蚁找到最短的路径，那么需要计算所有可能的路径并且⽐较它们的⼤⼩，⽽且更重要的是，你要⼩⼼翼翼的编程，因为程序的错误也许会让你前功尽弃。

这是多么不可思议的程序！太复杂了，恐怕没⼈能够完成这样繁琐冗余的程序。

然⽽，事实并没有你想得那么复杂，上⾯这个程序每个蚂蚁的核⼼程序编码不过100多⾏！为什么这么简单的程序会让蚂蚁⼲这样复杂的事情？答案是：简单规则的涌现。

事实上，每只蚂蚁并不是像我们想象的需要知道整个世界的信息，他们其实只关⼼很⼩范围内的眼前信息，⽽且根据这些局部信息利⽤⼏条简单的规则进⾏决策，这样，在蚁群这个集体⾥，复杂性的⾏为就会凸现出来。

蚁群算法步骤

蚁群算法（Ant Colony Optimization, ACO）是一种基于蚁群的群体智能算法，用于求解组合优化问题。

下面是蚁群算法的基本步骤：
1.初始化
在算法开始前，需对相关参数进行初始化，例如：蚂蚁群大小、信息素参数等。

此外，需要定义问题空间中每个解的初始状态，以及预设的目标函数。

2.蚁群搜索
在搜索阶段，蚂蚁会基于启发式信息（包括距离信息和信息素信息）进行路径选择，从而寻找到一组解来尽可能地优化目标函数。

对于每个蚂蚁，它将从初始位置出发，经过一系列的决策，最终到达目标位置，同时产生一条路径。

3.更新信息素
当所有的蚂蚁完成搜索后，将根据每个蚂蚁的路径更新信息素表。

结合各蚂蚁的贡献，信息素的浓度将被不断变化以反映出对当前问题具有的经验。

通过信息素的积累，越来越多的蚂蚁会选择这些较优的路径，从而找到更优的解。

4.重复搜索
重复执行步骤2和3，直到满足预设的停止条件。

通常停止条件是指已经经过了预设的搜索迭代次数或运行时间已过期等等。

在整个搜索过程中，各个蚂蚁将会逐渐集中于最优路径周围，以最小化目标函数。

5.解码和输出
最后，需要通过对最优路径进行解码来获得最佳解，并输出到相应的应用中。

总之，蚁群算法是一种有效的算法，在组合优化问题中具有优异的性能，例如旅行商问题、网络路径优化、调度安排等。

掌握蚁群算法的基本步骤和优化策略，可以为相关问题的求解提供有力的支持。

蚁群优化算法PPT

ACO首次被系统的提出
自然界中真实蚁群集体行为
4
蚁群算法原理
如何找到最短路径？
• 信息素：信息素多的地方显然经过这里的蚂蚁多，因而会有更多的蚂蚁聚集过来。
• 正反馈现象：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。
类比：
大肠杆菌在人体肠道内觅食的过程
5
蚁群算法原理
自然蚂蚁的智能特点
Meet the requirement of the solution
Y
output
31
实现过程
32
实现过程
33
实现过程
·
当比较小时，搜索的全局性好，但收敛速度变慢; 当比较大时，收敛速度比较快，但是容易陷入局部最优。
13
蚁群算法参数选择
因子和的选取
启发式因子的大小则反映了在蚁群路径搜索中的随机性因素作用的强度;
启发式因子的大小反映了在蚁群路径搜索中确定性因素作用的强度。
1.Ant-cycle
Q / Lk，第k只蚂蚁从城市i访问城市j k ii 0, 其他
k ii
Q / dij，第k只蚂蚁从城市i访问城市j 2.Ant-quantity 0, 其他
Q，第k只蚂蚁从城市i访问城市j 3.Ant-density 0, 其他
8
求解组合优化问题的蚁群算法
9
基本蚁群算法
蚂蚁k(k=1,2，…,m)根据各个城市间连接路径上的信息素浓度决定其下一个访问城市，设 Pijk t 表示t时刻蚂蚁 k从城市i转移到城市j的概率，其计算公式为：
is (t )is (t ) , s allowk Pijk (t ) is (t )is (t ) xallowk 0, s allowk

蚁群算法、遗传算法、模拟退火算法介绍

蚁群算法、遗传算法、模拟退火算法介绍穷举法列举所有可能,然后一个个去,得到最优的结果。

如图一，需要从A点一直走到G点，才能知道，F是最高的（最优解）。

这种算法得到的最优解肯定是最好的，但也是效率最低的。

穷举法虽然能得到最好的最优解，但效率是极其低下的。

为了能提高效率，可以不要枚举所有的结果，只枚举结果集中的一部分，如果某个解在这部分解中是最优的，那么就把它当成最优解。

显然这样有可能不能得到真正的最优解，但效率却比穷举法高很多。

只枚举部分解的方法很多。

贪心法在枚举所有解时，当遇到的解在当前情况下是最优时，就认为它是最优解。

如图一，当从A 点到B点时，由于B点比A点的解更优，所以会认为B点是最优解。

显然这样的效率很高，但得到的最优解质量也很差。

爬山法贪心法是只和前面的一个比较，为了提高最优解的质量，可以不仅和前一个解比较，也和后一个解比较，如果比前面和后面的解都优，那么就认为它是最优解。

如图一，当到C点时，发现它比前面的B和后面的D点的解都好，所以认为它是最优解。

模拟退火算法爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。

如图一，搜索到A点后就停止了搜索。

如果能跳出局部最优解，那么得到的最优解的质量相对就会好很多。

如当搜索到A点时以一定的概率跳转到另外一个地方。

这样就有可能跳出局部最优解A。

如果经过一定次数的跳跃，跳到了E 点，那么就会找到全局的最优解了。

如果这个概率不变，那么就会一直跳跃下去，不会结束。

可以让这个概率逐渐变小，到最后趋于稳定。

这里的概率逐渐减小类似于金属冶炼的退火过程，所以称之为模拟退火算法。

模拟退火算法(Simulated Annealing，SA)最早由Kirkpatrick等应用于组合优化领域，它是基于Mente-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。

模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。

《蚁群算法》课件

《蚁群算法整理》ppt课件
目
CONTENCT
录
• 蚁群算法简介 • 蚁群算法的基本原理 • 蚁群算法的实现过程 • 蚁群算法的改进策略 • 蚁群算法的性能评价 • 蚁群算法的应用案例
01
蚁群算法简介
蚁群算法的基本概念
蚁群算法是一种模拟自然界中蚂蚁觅食行为的优化算法，通过模拟蚂蚁的信息素传递机制来寻找最优解。
02
蚁群算法的基本原理
信息素的挥发与更新
信息素挥发与更新是蚁群算法中一个重要的过程，它影响着蚂蚁的移动和信息传递。
在蚁群算法中，信息素是蚂蚁之间传递的一种化学物质，用于标识路径的优劣。信息素会随着时间的推移而挥发，同时蚂蚁在移动过程中会释放新的信息素。挥发和更新的过程是动态的，影响着蚂蚁对路径的选择。
要点一
总结词
信息素更新规则是蚁群算法中的重要环节，通过改进信息素更新规则，可以提高算法的性能。
要点二
详细描述
在蚁群算法中，信息素更新规则决定了蚂蚁在移动过程中如何更新信息素。改进信息素更新规则可以提高算法的全局搜索能力和局部搜索能力。例如，可以采用动态调整策略，根据蚂蚁的移动路径和状态动态调整信息素的更新量，或者采用自适应策略，根据问题的特性和求解结果自适应地调整信息素更新规则，以提高算法的性能。
详细描述
在蚁群算法中，信息素挥发速度决定了信息素消散的快慢。较慢的挥发速度可以使信息素积累，有利于增强算法的全局搜索能力；较快的挥发速度则有利于算法的局部搜索。通过调整信息素的挥发速度，可以在全局搜索和局部搜索之间取得平衡，提高算法的效率和稳定性。
蚂蚁数量与移动规则的调整
总结词
蚂蚁数量和移动规则是蚁群算法中的重要参数，通过调整这些参数，可以改善算法的性能。

23个基本测试函数蚁群算法

23个基本测试函数蚁群算法蚁群算法是一种模拟蚂蚁行为的启发式算法，它通过模拟蚁群寻找食物的行为，来解决各种优化问题。

蚁群算法的核心思想是通过信息交流和反馈机制来寻找问题的最优解。

本文将介绍蚁群算法的基本原理，并以23个基本测试函数为例，展示蚁群算法在解决优化问题中的应用。

1. 算法简介蚁群算法最早由意大利学者Dorigo在1992年提出，其灵感来自于观察蚂蚁在寻找食物时的行为。

蚁群算法将问题抽象成一个图论模型，其中蚂蚁代表解空间中的候选解，信息素则代表蚂蚁之间的信息交流。

蚂蚁根据信息素的浓度和距离选择路径，并在路径上释放信息素，从而影响其他蚂蚁的选择。

通过多次迭代，蚂蚁群体逐渐收敛于最优解。

2. 蚁群算法的基本步骤蚁群算法主要包括初始化、路径选择、信息素更新和收敛判断等步骤。

2.1 初始化在蚁群算法中，需要初始化蚂蚁的位置和信息素的浓度。

蚂蚁的初始位置可以随机选择或者根据问题的特点进行设置。

信息素的初始浓度通常设置为一个较小的常数。

2.2 路径选择在路径选择阶段，蚂蚁根据信息素的浓度和距离选择路径。

通常情况下，信息素浓度较高的路径会有更多的蚂蚁选择，但也存在一定的随机性，以保证算法能够全局搜索。

2.3 信息素更新在信息素更新阶段，蚂蚁根据问题的优化目标更新路径上的信息素。

通常情况下，蚂蚁在路径上释放的信息素与路径的优化程度成正比。

信息素的更新规则可以根据具体问题进行设计。

2.4 收敛判断在每轮迭代之后，需要判断算法是否收敛。

通常情况下，可以通过设定一个停止准则来判断算法是否继续迭代。

常用的停止准则包括迭代次数、目标函数值的变化幅度等。

3. 蚁群算法在优化问题中的应用蚁群算法在解决各种优化问题中具有广泛的应用。

下面以23个基本测试函数为例，展示蚁群算法在不同问题中的应用。

3.1 球面函数球面函数是一个简单的优化问题，目标是找到一个全局最小值。

蚁群算法通过信息素的交流和反馈机制，可以在搜索空间中快速找到最优解。

人工智能：蚁群算法及其应用

●20世纪90年代初，意大利科学家Marco Dorigo 等受蚂蚁觅食行为的启发，提出蚁群算法(Ant Colony Optimization ，ACO)。

●一种应用于组合优化问题的启发式搜索算法。

●在解决离散组合优化方面具有良好的性能。

产生背景基本思想●信息素跟踪：按照一定的概率沿着信息素较强的路径觅食。

●信息素遗留：会在走过的路上会释放信息素，使得在一定的范围内的其他蚂蚁能够觉察到并由此影响它们的行为。

（1）环境：有障碍物、有其他蚂蚁、有信息素。

（2）觅食规则：范围内寻找是否有食物，否则看是否有信息素，每只蚂蚁都会以小概率犯错。

（3）移动规则：都朝信息素最多的方向移动，无信息素则继续朝原方向移动，且有随机的小的扰动，有记忆性。

（4）避障规则：移动的方向如有障碍物挡住，蚂蚁会随机选择另一个方向。

（5）信息素规则：越靠近食物播撒的信息素越多，越离开食物播撒的信息素越少。

6.7.1基本蚁群算法模型6.7.2蚁群算法的参数选择6.7.3蚁群算法的应用6.7.1 基本蚁群算法模型蚁群优化算法的第一个应用是著名的旅行商问题。

旅行商问题阐明蚁群系统模型旅行商问题（Traveling Salesman Problem ，TSP ）：在寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点的最小路径成本。

蚂蚁搜索食物的过程：通过个体之间的信息交流与相互协作最终找到从蚁穴到食物源的最短路径。

蚁群系统的模型6.7.1 基本蚁群算法模型m 是蚁群中蚂蚁的数量表示元素(城市) 和元素(城市) 之间的距离表示能见度，称为启发信息函数，等于距离的倒数，即表示t 时刻位于城市x 的蚂蚁的个数，表示t 时刻在xy 连线上残留的信息素，初始时刻，各条路径上的信息素相等即蚂蚁k 在运动过程中，根据各条路径上的信息素决定转移方向。

(,1,...,)xy d x y n =)(t xy ηxyxy d t 1)(=η()x b t ∑==nx x t b m 1)()(t xy τ)()0(const C xy =τ表示在t 时刻蚂蚁k 选择从元素(城市) x 转移到元素(城市) y 的概率，也称为随机比例规则。

蚁群算法求解函数最小值

蚁群算法求解函数最小值蚁群算法是一种群体智能算法，它模拟蚂蚁在寻找食物时留下信息、跟随信息和更新信息的行为。

其主要思想是让一群智能体（蚂蚁）在问题空间中随机游走，通过留下信息来指导其他蚂蚁的搜索，最终找到问题的最优解。

本文将介绍如何使用蚁群算法求解函数最小值问题。

1. 问题描述我们要求解函数f(x)的最小值，其中x是一个d维向量，f(x) = ∑(x_i^2)，i=1,2,...,d。

因为所有维度上的值都是正的，所以函数的最小值为0。

但在搜索过程中，优化器需要在向量空间中寻找最小值。

2. 蚁群算法基本思想3. 蚁群算法具体实现1）初始化初始化迭代次数、蚁群大小、信息素浓度以及每只蚂蚁的位置和速度。

对于每个蚂蚁的初始位置和速度，可以使用随机值来生成。

同时，需要记录当前所有蚂蚁中最优的位置和最优的适应度值。

2）信息素选取蚂蚁在搜索过程中留下信息，用于指导其他蚂蚁的行动。

信息素的选择需要权衡两个因素，即蚂蚁个体的局部搜索策略和群体策略。

在局部策略方面，蚂蚁会在已经访问的路径上留下信息素，吸引其他蚂蚁走向已经访问过的区域。

在群体策略方面，信息素可以加速全局搜索，吸引更多的蚂蚁在全局范围内搜索。

3）更新信息素蚂蚁在搜索过程中留下信息，导致当前路径上信息素的浓度增加。

信息素的浓度会随着时间的推移而逐渐降低。

信息素的更新根据当前路径的质量，决定增加或者减少信息素的浓度。

4）更新速度和位置根据留下的信息素和当前位置，更新蚂蚁的速度和位置。

5）计算适应度根据当前位置计算适应度。

这里的适应度即函数的值。

6）更新最优值如果当前的适应度比已记录的最优适应度更优，则更新记录的最优适应度值和位置。

7）终止条件循环运行以上步骤，直到达到指定的迭代次数或满足特定的终止条件。

4. 代码实现示例以Python语言为例，下面给出了求解函数最小值的蚁群算法实现示例：```pythonimport numpy as npclass Ant(object):def __init__(self, dim, max_pos, min_pos):self.dim = dimself.max_pos = max_posself.min_pos = min_posself.pos = np.random.uniform(min_pos, max_pos, size=dim)self.velocity = np.random.uniform(min_pos, max_pos, size=dim)self.pbest = self.posself.pbest_fitness = float('inf')self.fitness = float('inf')def evaluate(self, f):self.fitness = f(self.pos)if self.fitness < self.pbest_fitness:self.pbest = self.posself.pbest_fitness = self.fitnessdef update_velocity(self, other_ant_pos, w, c1, c2, max_velocity):r1 = np.random.rand(self.dim)r2 = np.random.rand(self.dim)self.velocity = w * self.velocity + c1 * r1 * (self.pbest - self.pos) + c2 * r2 * (other_ant_pos - self.pos)self.velocity = np.clip(self.velocity, -max_velocity, max_velocity)def update_pos(self):self.pos = self.pos + self.velocityself.pos = np.clip(self.pos, self.min_pos, self.max_pos)class ACO(object):def __init__(self, f, dim=2, max_iter=100, n_ant=10, max_velocity=1, w=0.5, c1=1, c2=1, max_pos=10, min_pos=-10):self.f = fself.dim = dimself.max_iter = max_iterself.n_ant = n_antself.max_velocity = max_velocityself.w = wself.c1 = c1self.c2 = c2self.max_pos = max_posself.min_pos = min_posself.global_best_fitness = float('inf')self.global_best_pos = np.zeros(dim)self.ants = [Ant(dim, max_pos, min_pos) for i in range(n_ant)]self.init_random_ant()def init_random_ant(self):for ant in self.ants:ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef search(self):for i in range(self.max_iter):for ant in self.ants:for other_ant in self.ants:if ant != other_ant:ant.update_velocity(other_ant.pos, self.w, self.c1, self.c2, self.max_velocity)ant.update_pos()ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef run(self):self.search()print("best fitness: {:.6f}, best position:{}".format(self.global_best_fitness, self.global_best_pos))def f(x):return np.sum(x**2)aco = ACO(f)aco.run()```在这个实现中，我们用Ant表示每个蚂蚁，包含了位置、速度、适应度等信息。

蚁群算法蚁狮算法

蚁群算法蚁狮算法
蚁群算法（Ant Colony Algorithm）是一种模拟蚂蚁觅食行为的启发式优化算法。

它通过模拟蚂蚁在寻找食物过程中释放信息素的行为，来解决组合优化问题。

蚂蚁在寻找食物时会在路径上释放一种化学物质，称为信息素，其他蚂蚁通过感知到信息素的浓度来选择路径，从而实现最优路径的搜索。

蚁群算法的基本思想是：在解空间中随机生成一群蚂蚁，每只蚂蚁根据当前位置和信息素浓度选择下一个移动位置，移动后释放信息素。

信息素浓度会随着时间的推移逐渐蒸发。

蚂蚁根据信息素浓度和启发函数来选择下一个位置，启发函数一般根据问题的特性来设计。

最终，通过迭代更新信息素浓度和蒸发，蚂蚁群体会逐渐收敛到最优解。

蚁狮算法（Ant Lion Optimizer）是一种基于蚁狮捕食行为的启发式优化算法。

蚁狮是一种昆虫，它会在沙地上挖掘坑穴，然后隐藏在坑穴中等待猎物。

当猎物掉进坑穴时，蚁狮会迅速捕捉并吃掉它。

蚁狮算法模拟了蚁狮捕食行为，通过追踪猎物的行为来寻找最优解。

蚁狮算法的基本思想是：在解空间中随机生成一群蚂蚁，每只蚂蚁根据当前位置和信息素浓度选择下一个移动位置。

与蚁群算法不同的是，蚁狮算法引入了一个蚁狮，它代表了当前最优解，蚂蚁会追踪蚁狮的位置。

当蚂蚁接近蚁狮时，它会增加信息素浓度，从而吸引其他蚂蚁朝着蚁狮方向移动。

蚁狮会不断更新自身位置，以寻找
更优解。

最终，通过迭代更新信息素浓度和蚁狮位置，蚂蚁群体会逐渐收敛到最优解。

蚁群算法ppt课件

，则以概率
pij
ij (k 1) , j T ij (k 1)
， pij 0, j T
lT
到达j，L(s) L(s) { j},i : j；若L(s) N且T {l | (i,l) A,l L(s)}{i0}
则到达 i0, L(s) L(s) {i0},i : i0; 重复STEP 2。 16
在STEP 3中，蚁群永远记忆到目前为止的最优解。
19
图的蚁群系统（GBAS）
四个城市的非对称TSP问题，距离矩阵和城市图示如下：
0 1 0.5 1
D
(dij
)
1
1.5
0 5
1 0
1
1
1 1 1 0
20
5 初始的蚁群优化算法—基于图的蚁群系统（GBAS）
假设共4只蚂蚁，所有蚂蚁都从城市A出发，挥发因子
出蚂计蚁s算行得走到的的城最市好集解合。，否初则始使L蚂(s蚁) 为s从空起集点，1i0出s发，m用。L(s) 表示
STEP 2 (内循环) 按蚂蚁1 s m的顺序分别计算。当蚂蚁在城市i，若 L(s) N或{l | (i,l) A,l L(s)}
完成第s只蚂蚁的计算。否则，若
L(s) N且T {l | (i,l) A,l L(s)} {i0}
31 168
1 24
0
这是第一次外循环结束的状态。
为了说明蚁群算法的原理，先简要介绍一下蚂蚁搜寻食物的具体过程。在蚁群寻找食物时，它们总能找到一条从食物到巢穴之间的最优路径。这是因为蚂蚁在寻找路径时会在路径上释放出一种特殊的信息素。当它们碰到一个还没有走过的路口时．就随机地挑选一条路径前行。与此同时释放出与路径长度有关的信息素。路径越长，释放的激索浓度越低.当后来的蚂蚁再次碰到这个路口的时候．选择激素浓度较高路径概率就会相对较大。这样形成一个正反馈。最优路径上的激索浓度越来越大．而其它的路径上激素浓度却会随着时间的流逝而消减。最终整个蚁群会找出最优路径。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

$
{
)" $%%&’ *#
" $ （（ ! &’ ( ） &’ ( ） # ， ’ " $%%&’ *# ， " $ （（ &) ( ） &) ( ） # !!
（"）
（#）（0）
& !&’ !
#
& !&’ ， ! #!"
#
& !&’ 表示第 # 只蚂蚁作本次循环中留在路径 &’ 上的信息量， & !&’ 表示本次循环中路径 &’ 上的信息量的增量（局部调整准则） ! / ，若第 # 只蚂蚁在本次循环中经过 &’ # 0 # （1） & !&’ ! (，否则其中，（ ( ）! /是常数， 0# 表示第 # 只蚂蚁在本次循环中所走路径的长度 ! 在初始时刻， !&’ …， "， ( &， ’ ! (， "， + , "） 1"， & !&’ ! （ $ 分别表示蚂蚁在运动过程中所积累的信息及启发式因子在可根据某种启发式算蚂蚁选择路径中所起的不同作用 ! #&’ 表示出城市 & 转移到城市 ’ 的期望程度，法具体确定 ! 根据具体算法的不同，（，（及 %（的表达形式可以不同，要根据具体问题 ! & ! &’ ( ） &’ ( ） &’ ( ）而定 ! 2&,-3& 4 曾给出三种不同模型，分别称之为 $5)6787%+ .8.)+9、 $5)6:;$5)-)8 .8.)+9、 $5)6<+5.-)8 ! 它们的差别在于表达式（1）的不同 ! 在 $5)6:;$5)-)8 .8.)+9 模型中：
第 !’ 卷第 ’ 期 &""! 年 !& 月
宁波大学学报（理工版）（@6GG） <=>?@AB =C @D@E/= >@DFG?6D-H
F1I+ !’ @1+ ’ 0JK+ &""!
文章编号：（&""!） !""!#$!%& "’#""$&#"’
用于一般函数优化的蚁群算法
魏平，熊伟清
’
"$ ! * )* # " ）（
，
$） #)*
（%）
（ !* " *"$
其中，将（$）式中的轨迹强度!)* 改为即目标函 !* 称为蚂蚁 * 的邻域吸引强度， #)* 我们定义为 #) + #* ，数差异值；参数"，［$，，可得（%）式’ &］ $! 强度更新方程
!*
, -$
人工蚁群算法是受到人们对自然界中真实的蚁群集体行为的研究成果的启发而提出的一种基于种群的模拟进化算法，属于随机搜索算法 + 由意大利学者 012341 5 等人首先提出，充分利用了蚁群搜索食物的过程与著名的旅行商问题（ -6.）之间的相似性，通过人工模拟蚂蚁搜索食物的过程（即：通过个体之间的信息交流与相互协作最终找到从蚁穴到食物源的最短路径）来求解 -6.，为了
{ {
{
# & &’
!
/ ，若第 # 只蚂蚁在时刻 ( 和 ( . " 本次循环中经过 &’ ， *&’
（=）
否则 1 (1 在 $5)6<+5.-)8 .8.)+9 模型中： / ，若第 # 只蚂蚁在时刻 ( 和 ( . " 本次循环中经过 &’ ， # （>） & !&’ ! 否则 1 (1 它们的区别在于：后两种模型中，利用的是局部信息，而前者利用的是整体信息，在求解 ?@A 问题时，性能较好，因而通常采用它作为基本模型 ! 蚁群算法主要包含 # 个基本阶段：适应阶段和协作阶段 ! 在适应阶段，各候选解根据积累的信息不断调整自身结构；在协作阶段，候选解之间通过信息该算法复杂度为 B （ +2 ・ + 0）其中 +2 交流，以期望产生性能更好的解 ! 由算法复杂性分析理论可知，表示循环次数 ! 算法中的参数设定目前尚无理论上的依据，经验结果为：（"）（#）（0） "# "# ( ! =# ! #=； #=； # " # ［0］（1） ( ! CC， " # / # "( (((， / 对算法的影响不大 ! #取 ( ! D 左右为佳；
［&］来寻求最优解 + 蚁群算法具有如下优点：
（!）较强的鲁棒性：对基本蚁群算法模型稍加修改，便可以应用于其它问题；（&）分布式计算：蚁群算法是一种基于种群的进化算法，具有本质并行性，易于并行实现；（%）易于与其它方法给合：蚁群算法很容易与多种启发式算法绪合，以改善算法的性能 + 众多研究已经证明蚁群算法具有很强的发现较好解的能力，这是因为该算法不仅利用了正反馈原理，在一定程度上可以加快进化过程，而且是一种本质并行的算法，不同个体之间不断进行信息交流和传递，从而能够相互协作，有利于发现较好解 + 本文探讨利用蚁群算法来求解一般函数化 +
［!］区别于真实蚂蚁群体系统，我们称这种算法为 “人工蚁群算法” 分配 + 并用该方法求解 -6. 问题、问题、取得了较好的实验结果 + 虽然对此方法的研究刚刚起步，但研究表明蚁群 718#9:1; 调度问题，
算法在求解复杂优化问题（特别是离散优化问题）方面的一些优越性，证明它是一种很有发展前景的方法，这种带有构造性特征的新的搜索方法已产生并被广泛应用 + 蚁群算法是一种随机搜索算法，与其它模拟进化算法一样，通过后选解组成的群体在进化过程
3
实验结果
下面的函数各参数取值为： / " $， 4 " *5&5 " " $， $ " $， % " * 5 %，著名的 9/:;#-</.= 函数：
2 （ $2 + $2 （$ + $ $），［ + 2 5 *4(， 6 $ " $** $) ! 2 5 *4(］ 5 ) " $， 2 $ ）最大值解有 2 个（ # 2 5 *4(，+ 2 5 *4(）" 3 ()% 5 %34 2 和（ # + 2 5 *4(，+ 2 5 *4(）" 3 )*& 5 )26 2 5 我们用标准遗传算法求解多数收敛在（要收敛在最优解采取了许多 # 2 5 *4(，+ 2 5 *4(）" 3 ()% 5 %34 2，［4］万方数据措施 ’ 该问题采用蚁群算法，迭代次数 > $* 就能得到最优解（ ’ " $* ， # + 2 5 *4( ， + 2 5 *4( ）"
万方数据
平（!,*$ ( ），女，汉族，山东平度人，讲师 +
第1期
魏
平等：用于一般函数优化的蚁群算法
=0
（ # ! "， …，根据各条路径上的信息量决定转移方向， ! 蚂蚁 # #， $ ）在运动过程中， ! "（常数） # 表示在 ( 时刻蚂蚁 # 由位置 & 转移到位置 ’ 的概率（称为转移概率准则） %（ &’ ( ）
#
用于函数优化的蚁群算法模型及其实现
在一般函数优化问题中，由于最初的蚁群算法思想起源于离散型的网络路径问题，因此，必须万方数据对许多实施细节加以修正 ! 我们先来考察简单一维搜索 !
&4
宁波大学学报（理工版）
2**$
假定优化函数为 !"# ! " （， $! ［ %，，转移概率准则： # $） &］设 ’ 个人工蚂蚁，刚开始时位于区间［ %，的 ’ 等分处，蚂蚁的转移概率定义为 &］ ()* "
%# &’ !
(， &)*+,’-.+ 其中， …，人 $%%&’+ *# ! ｛ (， "， + , "｝, )$/ -# 表示蚂蚁 # 下一步允许选择的城市 ! 与实际蚁群不同，工蚁群系统具有记忆功能， …，集合随着 )$/ -（ #， $ ）用以记录蚂蚁 # 当前所走过的城市， # # ! "，以前留下的信息逐渐消逝，用参数 " , % 表示信息消 )$/ -# 进化过程作动态调整 ! 随着时间的推移，蚂蚁完成一次循环，各路径上信息量要根据下式作调整（全局调整准则）：逝程度，经过 + 个时刻，（（ ! ! !&’ ， &’ ( . + ）! %・ &’ ( ）. &
!
基本蚁群系统模型
为了便于理解，我们以求解平面上 ! 个城市的 -6. 问题（"， …，! " # 表示城市序号）为例说 !，明蚁群系统模型 + 为模拟实际蚂蚁行为，首先引进如下记号：设 $ 为蚂蚁群中蚂蚁的数目，%（ ’ &’ & ， … !）表示城市 & 和城市 ’ 之间的距离，) （ &， ( !， & * ）表示 * 时刻位于城市 & 的蚂蚁的个数，$ (

用于一般函数优化的蚁群算法

蚁群算法

蚁群算法及案例分析精选全文

蚁群算法

一种求解函数优化的自适应蚁群算法

用于求解函数优化的蚁群算法设计

蚁群算法（ACO）解决TSP问题

蚁群算法求函数最大值的程序

蚁群算法求解函数优化的算法设计

用于求解函数优化的蚁群算法设计

蚁群算法matlab代码

蚁群算法（C语言实现）

蚁群算法步骤

蚁群优化算法PPT

蚁群算法、遗传算法、模拟退火算法介绍

《蚁群算法》课件

23个基本测试函数 蚁群算法

人工智能：蚁群算法及其应用

蚁群算法求解函数最小值

蚁群算法 蚁狮算法

蚁群算法ppt课件

23个基本测试函数蚁群算法

蚁群算法蚁狮算法