理科数学2010-2019高考真题分类训练专题五平面向量第十四讲向量的应用

合集下载

高考数学真题分类专题五平面向量第十四讲向量的应用答案

专题五平面向量第十四讲向量的应用答案部分2019年1.解析设()2AD AB A AO C λλ==+，1()(1)3AO AE EO AE EC AE AC AE AE AC AB AC μμμμμμ-=+=+=+-=-+=+，所以1232λμλμ-⎧=⎪⎪⎨⎪=⎪⎩，解得1214λμ⎧=⎪⎪⎨⎪=⎪⎩，所以11()24AO AD AB AC ==+，13EC AC AE AB AC =-=-+， 221131266()()()43233AO EC AB AC AB AC AB AB AC AC ⋅=⨯+⨯-+=-+⋅+=221322AB AB AC AC -+⋅+，因为221322AB AC AB AB AC AC ⋅=-+⋅+，所以221322AB AC =，所以223AB AC=，所以ABAC=. 2.解析：正方形ABCD 的边长为1，可得AB AD AC +=，BD AD AB =-，0AB AD ⋅=，123456||AB BC CD DA AC BD λλλλλλ+++++12345566||AB AD AB AD AB AD AD AB λλλλλλλλ=+--+++- 13562456|()()|AB AD λλλλλλλλ=-+-+-++ =由于(1,2,3,4,5,6)i i λ=错误!未找到引用源。

2，3，4，5，错误!未找到引用源。

取遍1±，可得13560λλλλ-+-=，24560λλλλ-++=，可取5613241,1,1,1λλλλλλ=====-=，可得所求最小值为0；由13564λλλλ-+-=，24564λλλλ-++=，可取2456131,1,1,1,1,λλλλλλ==-====-可得所求最大值为3.解析因为AB BE =，//AD BC ，30A ∠=，所以在等腰三角形ABE 中，120BEA ∠=，又AB =，所以25BE AD =-. 因为AE AB BE =+，所以25AE AB AD =-. 又BD BA AD AB AD =+=-+，所以()22272555BD AE AB AD AB AD AB AB AD AD ⎛⎫⋅=-+⋅-=-+⋅-= ⎪⎝⎭2272cos 55AB AB AD A AD -+⋅-=7212525155-+⨯⨯-⨯=-. 2010-2018年1．A 【解析】以A 为坐标原点，AB 所在直线为x 轴，建立如图的平面直角坐标系，因为在平面四边形ABCD 中，1AB AD ==，120BAD ∠=︒，所以(0,0)A ，(1,0)B，1(,22D -，设(1,)C m ,(,)E x y ，所以3(,2DC m=，1(2AD =-，因为AD CD ⊥，所以31(,(022m ⋅-=，即31()02222m ⨯-+-=，解得m =C ，因为E 在CD上，所以2y ≤CE CD k k =，2112=+，即2x =-，因为(,)AE x y =，(1,)BE x y =-，所以2222(,)(1,)2)2AE BE x y x y x x y y ⋅=⋅-=-+=--++246y =-+，令2()46f y y =-+，y ∈．因为函数2()46f y y =-+在上单调递减，在上单调递增，所以2min 21()4(68816f y =⨯-+=．所以⋅AE BE 的最小值为2116，故选A ． 2．A 【解析】解法一设O 为坐标原点，OA =a ，(,)OB x y ==b ，=(1,0)e ，由2430-⋅+=b e b 得22430x y x +-+=，即22(2)1x y -+=，所以点B 的轨迹是以(2,0)C 为圆心，l 为半径的圆．因为a 与e 的夹角为3π，所以不妨令点A在射线y =(0x >)上，如图，数形结合可知min ||||||31CA CB -=-=-a b ．故选A ．解法二由2430-⋅+=b e b 得2243()(3)0-⋅+=-⋅-=b e b e b e b e ．设OB =b ，OE =e ，3OF =e ，所以EB -=b e ，3FB -b e =，所以0EB FB ⋅=，取EF 的中点为C ．则B 在以C 为圆心，EF 为直径的圆上，如图．设OA =a ，作射线OA ，使得3AOE π∠=，所以|||(2)(2)|-=-+-≥a b a e e b|(2)||(2)|||||31CA BC ---=-≥a e e b ．故选A ．3．A 【解析】如图建立直角坐标系，则(0,1)A ，(0,0)B ，(2,1)D ，(,)P x y 所以圆的方程为224(2)5x y -+=，所以(,1)AP x y =-，(0,1)AB =-，(2,0)AD =，由AP AB AD λμ=+，得21x y μλ=⎧⎨-=-⎩，所以λμ+=12xy -+，设12x z y =-+，即102xy z -+-=，点(,)P x y 在圆上，所以圆心到直线102xy z -+-=的距离小于半径，≤，解得13z ≤≤，所以z 的最大值为3，即λμ+的最大值为3，选A ．4．B 【解析】如图，以BC 为x 轴，BC 的垂直平分线DA 为y 轴，D 为坐标原点建立平面直角坐标系，则 (0,3)A ，(1,0)B -，(1,0)C ，设(,)P x y ，所以 (,3)PA x y =--，(1,)PB x y =---，(1,)PC x y =--，所以 (2,2)PB PC x y +=--，22()22)22(PA PB PC x y y x y ⋅+=-=+-23322--≥，当P 时，所求的最小值为32-，故选B ． 5．C 【解析】如图所示，四边形ABCE 是正方形，F 为正方形的对角线的交点，易得AO AF <，而90AFB ∠=，∴AOB ∠与COD ∠为钝角，AOD ∠与BOC ∠为锐角．根据题意12()I I OA OB OB OC OB OA OC OB CA -=⋅-⋅=⋅-=⋅=||||cos 0OB CA AOB ∠<，∴12I I <，同理23I I >．做AG BD ⊥于G ，又AB AD =．∴OB BG GD OD <=<，而OA AF FC OC <=<，∴||||||||OA OB OC OD ⋅<⋅，而cos cos 0AOB COD ∠=∠<， ∴OA OB OC OD ⋅>⋅，即13I I >， ∴312I I I <<，选C ．G FEOABCD6．B【解析】由2DA DB DC ===知,D 为ABC ∆的外心．由DA DB ⋅=DB DC ⋅=DC DA ⋅ 知D 为ABC ∆的内心，所以ABC ∆为正三角形，易知其边长为23，取AC 的中点E ，因为M 是PC 的中点，所以1122EM AP ==，所以max 17||||22BM BE =+=，则2max49||4BM =．故选B ． 7．D 【解析】由菱形ABCD 的边长为a ，60ABC ∠=可知18060120BAD ∠=-=，2223()()cos1202BD CD AD AB AB AB AD AB a a a a ⋅=-⋅-=-⋅+=-⋅+=．8．A 【解析】由题意得111333=+=+=+-AD AC CD AC BC AC AC AB1433=-+AB AC ．9．A 【解析】以题意，以点A 为坐标原点，以AB 所在的直线为x 轴，AC 所在的直线为y 轴建立如图所示的平面直角坐标系，所以点(1,4)P ，1(,0)B t，(0,)C t ，所以11(1,4)(1,4)(1)(1)4(4)PB PC t t t t⋅=----=-⨯--⨯-=1174t t --117413t t -⨯=≤（当且仅当14t t =，即12t 时取等号），所以PB PC ⋅的最大值为13．故选A ．10．C【解析】311 ,443AM AB AD NM CM CN AD AB=+=-=-+，所以11(43)(43)412AM NM AB AD AB AD⋅=+⋅-2211(169)(1636916)94848AB AD=-=⨯-⨯=，选C．11．B 【解析】由题意得，AC为圆的直径，故可设),(nmA，),(nmC--，),(yxB ，∴(6,)PA PB PC x y++=-，而491237)6(22≤-=+-xyx，∴PA PB PC++的最大值为7，故选B．12．A【解析】设(1,0),(0,1)a b==，则(cos,sin)OPθθ=，(2,2)OQ=，所以曲线C是单位元，区域Ω为圆环（如图）∵||2OQ=，∴13r R<<<．13．C【解析】因为120BAD，所以cos1202AB AD AB AD.因为BE BC，所以AE AB AD，AF AB AD.因为1AE AF，所以1AB AD AB AD，即3222①同理可得23②，①+②得56.14．B【解析】如图，设,AB b AC c==，则1,2,0b c b c==•=，CBQP又(1)BQ BA AQ b c λ=+=-+-，CP CA AP c b λ=+=-+，由2-=•得22[(1)]()(1)4(1)2b c c b c b λλλλλλ-+-•-+=--=--=-，即32,23==λλ，选B. 15．A 【解析】【方法一】设34(10cos ,10sin )cos ,sin 55OP θθθθ=⇒==则33(10cos(),10sin())(44OQ ππθθ=++=-．【方法二】将向量(6,8)OP =按逆时针旋转32π后，可知Q 点落在第三象限，则可排除B 、D ，代入A ，由向量的夹角公式可得cos 2QOP ∠=-，∴34QOP π∠=． 16．C 【解析】首先观察集合113{|},1,,0,,1,,2,2222nn Z ⎧⎫∈=⋅⋅⋅--⋅⋅⋅⎨⎬⎩⎭，从而分析a b和b a 的范围如下：因为(0,)4πθ∈，∴cos 12θ<<，而||cos ||θ⋅==⋅b a b b a a a a ，且||||0>a b ，可得||0cos 1||θ<<b a ，又∵∈b a {|}2∈nn Z 中，∴||1cos ||2θ=b a ，从而||1||2cos θ=b a ，∴2||cos 2cos ||θθ⋅===⋅a b a a b b b b ，所以12<<a b ．且a b 也在集合{|}2∈nn Z 中，故有32=a b ． 17．D 【解析】根据已知得(,0)(0,0)[(1,0)(0,0)]c λ-=-，即(,0)(1,0)c λ=，从而得c λ=；(,0)(0,0)[(1,0)(0,0)]d μ-=-，即(,0)(1,0)d μ=，得d μ=，根据112λμ+=，得112c d+=．线段AB 的方程是0y =，[0,1]x ∈．若C 是线段AB 的中点，则12c =，代入112c d +=，得10d=．此等式不可能成立，故选项A 的说法不成立；同理选项B 的说法也不成立；若,C D 同时在线段AB 上，则01c <≤，01d <≤，此时11c ≥，11d≥，112c d +≥，若等号成立，则只能1c d ==，根据定义，,C D 是两个不同的点，故矛盾，故选项C 的说法也不正确，若,C D 同时在线段AB 的延长线上，若1c >，1d >，则112c d+<，与112c d +=矛盾，若0,0c d <<，则11c d +是负值，与112c d+=矛盾，若1c >，0d <，则11c <，10d <，此时111c d +<，与112c d+=矛盾，故选项D 的说法是正确的．18．3-【解析】设(0,)E t ，(0,2)±F t ，所以(1,)(2,2)⋅=⋅-±AE BF t t222(2)22(1)3=-+±=±-=±-t t t t t ，当1=±t 时，AE BF ⋅取得最小值3-．19．[-【解析】设(,)P x y ，由20PA PB ⋅≤，得250x y -+≤，x如图由250x y -+≤可知，P 在MN 上，由2225050x y x y -+=⎧⎨+=⎩，解得(1,7)M ，(5,5)N --，所以P 点横坐标的取值范围为[-．20．311【解析】032cos603AB AC ⋅=⨯⨯=，1233AD AB AC =+,则12212()()34934333333AD AE AB AC AC AB λλλ⋅=+-=⨯+⨯-⨯-⨯=-，311λ=．21．12【解析】由题意令(1,0)=e ，(cos ,sin )αα=a ，(2cos ,2sin )ββ=b ，则由||||6+ae be 可得|cos |2|cos |6αβ+ ①，令sin 2sin m αβ+= ②22①+②得24[|cos cos |sin sin ]1m αβαβ++对一切实数,αβ恒成立，所以4[|cos cos |sin sin ]1αβαβ+．故12(cos cos sin sin )2[|cos cos |sin sin ]2αβαβαβαβ⋅=++a b ．故最大值为12． 22．12 16 【解析】由1111()3232MN MC CN AC CB AC AB AC =+=+=+-1126AB AC xAB y AC =-=+．所以12x，16y ． 23．2918 【解析】因为19DF DC λ=，12DC AB =，119199918CF DF DC DC DC DC AB λλλλλ--=-=-==，AE AB BE AB BC λ=+=+，19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+， ()1918AE AF AB BC AB BC λλλ+⎛⎫⋅=+⋅+ ⎪⎝⎭22191911818AB BC AB BC λλλλλλ++⎛⎫=+++⋅ ⎪⎝⎭ 19199421cos1201818λλλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥=当且仅当2192λλ=即23λ=时的最小值为2918． BA24．1(1)(1)(cos,sin cos )(cos ,sin 66666k k k k k k k a a πππππ+++⋅=+⋅+(1)cos )6k π+2(1)2cos sincos cos sin 66666k k k k πππππππ+++=+++1(21)cos 26k π+，因此11103312k k k a a +=⋅==∑ 25．2【解析】因为120BAD，菱形的边长为2，所以2AB AD .因为113AE AFABAD ADAB λ，由1AE AF，所以4412(1)133λλ+-+=，解得2λ=． 26．1+(,)D x y ，由||1CD =，得22(3)1x y -+=，向量OA OB OD ++(1,x y =-+，故||(OA OB OC x ++=的最大值为圆22(3)1x y -+=上的动点到点(1,距离的最大值，其最大值为圆22(3)1x y -+=的圆心(3,0)到点(1,的距离加上圆的半径，11=27．2【解析】以A 为坐标原点，AB ，AD 所在的直线分别为x ，y 轴建立直角坐标系，则B ，E ，(0,2)D ，2)C ．设(,2)F x (0≤x ≤2)，由21AB AF x ⋅=⇒=，∴(1,2)F ，AE BF =()1,2⋅(1-2,2)=2．28．(2sin 2,1cos 2)--【解析】如图过P 作x 轴的垂线，垂足为E ，过C 作y 轴的垂线，垂足为A ，根据题意可知圆滚动了2个单位的弧长，BAC E∴2PCD ∠=，可知22PCB π∠=-，此时点P 的坐标为2cos(2)2sin 2,2P x π=--=-1sin(2)1cos 2,2P y π=+-=-另解1：根据题意可知滚动制圆心为（2,1）时的圆的参数方程为⎩⎨⎧+=+=θθsin 1cos 2y x ，且223,2-==∠πθPCD ，则点P 的坐标为⎪⎩⎪⎨⎧-=-+=-=-+=2cos 1)223sin(12sin 2)223cos(2ππy x ，即)2cos 1,2sin 2(--=OP . 29．14-【解析】根据已知得1()2AD AB AC =+，23BE AC AB =-，所以AD BE ⋅=1()2AB AC +⋅（23AC AB -）=1211(1)2334AB AC --⋅=-．30．【解析】(1)∵⊥m n ，∴0⋅=m n，故cos 022x x -=，∴tan 1x ．（2）∵m 与n 的夹角为3π，∴122cos ,112x x⋅<>===⨯m n m n |m ||n |，故1sin()42x π-=，又(0,)2x π∈，∴(,)444x πππ-∈-，46x ππ-=，即512x π．故x 的值为512π．31．【解析】（Ⅰ）已知()sin2cos2f x m x n x =⋅=+a b ，)(x f 过点)2,32(),3,12(-ππ，∴()sin cos 1266f m n πππ=+=234cos 34sin )32(-=+=πππn m f∴12122m ⎧+=⎪⎪⎨⎪-=-⎪⎩解得⎩⎨⎧==13n m（Ⅱ）由（Ⅰ）知)62sin(22cos 2sin 3)(π+=+=x x x x f由题意知()()2sin(22)6g x f x x πϕϕ=+=++设()y g x =的图象上符合题意的最高点为0(,2)x由题意知2011x +=．所以00x =，即到点(0,3)的距离为1的最高点为(0,2)．将其代入()y g x =得sin 216πϕ⎛⎫+= ⎪⎝⎭，又∵0ϕπ<<，所以6πϕ=，因此()2sin 22cos 22g x x x π⎛⎫=+= ⎪⎝⎭由222,k x k k Z πππ-+≤≤∈，得z k k x k ∈≤≤+-,2πππ∴()f x 的单调增区间为[,],2k k k πππ-+∈Z ．32．【解析】（Ⅰ）∵1cos ,3,cos 233acB b BA BC ca B ==⋅===，且222-cos 2a c b B ac+=，∴c 6,5a a c =+=，∵a c >，∴解得3,2a c ==．所以3,2a c ==．（Ⅱ）∵1cos 3B =，∴sin B =，∵3,3,2a b c ===，222-c 7cos 29a b C ab +==，sin 9C =，∴23cos(-)cos cos sin sin 27B C B C B C =+=，故23cos(-)27B C =． 33．【解析】（1）-a b ＝(cos cos ,sin sin )αβαβ--，2||-a b ＝22(cos cos )(sin sin )αβαβ-+-＝22(cos cos sin sin )2αβαβ-⋅+⋅=．所以，cos cos sin sin 0αβαβ⋅+⋅=，所以，b a ⊥．（2）⎩⎨⎧=+=+②1sin sin ①0cos cos βαβα，①2＋②2得：1cos()2αβ-=-．所以，αβ-＝π32，α＝π32＋β，带入②得：sin (π32＋β)＋sin β＝23cos β＋12sin β＝sin (3π＋β)＝1，所以，3π＋β＝2π．所以，α＝65π，β＝6π．34．【解析】由题意，抛物线E 的焦点为(0,)2p F ，直线1l 的方程为12py k x =+．由1222p y k x x py⎧=+⎪⎨⎪=⎩得22120x pk x p --=．设A ，B 两点的坐标分别为11(,)A x y ，22(,)B x y ，则1x 、2x 是上述方程的两个实数根．从而1212x x pk +=，212121()2y y k x x p pk p +=++=+．所以点M 的坐标为211(,)2ppk pk +，211(,)FM pk pk =．同理可得点N 的坐标为222(,)2p pk pk +，222(,)FN pk pk =．于是2221212()FM FN p k k k k ⋅=+．由题设，有k 1＋k 2＝2，k 1>0，k 2>0，k 1≠k 2，所以212120()12k k k k +<<=．故222(11)2FM FN p p ⋅<+=．(2)【解析】由抛物线的定义得1||2p FA y =+，2||2p FB y =+，所以2121||22AB y y p pk p =++=+，从而圆M 的半径211r pk p =+．故圆M 的方程为22222111()()()2p x pk y pk pk p -+--=+．化简得22221132(21)04x y pk x p k y p +--+-=．同理可得圆N 的方程为22222232(21)04x y pk x p k y p +--+-=．于是圆M ，圆N 的公共弦所在直线l 的方程为222121()()0k k x k k y -+-=．又k 2－k 1≠0，k 1＋k 2＝2，则l 的方程为x ＋2y ＝0. 因为p >0，所以点M 到直线l 的距离222117[2()]p k d ++===故当114k =-时，d．，解得8p =．故所求的抛物线E 的方程为216x y =． 35．【解析】（I）由2222)(sin )4sin ax x x =+=，222(cos )(sin )1b x x =+=，及2,4sin 1a b x ==得又1[0,],sin 22x x π∈=从而，所以6x π=.（II）2()cos sin f x a b x x x =⋅=⋅+=1112cos 2sin(2)22262x x x π-+=-+. 当[0.]sin 2- 1.326x x πππ=∈时，（）取最大值所以3().2f x 的最大值为 36．【解析】（1）由(2,1)MA x y =---，(2,1)MB x y =--，(MA MB +=-()(,)(0,2)2OM OAOB x y y ⋅+=⋅=，=22y +．化简得曲线C 的方程：24x y =．（2）假设存在点(0,)(0)P t t >满足条件，则直线PA 的方程是12t y x t -=+，PB 的方程是12ty x t -=+．曲线C 在Q 处的切线l 的方程是20024x x y x =-，它与y 轴的交点为2(0,)4x F - 由于022x -<<，因此0112x -<<． ①当10t -<<时，11122t --<<-，存在0(2,2)x ∈-，使得0122x t -=．即l 与直线PA 平行，故当10t -<<时不符合题意． ②1t-时，011,22x t --<1122x t ->，所以l 与直线,PA PB 一定相交．分别联立方程组0201224t y x t x x y x -⎧=+⎪⎪⎨⎪=-⎪⎩，解得,D E 的横坐标分别是 20042(1)D x t x x t +=+-，20042(1)E x t x x t +=+-，则202204(1)(1)E D x tx x t x t +-=--- 又204x FP t =--，有220220(4)1128(1)PDE E D x t t S FP x x t x ∆+-=⋅⋅-=⋅--，又2200414(1)242QABx x S ∆-=⋅⋅-=，于是22200220(4)(1)41(4)QAB PDEx x t S S t x t ∆∆⎡⎤---⎣⎦=⋅-+=422200422004(1)4(1)41816x t x t t x tx t⎡⎤-+-+-⎣⎦⋅-++，对任意0(2,2)x ∈-，要使QAB PDES S ∆∆为常数，即只需t 满足2224(1)84(1)16t tt t⎧---=⎨-=⎩，解得1t =-，此时2QAB PDES S ∆∆=，故存在1t =-，使得QAB ∆与PDE ∆的面积之比是常数2．37．【解析】由λ=知Q ，M ，P 三点在同一条垂直于x 轴的直线上，故可设 .)1(),(),,(),,(),,(2020220y x y x y y x x x M y x Q y x P λλλ-+=-=-则则 ①再设),1,1().(,),,(010111y x y y x x y x B --=--=λλ即由解得⎩⎨⎧-+=-+=.)1(,)1(011λλλλy y x x ②将①式代入②式，消去0y ，得⎩⎨⎧-+-+=-+=.)1()1(,)1(2211λλλλλλy x y x x ③ 又点B 在抛物线2x y =上，所以211x y =，再将③式代入211x y =，得.012),1(,0.0)1()1()1(2,)1(2)1()1()1(,))1(()1()1(22222222=--+>=+-+-+++-+=-+-+-+=-+-+y x y x x x y x x y x 得两边同除以因λλλλλλλλλλλλλλλλλλλλλλλ故所求点P 的轨迹方程为.12-=x y38．【解析】（1）（方法一）由题设知(3,5),(1,1)AB AC ==-，则(2,6),(4,4).AB AC AB AC +=-=所以||210,||4 2.AB AC AB AC +=-=故所求的两条对角线的长分别为．（方法二）设该平行四边形的第四个顶点为D ，两条对角线的交点为E ，则: E 为B 、C 的中点，E （0，1）又E （0，1）为A 、D 的中点，所以D （1，4）故所求的两条对角线的长分别为BC =、AD = （2）由题设知：OC =(－2,－1)，(32,5)AB tOC t t -=++．由(OC t AB -)·OC =0，得：(32,5)(2,1)0t t ++⋅--=，从而511,t =-所以115t =-．或者：2· AB OC tOC =，(3,5),AB =2115||AB OC t OC ⋅==-．。

2010—2019“十年高考”数学真题分类汇总平面向量专题解析版 (可下载)

2010—2019“十年高考”数学真题分类汇总平面向量专题（附详细答案解析）一、选择题。

1.（2019全国Ⅰ文8）已知非零向量a ，b 满足a =2b ，且（a –b ）⊥b ，则a 与b 的夹角为 A ．π6 B ．π3 C ．2π3 D ．5π6【答案】B ．【解析】因为()-⊥a b b ，所以()22cos ,0-⋅⋅-=⋅<>-=a b b =a b b a b a b b ，所以22cos ,2<>===⋅bba b a bb又因为0,]π[<>∈，a b ，所以π,3<>=a b ．故选B ． 2.（2019全国Ⅱ文3）已知向量a =(2，3)，b =(3，2)，则|a –b |= AB ．2C ．D ．50 【答案】A ．【解析】因为(2,3)=a ，(3,2)=b ，所以-(1,1)=-a b ，所以-==a b A.3.（2018全国卷Ⅰ）在∆ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB = A ．3144AB AC - B ．1344AB AC - C ．3144AB AC + D ．1344AB AC + 【答案】A.【解析】法一、通解如图所示，CB AD DB ED EB 2121+=+= ()()AC AB AC AB -++⨯=212121 3144=-AB AC ．故选A ．CB法二、优解111()222=-=-=-⨯+EB AB AE AB AD AB AB AC 3144=-AB AC ．故选A ． 4.（2018全国卷Ⅱ）已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b A ．4B ．3C ．2D ．0【答案】B.【解析】2(2)22(1)3⋅-=-⋅=--=a a b a a b ，故选B ．5.（2018天津）在如图的平面图形中，已知1OM =，2ON =，120MON ∠=，2BM MA =， 2CN NA =，则·BC OM 的值为 A ．15- B ．9- C ．6- D ．0【答案】C.【解析】由2BM MA =，可知||2||BM MA =，∴||3||BA MA =．由2CN NA =，可知||2||CN NA =，∴||3||CA NA =，故||||3||||BA CA MA NA ==，连接MN ，则BC MN ∥，且||3||BA MN =， ∴33()BC MN ON OM ==-，∴23()3()BC OM ON OM OM ON OM OM ⋅=-⋅=⋅-23(||||cos120||)6ON OM OM =-=-．故选C ．6.（2018浙江）已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430-⋅+=b e b ，则||-a b 的最小值是A 1B 1C ．2D ．2 【答案】A.【解析】解法一设O 为坐标原点，OA =a ，(,)OB x y ==b ，=(1,0)e ，由2430-⋅+=b e b 得22430x y x +-+=，即22(2)1x y -+=，所以点B 的轨迹是以(2,0)C 为圆心，l 为半径的圆．NMOCBA因为a 与e 的夹角为3π，所以不妨令点A在射线y =(0x >)上，如图，数形结合可知min ||||||31CA CB -=-=-a b ．故选A ．解法二由2430-⋅+=b e b 得2243()(3)0-⋅+=-⋅-=b e b e b e b e ．设OB =b ，OE =e ，3OF =e ，所以EB -=b e ，3FB -b e =，所以0EB FB ⋅=，取EF 的中点为C ．则B 在以C 为圆心，EF 为直径的圆上，如图．设OA =a ，作射线OA ，使得3AOE π∠=，所以|||(2)(2)|-=-+-≥a b a e e b|(2)||(2)|||||31CA BC ---=-≥a e e b ．故选A ．7.（2017北京）设m , n 为非零向量，则“存在负数λ，使得λ=m n ”是“0⋅<m n ”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A.【解析】因为,m n 为非零向量，所以||||cos ,0⋅=<><m n m n m n 的充要条件是cos ,0<><m n ．因为0λ<，则由λ=m n 可知,m n 的方向相反，,180<>=m n ，所以cos ,0<><m n ，所以“存在负数λ，使得λ=m n ”可推出“0⋅<m n ”；而0⋅<m n 可推出cos ,0<><m n ，但不一定推出,m n 的方向相反，从而不一定推得“存在负数λ，使得λ=m n ”，所以“存在负数λ，使得λ=m n ”是“0⋅<m n ”的充分而不必要条件．8.（2017浙江）如图，已知平面四边形ABCD ，AB BC ⊥,2AB BC AD ===,3CD =， AC 与BD 交于点O ，记1I OA OB =⋅，2·I OB OC ＝，3·I OC OD ＝，则 OABCDA ．1I <2I <3IB ．1I <3I <2IC ．3I < 1I <2ID ．2I <1I <3I【答案】C 。

理科数学2010-2019高考真题分类训练专题五平面向量第十四讲向量的应用答案

专题五平面向量第十四讲向量的应用答案部分2019年1.解析设()2AD AB A AO C λλ==+u u u u r u u u u u r u u u rr ，1()(1)3AO AE EO AE EC AE AC AE AE AC AB ACμμμμμμ-=+=+=+-=-+=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ，所以1232λμλμ-⎧=⎪⎪⎨⎪=⎪⎩，解得1214λμ⎧=⎪⎪⎨⎪=⎪⎩，所以11()24AO AD AB AC ==+u u u r u u u r u u u r u u u r ，13EC AC AE AB AC =-=-+u u u r u u u r u u u r u u ur u u u r ，221131266()()()43233AO EC AB AC AB AC AB AB AC AC ⋅=⨯+⨯-+=-+⋅+=u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r u u u r u u u r221322AB AB AC AC -+⋅+u u ur u u u r u u u r u u u r ，因为221322AB AC AB AB AC AC ⋅=-+⋅+u u u r u u u r u u u r u u u r u u u r u u u r ，所以221322AB AC =u u ur u u u r ，所以223AB AC=u u u r u u u r ，所以3AB AC =. 2.解析：正方形ABCD 的边长为1，可得AB AD AC +=u u u r u u u r u u u r ，BD AD AB =-u u u r u u u r u u u r ，0AB AD ⋅=u u ur u u u r ，123456||AB BC CD DA AC BD λλλλλλ+++++u u u r u u u r u u u r u u u r u u u r u u u r12345566||AB AD AB AD AB AD AD AB λλλλλλλλ=+--+++-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r 13562456|()()|AB AD λλλλλλλλ=-+-+-++u u u r u u u r2213562456()()λλλλλλλλ=-+-+-++,由于(1,2,3,4,5,6)i i λ=2，3，4，5，取遍1±，可得13560λλλλ-+-=，24560λλλλ-++=，可取5613241,1,1,1λλλλλλ=====-=，可得所求最小值为0；由13564λλλλ-+-=，24564λλλλ-++=，可取2456131,1,1,1,1,λλλλλλ==-====-可得所求最大值为3.解析因为AB BE =，//AD BC ，30A ∠=o ，所以在等腰三角形ABE 中，120BEA ∠=o ，又AB =，所以25BE AD =-u u u r u u u r .因为AE u u u r 25AE AB AD =-u u u r u u u r u u u r .又BD BA AD AB AD =+=-+u u u r u u u r ，所以()22272555BD AE AB AD AB AD AB AB AD AD ⎛⎫⋅=-+⋅-=-+⋅-= ⎪⎝⎭u u u r u u u ru u u ru u u r u u u ru u ur u u u r u u u r u u u r u u u r 2272cos 55AB AB AD A AD-+⋅-=u u u r u u u r u u u r u u ur 7212525155-+⨯⨯-⨯=-. 2010-2018年1．A 【解析】以A 为坐标原点，AB 所在直线为x 轴，建立如图的平面直角坐标系，因为在平面四边形ABCD 中，1AB AD ==，120BAD ∠=︒，所以(0,0)A ，(1,0)B ，1(,22D -，设(1,)C m ,(,)E x y ，所以3(,2DC m =-u u u r ，1(2AD=-u u u r ，因为AD CD ⊥，所以31(,(022m ⋅-=，即31()02222m ⨯-+-=，解得m =C ，因为E 在CD上，所以2y CE CD k k =，2112=+，即2x =-，因为(,)AE x y =u u u r ，(1,)BE x y =-u u u r ，所以2222(,)(1,)2)2AE BE x y x y x x y y ⋅=⋅-=-+=--++u u u r u u u r246y =-+，令2()46f y y =-+，y ∈．因为函数2()46f y y =-+在上单调递减，在上单调递增，所以2min 21()4(68816f y =⨯-+=．所以⋅uu u r uur AE BE 的最小值为2116，故选A ．2．A 【解析】解法一设O 为坐标原点，OA =u u u r a ，(,)OB x y ==u u u rb ，=(1,0)e ，由2430-⋅+=b e b 得22430x y x +-+=，即22(2)1x y -+=，所以点B 的轨迹是以(2,0)C 为圆心，l 为半径的圆．因为a 与e 的夹角为3π，所以不妨令点A在射线y =(0x >)上，如图，数形结合可知min ||||||1CA CB -=-u u u r u u u ra b ．故选A ．解法二由2430-⋅+=b e b 得2243()(3)0-⋅+=-⋅-=b e b e b e b e ．设OB =u u u r b ，OE =u u u r e ，3OF =u u u r e ，所以EB -=u u u r b e ，3FB -u u u r b e =，所以0EB FB ⋅=u u u r u u u r，取EF 的中点为C ．则B 在以C 为圆心，EF 为直径的圆上，如图．设OA =u u u r a ，作射线OA ，使得3AOE π∠=，所以|||(2)(2)|-=-+-≥a b a e e b|(2)||(2)|||||1CA BC ---=-u u u r u u u ra e eb ．故选A ．3．A 【解析】如图建立直角坐标系，则(0,1)A ，(0,0)B ，(2,1)D ，(,)Px y 所以圆的方程为224(2)5x y -+=，所以(,1)AP x y =-u u u r ，(0,1)AB =-u u u r ，(2,0)AD =u u u r，由AP AB AD λμ=+u u u r u u u r u u u r ，得21x y μλ=⎧⎨-=-⎩，所以λμ+=12x y -+，设12x z y =-+，即102xy z -+-=，点(,)P x y 在圆上，所以圆心到直线102xy z -+-=的距离小于半径，，解得13z≤≤，所以z的最大值为3，即λμ+的最大值为3，选A．4．B【解析】如图，以BC为x轴，BC的垂直平分线DA为y轴，D为坐标原点建立平面直角坐标系，则A，(1,0)B-，(1,0)C，设(,)P x y，所以()PA x y=-u u u r，(1,)PB x y=---u u u r，(1,)PC x y=--u u u r，所以(2,2)PB PC x y+=--u u u r u u u r，22()22)22(PA PB PC x y y x y⋅+=-=+-u u u r u u u r u u ur23322--≥，当P时，所求的最小值为32-，故选B．5．C【解析】如图所示，四边形ABCE是正方形，F为正方形的对角线的交点，易得AO AF<，而90AFB∠=o，∴AOB∠与COD∠为钝角，AOD∠与BOC∠为锐角．根据题意12()I I OA OB OB OC OB OA OC OB CA-=⋅-⋅=⋅-=⋅=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r||||cos0OB CA AOB∠<u u u r u u u r，∴12I I<，同理23I I>．做AG BD⊥于G，又AB AD=．∴OB BG GD OD<=<，而OA AF FC OC<=<，∴||||||||OA OB OC OD⋅<⋅u u u r u u u r u u u r u u u r，而cos cos0AOB COD∠=∠<，∴OA OB OC OD⋅>⋅u u u r u u u r u u u r u u u r，即13I I>，∴312I I I<<，选C．G FEOABCD6．B【解析】由2DA DB DC ===u u u r u u u r u u u r 知,D 为ABC ∆的外心．由DA DB ⋅u u u r u u u r =DB DC ⋅u u ur u u u r=DC DA ⋅u u u r u u u r知D 为ABC ∆的内心，所以ABC ∆为正三角形，易知其边长为23，取AC 的中点E ，因为M 是PC 的中点，所以1122EM AP ==，所以max 17||||22BM BE =+=u u u u r ，则2max 49||4BM =u u u u r ．故选B ．7．D 【解析】由菱形ABCD 的边长为a ，60ABC ∠=o可知18060120BAD ∠=-=o o o，2223()()cos1202BD CD AD AB AB AB AD AB a a a a ⋅=-⋅-=-⋅+=-⋅+=o u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ．8．A 【解析】由题意得111333=+=+=+-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u rAD AC CD AC BC AC AC AB1433=-+u u ur u u u r AB AC ．9．A 【解析】以题意，以点A 为坐标原点，以AB 所在的直线为x 轴，AC 所在的直线为y 轴建立如图所示的平面直角坐标系，所以点(1,4)P ，1(,0)B t，(0,)C t ，所以11(1,4)(1,4)(1)(1)4(4)PB PC t t t t⋅=----=-⨯--⨯-u u u r u u u r=1174t t --117413t t -⨯=≤（当且仅当14t t =，即12t =时取等号），所以PB PC ⋅u u u r u u u r的最大值为13．故选A ．10．C【解析】311,443 AM AB ADNM CM CN AD AB=+=-=-+u u u u r u u u r u u u r u u u u r u u u u r u u u r u u u r u u u r，所以11(43)(43)412AM NM AB AD AB AD⋅=+⋅-u u u u r u u u u r u u u r u u u r u u u r u u u r2211(169)(1636916)94848AB AD=-=⨯-⨯=u u u r u u u r，选C．11．B【解析】由题意得，AC为圆的直径，故可设),(nmA，),(nmC--，),(yxB，∴(6,)PA PB PC x y++=-u u u r u u u r u u u r，而491237)6(22≤-=+-xyx，∴PA PB PC++u u u r u u u r u u u r的最大值为7，故选B．12．A【解析】设(1,0),(0,1)a b==r r，则(cos,sin)OPθθ=u u u r，(2,2)OQ=u u u r，所以曲线C是单位元，区域Ω为圆环（如图）∵||2OQ=u u u r，∴13r R<<<．13．C【解析】因为120BAD?o，所以cos1202AB AD AB AD?鬃=-ou u u r u u u r u u u r u u u r.因为BE BCl=，所以AE AB ADl=+u u u r u u u r u u u r，AF AB ADm=+u u u r u u u r u u u r.因为1AE AF?u u u r u u u r，所以()()1AB AD AB ADu u u r u u u r u u u r u u u rl m+?=，即3222l m l m+-=①同理可得23l m l m--=-②，①+②得56l m+=.14．B【解析】如图，设,AB b AC c==u u u r r u u u r r，则1,2,0b c b c==•=r r r r，CBQP又(1)BQ BA AQ b c λ=+=-+-u u u r u u u r u u u r r r ，CP CA AP c b λ=+=-+u u u r u u u r u u u r r r，由2-=•得22[(1)]()(1)4(1)2b c c b c b λλλλλλ-+-•-+=--=--=-r r r r r r ，即32,23==λλ，选B. 15．A 【解析】【方法一】设34(10cos ,10sin )cos ,sin 55OP θθθθ=⇒==u u u r则33(10cos(),10sin())(44OQ ππθθ=++=-u u u r ．【方法二】将向量(6,8)OP =u u u r 按逆时针旋转32π后，可知Q 点落在第三象限，则可排除B 、D ，代入A ，由向量的夹角公式可得cos 2QOP ∠=-，∴34QOP π∠=． 16．C 【解析】首先观察集合113{|},1,,0,,1,,2,2222nn Z ⎧⎫∈=⋅⋅⋅--⋅⋅⋅⎨⎬⎩⎭，从而分析a b o和b a o 的范围如下：因为(0,)4πθ∈，∴cos 12θ<<，而||cos ||θ⋅==⋅o b a b b a a a a ，且||||0>…a b ，可得||0cos 1||θ<<b a ，又∵∈o b a {|}2∈nn Z 中，∴||1cos ||2θ=b a ，从而||1||2cos θ=b a ，∴2||cos 2cos ||θθ⋅===⋅o a b a a b b b b ，所以12<<o a b ．且a b o 也在集合{|}2∈nn Z 中，故有32=o a b ． 17．D 【解析】根据已知得(,0)(0,0)[(1,0)(0,0)]c λ-=-，即(,0)(1,0)c λ=，从而得c λ=；(,0)(0,0)[(1,0)(0,0)]d μ-=-，即(,0)(1,0)d μ=，得d μ=，根据112λμ+=，得112c d+=．线段AB 的方程是0y =，[0,1]x ∈．若C 是线段AB 的中点，则12c =，代入112c d +=，得10d=．此等式不可能成立，故选项A 的说法不成立；同理选项B 的说法也不成立；若,C D 同时在线段AB 上，则01c <≤，01d <≤，此时11c ≥，11d≥，112c d +≥，若等号成立，则只能1c d ==，根据定义，,C D 是两个不同的点，故矛盾，故选项C 的说法也不正确，若,C D 同时在线段AB 的延长线上，若1c >，1d >，则112c d+<，与112c d +=矛盾，若0,0c d <<，则11c d +是负值，与112c d+=矛盾，若1c >，0d <，则11c <，10d <，此时111c d +<，与112c d+=矛盾，故选项D 的说法是正确的．18．3-【解析】设(0,)E t ，(0,2)±F t ，所以(1,)(2,2)⋅=⋅-±u u u r u u u rAE BF t t 222(2)22(1)3=-+±=±-=±-t t t t t ，当1=±t 时，AE BF ⋅u u u r u u u r取得最小值3-．19．[-【解析】设(,)P x y ，由20PA PB ⋅u u u r u u u r≤，得250x y -+≤，x如图由250x y -+≤可知，P 在¼MN上，由2225050x y x y -+=⎧⎨+=⎩，解得(1,7)M ，(5,5)N --，所以P 点横坐标的取值范围为[-．20．311【解析】032cos603AB AC ⋅=⨯⨯=u u u r u u u r ，1233AD AB AC =+u u u r u u u r u u u r ,则12212()()34934333333AD AE AB AC AC AB λλλ⋅=+-=⨯+⨯-⨯-⨯=-u u u r u u u r u u u r u u u r u u u r u u u r ，311λ=．21．12【解析】由题意令(1,0)=e ，(cos ,sin )αα=a ，(2cos ,2sin )ββ=b ，则由||||+„ae be 可得|cos |2|cos |αβ+„①，令sin 2sin m αβ+= ②22①+②得24[|cos cos |sin sin ]1m αβαβ++„对一切实数,αβ恒成立，所以4[|cos cos |sin sin ]1αβαβ+„．故12(cos cos sin sin )2[|cos cos |sin sin ]2αβαβαβαβ⋅=++剟a b ．故最大值为12． 22．12 16- 【解析】由1111()3232MN MC CN AC CB AC AB AC u u u u r u u u u r u u u r u u u r u u u r u u u r u u u r u u u r =+=+=+-1126AB AC xAB y AC u u u r u u u r u u u r u u u r =-=+．所以12x =，16y =-． 23．2918 【解析】因为19DF DC λ=u u u r u u u r ，12DC AB =u u u r u u u r ，119199918CF DF DC DC DC DC AB λλλλλ--=-=-==u u u r u u u r u u u r u u u r u u u r u u u r u u u r ，AE AB BE AB BC λ=+=+u u u r u u u r u u u r u u u r u u u r ，19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ，()1918AE AF AB BC AB BC λλλu u u r u u u r u u u r u u u r u u u r u u u r +⎛⎫⋅=+⋅+ ⎪⎝⎭22191911818AB BC AB BC λλλλλλu u u r u u u r u u ur u u u r ++⎛⎫=+++⋅ ⎪⎝⎭ 19199421cos1201818λλλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥=当且仅当2192λλ=即23λ=时的最小值为2918． BA24．1(1)(1)(cos ,sin cos )(cos ,sin 66666k k k k k k k a a πππππ+++⋅=+⋅+u u r u u u r(1)cos )6k π+2(1)2cos sincos cos sin 66666k k k k πππππππ+++=++=++1(21)cos 26k π+，因此111012k k k a a +=⋅==∑u u r u u u r 25．2【解析】因为120BAD?o，菱形的边长为2，所以2AB AD?-u u u r u u u r.因为113AE AFAB AD AD AB λu u u r u u u r u u u r u u u r u u u r u u ur 骣骣鼢珑?+?鼢珑鼢珑桫桫，由1AE AF?u u u r u u u r ，所以4412(1)133λλ+-+=，解得2λ=．26．1+(,)D x y ，由||1CD =u u u r ，得22(3)1x y -+=，向量OA OB OD ++u u u r u u u r u uu r (1,x y =-+，故||OA OB OC ++=u u u r u u u r u u u r的最大值为圆22(3)1x y -+=上的动点到点(1,距离的最大值，其最大值为圆22(3)1x y -+=的圆心(3,0)到点(1,的距离加上圆的半径，11=27．2【解析】以A 为坐标原点，AB ，AD 所在的直线分别为x ，y轴建立直角坐标系，则B ，E ，(0,2)D ，2)C ．设(,2)F x (0≤x ≤2)，由1AB AF x ⋅=⇒=u u u r u u u r ，∴(1,2)F ，AE BF u u u r u u u rg =()1,2(12,2)=2．28．(2sin 2,1cos 2)--【解析】如图过P 作轴的垂线，垂足为E ，过C 作y 轴的垂线，垂足为A ，根据题意可知圆滚动了2个单位的弧长，BAC E∴2PCD ∠=，可知22PCB π∠=-，此时点P 的坐标为2cos(2)2sin 2,2P x π=--=-1sin(2)1cos 2,2P y π=+-=-另解1：根据题意可知滚动制圆心为（2,1）时的圆的参数方程为⎩⎨⎧+=+=θθsin 1cos 2y x ，且223,2-==∠πθPCD ，则点P 的坐标为⎪⎩⎪⎨⎧-=-+=-=-+=2cos 1)223sin(12sin 2)223cos(2ππy x ，即)2cos 1,2sin 2(--=OP .29．14-【解析】根据已知得1()2AD AB AC =+u u u r u u u r u u u r ，23BE AC AB =-u u u r u u u r u u u r ，所以AD BE ⋅=u u u v u u u v 1()2AB AC +⋅u u u r u u u r （23AC AB -u u u r u u u r ）=1211(1)2334AB AC --⋅=-u u u r u u u r ．30．【解析】(1)∵⊥m n ，∴0⋅=m n，故cos 022x x -=，∴tan 1x =．（2）∵m 与n 的夹角为3π，∴122cos ,112x x-⋅<>===⨯m n m n |m ||n |，故1sin()42x π-=，又(0,)2x π∈，∴(,)444x πππ-∈-，46x ππ-=，即512x π=．故x 的值为512π．31．【解析】（Ⅰ）已知()sin2cos2f x m x n x =⋅=+a b ，)(x f Θ过点)2,32(),3,12(-ππ，∴()sin cos 1266f m n πππ=+= 234cos 34sin )32(-=+=πππn m f∴12122m n ⎧+=⎪⎪⎨⎪-=-⎪⎩解得⎩⎨⎧==13n m（Ⅱ）由（Ⅰ）知)62sin(22cos 2sin 3)(π+=+=x x x x f由题意知()()2sin(22)6g x f x x πϕϕ=+=++设()y g x =的图象上符合题意的最高点为0(,2)x由题意知2011x +=．所以00x =，即到点(0,3)的距离为1的最高点为(0,2)．将其代入()y g x =得sin 216πϕ⎛⎫+= ⎪⎝⎭，又∵0ϕπ<<，所以6πϕ=，因此()2sin 22cos 22g x x x π⎛⎫=+= ⎪⎝⎭由222,k x k k Z πππ-+≤≤∈，得z k k x k ∈≤≤+-,2πππ∴()f x 的单调增区间为[,],2k k k πππ-+∈Z ．32．【解析】（Ⅰ）∵1cos ,3,cos 233acB b BA BC ca B ==⋅===u u u r u u u r ，且222-cos 2a c b B ac+=，∴c 6,5a a c =+=，∵a c >，∴解得3,2a c ==．所以3,2a c ==．（Ⅱ）∵1cos 3B =，∴sin B =，∵3,3,2a b c ===，222-c 7cos 29a b C ab +==，sin 9C =，∴23cos(-)cos cos sin sin 27B C B C B C =+=，故23cos(-)27B C =． 33．【解析】（1）-a b ＝(cos cos ,sin sin )αβαβ--，2||-a b ＝22(cos cos )(sin sin )αβαβ-+-＝22(cos cos sin sin )2αβαβ-⋅+⋅=．所以，cos cos sin sin 0αβαβ⋅+⋅=，所以，b a ⊥．（2）⎩⎨⎧=+=+②1sin sin ①0cos cos βαβα，①2＋②2得：1cos()2αβ-=-．所以，αβ-＝π32，α＝π32＋β，带入②得：sin (π32＋β)＋sin β＝23cos β＋12sin β＝sin (3π＋β)＝1，所以，3π＋β＝2π．所以，α＝65π，β＝6π．34．【解析】由题意，抛物线E 的焦点为(0,)2p F ，直线1l 的方程为12py k x =+．由1222p y k x x py⎧=+⎪⎨⎪=⎩得22120x pk x p --=．设A ，B 两点的坐标分别为11(,)A x y ，22(,)B x y ，则1x 、2x 是上述方程的两个实数根．从而1212x x pk +=，212121()2y y k x x p pk p +=++=+．所以点M 的坐标为211(,)2ppk pk +，211(,)FM pk pk =u u u u r ．同理可得点N 的坐标为222(,)2p pk pk +，222(,)FN pk pk =u u u r ．于是2221212()FM FN p k k k k ⋅=+u u u u r u u u r ．由题设，有1＋2＝2，1>0，2>0，1≠2，所以212120()12k k k k +<<=．故222(11)2FM FN p p ⋅<+=u u u u r u u u r ．(2)【解析】由抛物线的定义得1||2p FA y =+，2||2p FB y =+，所以2121||22AB y y p pk p =++=+，从而圆M 的半径211r pk p =+．故圆M 的方程为22222111()()()2p x pk y pk pk p -+--=+．化简得22221132(21)04x y pk x p k y p +--+-=．同理可得圆N 的方程为22222232(21)04x y pk x p k y p +--+-=．于是圆M ，圆N 的公共弦所在直线l 的方程为222121()()0k k x k k y -+-=．又2－1≠0，1＋2＝2，则l 的方程为＋2y ＝0. 因为p >0，所以点M 到直线l 的距离222117[2()]p k d ++===故当114k =-时，d．，解得8p =．故所求的抛物线E 的方程为216x y =． 35．【解析】（I）由2222)(sin )4sin ax x x =+=，222(cos )(sin )1b x x =+=，及2,4sin 1a b x ==得又1[0,],sin 22x x π∈=从而，所以6x π=.（II）2()cos sin f x a b x x x =⋅=⋅+=1112cos 2sin(2)22262x x x π-+=-+. 当[0.]sin 2- 1.326x x πππ=∈时，（）取最大值所以3().2f x 的最大值为 36．【解析】（1）由(2,1)MA x y =---u u u r ，(2,1)MB x y =--u u u r，MA MB +=u u u r u u u r ()(,)(0,2)2OM OA OB x y y ⋅+=⋅=u u u u r u u u r u u u r ，22y +．化简得曲线C 的方程：24x y =．（2）假设存在点(0,)(0)P t t >满足条件，则直线PA 的方程是12t y x t -=+，PB 的方程是12ty x t -=+．曲线C 在Q 处的切线l 的方程是20024x x y x =-，它与y 轴的交点为2(0,)4x F - 由于022x -<<，因此0112x -<<． ①当10t -<<时，11122t --<<-，存在0(2,2)x ∈-，使得0122x t -=．即l 与直线PA 平行，故当10t -<<时不符合题意． ②1t -„时，011,22x t --<„01122x t ->…，所以l 与直线,PA PB 一定相交．分别联立方程组0201224t y x t x x y x -⎧=+⎪⎪⎨⎪=-⎪⎩，解得,D E 的横坐标分别是 20042(1)D x t x x t +=+-，20042(1)E x t x x t +=+-，则202204(1)(1)E D x tx x t x t +-=--- 又204x FP t =--，有220220(4)1128(1)PDE E D x t t S FP x x t x ∆+-=⋅⋅-=⋅--，又2200414(1)242QABx x S ∆-=⋅⋅-=，于是22200220(4)(1)41(4)QAB PDEx x t S S t x t ∆∆⎡⎤---⎣⎦=⋅-+=422200422004(1)4(1)41816x t x t t x tx t⎡⎤-+-+-⎣⎦⋅-++，对任意0(2,2)x ∈-，要使QAB PDES S ∆∆为常数，即只需t 满足2224(1)84(1)16t tt t⎧---=⎨-=⎩，解得1t =-，此时2QAB PDES S ∆∆=，故存在1t =-，使得QAB ∆与PDE ∆的面积之比是常数2．37．【解析】由λ=知Q ，M ，P 三点在同一条垂直于轴的直线上，故可设 .)1(),(),,(),,(),,(2020220y x y x y y x x x M y x Q y x P λλλ-+=-=-则则 ①再设),1,1().(,),,(010111y x y y x x y x B --=--=λλ即由解得⎩⎨⎧-+=-+=.)1(,)1(011λλλλy y x x ②将①式代入②式，消去0y ，得⎩⎨⎧-+-+=-+=.)1()1(,)1(2211λλλλλλy x y x x ③ 又点B 在抛物线2x y =上，所以211x y =，再将③式代入211x y =，得.012),1(,0.0)1()1()1(2,)1(2)1()1()1(,))1(()1()1(22222222=--+>=+-+-+++-+=-+-+-+=-+-+y x y x x x y x x y x 得两边同除以因λλλλλλλλλλλλλλλλλλλλλλλ故所求点P 的轨迹方程为.12-=x y38．【解析】（1）（方法一）由题设知(3,5),(1,1)AB AC ==-u u u r u u u r，则(2,6),(4,4).AB AC AB AC +=-=u u u r u u u r u u u r u u u r所以|||AB AC AB AC +=-=u u u r u u u r u u u r u u u r故所求的两条对角线的长分别为、（方法二）设该平行四边形的第四个顶点为D ，两条对角线的交点为E ，则 E 为B 、C 的中点，E （0，1）又E （0，1）为A 、D 的中点，所以D （1，4）故所求的两条对角线的长分别为BC =、AD =（2）由题设知：OC u u u r =(－2,－1)，(32,5)AB tOC t t -=++u u u r u u u r．由(OC t AB -)·OC =0，得：(32,5)(2,1)0t t ++⋅--=，从而511,t =-所以115t =-．或者：2· AB OC tOC =u u u r u u u r u u u r ，(3,5),AB =u u u r2115||AB OC t OC ⋅==-u u u r u u u r u u u r ．。

十年高考理科数学真题专题五平面向量十四向量的应用及答案【精选】

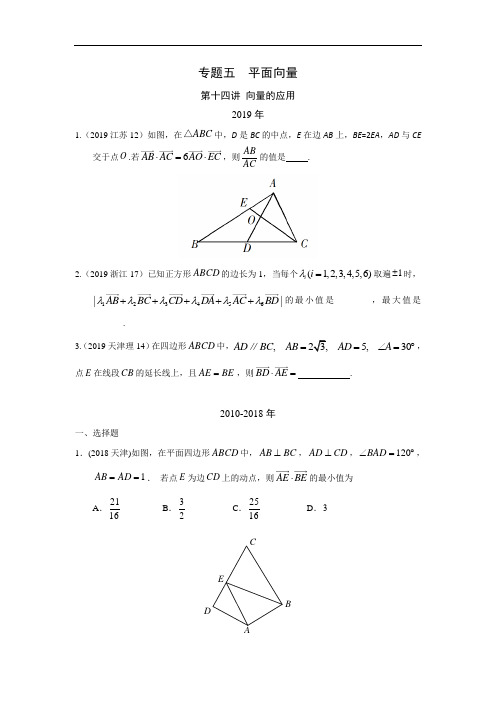
专题五平面向量第十四讲向量的应用2019年1.（2019江苏12）如图，在ABC △中，D 是BC 的中点，E 在边AB 上，BE =2EA ，AD 与CE交于点O .若6AB AC AO EC ⋅=⋅，则AB AC的值是 .2.（2019浙江17）已知正方形ABCD 的边长为1，当每个(1,2,3,4,5,6)i i λ=取遍1±时，123456||AB BC CD DA AC BD λλλλλλ+++++的最小值是________，最大值是_______.3.（2019天津理14）在四边形ABCD 中，,23,5,30AD BC AB AD A ==∠=︒∥，点E 在线段CB 的延长线上，且AE BE =，则BD AE ⋅= .2010-2018年一、选择题1．(2018天津)如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==．若点E 为边CD 上的动点，则⋅AE BE 的最小值为A ．2116B ．32C ．2516D ．3EDC B2．(2018浙江)已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430-⋅+=b e b ，则||-a b 的最小值是A1 B1 C ．2 D．23．（2017新课标Ⅲ）在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为A ．3 B． CD ．24．（2017新课标Ⅱ）已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是A ．2-B ．32-C ．43- D ．1- 5．（2017浙江）如图，已知平面四边形ABCD ，AB BC ⊥，2AB BC AD ===，3CD =，AC 与BD 交于点O ，记1I OA OB =⋅，2·I OB OC ＝，3·I OC OD ＝，则OAB CDA ．1I <2I <3IB ．1I <3I <2IC ．3I < 1I <2ID ．2I <1I <3I6．（2016四川）在平面内，定点A ，B ，C ，D 满足DA =DB =DC ，DA DB ⋅=DB DC ⋅=DC DA ⋅=-2，动点P ，M 满足AP =1，PM =MC ，则2BM 的最大值是A ．434B ．494 CD7．(2015山东)已知菱形ABCD 的边长为a ，60ABC ∠=，则BD CD ⋅＝A ．232a -B ．234a - C ．234a D ．232a8．（2015新课标）设D 为ABC ∆所在平面内一点，3BC CD =，则A ．1433AD AB AC =-+ B ．1433AD AB AC =- C ．4133AD AB AC =+ D ．4133AD AB AC =- 9．（2015福建）已知AB AC ⊥， 1AB t =， AC t =，若点P 是ABC ∆所在平面内一点，且4ABACAP AB AC =+ ，则PB PC ⋅ 的最大值等于A ．13B ．15C ．19D ．2110．（2015四川）设四边形ABCD 为平行四边形，6AB =，4AD =．若点,M N 满足3BM MC =，2DN NC =，则AM NM ⋅=A ．20B ．15C ．9D ．611．（2015湖南）已知点,,A B C 在圆221x y +=上运动，且AB BC ⊥．若点P 的坐标为(2,0)，则PA PB PC ++的最大值为A ．6B ．7C ．8D ．912．（2014安徽）在平面直角坐标系xOy 中，已知向量,a b ，||||1==a b ，0⋅=a b ，点Q 满足2()OQ =+a b ．曲线{|cos sin ,02}C P OP θθθπ==+a b ≤≤，区域 {|0||,}P r PQ R r R Ω=<<≤≤．若C Ω为两段分离的曲线，则A ．13r R <<<B ．13r R <<≤C ．13r R ≤<<D ．13r R <<< 13．（2014天津）已知菱形ABCD 的边长为2，120BAD，点,E F 分别在边,BC DC 上，BEλBC ，DF μDC .若1AE AF ，23CE CF ，则λμ A ．12 B ．23 C ．56 D ．71214．（2012天津）在△ABC 中，∠A =90°，AB =1，设点P ，Q 满足AP AB λ=，(1)AQ AC λ=-，R λ∈．若2BQ CP ⋅=-，则λ=A ．13B ．23C ．43D ．215．(2012安徽)在平面直角坐标系中，(0,0),(6,8)O P ，将向量OP 绕点O 按逆时针旋转34π后得向量OQ ，则点Q 的坐标是A ．(-B ．(-C ．(2)--D ．(-16．（2012广东）对任意两个非零的平面向量α和β，定义αβαβββ⋅=⋅．若平面向量,a b 满足||||0>a b ，a 与b 的夹角(0,)4πθ∈，且a b 和b a 都在集合{|}2∈n n Z 中，则a b =A ．12B ．1C ．32D ．5217．（2011山东）设1A ，2A ，3A ，4A 是平面直角坐标系中两两不同的四点，若1312A A A A λ=(λ∈R )，1412A A A A μ=(μ∈R )，且112λμ+=，则称3A ，4A 调和分割1A ，2A ，已知点(,0)C c ，(,0)D d ，(,c d ∈R )调和分割点(0,0)A ，(1,0)B ，则下面说法正确的是A ．C 可能是线段AB 的中点B ．D 可能是线段AB 的中点C ．C ，D 可能同时在线段AB 上D ．C ，D 不可能同时在线段AB 的延长线上二、填空题18．(2018上海)在平面直角坐标系中，已知点(10)A -，，(2,0)B ，E ，F 是y 轴上的两个动点，且||2EF =，则AE BF ⋅的最小值为______．19．（2017江苏）在平面直角坐标系xOy 中，(12,0)A -，(0,6)B ，点P 在圆O ：2250x y +=上，若20PA PB ⋅≤，则点P 的横坐标的取值范围是．20．（2017天津）在ABC △中，60A =︒∠，3AB =，2AC =．若2BD DC =， AE AC AB λ=-()λ∈R ，且4AD AE ⋅=-，则λ的值为___________．21．（2016年浙江）已知向量,a b ，||1=a ，||2=b ，若对任意单位向量e ，均有||||6+ae be ，则⋅a b 的最大值是．22．(2015北京)在ABC △中，点M ，N 满足2AM MC =，BN NC =．若MN xAB yAC =+，则x = ；y = ．23．（2015天津）在等腰梯形ABCD 中,已知AB DC ∥,2AB =,1BC =,60ABC ∠=．动点E 和F 分别在线段BC 和DC 上，且BE BC λ=，19DF DC λ=，则AE AF ⋅的最小值为．24．（2015江苏）设向量(cos ,sin cos )666k k k k πππ=+a (0,1,2,,12)k =⋅⋅⋅，则∑=+⋅1201)(k k k a a 的值为．25．（2014天津）已知菱形ABCD 的边长为2，120BAD ∠=︒，点E ，F 分别在边BC 、DC 上，3BC BE =，DC DF λ=．若1AE AF ⋅=，则λ的值为________．26．（2014湖南）在平面直角坐标系中，O 为原点，(1,0),(0,3),(3,0),A B C -动点D 满足||1CD =，则||OA OB OD ++的最大值是．27．（2012江苏）如图，在矩形ABCD 中，22AB BC ==，，点E 为BC 的中点，点F 在边CD 上，若2AB AF =，则AE BF 的值是．28．（2012山东）如图，在平面直角坐标系xoy 中，一单位圆的圆心的初始位置在()1,0，此时圆上一点P 的位置在()0,0，圆在x 轴上沿正向滚动。

2019年高考真题理科数学解析汇编：平面向量word资料6页

第 1 页2019年高考真题理科数学解析汇编：平面向量一、选择题1 ．（2019年高考（天津理））已知△ABC 为等边三角形,=2AB ,设点P,Q 满足=A P A Bλ,=(1)AQ AC λ-,R λ∈,若3=2BQ CP ⋅-,则=λ （）A ．12B．12CD．32-± 2 ．（2019年高考（浙江理））设a ,b 是两个非零向量.（）A ．若|a +b |=|a |-|b |,则a ⊥bB ．若a ⊥b ,则|a +b |=|a |-|b |C ．若|a +b |=|a |-|b |,则存在实数λ,使得a =λbD ．若存在实数λ,使得a =λb ,则|a +b |=|a |-|b |3 ．（2019年高考（重庆理））设,x y ∈R,向量()()()4,2,,1,1,-===c y b x a ,且c b c a //,⊥,则_______=（）ABC．D ．104 ．（2019年高考（四川理））设a 、b 都是非零向量,下列四个条件中,使||||a ba b =成立的充分条件是（）A ．a b =-B ．//a bC ．2a b =D ．//a b 且||||a b =5 ．（2019年高考（辽宁理））已知两个非零向量a ,b 满足|a +b |=|a -b |,则下面结论正确的是（）A ．a ∥bB ．a ⊥bC ．{0,1,3}D ．a +b =a -b6 ．（2019年高考（湖南理））在△ABC 中,AB=2,AC=3,AB BC = 1则___BC =.（）ABC． D 7 ．（2019年高考（广东理））对任意两个非零的平面向量α和β,定义⋅⋅=⋅αβαβββ,若平面向量a 、b 满足0≥>a b ,a 与b 的夹角0,4πθ⎛⎫∈ ⎪⎝⎭,且a b 和b a 都在集合2n n Z ⎧⎫∈⎨⎬⎩⎭中,则=a b（）A ．12B ．1C ．32D ．528 ．（2019年高考（广东理））(向量)若向量()2,3BA =,()4,7CA =,则BC =（）第 2 页A ．()2,4--B ．()2,4C ．()6,10D ．()6,10--9 ．（2019年高考（大纲理））ABC ∆中,AB 边上的高为CD ,若,,0,||1,||2CB a CA b a b a b ==⋅===,则AD =（）A ．1133a b -B ．2233a b - C ．3355a b - D ．4455a b - 10．（2019年高考（安徽理））在平面直角坐标系中,(0,0),(6,8)O P ,将向量OP 按逆时针旋转34π后,得向量OQ则点Q 的坐标是（）A．(- B．(-C．(2)--D．(2)-二、填空题11．（2019年高考（新课标理））已知向量,a b 夹角为45︒,且1,210a a b =-=;则_____b =[来源:shulihuashulihua]12．（2019年高考（浙江理））在∆ABC 中,M 是BC 的中点,AM =3,BC =10,则AB AC ⋅=______________. 13．（2019年高考（上海理））在平行四边形ABCD 中,∠A=3π, 边AB 、AD 的长分别为2、1. 若M 、N 分别是边BC 、CD 上的点,且满足||||CD CN BC BM =,则AN AM ⋅的取值范围是_________ .[来源:shulihua]14．（2019年高考（江苏））如图,在矩形ABCD 中,2AB BC ==，点E 为BC 的中点,点F 在边CD 上,若2AB AF =,则AE BF 的值是____.15．（2019年高考（北京理））已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为________; DE DC ⋅的最大值为________.16．（2019年高考（安徽理））若平面向量,a b 满足:23a b -≤;则a b 的最小值是_____第 3 页2019年高考真题理科数学解析汇编：平面向量参考答案一、选择题 1. 【答案】A【命题意图】本试题以等边三角形为载体,主要考查了向量加减法的几何意义,平面向量基本定理,共线向量定理及其数量积的综合运用.【解析】∵=BQ AQ AB -=(1)AC AB λ--,=CP AP AC -=AB AC λ-, [来源:数理化网] 又∵3=2BQ CP ⋅-,且||=||=2AB AC ,0<,>=60AB AC ,0=||||cos 60=2AB AC AB AC ⋅⋅,∴3[(1)]()=2AC AB AB AC λλ----,2223||+(1)+(1)||=2AB AB AC AC λλλλ--⋅-,所以234+2(1)+4(1)=2λλλλ---,解得1=2λ. 2. 【答案】C【解析】利用排除法可得选项C 是正确的,∵|a +b |=|a |-|b |,则a ,b 共线,即存在实数λ,使得a =λb .如选项A:|a +b |=|a |-|b |时,a ,b 可为异向的共线向量;选项B:若a ⊥b ,由正方形得|a +b |=|a |-|b |不成立;选项D:若存在实数λ,使得a =λb ,a ,b 可为同向的共线向量,此时显然|a +b |=|a |-|b |不成立. 3. 【答案】B【解析】由0240a c a c x x ⊥⇒⋅=⇒-=⇒=,由//422b c y y ⇒-=⇒=-,故||(21)a b +=+=【考点定位】本题主要考查两个向量垂直和平行的坐标表示,模长公式.解决问题的关键在于根据a c ⊥、//b c ,得到,x y 的值,只要记住两个向量垂直,平行和向量的模的坐标形式的充要条件,就不会出错,注意数字的运算.4. [答案]D[解析]若使||||a ba b =成立,则方向相同，与选项中只有D 能保证,故选D. [点评]本题考查的是向量相等条件⇔模相等且方向相同.学习向量知识时需注意易考易错零向量,其模为0且方向任意. 5. 【答案】B【解析一】由|a +b |=|a -b |,平方可得a ⋅b =0, 所以a ⊥b ,故选B【解析二】根据向量加法、减法的几何意义可知|a +b |与|a -b |分别为以向量a ,b 为邻边的平行四边形的两条对角线的长,因为|a +b |=|a -b |,所以该平行四边形为矩形,所以a ⊥b ,故选B【点评】本题主要考查平面向量的运算、几何意义以及向量的位置关系,属于容易题.解析一是利用向量的运算来解,解析二是利用了向量运算的几何意义来解. [来源:shulihua]C第 4 页6. 【答案】A【解析】由下图知AB BC = cos()2(cos )1AB BC B BC B π-=⨯⨯-=.1cos 2B BC ∴=-.又由余弦定理知222cos 2AB BC AC B AB BC +-=⋅,解得BC =.【点评】本题考查平面向量的数量积运算、余弦定理等知识.考查运算能力,考查数形结合思想、等价转化思想等数学思想方法.需要注意,AB BC 的夹角为B ∠的外角.7. 【解析】C;因为||cos cos 1||b a b ba a a a θθ⋅==≤<⋅,且a b 和b a 都在集合|2n n Z ⎧⎫∈⎨⎬⎩⎭中,所以12b a =,||12cos ||b a θ=,所以2||cos 2cos 2||a ab b θθ==<,且22cos 1a b θ=>,所以12a b <<,故有32a b =,选 C. 【另解】C;1||cos 2||k a a b b θ==,2||cos 2||k b b a a θ==,两式相乘得212cos 4k k θ=,因为0,4πθ⎛⎫∈ ⎪⎝⎭,12,k k 均为正整数,于是cos 12θ<=<,所以1224k k <<,所以123k k =,而0a b ≥>,所以123,1k k ==,于是32a b =,选C. [来源:数理化网] 8. 解析:A.()2,4BC BA CA =-=--. 9. 答案D【命题意图】本试题主要考查了向量的加减法几何意义的运用,结合运用特殊直角三角形求解点D 的位置的运用. [来源:shulihua]【解析】由0ab ⋅=可得90ACB ∠=︒,故AB =用等面积法求得CD =,所以AD =,故4444()5555AD AB CB CA a b ==-=-,故选答案D 10. 【解析】选A【方法一】设34(10cos ,10sin)cos ,sin 55OP θθθθ=⇒== [来源:数理化网]则33(10cos(),10sin())(44OQ ππθθ=++=- C第 5 页【方法二】将向量(6,8)OP =按逆时针旋转32π后得(8,6)OM =-则)(OQ OP OM =+=- 二、填空题[来源:shulihuashulihua] 11. 【解析】b=12. 【答案】16-【解析】此题最适合的方法是特例法.假设∆ABC 是以AB =AC 的等腰三角形,如图,AM =3,BC =10,AB =ACcos∠BAC =3434100823417+-=-⨯.AB AC ⋅=cos 16AB AC BAC ⋅∠=-13. [解析] 如图建系,则A (0,0),B (2,0),D (21,23),C (25,23).t CD BC ==||||∈[0,1],则t BM =||,t CN 2||=, 所以M (2+2t ,23t ),N (25-2t ,23),故AN AM ⋅=(2+2t)(25-2t )+23t ⋅23=)(6)1(5222t f t t t =++-=+--,因为t ∈[0,1],所以f (t )递减,(AN AM ⋅)max = f (0)=5,(AN AM ⋅)min = f (1)=2.[评注] 当然从抢分的战略上,可冒用两个特殊点:M 在B (N 在C )和M 在C (N 在D ),而本案恰是在这两点处取得最值,蒙对了,又省了时间!出题大虾太给蒙派一族面子了!14. .【考点】向量的计算,矩形的性质,三角形外角性质,和的余弦公式,锐角三角函数定义. 【解析】由2AB AF=,得cos ABAF FAB ∠=由矩形的性质,得cos =AF FAB DF ∠.记AE BF 和之间的夹角为,AEB FBC θαβ∠=∠=，,则θαβ=+. 又∵2BC =，点E 为BC 的中点,∴1BE =.本题也可建立以, AB AD 为坐标轴的直角坐标系,求出各点坐标后求解.15. 【答案】1;1 [来源:shulihuashulihua]【解析】根据平面向量的点乘公式||||cos DE CB DE DA DE DA θ⋅=⋅=⋅,可知||cos ||DE DA θ=,因此2||1DE CB DA ⋅==;||||cos ||cos DE DC DE DC DE αα⋅=⋅=⋅,而||cos DE α就是向量DE 在DC 边上的射影,要想让DE DC ⋅最大,即让射影最大,此时E 点与B 点重合,射影为||DC ,所以长度为1【考点定位】本题是平面向量问题,考查学生对于平面向量点乘知识的理解,其中包含动点问题,考查学生最值的求法. [来源:shulihuashulihua]16. 【解析】a b的最小值是98第 6 页。

(2010-2019)十年高考数学真题分类汇编：平面向量(含解析)

(2010-2019)十年高考数学真题分类汇编：平面向量（含解析）1.(2019·全国2·文T3)已知向量a=(2，3)，b=(3，2)，则|a-b|=( ) A.√2 B.2 C.5√2 D.50【答案】A【解析】由题意，得a-b=(-1，1)，则|a-b|=√(-1)2+12=√2，故选A.2.(2019·全国·1理T7文T8)已知非零向量a ，b 满足|a|=2|b|，且(a-b)⊥b ，则a 与b 的夹角为( ) A.π6 B.π3C.2π3D.5π6【答案】B【解析】因为(a-b)⊥b ，所以(a-b )·b=a ·b-b 2=0，所以a ·b=b 2.所以cos<a ，b>=a ·b|a |·|b |=|b |22|b |2=12，所以a 与b 的夹角为π3，故选B.3.(2018·全国1·理T6文T7)在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB ⃗⃗⃗⃗⃗ =( ) A.34AB ⃗⃗⃗⃗⃗ −14AC ⃗⃗⃗⃗⃗ B.14AB ⃗⃗⃗⃗⃗ −34AC⃗⃗⃗⃗⃗ C.34AB ⃗⃗⃗⃗⃗ +14AC ⃗⃗⃗⃗⃗ D.14AB ⃗⃗⃗⃗⃗ +34AC ⃗⃗⃗⃗⃗ 【答案】A【解析】如图，EB ⃗⃗⃗⃗⃗ =-BE⃗⃗⃗⃗⃗ =-12(BA ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗ ) =12AB ⃗⃗⃗⃗⃗ −14BC ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ −14(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=3 4AB⃗⃗⃗⃗⃗ −14AC⃗⃗⃗⃗⃗ .4.(2018·全国2·T4)已知向量a，b满足|a|=1，a·b=-1，则a·(2a-b)=( )A.4B.3C.2D.0【答案】B【解析】a·(2a-b)=2a2-a·b=2-(-1)=3.5.(2018·北京·理T6)设a，b均为单位向量，则“|a-3b|=|3a+b|”是“a⊥b”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】C【解析】由|a-3b|=|3a+b|，得(a-3b)2=(3a+b)2.∵a，b均为单位向量，∴1-6a·b+9=9+6a·b+1.∴a·b=0，故a⊥b，反之也成立.故选C.6.(2018·浙江·T9)已知a，b，e是平面向量，e是单位向量.若非零向量a与e的夹角为π3，向量b满足b2-4e·b+3=0，则|a-b|的最小值是( )A.√3-1B.√3+1C.2D.2-√3【答案】A【解析】∵b2-4e·b+3=0，∴(b-2e)2=1，∴|b-2e|=1.如图所示，平移a，b，e，使它们有相同的起点O，以O为原点，向量e所在直线为x轴建立平面直角坐标系，则b的终点在以点(2，0)为圆心，半径为1的圆上，|a-b|就是线段AB的长度.要求|AB|的最小值，就是求圆上动点到定直线的距离的最小值，也就是圆心M到直线OA的距离减去圆的半径长，因此|a-b|的最小值为-1.7.(2018·天津·理T8)如图，在平面四边形ABCD 中，AB ⊥BC ，AD ⊥CD ，∠BAD=120°，AB=AD=1.若点E 为边CD 上的动点，则 A.2116 B.32C.2516D.3【答案】A【解析】如图，以D 为坐标原点建立直角坐标系.连接AC ，由题意知∠CAD=∠CAB =60°，∠ACD=∠ACB =30°，则D(0，0)，A(1，0)，B （32，√32），C(0，√3).设E(0，y)(0≤y≤√3)，则AE⃗⃗⃗⃗⃗ =(-1，y)，BE ⃗⃗⃗⃗⃗ =（-32，y-√32），∴AE ⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ =32+y 2-√32y=（y-√34）2+2116，∴当y=√34时，AE ⃗⃗⃗⃗⃗ ·BE⃗⃗⃗⃗⃗ 有最小值2116.8.(2018·天津·文T8)在如图的平面图形中，已知OM=1，ON=2，∠MON=120°，BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ，CN ⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗ ，则BC ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ 的值为( ) A.-15 B.-9 C.-6D.0【答案】C【解析】连接MN ，∵BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ，CN ⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗ ，∴AC ⃗⃗⃗⃗⃗ =3AN ⃗⃗⃗⃗⃗ ，AB ⃗⃗⃗⃗⃗ =3AM⃗⃗⃗⃗⃗⃗ .∴MN ∥BC ，且MN BC =13，∴BC ⃗⃗⃗⃗⃗ =3MN ⃗⃗⃗⃗⃗⃗ =3(ON ⃗⃗⃗⃗⃗ −OM ⃗⃗⃗⃗⃗⃗ )，∴BC ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =3(ON ⃗⃗⃗⃗⃗ −OM ⃗⃗⃗⃗⃗⃗ )·OM ⃗⃗⃗⃗⃗⃗ =3(ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ -|OM ⃗⃗⃗⃗⃗⃗ |2)=3[2×1×(-12)-1]=-6.9.(2017·全国2·理T12)已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA ⃗⃗⃗⃗ ·(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗ )的最小值是( ) A.-2 B.-32 C.-43 D.-1【答案】B【解析】以BC 所在的直线为x 轴，BC 的垂直平分线AD 为y 轴，D 为坐标原点建立平面直角坐标系，如图.可知A(0，√3)，B(-1，0)，C(1，0).设P(x ，y)，则PA ⃗⃗⃗⃗ =(-x ，√3-y)，PB ⃗⃗⃗⃗⃗ =(-1-x ，-y)，PC ⃗⃗⃗⃗ =(1-x ，-y).所以PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗ =(-2x ，-2y).所以PA ⃗⃗⃗⃗ ·(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗ )=2x 2-2y(√3-y)=2x 2+2(y -√32)2−32≥-32. 当点P 的坐标为(0，√32)时，PA ⃗⃗⃗⃗ ·(PB⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗ )取得最小值为-32，故选10.(2017·全国3·理T12)在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上.若AP ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAD ⃗⃗⃗⃗⃗ ，则λ+μ的最大值为( ) A.3 B.2√2C.√5D.2【答案】A【解析】建立如图所示的平面直角坐标系，则A(0，1)，B(0，0)，D(2，1).设P(x ，y)，由|BC|·|CD|=|BD|·r ，得r=|BC |·|CD ||BD |=5=2√55，即圆的方程是(x-2)2+y 2=45. 易知AP ⃗⃗⃗⃗⃗ =(x ，y-1)，AB ⃗⃗⃗⃗⃗ =(0，-1)，AD ⃗⃗⃗⃗⃗ =(2，0).由AP ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAD ⃗⃗⃗⃗⃗ ，得{x =2μ，y -1=-λ，所以μ=x2，λ=1-y ，所以λ+μ=12x-y+1. 设z=12x-y+1，即12x-y+1-z=0. 因为点P(x ，y)在圆(x-2)2+y 2=45上，所以圆心C 到直线12x-y+1-z=0的距离d≤r，即√14+1≤2√55，解得1≤z≤3，11.(2017·全国2·文T4)设非零向量a ，b 满足|a+b|=|a-b|，则( ) A.a ⊥b B.|a|=|b| C.a ∥b D.|a|>|b| 【答案】A【解析】由|a+b|=|a-b|，平方得a 2+2a ·b+b 2=a 2-2a ·b+b 2，即a ·b=0.又a ，b 为非零向量，故a ⊥b ，故选A.12.(2016·四川·文T9)已知正三角形ABC 的边长为2√3，平面ABC 内的动点P ，M 满足|AP ⃗⃗⃗⃗⃗ |=1，PM ⃗⃗⃗⃗⃗⃗ =MC ⃗⃗⃗⃗⃗⃗ ，则|BM ⃗⃗⃗⃗⃗⃗ |2的最大值是( ) A.434 B.494 C.37+6√34 D.37+2√334【答案】B【解析】设△ABC 的外心为D ，则|DA ⃗⃗⃗⃗⃗ |=|DB ⃗⃗⃗⃗⃗ |=|DC ⃗⃗⃗⃗⃗ |=2. 以D 为原点，直线DA 为x 轴，过D 点的DA 的垂线为y 轴，建立平面直角坐标系，则A(2，0)，B(-1，-√3)，C(-1，√3). 设P(x ，y)，由已知|AP⃗⃗⃗⃗⃗ |=1，得(x-2)2+y 2=1，∵PM ⃗⃗⃗⃗⃗⃗ =MC⃗⃗⃗⃗⃗⃗ ，∴M (x -12，y+√32). ∴BM ⃗⃗⃗⃗⃗⃗ =(x+12，y+3√32). ∴BM ⃗⃗⃗⃗⃗⃗ 2=(x+1)2+(y+3√3)24，它表示圆(x-2)2+y 2=1上点(x ，y)与点(-1，-3√3)距离平方的14，∴(|BM⃗⃗⃗⃗⃗⃗ |2)max =14[√32+(0+3√3)22=494，故选B.13.(2016·天津·文T7)已知△ABC 是边长为1的等边三角形，点D ，E 分别是边AB ，BC 的中点，连接DE 并延长到点F ，使得DE=2EF ，则AF ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ 的值为 ( ) A.-58 B.18C.14D.118【答案】B【解析】方法1(基向量法):如图所示，选取AB ⃗⃗⃗⃗⃗ ，AC ⃗⃗⃗⃗⃗ 为基底，则AF ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ +EF ⃗⃗⃗⃗ =AB⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =AC⃗⃗⃗⃗⃗ −12BC ⃗⃗⃗⃗⃗ +12DE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +12(AC ⃗⃗⃗⃗⃗ −AB⃗⃗⃗⃗⃗ )+12×12AC ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +34AC⃗⃗⃗⃗⃗ ，AB⃗⃗⃗⃗⃗ . 故AF ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =（12AB ⃗⃗⃗⃗⃗ +34AC ⃗⃗⃗⃗⃗ ）·(AC ⃗⃗⃗⃗⃗ −AB⃗⃗⃗⃗⃗ ) =34AC ⃗⃗⃗⃗⃗ 2−14AC ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ −12AB⃗⃗⃗⃗⃗ 2 =34−14×1×1×12−12=18.14.(2016·全国2·理T3)已知向量a=(1，m)，b=(3，-2)，且(a+b)⊥b ，则m=( ) A.-8B.-6C.6D.8【答案】D【解析】由题意可知，向量a+b=(4，m-2).由(a+b)⊥b ，得4×3+(m-2)×(-2)=0，解得m=8.故选D.15.(2015·全国2·文T4)向量a=(1，-1)，b=(-1，2)，则(2a+b )·a=( ) A.-1B.0C.1D.2【答案】C【解析】由已知2a+b=(1，0)，所以(2a+b )·a=1×1+0×(-1)=1.故选C.16.(2015·福建·文T7)设a=(1，2)，b=(1，1)，c=a+kb.若b ⊥c ，则实数k 的值等于( )A.-32 B.-53C.53D.32【答案】A【解析】∵a=(1，2)，b=(1，1)，∴c=(1+k ，2+k). ∵b ⊥c ，∴b ·c=1+k+2+k=0.∴k=-3217.(2015·广东·文T9)在平面直角坐标系xOy 中，已知四边形ABCD 是平行四边形，AB ⃗⃗⃗⃗⃗ =(1，-2)，AD ⃗⃗⃗⃗⃗ =(2，1)，则AD ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =( ) A.5 B.4 C.3 D.2 【答案】A【解析】AC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ =(3，-1)，所以AD⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =(2，1)·(3，-1)=2×3+1×(-1)=5. 18.(2015·山东·理T4)已知菱形ABCD 的边长为a ，∠ABC =60°，则BD ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =( ) A.-32a 2 B.-34a 2 C.34a 2 D.32a 2【答案】D【解析】如图，设BA ⃗⃗⃗⃗⃗ =a ，BC⃗⃗⃗⃗⃗ =b. 则BD ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =(BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )·BA⃗⃗⃗⃗⃗ =(a+b)·a=a 2+a ·b=a 2+a ·a ·c os 60°=a 2+12a 2=32a 2.19.(2015·四川·理T7)设四边形ABCD 为平行四边形，|AB ⃗⃗⃗⃗⃗ |=6，|AD ⃗⃗⃗⃗⃗ |=4.若点M ，N 满足BM ⃗⃗⃗⃗⃗⃗ =3MC ⃗⃗⃗⃗⃗⃗ ，DN ⃗⃗⃗⃗⃗ =2NC ⃗⃗⃗⃗⃗ ，则AM ⃗⃗⃗⃗⃗⃗ ·NM ⃗⃗⃗⃗⃗⃗ =( ) A.20B.15C.9D.6【答案】C【解析】如图所示，AM ⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +34AD ⃗⃗⃗⃗⃗ ，NM ⃗⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ −14AD ⃗⃗⃗⃗⃗ ，所以AM ⃗⃗⃗⃗⃗⃗ ·NM ⃗⃗⃗⃗⃗⃗ =(AB⃗⃗⃗⃗⃗ +34AD ⃗⃗⃗⃗⃗ )·（13AB ⃗⃗⃗⃗⃗ −14AD ⃗⃗⃗⃗⃗ ） =13|AB ⃗⃗⃗⃗⃗ |2-316|AD ⃗⃗⃗⃗⃗ |2+14AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ −14AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗=13×36-316×16=9.20.(2015·福建·理T9)已知AB ⃗⃗⃗⃗⃗ ⊥AC ⃗⃗⃗⃗⃗ ，|AB ⃗⃗⃗⃗⃗ |=1t ，|AC⃗⃗⃗⃗⃗ |=t.若点P 是△ABC 所在平面内的一点，且AP ⃗⃗⃗⃗⃗ =AB⃗⃗⃗⃗⃗⃗ |AB⃗⃗⃗⃗⃗⃗ |+4AC⃗⃗⃗⃗⃗ |AC ⃗⃗⃗⃗⃗ |，则PB⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ 的最大值等于( )A.13B.15C.19D.21【答案】A【解析】以点A 为原点，AB ⃗⃗⃗⃗⃗ ，AC ⃗⃗⃗⃗⃗ 所在直线分别为x 轴、y 轴建立平面直角坐标系，如图. 则A(0，0)，B (1t ，0)，C(0，t)， ∴AB ⃗⃗⃗⃗⃗⃗ |AB ⃗⃗⃗⃗⃗⃗ |=(1，0)，AC⃗⃗⃗⃗⃗ |AC ⃗⃗⃗⃗⃗ |=(0，1). ∴AP⃗⃗⃗⃗⃗ =AB⃗⃗⃗⃗⃗⃗ |AB⃗⃗⃗⃗⃗⃗ |+4AC⃗⃗⃗⃗⃗ |AC⃗⃗⃗⃗⃗ |=(1，0)+4(0，1)=(1，4). ∴点P 的坐标为(1，4)，PB⃗⃗⃗⃗⃗ =(1t-1，-4)，PC ⃗⃗⃗⃗ =(-1，t-4). ∴PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ =1-1t -4t+16=-(1t +4t)+17≤-4+17=13，当且仅当1t =4t ，即t=12时取“=”. ∴PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗ 的最大值为13.21.(2015·全国1·文T2)已知点A(0，1)，B(3，2)，向量AC ⃗⃗⃗⃗⃗ =(-4，-3)，则向量BC ⃗⃗⃗⃗⃗ =( ) A.(-7，-4) B.(7，4) C.(-1，4) D.(1，4) 【答案】A【解析】∵AB ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =(3，1)，AC ⃗⃗⃗⃗⃗ =(-4，-3)， ∴BC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =(-4，-3)-(3，1)=(-7，-4). 22.(2015·重庆·理T6)若非零向量a ，b 满足|a|=2√23|b|，且(a-b)⊥(3a+2b)，则a 与b 的夹角为 ( )A.π4B.π2C.3π4D .π【答案】A【解析】由(a-b)⊥(3a+2b)知(a-b)·(3a+2b)=0，即3|a|2-a ·b-2|b|2=0.设a 与b 的夹角为θ，则3|a|2-|a||b|cos θ-2|b|2=0，即3·(2√23|b |)2−2√23|b|2cos θ-2|b|2=0，整理，得cos θ=√22.故θ=π4.23.(2015·重庆·文T7)已知非零向量a ，b 满足|b|=4|a|，且a ⊥(2a+b)，则a 与b 的夹角为( ) A.π3 B.π2C.2π3D.5π6【答案】C【解析】因为a ⊥(2a+b)，所以a ·(2a+b)=0，即2|a|2+a ·b=0.设a 与b 的夹角为θ，则有2|a|2+|a||b|cos θ=0. 又|b|=4|a|，所以2|a|2+4|a|2cos θ=0，则cos θ=-12，从而θ=2π3.24.(2015·全国1·理T7)设D 为△ABC 所在平面内一点，BC ⃗⃗⃗⃗⃗ =3CD ⃗⃗⃗⃗⃗ ，则( ) A.AD ⃗⃗⃗⃗⃗ =-13AB ⃗⃗⃗⃗⃗ +43AC⃗⃗⃗⃗⃗ B.AD ⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ −43AC⃗⃗⃗⃗⃗ C.AD ⃗⃗⃗⃗⃗ =43AB ⃗⃗⃗⃗⃗ +13AC⃗⃗⃗⃗⃗ D.AD ⃗⃗⃗⃗⃗ =43AB ⃗⃗⃗⃗⃗ −13AC⃗⃗⃗⃗⃗ 【答案】A 【解析】如图，∵AD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗ ，BC ⃗⃗⃗⃗⃗ =3CD ⃗⃗⃗⃗⃗ ， ∴AD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +43BC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +43(AC ⃗⃗⃗⃗⃗ −AB⃗⃗⃗⃗⃗ ) =-13AB ⃗⃗⃗⃗⃗ +43AC ⃗⃗⃗⃗⃗ . 25.(2014·全国1·文T6)设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB ⃗⃗⃗⃗⃗ +FC ⃗⃗⃗⃗ =( ) A.AD ⃗⃗⃗⃗⃗B.12AD ⃗⃗⃗⃗⃗C.BC ⃗⃗⃗⃗⃗D.12BC⃗⃗⃗⃗⃗ 【答案】A【解析】EB ⃗⃗⃗⃗⃗ +FC ⃗⃗⃗⃗ =-12(BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )-12(CA ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ )=-12(BA ⃗⃗⃗⃗⃗ +CA⃗⃗⃗⃗⃗ )=12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=12×2AD ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ ，故选A.26.(2014·山东·文T7)已知向量a=(1，√3)，b=(3，m)，若向量a ，b 的夹角为π6，则实数m=( ) A.2√3 B.√3 C.0 D.-√3【答案】B【解析】∵cos<a ，b>=a ·b|a ||b |， ∴cos π6=√3m 2×√32+m 2，解得m=√3.27.(2014·北京·文T3)已知向量a=(2，4)，b=(-1，1)，则2a-b=( ) A.(5，7) B.(5，9) C.(3，7) D.(3，9) 【答案】A【解析】2a-b=(4-(-1)，8-1)=(5，7).故选A.28.(2014·广东·文T3)已知向量a=(1，2)，b=(3，1)，则b-a=( ) A.(-2，1) B.(2，-1) C.(2，0) D.(4，3) 【答案】B【解析】由题意得b-a=(3，1)-(1，2)=(2，-1)，故选B.29.(2014·福建·理T8)在下列向量组中，可以把向量a=(3，2)表示出来的是( ) A.e 1=(0，0)，e 2=(1，2)B.e 1=(-1，2)，e 2=(5，-2)C.e 1=(3，5)，e 2=(6，10)D.e 1=(2，-3)，e 2=(-2，3) 【答案】B【解析】对于A ，C ，D ，都有e 1∥e 2，故选B.30.(2014·全国2·理T3文T4)设向量a ，b 满足|a+b|=√10，|a-b|=√6，则a ·b=( ) A.1 B.2 C.3 D.5 【答案】A【解析】∵|a+b|=√10，∴(a+b)2=10.∴|a|2+|b|2+2a·b=10，①∵|a-b|=√6，∴(a-b)2=6，∴|a|2+|b|2-2a·b=6，②由①-②得a·b=1，故选A.31.(2014·大纲全国·文T6)已知a，b为单位向量，其夹角为60°，则(2a-b)·b=( )A.-1B.0C.1D.2【答案】B【解析】由已知得|a|=|b|=1，<a，b>=60°，∴(2a-b)·b=2a·b-b2=2|a||b|cos<a，b>-|b|2=2×1×1×c os 60°-12=0，故选B.32.(2014·大纲全国·理T4)若向量a，b满足:|a|=1，(a+b)⊥a，(2a+b)⊥b，则|b|=( )A.2B.√2C.1D.√22【答案】B【解析】∵(a+b)⊥a，|a|=1，∴(a+b)·a=0.∴|a|2+a·b=0.∴a·b=-1.又(2a+b)⊥b，∴(2a+b)·b=0.∴2a·b+|b|2=0.∴|b|2=2.∴|b|=√2.故选B.33.(2014·重庆·理T4)已知向量a=(k，3)，b=(1，4)，c=(2，1)，且(2a-3b)⊥c，则实数k=( )A.-92B.0 C.3 D.152【答案】C【解析】由已知(2a-3b)⊥c，可得(2a-3b)·c=0，即(2k-3，-6)·(2，1)=0，展开化简，得4k-12=0，所以k=3.故选C.34.(2012·陕西·文T7)设向量a=(1，cos θ)与b=(-1，2cos θ)垂直，则cos 2θ等于( )A.√22B.12C.0D.-1【答案】C【解析】∵a ⊥b ，∴a ·b=0， ∴-1+2cos 2θ=0，即cos 2θ=0.35.(2012·重庆·理T6)设x ，y ∈R ，向量a=(x ，1)，b=(1，y)，c=(2，-4)，且a ⊥c ，b ∥c ，则|a+b|= ( ) A.√5 B.√10 C.2√5 D.10【答案】B【解析】由a ⊥c ，得a ·c=2x-4=0，解得x=2.由b ∥c 得12=y-4，解得y=-2，所以a=(2，1)，b=(1，-2)，a+b=(3，-1)，|a+b|=√10.故选B.36.(2010·全国·文T2)a ，b 为平面向量，已知a=(4，3)，2a+b=(3，18)，则a ，b 夹角的余弦值等于( ) A.865 B.-865C.1665D.-1665【答案】C【解析】b=(2a+b)-2a=(3，18)-(8，6)=(-5，12)，因此cos<a ，b>=a ·b |a ||b |=165×13=1665.37.(2019·全国3·文T13)已知向量a=(2，2)，b=(-8，6)，则cos<a ，b>= . 【答案】−√210【解析】cos<a ，b>=a ·b|a ||b |=√22+22×√(-8)+62=2√2×10=-√210. 38.(2019·北京·文T9)已知向量a=(-4，3)，b=(6，m)，且a ⊥b ，则m= . 【答案】8【解析】∵a=(-4，3)，b=(6，m)，a ⊥b ， ∴a ·b=0，即-4×6+3m=0，即m=8.39.(2019·天津·T14)在四边形ABCD 中，AD ∥BC ，AB=2√3，AD=5，∠A=30°，点E 在线段CB 的延长线上，且AE=BE ，则BD ⃗⃗⃗⃗⃗ ·AE ⃗⃗⃗⃗⃗ = . 【答案】-1【解析】∵AD ∥BC ，且∠DAB=30°，∴∠ABE=30°. ∵EA=EB ，∴∠EAB=30°.∠AEB=120°.在△AEB 中，EA=EB=2， BD ⃗⃗⃗⃗⃗ ·AE ⃗⃗⃗⃗⃗ =(BA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )·(AB ⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ ) =-BA ⃗⃗⃗⃗⃗ 2+BA ⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ ·BE⃗⃗⃗⃗⃗ =-12+2√3×2×c os 30°+5×2√3×c os 30°+5×2×c os 180°=-22+6+15=-1.40.(2019·全国3·理T13)已知a ，b 为单位向量，且a ·b=0，若c=2a-√5b ，则cos<a ，c>= . 【答案】23【解析】∵a ，b 为单位向量， ∴|a|=|b|=1.又a ·b=0，c=2a-√5b ，∴|c|2=4|a|2+5|b|2-4√5a ·b=9，∴|c|=3. 又a ·c=2|a|2-√5a ·b=2， ∴cos<a ，c>=a ·c|a |·|c |=21×3=23.41.(2019·浙江·T17)已知正方形ABCD 的边长为1.当每个λi (i=1，2，3，4，5，6)取遍±1时，|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ |的最小值是，最大值是 . 【答案】0 2√5 【解析】(基向量处理)λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ =(λ1-λ3+λ5-λ6)AB ⃗⃗⃗⃗⃗ +(λ2-λ4+λ5+λ6)AD ⃗⃗⃗⃗⃗ ，要使|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ |的最小，只需要|λ1-λ3+λ5-λ6|=|λ2-λ4+λ5+λ6|=0，此时只需要取λ1=1，λ2=-1，λ3=1，λ4=1，λ5=1，λ6=1，此时|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ |min =0，由于λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ =±2AB ⃗⃗⃗⃗⃗ 或±2AD ⃗⃗⃗⃗⃗ ，取其中的一种λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ =2AB⃗⃗⃗⃗⃗ 讨论(其他三种类同)，此时λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ =(λ1-λ3+2)AB ⃗⃗⃗⃗⃗ +(λ2-λ4)AD ⃗⃗⃗⃗⃗ ，要使|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ |的最大，只需要使|λ1-λ3+2|，|λ2-λ4|最大，取λ1=1，λ2=1，λ3=-1，λ4=-1，此时|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD ⃗⃗⃗⃗⃗ |=|4AB ⃗⃗⃗⃗⃗ +2AD ⃗⃗⃗⃗⃗ |=2√5，综合几种情况可得|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD⃗⃗⃗⃗⃗ |max =2√42.(2019·江苏·T12)如图，在△ABC 中，D 是BC 的中点，E 在边AB 上，BE=2EA ，AD 与CE 交于点O.若AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =6AO ⃗⃗⃗⃗⃗ ·EC ⃗⃗⃗⃗ ，则ABAC 的值是 .【答案】√3【解析】如图，过点D 作DF ∥CE ，交AB 于点F ，由BE=2EA ，D 为BC 中点，知BF=FE=EA ，AO=OD.又AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =6AO ⃗⃗⃗⃗⃗ ·EC ⃗⃗⃗⃗ =3AD ⃗⃗⃗⃗⃗ ·(AC ⃗⃗⃗⃗⃗ −AE⃗⃗⃗⃗⃗ ) =32(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )·(AC ⃗⃗⃗⃗⃗ -13AB⃗⃗⃗⃗⃗ ) =32（AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ −13AB ⃗⃗⃗⃗⃗ 2+AC ⃗⃗⃗⃗⃗ 2−13AB ⃗⃗⃗⃗⃗ ·AC⃗⃗⃗⃗⃗ ） =32（23AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ −13AB ⃗⃗⃗⃗⃗ 2+AC⃗⃗⃗⃗⃗ 2） =AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ −12AB ⃗⃗⃗⃗⃗ 2+32AC⃗⃗⃗⃗⃗ 2，得12AB ⃗⃗⃗⃗⃗ 2=32AC ⃗⃗⃗⃗⃗ 2，即|AB⃗⃗⃗⃗⃗ |=√3|AC ⃗⃗⃗⃗⃗ |，故AB AC=√3. 43.(2018·北京·文T9)设向量a=(1，0)，b=(-1，m).若a ⊥(ma-b)，则m= . 【答案】-1【解析】由题意，得ma-b=(m+1，-m). ∵a ⊥(ma-b)，∴a ·(ma-b)=0，即m+1=0， ∴m=-1.44.(2018·上海·T8)在平面直角坐标系中，已知点A(-1，0)，B(2，0)，E ，F 是y 轴上的两个动点，且|EF ⃗⃗⃗⃗ |=2，则AE ⃗⃗⃗⃗⃗ ·BF ⃗⃗⃗⃗ 的最小值为 . 【答案】-3【解析】依题意，设E(0，a)，F(0，b)，不妨设a>b ，则 a-b=2，AE ⃗⃗⃗⃗⃗ =(1，a)，BF ⃗⃗⃗⃗ =(-2，b)，a=b+2，所以AE ⃗⃗⃗⃗⃗ ·BF ⃗⃗⃗⃗ =(1，a)·(-2，b)=-2+ab=-2+(b+2)b=b 2+2b-2=(b+1)2-3，故所求最小值为-3.45.(2018·江苏·T2)在平面直角坐标系xOy 中，A 为直线l:y=2x 上在第一象限内的点，B(5，0)，以AB 为直径的圆C 与直线l 交于另一点D.若AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =0，则点A 的横坐标为 . 【答案】3【解析】设A(a ，2a)(a>0)，则由圆心C 为AB 的中点得C (a+52，a)，☉C:(x-5)(x-a)+y(y-2a)=0.将其与y=2x 联立解得x D =1，D(1，2).因为AB ⃗⃗⃗⃗⃗ =(5-a ，-2a)，CD ⃗⃗⃗⃗⃗ =(1-a+52，2-a)，AB ⃗⃗⃗⃗⃗ ·CD⃗⃗⃗⃗⃗ =0，所以(5-a)·(1-a+52)+(-2a)(2-a)=0，即a 2-2a-3=0，解得a=3或a=-1.因为a>0，所以a=3.46.(2018·全国3·T13)已知向量a=(1，2)，b=(2，-2)，c=(1，λ).若c ∥(2a+b)，则λ= . 【答案】12【解析】2a+b=(4，2)，c=(1，λ)，由c ∥(2a+b)，得4λ-2=0，得λ=12.47.(2017·全国1·文T13)已知向量a=(-1，2)，b=(m ，1)，若向量a+b 与a 垂直，则m= . 【答案】7【解析】因为a=(-1，2)，b=(m ，1)，所以a+b=(m-1，3).因为a+b 与a 垂直，所以(a+b )·a=0，即-(m-1)+2×3=0，解得m=7.48.(2017·山东·文T11)已知向量a=(2，6)，b=(-1，λ).若a ∥b ，则λ= . 【答案】-3【解析】∵a ∥b ，∴2λ-6×(-1)=0，∴λ=-3.49.(2017·全国1·理T13)已知向量a ，b 的夹角为60°，|a|=2，|b|=1，则|a+2b|= . 【答案】2【解析】因为|a+2b|2=(a+2b)2=|a|2+4·|a|·|b|·c os 60°+4|b|2=22+4×2×1×12+4×1=12，所以|a+2b|=√12=2√3.50.(2017·天津，理13文14)在△ABC 中，∠A =60°，AB=3，AC=2.若BD ⃗⃗⃗⃗⃗ =2DC ⃗⃗⃗⃗⃗ ，AE ⃗⃗⃗⃗⃗ =λAC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ (λ∈R)，且AD ⃗⃗⃗⃗⃗ ·AE ⃗⃗⃗⃗⃗ =-4，则λ的值为 . 【答案】311【解析】由题意，知|AB ⃗⃗⃗⃗⃗ |=3，|AC ⃗⃗⃗⃗⃗ |=2， AB ⃗⃗⃗⃗⃗ ·AC⃗⃗⃗⃗⃗ =3×2×c os 60°=3， AD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +23BC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +23(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=13AB ⃗⃗⃗⃗⃗ +23AC⃗⃗⃗⃗⃗ ，所以AD ⃗⃗⃗⃗⃗ ·AE ⃗⃗⃗⃗⃗ =（13AB ⃗⃗⃗⃗⃗ +23AC ⃗⃗⃗⃗⃗ ）·(λAC ⃗⃗⃗⃗⃗ −AB⃗⃗⃗⃗⃗ ) =λ-23AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ −13AB ⃗⃗⃗⃗⃗ 2+2λ3AC ⃗⃗⃗⃗⃗ 2 =λ-23×3-13×32+2λ3×22=113λ-5=-4，解得λ=311.51.(2017·江苏·T12)如图，在同一个平面内，向量OA ⃗⃗⃗⃗⃗ ，OB ⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ 的模分别为1，1，√2，OA ⃗⃗⃗⃗⃗ 与OC ⃗⃗⃗⃗⃗ 的夹角为α，且tan α=7，OB ⃗⃗⃗⃗⃗ 与OC ⃗⃗⃗⃗⃗ 的夹角为45°.若OC ⃗⃗⃗⃗⃗ =m OA ⃗⃗⃗⃗⃗ +n OB ⃗⃗⃗⃗⃗ (m ，n ∈R)，则m+n= . 【答案】3【解析】由tan α=7可得cos α=5√2，sin α=5√2，则5√2=OA⃗⃗⃗⃗⃗⃗ ·OC ⃗⃗⃗⃗⃗⃗ |OA⃗⃗⃗⃗⃗⃗ |·|OC ⃗⃗⃗⃗⃗⃗ |=⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗⃗ √2，由cos ∠BOC=√22可得√22=OB ⃗⃗⃗⃗⃗⃗ ·OC ⃗⃗⃗⃗⃗⃗ |OB ⃗⃗⃗⃗⃗⃗ |·|OC⃗⃗⃗⃗⃗⃗ |=⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗⃗ √2，因为cos ∠AOB=cos (α+45°)=cos αc os 45°-sin αsin45°=5√2×√22−5√2×√22=-35，所以OA ⃗⃗⃗⃗⃗ ·OB⃗⃗⃗⃗⃗ =-35，所以m-35n=15，-35m+n=1，所以25m+25n=65，所以m+n=3.52.(2017·山东·理T12)已知e 1，e 2是互相垂直的单位向量，若√3 e 1-e 2与e 1+λe 2的夹角为60°，则实数λ的值是 . 【答案】√33【解析】∵e 1，e 2是互相垂直的单位向量， ∴可设a=√3e 1-e 2=(√3，-1)，b=e 1+λe 2=(1，λ). 则<a ，b >=60°.∴cos<a ，b>=c os 60°=a ·b|a ||b |=√3-2=12，即√3-λ=2+1，解得λ=√33.53.(2017·江苏·理T13)在平面直角坐标系xOy 中，A(-12，0)，B(0，6)，点P 在圆O:x 2+y 2=50上.若PA ⃗⃗⃗⃗ ·PB ⃗⃗⃗⃗⃗ ≤20，则点P 的横坐标的取值范围是 . 【答案】[-5√2，1]【解析】设P(x ，y)，由PA ⃗⃗⃗⃗ ·PB ⃗⃗⃗⃗⃗ ≤20，易得x 2+y 2+12x-6y≤20.把x 2+y 2=50代入x 2+y 2+12x-6y≤20得2x-y+5≤0. 由{2x -y +5=0，x 2+y 2=50，可得{x =-5，y =-5或{x =1，y =7.由2x-y+5≤0表示的平面区域及P 点在圆上，可得点P 在圆弧EPF 上，所以点P 横坐标的取值范围为[-5√2，1].54.(2017·北京·文T12)已知点P 在圆x 2+y 2=1上，点A 的坐标为(-2，0)，O 为原点，则AO ⃗⃗⃗⃗⃗ ·AP ⃗⃗⃗⃗⃗ 的最大值为 .【答案】6【解析】方法1:设P(cos α，sin α)，α∈R ，则AO ⃗⃗⃗⃗⃗ =(2，0)，AP ⃗⃗⃗⃗⃗ =(cos α+2，sin α)，AO ⃗⃗⃗⃗⃗ ·AP ⃗⃗⃗⃗⃗ =2cos α+4.当α=2k π，k ∈Z 时，2cos α+4取得最大值，最大值为6. 故AO ⃗⃗⃗⃗⃗ ·AP⃗⃗⃗⃗⃗ 的最大值为6. 方法2:设P(x ，y)，x 2+y 2=1，-1≤x≤1，AO ⃗⃗⃗⃗⃗ =(2，0)，AP ⃗⃗⃗⃗⃗ =(x+2，y)，AO ⃗⃗⃗⃗⃗ ·AP ⃗⃗⃗⃗⃗ =2x+4，故AO ⃗⃗⃗⃗⃗ ·AP ⃗⃗⃗⃗⃗ 的最大值为6.55.(2016·北京·文T9)已知向量a=(1，√3)，b=(√3，1)，则a 与b 夹角的大小为 . 【答案】π6【解析】设a 与b 的夹角为θ，则cos θ=a ·b|a ||b |=2√32×2=√32，且两个向量夹角范围是[0，π]，∴所求的夹角为π6.56.(2016·全国1·文T13)设向量a=(x ，x+1)，b=(1，2)，且a ⊥b ，则x= . 【答案】−23【解析】∵a ⊥b ，∴a ·b=x+2(x+1)=0，解得x=-23.57.(2016·山东·文T13)已知向量a=(1，-1)，b=(6，-4).若a ⊥(ta+b)，则实数t 的值为 . 【答案】-5【解析】由a ⊥(ta+b)可得a ·(ta+b)=0，所以ta 2+a ·b=0，而a 2=12+(-1)2=2，a ·b=1×6+(-1)×(-4)=10，所以有t×2+10=0，解得t=-5. 58.(2016·全国2·文T13)已知向量a=(m ，4)，b=(3，-2)，且a ∥b ，则m= . 【答案】-6【解析】因为a ∥b ，所以-2m-4×3=0，解得m=-6.59.(2016·全国1·理T13)设向量a=(m ，1)，b=(1，2)，且|a+b|2=|a|2+|b|2，则m= . 【答案】-2【解析】∵|a+b|2=|a|2+|b|2， ∴(m+1)2+32=m 2+1+5，解得m=-2.60.(2015·浙江·文T13)已知e 1，e 2是平面单位向量，且e 1·e 2=12.若平面向量b 满足b ·e 1=b ·e 2=1，则|b|= . 【答案】2√33【解析】因为b ·e 1=b ·e 2=1，|e 1|=|e 2|=1，由数量积的几何意义，知b 在e 1，e 2方向上的投影相等，且都为1，所以b 与e 1，e 2所成的角相等.由e 1·e 2=12知e 1与e 2的夹角为60°，所以b 与e 1，e 2所成的角均为30°，即|b|c os 30°=1，所以|b|=1cos30°=2√33. 61.(2015·全国2·理T13)设向量a ，b 不平行，向量λa+b 与a+2b 平行，则实数λ= . 【答案】12【解析】由题意知存在实数t ∈R ，使λa+b=t(a+2b)，得{λ=t ，1=2t ，解得λ=12.62.(2015·北京·理T13)在△ABC 中，点M ，N 满足AM ⃗⃗⃗⃗⃗⃗ =2MC ⃗⃗⃗⃗⃗⃗ ，BN ⃗⃗⃗⃗⃗ =NC ⃗⃗⃗⃗⃗ .若MN ⃗⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗⃗ +y AC ⃗⃗⃗⃗⃗ ，则x= ，y= . 【答案】12−16【解析】如图，∵MN ⃗⃗⃗⃗⃗⃗ =MC ⃗⃗⃗⃗⃗⃗ +CN ⃗⃗⃗⃗⃗ =13AC ⃗⃗⃗⃗⃗ −12BC⃗⃗⃗⃗⃗ =13AC ⃗⃗⃗⃗⃗ −12(AC ⃗⃗⃗⃗⃗ −AB⃗⃗⃗⃗⃗ ) =12AB ⃗⃗⃗⃗⃗ −16AC⃗⃗⃗⃗⃗ ， ∴x=12，y=-16.63.(2014·湖北·理T11)设向量a=(3，3)，b=(1，-1).若(a +λb)⊥(a-λb)，则实数λ= . 【答案】±3【解析】由题意得(a+λb)·(a-λb)=0，即a 2-λ2b 2=0，则a 2=λ2b 2， λ2=a 2b 2=(√32+32)2[√12+(-1)]=182=9.故λ=±3.64.(2014·陕西·理T3)设0<θ<π2，向量a=(sin 2θ，cos θ)，b=(cos θ，1)，若a ∥b ，则tan θ= .【答案】12【解析】由a ∥b ，得sin 2θ=cos 2θ，即2sin θcos θ=cos 2θ，因为0<θ<π2，所以cos θ≠0，所以2sin θ=cos θ. 所以tan θ=12.65.(2014·重庆·文T12)已知向量a 与b 的夹角为60°，且a=(-2，-6)，|b|=√10，则a ·b= . 【答案】10【解析】由题意得|a|=2√10，所以a ·b=|a||b|cos<a ，b>=2√10×√10×12=10.66.(2014·全国1·理T15)已知A ，B ，C 为圆O 上的三点，若AO ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )，则AB ⃗⃗⃗⃗⃗ 与AC⃗⃗⃗⃗⃗ 的夹角为 . 【答案】90°【解析】由AO ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )，可得O 为BC 的中点，则BC 为圆O 的直径，即∠BAC =90°.故AB⃗⃗⃗⃗⃗ 与AC⃗⃗⃗⃗⃗ 的夹角为90°. 67.(2014·湖北·文T12)若向量OA ⃗⃗⃗⃗⃗ =(1，-3)，|OA ⃗⃗⃗⃗⃗ |=|OB ⃗⃗⃗⃗⃗ |，OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =0，则|AB ⃗⃗⃗⃗⃗ |= . 【答案】2√5【解析】设B(x ，y)，由|OA ⃗⃗⃗⃗⃗ |=|OB ⃗⃗⃗⃗⃗ |，可得√10=√x 2+y 2， ① OA⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =x-3y=0， ② 由①②得x=3，y=1或x=-3，y=-1，所以B(3，1)或B(-3，-1)，故AB ⃗⃗⃗⃗⃗ =(2，4)或AB ⃗⃗⃗⃗⃗ =(-4，2)，|AB⃗⃗⃗⃗⃗ |=2√5， 68.(2013·江苏·T10)设D ，E 分别是△ABC 的边AB ，BC 上的点，AD=12AB ，BE=23BC.若DE ⃗⃗⃗⃗⃗ =λ1AB ⃗⃗⃗⃗⃗ +λ2AC ⃗⃗⃗⃗⃗ (λ1，λ2为实数)，则λ1+λ2的值为 . 【答案】12【解析】由题意作图如图.∵在△ABC 中，DE ⃗⃗⃗⃗⃗ =DB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +23BC ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +23(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=-16AB ⃗⃗⃗⃗⃗ +23AC ⃗⃗⃗⃗⃗ =λ1AB ⃗⃗⃗⃗⃗ +λ2AC ⃗⃗⃗⃗⃗ ，∴λ1=-16，λ2=23.故λ1+λ2=12.69.(2013·北京·理T13)向量a ，b ，c 在正方形网格中的位置如图所示，若c =λa +μb(λ，μ∈R)，则λμ= .【答案】4【解析】可设a=-i+j ，i ，j 为单位向量且i ⊥j ，则b=6i+2j ，c=-i-3j.∵c =λa +μb=(6μ-λ)i+(λ+2μ)j ，∴{6μ-λ=-1，λ+2μ=-3，解得{λ=-2，μ=-12.∴λμ=4. 70.(2013·全国1·T13)已知两个单位向量a ，b 的夹角为60°，c=ta+(1-t)b.若b ·c=0，则t= .【答案】2【解析】b ·c=ta ·b+(1-t)|b|2.又|a|=|b|=1，且a 与b 的夹角为60°，b ·c=0，∴0=t|a||b|c os 60°+(1-t)，0=12t+1-t.∴t=2.71.(2013·全国2·理T13文T14)已知正方形ABCD 的边长为2，E 为CD 的中点，则AE⃗⃗⃗⃗⃗ ·BD⃗⃗⃗⃗⃗ = .【答案】2【解析】以{AB ⃗⃗⃗⃗⃗ ，AD ⃗⃗⃗⃗⃗ }为基底，则AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ =0，而AE ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ ，BD ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ， ∴AE ⃗⃗⃗⃗⃗ ·BD ⃗⃗⃗⃗⃗ =(12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )·(AD ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ) =-12|AB ⃗⃗⃗⃗⃗ |2+|AD ⃗⃗⃗⃗⃗ |2=-12×22+22=2.72.(2013·天津·理T12)在平行四边形ABCD 中，AD=1，∠BA D=60°，E 为CD 的中点.若AC⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ =1，则AB 的长为 .【答案】12【解析】如图所示，在平行四边形ABCD 中，AC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ ，BE ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗ =-12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ . 所以AC ⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )·(-12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )=-12|AB ⃗⃗⃗⃗⃗ |2+|AD ⃗⃗⃗⃗⃗ |2+12AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ =-12|AB ⃗⃗⃗⃗⃗ |2+14|AB ⃗⃗⃗⃗⃗ |+1=1，解方程得|AB ⃗⃗⃗⃗⃗ |=12(舍去|AB ⃗⃗⃗⃗⃗ |=0).所以线段AB 的长为12.73.(2013·北京·文T14)已知点A(1，-1)，B(3，0)，C(2，1).若平面区域D 由所有满足AP ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAC⃗⃗⃗⃗⃗ (1≤λ≤2，0≤μ≤1)的点P 组成，则D 的面积为 . 【答案】3【解析】AP ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAC ⃗⃗⃗⃗⃗ ，AB ⃗⃗⃗⃗⃗ =(2，1)，AC⃗⃗⃗⃗⃗ =(1，2). 设P(x ，y)，则AP⃗⃗⃗⃗⃗ =(x-1，y+1). ∴{x -1=2λ+μ，y +1=λ+2μ，得{λ=2x -y -33，μ=2y -x+33，∵1≤λ≤2，0≤μ≤1，可得{6≤2x -y ≤9，0≤x -2y ≤3，如图.可得A 1(3，0)，B 1(4，2)，C 1(6，3)，|A1B1|=√(4-3)2+22=√5，两直线间距离d=√22+1=√5，∴D的面积S=|A1B1|·d=3.74.(2012·全国·理T13文T15)已知向量a，b夹角为45°，且|a|=1，|2a-b|=√10，则|b|= .【答案】3√2【解析】∵a，b的夹角为45°，|a|=1，∴a·b=|a|×|b|c os 45°=√22|b|，|2a-b|2=4-4×√22|b|+|b|2=10，∴|b|=3√2.75.(2012·安徽·文T11)设向量a=(1，2m)，b=(m+1，1)，c=(2，m)，若(a+c)⊥b，则|a|= . 【答案】√2【解析】由题意，可得a+c=(3，3m).由(a+c)⊥b，得(a+c)·b=0，即(3，3m)·(m+1，1)=3(m+1)+3m=0，解之，得m=-12.∴a=(1，-1)，|a|=√2.76.(2011·全国·文T13)已知a与b为两个不共线的单位向量，k为实数，若向量a+b与向量ka-b垂直，则k= .【答案】1【解析】由已知可得|a|=|b|=1，且a与b不共线，所以a·b≠1，a·b≠-1.由已知向量a+b与向量ka-b垂直，所以(a+b)·(ka-b)=0，即ka2-b2+(k-1)a·b=0，即k-1+(k-1)a·b=0，所以(k-1)(1+a·b)=0.因为a·b≠-1，即a·b+1≠0，所以k-1=0，即k=1.(2010-2019)十年高考数学真题分类汇编：平面向量（含解析）。

2010—2019“十年高考”数学真题分类汇总平面向量专题解析版 (可下载)

解法二由 b2 4e b 3 0 得 b2 4e b 3e2 (b e) (b 3e) 0 ．

设 b OB ， e OE ， 3e OF ，所以 b e EB ， b 3e = FB ，
7.（2017 北京）设 m , n 为非零向量，则“存在负数，使得 m n ”是“ m n 0 ”的
A．充分而不必要条件
B．必要而不充分条件
C．充分必要条件
D．既不充分也不必要条件
【答案】A.
【解析】因为 m, n 为非零向量，所以 m n | m || n | cos m, n 0 的充要条件是
cos m, n 0 ．
因为 0 ，则由 m n 可知 m, n 的方向相反， m, n 180 ，所以
法二、优解
EB

AB

AE

AB

1
AD

AB

1
1
(AB

AC
)
2
22

3
AB

1
AC
．故选
A．
44
4.（2018 全国卷Ⅱ）已知向量 a ， b 满足 | a | 1 ， a b 1 ，则 a (2a b)
所以 cos a, b b 2 b 2 1 ． ab 2b 2
又因为 a, b [0，π] ，所以 a, b π ．故选 B． 3
2.（2019 全国Ⅱ文 3）已知向量 a=(2，3)，b=(3，2)，则|a–b|=

理科数学2010-2019高考真题分类训练14专题五平面向量第十四讲向量的应用—附解析答案

求 y g x 的单调递增区间．
32．（2014 辽宁）在 ABC 中，内角 A, B,C 的对边 a,b, c ，且 a c ，已知 BA BC 2 ， cos B 1 ， b 3 ，求： 3 （Ⅰ） a 和 c 的值；
（Ⅱ） cos(B C) 的值．
33．（2013 江苏）已知 a (cos,sin) ， b (cos ,sin ) ， 0 ．
{P | 0 r ≤| PQ |≤ R, r R}．若 C 为两段分离的曲线，则
A．1 r R 3 B．1 r 3 R C． r 1 R 3 D．1 r 3 R
13．（2014 天津）已知菱形 ABCD 的边长为 2，? BAD 120 ，点 E, F 分别在边 BC, DC
存在定点 P(0,t)(t 0) ，使得 l 与 PA, PB 都相交，交点分别为 D, E ，且 QAB 与 PDE 的面积之比是常数？若存在，求 t 的值．若不存在，说明理由． 37．（2011 安徽）设，点 A 的坐标为 (1,1) ，点 B 在抛物线 y x 上运动，点 Q 满足
36．（2012 江西）已知三点 O(0, 0) ， A(2,1) ， B(2,1) ，曲线 C 上任意一点 M (x, y) 满足
| MA MB | OM (OA OB) 2 ．（1）求曲线 C 的方程；（2）动点 Q(x0, y0 )(2 x0 2) 在曲线 C 上，曲线 C 在点 Q 处的切线为 l 。问：是否
（II）若点 M 到直线 l 的距离的最小值为 7 5 ，求抛物线 E 的方程． 5
35．（2013 辽宁）设向量 a
3 sin x,sin x
,
b
cos
x,
sinx
,

专题14 平面向量-2019年高考理数母题题源系列(天津专版)(解析版)

【母题原题1】【2019年高考天津卷理数】在四边形ABCD中，,AD BC AB =∥5,30AD A =∠=︒，点E 在线段CB 的延长线上，且AE BE =，则BD AE ⋅=___________．【答案】1-【解析】建立如图所示的直角坐标系，∠DAB =30°，5,AB AD ==则B，5)2D ．因为AD ∥BC ，30BAD ∠=︒，所以30ABE ∠=︒，因为AE BE =，所以30BAE ∠=︒，所以直线BE的斜率为3，其方程为(3y x =-，直线AE的斜率为y x =．由(33y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩得x =1y =-，所以1)E -．所以35(,)(3,1)122BD AE =-=-．专题14 平面向量【名师点睛】平面向量问题有两大类解法：基向量法和坐标法，在便于建立坐标系的问题中使用坐标方法更为方便．【母题原题2】【2018年高考天津卷理数】如图，在平面四边形ABCD 中，,,AB BC AD CD ⊥⊥120,BAD ∠=1,AB AD ==若点E 为边CD 上的动点，则AE BE ⋅的最小值为A ．2116 B ．32C ．2516D ．3【答案】A【解析】连接AD ，取AD 中点为O ，可知ABD △为等腰三角形，而,AB BC AD CD ⊥⊥，所以BCD △为等边三角形，BD =设()01DE tDC t =≤≤，AE BE ⋅ ()()()2232AD DE BD DE AD BD DE AD BD DE BD DE DE =+⋅+=⋅+⋅++=+⋅+ =233322t t -+ ()01t ≤≤，所以当14t =时，上式取最大值2116，故选A ．【名师点睛】本题考查的是平面向量基本定理与向量的拆分，需要选择合适的基底，再把其它向量都用基底表示，同时利用向量共线转化为函数求最值．【母题原题3】【2017年高考天津卷理数】在ABC △中，60A =︒∠，3AB =，2AC =．若2B D D C =，AE AC λ=-()AB λ∈R ，且4AD AE ⋅=-，则λ的值为___________．【答案】311【解析】由题可得1232cos603,33AB AC AD AB AC ⋅=⨯⨯︒==+，则12()33AD AE AB AC ⋅=+2123()34934333311AC AB λλλλ-=⨯+⨯-⨯-⨯=-⇒=．【名师点睛】根据平面向量基本定理，利用表示平面向量的一组基底可以表示平面内的任一向量，利用向量的定比分点公式表示向量，则可获解．本题中,AB AC 已知模和夹角，作为基底易于计算数量积．【命题意图】主要考查考生的直观想象能力、数学运算能力和方程思想、数形结合思想的运用．【命题规律】在高考中的命题重点有平面向量的线性运算、共线向量定理、平面向量基本定理及向量的坐标运算，主要以选择题和填空题的形式呈现，难度不大．【答题模板】1．向量的坐标运算主要是利用向量加、减、数乘运算的法则来进行求解，若已知有向线段两端点的坐标，则应先求向量的坐标．2．解题过程中，常利用向量相等则其坐标相同这一原则，通过列方程（组）来进行求解． 3．两平面向量共线的充要条件有两种形式：（1）若a ＝（x 1，y 1），b ＝（x 2，y 2），则a ∥b 的充要条件是x 1y 2－x 2y 1＝0；（2）若a ∥b （a ≠0），则b ＝λa ，应视题目条件灵活选择．【知识总结】 1．向量的有关概念向量的定义及表示：既有大小又有方向的量叫作向量．以A 为起点、B 为终点的向量记作 AB ，也可用黑体的单个小写字母a ，b ，c ，…来表示向量．向量的长度（模）：向量AB 的大小即向量AB 的长度（模），记为|AB |．（1）向量不同于数量，向量不仅有大小，而且还有方向．（2）任意向量a 的模都是非负实数，即|a |≥0．（3）向量不能比较大小，但|a |是实数（正数或0），所以向量的模可以比较大小． 2．几种特殊向量说明：（1）要注意0与0的区别，0是一个实数，0是一个向量，且|0|=0；（2）单位向量有无数个，它们大小相等，但方向不一定相同；（3）任一组平行向量都可以平移到同一直线上，因此平行向量也叫作共线向量；（4）与向量a 平行的单位向量有两个，即向量||a a 和–||aa ． 3．平面向量运算的坐标表示说明：（1）相等的向量坐标相同；（2）向量的坐标与表示该向量的有向线段的端点无关，只与其相对位置有关． 4．平面向量共线的坐标表示（1）如果a =（x 1，y 1），b =（x 2，y 2），则a ∥b 的充要条件为x 1y 2–x 2y 1=0．（2）A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）三点共线的充要条件为（x 2–x 1）（y 3–y 1）–（x 3–x 1）（y 2–y 1）=0，或（x2–x1）（y3–y2）=（x3–x2）（y2–y1），或（x3–x1）（y3–y2）=（x3–x2）（y3–y1）．5．向量的数量积（1）平面向量数量积的定义已知两个非零向量a与b，它们的夹角为θ，则数量|a||b|cos θ叫作a与b的数量积，记作a·b，即a·b=|a||b|cos θ．规定：零向量与任一向量的数量积为零．（2）向量数量积的性质设a，b为非零向量，它们的夹角为θ，则①设e是单位向量，且e与a的夹角为θ，则e·a=a·e=|a|cos θ；②a⊥b⇔a·b=0；③当a与b同向时，a·b=|a||b|；当a，b反向时，a·b=–|a||b|．特别地，a·a=a2=|a|2或|a④|a·b|≤|a||b|，当且仅当a与b共线，即a∥b时等号成立；⑤cos θ=·||||a ba b．（3）向量数量积的运算律①交换律：a·b=b·a；②数乘结合律：（λa）·b=λ（a·b）=a·（λb）；③分配律：（a+b）·c=a·c+b·c．（4）平面向量数量积的几何意义①一个向量在另一个向量方向上的投影设θ是a，b的夹角，则|b|cos θ叫作向量b在向量a的方向上的投影，|a|cos θ叫作向量a在向量b的方向上的投影．②a·b的几何意义数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos θ的乘积．注意：投影和两向量的数量积都是数量，不是向量．设两个非零向量a与b的夹角为θ，则①θ为锐角⇔a·b>0且向量a，b不共线；②θ为钝角⇔a·b<0且向量a，b不共线；③当a ·b >0时，cos θ>0，则θ是锐角或θ=0°（此时cos θ=1）； ④当a ·b <0时，cos θ<0，则θ是钝角或θ=180°（此时cos θ=–1）．【方法总结】1．只有非零向量才能表示与之共线的其他向量，要注意待定系数法和方程思想的运用．（1）基底e 1，e 2必须是同一平面内的两个不共线向量，零向量不能作为基底；（2）基底给定，同一向量的分解形式唯一；（3）如果对于一组基底e 1，e 2，有a =λ1e 1+λ2e 2=μ1e 1+μ2e 2，则可以得到1122,.λμλμ=⎧⎨=⎩2．平面向量的线性运算的求解策略：（1）进行向量运算时，要尽可能转化到平行四边形或三角形中，选用从同一顶点出发的向量或首尾相接的向量，运用向量加、减法运算及数乘运算来求解．（2）除了充分利用相等向量、相反向量和线段的比例关系外，有时还需要利用三角形中位线、相似三角形对应边成比例等平面几何的性质，把未知向量转化为与已知向量有直接关系的向量来求解． 3．向量的线性运算（1）向量的线性运算集中体现在三角形中，可构造三角形，利用向量加减法的三角形法则表示相关的向量，利用三角形中位线、相似三角形对应边成比例等平面几何的性质，得出含相关向量的关系式．（2）向量线性运算的常用结论： ①在△AB C 中，若D 是BC 的中点，则AD =12（AC +AB ）； ②O 为△ABC 的重心的充要条件是OA +OB +OC =0；③四边形ABCD 中，若E 为AD 的中点，F 为BC 的中点，则AB +DC =2EF ． 4．利用共线向量定理解题的策略（1）a ∥b ⇔a =λb （b ≠0）是判断两个向量共线的主要依据．注意待定系数法和方程思想的运用．（2）证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得出三点共线．即A ，B ，C 三点共线⇔,AB AC 共线．（3）若a 与b 不共线且λa =μb ，则λ=μ=0．（4）OA =λOB +μOC （λ，μ为实数），若A ，B ，C 三点共线，则λ+μ=1． 5．利用平面向量基本定理解题的策略（1）先选择一组基底，并运用平面向量基本定理将条件和结论表示成该基底的线性组合，再进行向量的运算．（2）在基底未给出的情况下，合理地选取基底会给解题带来方便，另外，要熟练运用线段中点的向量表达式．注意：（1）若a，b为非零向量，且a∥b，则a，b的夹角为0°或180°，求解时容易忽视其中一种情形而导致出错．（2）零向量和共线向量不能作基底，基底通常选取确定整个几何图形的从同一结点出发的两边所对应的向量．6．向量坐标运算问题的一般思路（1）向量问题坐标化：向量的坐标运算，使得向量的线性运算都可用坐标来进行，实现了向量运算完全代数化，将数与形紧密结合起来，通过建立平面直角坐标系，使几何问题转化为数量运算．（2）巧借方程思想求坐标：向量的坐标运算主要是利用加法、减法、数乘运算法则进行，若已知有向线段两端点的坐标，则应先求出向量的坐标，求解过程中要注意方程思想的运用．（3）妙用待定系数法求系数：利用坐标运算求向量的基底表示，一般先求出基底和被表示向量的坐标，再用待定系数法求出系数．7．求向量模长利用数量积求模是数量积的重要应用，要掌握此类问题的处理方法：（1）a2=a·a=|a|2或|a（2）|a±b；（3）若a=（x，y），则|a8．求向量模的最值（范围）的方法（1）代数法，把所求的模表示成某个变量的函数，再用求最值的方法求解；（2）几何法（数形结合法），弄清所求的模表示的几何意义，结合动点表示的图形求解；（3）利用绝对值三角不等式||a|–|b||≤|a±b|≤|a|+|b|求模的取值范围．9．求向量夹角问题的方法（1）定义法：当a，b是非坐标形式，求a与b的夹角θ时，需求出a·b及|a|，|b|或得出它们之间的关系，由cos θ=·||||a ba b求得；（2）坐标法：若已知a =（x 1，y 1）与b =（x 2，y 2），则cos<a ，b<a ，b >∈[0，π]．10．用向量法解决平面（解析）几何问题的两种方法：（1）几何法：选取适当的基底（基底中的向量尽量已知模或夹角），将题中涉及的向量用基底表示，利用向量的运算法则、运算律或性质计算；（2）坐标法：建立平面直角坐标系，实现向量的坐标化，将几何问题中的长度、垂直、平行等问题转化为代数运算．一般地，存在坐标系或易建坐标系的题目适合用坐标法．11．平面向量常与几何问题、三角函数、解三角形等问题综合起来考查，解题关键是把向量关系转化为向量的有关运算，进一步转化为实数运算，进而利用相关知识求解．1．【天津市新华中学2019届高三下学期第八次统练（一模）数学】已知点C 为线段AB 上一点，P 为直线AB 外一点，PC 是APB ∠的角平分线，I 为PC 上一点，满足BI BA =+||||AC AP AC AP λ⎛⎫+ ⎪⎝⎭(0)λ>，4PA PB -=，10PA PB -=，则BI BA BA⋅的值为A ．2B ．3C ．4D ．5【答案】B【解析】由BI BA =+||||AC AP AC AP λ⎛⎫+⎪⎝⎭(0)λ>可得||||AC AP AI AC AP λ⎛⎫=+ ⎪⎝⎭，∴I 在∠BAP 的角平分线上，由此得I 是△ABP 的内心，过I 作IH ⊥AB 于H ，I 为圆心，IH 为半径，作△PAB 的内切圆，如图，分别切PA ，PB 于E ，F ，||||4,||10PA PB PA PB -=-=，则10AB =，11||||(||||||)[||(||||)223 ]BH BF PB AB PA AB PA PB ==+-=--=，在直角三角形BIH 中，||cos ||BH IBH BI ∠=， ∴||cos 3||BI BABI IBH BH BA ⋅=∠==．故选B ．【名师点睛】本题主要考查向量的运算法则，内切圆的性质，向量数量积的定义与应用等知识，意在考查学生的转化能力和计算求解能力．2．【天津市红桥区2019届高三二模数学】已知点O 是ABC △内一点，满足2OA OB mOC +=，47AOB ABC S S =△△，则实数m 为 A ．2 B ．–2 C ．4 D ．–4【答案】D【解析】由2OA OB mOC +=得：12333mOA OB OC +=，设3m OC OD =，则1233OA OB OD +=，,,A B D ∴三点共线，如下图所示．OC 与ODuuu r 反向共线，3OD m m CD ∴=-，437AOB ABC O S m S D m CD =∴==-△△，4m ⇒=-，故选D ．【名师点睛】本题考查向量的线性运算性质及向量的几何意义，关键是通过向量线性运算关系得到三点共线的结果，从而得到向量模长之间的关系．3．【天津市河西区2018–2019学年高三第二学期总复习质量调查（二）数学】在平行四边形ABCD 中，||2,||4,60,,AD CD ABC E F ==∠=︒分别是,BC CD 的中点，DE 与AF 交于H ，则AH DE ⋅的值A ．12B ．16C ．125 D ．165【答案】C【解析】1cos1204242AB AD AB AD ⎛⎫⋅=⋅︒=⨯⨯-=- ⎪⎝⎭，取DE 中点M ，则1,2FM CE =∴445AH AD AH AF HE FM ==∴=，，因此()()4441155522AH DE AF DE AD DF DC CE AD AB AB AD ⎛⎫⎛⎫⋅=⋅=+⋅+=+⋅- ⎪ ⎪⎝⎭⎝⎭()2243114311124164542254225AD AB AB AD ⎛⎫⎛⎫=⋅+-=⨯-+⨯-⨯= ⎪ ⎪⎝⎭⎝⎭，故选C ．【名师点睛】本题考查向量数量积，考查基本分析求解能力，属中档题．4．【天津市河西区2019届高三一模数学】如图梯形ABCD ，AB CD ∥且5AB =，24AD DC ==，E 在线段BC 上，0AC BD ⋅=，则AE DE ⋅的最小值为A ．1513B ．9513 C ．15 D ．1513-【答案】B【解析】以A 为坐标原点，AB所在直线为x 轴，建立平面直角坐标系，设(,),(2,),(0,0)D m n C m n m n +>>，因此22222221616,(2,)(5,)03100,m m n m n m n m n n m n m =⎧⎧+=⎧⎨+=⎪⎪∴⎨⎨+⋅-==+--⎩=⎪⎪⎩⎩因此:5),5)BC y x y x=-=--，设(,5)),45,E x x x --≤≤∴(,5))(2,5)AE DE x x x x ⋅=--⋅----2(,5))(2,5)13110240x x x x x x =--⋅----=-+，当55[4,5]13x =∈时，AE DE ⋅最小值为95.13故选B ．【名师点睛】以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数等相结合的一类综合问题．通过向量的坐标运算，将问题转化为解不等式或求函数值域，是解决这类问题的一般方法． 5．【天津市和平区2018–2019学年度第二学期高三年级第三次质量调查数学】已知菱形ABCD 的边长为2，120BAD ∠=︒，点E ，F 分别在边BC ，DC 上，3BC BE =，DC DF λ=，若1AE AF ⋅=，则λ的值为 A ．3 B ．2 C ．23 D ．52【答案】B【解析】由题意可得：()()AE AF AB BE AD DF ⋅=+⋅+=113AB BC BC AB λ⎛⎫⎛⎫+⋅+ ⎪ ⎪⎝⎭⎝⎭22111133AB BC AB BC λλ⎛⎫=+++⋅ ⎪⎝⎭，且224,22cos1202AB BC AB BC ==⋅=⨯⨯︒=-，故()44112133λλ⎛⎫+++⨯-= ⎪⎝⎭，解得2λ=．故选B ．【名师点睛】本题主要考查平面向量数量积的定义与运算法则，平面向量基本定理及其应用等知识，意在考查学生的转化能力和计算求解能力．6．【天津市北辰区2019届高考模拟考试数学】已知边长为2的菱形ABCD 中，点F 为BD 上一动点，点E 满足223BE EC AE BD =⋅=-，，则AF EF ⋅的最小值为 A ．23- B ．43- C ．15275- D ．7336-【答案】D【解析】由题意知：23BE BC =，设DAB θ∠=， ()()22233AE BD AB BE AD AB AB AD AB BC AD BC AB ∴⋅=+⋅-=⋅-+⋅-⋅8824cos 4cos 333θθ=-+-=-，1πcos 23θθ∴=⇒=，以AC 与BD 交点为原点，AC 为x 轴，BD 为y 轴建立如下图所示的平面直角坐标系：()13A E ⎫∴-⎪⎪⎝⎭，，设()0F t ，，则()2133AF t EF t ⎛⎫==-+ ⎪ ⎪⎝⎭，，， 2112233AF EF t t t t ⎛⎫∴⋅=-++=+- ⎪⎝⎭，当16t =-时，()min11732361836AF EF⋅=--=-，故选D ．【名师点睛】本题考查向量数量积的运算问题，涉及到利用定义的运算和数量积的坐标运算，解题关键是能够通过线性运算进行变换，通过数量积运算的定义求得夹角；再通过建立平面直角坐标系的方式，将问题转化为坐标运算，通过函数关系求解得到最值．7．【天津市红桥区2019届高三二模数学】已知点M 是ABC △所在平面内一点，满足2134AM AB AC =+，则ABM △与BCM △的面积之比为 A ．38B ．83 C ．3 D ．13【答案】C【解析】设点D 是AB 上一点，且23AD AB =，点E 是AC 上一点，且14AE AC =，如下图所示：由2134AM AB AC =+，可知AM AD AE =+，以AD AE ，为邻边作平行四边形ADME ，连接BM CM ，，延长DM ，交BC 于F ，设BDM S S =△，∵23AD AB =，∴3BAM S S =△，由平行四边形ADME ，可知12BD BF DF AC DA FC ⇒==，设AE DM a MF x ===，，133FD BD a DF AC x CA BA ⇒==⇒=，∴13BFM BCM S S S S ==△△，，因此ABM △与BCM △的面积之比为3，故选C ．【名师点睛】本题考查了向量加法的几何意义，三角形的面积，平行线成比例定理．考查了运算能力． 8．【天津南开中学2019届高三月考数学】在ABC △中，23120AB AC BAC ==∠=︒，，，AH BC ⊥于点H ，M 为AH 的中点，若AM AB AC λμ=+，则实数λ=A ．619 B ．738 C ．514D ．37【答案】A【解析】在ABC △中，23120AB AC BAC ==∠=︒，，，由余弦定理可得22223223cos12019BC =+-⨯⨯︒=，即BC =又由ABC △的面积为11sin120232222S AB AC =︒=⨯⨯⨯=，∴11222BC AH AH ⋅==，解得AH =，在Rt ABH △中，由勾股定理得BH ===CH = ∴719BH BC =，则11171767()()[()]222192191938AM AH AB BH AB BC AB AC AB AB AC ==+=+=+-=+，又由AM AB AC λμ=+，∴619λ=，故选A ．【名师点睛】本题主要考查了三角形余弦定理和面积公式的应用，以及平面向量的基本定理的应用，其中解答中熟练应用余弦定理和面积公式，求得,BH CH 的值，再利用平面向量的运算和平面向量的基本定理求解是解答的关键，着重考查了分析问题和解答解答问题的能力，属于中档试题．9．【天津市和平区2018–2019学年度第二学期高三年级第二次质量调查数学】在ABC △中，26AB AC ==，2BA BC BA ⋅=，点P 是ABC △所在平面内的一点，则当222PA PB PC ++取得最小值时，AP BC ⋅= A ．35B ．9-C ．7D ．25-【答案】B 【解析】2||||cos ||BA BC BA BC B BA ⋅=⋅=，||cos ||BC B BA ∴⋅=，CA AB ∴⊥，2CAB π∠=，以A 为坐标原点建如图所示的平面直角坐标系，则(6,0),(0,3)B C ，设(,)P x y ，则222222222(6)(3)PA PB PC x y x y x y ++=++-+++-222231236453(2)(1)10x x y y x y ⎡⎤=-+-+=-+-+⎣⎦，∴当x =2，y =1时222PA PB PC ++取最小值，此时(2,1)(6,3)9AP BC ⋅=⋅-=-．故选B ．【名师点睛】本题主要考查平面向量的数量积运算法则，平面向量的坐标运算，二次函数最值的求解等知识，意在考查学生的转化能力和计算求解能力．10．【天津市十二重点中学2019届高三下学期毕业班联考（二）数学】已知ABC △为直角三角形，2AC BC ==，点D 为斜边AB 的中点，点P 是线段CD 上的动点，则PA PB ⋅的最小值为A ．2-B ．14-C ．12-D ．0【答案】A【解析】由图形可知：()()()2CA CP CB CP CA CB CA CB CP B P P P C A =-⋅⋅-+⋅+⋅-=，ABC △为直角三角形，斜边为AB CA CB ∴⊥，即0CA CB ⋅=，且2AC BC ==，则AB =又D 为AB 中点，2CA CB CD ∴+=且12CD AB ==，设CP CD λ=，[]0,1λ∈，则()222222224CD CD C P D B D PA C λλλλλλ=-⋅⋅+=-+⋅=-，当1λ=时，()min2PA PB⋅=-，故选A ．【名师点睛】本题考查向量数量积取值范围的求解，关键是能够通过线性运算将所求数量积向已知模长和夹角的向量进行转化，利用向量共线定理，构造出二次函数的形式，从而可以利用二次函数最值的求解方法得到结果．11．【天津市河西区2018–2019学年高三第二学期总复习质量调查（二）数学】在平行四边形ABCD 中，||2,||4,60AD CD ABC ︒==∠=，,E F 分别是,BC CD 的中点，DE 与AF 交于H ，则AH DE ⋅的值 A ．16 B ．12 C ．165 D ．125【答案】D【解析】以B 为原点，BC 所在直线为x 轴建立如图所示的直角坐标系，则()0,0B，(2,A ，()2,0C，(D ，故(1,0)E，(F ，∴:AF y =+:DE y x =，由y y y x ⎧=+⎪⎨==⎪⎩，可得14,55H ⎛ ⎝⎭，4,5AH ⎛= ⎝⎭，(3,DE =--，故122412555AH DE =-+=，故选D ．【名师点睛】向量的数量积的计算，有四种途径：（1）利用定义求解，此时需要知道向量的模和向量的夹角；（2）利用坐标来求，把数量积的计算归结坐标的运算，必要时需建立直角坐标系；（3）利用基底向量来计算，也就是用基底向量来表示未知的向量，从而未知向量数量积的计算可归结为基底向量的数量积的计算；（4）靠边靠角，也就是利用向量的线性运算，把未知向量的数量积转化到题设中的角或边对应的向量．12．【天津市南开区南开中学2019届高三第五次月考数学】如图，在等腰三角形ABC 中，已知2AB AC ==，120,,A E F ∠=︒分别是,AB AC 上的点，且AE AB λ=，AF AC μ=（其中λ，()0,1μ∈），且41λμ+=，若线段,EF BC 的中点分别为,M N ，则MN 的最小值为_________．【答案】7【解析】连接,AM AN ，等腰三角形ABC 中，2,120AB AC A ===，||||cos1202AB AC AB AC ︒∴⋅=⋅=-，AM 是AEF △的中线，11()()22AM AE AF AB AC λμ∴=+=+同理，可得1()2AN AB AC =+，由此可得11()()22MN AN AM AB AC AB AC λμ=-=+-+11(1)(1)22AB AC λμ=-+-，2211(1)(1)22MN AB AC λμ⎡⎤=-+-⎢⎥⎣⎦2222111(1)(1)(1)(1)424AB AB AC AC λλμμ=-+--⋅+- ()22(1)(1)1(1)λμλμ=----+-．41λμ+=，∴14λμ-=，代入上式得222(4)4(1)(1)MN μμμμ=--+-22161μμ=-+， ,(0,1)λμ∈，∴当17μ=时，2MN 的最小值为47，此时MN 的最小值为．【名师点睛】本题主要考查平面向量的线性运算以及平面向量数量积的运算法则，考查零点二次函数的性质，属于难题．向量数量积的运算主要掌握两点：一是数量积的基本公式||||cos θ⋅=a b a b ；二是向量的平方等于向量模的平方22||=a a ．13．【天津市南开区2019届高三第二学期模拟考试（二）数学】在等腰梯形ABCD 中，已知ABDC ，AC 与BD 交于点M ，24AB CD ==，若1AC BD ⋅=-，则cos BMC ∠=_________．【答案】117【解析】∵等腰梯形ABCD 中，AB DC ，AC 与BD 交于点M ，24AB CD ==，2,1AM AB BM DCM BAM MC DC DM ∴∴===△∽△，设CM x =，则3,3AC x BD x ==，1AC BD ⋅=-，||||cos 1AC BD AMB ∴⋅∠=-，即29cos 1x AMB ⋅∠=-，21cos 9AMB x ∴∠=-，在ABM △中，224416cos 222x x AMB x x +-∠=⨯⨯，222181698x x x -∴-=，解得2179x =，1cos 17AMB ∴∠=-，而1cos cos 17BMC AMB ∠=-∠=，故答案为：117．【名师点睛】本题主要考查平面向量数量积公式以及余弦定理的应用，属于中档题．对余弦定理一定要熟记两种形式：（1）2222cos a b c bc A =+-；（2）222cos 2b c a A bc+-=，同时还要熟练掌握运用两种形式的条件．另外，在解与三角形、三角函数有关的问题时，还需要记住30,45,60︒︒︒等特殊角的三角函数值，以便在解题中直接应用．14．【天津市河东区2019届高三二模数学】如图，已知OA OB OC ==，2AB =，135ABC ∠=，2OA OB ⋅=，则OB OC ⋅=_________．【答案】【解析】设OA OB OC ==()0m m =>，AOB θ∠=，在△ABO 中，由余弦定理可得：2222cos 4m m m θ+-=，整理可得：()21cos 2m θ-=，①由平面向量数量积的定义可得：OA OB ⋅=2cos m θ2=，② 由①②有：()221co c s os m m θθ-=，解得：1cos ,602θθ=∴=，即△ABO 为等边三角形，2m =，由题意可得：01801354522OBC θθ︒︒-∠=-=+，18029030BOC OBC θ︒︒∠=-∠=-=，故OB OC ⋅=2cos cos3023OB OC BOC m ⨯∠=⨯=．【名师点睛】本题主要考查平面向量数量积的定义及其应用，余弦定理的应用等知识，意在考查学生的转化能力和计算求解能力．15．【天津市部分区2019届高三联考一模数学】在ABC △中，D 为AB 的中点，点O 满足2CO OD =，OA OB ⊥，若10AB =，则AC BC ⋅=_________．【答案】200【解析】ABC △中，D 为AB 的中点，点O 满足2CO OD =，OA OB ⊥， 10AB =，15,2102OD AB OC OD ∴====，且0OA OB ⋅=， ()()AC BC OC OA OC OB ⋅=-⋅-()2OC OC OA OB OA OB =-⋅++⋅22OC OC OD =-⋅22100100200OC OC =+=+=，故答案为：200．【名师点睛】本题主要考查平面向量的运算以及平面向量数量积的运算，属于中档题．平面向量数量积的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式．利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．16．【天津市河北区2019届高三一模数学】在△AB C 中，4AB =，6BC =，2ABC π∠=，D 是AC 的中点，E 在BC 上，且AE BD ⊥，则AE •BC =_________．【答案】16【解析】建立平面直角坐标系，如图所示．则A （0，4），B （0，0），C （6，0），D （3，2），设E （x ，0），则AE =（x ，–4），BD =（3，2），由AE ⊥BD ，得AE •BD =3x –8=0，解得x 83=，∴AE =（83，–4），又BC =（6，0），∴AE •83BC =⨯6–4×0=16．故答案为：16．【名师点睛】本题考查了平面向量坐标表示与数量积运算问题，考查计算能力，是中档题． 17．【天津市十二重点中学2019届高三下学期毕业班联考（一）数学】在梯形ABCD 中，ABCD ，22AB CD ==，π3BAD ∠=，若2BA BD ⋅=，CE ED =，点F 为边BC 上的动点，则FE FA ⋅的取值范围为_________．【答案】1,14⎡⎤⎢⎥⎣⎦【解析】设D 在AB 上的射影为H ，则,DH AB DH CD ⊥⊥，cos 2B BA BD D AB A B D ∴⋅=⋅∠=，1cos 12BD ABD BH AB ∴∠===，又∵1CD =，∴BCDH 是矩形，ABD ∴△是等腰三角形，又π3BAD ∠=，ABD ∴△为正三角形，DH =BC =，以,BA BC 为,x y 轴，建立坐标系，∵CE ED =，则()((12,0,,,2A C D E ⎛ ⎝，设()(0,0F y y ≤≤，则()1,3,2,2FE y FA y ⎛⎫=-=-⎪⎝⎭，)()221121224FE FA y y y y ⎛⎫⎡⎤⋅=⨯+-=+=-+ ⎪⎢⎥ ⎪⎣⎦⎝⎭，当2y =时，FE FA ⋅有最小值14；当0y =FE FA ⋅有最大值1，∴FE FA ⋅的取值范围是1,14⎡⎤⎢⎥⎣⎦，故答案为：1,14⎡⎤⎢⎥⎣⎦．【名师点睛】平面向量数量积的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用．18．【天津市红桥区2019届高三一模数学】已知两点()1,0A ，(B ，O 为坐标原点，点C 在第二象限，且120AOC ∠=︒，设2OA OB OC λ-+=，λ∈R ，则实数λ=_________（用数字填写）．【答案】1【解析】设点C 的坐标是（x ，y ），则由2OC OA OB λ=-+得，（x ，y ）=–2（1，0）+λ（1=（–2+λ），∴x =–2+λ，y =，又∵∠AOC =120°，∴cos120°||OA OC OA OC⋅=，即12-=λ=1．故答案为：1．【名师点睛】本题考查向量的数量积和向量的坐标运算的应用，即通过条件列出关系式，利用向量相等的坐标等价条件进行求值．19．【天津市部分区2019届高三联考一模数学】已知菱形ABCD 的边长为2，60ABC ∠=︒，点,E F 分别在边,AD DC 上，()12BE BA BD =+，13DF DC =，则BE BF ⋅=_________．【答案】223【解析】连接,AC BD 交于O ，以O 为原点，以,OC OD 为x 轴，y 轴的正半轴建立直角坐标系，菱形边长为2，60ABC ∠=，()(()(1,0,0,,1,0,A B C D ∴-，()12BE BA BD =+E ∴为AD 的中点，1,22E ⎛⎫- ⎪ ⎪⎝⎭， 11,33BF DC F ⎛=∴ ⎝⎭，13315,,23BE BF ⎛⎫⎛∴=-= ⎪ ⎝⎭⎝⎭， 11522623BE BF ∴⋅=-+=．故答案为：223．【名师点睛】本题主要考查平面向量的线性运算以及平面向量数量积的坐标表示，属于中档题．平面向量数量积的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用．20．【天津市实验中学2019届高三第六次阶段考数学】已知A ，B 是圆O ：224x y +=上的两个动点，2AB =，5233OC OA OB =-．若M 是线段AB 的中点，则OC OM ⋅的值为_________．【答案】3【解析】解法一：设11(,)A x y ，22(,)B x y ，则11(,)OA x y =，22(,)OB x y =，1212,22x x y y OM ++⎛⎫=⎪⎝⎭，()2121,AB x x y y =--， ∴1212525252,,333333OC OA OB x x y y ⎛⎫=-=-- ⎪⎝⎭．由2AB =，得()()2221214x x y y -+-=，① 又A ，B 在圆O 上，∴22114x y +=，22224x y +=，② 联立①②得12122x x y y +=， ∴121212125252,,333322x x y y OC OM x x y y ++⎛⎫⎛⎫⋅=--⋅⎪ ⎪⎝⎭⎝⎭化简并整理，得()()()222211221212511632x y x y x x y y +-+++511442632=⨯-⨯+⨯3=．解法二（优解）：由条件易知OAB △为正三角形．又由M 为AB 的中点，则1()2OM OA OB =+， ∴152()233OC OM OA OB OA OB ⎛⎫⋅=+⋅- ⎪⎝⎭22152||||233OA OA OB OB ⎛⎫=+⋅- ⎪⎝⎭3=．【名师点睛】本题主要考查平面向量的应用及平面向量数量积运算，由已知得出1OM (OA OB)2=+代入计算是解题的关键．21．【天津市北辰区2019届高考模拟考试数学】平行四边形ABCD 中，4,2,4AB AD AB AD ==⋅=，点P 在边CD 上，则AP PC ⋅的取值范围是_________．【答案】250,4⎡⎤⎢⎥⎣⎦【解析】∵点P 在边CD 上，∴设()01DP λDC λAB λ==≤≤，则 λAP AD DP A A D B =+=+，()1PC λAB -=， ∴()()1PC A AP D λλAB AB ⋅=+⋅-()()223 141161612445224λλλλλλ⎛⎫=-+-⨯=-++=-- ⎪⎝+⎭，又01λ≤≤，∴2504AP PC ≤⋅≤，故答案为：250,4⎡⎤⎢⎥⎣⎦．【名师点睛】本题主要考查了平面向量数量积的运算以及平面向量基本定理，转化为函数求值域问题是解题的关键，属于中档题．22．【天津市南开中学2019届高三模拟数学】已知四边形ABCD 中，3BC =，4AC =，M 为AB 中点且MD AB ⊥，则AB CD ⋅=_________．【答案】72- 【解析】()AB CD AB CM MD AB CM ⋅=⋅+=⋅，又AB CB CA =-，1()2CM CA CB =+， 22117=()==222AB CM CB CA CA CB CB CA ∴⋅-⋅+--（）（），故答案为：72-．【名师点睛】本题考查了平面向量基本定理的应用，考查了数量积的运算，属于中档题．23．【天津市南开区2018～2019学年度高三第二学期基础训练数学】在ABC △中，901A AB ∠=︒=，，AC =2，设点P Q ，满足()1AP AB AQ AC λλλ==-∈R ，，，若2BQ CP ⋅=-，则λ=_________．【答案】23【解析】11BQ AQ AB AQ AC BQ AC AB λλ=-=-∴=--，（），（），CP AP AC AP AB CP AB AC λλ=-=∴=-，，，90A ︒∠=，得AB AC ⊥，即0AB AC ⋅=，∵2BQ CP ⋅=-，∴12AC AB AB AC λλ⎡⎤--⋅-=-⎣⎦（）（），化简可得[]221110AC AB AC AB λλλλ--+-+⋅-=（）（），120AB AC AB AC ==⋅=，，，∴214123λλλ--⨯-⨯=-∴=（），．故答案为：23．【名师点睛】本题主要考查平面向量数量积的运算法则，考查了向量垂直的性质，属于中档题．向量数量积的运算主要掌握两点：一是数量积的基本公式||||cos θ⋅=a b a b ；二是向量的平方等于向量模的平方22||=a a ．24．【天津市十二重点中学2019届高三下学期毕业班联考（二）数学】在梯形ABCD 中，AB ∥CD ，2,1AB BC CD ===，M 是线段BC 上的动点，若3BD AM ⋅=-，则BA BC ⋅的取值范围是_________．【答案】[1，10]【解析】设,[0,1]BM tBC t =∈，则()BD AM BC CD AB BM⋅=+⋅+()()1122BC BA BA tBC BC BA BA tBC =+⋅-+=+⋅-+()14t 232t BC BA ⎛⎫=--⋅+-=- ⎪⎝⎭．∴8218822t BC BA t t +⋅==--∈--[1，10]．【名师点睛】本题考查向量数量积以及向量表示，考查基本分析求解能力，属中档题． 25．【天津市和平区耀华中学2019届高三第一次校模拟考试数学】在ABC △中，点M 满足14MB AB =，且对于边AB 上任意一点N ，恒有NB NC MB MC ⋅≥⋅．则()CA CB AB +⋅=_________．【答案】0【解析】以A 为原点，AB 为x 轴，建立直角坐标系，设()()()400B C a b N x ，，，，，，则()30M ，， ∴1033MB MC a b a ⋅=⋅-=-（，）（，），404NB NC x a x b x a x ⋅=-⋅-=--（，）（，）（）（）2224444424a a x a x a x a ++⎛⎫=-++=-+- ⎪⎝⎭（）（）2444a a +≥-（） ∵NB NC MB MC ⋅≥⋅，∴24434a a a +-=-（），解得2a AC BC =∴=，，∴()()()220+⋅=+⋅-=-=，故答案为：0．CA CB AB CA CB CB CA CB CA【名师点睛】平面向量数量积的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题以及最值问题时，往往先建立适当的平面直角坐标系，转化为解析几何问题或函数问题，可起到化繁为简的妙用．。

十年真题(2010-2019)高考数学(理)分类汇编专题06 平面向量(新课标Ⅰ卷)(原卷版)

专题06平面向量历年考题细目表题型年份考点试题位置单选题2019 平面向量的数量积2019年新课标1理科07单选题2018 平面向量基本定理2018年新课标1理科06单选题2015 平面向量基本定理2015年新课标1理科07单选题2011 平面向量的定义2011年新课标1理科10填空题2017 向量的模2017年新课标1理科13填空题2016 平面向量的数量积2016年新课标1理科13填空题2014 平面向量的数量积2014年新课标1理科15填空题2013 平面向量的数量积2013年新课标1理科13填空题2012 向量的模2012年新课标1理科13历年高考真题汇编1．【2019年新课标1理科07】已知非零向量，满足||＝2||，且（）⊥，则与的夹角为（）A．B．C．D．2．【2018年新课标1理科06】在△ABC中，AD为BC边上的中线，E为AD的中点，则（）A．B．C．D．3．【2015年新课标1理科07】设D为△ABC所在平面内一点，，则（）A．B．C．D．4．【2011年新课标1理科10】已知与均为单位向量，其夹角为θ，有下列四个命题P1：||＞1⇔θ∈[0，）；P2：||＞1⇔θ∈（，π]；P3：||＞1⇔θ∈[0，）；P4：||＞1⇔θ∈（，π]；其中的真命题是（）A．P1，P4B．P1，P3C．P2，P3D．P2，P45．【2017年新课标1理科13】已知向量，的夹角为60°，||＝2，||＝1，则|2|＝．6．【2016年新课标1理科13】设向量（m，1），（1，2），且||2＝||2+||2，则m＝﹣2．7．【2014年新课标1理科15】已知A，B，C为圆O上的三点，若（），则与的夹角为．8．【2013年新课标1理科13】已知两个单位向量，的夹角为60°，t（1﹣t）．若•0，则t ＝．9．【2012年新课标1理科13】已知向量夹角为45°，且，则．考题分析与复习建议本专题考查的知识点为：平面向量的线性运算，平面向量基本定理及坐标表示，平面向量的数量积，平面向量的综合应用等.历年考题主要以选择填空题型出现，重点考查的知识点为：平面向量的线性运算，平面向量基本定理及坐标表示，平面向量的数量积等，预测明年本考点题目会比较稳定，备考方向以知识点平面向量的线性运算，平面向量的数量积，平面向量的综合应用等为重点较佳.最新高考模拟试题1．在ABC ∆中，2AB AC AD +=u u u r u u u r u u u r ，0AE DE +=u u u r u u u r r ，若EB xAB y AC =+u u u r u u u r u u u r，则（） A ．3y x =B ．3x y =C ．3y x =-D ．3x y =-2．已知非零向量a r ,b r 的夹角为60o,且满足22a b -=r r ,则a b ⋅r r 的最大值为( ) A ．12B ．1C ．2D ．33．设a r ，b r 均为单位向量，则“a r 与b r 夹角为2π3”是“||a b +=r r ”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4．在矩形ABCD 中，4AB =uu u r ,2AD =u u u r ．若点M ，N 分别是CD ，BC 的中点，则AM MN ⋅=u u u u r u u u u r（）A ．4B ．3C ．2D ．15．已知P 为等边三角形ABC 所在平面内的一个动点，满足()BP BC R λλ=∈u u u r u u u r，若2AB =u u u r ，则()AP AB AC u u u v u u u v u u u v⋅+=（）A ．B ．3C ．6D ．与λ有关的数值6．已知向量(2,1),(,1)a b m ==-r r ，且()a a b ⊥-rr r ，则m 的值为（）A ．1B ．3C ．1或3D ．47．已知向量a r 、b r 为单位向量，且a b +r r 在a r 的方向上的投影为12+，则向量a r 与b r 的夹角为（）A ．6π B ．4π C ．3πD ．2π8．在矩形ABCD 中，3,4,AB AD AC ==与BD 相交于点O ，过点A 作AE BD ⊥，垂足为E ，则AE EC ⋅=u u u v u u u v（）A ．725B ．14425C ．125D ．1225 9．已知直线y=+m 和圆2+y 2=1交于A 、B 两点，O 为坐标原点，若3AO AB 2⋅=u u u r u u u r ，则实数m=（）A ．1±B ．3±C ．2±D ．12±10．已知菱形ABCD 的边长为2，120BAD ∠=︒，点E ，F 分别在边BC ，DC 上，3BC BE =，DC DF λ=，若1AE AF ⋅=u u u r u u u r，则λ的值为（）A ．3B ．2C ．23D ．5211．已知正ABC ∆的边长为4，点D 为边BC 的中点，点E 满足AE ED u u u r u u u r=，那么EB EC ⋅u u u r u u u r 的值为（）A ．83-B ．1-C ．1D ．312．在ABC ∆中，3AC =，向量AB u u u v 在AC u u u v上的投影的数量为2,3ABC S ∆-=，则BC =( ) A ．5B ．27C ．29D ．4213．在△ABC 中，,2,BD DC AP PD BP AB AC u u u r u u u r u u u r u u u r u u u r u u u r u u u rλμ===+，则λμ+= （）A ．1-3B ．13C ．1-2D ．1214．在ABC ∆中，543AB BC BC CA CA AB →→→→→→==g g g ，则sin :sin :sin A B C =（） A ．9:7:8B ．9:7:8C ．6:8:7D ．6:8:715．在平行四边形ABCD 中，113,2,,,32AB AD AP AB AQ AD ====u u u r u u u r u u u r u u u v 若12,CP CQ ⋅=u u u v u u u v则ADC ∠=( )A ．56πB ．34π C ．23π D ．2π16．已知△ABC 中，22BC BA BC =⋅=-u u u r u u u r u u u r ，．点P 为BC 边上的动点，则()PC PA PB PC ⋅++u u u r u u u r u u u r u u u r的最小值为（） A ．2B ．34-C ．2-D ．2512-17．如图Rt ABC ∆中，2ABC π∠=，2AC AB =，BAC ∠平分线交△ABC 的外接圆于点D ，设AB a =u u u r r ，AC b =u u u r r ，则向量AD =u u u r（）A ．a b +r rB ．12a b +r rC ．12a b +r rD ．23a b +r r18．在ABC ∆中，90A ∠=︒，1AB =，2AC =，设点D 、E 满足AD AB λ=u u u r u u u r ，(1)AE λ=-u u ur ()AC R λ∈u u u r ，若5BE CD ⋅=u u u r u u u r，则λ=（） A ．13-B ．2C ．95D ．319．已知点C 为扇形AOB 的弧AB 上任意一点，且120AOB ∠=︒，若(,)OC OA OB R λμλμ=+∈u u u r u u u r u u u r，则λμ+的取值范围为（）A ．[2,2]-B ．(1,2]C ．[1,2]D ．[1,2]20．在同一平面内，已知A 为动点，B ，C 为定点，且∠BAC=3π，2ACB π∠≠，BC=1，P 为BC 中点．过点P 作PQ⊥BC 交AC 所在直线于Q ，则AQ uuu r 在BC uuu r方向上投影的最大值是（）A ．13B ．12C ．33D ．2321．已知圆22450x y x ++-=的弦AB 的中点为(1,1)-，直线AB 交x 轴于点P ，则PA PB ⋅u u u r u u u r的值为______．22．已知向量(2,1),(,1)a b λ=-=rr，若||||a b a b +=-rrrr，则λ=______．23．向量()1,2a v=-，()1,0b =-r ，若()()a b a b λ-⊥+r r r r ，则λ=_________.24．设向量12,e e r r的模分别为1,2，它们的夹角为3π，则向量21e e -r r 与2e r 的夹角为_____． 25．已知平面向量a r ，m v ，n v ，满足4a =r ，221010m a m n a n ⎧-⋅+=⎨-⋅+=⎩v v v v v v ，则当m n -=u r r _____，则m v 与n v的夹角最大．26．如图，已知P 是半径为2，圆心角为3π的一段圆弧AB 上一点，2A B B C =u u u v u u u v ，则PC PA ⋅u u u r u u u r 的最小值为_______．27．如图，在边长为2的正三角形ABC 中，D 、E 分别为边BC 、CA 上的动点，且满足CE mBD =（m为定常数，且(0,1]m ∈），若AD DE ⋅u u u r u u u r的最大值为34-，则m =________.28．在ABC ∆中，已知AB 边上的中线1CM =，且1tan A ，1tan C ，1tan B成等差数列，则AB 的长为________.29．如图，在平面四边形ABCD 中，90CBA CAD ∠=∠=︒，30ACD ∠=︒，AB BC =，点E 为线段BC的中点．若AC AD AE λμ=+u u u r u u u r u u u r(,R λμ∈)，则λμ的值为_______．30．在平面直角坐标系xOy 中，已知()11,A x y ，()22,B x y 为圆221x y +=上两点，且121212x x y y +=-．若C 为圆上的任意一点，则CA CB u u u r u u u rg 的最大值为______．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题五平面向量第十四讲向量的应用2019年1.（2019江苏12）如图，在ABC △中，D 是BC 的中点，E 在边AB 上，BE =2EA ，AD 与CE 交于点O .若6AB AC AO EC ⋅=⋅，则ABAC的值是.2.（2019浙江17）已知正方形ABCD 的边长为1，当每个(1,2,3,4,5,6i i λ=取遍1±时，123456||AB BC CD DA AC BD λλλλλλ+++++的最小值是________，最大值是_______.3.（2019天津理14）在四边形ABCD中，,5,30AD BC AB AD A ==∠=︒∥，点E 在线段CB 的延长线上，且AE BE =，则BD AE ⋅= .2010-2018年一、选择题1．(2018天津)如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==．若点E 为边CD 上的动点，则⋅uu u r uurAE BE 的最小值为A ．2116B ．32C ．2516D ．3E DCBA2．(2018浙江)已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430-⋅+=b e b ，则||-a b 的最小值是A1B1C ．2D．23．（2017新课标Ⅲ）在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为A ．3 B． CD ．24．（2017新课标Ⅱ）已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是A ．2-B ．32-C ．43- D ．1- 5．（2017浙江）如图，已知平面四边形ABCD ，AB BC ⊥，2AB BC AD ===，3CD =，AC 与BD交于点O ，记1I OA OB =⋅，2·I OB OC ＝，3·I OC OD ＝，则 OABCDA ．1I <2I <3IB ．1I <3I <2IC ．3I < 1I <2ID ．2I <1I <3I6．（2016四川）在平面内，定点A ，B ，C ，D 满足DA =DB =DC ，DA DB ⋅=DB DC ⋅=DC DA ⋅=-2，动点P ，M 满足AP =1，PM =MC ，则2BM 的最大值是A ．434 B ．494C．374+ D．374+7．(2015山东)已知菱形ABCD 的边长为a ，60ABC ∠=，则BD CD ⋅＝A ．232a -B ．234a - C ．234a D ．232a8．（2015新课标）设D 为ABC ∆所在平面内一点，3BC CD =，则A ．1433AD AB AC =-+ B ．1433AD AB AC =-C ．4133AD AB AC =+ D ．4133AD AB AC =- 9．（2015福建）已知AB AC ⊥， 1AB t=， AC t =，若点P 是ABC ∆所在平面内一点，且4AB AC AP ABAC=+，则PB PC ⋅ 的最大值等于A ．13B ．15C ．19D ．2110．（2015四川）设四边形ABCD 为平行四边形，6AB =，4AD =．若点,M N 满足3BM MC =，2DN NC =，则AM NM ⋅=A ．20B ．15C ．9D ．611．（2015湖南）已知点,,A B C 在圆221x y +=上运动，且AB BC ⊥．若点P 的坐标为(2,0)，则PA PB PC ++的最大值为A ．6B ．7C ．8D ．912．（2014安徽）在平面直角坐标系xOy 中，已知向量,a b ，||||1==a b ，0⋅=a b ，点Q 满足2()OQ =+a b ．曲线{|cos sin ,02}C P OP θθθπ==+a b ≤≤，区域 {|0||,}P r PQ R r R Ω=<<≤≤．若C Ω为两段分离的曲线，则A ．13r R <<<B ．13r R <<≤C ．13r R ≤<<D ．13r R <<<13．（2014天津）已知菱形ABCD 的边长为2，120BAD ?，点,E F 分别在边,BC DC 上，BE λBC =，DF μDC =.若1AE AF?，23CE CF?-，则λμ+= A ．12 B ．23 C ．56 D ．71214．（2012天津）在△ABC 中，∠A =90°，AB =1，设点P ，Q 满足AP AB λ=，(1)AQ AC λ=-，R λ∈．若2B Q C P ⋅=-，则λ=A ．13 B ．23 C ．43D ．2 15．(2012安徽)在平面直角坐标系中，(0,0),(6,8)O P ，将向量OP 绕点O 按逆时针旋转34π后得向量OQ ，则点Q 的坐标是A ．(-B ．(-C ．(2)--D ．(2)-16．（2012广东）对任意两个非零的平面向量α和β，定义αβαβββ⋅=⋅．若平面向量,a b 满足||||0>…a b ，a 与b 的夹角(0,)4πθ∈，且a b 和b a 都在集合{|}2∈nn Z 中，则a b =A ．12B ．1C ．32D ．5217．（2011山东）设1A ，2A ，3A ，4A 是平面直角坐标系中两两不同的四点，若1312A A A A λ=(λ∈R )，1412A A A A μ=(μ∈R )，且112λμ+=，则称3A ，4A 调和分割1A ，2A ，已知点(,0)C c ，(,0)D d ，(,c d ∈R )调和分割点(0,0)A ，(1,0)B ，则下面说法正确的是 A ．C 可能是线段AB 的中点 B ．D 可能是线段AB 的中点 C ．C ，D 可能同时在线段AB 上D ．C ，D 不可能同时在线段AB 的延长线上二、填空题18．(2018上海)在平面直角坐标系中，已知点(10)A -，，(2,0)B ，E ，F 是y 轴上的两个动点，且||2EF =，则AE BF ⋅的最小值为______．19．（2017江苏）在平面直角坐标系xOy 中，(12,0)A -，(0,6)B ，点P 在圆O ：2250x y +=上，若20PA PB ⋅≤，则点P 的横坐标的取值范围是．20．（2017天津）在ABC △中，60A =︒∠，3AB =，2AC =．若2BD DC =，AE AC AB λ=-()λ∈R ，且4AD AE ⋅=-，则λ的值为___________．21．（2016年浙江）已知向量,a b ，||1=a ，||2=b ，若对任意单位向量e ，均有||||+…ae be ，则⋅a b 的最大值是．22．(2015北京)在ABC △中，点M ，N 满足2AM MC =，BN NC =．若MN x AB y AC =+，则x =；y =．23．（2015天津）在等腰梯形ABCD 中,已知AB DC ∥,2AB =,1BC =,60ABC ∠=．动点E 和F 分别在线段BC 和DC 上，且BE BC λ=，19DF DC λ=，则AE AF ⋅的最小值为．24．（2015江苏）设向量(cos ,sin cos )666k k k k πππ=+a (0,1,2,,12)k =⋅⋅⋅，则∑=+⋅121)(k k k a a 的值为． 25．（2014天津）已知菱形ABCD 的边长为2，120BAD ∠=︒，点E ，F 分别在边BC 、DC 上，3BC BE =，DC DF λ=．若1AE AF ⋅=，则λ的值为________．26．（2014湖南）在平面直角坐标系中，O 为原点，(1,0),(3,0),A B C -动点D 满足||1CD =，则||OA OB OD ++的最大值是．27．（2012江苏）如图，在矩形ABCD 中，2AB BC ==，点E 为BC 的中点，点F 在边CD 上，若2AB AF =，则AE BF 的值是．28．（2012山东）如图，在平面直角坐标系xoy 中，一单位圆的圆心的初始位置在()1,0，此时圆上一点P的位置在()0,0，圆在x 轴上沿正向滚动。

当圆滚动到圆心位于()1,2时，OP 的坐标为．29．（2010湖南）在边长为1的正三角形ABC 中, 设2,3,BC BD CA CE ==则AD BE ⋅=______．三、解答题30．（2015广东）在平面直角坐标系xoy 中，已知向量=m ，(sin ,cos )x x =n ， (0,)2x π∈．（1）若⊥m n ，求tan x 的值；（2）若m 与n 的夹角为3π，求x 的值． 31．（2014山东）已知向量()(),cos2,sin 2,m x x n ==a b ，函数()f x =⋅a b ，且()y f x = 的图像过点12π⎛ ⎝和点2,23π⎛⎫- ⎪⎝⎭．（Ⅰ）求,m n 的值；（Ⅱ）将()y f x =的图像向左平移()0ϕϕπ<<个单位后得到函数()y g x =的图像，若()y g x =图像上各最高点到点()0,3的距离的最小值为1，求()y g x =的单调递增区间．32．（2014辽宁）在ABC ∆中，内角,,A B C 的对边,,a b c ，且a c >，已知2BA BC ⋅=，1cos 3B =，3b =，求：（Ⅰ）a 和c 的值；（Ⅱ）cos()B C -的值．33．（2013江苏）已知(cos ,sin )αα=a ，(cos ,sin )ββ=b ，0βαπ<<<．(1) 若||-=a b ⊥a b ；(2) 设(0,1)=c ，若+=a b c ，求α，β的值．34．（2013湖南）过抛物线2:2(0)E x py p =>的焦点F 作斜率分别为12,k k 的两条不同的直线12,l l ，且122k k +=，1l E 与相交于点A ，B ，2l E 与相交于点C ，D ．以AB ，CD 为直径的圆M ，圆N （M ，N为圆心）的公共弦所在的直线记为l ．（I ）若120,0k k >>，证明：22FM FN p ⋅<；（II ）若点M 到直线l 的距离的最小值为，求抛物线E 的方程．35．（2013辽宁）设向量)(),sin ,cos ,sinx ,0,.2x x x x π⎡⎤==∈⎢⎥⎣⎦a b（I ）若||||=a b ，求x 的值；（II ）设函数()f x =⋅a b ，求()f x 的最大值．36．（2012江西）已知三点(0,0)O ，(2,1)A -，(2,1)B ，曲线C 上任意一点(,)M x y 满足||()2MA MB OM OA OB +=⋅++．（1）求曲线C 的方程；（2）动点000(,)(22)Q x y x -<<在曲线C 上，曲线C 在点Q 处的切线为l 。

理科数学2010-2019高考真题分类训练专题五 平面向量第十四讲 向量的应用

高考数学真题分类专题五 平面向量第十四讲 向量的应用答案

2010—2019“十年高考”数学真题分类汇总 平面向量专题解析版 (可下载)

理科数学2010-2019高考真题分类训练专题五平面向量第十四讲向量的应用答案

十年高考理科数学真题 专题五 平面向量 十四 向量的应用及答案【精选】

2019年高考真题理科数学解析汇编：平面向量word资料6页

(2010-2019)十年高考数学真题分类汇编：平面向量(含解析)

2010—2019“十年高考”数学真题分类汇总 平面向量专题解析版 (可下载)

理科数学2010-2019高考真题分类训练14专题五 平面向量第十四讲 向量的应用—附解析答案

专题14 平面向量-2019年高考理数母题题源系列(天津专版)(解析版)

十年真题(2010-2019)高考数学(理)分类汇编专题06 平面向量(新课标Ⅰ卷)(原卷版)

理科数学2010-2019高考真题分类训练专题五平面向量第十四讲向量的应用

高考数学真题分类专题五平面向量第十四讲向量的应用答案

2010—2019“十年高考”数学真题分类汇总平面向量专题解析版 (可下载)

十年高考理科数学真题专题五平面向量十四向量的应用及答案【精选】

2010—2019“十年高考”数学真题分类汇总平面向量专题解析版 (可下载)

理科数学2010-2019高考真题分类训练14专题五平面向量第十四讲向量的应用—附解析答案