求J积分
J积分理论

汇报人: 孙明 指导老师: 王吉会
目录
断裂力学背景 J积分理论应用 全文塑性断裂
Dugdale理论 J理论 COD理论
有限元法
边界元法
无网格法
小波数值法
对材料和结构的安全性评估
一、背景
理论发展
1960年 Dugdale运用 Muskhelishvil i的方法,研究 了裂纹尖端的 塑性区 (D-M模型)
一、背景
计算理论3:
无网格法起源于20世纪80年代,现在已经得到工程界的广泛关 注。该方法将整个求解域离散为独立的节点,而无须将节点连成单 元,它不需要划分网格,从而克服了有限元法在计算过程中更新网 格很麻烦的缺陷。另外,无网格法只需要计算域的几何边界点及计 算点,不需要单元信息,因此具有边界元的优点,而且无网格法的 基本方程和数学基础与有限元法相同,所以它又具有有限元法的优 点,还具有比边界元法更广泛的应用范围。
试验条件:
母材:日本WEL-TEN590焊接结构用高强钢,原始板厚 16mm。 填充金属:YM-60C YM-70C YM-80A ,直径1.2mm 母材及三种焊丝熔敷金属的化学成分与焊后实际测定力学性 能如下:
二、J积分理论应用
高组配焊接接头表面裂纹积分试验研究
试验过程:
焊接试板经机械加工,铣削成为l2mmX70mmX450mm的 板状试样,焊缝位于试板的中心,并垂直于试验中的拉伸加载 方向。首先采用 电火花机床 ,在预定位置垂直于试板表面, 制造长2C0=l0mm,深a0=3mm的裂纹源,然后利用三点弯曲 加载方式预制疲劳裂纹。裂纹开 在焊缝区的中心。选取积分 回路为G-F-E-D-C-B-A.考虑到试板结构与 材质的对称性,因 此只沿1/2积分回路在试样表面布置应变片及引伸 计,加工配 置完成后的试样如图 试验在万能材料试验机上进行。试样装夹后,施加初始的拉 伸载荷,待仪器设备稳定后,逐步加大载荷,在预订的载荷点 上测量相应的应变及位移值。直至试样出现一定量的屈服后, 停机卸载。实验完成后,试样经热氧化发蓝处理,二次疲劳后 压断,测量裂纹尺寸。
J积分

为什么J 积分能作为弹塑性断裂力学的判据工程上应用的中、低强度高韧钢含裂纹构件,甚至高强钢中存在微小裂纹的问题,都是大范围屈服问题。
对大范围屈服问题,人们自然会想到用类似 K 理论的方法,找到描述裂尖弹塑性应力应变场强度的参量,从而建立工程应用判据。
然而线弹性断裂力学应用的前提—“小范围屈服”条件过于苛刻。
包含以下原因1)结构中存在高应力集中的塑性区2)大量韧性较好的材料的应用,如中低强度钢3)高韧性材料的KIC 测量很难进行4) 塑性状态下材料力学行为不能用弹性力学描述。
针对这些情况,必须采用弹塑性力学观点研究。
用弹塑性力学的理论研究裂纹扩展规律及断裂问题的学科叫弹塑性断裂力学。
弹塑性断裂力学的要解决的中心问题是:如何在大范围屈服的条件下,确定出能定量描述裂纹尖端区域应力应变场强度的参量,以便能用理论建立这些参量与裂纹几何特性、外载荷之间的关系。
又易于用试验测定它们,最后建立便于工程应用的判据。
目前应用最多的是J 积分和COD 理论。
由于塑性应力应变关系与加载路线或加载的历史有关。
因此,离开加载路线来建立应力与全量塑性应变之间的普遍关系是不可能的。
一般只能建立应力与应变增量之间的关系仅在简单加载下,才可以建立全量关系。
COD 理论裂纹尖端的张开位移(COD)是裂纹尖端塑性应变的一种度量。
1963年Wells 提出了COD 断裂准则,即当裂纹尖端的张开位移达到其临界值时失稳扩展:是材料常数,相当于裂纹扩展阻力,由试验测定。
是外载、构件形状和尺寸的函数,由计算得到。
然而COD 的几种定义有所不同:① 考虑线弹性断裂力学塑性区修正后,裂纹顶端由O → O ’,此时原始的裂纹顶端位置的张开位移成为COD 。
② 以弹塑性区交界点处的位移作为COD③ 将受载后裂纹自由表面延长,与尖端垂线交线处位移作为CODCOD 理论虽然测量方法简单,而且也能有效地解决工程,但COD 理论缺乏严密的理论基础和分析手段,确切的定义和标定至今仍有不同意见,并且在弹塑性条件下,COD 还不是一个直接与裂纹尖端应力应变场相关联的参量,所以不能从COD 来描述弹塑性情况下裂纹尖端应力场的奇异性。
三维裂纹J积分求解
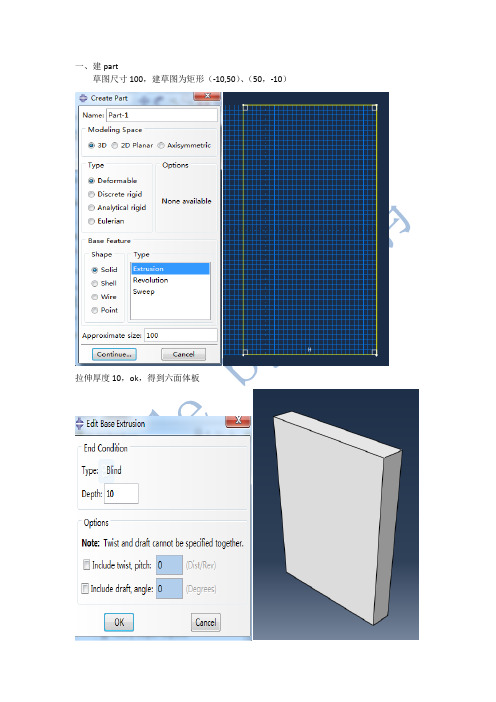
一、建part草图尺寸100,建草图为矩形(-10,50)、(50,-10)拉伸厚度10,ok,得到六面体板二、材料属性,具体参数自己设置吧,一步步都应该清楚。
3、装配(creat instance)装配要用第二个(独立的),装配之后要切出一条缝,为后面定义seam,用下图右边的那个这个是选择分割草图的一条边这里应该选择红色面的右边, 这个是分割需要的草图,黄色的线就是分割线,然后,分割tool-partition选择cell-extrude/sweep edges选择红色的圈这个选择选中的这个然后选择z轴,看好方向如果方向正确就选ok,如果不正确就选flip然后再选按住shfit选择涂黄的两条线(就是裂纹线)(1)先定义seam,special-creat-assign选择红色的区域,就定义了seam(2)定义crake,special-creat-crake,用围线积分继续,这里选择的时候容易选择的只是一个面所以先隐藏那个小圆面,选择的那个就是隐藏的命令,隐藏小圆面后就可以选择crake front了。
Crake Front 亮红色的就是选择的裂纹线学裂纹尖端有奇异性,所以这儿要按下图设置,不懂的看理论吧。
此时crake定义好了5、荷载步按静力学分析,继续默认设置就行,谈后在历史输出步中要编辑Domain这个要选择之前定义的crake-1下面的围线数我一般用的是8,这个我感觉8左右就行,但是不能就2,3个,也不必要太多(路径无关性)。
6、load这个我简单加载两端均布拉力,做好加一个约束边界条件,这里我加了一个右边的UZ7、划分网格,感觉断裂最麻烦的就是划分网格了,划分网格之前必须对实体分割能比较规则的,而且在裂纹尖端需要时放射状,其实尖端是四边形也能算,但是所有的例子都是放射状的。
因为划分网格比较麻烦我就补一步步的说了那个之前做的例子来示意一下最好是按照下图进行分割,矩形里面最好再分一个圆这样可以有效保证网格效果比较好。
第二章 弹塑性断裂力学

J积分的第一项:
Wdy
/2
Wr
/ 2
cos d
(1
v)(1 4E
2v)
K2
J积分的第二项(平面应变状态下):
Tx
ux x
Ty
uy y
ds
1
v3
4E
2v
K2
所以,有J积分:
J
(Wdy
Ti
ui x
ds)
(1
v)(1 4E
2v)
K2
1
v3 2v
4E
K
2
1 v2 E
K2
G
类似的,平面应力状态下有:
ds)
(Wdy '
T
i
ui x
ds)
BC
(Wdy
T
i
ui x
ds)
(Wdy DA
T
i
ui x
ds)
(2.7)
由于在BC和DA段上dy 0及 Ti 0,所以(2.7)中后两个积分为零,即:
J
(Wdy
Ti
ui x
ds)
(Wdy '
T
i
ui x
ds)
所以J积分与路径无关。
J积分理论
J积分使用范围的前提条件:
ui x
ds]
应用Green公式,上式可写成:
I
W
x
dxdy
xi
ij
ui x
dxdy
(2.4)
J积分理论
又
W
x
W ij ij x
ij
ij
x
ij
x
1 2
ui,
j u j,i
定积分计算方法总结

摘要定积分是数学分析中的一个基本问题,而计算定积分是最基本最重要的问题.它在许多实际问题有着广泛的应用.下面针对定积分的计算方法做一个比较详细的总结,常见的包括分项积分、分段积分法、换元积分法、分部积分法.但对于不能直接找出原函数的定积分,或者被积函数比较复杂时,往往是比较难求出原函数的,从而无法用牛顿-莱布尼兹公式求解.针对这样的情形,本文总结用欧拉积分求解定积分、留数在定积分上的运用、巧用二重积分求解定积分、反函数求解定积分以及带积分型余项的泰勒公式在定积分上的应用,并列举相应的例子进行说明.关键词: 定积分; 被积函数; 原函数; 牛顿-莱布尼兹公式目录1 引言2 定计算的计算方法2.1 分项积分法 (1)2.2 分段积分法 (2)2.3 换元积分法 (3)2.4 分部积分法 (5)2.5 欧拉积分在定积分计算中的应用 (9)2.6 留数在定积分计算上的应用 (10)2.7 巧用二重积分求解定积分 (10)2.8 反函数法求解定积分 (10)2.9 带积分型余项的泰勒公式在定积分上的应用 (11)3 总结 (12)浅谈定积分的计算1.引言定积分的计算是微积分学的重要内容,其应用十分广泛,它是包括数学及其其他学科的基础.本文归纳总结了常见的定积分计算方法(如[1-4]),其中包括分项积分法、分段积分法、换元积分法以及分部积分法.另外对于找不出原函数的定积分,或者被积函数十分复杂时,往往是很难求出其原函数,从而无法用牛顿-莱布尼兹公式求解.针对这样的情形,我们有必要在此基础上研究出新的计算方法.对此本文总结了一些另外的方法(如[5-9]),其中包括欧拉积分求解定积分、运用留数计算定积分、巧用二重积分求解定积分、反函数法求解定积分以及带积分型余项的泰勒公式在定积分上的应用,进行了一一列举,并通过例子加以说明.2.定积分的计算方法2.1 分项积分法我们常把一个复杂的函数分解成几个简单的函数之和:1122()()f x k g x k g x ()+,若右端的积分会求,则应用法则1122()()b b baaaf x dx kg x dx k g x dx =⎰⎰⎰()+,其中1k ,2k 是不全为零的任意常数,就可求出积分()baf x dx ⎰,这就是分项积分法.例2-1[1]计算定积分414221(1)dxx x π+⎰.解 利用加减一项进行拆项得414221(1)dx x x π+⎰=2241422(1)(1)x x dx x x π+-+⎰=41421dx x π⎰-2241222(1)(1)x x dx x x π+-+⎰ =41421dx x π⎰-41221dx x π⎰+412211dx x π+⎰=-313x 412π+4121xπ+arctan x412π.=364415arctan 323ππ-+-+. 例2-2计算定积分21⎰.解 记J=21⎰=1⎰=3221x dx ⎰+21⎰再将第二项拆开得 J=3221x dx ⎰+3221(1)x dx -⎰+1221(1)x dx -⎰=522125x +52212(1)5x -+32212(1)3x -=52225+23. 2.2 分段积分法分段函数的定积分要分段进行计算,这里重要的是搞清楚积分限与分段函数的分界点之间的位置关系,以便对定积分进行正确的分段.被积函数中含有绝对值时,也可以看成分段函数,这是因为正数与负数的绝对值是以不同的方式定义的,0就是其分界点.例2-3[2]计算定积分221(1)min ,cos 2x x dx ππ-⎧⎫+⎨⎬⎩⎭⎰.解 由于1min ,cos 2x ⎧⎫⎨⎬⎩⎭为偶函数,在0,2π⎡⎤⎢⎥⎣⎦上的分界点为3π,所以221(1)min ,cos 2x x dx ππ-⎧⎫+⎨⎬⎩⎭⎰=221min ,cos 2x x dx ππ-⎧⎫⎨⎬⎩⎭⎰+2012min ,cos 2x dx π⎧⎫⎨⎬⎩⎭⎰ =0+320312(cos )2dx xdx πππ+⎰⎰=23π+.例2-4 计算定积分2(1)f x dx -⎰,其中1,011,01()xx x x e f x ≥+<+⎧⎪=⎨⎪⎩.解 由于函数()f x 的分界点为0,所以,令1t x =-后,有2(1)f x dx -⎰=11()f t dt -⎰=0111x dx e -+⎰+1011dx x +⎰ =011x xe dx e ---+⎰+10ln(1)x +=01ln(1)xe ---++ln 2=ln(1)e +.2.3 换元积分法(变量替换法) 换元积分法可以分为两种类型:2.3.1 第一类换元积分法(也被俗称为“凑微分法”) 例2-5[3]计算定积分21sin tan dxx xπ+⎰.解21sin tan dxx x π+⎰=21cos sin (1cos )xdx x x π+⎰=22213cos sin 224sin cos 22x x dx x x π-⎰ =2211tan 2tan 22tan2xx d x π-⎰ =2111(tan )tan 222tan 2x x d x π-⎰ =2221111ln tan tan 2242x xππ-=21111ln tan tan 2424-+-.例2-6计算定积分241x dx x-+.解241x dx x -+=222111x dx xx -+=02211()1d x x x x -++=0211()1()2d x x x x-++-= 0011()()11()()d x d x x x x x x x ⎡⎤++⎢⎥-⎢⎢+-++⎣=15.2.3.2 第二换元积分法常用的变量替换有:①三角替换;②幂函数替换;③指数函数替换④倒替换. 下面具体介绍这些方法. ① 三角替换例2-7[4] 计算定积分31240(1)x x dx -⎰.解 由于31240(1)x x dx -⎰=3124201(1)2x dx -⎰,故可令2sin x t =,于是 31240(1)x x dx -⎰=arcsin1401cos 2tdt ⎰=2arcsin101(1cos 2)8t dt +⎰=arcsin101(12cos 28t ++⎰1cos 4)2t dt + =arcsin1011(32sin 2sin 4)164t t t ++=1(34sin 16t +2arcsin10sin sin ))t -=224101(3arcsin 4(1216x x x x +-=2101(3arcsin 5216x x x +=3arcsin116.②幂函数替换例2-8 计算定积分220sin sin cos xdx x xπ+⎰. 解 作变量代换2x t π=-,得到220sin sin cos x dx x xπ+⎰=220cos sin cos t dt t t π+⎰,因此220sin sin cos x dx x x π+⎰=2222001sin cos ()2sin cos sin cos x t dx dt x x t t ππ+++⎰⎰= 20112sin cos dx x x π+⎰201sin()4dx x ππ+⎰3441sin dx x ππ⎰= 3441cos )sin x x ππ-. ③倒替换例2-9计算定积分1解11令1t x=得1=11-=1arcsin-=6π. 2.4 分部积分法定理 3-1[5]若()x μ',()x ν'在[],a b 上连续,则bb b a aauv dx uv u vdx ''=-⎰⎰或b bba aaudv uv vdu =-⎰⎰.利用分部积分求()baf x dx ⎰的解题方法(1)首先要将它写成b audv ⎰()bauv dx '⎰或得形式.选择,u v ,使用分布积分法的常见题型: 表一(2)多次应用分部积分法,每分部积分一次得以简化,直至最后求出. (3)用分部积分法有时可导出()ba f x dx ⎰的方程,然后解出.(4)有时用分部积分法可导出递推公式. 例2-10[6]计算定积分2220sin x xdx π⎰.解 于21sin (1cos 2)2x x =-,所以2220sin x xdx π⎰=2201(1cos 2)2x x dx π-⎰=322211sin 264x x d x ππ-⎰ 连续使用分部积分得222sin x xdx π⎰=3222111(sin 2)sin 2642x x x x xdx ππ-+⎰ =3222111(sin 2)cos 2644x x x xd x ππ--⎰ =32201111(sin 2cos 2sin 2)6448x x x x x x π--+=3488ππ+.例2-11[7]计算定积分220sin x x e xdx π⎰.解 因为20sin x e xdx π⎰=20sin xxde π⎰=2sin xe xπ-20cos x xde π⎰=20(sin cos )xe x x π-20sin x e xdx π-⎰ 所以2sin xe xdx π⎰=1220(sin cos )xe x x π- =21(1)2e π+ 于是 20cos x e xdx π⎰=cos xe x20π+20sin x e xdx π⎰=201(sin cos )2x e x x π+=21(1)2e π- 从而220s i n xx e x d x π⎰=2201(sin cos )2x x d e x x π⎡⎤-⎢⎥⎣⎦⎰=2201(sin cos )2x x e x x π-20(sin cos )x xe x x dx π--⎰=2201(sin cos )2x x e x x π-201(sin cos )2x xd e x x π⎡⎤--⎢⎥⎣⎦⎰201(sin cos )2x xd e x x π⎡⎤++⎢⎥⎣⎦⎰=2201(sin cos )2x x e x x π-201(sin cos )2x xe x x π--201(sin cos )2x e x x dx π+-⎰ 201(sin cos )2x xe x x π++201(sin cos )2x e x x dx π-+⎰ =2201(sin cos )2x x e x x π-20cos xxe xπ+20cos x e xdx π-⎰=2201(sin cos )2x x e x x π-20cos xxe xπ+-201(sin cos )2x e x x π+=2221(1)sin (1)cos 2x e x x x x π⎡⎤---⎣⎦=221(1)242e ππ-+. 例2-12[8]计算定积分0sin n x x dx π⎰,其中n 为正整数.解(21)2s i n k k x x d x ππ+⎰=(21)2sin k k x xdx ππ+⎰作变量替换2t x k π=-得(21)2sin k k x xdx ππ+⎰=0(2)sin t k tdt ππ+⎰=0sin 2sin t tdt k tdt πππ+⎰⎰=0cos cos 2cos t ttdt k tππππ-+-⎰=(41)k π+(22)(21)sin k k x xdx ππ++⎰=(22)(21)sin k k x xdx ππ++-⎰作变量替换2t x k π=-得(22)(21)sin k k x xdx ππ++-⎰=2(2)sin t k tdt πππ-+⎰=-22sin 2sin t tdt k tdt πππππ--⎰⎰=222cos cos 2cos t tdttdt k tπππππππ-+⎰=(43)k π+ 当n 为偶数时,sin n x x dx π⎰=12(21)(22)2(21)0(sin sin )nk k k k k x xdx x xdx ππππ-+++=+∑⎰⎰=[]12(41)(43)n k k k ππ-=+++∑(1)224222n n n π⎡⎤-⎢⎥=⋅+⎢⎥⎢⎥⎣⎦=2n π 当n 为奇数时,sin n x x dx π⎰=32(21)(22)2(21)(1)0(sin sin )sin n k k n k k n k x xdx x xdx x x dx ππππππ-+++-=++∑⎰⎰⎰=[]321(41)(43)(41)2n k n k k πππ-=-++++⋅+∑ =324(21)(21)n k k n ππ-=++-∑=31()()12242(21)22n n n n ππ--⎡⎤⋅⎢⎥-⋅++-⎢⎥⎢⎥⎣⎦=2n π.2.5 欧拉积分在定积分计算中的应用定义 2-1[4]形如(,)p q B =1110(1)p q x x dx ---⎰的含参变量积分称为Beta 函数,或第一类Euler 积分。
J 积分new

恒成立,因此首两项分别为零。利用应变位移
关系,其余的项可化为
•
cTi
ui x
因此
ds
A x
x
x
y
y
x
Wdy
C
Ti
ui x
ds
0
2
xy
xy
x
dxdy
A ij
ij dxdy
x
• 因为在路段C3=0和C4上,dy=0,同时裂纹表 面应力自由,即Tx=0和Ty=0,所以对积分值没 有贡献,因此证明了上式的成立。相当于证明
;
w1为内能密度;D为损耗能。
• 当大于号成立时,表示裂纹在扩展,动能 在改变。现在假设是准静态,等号成立。 设损耗能D只用来形成裂纹新面积,则,
dD / dt G • da / dt
• 这里G是一参数,a是裂纹长度,则有:
cTi
dui dt
ds
d dt
AW1dA
G
da dt
• 因为:
d da dt a dt
直接计算裂端区复杂的应力场,这是J积分对断
裂力学的重大贡献。为什么?
2 J积分的线路无关性
• 如图,任意选取两逆时 针方向的线路C1和C2, 加上裂纹表面上的积分 线路C3(由P’至Q’)和 C4(由Q至P),可定义 线路C C1 C3 C,2 是C4封闭 回路。设封闭回路内的 面积为A,现欲证明
A
Q x
P y
dxdy
cPdx
Qdy
A
Q x
P y
dxdy
cPdx
Qdy
G
W1 dA A x
cTi
ui ds x
• 现在Q=W1,P=0,故上式变成:
05 J积分理论
© Kylinsoft, 2010
J积分理论-31
得出两裂纹板单位厚势能的差:
d
© Kylinsoft, 2010
J积分理论-32
3 形变功率J积分定义应用:
du i 1 1 U J Ti ds B a B a C da
1 dU d J P B da da
© Kylinsoft, 2010 J积分理论-13
弹塑性HRR解
线弹性
EJ ij 0 2I r 0 n
1 n 1
Fij , n
0 EJ ij 2 E I r 0 n
其中:
n n 1
© Kylinsoft, 2010 J积分理论-12
三 裂纹顶端应力、应变场与J积分判据
1 HRR理论
1968年Hutchinson,Rice与Rosengren建立了HRR理论: (1) 给出了硬化材料裂纹尖端应力场的HRR解,指出裂纹尖 端附近应力具有HRR奇异性。 (2) 指出弹塑性或非线性情况下,裂纹尖端附近应力场的强 度由J积分决定,J积分是度量裂纹尖端弹塑性应力应变 场强度的参量。 求解方法: 应用J积分守恒性及材料的硬化规律确定应力和应变的幂, 然后选择满足平衡方程的应力函数,从而得出裂纹尖端的应 力和应变场的局部解。 重要矛盾: 既然考虑了塑性变形,裂纹尖端的应力就不应该是奇异的
J JC
© Kylinsoft, 2010
J积分理论-23
四 J积分的形变功率定义
形变功率J积分定义也是由Rice首先提出的。
du i 1 1 U ui J Ti ds wdx T ds 2 i B a B a C da x 1
电测法测量J-积分的实验方法研究
电测法测量J-积分的实验方法研究摘要:J-积分是一种重要的断裂力学参数,用于描述裂纹尖端附近在弹塑性情况下的应力应变场;电测法是比较成熟的固体力学实验方法,具有适用性强、测量准确等特点。
本文严格遵循J-积分定义,通过严谨的数学推导,得到了以离散点应变表达的J-积分公式;然后借助有限元分析对测量围道进行了优化,提出了“十点测量法”,并采用电测法进行了实验验证。
本文所提出的电测法测定J-积分的实验方法适用于在役一般结构件,具有严谨的理论基础和良好的可行性,因而具有一定的理论意义和广泛的工程应用前景。
关键词:断裂力学J-积分电测法1 引言J-积分是J.R.Rice[1]在1968年提出的一个弹塑性断裂力学中的重要参数,用于描述裂纹尖端附近弹塑性应力应变场,并且具有良好的守恒性,是结构材料断裂破坏的重要判据。
目前,J-积分可以通过三种方法得到:理论分析与估算、数值计算和实验测定,实验测定是其他两种方法无法替代的直接依据。
实验常用方法有:单试件法、多试件法和光测法等,它们都有自身难以克服的缺点。
多试件法的主要问题是需要较多的实验件和花费较多的试验测量工作[2]。
单试件法[3]虽然避免了前者的问题,但需要的设备条件较高,且不能用于在役结构件测量。
光测法[4、5]理论精度较高,便于得到全场信息,但存在等差线条纹过密、条纹序数难以确定等问题,另外,光测法也存在对试件表面质量要求过高、试件加工工艺复杂和成本高昂等问题。
1983年,D.T.Read[6]提出了二维单边裂纹J-积分的直接测试法,此方法充分利用了试件的自由边界,但由于测量的限制,理论公式作了较大简化,只适用于较薄的试件。
本文严格遵循J-积分定义,建立了严谨的离散型计算公式,并结合电测法测量,具有广泛的适用性。
2 实验公式推导2.1 J-积分的定义,图1对于一端有一直线切口的二维断裂问题中,J-积分可以用回路上的应力、应变和位移给出,其表达式为:综上所述,综合式(3)、(5)、(9)、(12)以及(13)~(16),可知式(1)所示的J-积分可用积分围道上的应力、应变来表示。
ABAQUS计算J积分细节
ABAQUS计算J积分细节Abaqus计算J积分,主要是指派裂纹及定义裂纹的方向,同时在step中的历程模型:10×50裂纹:定义一个尖端;另一方面指明裂纹的扩展方向(1.0,0.0),说白了就是X积分数值,图中输入10,则输出10个J积分值计算包含裂纹尖端的包络区域的面积即为J积分避开裂纹尖端塑形区域的不可计算的特性。
同时J积分的计算数值与积分路径无从以上图例可以看出J积分数值区域稳定。
疑问:为何计算多个积分点,是否最后的稳定数值就是需要计算的J积分数值?J积分应该是数值,而不是多个不同的数值。
我个人觉得最后的稳定数值应该是需要计算的积分数值。
从dat文件到inp文件,找到积分区域。
pickseted12以及pickseted13都是节点4,坐标如图所示,在cad模型中的位置如箭头指向,即裂纹尖端。
详细的需要看一下abaqus帮助文档,关于J积分的计算细节。
积分点的个数的意义我还没有搞清楚。
对于应力强度因子K,表征裂纹尖端受力的一个参量,在裂纹尖端的应力场的一定范围内,不同的节点计算数值大体是相同的。
计算应力强度因子:可以利用abaqus直接输出,也可以利用公式计算应力强度因子,以下为利用有限元法计算应力强度因子:计算应力强度因子:从上图可以看出,计算应力强度应力的点与计算J积分的点是一致的。
Abaqus计算的应力强度因子为裂尖处的应力强度因子。
下面我们利用有限元法计算y=0处的应力强度因子,最后外推到裂尖处的应力强度因子。
选取不同的半Abaqus计算J积分注意事项:(1)一、Interaction模块1.1 预制裂纹(步骤:菜单/special/crack/assign seam)注意:并不是作裂纹分析都要定义seam,如果你的裂纹不是一条缝,而是一个缺口,则不需要assign seam,直接走下一步(定义裂纹)就行。
1.2 创建裂纹(步骤:菜单/special/crack/create,type:contour integral)—crack front:crack front是用来定义第一围线积分的区域,2D下我们可以选择包围裂尖点的面,3D则选择包围裂尖线的面;另外还有一种定义crack front的方法,就是直接选择裂尖点(2D)或裂尖线3D),用这个方法定义crack front不需要再定义下一步的crack tip/line,比较简便,两种方法算出的结果没有明显的差别,其实只是影响积分路线的问题,但是J积分值是路径无关的,看个人喜好吧—crack tip/line:这个比较好理解就是裂尖点(2D)或线(3D),如果我们在上一步中用方法二定义crack front,这一步就直接跳过了—crack extension direction(定义裂纹扩展方向):这里定义的其实是一个虚拟的裂纹扩展方向,定义了这个参考方向后,我们才能通过输出的角度判断裂纹扩展方向,可以通过两种方法:(1)q vector:输入一个方向,用来作为计算裂纹的扩展方向的参考方向;(2)normal to crack plane:crack plane表示裂纹的对称面(当裂纹在一个平面内时,可能需要分开定义多个裂纹),这种方法下我们只需定义裂纹面的法线方向,通过(t表示裂纹尖端的切线), 会在每个节点得出一个q方向;(3)注意:q的方向对输出的应力强度因子,J积分等都会有影响,一般情况下,q最好在裂纹平面内,且垂直于裂尖线的切线,否则算出的应力强度因子,J积分值等等在不同围线积分中会差别较大。
用ANSYS计算J积分的具体步骤,其实是帮助文件中的翻译
用ANSYS 算J 积分的步骤:建模、网格划分、加载、求解,这些我就不说了,我主要说说后处理中是怎么求解J 积分的。
2D 情况下,J 积分的公式为:d ()d y x x y u u J w y t t s x yΓΓ∂∂=-+∂∂⎰⎰ (1) 式中,各参数意义如下:Γ:围绕裂纹尖端的积分路径。
w :应变能密度(单位体积的应变能)x t :X 轴的引力分量,x x x xy y t n n σσ=+y t :Y 轴的引力分量,y y y xy x t n n σσ=+σ:应力分量n :路径Γ的单位外法线向量。
u :位移向量s :路径Γ的距离。
下面是计算J 积分的具体步骤:1、读入所要结果Command:SETGUI: Main Menu →General Postproc →Last Set2、存贮每个单元的应变能和体积Command: ETABLEGUI: Main Menu → General Postproc →Element Table →Define Table3、计算每个单元的应变能密度Command: SEXPGUI: Main Menu → General Postproc →Element Table →Exponentiate4、定义线积分路径Command: PATH,PPATHGUI: Main Menu → General Postproc →Path Opertions →Define Path5、将应变能密度映射到路径上Command: PDEFGUI: Main Menu → General Postproc →Path Opertions →Map Onto Path6、对Y 轴积分Command: PCALCGUI: Main Menu → General Postproc →Path Opertions →Intergrate7、将积分结果的最后值赋值给参数,该结果为(1)式的第一项Command: *GET,Name,PATH,,LASTGUI: Utility Menu →Parameters →Get Scalar Data8、将应力分量SX 、SY 、SXY 映射到路径上Command: PDEFGUI: Main Menu → General Postproc →Path Opertions →Map Onto Path9、定义路径的单位法向量Command: PVECTGUI: Main Menu → General Postproc →Path Opertions →Unit Vector10.计算式(1)中的x t 和y tCommand: PCALCGUI: Main Menu → General Postproc →Path Opertions →Operation11.沿x 轴正方向和负方向把路径移动一小段距离,计算位移向量的导数x u x ∂∂和y u y∂∂ 步骤:a 、计算路径移动的距离DX 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本例中原始的python文件位于Abaqus Benchmarks Manual中1.16.1Contour integral evaluation: two-dimensional case中,两个原始文件是
2DDoubleEdgedNotchCPE8R_model.py,2DDoubleEdgedNotchCPE8R_job.py。
在命令行下提取它们的命令:
abaqus fetch job=2DDoubleEdgedNotchCPE8R_model.py
abaqus fetch job=2DDoubleEdgedNotchCPE8R_job.py
在abaqus/CAE中运行Run Script便可得到结果。
J积分是保存在.dat文件中的。
我仔细看了python文件,感觉其分析建模过程乱七八糟,很容易把人搞糊涂;从python文件看,其模型初始数据也有错(根据python文件,高度应该是100 in,而不是60 in);
机器软件配置:
操作系统:32位windows XP SP3; ABAQUS:6.9
根据我自己的理解,将题目重新做了一下,详细如下:
第一步,进入Part模块
在草图上随便画个矩形
给矩形标尺寸
尺寸确定后便可结束草图操作,返回part功能模块。
第二步,进入Property 模块,将刚才的模型赋予材料特性。
完成后的结果如下:
第三步,进入Assembly模块。
注意Instance Type选项。
在这里需要分割图形,主要是为裂尖处网格作准备。
进入草图模式
裂纹在中央的侧面,所以先在中央划线。
这里划成相等的两段。
在刚才作出的线上,随便画两个圆
对圆进行约束,尺寸如下:
结束分割,返回到Assembly
下面找出裂尖,采用分割直线的办法。
(其实刚才画出来更简便)
在直径上随便点击一下,根据下面的提示就可完成分割。
在model tree 中可以看到刚才的分割点,右击Edit ,因为是等分,所以在Edge Parameter 中填入0.5。
第四步,进入Interaction模块。
先定义seam,然后设置crack。
选择左边两段线,完成左边seam;同理完成右边seam。
完成后的效果:
下面设置crack。
A.选择裂尖点
选择裂纹扩展方向。
左边裂纹向右扩展,因此向量选择是(0,0)到(1,0)
下面对奇异性(Singularity)进行设置:
裂尖的奇异性用1/4节点来模拟,所以填0.25;此处裂纹尖端处是单节点。
同理完成右边crack设置,但其向量是由(0,0)指向(-1,0)的。
第五步,进入step模块,设置J积分输出。
A.生成一个分析步。
B.设置J积分输出。
因为有两条裂纹,所以要设置两项历史输出报告。
点击Edit ,设置左裂纹J 积分输出。
C.同理,再生成一个输出,设置右裂纹的J积分输出。
完成J积分输出设置的效果如下:
第六步,进入Load模块,设置边界条件和载荷。
边界条件为中心点1方向位移为0,中央两条短线2方向位移为0;载荷:上下两条边上的Pressure均为-100,完成后的效果如下。
第七步,进入Mesh模块,生成裂尖处网格和其他区域网格。
A.在裂尖区域边界布点
先布置左裂纹尖端。
bias = 2 , number = 6。
注意选线段时点击线段靠圆心处,不然不是由里向外逐渐稀疏。
同理设置右边裂纹。
最终效果如下:
设置四条圆弧,分成12份。
完成后的效果如下:
设置中间四条短线,分成4份。
完成后的效果如下:
设置左右四条边,分成24份;设置上下两条边,分成14份。
最终效果下:
B.控制裂尖处网格生成。
点击Assign Mesh Controls,选择裂尖区域。
点击Assign Element Type,选中裂尖区域,选择单元。
第八步,进入Job 模块,生成一个Job(均按缺省设置),提交分析便可。
查看结果:
J 积分在job-1.dat 中,打开如下:
同理设置剩余区间。
网格控制如下:
单元类型如下:
网格划分完成后的效果如下:
最后,进入Job模块,按缺省值生成一个Job,submit,点击result,结果如下:
J积分在Job-1.dat中,打开如下:
求J积分详细过程Page 31 of 31
非赢利目的,请随便拷贝;赢利目的,请联系灰太狼(Email: 71494617@ )。
