关于有理数的加法法则课件
合集下载
1.6 有理数的加法 2.有理数加法的运算律课件(共21张PPT)

知识点2 有理数加法运算律的应用
解:2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]=8+(-4)=4.30×10+4=304(千克).答:这10筐苹果总共重304千克.
还有其他方法吗?哪种更简便?
解:(1)原式=(26+5)+[(-18)+(-16)]=31+(-34)=-3.(2)原式=[(-1.75)+(-2.25)]+[1.5+(-8.5)]+7.3=(-4)+(-7)+7.3=(-4)+[(-7)+7.3]=(-4)+0.3=-3.7.
同号结合
凑整
例3 10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下: 2,-4,2.5,3,-0.5,1.5,3,-1,0,-2.5.问这10筐苹果总共重多少?
( )
探索:
(2)任意选择三个有理数(至少有一个是负数),分别填入下列、◯和◇内,并比较两个运算结果:
和
+
+
+
+
( )
2
(-5)
4
2
(-5)
4
[2+(-5)]+4=1=2+[(-5)+4]
有理数的加法仍满足交换律和结合律
1.加法交换律:两个数相加,交换加数的位置,和不变.
B
解:2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]=8+(-4)=4.30×10+4=304(千克).答:这10筐苹果总共重304千克.
还有其他方法吗?哪种更简便?
解:(1)原式=(26+5)+[(-18)+(-16)]=31+(-34)=-3.(2)原式=[(-1.75)+(-2.25)]+[1.5+(-8.5)]+7.3=(-4)+(-7)+7.3=(-4)+[(-7)+7.3]=(-4)+0.3=-3.7.
同号结合
凑整
例3 10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下: 2,-4,2.5,3,-0.5,1.5,3,-1,0,-2.5.问这10筐苹果总共重多少?
( )
探索:
(2)任意选择三个有理数(至少有一个是负数),分别填入下列、◯和◇内,并比较两个运算结果:
和
+
+
+
+
( )
2
(-5)
4
2
(-5)
4
[2+(-5)]+4=1=2+[(-5)+4]
有理数的加法仍满足交换律和结合律
1.加法交换律:两个数相加,交换加数的位置,和不变.
B
第1课时有理数的加法法则(39张PPT)数学

B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
解析
答案
解析 -(-1)+|-1|=-(-1)+1=1+1=2,故选B.
3.下列运算正确的是( )A.(-2)+(-2)=0 B.(-6)+(+4)=-10C.0+(-3)=3 D.0.56+(-0.26)=0.3
1
2
3
4
5
6
7
8
9
10
11
答案
同号两数相加,取与 相同的符号,并把 相加;异号两数相加,取 的符号,并用 减去_____________;互为 的两个数相加得0;一个数同0相加,仍得这个数.
类型2
利用有理数的加法法则运算
解
例2 (教材例1针对训练)计算:
(2)(-39)+(-11).
解 (-39)+(-11)=-(39+11)=-50.
解
(4)(-10)+0.
解 (-10)+0=-10.
归纳总结 两个有理数相加的运算方法:(1)同号→确定符号(与加数同号)→把绝对值相加;(2)异号→确定符号(取绝对值较大的加数符号)→较大绝对值减较小绝对值;(3)数+0=原数.
0
-8
典例精析
类型1
利用数轴表示两个有理数相加
例1 (教材补充例题)在数轴上表示以下两数相加,并写出结果.(1)(-5)+(+3).
解
解 (-5)+(+3)=-2.
解
(2)(-2)+(-4).
解 (-2)+(-4)=-6.
归纳总结 利用数轴表示两个有理数相加的步骤:(1)画数轴;(2)从0开始进行移动;(3)根据终点确定和.
有理数的加法法则ppt课件

解:(1) (+2) + (-11) = -(11 - 2)=-9.
(2) (-12) + (+12) =0.
3
1 2
2 3
1 2
2 3
1
1 6
.
试说出每 小题计算 的依据.
(4) (-3.4) + 4.3 = +(4.3 - 3.4) = 0.9.
课堂练习
1. 计算:
(1) 180 + (-10);
误的是( C )
c b0 a
A. a+c<0 C. –b+a<0
B. b+c<0 D.–a+b+c<0
3.已知一辆送货物的卡车从 A 站出发,先向东行驶 15 千 米,卸货之后再向西行驶 25 千米,装上另一批货物,然 后又向东行驶 20 千米后停下来,问卡车最后停在何处?
解:设 A 站为原点,向东行驶为正,则有 (+15)+(-25)+(+20) =-(25-15)+(+20) =(-10)+20=10 (km). 答:卡车最后停在 A 站东面 10 km 处.
﹣5 ﹣6 +3 +2
(5) 第一次向西走了 3 m,第二次向东走了 3m. (-3) + (+3)=0
(6) 第一次向西走了 3 m,第二次没走 (-3) + 0=-3
概括
有理数 加法法则
1. 同号两数相加,取与加数相同的正负号,并 把绝对值相加;
2. 绝对值不相等的异号两数相加,取绝对值较
大的加数的正负号,并用较大的绝对值减去较
第一章 有理数
1.6 有理数的加法
1 有理数的加法法则
华师版七年级(上)
有理数的加法ppt课件

03
CATALOGUE
有理数加法的运算律
交换律
总结词
有理数加法的交换律是指加法满足交换律,即加法运算不改变数的顺序。
详细描写
交换律是数学中的基本运算律之一,适用于有理数加法。交换律意味着无论数的顺序如何,加法的结 果都是相同的。例如,在有理数中,3 + 4 = 4 + 3,即加数的顺序可以交换,不影响加法的结果。
在0的左边。
绝对值表示一个数到数轴上原点 的距离,正数的绝对值等于其本 身,负数的绝对值等于其相反数
。
有理数的加法、减法、乘法和除 法等运算在数轴上可以通过相应
的位置移动来实现可视化。
02
CATALOGUE
有理数的加法规则
同号有理数相加
总结词
同号有理数相加,取相同的符号,并将绝对值相加。
详细描写
结合律
总结词
有理数加法的结合律是指加法满足结合 律,即加法运算不改变数之间的组合方 式。
VS
详细描写
结合律也是数学中的基本运算律之一,适 用于有理数加法。结合律意味着无论数如 何分组,加法的结果都是相同的。例如, 在有理数中,(3 + 4) + 5 = 3 + (4 + 5),即加数的组合方式可以改变,不 影响加法的结果。
整数与有理数相加
总结词
整数与有理数相加时,先将整数视为特殊的有理数,然后依 照有理数的加法规则进行运算。
详细描写
整数可以视为正有理数或负有理数,因此与任何有理数相加 时,都可以先将其视为特殊的有理数,然后依照有理数的加 法规则进行运算。例如,3(视为+3)和-5相加得到-2。
分数与有理数相加
总结词
04
有理数的加法ppt课件
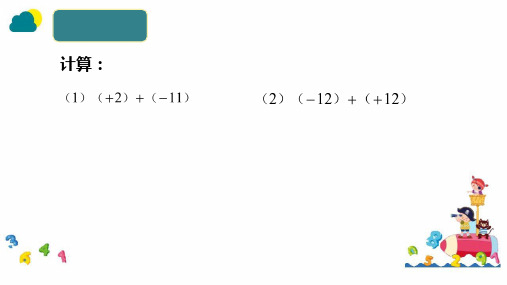
计算:
计算:
七年级上册有理数
有理数加法的运算律
教学目标
知识与技能
通过验证小学学过 的加法运算律适用 于有理数,并能熟 练运用加法运算律 进行计算。
过程与方法
由加法运算律扩大 到有理数,培养学 生用联系发展的眼 光看待问题。
情感与价值
通过对有理数加 法运算律的探究, 激发学生的求知 欲,体验简单运 算的价值。
巩固练习
计算,并说出它的解题依据和简便方法
解:①23+(-27)+6+(-22) 解题依据
=(23+6) +[(-27)+(-22)]
加法交换律、 加法结合律
=29+(-49)
加法法则
=-20
加法法则
简便方法
正数与正数、负数 与负数分别结合
小结小结
小结有理数加法法则
课外作业: 1. 2、课本第31页2题
a+b=b+a
(a+b)+c=a+(b+c)
例题解析
例1 计算: 16+(-25)+24+(-35)
你能进行简 便运算吗?
解: =[(16+24)]+[(-25)+(-35)] = 40+(-60) = -20
归 纳: 探索了有理数的加法运算律,灵活运 用加法运算律可使运算简便。
有理数加法
巩固练习1 拖动ቤተ መጻሕፍቲ ባይዱ案于对应横线上
重点:有理数加法运算律的验证和运用 难点:灵活利用运算律简化运算
小学学过的加法交换律和结合律 1 两数相加,交换加数的位置,和不变。 a+b=b+a
计算:
七年级上册有理数
有理数加法的运算律
教学目标
知识与技能
通过验证小学学过 的加法运算律适用 于有理数,并能熟 练运用加法运算律 进行计算。
过程与方法
由加法运算律扩大 到有理数,培养学 生用联系发展的眼 光看待问题。
情感与价值
通过对有理数加 法运算律的探究, 激发学生的求知 欲,体验简单运 算的价值。
巩固练习
计算,并说出它的解题依据和简便方法
解:①23+(-27)+6+(-22) 解题依据
=(23+6) +[(-27)+(-22)]
加法交换律、 加法结合律
=29+(-49)
加法法则
=-20
加法法则
简便方法
正数与正数、负数 与负数分别结合
小结小结
小结有理数加法法则
课外作业: 1. 2、课本第31页2题
a+b=b+a
(a+b)+c=a+(b+c)
例题解析
例1 计算: 16+(-25)+24+(-35)
你能进行简 便运算吗?
解: =[(16+24)]+[(-25)+(-35)] = 40+(-60) = -20
归 纳: 探索了有理数的加法运算律,灵活运 用加法运算律可使运算简便。
有理数加法
巩固练习1 拖动ቤተ መጻሕፍቲ ባይዱ案于对应横线上
重点:有理数加法运算律的验证和运用 难点:灵活利用运算律简化运算
小学学过的加法交换律和结合律 1 两数相加,交换加数的位置,和不变。 a+b=b+a
有理数的加法ppt课件

22
在运算过程中,“先 定和的符号、再算和的 绝对值”是一种有效 的方法.
新知探究 知识点1 有理数加法法则
➢ 有理数加法的运算步骤:
一看 一要辨别加数的类型(同号、异号);
二定 三算
二要确定和的符号; 三要计算绝对值的和(或差).
新知探究 知识点2 一个数加上正(负)数 思考
任何一个数加上一个正数,和与原来的数有怎样的大小关 系?加上一个负数呢?请你先借助数轴直观地得出结论,再利用 有理数的加法法则进行说明.
(1)如果物体沿着一条直线先向右运动5 m,再向右运动3 m,
那么两次运动的最后结果是什么?可以用怎样的算式表示?
5
+3
-1 0 1 2 3 4 5 6 7 8
8 (+5)+(+3)=8
新知探究 知识点1 有理数加法法则 思考
(2)如果物体沿着一条直线先向左运动5 m,再向左运动3 m,
那么两次运动的最后结果是什么?可以用怎样的算式表示?
取绝对值较大 的加数的符号
新知探究 知识点1 有理数加法法则 例1 计算: (1)(-3)+(-9); (2)(-8)+0; (3)12+(-8); (4)(-4.7)+3.9;(5)(-1)+(+1).
22
解: (4) (-4.7)+3.9=-(4.7-3.9)=-0.8;
(5) (-1)+(+1)=0.
22
把绝对值相加
解:(1)(-3)+(-9)=-(3+9)=-12;
同号两数相加 取相同符号
新知探究 知识点1 有理数加法法则 例1 计算: (1)(-3)+(-9); (2)(-8)+0; (3)12+(-8); (4)(-4.7)+3.9;(5)(-1)+(+1).
在运算过程中,“先 定和的符号、再算和的 绝对值”是一种有效 的方法.
新知探究 知识点1 有理数加法法则
➢ 有理数加法的运算步骤:
一看 一要辨别加数的类型(同号、异号);
二定 三算
二要确定和的符号; 三要计算绝对值的和(或差).
新知探究 知识点2 一个数加上正(负)数 思考
任何一个数加上一个正数,和与原来的数有怎样的大小关 系?加上一个负数呢?请你先借助数轴直观地得出结论,再利用 有理数的加法法则进行说明.
(1)如果物体沿着一条直线先向右运动5 m,再向右运动3 m,
那么两次运动的最后结果是什么?可以用怎样的算式表示?
5
+3
-1 0 1 2 3 4 5 6 7 8
8 (+5)+(+3)=8
新知探究 知识点1 有理数加法法则 思考
(2)如果物体沿着一条直线先向左运动5 m,再向左运动3 m,
那么两次运动的最后结果是什么?可以用怎样的算式表示?
取绝对值较大 的加数的符号
新知探究 知识点1 有理数加法法则 例1 计算: (1)(-3)+(-9); (2)(-8)+0; (3)12+(-8); (4)(-4.7)+3.9;(5)(-1)+(+1).
22
解: (4) (-4.7)+3.9=-(4.7-3.9)=-0.8;
(5) (-1)+(+1)=0.
22
把绝对值相加
解:(1)(-3)+(-9)=-(3+9)=-12;
同号两数相加 取相同符号
新知探究 知识点1 有理数加法法则 例1 计算: (1)(-3)+(-9); (2)(-8)+0; (3)12+(-8); (4)(-4.7)+3.9;(5)(-1)+(+1).
1.6 有理数的加法(第1课时 有理数加法法则)(课件) 七年级数学上册(华东师大版2024)

A. -5
B. 5
C. -1
D. 1
)
和的绝对值
和
20
20
20
-20
5. [2023·连云港]如图,数轴上的点 A , B 分别对应数 a , b ,
则a+b
<
0.(用“>”“<”或“=”填空)
【解析】由数轴可得 a <0< b ,| a |>| b |,根据异号两
数相加,取绝对值较大的数的符号,再用绝对值较大的数减去较小的
【解】因为| a |= ,所以 a =± .
因为| b |= ,所以 b =± .因为 a > b ,
所以 a = , b = 或- .所以 a + b =
或
.
11. [立德树人 民族精神]在某次抗洪抢险中,解放军战士的冲锋舟沿东西方向的河
流抢救灾民,早晨从甲村出发,晚上到达乙村,约定向东为正方向,当天的航
4
–2 –1 0
1
2
3
4
10
3
Байду номын сангаас
–7 –6 –5 –4 –3 –2 –1 0
7
1
2
3
4
5
–6 –5 –4 –3 –2 –1 0
2
1
2
3
1
2
3
6
–6 –5 –4 –3 –2 –1 0
还有两种特殊情形:
(5)第一次向西走了30米,第二次向东走了30米写成算式是.
(-30)+(+30)=( 0 )
(6)第一次向西走30米,第二次没走.写成算式是.
B. 5
C. -1
D. 1
)
和的绝对值
和
20
20
20
-20
5. [2023·连云港]如图,数轴上的点 A , B 分别对应数 a , b ,
则a+b
<
0.(用“>”“<”或“=”填空)
【解析】由数轴可得 a <0< b ,| a |>| b |,根据异号两
数相加,取绝对值较大的数的符号,再用绝对值较大的数减去较小的
【解】因为| a |= ,所以 a =± .
因为| b |= ,所以 b =± .因为 a > b ,
所以 a = , b = 或- .所以 a + b =
或
.
11. [立德树人 民族精神]在某次抗洪抢险中,解放军战士的冲锋舟沿东西方向的河
流抢救灾民,早晨从甲村出发,晚上到达乙村,约定向东为正方向,当天的航
4
–2 –1 0
1
2
3
4
10
3
Байду номын сангаас
–7 –6 –5 –4 –3 –2 –1 0
7
1
2
3
4
5
–6 –5 –4 –3 –2 –1 0
2
1
2
3
1
2
3
6
–6 –5 –4 –3 –2 –1 0
还有两种特殊情形:
(5)第一次向西走了30米,第二次向东走了30米写成算式是.
(-30)+(+30)=( 0 )
(6)第一次向西走30米,第二次没走.写成算式是.
有理数的加法ppt课件

在财务管理中,有理数的加法用于计算总收入、总支出和净利润。 例如,一家公司的日收入为200元,支出为150元,净利润是多少呢?
200 + (-150) = 50(元)
Байду номын сангаас
日常生活中的应用
在日常生活中,有理数的加法用于计算购物的总花费、 旅行的总距离等。
例如, 一个人带了100元在超市购物,在超市购买了价值10元、20元 和30元的商品,还有多少钱呢?
0+ (-11) =
加法的结合律
加法的结合律表明,加数的分组方式可以改变,但和不变。 加法结合律: a + (b + c ) = (a + b ) + c
8 + (-10) + (- 8) =[8 + (- 8)] + (- 10) =0 +(- 10) =- 10
有理数加法的实际应用
财务计算中的应用
11 + 0= 11 0+0= 0
有理数加法的运算律
加法的交换律
加法的交换律表明,加数的顺序可以改变,但和不变。 加法交换律: a + b = b + a
5 + 10= 15
10 + 5=
(-11) +(-1) = -12
(-1) + (-11) =
(-5) + 1= -4
1 + (-5)=
(-11) + 0 = -11
加法的基本概念
(1)如果物体沿着一条直线先向左运动3m,再向右运动5m,那 么两次运动的最后结果是什么?如何用算式表示?
(2)如果物体沿着一条直线先向右运动3m,再向左运动5m,那 么两次运动的最后结果是什么?如何用算式表示?
200 + (-150) = 50(元)
Байду номын сангаас
日常生活中的应用
在日常生活中,有理数的加法用于计算购物的总花费、 旅行的总距离等。
例如, 一个人带了100元在超市购物,在超市购买了价值10元、20元 和30元的商品,还有多少钱呢?
0+ (-11) =
加法的结合律
加法的结合律表明,加数的分组方式可以改变,但和不变。 加法结合律: a + (b + c ) = (a + b ) + c
8 + (-10) + (- 8) =[8 + (- 8)] + (- 10) =0 +(- 10) =- 10
有理数加法的实际应用
财务计算中的应用
11 + 0= 11 0+0= 0
有理数加法的运算律
加法的交换律
加法的交换律表明,加数的顺序可以改变,但和不变。 加法交换律: a + b = b + a
5 + 10= 15
10 + 5=
(-11) +(-1) = -12
(-1) + (-11) =
(-5) + 1= -4
1 + (-5)=
(-11) + 0 = -11
加法的基本概念
(1)如果物体沿着一条直线先向左运动3m,再向右运动5m,那 么两次运动的最后结果是什么?如何用算式表示?
(2)如果物体沿着一条直线先向右运动3m,再向左运动5m,那 么两次运动的最后结果是什么?如何用算式表示?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(-5)+ 0 = -5
讨论 归纳
观察、比较上述两例的几个 式子,看能否从这些算式中得到 启发,想办法归纳出有理数加法 的法则?
讨论
研究 三、有理数加法的类型
1. 5 + 3 = 8 2.(-5)+(-3)= - 8 3. 5+(-3)=2 4. 3+(-5)=-2 5. 5+(-5)=0
同号两数相加 异号两数相加
(6)(-1/4)+(-1/4)( -1/2)
(7) (-1.25)+(-15/2) ( -8.75)
归纳 小结:
1.有理数加法分三类:同号相加 , 异号相加 , 数与0相加;
2.有理数加法法则 有理数加法运算须确定: 和的 符号与和的 绝对值 ;
思考: 1.两数和一定大于每一个加数吗? 2.两数和的绝对值与两数绝对值的和或差
8
(+5)+(+3)=8
2、向西走5米,再向西走3米,
两次一共向东走了多少米?
-3 +
-5
-8 -7 -6 -5 -4 -3 -2 -1 0 1
-8
(-5)+(-3)=-8
3、 向东走5米,再向西走3米, 两次一共向东走了多少米?
-1 0 1
2
-3 5
234
ቤተ መጻሕፍቲ ባይዱ
+
56
5+(-3)=2
4、 向东走3米,再向西走5米,
的加法有什么区别和联系?
回答: 有理数加法运算,先要根据具体情况正确选用法则, 确定“和”的符号;再计算“和”的绝对值,用的就 是小学里学过的加法运算。
注意:1、确定和的符号;
2、确定和的绝对值。
应 五、有理数的加法运算
用 例一:
1、(-4)+(-5 ) (同号两数相加)
=-(
) (取相同的符号)
两次一共向东走了多少米 ?
-5 3
+
-3 -2 -1 0 1 2 3 4
-2
3+(-5)=-2
5、向东走5米,再向西走5米, 两次一共向东走了多少米?
-5 5
-1 0 1 2 3 4
+
56
5+(-5)=0
6、向西走5米,再向东走0米, 两次一共向东走了多少米?
-5
+0
-5 -4 -3 -2 -1 0 1
=-(4 + 5) (把绝对值相加)
=- 9
2、( -6) + 2 (绝对值不相等的异号两数相加)
=-(
) (取绝对值较大的加数符号)
=-(6 – 2 ) (用较大的绝对值减去较小的绝对值)
=- 4
例二: 计算
(1) (-3)+(-9)
(2) (-1/2)+(+1/3)
(3) 0 +( -0﹒1 )
关于有理数的加法法则
小明在一条东西向的跑道上,先走了5米, 又走了3米,问:他现在位于原来位置的 哪个方向,与原来位置相距多少米?
答案确定吗?有多少种情况? 与你的同桌交流一下。
研究
二、有理数加法的意义
1、向东走5米,再向东走3米, 两次一共向东走了多少米?
5
+3
-1 0 1 2 3 4 5 6 7 8
6.(-5)+0=-5
一数和零相加
学生归纳
四、有理数加法法则
1、 同号两数相加,取相同的符号,并 把绝对值相加。
2、 异号两数相加,取绝对值较大的加数 的符号,并用较大的绝对值减去较小的绝 对值。互为相反数 的两个数相加得0。
3、 一个数同0相加,仍得这个数。
比 较 比较“有理数加法”与小学里学过的数
解:(1)原式 =-(3+9) (2)原式=-(1/2-1/3)
=-12
=-1/6
(3) 原式= -0﹒1
巩固 练习
接力口答:
1、 (+4)+(-7) 2、 (-8)+(-3) 3、 (-9)+(+5) 4、 (-6)+(+6) 5、 (-7)+0 6、 8+(-1) 7、 (-7)+1 8、 0+(-10)
的关系?
同步第11页6
判断题
1 两个负数的和一定是负数
√
2 两个数的和一定大于每个加数
×
3 绝对值相等的两个数的和等于零 ×
4 若两个有理数之和是正数,则这 两个有理数一定都是正数
×
5 两个绝对值不相等的有理数的和一定不
等于零
√
6 正负两数的和不是正数就是负数 ×
1、 -3
2、 -11 3、 -4 4、 0 5、 -7 6、 7 7、 -6 8、-10
计算,并说明理由:
(1)15+(-22)
( -7 )
(2)(-13)+(-8) ( -21 )
(3)(-0.9)+1.5 (4)2.7+(-3.5)
( 0.6 ) ( -0.8)
(5)1/2+(-2/3) (1/6)
