力学中的泛函分析和变分原理第六讲
弹性力学变分原理PPT课件

fiuikdv
tiuikds
s
ij
k ij
dv
V
S
V
并取
s ij
ij
fi (ui ui )dv ti (ui ui )ds
外荷载做功的增量: W
弹性体 应 变能增 量: V
对于弹性静力学问题,根据热力学第一定律:
W V
第21页/共83页
微元体在某一应变状态获得的应变能增量为
V fiuidv tiuids
V
V
其中,ui为弹性体变形过程中的位移增量。
利用高斯公式得:
fiδ uidv σij n jδ uids
弹性体应变能是状态函数,故上式积分与 路径无关。
对于线性问题,可假设在变形过程中应力、 应变分量等比例增长。
* ij
:
0
tij
(0
t
1)
* ij
:
0
t
ij
(0
t
1)
v
1
σ
* ij
δε
* ij
1
tσij εijt
0
0
1 2
σij εij
第27页/共83页
2. 余应变能、余应变能密度
对于单向拉伸问题
a
a
结论:变分运算和积分运算可以交换次序
第11页/共83页
四、泛函的驻值与极值
1、函数的驻值和极值
如果函数y(x)在x=x0的邻近任一点上的值都 不大于或都不小于y(x0),即
y(x)-y(x0)≤0或≥0
则称函数y(x)在x=x0处达到极大值或极小
值。极值的必要条件为
dy dx
0
第12页/共83页
弹性力学的变分解法
七、弹性力学参量的下标表示法前面给出的力分量、应力分量、应变分量和位移分量,其表示方法引用的是记号法;这是一种公认的弹性力学参量表示方法。
下标表示法书写简洁,便于力学问题的理论推导。
1. 下标符号具有相同性质的一组物理量,可用一个带下标的字母表示:如:位移分量u, v, w 表示为u 1, u 2, u 3,缩写为u i (i =1,2,3)坐标x, y, z 表示为x 1, x 2, x 3,缩写为x i (i =1,2,3)单位矢量i, j, k 表示e i (i =1,2,3)。
体力分量X, Y, Z 表示为X 1, X 2, X 3,缩写为X i (i =1,2,3)应力分量:z zy zx yz y yxxz xy x 可表示为:333231232221131211 缩写为:)3,2,1;3,2,1( j i ij4. 克罗内克(Kroneker)符号具有如下性质 )cos(j i ij e ej i e eji ji ij 01 100010001333231232221131211 ij ij (1)3ii j i ij A A ij 也称换名算子同理:ijkj ik A a (2)选取可能位移:十、利用位移变分原理的近似解法m mm m mm mm m w C w w v B v v u A u u 000其中系数是完全任意的m m m C B A 、、1、瑞雷—里兹法(1)是在边界上满足位移边界条件的设定函数000w v u 、、(2)是在边界上为零的设定函数m m m w v u 、、可见,由(1)、(2)选取出来的是可能位移w v u 、、。
(53页PPT幻灯片修改版)泛函分析课件

例子
n维Euclid空间是可分的 连续函数集C[a, b]是可分的
目的:用简单的逼近复杂的
距离空间的完备性
柯西序列
设{xn}是(X, ρ)中的点列,若对任意的ε>0,存在N>0,当 n, m>N时,有ρ(xn, xm)< ε. 则称 {xn}是X中的柯西(Cauchy) 序 列,或称基本序列
距离空间:定义
设 X 是非空集合,对于X中的任意两元素x与y,按某一法则都 对 应唯一的实数ρ(x, y),并满足以下三条公理(距离公理) :
1. 2.
3.
非负性: ρ(x, y) ≥0, ρ(x, y) =0当且仅当x=y; 对称性: ρ(x, y) =ρ(y, x); 三角不等式;对任意的x, y, z ρ(x, y) ≤ ρ(x, z) + ρ(z, y)
取 x (1,1,...,1,...), (0, 0,..., 0,...)
1 2 1 ( x, ) i 2 i 1 2 1 1
(2 x, )
i 1
1 2 2 i 2 1 2 3
2 ( x, ) (2 x, )
巴拿赫(Banach)空间
极限是数学分析中的基本概念之一,有了它可以派 生 出许多其它概念.泛函分析用距离来导出一般化 的极 限概念.
如n→∞时xn→a,我们应理解为xn与a的距离当n→∞时趋向 于零.
距离空间: Rn
n 维实(或复)Euclid空间 Rn 是 n 维向量x = (a1,a2,…,an)的全体,其中ai是实(或复)数. 对 任何的x = (a1,a2,…,an), y = (b1,b2,…,bn),规定
有限元基础(泛函、变分与变分法)

因此
aT K a = aT K a
= aT( Ka - P ) = 0 由 a 的任意性,就得到(1.3.6)式:
Ka — P = 0
1.3.2 变分原理的建立
1.线性、自伴随微分算子
线性算子
具有以下性质的算子 L 称为线性算子
其中和是两个常数
内积
算子L(u)与任意函数v的 内积 定义为
则被积函数 (x) 在区间 a ≤x≤b 上必处处为零,即
1.3 变分原理和里兹方法
1.3.1 变分原理
变分原理定义
部分物理问题存在一个泛函: 而问题的解 u 使泛函取驻值,即 利用此式求解的方法称为变分法或变分原理
里兹(Ritz)法
选择试探函数:
其中N为已知函数,a为待定参数
代入泛函积分式,泛函变为普通实函数 令泛函变分为零
5. 变分法
求泛函极值的数学方法称为变分法。 泛函极值的必要条件: J = 0
充分条件:J = 0 且:2J >0 极小值 2J < 0 极大值
变分法基本预备定理:
设 (x) 是闭区间 a ≤x≤b 上的连续函数,y 是该区间上自变函数 y(x) 的变分,如果 y 在满足 约束条件的前提下任意变化时,下式始终成立
与以上微分提法相等效的伽辽金提法为
(1.3.21)
若算子L是线性、自伴随的,则有如下关系:
将其代入(1.3.21)式得
若令 则上式可表示为变分原理:
(1.3.23) 此处Π就是原问题的泛函,因为此泛函中u的最高 次为二次,所以是二次泛函。
3. 泛函的极值性
条件:
1.算子L是偶数(2m)阶的;
由于 y 与 y, y, , y(n) 无关,所以
实变函数论泛函分析课件

02 实变函数的定义与性质
实变函数的定义
01
02
03
定义域
实变函数的定义域是实数 集的一个子集,可以是有 限或无限的。
值域
实变函数的值域是实数集 的一个子集,可以是有限 或无限的。
函数表达式
实变函数可以表示为从定 义域到值域的映射关系, 通常用符号 f(x) 表示。
实变函数的性质
单调性
如果对于任意 x1<x2,都有 f(x1)≤f(x2),则称 f(x) 在其定义
微积分的应用
介绍微积分在各个领域的应用,如物理学、工程学、经济学等。
微积分的进一步发展
介绍微积分的进一步发展,如变分法、最优控制等。
04 泛函分析的基本概念
泛函的定义与性质
定义
泛函是将函数空间的每一个元素作为自变量,其值是实数或 复数的函数。
性质
泛函是定义在函数空间上的,它具有连续性、可加性、线性 等性质。
么该空间是自完备的。
共鸣定理
在赋范线性空间中,如果存在 一个与所有单位球相交的集合,
那么该空间是自完备的。
开映射定理
如果X和Y是赋范线性空间,T 是X到Y的开映射,那么T是满
射。
闭图像定理
如果X和Y是赋范线性空间,T 是X到Y的连续线性映射,那
么T的像集是闭的。
05 泛函分析的应用领域
微分方程的求解
分析中的某些问题。
应用领域
实变函数论和泛函分析 在许多应用领域都有交 叉,如 质
线性性质
对于任意实数k和函数f,g,有 $k(f+g)=(kf)+(kg)$, $(kf)+(kg)=(k+k)(f)$。
连续性质
如果f_n(x)是函数空间中的收敛序列, 那么$f_n(x)$的极限函数也是连续的。
变分法泛函极值问题PPT课件

F x
d dt
(
F x
)
0
(3-3)
上式称为欧拉——拉格朗日方程。
(3-2)式中第二项为零的条件要分两种情况来讨论:
.
15
1、 固定端点的情况
这时 x(t0 ) x0 , x(t f ) x f,它们不发生变化,所 以 x(t0 ) x(t f ) 0 。而(3-2)中第二项可写成
F x
x
JX ,X X
这里,JX ,X 是X 的线性泛函,若 X 0时, 有 0,则称JX ,X 是泛函 JX 的变分。J 是 J
的线性主部。
.
9
6、泛函的极值:若存在 0 ,对满足的
X X一* 切 X,
J (X ) 具J (有X *同) 一符号,则
称 J ( X ) 在 X X *处有极值。
(3-21)与(3-22)一起称为哈密顿正则程。
.
39
(3-23)是控制方程,它表示 H 在最优控制处取 极值。
注意,这是在U为任意时得出的方程,当 U (t)有界且 在边界上取得最优值时,就不能用这方程,这时要用 极小值原理求解。
(3-24)是在 固定、t f
自X (t由f ) 时得出的横截条件。
容易验证 x(t) 0时, J 0 对应局部极小;x(t) 2t 3
时, J 4 27 ,对应局部极大。
.
28
3.3 有约束条件的泛函极值 ——动态系统的最优控制问题
前面讨论泛函极值问题时,对极值轨迹 X *(t) 没有附 加任何约束条件。但在动态系统最优控制问题中, 极值轨迹必须满足系统的状态方程,也就是要受到 状态方程的约束。考虑下列系统
是指同属于函数类X (t)中两个函数X1(t) 、X 2 (t) 之差
2+弹性力学、泛函、变分等基本知识
2013-7-31 有限元法预备知识
σ
来表
7
2.1 弹性力学基本知识 [ 位 移 ]
z
z
x
x
x
E
(6)
y
y
式中,E为弹性模量。弹性体在x方 向的伸长还伴随有侧向收缩,即在y 和z方向的单位缩短可表示为:
x
z
0 x
图 1-7
y
x x y , z (7) E E
式中,μ 为泊松比。 上述两个方程可用于简单和压缩。
2013-7-31
有限元法预备知识
x y z xy yz zx 0
有 u 0,v 0,w 0,u v 0,v w 0,w u 0 x y z y z z x x y
积分得
式中,u0、v0、w0、 x、 y、 z、为积分常数,即刚体位移。
2013-7-31
有限元法预备知识
4
2.1 弹性力学基本知识 [ 应力的概念 ]
•正应力 为了表明这个正应力的作用面和 作用方向,加上一个角码,例如, 正应力σx是作用在垂直于x轴的面 上同时也沿着x轴方向作用的。 •剪应力 加上两个角码,前一个角 码表明作用面垂直于哪一个坐 标轴,后一个角码表明作用方 向沿着哪一个坐标轴。例如, 剪应力τxy是作用在垂直于x轴 的面上而沿着y轴方向作用的。
由
F 0 ,得
x
x
xy
Gx
x
Gy
yx
泛函与变分概念
1 xy 2
e yy e m
1 zy 2
1 xz 2 1 yz 2
e zz
em
应变球张量
应变偏张量
§i1 张量5
求和定约
张量表达式的某一项内的一个下标出现两次, 则对此下标从1到3求和。
aii a11 a22 a33
aijbij a1 j b1 j a2 j b2 j a3 j b3 j (a11b11 a12b12 a13b13 ) (a21b21 a22b22 a23b23 ) (a31b31 a32b32 a33b33 )
i=1,2,3 j=1,2,3
s z 2e z
§i1 张量10
(4)边界条件
应力边界条件
f x s x l yx m zx n f y xy l s y m zy n f z xz l yz m s z n
位移边界条件
设(n1 , n2 , n3 ) (l , m, n)
a b
f f dy dy) dy及dy高阶项) ]dx y y
b a
J [df dy及dy高阶项) ]dx
取线性主部
dJ dfdx
a
b
k d J d a fdx 函数的变分与积分运算可以交换. k
b
§i2 变分法9
三. 泛函极值与驻值
1、函数的极值 如果函数y(x) 在x=x0的邻近任一点上的值都不大于(不 小于)y(x0),即
1 e ij s ij s kkd ij E E
s kk s x s y s z
s x 2e x
泛函极值及变分法
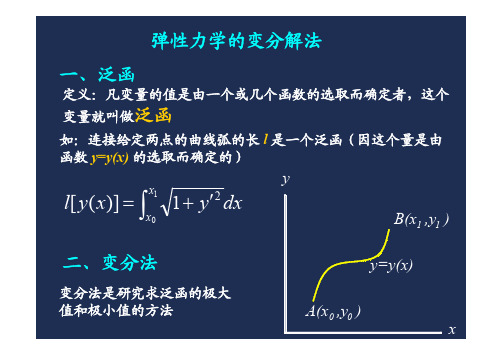
第二章 泛函极值及变分法(补充内容)2.1 变分的基本概念2.1.1 泛函和变分泛函是一种广义的函数,是指对于某一类函数{y (x )}中的每一个函数y (x ),变量J 有一值与之对应,或者说数J 对应于函数y (x )的关系成立,则我们称变量J 是函数y (x )的泛函,记为J [y (x )]。
例1:如果表示两固定端点A (x A ,y A ),B (x B ,y B )间的曲线长度J (图2.1.1),则由微积分相关知识容易得到:dx dx dy J BAx x ⎰+=2)/(1 (2.1.1)显然,对于不同的曲线y (x ),对应于不同的长度J ,即J 是函数y (x )的函数,J =J [y (x )]。
图2.1.1 两点间任一曲线的长度例2:历史上著名的变分问题之一——最速降线问题,如果2.1.2所示。
设在不同铅垂线上的两点P 1与P 2连接成某一曲线,质点P 在重力作用下沿曲线由点P 1自由滑落到点P 2,这里不考虑摩擦作用影响,希望得到质点沿什么样的曲线滑落所需时间最短。
图2.1.2 最速降线问题选取一个表示曲线的函数y (x ),设质点从P 1到P 2沿曲线y =y (x )运动,则其运动速度为:dsv dt ==其中,S 表示曲线的弧长,t 表示时间,于是:dt =设重力加速度为g ,则gy v 2=。
因为P 1和P 2点的横坐标分别为x 1到x 2,那么质点从P 1到P 2所用时间便为:1[()]x x J y x =⎰211/2211[()]2[()()]x x y x dx g y x y x ⎧⎫'+=⎨⎬-⎩⎭⎰(2.1.2)则最速降线问题对应于泛函J [y (x )]取最小值。
回顾函数的微分:对于函数的微分有两种定义: 一种是通常的定义,即函数的增量:),()()()(x x x x A x y x x y y ∆+∆=-∆+=∆ρ (2.1.3) 其中A (x )与∆x 无关,且有∆x →0时ρ(x ,∆x )→0,于是就称函数y (x )是可微的,其线性部分称为函数的微分()()dy A x x y x x '=∆=∆,函数的微分就是函数增量的主部。
力学的变分原理PPT课件
如果F不显含自变量 t , 则欧拉方程有初积分 :
F - q F 常 数
2021/3/7
q
CHENLI
13
例 : 求 最 速 落 径 方 程 . ( 已 知 F 1 y '2 ) 2 gy
解:
因F
不显含
x,
则有 F
-
y'
f y '
C1.
即:
1 y '2 2gy
y
'
y
'
1 y '2 2gy
其中t为自变量,q为力学系统的广义坐标,此函数关系
如图中曲线所示。当自变量
t有微小增量dt时,对应的
q
函数q的微小增量的线性主部
dq称为函数的微分,记为
d qq'(t)d t
(1 )
或: q' (t) dq dt
2021/3/7
o
CHENLI
, q=q(t)+εη(t)
p δq dq q=q(t)
常
数
1
y '2
y '
y'
常数
2gy
2 g y (1 y '2 )
2 g y (1 y '2 ) 常 数 y (1 y '2 ) C 1 引 入 参 数 , 使 y ' c tg y C 1 C 1 (1 c o s 2 )
1 ctg 2 2
2021/3/7
CHENLI
比如,牛顿提出的力学三大定律,就是力学的基本原理,由这些基本原理出发,经过严 格的逻辑推理和数学演绎,可以获得经典力学的整个理论框架。
力学原理可以分为两大类:不变分原理和变分原理。每一类又可 分为微分形式和积分形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定理4:设������是Hilbert空间ℍ中的闭凸子集, ������ ∈ ℍ\������,则下列命题等价
(i) ������ ∈ ������是������的最佳元,即对任意的������ ∈ ������,均有 ������ − ������ ≤ ������ − ������ ; (ii) ������ ∈ ������满足:对任意的������ ∈ ������,均有 ������ − ������ , ������ − ������ ≤ 0; (iii) ������ ∈ ������满足:对任意的������ ∈ ������,均有 ������ − ������, ������ − ������ ≥ 0.
算子的图像
令������是定义在������ ������ ⊂ ������上并在������1 中取值的线性算子,������的图像是指������ × ������1 中 元素 ������, ������ ������ 的全体,记为������ ,其中������取遍整个定义域������ ������ . ������
§3.1 线性算子
算子范数
设������: ������ → ������为有界线性算子,则对于一切������ ∈ ������ ������ 使得不等式 ������ ������ ������ ������ 为
������ 成立的正数������的下确界称为算子������的范数。或者说数集 ������
§3.2 有界线性算子空间
设������和������都是线性赋范空间,定义在整个������上,而在������上����, ������ . 如果规定������ ������, ������ 中任意两个算子
(1) 加法为: ������ + ������ ������ = ������ ������ + ������ ������ 1 2 1 1 (2) 数与算子乘积为: ������������ ������ = ������������ ������ 则������ ������, ������ 便成为线性空间。 定理:设������为线性赋范空间,而������为Banach空间,则������ ������, ������ 为Banach空间。
子”。
§3.1 线性算子
线性算子
设������和������是给定的两个线性空间,算子������: ������ → ������,且������满足 (1)∀ ������, ������ ∈ ������ ������ ; ������ ������ + ������ = ������ ������ + ������ ������ ; (2)∀ ������ ∈ ������ ������ , ∀ ������ ∈ ℝ; ������ ������������ = ������������ ������ ; 则称������为由������到������的线性算子。
2
= ������
2;
(ii) 若有一元素������ ∈ ℍ与每个������������ 都正交,则������ = ������.
正交补
设������为ℍ中的子集,ℍ中所有正交于������的元素集合称为������的正交补,记为������⊥ . 定理:设������是ℍ中的闭子空间,则ℍ = ������⨁������⊥ ,且 ������⊥
������ ������ 1/2 2 ������������
������ =
������
������ ������
+
������
������′ ������
2 ������������
2.4.2
空间ℍ1 ������, ������ 在范数(2.4.2)意义下的完备化空间记为ℍ1 ������, ������ ,称为Sobolev空间。
������∈������
推论:设������是ℍ中的闭子空间,������ ∈ ℍ\������,则存在������ ∈ ������,使得 ������ − ������ = ������ ������, ������ 定理2:若������ ⊥ ������,则 ������ + ������
研究生课程
力学中的泛函分析 与变分原理
第六讲:有界线性算子
授课教师:郭旭教授
大连理工大学工程力学系
课 程 回 顾
定理1:设������是ℍ中的闭凸子集,������ ∈ ℍ\������,则必存在唯一的������ ∈ ������,使得 ������ − ������ = inf ������ − ������
课 程 回 顾
第三章 有界线性算子
算子
设������和������是给定的两个线性赋范空间,集合������ ⊂ ������,若对������中每一个元素������,均对 应������中一个确定的元素������,就说这种对应关系确定了一个算子,用花体大写字母 ������, ������, …表示,记为������ = ������������或������ = ������ ������ .������称为������的像,������称为������的原像。集合������称
⊥
= ������.
课 程 回 顾
索伯列夫空间
将区间 ������, ������ 上一阶连续可微函数全体构成的集合记为ℍ1 ������, ������ .在通常的函数 加法、数乘意义下,ℍ1 ������, ������ 是线性空间.对于任意的������ ������ ,������ ������ ∈ ℍ1 ������, ������ ,定义
算子有界
如果存在正常数������,使得对每一个������ ∈ ������ ������ ,均有: ������ ������
������
≤ ������ ������
������
则称算子������: ������ → ������是有界的。
算子连续
设������: ������ → ������,������在������0 ∈ ������的邻域内有定义,如果当 ������������ − ������0 → 0, ������ → ∞ 时, 有 ������ ������������ − ������ ������0 → 0, ������ → ∞ ,则称算子������ 在������0 处是连续的,如果������ 在 ������ ������ 的每一点处都连续,则称������是连续的算子。 定理:设������: ������ → ������是线性算子,假定������ 在某一点������0 ∈ ������ ������ 连续,则������ 在 ������ ������ 内处处连续;������连续的充分必要条件是������有界。 2
≤
������ ������ ������ (简记 ������ ������
������ ������ ������
)是有上界的,取其最小者为������的范数,即: ������ = sup
������ ≠0
������ ������ ������
定理:设������: ������ → ������为有界线性算子,则 ������ = sup
为算子������的定义域,常记为������ ������ .而集合
������ ������ = ������ ∈ ������; ������ = ������ ������ , ������ ∈ ������ ������ 称为算子������的值域。对于算子������,常用记号"������: ������ → ������",读作“������是由������到������的算
算子强收敛
设 ������ ⊂ ������ ������, ������ ,������ ⊂ ������ ������, ������ , 如果对∀ ������ ∈ ������, 均有 ������ ������ − ������ ������ ������ ������ 称算子 ������ 强收敛于������. ������ → 0, 则
∞ ������=1 ������������ ������������ ,其中������������
= ������, ������������ ,
(i) 对于∀ ������~
∞ ������=1 ������������ ������������
∈ ℍ,均有
∞ ������=1
������������
课 程 回 顾
正交化方法
设 ������1 , ������2 , … 是 ℍ 的 一 组 元 素 , 如 果 对 任 意 的 ������ ≠ ������, ������, ������ ∈ ℕ+ , 均 有 ������������ , ������������ = 0,则称 ������1 , ������2 , … 是ℍ中的正交集;如果每个������������ 都是单位元素(即 范数为1),则称之为规范正交集. 设 ������������ 是ℍ的规范正交集,若对∀ ������ ∈ ℍ,均有������ = 则称 ������1 , ������2 , … 是完全的。 定理:设 ������1 , ������2 , … 是ℍ中的规范正交集,则其为完全的充分必要条件是
2 2 2.
= ������
+ ������
定理3(投影定理):设������是ℍ的闭子空间,������ ∈ ℍ\������,则������ 是������在������中的最佳元 的充要条件是 ������ − ������ ⊥ ������,即对∀ ������ ∈ ������,均有 ������ − ������ , ������ = 0. ������ 称为元素������在 闭子空间������上的投影。
