混凝土简支梁斜截面抗剪强度
《混凝土结构设计原理》第4章 受弯构件斜截面承载力计算

计算剪力值的确定
《公路桥规》规定:取离支点中心线梁高一半处的剪力 设计值 V ;其中不少于60%由混凝土和箍筋共同承担; 不超过40%由弯起钢筋(按45º弯起)承担,并且用水平 线将剪力设计值包络图分割;
箍筋设计 假设箍筋直径和种类,箍筋间距为
箍筋可减小斜裂缝宽度,从而提高斜截面上的骨料咬力。
箍筋限制了纵向钢筋的竖向位移,阻止混凝土沿纵向 钢筋的撕裂,提高了纵向钢筋的销栓作用。
可见,箍筋对提高斜截面受剪承载力的作用是多方面的和 综合性的。
2、剪力传递机理(见下图)——桁架-拱模型:
拱I: 相当于上弦压杆 拱Ⅱ、拱Ⅲ: 相当于受压腹杆
否
是否通过 是
计算结束
§4.3 受弯构件的斜截面抗剪承载力
计算依据:以剪压破坏为基础 一般是采用限制截面最小尺寸防止发生斜压破坏; 限制箍筋最大间距和最小配箍率防止发生斜拉破坏
一、基本公式及适用条件 计算图式:
基本公式:(半经验半理论)
Vu Vc Vsv Vsb Vcs Vsb
抗剪能力:
斜截面受剪承载力主要取决于构件截面尺寸和混凝土抗 压强度,受剪承载力比剪压破坏高。
破坏性质:属脆性破坏
除上述三种主要破坏形态外,有时还可能发生局部挤压 或纵向钢筋锚固等破坏。
四、有腹筋简支梁斜裂缝出现后的受力状态
无腹筋梁斜截面受剪承载力很低,且破坏时呈脆性。 故《公桥规》规定,一般的梁内都需设置腹筋。配置腹筋是 提高梁斜截面受剪承载力的有效方法。在配置腹筋时,一般 首先配置一定数量的箍筋,当箍筋用量较大时,则可同时配 置弯起钢筋。
V fcbh00
0. 0. 0. 0. 0.1
混凝土简支T梁桥结构桥梁设计指导书
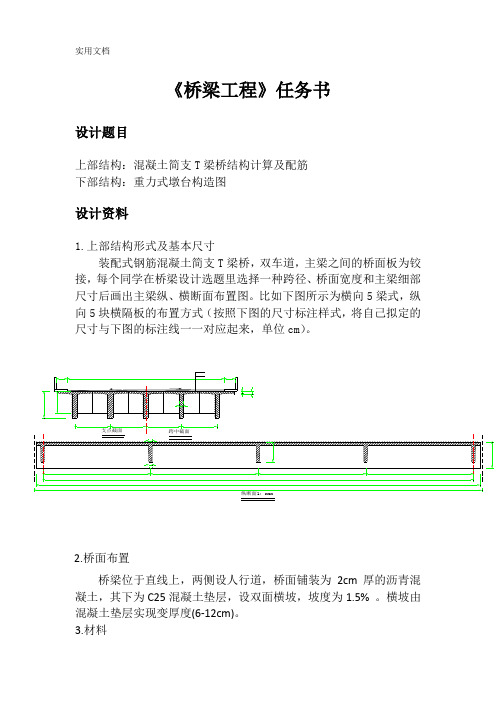
《桥梁工程》任务书设计题目上部结构:混凝土简支T梁桥结构计算及配筋下部结构:重力式墩台构造图设计资料1.上部结构形式及基本尺寸装配式钢筋混凝土简支T梁桥,双车道,主梁之间的桥面板为铰接,每个同学在桥梁设计选题里选择一种跨径、桥面宽度和主梁细部尺寸后画出主梁纵、横断面布置图。
比如下图所示为横向5梁式,纵向5块横隔板的布置方式(按照下图的尺寸标注样式,将自己拟定的尺寸与下图的标注线一一对应起来,单位cm)。
2.桥面布置桥梁位于直线上,两侧设人行道,桥面铺装为2cm厚的沥青混凝土,其下为C25混凝土垫层,设双面横坡,坡度为1.5% 。
横坡由混凝土垫层实现变厚度(6-12cm)。
3.材料1)混凝土:上部结构C30(容重为25kN/m 3)下部结构C25(容重为23kN/m 3主筋:II级钢筋;构造钢筋:I级钢筋2)桥面铺装:沥青混凝土(容重为21kN /m 3);混凝土垫层C25(容重为23kN/m 3)4)人行道:人行道包括栏杆荷载集度为6 kN/m;4.设计规范及参考书目1)《公路桥涵设计通用规范》2)《公路钢筋混凝土及预应力混凝土桥涵设计规范》3)《桥梁工程》4)《混凝土结构设计原理》5)《结构力学》6)《桥梁通用构造及简支梁桥》设计与计算要求(1)取行车道板(单位板宽即1m宽)、边梁和中梁进行恒载、活载内力计算。
(2)选取合适的方法进行荷载横向分布系数计算,并根据规范公式计算主梁自振频率和冲击系数。
(3)按规范进行作用组合(分别对应承载能力极限状态和正常使用极限状态)(4)根据作用组合进行行车道板和一片梁的截面配筋设计(主要是正截面抗弯验算与斜截面抗剪验算)成果要求1.完整的计算书,要求条理清楚,格式整齐。
计算说明书包括:行车道板的内力计算、配筋、验算;主梁的荷载横向分布系数的计算;主梁内力计算、配筋、验算。
2.绘制相关图纸:墩台构造图、桥面板、主梁钢筋布置图(纵断面和横断面及局部构造图)。
图纸可以打印或手绘,但同等条件下,打印图纸较手绘的可优先评较高一个等级。
农业设施设计与建造第三章(四)混凝土构件斜截面受剪一

在剪弯区段截面的下边缘,主拉应力还是水平向 的。所以,在这些区段仍可能首先出一些较短的垂直 裂缝,然后延伸成斜裂缝,向集中荷载作用点发展, 这种由垂直裂缝引伸而成的斜裂缝的总体,称为弯剪
斜裂缝,这种裂缝上细下宽,是最常见的,如下图所
示。
弯剪斜裂缝
腹剪斜裂缝(薄腹梁) 两种斜裂缝 弯剪斜裂缝(一般梁)
存在问题:
所以工程上往往首选垂直箍筋,然后再考虑弯 起钢筋。 纵筋受力筋,架立筋,箍筋(腹筋)形成 -----------钢筋骨架
弯起钢筋
架立钢筋
腰筋
箍筋
纵向钢筋
梁的钢筋构造
小贴士:(1)板通常跨高比很大,具有足够的斜
截面承载力,一般只计算正截面承载力,只 配纵筋,不配腹筋。但厚板(例如桩承台) 例外。 (2)斜截面承载力包括斜截面受剪承载力 和斜截面受弯承载力。
线性关系。
三、破坏形态
正截面破坏形态:用纵筋配筋率
划分,
少筋梁破坏
适筋梁破坏
超筋梁破坏
max
min max
min
斜截面破坏形态:用配箍率 sv 和剪跨比 划分, 剪压破坏 (适箍梁) 斜压破坏 (超箍梁) 斜拉破坏 (少箍梁)
1. 斜压破坏(超箍梁破坏)
设计中斜压破坏和斜拉破坏主要靠构造要求来避免, 而剪压破坏则通过配箍计算来防止。
对有腹筋梁来说,只要截面尺寸合适,箍筋数量适当,剪压 破坏是斜截面受剪破坏中最常见的一种破坏形式。
第三节 斜截面受剪破坏的主要影响因素
1 剪跨比
试验表明,剪跨比越大,有腹筋梁的抗剪承载力越低。对无腹筋 梁来说,剪跨比越大,抗剪承载力也越低,但当λ≥3 ,剪跨比的影响 不再明显。
以上这些斜截面都是受剪承载力较薄弱之处, 计算时应取这些斜截面范围内的最大剪力,即取斜 截面起始端处的剪力作为计算的外剪力。
混凝土结构设计原理-第四章斜截面受弯习题讲解学习

第四章小结1、斜截面强度计算是钢筋混凝土结构的一个重要问题。
设计受弯构件时,必须同时解决正截面强度和斜截面强度的计算与构造问题。
2、梁沿斜截面破坏的主要形态有斜压、剪压和斜拉三种。
影响斜截面抗剪强度的主要因素有:剪跨比、混凝土强度、纵向受拉钢筋配筋率和箍筋数量及强度等。
3、斜截面抗剪强度的计算公式是以剪压破坏为基础建立的。
对于斜压和斜拉破坏,一般采用截面限制条件和构造措施予以避免。
斜截面抗剪强度的计算图式、基本计算公式和适用条件,斜截面抗剪设计和复核的方法及步骤。
4、斜截面强度有两个方面:一是斜截面抗剪强度,通过计算配置箍筋或配置箍筋和弯起钢筋来保证,一是斜截面抗弯强度,通过采用一定的构造措施来保证。
第四章 受弯构件斜截面承载力计算一、填空题:1、在钢筋混凝土受弯构件中,( ) 和 ( )称为腹筋或剪力钢筋。
2、影响受弯构件斜截面抗剪力的主要因素( ) 、( ) 、( )和( )。
3、受弯构件斜截面破坏的主要形态( )、( ) 和( )。
桥规抗剪承载力公式是以( )破坏形态的受力特征为基础建立的。
4、梁中箍筋的配箍率公式:( )。
5、纵筋的配筋率越大,受剪承载力越高,这是由于( )和( )。
6、梁式结构受拉主钢筋应有不少于( )根并不少于( )的受拉主钢筋通过支点。
7、支座中心向跨径方向长度在一倍梁高范围内,箍筋间距应不大于( )。
8、控制最小配箍率的目的( ),限制截面最小尺寸的目的( )。
9、影响有腹筋梁斜截面抗剪能力的主要因素有:( )、 ( ) 、 ( )、 ( ) 。
10、钢筋混凝土梁沿斜截面的主要破坏形态有斜压破坏、斜拉破坏和剪压破坏等。
在设计时,对于斜压和斜拉破坏,一般是采用( ) 和 ( ) 予以避免,对于常见的剪压破坏形态,梁的斜截面抗剪能力变化幅度较大,故必须进行斜截面抗剪承载力的计算。
《公路桥规》规定,对于配有腹筋的钢筋混凝土梁斜截面抗剪承载力的计算采用下属半经验半理论的公式:ssb sd sv sv k cu u d A f f f p bh V V θραααγsin )1075.0()6.02()1045.0(3,033210∑⨯++⨯=≤--11、对于已经设计好的等高度钢筋混凝土简支梁进行全梁承载能力校核,就是进一步检查梁沿长度上的截面的( )、 ( )和 ( 是否满足要求。
(整理)13M跨普通钢筋混凝土梁计算书-桥梁博士.

1工程说明本上部结构采用10+13+10m普通钢筋混凝土简支梁。
桥梁桥面分左右两幅布置,桥面宽度为:0.3米(栏杆)+2.7米(人行道)+3.5米(非机动车道)+1.5米(机非分隔带)+8.25米(机动车道)+2.5米(中央分隔带)+8.25米(机动车道)+1.5米(机非分隔带)+3.5米(非机动车道)+2.7米(人行道)+0.3米(栏杆)。
下图是桥梁中墩1/2横断面布置图和侧面图。
2 设计标准2.1设计标准1、公路等级:二级道路2、行车道数:2车道;3、荷载标准:城--B4、人群荷载:5KN/㎡2.2设计规范1、《公路工程技术标准》(JTG B01-2003)2、《公路桥涵设计通用规范》(JTG D60-2004)3、《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)4、《公路桥涵施工技术规范》(JTJ 041-2000)5、《公路桥涵地基与基础设计规范》(JTJ024-85)6、《混凝土结构设计规范》(GB50010-2002)7、上海市工程建设规范《地基基础设计规范》(DGJ08-11-1999)8 、《城市桥梁设计荷载标准》(CJJ 77-98)3 设计参数3.1 混凝土各项力学指标见表3.2普通钢筋采用R235、HRB335钢筋:直径8~25mm弹性模量:R235 :210000 Mpa/ HRB335 :200000 Mpa抗拉强度标准值:R2355 235 Mpa/ HRB335: 335 Mpa热膨胀系数:0.0000124上部结构单孔荷载计算1、梁体自重梁体截面尺寸,从CAD图上得到截面的面积中梁为0.31m2、边梁为0.35 m2 。
中梁梁重:0.4×13×26=135.2KN边梁梁重:0.443×13×26=149.7KN2、单片中板铺装层:(0.07×23+0.08×25)×(3.5+8.25)×13=48KN10363610799103679910362、人行道断面截面积=(2.7+1.17×0.08+0.32×0.2+0.26×0.19+0.43×0.35+0.32×0.17×2=0.69m2人行道总重=0.69×25×13=224KN,平均作用人行道下面的三块空心板上。
影响斜截面抗剪承载力的主要因素

对于混凝土梁,由于混凝土的抗拉强度很低,因此 随着荷载的增加。当主拉应力值超过混凝土抗拉强 度时,首先在达到该强度的部位产生裂缝,其裂缝 的走向与主应力的方向垂直,故为斜裂缝。 通常情况下,斜裂缝往往是由梁底的弯曲裂缝发展 而成的,称为弯剪型裂缝。 当梁的腹板很薄或集中荷载至支座距离很小时,斜 裂缝可能首先在梁的腹部出现,称为腹剪型裂缝。
当荷载继续增加后,随着斜裂缝条数的增多和裂缝 宽度增加,骨料的咬合力下降;沿纵向钢筋的混凝 土保护层也有可能被撕裂、钢筋的销栓作用也逐步 减弱;斜裂缝中的一条发展成为主要裂缝,称为临 界斜裂缝。
无腹筋梁此时如同拱结构(如图5-6),纵向钢筋成 为拱的拉杆。
图5-6 无腹筋梁的拱体受力机制
一种常见的破坏情形是:临界斜裂缝的发展导致混凝 土剪压区高度不断减小,最后在切应力和压应力的共 同作用下,剪压区混凝土被压碎(拱顶破坏),梁发 生破坏。 破坏时纵向钢筋拉应力往往低于其屈服强度。
3. 纵筋配筋率 纵筋的配筋越大,斜截面的承载力也越大。试验 表明:而者也大致呈线性关系(图5-13)。
★混凝土剪压区面积因斜裂缝出现和发展而减小, 剪压区内的混凝土压应力将大大增加;
★与斜裂缝相交处的纵向钢筋应力,由于斜裂缝 的出现而突然增加;
★纵向钢筋拉应力的增加导致钢筋与混凝土之间 粘结应力的增加,有可能出现沿纵向钢筋的粘结 裂缝(图5-5a)或撕裂裂缝(图5-5b);
图5-5 粘结裂缝和撕裂裂缝
§5.1 概述
1)受力破坏分析 1.斜截面开裂前的受力分析
如图5-1所示,简支梁在两个对称荷载作用下 产生的效应是弯矩和剪力。在梁开裂前可将梁视为 匀质弹性体,按材力公式分析。
图 5-1 主应力轨迹线
混凝土结构设计原理-05章-受弯构件的斜截面承载力

第5章 受弯构件的斜截面承载力
主要内容
● ● ● ●
重点
斜裂缝、剪跨比及斜截面受剪破坏形态 简支梁斜截面受剪机理 斜截面受剪承载力计算公式及设计计算 保证斜截面受剪承载力的构造措施
● 斜裂缝、剪跨比及斜截面受剪破坏形态 ● 简支梁斜截面受剪机理 ● 斜截面受剪承载力的设计计算 ● 保证斜截面受剪承载力的构造措施
图形。 材料抵抗弯矩图:按实际配置的受力钢筋计算的各个
正截面受弯承载力 Mu 所绘制的图形。
5.5 保证斜截面受弯承载力的构造措施
第5章 受弯构件的斜截面承载力
对承受均布荷载的单筋矩形截面简支梁:
Mu
As
fsd (h0
fsd As ) 2 fcdb
每根纵筋所承担的
M ui可近似按钢筋面积分配, M ui
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
公式的适用范围 ■ 截面的最小尺寸(上限值) 为防止斜压破坏,要求:
0Vd (0.51 103 ) fcu,k bh0
否则,应加大截面尺寸或提高混凝土强度等级。 ■ 构造配箍条件(下限值)
0Vd (0.5 103 ) 2 f tdbh0
而略有降低。 T形截面梁的受剪承载力高于矩形截面梁。
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
2. 斜截面受剪承载力计算公式
由于抗剪机理和影响因素的复杂性,目前各国规范的斜
截面受剪承载力计算公式均为半理论半经验的实用公式。
《公路桥规》中的斜截面受剪承载力计算公式以剪压破
坏为建立依据,假定梁的斜截面受剪承载力Vu由剪压区混凝 土的抗剪能力Vc、与斜裂缝相交的箍筋的抗剪能力Vsv 和与斜 裂缝相交的弯起钢筋的抗剪能力Vsb 三部分所组成。
斜截面受剪承载力计算步骤

第5章
6. 斜截面承载力计算步骤
⑴ 确定计算截面及其剪力设计值;
⑵ 验算截面尺寸是否足够; ⑶ 验算是否可以按构造配筋; ⑷ 当不能按构造配箍筋时,计算腹筋用量; ⑸ 验算箍筋间距、直径和最小配箍率是否
满足要求。
混凝土结构设计原理
第5章
截面设计:
一般:V
0.7
ft bh0
fyv
解:本例采用C30混凝土,取
as 35mm , h0 h as 550mm 35mm 515mm (1)复核截面的确定和剪力设计值计算
Asv s
h0
0.8 fy Asb sin
特殊:V
1.75
1
ftbh0
f yv
Asv s
h0
0.8 fy Asb
sin
已知 :b、 h0、 V 、 f c、 f t、 f yv、 f y、 、
求:
Asv s
、Asb
未知数:Asv、Asb、s
混凝土结构设计原理
第5章
例5-1 某宿舍钢筋混凝土矩形截面简支梁,设计使用年限为 50年,环境类别为一类,两端支承在砖墙上,净跨度ln 3660mm 截面尺寸b h 200mm 500mm 。该梁承受均布荷载,其中恒荷 载标准值gk 25kN/m(包括自重),荷载分项系数G 1.2,活 荷载qk 38kN/m ,荷载分项系数Q 1.4 ;混凝土强度等级为 C20;箍筋为HPB300级钢筋,按正截面受弯承载力计算; 已选配HRB335级钢筋为纵向受力钢筋。试根据斜截面受剪 承载力要求确定腹筋。 g q
99
kN
< Vcs
混凝土结构设计原理
第5章
故不需要第二排弯起钢筋。其配筋图如下图(b)所示
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混凝土简支梁斜截面抗剪强度1 影响混凝土抗剪强度Vc的主要参数的分析1.1 混凝土强度的影响试验表明,混凝土梁抗剪强度的增长与混凝土抗压强度fcu并非直线关系,而是按抛物线变化。
图1表示前苏联学者无箍筋梁抗剪强度与混凝土强度fcu的关系,梁混凝土立方体强度fcu 从20kg/cm2到1000kg/cm2变化,曲线为采用fct为参数的Vc 表达式,Vc=Kfctbh2/a=Kfctbh/m,m=a/h为剪跨比;直线表示采用fc为参数的波氏公式,Vc =0.15fcbh2/c=0.15fcbh/m。
从图可明显地看出,采用fct为混凝土强度影响参数与试验结果比较相符合,而如果采用fcu 或fc为参数时,混凝土强度低时,试验值高于计算值;中等强度时,两者相接近;高强度时,试验值大大低于计算值,这是很不安全的。
因此,苏联规范对波氏抗剪强度公式进行了修改,将混凝土强度从fc 改为fct。
CEB/FIP规范对无抗剪钢筋构件Vc计算式实际是采用fct 为参数。
西南交大抗剪试验[2,3]表明,把混凝土抗拉强度fct做为混凝土强度对Vc影响参变量是合适的。
考虑到铁路桥梁多使用高强度混凝土,而采用fct为参数,能更明确地反映问题的实质,并可避免单位变换时引起不同系数的因次带来的麻烦。
因此,选取fct为混凝土强度的影响参数。
图1 苏联无箍筋梁抗剪强度Vc 与混凝土fct的关系1.2 剪跨比m的影响大量试验表明,剪跨比m是影响混凝土抗剪强度的主要参数之一。
V c 随m的增大而减小,当m>3~4,Vc基本上就不受m的影响,其变化较小。
各规范在Vc表达式中,对m影响的处理上有所不同。
CEB/FIP,BS5400和《苏联СНИПⅡ-21-75》等规范,其Vc取较低值,考虑小剪距比时,乘一个2/m(m<2)的提高系数。
我国铁路、公路桥规直接取1/m,文中分析时选取1/m为参数。
1.3 预应力度的影响[2,3,5]PPC简支T梁试验结果证明,预应力大小对无箍、有箍PPC简支梁的混凝土抗剪强度Vc有提高作用。
这主要是因为预压应力推迟了斜裂缝的出现和发展,增加了梁混凝土剪压区的高度,从而提高了混凝土剪压区的抗剪能力。
试验分析时,曾采用了两个与预应力度λ相关的提高系数β或β′来表达预应力对Vc的提高作用。
式中:λ为预应力度;M为梁的消压弯矩;M为梁的使用荷载作用下的弯矩;Mu 为梁的破坏弯矩;考虑到同一配筋的试验梁,M不确定,而Mu较为固定,试验分析时用M0/Mu反映预应力度的影响较为确定。
图2示出16片3种不同预应力度PPC T型试验梁V sc /fctbh与β′的关系[5],它说明Vc随β′值的增大而提高,基本呈线性关系。
对铁路PPC梁而言,可令Mu=2M,采用β或β′为预应力提高系数都是合适的。
而统计分析结果表明,采用β作为预应力提高系数,有利于把混凝土矩形和T形梁的抗剪强度表达式统一起来。
因此,表达式选用β为提高系数的参数。
图2 PPC T梁V sc /fctbh与β′的关系1.4 纵向配筋率的影响(p=100μ)纵向钢筋对斜截面抗剪起梢栓作用外,还对斜裂缝向下翼缘扩展起约束作用,间接地影响混凝土的抗剪强度。
现行《铁路桥规》的抗剪强度公式对纵向配筋率的影响(p=100μ)采用(2+p)线性增加的关系式。
根据收集的试验资料,对剪跨比1.33~3.0的RC无箍筋矩形梁试验数据,按照V sc /fctbh与(k+p)关系进行回归分析,结果表明,41片m=3试验数据求得k=2.07,而m=1.33~3.0五组试验数据求得k平均值为2.6,k 值为2.0~2.6左右。
西南交大专题分析时仍取(2+p)为参数。
1.5 截面形状的影响试验表明[2],PPC无箍筋T梁抗剪强度比PPC矩形梁的要高,应考虑受压区翼缘的有利作用。
在对PPC T梁混凝土抗剪强度分析时,建议采用α=1+kh′f 2/bh系数考虑T梁压区翼缘对抗剪的有利作用。
k值根据PPC T梁与矩形梁资料分析求得k=1,因此分析时取α=1+hf 2/bh≯1.2。
2 影响箍筋抗剪能力V s主要参数的分析试验表明[3],梁斜裂缝出现前,箍筋的应力几乎为零,它对斜裂缝出现时的剪力没有多大影响。
当斜裂缝一旦出现,其应力便突然增大,箍筋才发挥作用,除承担部分剪力外,还对斜裂缝的宽度和扩展起约束作用。
大多试验表明,有箍筋梁剪力破坏时与主斜裂缝相交的箍筋大都可达到屈服强度f vst ,ρsvf vst和斜裂缝水平投影长度C是影响Vs的主要因素。
图3表示将西南交大完成的20片PPC T梁(m=3)试验结果,按预应力提高系数β′值分为4组,每组又包括4种不同配箍率(ρsv=0,0.34%,0.44%,0.59%)的试验梁剪力破坏值点绘于以V su /fct(2+p)bh为纵坐标,以ρsv f vst/fct(2+p)为横坐标的图上。
从图可见,预应力度不同的4条直线大致平行,V su 随ρsvf vst的增加而线性增大,随β′值增大直线向上提高,这充分说明ρsv f vst对Vs的提高作用,又说明预应力对Vc的提高作用。
为了使C值具有代表性,现根据收集到的200多片PPC,PC T梁和矩形梁剪力破坏时的实测值,按C SP /h=A+Bm线性公式回归统计,求得A=0.35,B=0.4。
(1)图3 PPC T梁V su /fct(2+p)bh与β′和ρsvf vst的关系图4表示与《铁路桥规》、文献[3]和文献[7]计算式比较情况,说明式(1)居中更为合理。
按上述分析,建议Vs计算式如下(2)图4 Cp /h与m的关系3 混凝土梁斜截面抗剪强度表达式的选定现收集到国内外结构混凝土简支梁抗剪强度可利用的试验数据有:(1) RC矩形梁526片;(2) PPC矩形梁133片;(3) PPC T梁212片。
其中有西南交大专题组后张PPC T形截面试验梁44片,并包括4片具有弯起预筋的PPC T梁4片;铁研院、北方交大的先张PPC T形试验梁19片以及重庆交通学院PPCT形试验梁50余片[9]。
PPC T梁试验数据既有较多的后张PPC梁,也有先张PPC梁,多数为直线预筋T梁,也含有弯起预筋的T梁,具有良好的代表性,为《铁路桥规》修改提供了较全面的试验依据。
根据上述对影响混凝土梁抗剪强度主要因素的分析,在对所做试验的结果及所收集到的国内外试验数据进行综合分析研究时,对混凝土简支梁斜截面抗剪强度推荐采用统一的表达式(3)(4)式中:C为待定系数,对大量试验数据统计回归求得,并根据验算可靠度指标来最后选定;m 为计算截面处的剪跨比,m=MV /Vmh或m=a/h,当m>3时,取m=3;m<1时,取m=1;p=100ρ,ρ为斜截面处受拉纵向主筋的配筋率,ρ=(Ap +Apb+As)/bh,当p>3时,取p=3;β 为考虑预应力影响的提高系数,β=1+M/M=1+λ≤2;α为考虑T形截面受压区翼缘有利作用系数,α=1+h2f /bh≯1.2;Vs为斜截面上箍筋承担的抗剪能力,采用式(2),则有(5)现采用推荐的表达式(4)和式(5),分别为RC矩形梁、PPC矩形梁和PPC T 梁3组试验数据,并按无箍筋梁、有箍筋梁、无箍+有箍梁综合等3种情况进行回归统计分析,求出相应的C 值。
同时求出V s c /v j c 的平均值c 、标准差σc 和变异系数c vc ,又按V j u =V c +V s ,求出V s u /V j u 的平均值u、标准差σu ,及变异系数c uc 。
对所有试验数据按剪跨比m>3取m=3限制条件进行回归统计,结果列于表1。
从表可知,C=0.42~0.44,3组梁C值基本相当。
如果以无箍+有箍梁综合等情况为准,混凝土梁混凝土抗剪强度回归统一表达式和具有95%保证率表达式为(6)(7)按照建议的回归公式及其统计参数,应用可靠性理论的分位值法对铁路RC和PC标准设计梁(RC梁Lp =8 m,12 m,16 m;PC梁Lp=16 m,20 m,24 m,32 m)抗剪强度可靠指标进行了校准[9],其危险截面的可靠指标β值,RC梁β=2.84~3.91,=3.47,PC梁β=3.25~3.59,=3.44。
计算结果表明,采用回归式可靠指标低于新《铁路桥规》目标可靠指标βmon =5.2的要求。
因此,建议采用具有95%保证率的Vc0.05公式,基本可以满足目标可靠指标的要求。
4 新《铁路桥规》混凝土简支梁抗剪强度建议式西南交大与铁研院、北方交大两专题组分别提出了斜截面抗剪强度建议式,表达式虽不同,而在选取影响抗剪强度的主要参数上基本一致。
两专题组通过讨论研究认为,抗剪强度计算表达式应是对混凝土梁均能适用的统一表达式为好,参数形式宜简单些。
以西南交大所推荐的统一表达式为基础,Vc表达式中宜适当降低配筋率p的影响,对通常配筋情况建议将(2+p)改为(2+0.7p),西南交大专题组根据试验结果以及收集的国内外数据,重新回归分析,并为新《铁路桥规》抗剪强度计算提出建议公式。
建议的混凝土梁斜截面抗剪强度表达式可写为(8)Vs仍采用式(2),则(9)现按照建议式(8)和式(9),根据试验结果和所收集的国内外数据重新分析计算。
仍分别对RC矩形梁、PPC矩形梁和PPC T梁的试验数据,按无箍筋、有箍筋和无箍+有箍综合等种情况进行回归统计,求得相应C值,同时求出V sc /V jc平均值c,标准差σc和变异系数cvc及V su/V ju的平均值u ,标准差σu和变异系数cvu,所得结果也列于表1。
从表1可知,C值回归计算求得结果为C=0.50~0.55,3组梁C值也基本相同,可取C=0.5。
对全部试验数据,综合回归统计c=1.042,σc =0.247,cvc=0.235。
则斜截面抗剪强度建议公式回归表达式和具有95%保证率的公式可写为(10)(11)现将全部试验数据点绘在以剪跨比m为x轴,V sc /(2+0.7p)fctbhβα为y轴的坐标图上(图5),同时将回归式(式10)和具有95%保证率表达式(式11)也绘于图上。
从图可知,具有95%保证率表达式基本接近该试验点下限值。
图5 试验梁V sc /(2+0.7p)fctbhβα与m的关系根据可靠指标的要求,Vc应采用具有95%保证率的公式,新《铁路桥规》混凝土简支梁抗剪强度建议计算公式则为下式(12)上述建议公式已被正式纳入新的《铁路桥涵规范(上册)》送审稿中。
5 结论表达式统一(1) 通过回归计算与分析,并考虑要把混凝土矩形、T形梁Vc选用(4)与式(8)为表达式。
起来,推荐Vc(2) 文中通过200多片PPC和PC T梁资料分析,提出了箍筋抗剪能力Vs 的计算公式(式2)。
(3) 通过对专题组试验结果和国内外871片梁试验数据回归统计和综合分析,提出了混凝土简支梁抗剪强度统一表达式(式(9)),为《铁路桥规》修改提供了依据。
