工程弹塑性力学题库及答案
弹塑性力学试题(06研)
弹塑性力学试题(土建院06研)考试时间：2小时考试形式：笔试，开卷一、是非题（下列各题，你认为正确的在括号内打“√”，错误的打“×”。
每小题3 分，共27分）1．外力（面力、体力）均以沿坐标轴正方向为正，面力的正负号与所处面的正负无关。
（ ）2．若物体内一点的位移u 、v 、w 均为零，则该点的正应变x ε＝y ε＝z ε＝0。
（ ）3．满足平衡方程和全部应力边界条件的应力必为正确解（本问题的边界条件均为应力边界条件）。
（ ）4．弹性体中任一点的柱坐标应力分量之和z r σσσθ++与三个主应力分量之和321σσσ++一定相等。
（ ）5．塑性理论的主要特点是应力应变关系不同于弹性理论，对于给定的应变，不能确定应力。
（ ）6． 薄壳与薄板一样，是以物体内一点的位移、形变、应力为研究对象的。
（ ）7． 对于等截面实心杆扭转问题，普朗都（Prandtl ）应力函数ϕ的边界值s ϕ＝0。
（ ）8． 任何边界上都可应用圣维南（St. Venant ）原理，条件是静力等效。
（ ）9．Ritz 法和Galerkin 法解薄板小挠度弯曲问题时，都设∑=mm m w C w ，但Ritz法中m w 必须满足全部边界条件，Galerkin 法中m w 只需满足几何边界条件。
（ ）二﹑填空题（每小题3分，共12分）1．z y x εεε++称为（ ），z y x σσσ++称为（ ），)21/(μ-E 称为（ ）。
2．球坐标系（ϕθ,,r ）中（ϕϕθϕθcos ,sin sin ,sin cos r z r y r x ===）的拉密系数1H 、2H 、3H 分别为（ ）、（ ）、（ ）。
3．矩形薄板小挠度问题Navier 解法与Levy 解法的特点分别是（ ）、（ ）。
4．Mises 屈服准则可用方程表示为（ ）。
61分）(L>>h)，厚度为1，右端顶部受与水平方向成α角的集试检验函数332Dy Cxy Bxy Ay +++=ϕ能否作为应力函数？若可以作为应力函数，求出应力分量xy y x τσσ , ,（不计体力） (15分)2. 内半径为a 、外半径为b 的圆环板，板面无分布荷载作用，板边作用有均布弯矩和横向力，作用方向及板的支承如图所示，试求圆环板的挠度和内力。
弹塑性理论考试题及答案
弹塑性理论考试题及答案一、单项选择题（每题2分，共10分）1. 弹塑性理论中，材料的屈服准则通常用以下哪个参数表示？A. 应力B. 应变C. 弹性模量D. 屈服应力答案：D2. 弹塑性材料在循环加载下，其行为主要受哪个参数的影响？A. 最大应力B. 最大应变C. 应力幅值D. 应变幅值答案：C3. 根据弹塑性理论，材料的硬化指数n通常用来描述什么？A. 材料的弹性B. 材料的塑性C. 材料的断裂特性D. 材料的疲劳特性答案：B4. 在弹塑性理论中，哪个参数用来描述材料在塑性变形后能否恢复原状？A. 弹性模量B. 屈服应力C. 塑性应变D. 弹性应变答案：D5. 弹塑性材料在受到拉伸应力作用时，其应力-应变曲线通常呈现哪种形状？A. 线性B. 非线性C. 抛物线D. 指数曲线答案：B二、多项选择题（每题3分，共15分）6. 弹塑性理论中，材料的屈服准则可以由以下哪些因素确定？A. 应力状态B. 应变状态C. 温度D. 材料的微观结构答案：A|B|C|D7. 弹塑性材料在循环加载下，其疲劳寿命主要受哪些因素的影响？A. 应力幅值B. 材料的屈服应力C. 循环加载频率D. 材料的微观缺陷答案：A|B|C|D8. 在弹塑性理论中，材料的硬化行为可以通过以下哪些方式来描述？A. 硬化指数B. 硬化模量C. 应力-应变曲线D. 屈服应力答案：A|B|C9. 弹塑性材料在受到压缩应力作用时，其应力-应变曲线通常呈现以下哪些特点？A. 初始阶段为弹性B. 达到屈服点后进入塑性变形C. 塑性变形后材料体积不变D. 卸载后材料能够完全恢复原状答案：A|B|C10. 弹塑性理论中，材料的断裂特性可以通过以下哪些参数来描述？A. 断裂韧性B. 应力集中系数C. 材料的硬度D. 材料的塑性应变答案：A|B|C|D三、简答题（每题5分，共20分）11. 简述弹塑性理论中材料的屈服现象。
答：在弹塑性理论中，材料的屈服现象是指材料在受到一定的应力作用后，从弹性变形转变为塑性变形的过程。
弹塑性力学复习-1
二、计算题
1.已知一点的应力
500 σij = -100
-100
-100 400
0
-100
0
MPa
400
计算（1）主应力 （2）主方向 （3）最大切应力 （3）正八面体上的正应力 （4）正八面体上的切应力 （5）正八面体上的全应力
2.已知一点的应变
u (x1 x2 )2 e1 (x2 x3 )2 e2 x1x2e3
解(1): 管的两端是自由的应力状态
1 6
[(1
2
)2
(
2
3 )2
(
3
1)2
]
2 s
(Mises)
1 3 2 s (Tresca)
1
pR t
,
2
z
0, 3
r
0, zr
r
z
0
1 6
[(
pR t
)2
(
pR t
一、概念题
1.若物体内一点的位移均为零，则该点的应变也 为零。
2.在x为常数直线上，u=0，则沿该线必有 x 0 。 34..在满足y为平常衡数微直分线方上程，又u满=0足，力则边沿界该条线件必的有应 x力 0是。
否是实际应力。 5.应变状态 x k(x2 y2 ), y ky2, xy 2kxy 不可能存在。 6.若 是平面调和函数，1 (x2 y2 ) 是否可以作为
应力函数。
一、概念题
7.平面应力与平面应变主要的异同是什么。 8.切应变的含义是什么。 9.变形协调方程的物理意义是什么。 10.应力主轴与应变主轴在什么情况下重合。 11.什么是横向各向同性材料。 12.受内压压圆环（筒）的应力分析 。 13.逆解法、半逆解法的理论依据是什么？为什么？ 14.为什么最小势能原理等价于平衡方程与应力边 界条件？ 15.里兹法与伽辽金法的近似性表现在哪里？
工程弹塑性力学课后答案
工程弹塑性力学课后答案【篇一：弹塑性力学思考题答案】一点的应力状态？答：通过一点p 的各个面上应力状况的集合⒉一点应变状态？答：[受力物体内某点处所取无限多方向上的线应变与剪应变(任意两相互垂直方向所夹直角的改变量)的总和，就表示了该点的应变状态。
]代表一点 p 的邻域内线段与线段间夹角的改变⒊应力张量？应力张量的不变量？应力球张量？体积应力？平均应力？应力偏张量？偏应力第二不变量j2的物理意义？单向应力状态、纯剪应力状态的应力张量？给出应力分分量，计算第一，第二不变量。
答：应力张量：代表一点应力状态的应力分量，当坐标变化时按一定的规律变化，其变换关系符合??x?xy?xz???????????yxyyz???zx?zy?z???。
其中：?=?，?=?，?=?。
xzzxxyyxyzzy应力张量的不变量：对于一个确定的应力状态,只有一组(三个)主应力数值,即j1,j2,j3是不变量,不随着坐标轴的变换而发生变化。
所以j1,j2,j3分别被称为应力张量的第一、第二、第三不变量。
应力张量可分解为两个分量0???x-?m?xy?xz???m0??+???ij??0?0????mymyz?，等式右端第一个张量称为应力球张量，第二个张量称为应???yx?0?m??zy?z??m??0????zx?力偏张量。
应力球张量：应力球张量，表示球应力状态（静水应力状态），只产生体积变形，不产生形状变形，任何切面上的切应力都为零，各方向都是主方向。
应力偏张量：应力偏张量，引起形状变形，不产生体积变形，切应力分量、主切应力、最大正应力11平均应力：?m?(?x??y??z)?(?1??2??3)，?m为不变量,与坐标无关。
33偏应力第二不变量j2的物理意义：形状变形比能。
单向应力状态：两个主应力为零的应力状态。
纯剪应力状态的应力张量:给出应力分分量，计算第一，第二不变量。
（带公式）⒋应变张量？应变张量的不变量？应变球张量？体积应变？平均应变？应变偏张量？应变张量：几何方程给出的应变通常称为工程应变，这些应变分量的整体，构成一个二阶的对称张版权所有，翻版必究量，称为应变张量，记为：即。
弹塑性力学习题集_很全有答案_
ε x = a 0 + a1 ( x 2 + y 2 ) + x 4 + y 4 , ε y = b0 + b1 ( x 2 + y 2 ) + x 4 + y 4 , γ xy = c 0 + c1 xy ( x 2 + y 2 + c 2 ), ε z = γ zx = γ yz = 0.
试求式中各系数之间应满足的关系式。 2—38* 试求对应于零应变状态（ ε ij = 0 ）的位移分量。
(2) J 3 = I 3 + (4) J 2 = (6)
1 2 3 I1 I 2 + I1 ; 3 27
1 S ij S ij ; 2
∂J 2 = S ij . ∂σ ij
1 S ik S km S mi 。 3 2—22* 试证在坐标变换时， I 1 为一个不变量。要求：(a) 以普通展开式证明； (b) 用 张量计算证明。 5 3 8 2—23 已知下列应力状态： σ ij = 3 0 3 MPa ，试求八面体单元的正应力 σ 8 与剪 8 3 11
题 2—41 图
题 2—42 图
第三章 弹性变形·塑性变形·本构方程
试证明在弹性变形时，关于一点的应力状态，下式成立。 1 (1) γ 8 = τ 8 ; (2) σ = kε （设ν = 0.5 ） G 3—2* 试以等值拉压应力状态与纯剪切应力状态的关系， 由应变能公式证明 G、 E、 ν之 间的关系为： 1 G= 2(1 + ν ) 1 1 3—3* 证明：如泊松比ν = ，则 G = E ， λ → ∞ ， k → ∞ , e = 0 ，并说明此时上述 2 3 各弹性常数的物理意义。 3—4* 如设材料屈服的原因是形状改变比能（畸形能）达到某一极值时发生，试根据 单向拉伸应力状态和纯剪切应力状态确定屈服极限 σ s 与 τ s 的关系。 3—5 试依据物体单向拉伸侧向不会膨胀，三向受拉体积不会缩小的体积应变规律来 1 证明泊松比ν 的上下限为： 0 < ν < 。 2 2 3—6* 试由物体三向等值压缩的应力状态来推证：K = λ + G 的关系， 并验证是否与 3 E K= 符合。 3(1 − 2v) 3—7 已知钢材弹性常数 E1 = 210Gpa，v1 = 0.3， 橡皮的弹性常数 E 2 =5MPa，v 2 = 0.47， 试比较它们的体积弹性常数（设 K1 为钢材，K2 为橡皮的体积弹性模量） 。 3—8 有一处于二向拉伸应力状态下的微分体（ σ 1 ≠ 0, σ 2 ≠ 0, σ 3 = 0 ） ，其主应变
弹塑性力学习题答案
第二章 习题解答2-1解：已知 0,0,===-==y x xy y xf f q τσσ1）⎪⎪⎩⎪⎪⎨⎧+∂∂+∂∂+∂∂+∂∂xy y yxx x y yx τστσ23()()⎩⎨⎧++s xy y s yx x l m m l σστστσ 有：lq t x -=代入（*4理、几何方程得：E x u x ==∂∂ε11E y v y ==∂∂ε0==∂∂+∂∂xy yux v γ ()()⇒=+∴0dyy df dx x dg 类似于教材题2-3，可求出 ()()wx v x g wy u y f +=-=00,001;1v wx qy Ev u wy qx Eu ++--=+---=∴υυ从v u ,表达式可见，位移分量是坐标的单值函数，满足位移单值条件。
综合1）～4），。
q xy y x 为问题的正确解答0,=-==τσσ2-2x =σxy τ注意：y x ，代入均满足。
2）验证相容方程：0)(2=+∇y x σσ 亦满足。
3）验证应力边界条件： i) 主要边界：()0,2=±=h y yx yτσ满足ii) 次要边界：()()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧===⎰⎰⎰-=-=-=222222320)1(0h h lx xy h h l x x h h l x x Pdy ydy dy τσσ （1）、（2）满足，（3）式左=⎰-===⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-223332212*41*618218hh P h I P h h I P dy y h I P 右 结论：所列xy y x τσσ,,满足平衡方程、相容方程；在主要边界上严格满足应力边界条件，次要边界近似满足应力边界条件，又为单连体，故在圣维南原理的前提下为问题的正确解。
2-3、证明：1）由,,yVf xV fy x∂∂-=∂∂-=则平衡微分方程为： ()()⎪⎪⎩⎪⎪⎨⎧=∂τ∂+∂-σ∂=∂τ∂+∂-σ∂⇒⎪⎪⎩⎪⎪⎨⎧=∂∂-∂τ∂+∂σ∂=∂∂-∂τ∂+∂σ∂0x y V 0yx V 0y V x y 0x V y x yx y xyx yx y xy x （*） 类似于题2-10的推证过程，（*）式的通解为：y x x V yV 2xy 22y 22x ∂∂ϕ∂-=τ∂ϕ∂=-σ∂ϕ∂=-σ;;即： yx V xV y2xy 22y 22x ∂∂ϕ∂-=τ+∂ϕ∂=σ+∂ϕ∂=σ;;2） 对于平面应力问题，相容方程为：()()⎪⎪⎭⎫⎝⎛∂∂+∂∂+-=+∇y f x f y x y xυσσ12即：2222 2-4、x, y n l σσ2==2l 应力主向成∴l σn3-3、解： 1由x=0得： 2由 得： Fx Ex Cx Bx Ax y ++++=∴注：公式中已略去ϕ中与应力分量无关的一次项和常数项。
弹塑性力学课程作业 参考答案
弹塑性力学课程作业1 参考答案一．问答题1. 答：请参见教材第一章。
2. 答：弹塑性力学的研究对象比材料力学的研究对象更为广泛，是几何尺寸和形态都不受任何 限制的物体。
导致这一结果的主要原因是两者研究问题的基本方法的不同。
3. 答：弹塑性力学与材料力学、结构力学是否同属固体力学的范畴，它们各自求解的主要问题都是变形问题，求解主要问题的基本思路也是相同的。
这一基本思路的主线是：（1）静 力平衡的受力分析；（2）几何变形协调条件的分析；（3）受力与变形间的物理关系分析； 4. 答：“假设固体材料是连续介质”是固体力学的一条最基本假设，提出这一基本假设得意义是为利用数学中的单值连续函数描述力学量（应力、应变和位移）提供理论依据。
5. 答：请参见本章教材。
6. 答：略（参见本章教材）7. 答：因为物体内一点某微截面上的正应力分量 σ 和剪应力分量τ 同材料的强度分析 问题直接相关，该点微截面上的全应力则不然。
8. 答：参照坐标系围绕一点截取单元体表明一点的应力状态，对单元体的几何形状并不做 特定的限制。
根据单元体所受力系的平衡的原理研究一点的应力状态。
研究它的目的是： 首先是了解一点的应力状态任意斜截面上的应力，进一步了解该点的主应力、主方向、 最大（最小）剪应力及其作用截面的方位，最终目的是为了分析解决材料的强度问题。
9．答：略（请参见教材和本章重难点剖析。
） 10. 答：略（请参见教材和本章重难点剖析。
）11. 答：略（请参见教材和本章重难点剖析。
） 这样分解的力学意义是更有利于研究材料的塑性变形行为。
12. 答：略（请参见教材和本章重难点剖析。
）纳唯叶 (Navier) 平衡微分方程的力学意义是：只有满足该方程的应力解和体力才是客观上可能存在的。
13. 答：弹塑性力学关于应力分量和体力分量、面力分量的符号规则是不一样的。
它们的区别请参见教材。
14、答：弹塑性力学的应力解在物体内部应满足平衡微分方程和相容方程（关于相容方程详见第3、5、6章），在物体的边界上应满足应力边界条件。
(完整版)弹塑性力学习题题库加答案
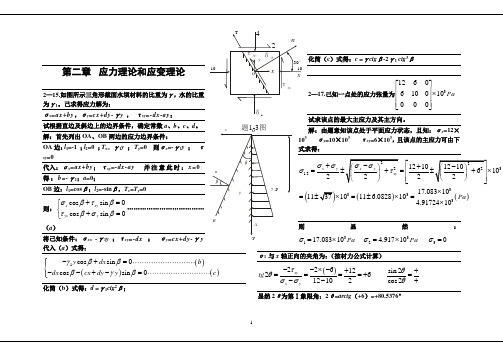
第二章 应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ，水的比重为γ1。
己求得应力解为：σx =ax+by ，σy =cx+dy-γy ， τxy =-dx-ay ；试根据直边及斜边上的边界条件，确定常数a 、b 、c 、d 。
解：首先列出OA 、OB 两边的应力边界条件：OA 边：l 1=-1 ；l 2=0 ；T x = γ1y ； T y =0 则σx =-γ1y ； τxy =0代入：σx =ax+by ；τxy =-dx-ay 并注意此时：x =0 得：b=-γ1；a =0；OB 边：l 1=cos β；l 2=-sin β，T x =T y =0则：cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………（a ）将己知条件：σx= -γ1y ；τxy =-dx ； σy =cx+dy-γy 代入（a ）式得：()()()1cos sin 0cos sin 0y dx b dx cx dy y c γβββγβ-+=⎧⎪⎨--+-=⎪⎩化简（b ）式得：d =γ1ctg 2β；化简（c ）式得：c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。
解：由题意知该点处于平面应力状态，且知：σx =12×103 σy =10×103 τxy =6×103，且该点的主应力可由下式求得：(()()31.233331210102217.0831******* 6.082810 4.9172410x yPa σσσ⎡++⎢=±=⨯⎢⎣⨯=⨯=±⨯=⨯则显然：3312317.08310 4.917100Pa Pa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为：（按材力公式计算）()22612sin 22612102cos 2xyx ytg τθθσσθ--⨯-++====+=--+显然2θ为第Ⅰ象限角：2θ=arctg （+6）=+80.5376°题图1-3则：θ=+40.268840°16＇ 或（-139°44＇）2—19.己知应力分量为：σx =σy =σz =τxy =0，τzy =a ，τzx =b ，试计算出主应力σ1、σ2、σ3并求出σ2的主方向。
工程弹塑性力学题库及答案
(2)如将该曲线表示成
解：（1）由 在
处连续，有
形式，试给出 的表达式。
（a）
由在
处连续，有
（a）、（b）两式相除，有
由（a）式，有
（2）取
形式时，
当
：
即
当
：应力相等，有
解出得，
（代入 值）
（b） （c） （d）
（代入 值） 5.6已知简单拉伸时的应力-应变曲线
如图5-1所示，并表示如下：
问当采用刚塑性模型是，应力-应变曲线应如何表 示？
解：1） OD 边：
GD 边：
沿
线，
，
2）
沿 OB 线，
，
8.7 Mises 线性等强化材料，在平面应变（ 试导出用表示的强化规律和本构关系。
解：当 时，在弹性阶段有
）和泊松比 条件下，
得
平均应力 因此在弹性阶段有
，进入塑性后有
对平均应变
刚进入塑性时
。由上式导出
。因此进入塑性
后还满足
（2）当 = 时，继续加载，使 解：1）开始屈服时
，求此时的 、 、 。 ，代入 Mises 屈服准则
得
；
2）屈服后对应的塑性应变增量为
由 及屈服条件的微分形式
， 式子得到答案结果。
7.9 在如下两种情况下，试求塑性应变增量的比。
（1）单向拉伸应力状态，
；
，联列可得 ，代入
（2）纯剪力状态，
。
解：（1）单向拉伸应力状态
在
中：
沿
线，
中： ，
中：
,
，
，
, 情况二见图（1），与①一样
所以
8.6 已知具有尖角为 的楔体，在外力 P 的作用下，插入具有相同角度的 V 形缺口 内，试分别按如下两中情况画出滑移线场并求出两种情况的极限荷载。 1）、楔体与 V 形缺口之间完全光滑；2）、楔体与 V 形缺口接触处因摩擦作用其剪应 力为 k。
弹塑性力学部分习题及答案
厚壁筒应力问题
要点一
总结词
厚壁筒应力问题主要考察了弹塑性力学中厚壁筒结构的应 力分析和变形计算。
要点二
详细描述
厚壁筒应力问题涉及到厚壁筒结构在受到内压、外压或其 他复杂载荷作用时的应力分布和变形情况。在解题过程中 ，需要运用弹塑性力学的相关理论，如应力分析、应变分 析等，来求解结构的应力分布和变形情况。同时，还需要 考虑厚壁筒结构的特殊性，如不同材料的组合、多层结构 等，对结构应力和变形的影响。
02
弹塑性力学基础知识
应力和应变
基本概念
详细描述：应力和应变是弹塑性力学中的基本概念。应力表示物体内部相邻部分之间的相互作用力，而应变则表示物体在应 力作用下的变形程度。
屈服条件与应力-应变关系
屈服准则与流动法则
详细描述：屈服条件决定了材料在应力作用下的屈服点，是判断材料是否进入塑性状态的重要依据。 应力-应变关系则描述了材料在受力过程中应力与应变的变化规律。
弹塑性力学特点
弹塑性力学具有广泛的应用背景，涉及到众多工程领域，如结构工程、机械工 程、航空航天等。它既适用于脆性材料，也适用于塑性材料，并考虑了材料的 非线性特性。
弹塑性力学的基本假设
连续性假设
小变形假设
假设固体内部是连续的，没有空隙或 裂纹。
假设物体在外力作用下发生的变形是 微小的，不会影响物体内部应力分布。
弹塑性力学部分习题及答 案
• 弹塑性力学概述 • 弹塑性力学基础知识 • 弹塑性力学典型习题解析 • 弹塑性力学部分习题的定义与特点
弹塑性力学的定义
弹塑性力学是一门研究固体在受到外力作用时，其内部应力、应变和位移之间 关系的学科。它主要关注材料在受力过程中发生的弹性变形和塑性变形。
塑性力学考试题及答案
塑性力学考试题及答案一、单项选择题（每题2分，共10题）1. 塑性力学中，材料进入塑性变形阶段的条件是应力达到（）。
A. 屈服强度B. 抗拉强度C. 弹性极限D. 断裂强度答案：A2. 塑性变形与弹性变形的主要区别在于（）。
A. 变形量的大小B. 是否可逆C. 材料硬度的变化D. 变形速率的快慢答案：B3. 根据塑性力学理论，下列哪种材料不属于塑性材料（）。
A. 低碳钢B. 铝合金C. 玻璃D. 橡胶答案：C4. 塑性力学中，材料的屈服点是指（）。
A. 材料开始发生塑性变形的应力值B. 材料发生断裂的应力值C. 材料弹性极限的应力值D. 材料达到最大强度的应力值答案：A5. 在塑性力学中，安全系数的计算公式为（）。
A. 安全系数 = 材料强度 / 工作应力B. 安全系数 = 工作应力 / 材料强度C. 安全系数 = 材料强度 / 材料屈服强度D. 安全系数 = 材料屈服强度 / 工作应力答案：A6. 塑性力学中，材料的硬化指数n的物理意义是（）。
A. 材料的塑性变形能力B. 材料的弹性模量C. 材料的屈服强度D. 材料的硬化程度答案：D7. 塑性力学中，真应力-真应变曲线的斜率代表的是（）。
A. 弹性模量B. 屈服强度C. 强度极限D. 硬化模量答案：D8. 塑性力学中，材料的塑性变形通常发生在（）。
A. 弹性阶段B. 屈服阶段C. 强化阶段D. 断裂阶段答案：C9. 塑性力学中，材料的塑性变形与温度的关系是（）。
A. 温度升高，塑性变形能力增强B. 温度升高，塑性变形能力减弱C. 温度降低，塑性变形能力增强D. 温度对塑性变形能力无影响答案：A10. 塑性力学中，材料的塑性变形与应变率的关系是（）。
A. 应变率增加，塑性变形能力增强B. 应变率增加，塑性变形能力减弱C. 应变率对塑性变形能力无影响D. 应变率降低，塑性变形能力增强答案：A二、简答题（每题5分，共4题）1. 简述塑性力学与弹性力学的主要区别。
(完整版)弹塑性力学习题题库加答案
第二章 应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ，水的比重为γ1。
己求得应力解为：σx =ax+by ，σy =cx+dy-γy ， τxy =-dx-ay ；试根据直边及斜边上的边界条件，确定常数a 、b 、c 、d 。
解：首先列出OA 、OB 两边的应力边界条件：OA 边：l 1=-1 ；l 2=0 ；T x = γ1y ； T y =0 则σx =-γ1y ； τxy =0代入：σx =ax+by ；τxy =-dx-ay 并注意此时：x =0 得：b=-γ1；a =0；OB 边：l 1=cos β；l 2=-sin β，T x =T y =0则：cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………（a ）将己知条件：σx= -γ1y ；τxy =-dx ； σy =cx+dy-γy 代入（a ）式得：()()()1cos sin 0cos sin 0y dx b dx cx dy y c γβββγβ-+=⎧⎪⎨--+-=⎪⎩化简（b ）式得：d =γ1ctg 2β；化简（c ）式得：c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。
解：由题意知该点处于平面应力状态，且知：σx =12×103 σy =10×103 τxy =6×103，且该点的主应力可由下式求得：(()()31.233331210102217.0831******* 6.082810 4.9172410x yPa σσσ⎡++⎢=±=⨯⎢⎣⨯=⨯=±⨯=⨯则显然：3312317.08310 4.917100Pa Pa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为：（按材力公式计算）()22612sin 22612102cos 2xyx ytg τθθσσθ--⨯-++====+=--+显然2θ为第Ⅰ象限角：2θ=arctg （+6）=+80.5376°题图1-3则：θ=+40.268840°16＇ 或（-139°44＇）2—19.己知应力分量为：σx =σy =σz =τxy =0，τzy =a ，τzx =b ，试计算出主应力σ1、σ2、σ3并求出σ2的主方向。
弹塑性力学习题集_很全有答案_
σ y = cx + dy − γy , τ xy = − dx − ay ，其它应力分量为零。试根据
直边及斜边上的边界条件，确定常数 a、b、c、d。 2—16* 已知矩形截面高为 h， 宽为 b 的梁受弯曲时的正 My 12 M 应力 σ z = = y， 试求当非纯弯时横截面上的剪应力公 J bh 3 式。 （利用弹塑性力学平衡微分方程）
题 2—15 图
12 6 0 2—17 已知一点处的应力张量为： σ ij = 6 10 0 MPa ，试求该点的最大主应力及 0 0 0 其主方向。 2—18* 在物体中某一点 σ x = σ y = σ z = τ xy = 0 ，试以 τ yz 和 τ zx 表示主应力。
3—1
为 ε 1 = 1.7 × 10 −4 ， ε 2 = 0.4 × 10 −4 。已知ν = 0.3，试求主应变 ε 3 。
3—9 如题 4—9 图示尺寸为 1×1×1cm 的铝方块，无间隙地嵌入——有槽的钢块中。 设钢块不变形，试求：在压力 P = 6KN 的作用下铝块内一点应力状态的三个主应力及主应 变，铝的弹性常数 E=70Gpa，ν = 0.33。 3—10* 直径 D = 40mm 的铝圆柱体， 无间隙地放入厚度为 δ = 2mm 的钢套中， 圆柱受
v = b0 + b1 x + b2 y + b3 z w = c 0 + c1 x + c 2 y + c3 z
式中 a 0 L , a1 L , a 2 L 为常数，试证各点的应变分量为常数。 2—29 设已知下列位移，试求指定点的应变状态。
(1) u = (3x 2 + 20) × 10 −2 , v = (4 yx) × 10 −2 ，在（0，2）点处。 (2) u = (6 x 2 + 15) × 10 −2 , v = (8 zy ) × 10 −2 , w = (3z 2 − 2 xy) × 10 −2 ，在（1，3，4）点处。 2—30 试证在平面问题中下式成立： εx + εy =ε′ x + ε′ y
(完整版)弹塑性力学习题题库加答案.docx
第二章 应力理论和应变理论2— 15.如 所示三角形截面水 材料的比重 γ，水的比重 γ 1。
己求得 力解 ：σ x = ax+by ， σy =cx+dy- γy ， τxy =-dx-ay ；根据直 及斜 上的 界条件，确定常数 a 、b 、c 、 d 。
解：首先列出OA 、 OB 两 的 力 界条件：OA ：l 1=-1 ；l 2=0 ；T x= γ1 y ； T y =0σx =-γ1y ； τxy =0代入： σx =ax+by ； τxy =-dx-ay 并 注 意 此 ： x =0得 ： b=- γ1； a=0；OB ： l 1=cos β ； l 2=-sin β， T x =T y =0：x cosxy sin0 yx cosy sin⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（ a ）将己知条件： σ x=1xy=-dxyγ y-γ y ； τ； σ =cx+dy-代入（ a ）式得：1 y cos dx sin0L L L L L L L L L bdx coscxdyy sin L L L L L L L L L化 （ b ）式得： d = γ12β；ctgT4n2τ 30° δ 30°30°化 （ c ）式得： c =γctg β -2γ 13y10x10Ox12 6τxy103 Pa2— 17.己知一点 的 力 量6 10 00 0δ y求 点的最大主 力及其主方向。
x题1-3 图解：由 意知 点 于平面 力状 ，且知：σx =12×O103σ y =10× 103 τ xy =6× 103，且 点的主 力可由下式求得：β212 101221.2xyxy21023n 22xy22610βγ 1y113710311 6.0828 10317.083 10 3 Paγ34.91724 10BA然：y117.083 10 3Pa2 4.917 10 3Pa30σ 1 与 x 正向的 角 ： （按材力公式 算）c2 xy2 6 12 sin 2tg 2121026xycos2然 2θ 第Ⅰ象限角： 2θ=arctg （ +6） =+80.5376 °则：θ=+40.2688 B 40° 16＇或（-139° 44＇）2— 19.己知应力分量为：σx=σy=σz=τxy=0，τzy=a，τzx=b，试计算出主应力σ1、σ2、σ3 并求出σ2 的主方向。
弹塑性力学部分习题及答案
解
根据梁的弯曲变形公式，y = Fx/L(L - x)，其中y为挠度，F 为力，L为梁的长度。代入题目给定的数据，得y = (frac{300 times (4 - x)}{8})。当x = 2时，y = (frac{300 times (4 - 2)}{8}) = 75mm。
习题三答案及解析
解析
和变形情况。
04
弹塑性力学弹塑性力学的基本假设。
答案
弹塑性力学的基本假设包括连续性假设、均匀性假设、各向同性假设和非线性假设。连 续性假设认为物质是连续的，没有空隙；均匀性假设认为物质的性质在各个位置都是相 同的；各向同性假设认为物质的性质在不同方向上都是相同的；非线性假设认为弹塑性
习题二答案及解析
01 02 03 04
解析
选择题主要考察基本概念的理解，如能量守恒定律、牛顿第二定律等 。
填空题涉及简单的力学计算，如力的合成与分解、牛顿第二定律的应 用等。
计算题要求应用能量守恒定律和牛顿第二定律进行计算，需要掌握基 本的力学原理和公式。
习题三答案及解析
01
答案
02
选择题
03
1. A
2. 解
根据牛顿第二定律，F = ma，其中F为力，m为质量，a 为加速度。代入题目给定的数据，得a = (frac{400}{5}) = 80m/s(}^{2})。再根据运动学公式s = ut + (frac{1}{2})at(}^{2})，得s = 10 × 2 + (frac{1}{2} times 80 times (2)^2) = 108m。
04
计算题要求应用胡克定律和动量守恒定律进行计算，需要掌握基本的 力学原理和公式。
习题二答案及解析
弹塑性力学综合测试答案
综合测试试题一二、填空题第1个为6第2个为平衡微分方程三、选择题 1 A 2 B 3 B 4 C四1、；；；2、五、计算题1、解：已知该点为平面应变状态，且知：k为已知常量。
则将应变分量函数代入相容方程得：2k+0=2k 成立，故知该应变状态可能存在。
2、解：球应力张量作用下，单元体产生体变。
体变仅为弹性变形。
偏应力张量作用下单元体只产生畸变。
塑性变形只有在畸变时才可能出现。
关于岩土材料，上述观点不成立。
3、解：，满足，是应力函数。
相应的应力分量为：，，；①应力边界条件：在x = h处，②将式①代入②得：，故知：，，；③由本构方程和几何方程得：④积分得：⑤⑥在x=0处u=0，则由式⑤得，f1(y)= 0；在y=0处v=0，则由式⑥得，f2(x)=0；因此，位移解为：4、解：据题意知一点应力状态为平面应力状态，如图示，且知，则，且= 0。
代入Mises屈服条件得：即：解得：200 MPa；轴力：P== 2×50×10－3×3×10－3×200×106=188.495kN扭矩：M== 2×502×10－6×3×10－3×200×106=9.425 kN·m综合测试试题二二、填空题第1个为9 5 2第2个为Tresca 屈服条件Mises屈服条件三、选择题 1 C 2 C 3 A 4 D四1、2、五、计算题1、解：应力解应再满足平衡微分方程即为弹性力学平面应力问题可能的应力解，代入平衡微分方程得：则知，只要满足条件a＝－f，e＝－d，b和c可取任意常数。
若给出一个具体的弹性力学平面应力问题，则再满足该问题的应力边界条件，该组应力分量函数即为一个具体的弹性力学平面应力问题的应力解。
2、解：由式（2—19）知，各应力不变量为、，代入式（2—18）得：也即（1）因式分解得：（2）则求得三个主应力分别为。
弹塑性力学试卷
二、填空题：（每空2分，共8分）1、在表征确定一点应力状态时，只需该点应力状态的-------个独立的应力分量，它们分别是-------。
（参照oxyz直角坐标系）。
2、在弹塑性力学应力理论中，联系应力分量与体力分量间关系的表达式叫---------方程，它的缩写式为-------。
三、选择题（每小题有四个答案，请选择一个正确的结果。
每小题4分，共16分。
）1、试根据由脆性材料制成的封闭圆柱形薄壁容器，受均匀内压作用，当压力过大时，容器出现破裂。
裂纹展布的方向是：_________。
A、沿圆柱纵向（轴向）B、沿圆柱横向（环向）C、与纵向呈45°角D、与纵向呈30°角2、金属薄板受单轴向拉伸，板中有一穿透形小圆孔。
该板危险点的最大拉应力是无孔板最大拉应力__________倍。
A、2B、3C、4D、53、若物体中某一点之位移u、v、w均为零（u、v、w分别为物体内一点，沿x、y、z直角坐标系三轴线方向上的位移分量。
）则在该点处的应变_________。
A、一定不为零B、一定为零C、可能为零D、不能确定4、以下________表示一个二阶张量。
A、B、C、D、四、试根据下标记号法和求和约定展开下列各式：（共8分）1、；（i ，j = 1，2，3 ）；2、；五、计算题（共计64分。
）1、试说明下列应变状态是否可能存在：；（）上式中c为已知常数，且。
2、已知一受力物体中某点的应力状态为：式中a为已知常数，且a＞0，试将该应力张量分解为球应力张量与偏应力张量之和。
为平均应力。
并说明这样分解的物理意义。
3、一很长的（沿z轴方向）直角六面体，上表面受均布压q作用，放置在绝对刚性和光滑的基础上，如图所示。
若选取＝ay2做应力函数。
试求该物体的应力解、应变解和位移解。
（提示：①基础绝对刚性，则在x＝0处，u＝0 ；②由于受力和变形的对称性，在y＝0处，v＝0 。
）题五、3图4、已知一半径为R＝50mm，厚度为t＝3mm的薄壁圆管，承受轴向拉伸和扭转的联合作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
式中：
是三个应力不变量，并有公式
代入已知量得
为了使方程变为 关系
形式，可令
代入，正好 项被抵消，并可得
代入数据得
，
，
1.7已知应力分量中
，求三个主应力
解：在
时容易求得三个应力不变量为
，
特征方程变为
。 ，
求出三个根，如记
，则三个主应力为
记
1.8已知应力分量
， 是材料的屈服极限，求 及主应力
。
解：先求平均应力
Mises 屈服条件：
故有
6.5 试用 Lode 应力参数 表达 Mises 屈服条件。 解：由定义：
即 Mises 屈服条件为 将上式代入，得：
即：
6.6 物体中某点的应力状态为
，该物体在单向拉伸
时
，试用 Mises 和 Tresca 屈服条件分别判断该点是处于弹性
状态还是塑性状态，如主应力方向均作相反的改变（即同值异号），则对被 研究点所处状态的判断有无变化? 解：（1）Mises 屈服条件判断
对，
，代入得
对，
，代入得
对，
，代入得
1.10当
时，证明
成立。
解： 由
，移项之得
证得
第五章 简单应力状态的弹塑性问题
5.1 简述 Bauschinger 效应： 解：拉伸塑性变形后使压缩屈服极限降低的现象
5.2 在拉杆中，如果 和 为试件的原始截面积和原长，而 和 为拉伸后的截
面积和长度。则截面收缩率为 时，有这样的关系： 证明： 体积不变，则有
解：的定义、物理意义：
；
1) 表征 Sij 的形式；2) 相等，应力莫尔圆相似，Sij 形式相同；3) 由可确定 S1：S2：S3。
1.4设某点应力张量 的分量值已知，求作用在过此点平面
力矢量
，并求该应力矢量的法向分量 。
解：该平面的法线方向的方向余弦为
上的应
而应力矢量的三个分量满足关系
而法向分量 满足关系
最后结果为：
1.5利用上题结果求应力分量为
时，过平
面
处的应力矢量 ，及该矢量的法向分量 及切向分量 。
解：求出
后，可求出
及 ，再利用关系
最终的结果为
可求得 。 ，
1.6 已知应力分量为 三次多项式
，求
，其特征方程为 。如设法作变换，把该方程变为形式
，求 以及 与 的关系。 解：求主方向的应力特征方程为
7.5 已知一长封闭圆筒半径为 r,壁厚为 t，受内压 p 的作用，从而产生塑性变形， 材料是各向同性的。如果忽略弹性应变，试求轴向、周向和径向应变增量的比。
解：在
方向的主应力分别为：
，则
，从而求得应力偏量 ，得最终结果为（-1）：1：0
，再根据增量理论
7.6 已知薄壁圆筒受拉应力
的作用，若使用 Mises 屈服条件，试求屈服时扭转应
，而应变
，试证明当体积不变
证毕！
5.3 对于线性弹塑性随动强化模型，若 （1）、已知给定应力路径为 （2）、已知给定应变路径为
，试求 ，求对应的应变值。 ，求对应的应力值。
（1）解：①、 ， ；②、
，
③、 ，
；④、
，
⑤、 ，
（2）解：①、 ， ；②、
，
③、 ，
；
④、
，
⑤、 ，
5.4 在拉伸试验中，伸长率为
z
且 利用平衡方程
当
时， 为（e）式。
（3）塑性阶段 平衡方程和几何方程同上。
本构方程 与（2）弹塑性阶段同样步骤：可得
（e） （f） （g）
5.9 如图所示等截面直杆，截面积为 ，且 。在 处作用一个逐渐增加 的力 。该杆材料为理想弹塑性，拉伸和压缩时性能相同。按加载过程分析
结构所处不同状态，并求力 作用截面的位移 与 的关系。 解：基本方程为
，截面收缩率为
，其中
和 为试件的初始横截面面积和初始长度，试证当材料体积不变时有如下关 系：
证明：将 和 的表达式代入上式，则有
5.5 为了使幂强化应力-应变曲线在 -应变关系：
时能满足虎克定律，建议采用以下应力
(1)为保证 及 在
处连续，试确定 、 值。
(2)如将该曲线表示成
解：（1）由 在
处连续，有
并从零开始增加，求三杆内力随 的变化规律．
解：基本方程为
几何方程： 协调关系：
本构方程：
（1）弹性阶段（
）
利用（a）、（b）及（c）第一式，联立求解得
（a) （b）
即
可看出 结构弹性极限：令
有
（2）弹塑性阶段（
）
取
，结构成为静定，由平衡方程
解得
若取
，即
此时 即当
时，内力为上列
值，当
时，杆1和杆2 已
的变化规律。
（a） 左边为体积变形，不论材料屈服与否，它要按弹性规律变化，即有
比较（a），（b）两式，得
（b）
将
表达式代入，即可得
。
5.8如图所示等截面直杆，截面积为 ，且 。在 处 作用一个逐渐增加的力 。该杆材料为线性强化弹塑性，拉伸和压缩时性能 相同。求左端反力 和力 的关系。
解：（1）弹性阶段 基本方程：平衡方程
解：刚塑性模型不考虑弹性阶段应变，因此刚塑性应力应变曲线即为
曲
线，这不难由原式推得
而在强化阶段，
，因为这时
将 都移到等式左边，整理之即得答案。
其中
5.7 已知简单拉伸时的 变的比值
曲线由（5.1）式给出，考虑横向应变与轴向应
在弹性阶段，
为材料弹性时的泊松比，但进入塑性阶段后 值开
始增大最后趋向于 。试给出 解：按题设在简单拉伸时总有
有
则
（2）纯剪切应力状态，
有
故 7.10 如何利用与 Tresca 屈服条件相关联的流动法则？
第八章 理想刚塑性的平面应变问题
8.1简述滑移线的概念： 解：在塑性区内，将各点最大剪应力方向作为切线而连接起来的线，称之为滑移 线。 剪切应力是最大剪应力。 平衡方程——沿线： 2k=C 或 =2k ；
沿线： +2k=C 或 = 2k ； 速度方程——沿线：dv v d=0；
，再求应力偏张量
，
，
，
，
，
。
由此求得：
然后求得：
，
，解出
然后按大小次序排列得到
，
，
1.9 已知应力分量中
，求三个主应力
，以及每个
主应力所对应的方向余弦
。
解：特征方程为
记
，则其解为
，
，
。对应于 的方向余弦 ， ， 应满足下列关系
由（a）,(b)式，·11得
（a） （b） （c）
， ，由此求得
，代入（c）式，得
解：1） OD 边：
GD 边：
沿
线，
，
2）
沿 OB 线，
，
8.7 Mises 线性等强化材料，在平面应变（ 试导出用表示的强化规律和本构关系。
解：当 时，在弹性阶段有
）和泊松比 条件下，
得
平均应力 因此在弹性阶段有
，进入塑性后有
对平均应变
刚进入塑性时
。由上式导出
。因此进入塑性
后还满足
保持不变； （2）平均应力与平均应变成比例； （3）应力偏量分量与应变偏量分量成比例； （4）等效正应力是等效正应变的函数，而这个函数对每个具体材料都应通过试 验来确定。
7.2 简述简单加载定理： 解：简单加载就是指单元体的应力张量各分量之间的比值，在加载过程中保持不 变，按同一参数单调增长。
7.3 简述单一曲线假定： 解：按不同应力组合所得的
6.8证明下列等式： （1）、 证明：（1）、右边
（2）、
=左边
证毕！
（2）、
证毕！
6.9 设 、 、 为应力偏量，试证明用应力偏量表示 Mises 屈服条件时，其形式为
，提示：
证明：Mises 屈服条件：
，
，
又 又
证毕！
第七章 塑性本构关系
7.1 塑性全量理论的成立条件： 解：（1）应力主方向与应变主方向是重合的，即应力 Mohr 圆与应变 Mohr 圆相 似，应力 Load 参数 和应变 Load 参数 相等，而且在整个加载过程中主方向
力为多大，并求此时塑性应变增量的比。
解：设扭转剪应力 入 Mises 屈服条件，得
，主应力为： 。
，
，代
7.7 证明等式：
证明：
将 对 求偏导，可得
，同理可得
，
，
，所以
；用同样的方法求得
。
7.8 一泊松比为 ，满足 Mises 屈服条件的单元体，已知其受力状态为
，
， ，x,y,z 是主方向。求： （1）当 从零增加到 时屈服，求 ；
沿线：dv +v d=0。 8.2 简述 Hencky 第一定理： 解：如果由一条滑移线 转到另一条滑移线 ，则沿任何一个 族的滑移线而 变化的 角和压力 的改变值而保持常数。
8.3推导 Levy—Mises 关系式 证明：对于平面应变问题，刚塑性材料的本构关系为：
证毕！
8.4在刚塑性平面应变条件下，用 Tresca 屈服条件下，证明公式 证明：Tresca 屈服线，
中： ，
中：
,
，
，
, 情况二见图（1），与①一样
所以
8.6 已知具有尖角为 的楔体，在外力 P 的作用下，插入具有相同角度的 V 形缺口 内，试分别按如下两中情况画出滑移线场并求出两种情况的极限荷载。 1）、楔体与 V 形缺口之间完全光滑；2）、楔体与 V 形缺口接触处因摩擦作用其剪应 力为 k。