第十二章 单相变压器的负载运行
合集下载
单相变压器的负载运行、等值电路

R1
X 1
I1
R2
' X 2
U1
Im
Rm
I
' 2
E1 E2
' U2
Xm
变压器的T形等效电路图
I1
' RK R2' R1 X K X 2 X 1
Rm
I2
U1
U2
Im
Xm
图 变压器的近似形等效电路图
短路电 阻
RK
短路电 抗
即
I2 U 2 U 2 kU 2 I2
(2)电流归算 根据归算前后的磁动势保持不变,有
N 2 N1 I 2 N2 I 2 N2
N2 N2 I 2 I2 I2 ' I2 N2 N1 k
(3)阻抗归算 根据归算前后副边绕组的铜耗和无功功率保持不变的 原则,有
XK
I 1 I
' 2
其中
' U2
Rk R1 R2 X k X1 X 2 Z k Rk jX k
U1
分别为短路电阻、短路电 抗和短路阻抗。
图 变压器的简化等效电路
U1 Ik ZK
由简化等效电路可知,短路阻抗起限制短路电流的作用,由 于短路阻抗值很小,所以变压器的短路电流值较大,一般可达额 定电流的10~20倍。
3、相量图 作相量图的步骤—— 对应T型等效电路, 假定变压器带感性负 载。
作相量图的步骤(假定变压器带感性负载)-对应简化等效电路
由等效电路可知
U 2 I 2 Z 2 I1 I 2 U1 U 2 I1RS jX S I1
单相变压器的负载运行(为录像用)

匝数为 N 2 的二次绕组,达到变比等于1 的目的。
第2章 变压器的基本理论
根据折算前、后磁动势不变,可得
N2 I2 N2 I2
I2
N2 N2 1 I2 I2 I2 N2 N1 k
1 I2 I2 k
根据折算前、后主磁通不变,可得
m N 2 4.44 fN 2 N1 E2 k E2 4.44 fN 2 m N 2 N 2
系,如果能将它体现在电路中,并将两个分离电路画在一起,则可得到描述变压器内 部电磁关系的一个纯电路,即变压器的等效电路。为此,需要进行绕组折算。
第2章 变压器的基本理论
1.绕组折算
折算目的:将变比为k 的变压器等效成变比为 1 的变压器, 从而可以把一、二次两个分离的电路画在一起。
通常是把二次绕组折算成一次绕组。
E I ( R jX ) U E I ( R jX ) U 1 1 1 1 1 2 2 2 2 2
根据方程式可 以画出变压器 的一、二次等 效电路。
表面上看,一、二次电路是两个分 离的电路,但事实上,二者之间通
I I /k I 0 1 2
过磁耦合(主磁通)相互联系在一起。磁动势平衡方程式定量地描述了这种磁耦合关
综合空载和负载电磁过程分析,可归纳出变压器负载运行时的基本方程式
E I ( R jX ) U 1 1 1 1 1 E I ( R jX ) U
2 2 2 2 2
I I /k I 0 1 2 kE E 1 2 I ( R jX ) E 1 0 m m I Z U
第2章 变压器的基本理论
2.2 单相变压器的负载运行
本节主要讲四个问题: 一、 负载时的电磁过程 二ቤተ መጻሕፍቲ ባይዱ 负载时的基本方程式 三、 负载时的等效电路
3.3单相变压器的负载运行
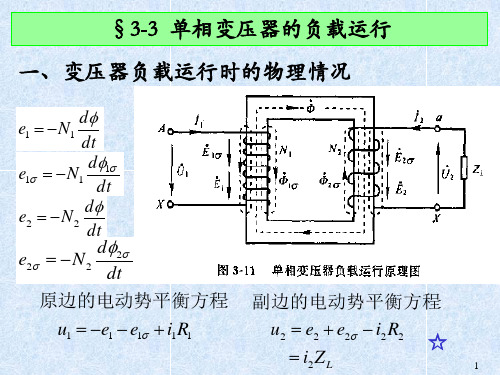
§3-3 单相变压器的负载运行 一、变压器负载运行时的物理情况
e1
N1
d
dt
e1
N1
d1
dt
e2
N2
d
dt
e2
N2
d2
dt
原边的电动势平衡方程: 副边的电动势平衡方程:
u1 e1 e1 i1R1
u2 e2 e2 i2R2 ☆
i2ZL
1
§3-3 单相变压器的负载运行
二、负载运行时的基本方程式
18
解 :(1)原、副边线电流: 变压器变比:
k U1N / 3 10000 25 U2N / 3 400
负载阻抗折算值:
ZL k 2ZL 252 (0.2 j0.07) 125 j43.75Ω
每相总阻抗:
Z zk ZL 1.546 j5.408125 j43.75Ω 126.546 j49.158 135.7621.23
X 2 k 2 X 2 3 0.055 0.165Ω
ZL k 2ZL 3 (4 j3) 12 j9Ω
14
根据题意,画出T形等值电路:
励磁阻抗:
Zm Rm jX m 30 j310 311.484.5
15
副边漏阻抗和负载阻抗和:
Z Z2 ZL 0.105 j0.165 12 j9 15.1837.1
『补例3-4』一台三相变压器,Y/y连接,SN=800kVA,U1N/U2N
=10000/400V;已知每相短路电阻rk=1.546,短路电抗xk=5.408
,该变压器原边接额定电压,副边接三相对称负载运行,每
相负载阻抗为:ZL=0.20+j0.07 。试用简化等值电路计算:
(1)变压器原、副边线电流; (2)副边线电压; (3)输入输出的有功功率及无功功率 (4)变压器效率
e1
N1
d
dt
e1
N1
d1
dt
e2
N2
d
dt
e2
N2
d2
dt
原边的电动势平衡方程: 副边的电动势平衡方程:
u1 e1 e1 i1R1
u2 e2 e2 i2R2 ☆
i2ZL
1
§3-3 单相变压器的负载运行
二、负载运行时的基本方程式
18
解 :(1)原、副边线电流: 变压器变比:
k U1N / 3 10000 25 U2N / 3 400
负载阻抗折算值:
ZL k 2ZL 252 (0.2 j0.07) 125 j43.75Ω
每相总阻抗:
Z zk ZL 1.546 j5.408125 j43.75Ω 126.546 j49.158 135.7621.23
X 2 k 2 X 2 3 0.055 0.165Ω
ZL k 2ZL 3 (4 j3) 12 j9Ω
14
根据题意,画出T形等值电路:
励磁阻抗:
Zm Rm jX m 30 j310 311.484.5
15
副边漏阻抗和负载阻抗和:
Z Z2 ZL 0.105 j0.165 12 j9 15.1837.1
『补例3-4』一台三相变压器,Y/y连接,SN=800kVA,U1N/U2N
=10000/400V;已知每相短路电阻rk=1.546,短路电抗xk=5.408
,该变压器原边接额定电压,副边接三相对称负载运行,每
相负载阻抗为:ZL=0.20+j0.07 。试用简化等值电路计算:
(1)变压器原、副边线电流; (2)副边线电压; (3)输入输出的有功功率及无功功率 (4)变压器效率
2-变压器负载运行
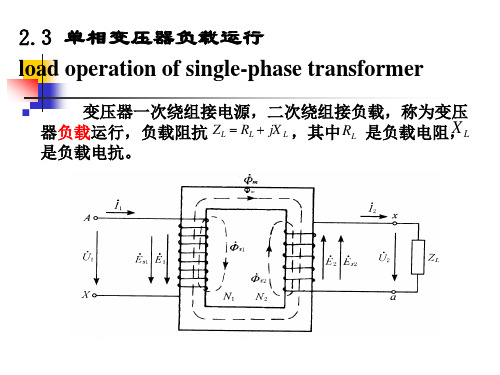
的大小
与空载运行时相比,负载时一次绕组的电流变化了,电源电压
不变,严格说来,负载时的
•
E
与空载时的不同。但在电力变压
1
器仍的然设还计是I中1N Z1I•0很U1小.仍,即存使在在U1额 E定1 由负载E1下 4运.44行fN1,I1Nm
比I0 大很多倍, 看出,空载、负
载与表运示空行。载,时其的主在磁数通值• m上的差数不值多差,仍别可很以小用,即同负一载个时符的号励I•磁0 N磁1或动势F• 0
因
,可认为 Zm
Z
' 2
Z
' L
无限Zm大而断开,于是等效电路变成了“一”型,
称为简化等效电路。如图:
单相变压器的负载运行
b.电压平衡方程式:
•
•
•
•
•
•
•
•
U1
I1
Z1
I 1 Z2'
U
' 2
I1
Z1
Z
' 2
U
' 2
I1 Zk
U
' 2
•
•
I1
I
' 2
•
•
U
' 2
Z
' L
单相变压器的负载运行
b.变压器接感性负载的相量图2-12a图:
单相变压器的负载运行
※相量图的绘制过程: 根据给定的条件不同,画法不同,但都是电压方程式 的相量图表示。
如给定U2, I2,cos2, k 及各参数,画图步骤为:
(((((((1234567)))))))根画在画画画E•1 据出出出出U•2'EU超•I2•'的•20' IE••前21相和E,•1,E量•910它/加I上Z•2的' m与,上,,主I其•I•1加画磁0R夹1上出通的,I角•2'U•相R•1再m为2' I量•,0加;和再上,2为加。它j上II••超11XjI•1;2前'得X2'到得•一m 出U•个1E•。2'铁耗;角;
变压器的负载运行解读

(3-39)
折算后,变压器负载运行时的基本方程式组可简化为如下的方程式组
U1 E1 I1z1 E1 I0zm U2 E2 I2 z2 U2 I2 zL E2 E1 I1 I2 I0
(3-40)
变压器的负载运行(续8)
2.等效电路
在将变压器副绕组的匝数折算为
与原绕组的匝数相等后,原、副绕组
负载增加时,I2 增加,副边磁动势N1 I2N2 增加,原
边电流的负载电流分量(-
N• I2
2
)也相应增加,
N
使 的其副产边生磁的动磁势动I2N势2 ,(以-维持NN12 I• 2励)磁1 Nl电得流以分抵量消增I0 加不了
变。可见,虽然变压器的原、副边没有直接的电
路联系,但负载电流的变化也会使原边电流相应
衡方程式。
变压器的负载运行(续2)
将磁动势平衡方程式表示成电流的形式,得
I
•
I
0
(
N
2
•
I2)
(3-26)
1
N
由上式看出,变压器负1 载运行时的原边电
流 I1 是大于变压器空载运行时的原边电流 I0 的, 它由反映主磁通 m 大小的励磁电流分量 I0 和反
映负载大小的负载电流分量(-
)组成。当 N • I2 2
s
s
s
图3.9 单相变压器负载运行 时的简化等效电路
变压器的负载运行(续9)
==308.00V例53/111,5已V其知,负一r1=载台0阻单.1抗相5为变,:压r2z器=L=的0.40数+2j43据为,。:x当S1N=外4.06k加.V2A7电,U压,1N /为xU22N 额定值时,用简化等效电路计算原、副边电流及副边电
单相变压器的负载运行
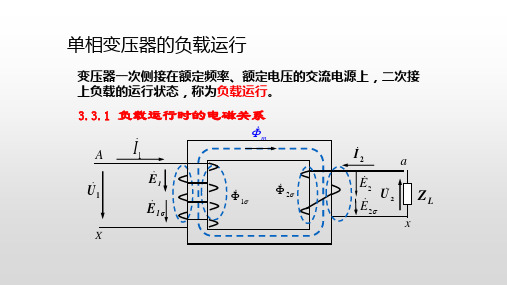
E 1 Zm I0 U 2 I2 Z L
二、等效电路 根据折算后的方程,可以作出变压器的等效电路。
T型等效电路:
近似等效电路
R1 X1
R2 X 2
R1 X1
R2 X 2
U 1
I1
I0
Rm
I2 U 2
I1
Z LU1
Xm
I1L I2
U 2 ZL
简化等效电路:
RS X S
I1 I2
U 1
3.3.3 等效电路及相量图
一、折算
折算:将变压器的二次(或一次)绕组用另一个绕组(N2=N1)来 等效,同时对该绕组的电磁量作相应的变换,以保持两侧的电磁 关系不变,用一个等效的电路代替实际的变压器。
折算原则:1)保持二次侧磁动势不变;2)保持二次侧各功率 或损耗不变。
方法:(将二次侧折算到一次侧)
I 2
I2 k
E2 kE2 E1 U2 kU2
r2 k 2r2 x2 k 2 x2 ZL k 2 ZL
折算后的方程式为
U1 E 1 I1R1 jI1 X1 E 1 I1Z1
U 2 E 2 I2 R2 jI2 X 2 E 2 I2 Z2 I1 I2 I0
E 2 E 1
次电流的增加或减少.
负载运行时,忽略空载电流有:
I1
I2 k
或
I1 I2
1 k
N2 N1
表明,一、二次电流比近似与匝数成反比。可见,匝数不
同,不仅能改变电压,同时也能改变电流。
二、电动势平衡方程
根据基尔霍夫电压定律可写出一、二次侧电动势平衡方程
U1 E 1 I1R1 jI1 X1 E 1 I1Z1 U 2 E 2 I2 R2 jI2 X 2 E 2 I2 Z2 U 2 I2 Z L
二、等效电路 根据折算后的方程,可以作出变压器的等效电路。
T型等效电路:
近似等效电路
R1 X1
R2 X 2
R1 X1
R2 X 2
U 1
I1
I0
Rm
I2 U 2
I1
Z LU1
Xm
I1L I2
U 2 ZL
简化等效电路:
RS X S
I1 I2
U 1
3.3.3 等效电路及相量图
一、折算
折算:将变压器的二次(或一次)绕组用另一个绕组(N2=N1)来 等效,同时对该绕组的电磁量作相应的变换,以保持两侧的电磁 关系不变,用一个等效的电路代替实际的变压器。
折算原则:1)保持二次侧磁动势不变;2)保持二次侧各功率 或损耗不变。
方法:(将二次侧折算到一次侧)
I 2
I2 k
E2 kE2 E1 U2 kU2
r2 k 2r2 x2 k 2 x2 ZL k 2 ZL
折算后的方程式为
U1 E 1 I1R1 jI1 X1 E 1 I1Z1
U 2 E 2 I2 R2 jI2 X 2 E 2 I2 Z2 I1 I2 I0
E 2 E 1
次电流的增加或减少.
负载运行时,忽略空载电流有:
I1
I2 k
或
I1 I2
1 k
N2 N1
表明,一、二次电流比近似与匝数成反比。可见,匝数不
同,不仅能改变电压,同时也能改变电流。
二、电动势平衡方程
根据基尔霍夫电压定律可写出一、二次侧电动势平衡方程
U1 E 1 I1R1 jI1 X1 E 1 I1Z1 U 2 E 2 I2 R2 jI2 X 2 E 2 I2 Z2 U 2 I2 Z L
变压器负载运行
' 2
E
' 2
&r I 1 1
& −E 1 &' −I 2 & I m
& I 1
& φ m
& & 90 0 的主磁通 φ (4)画出领先 E 1 m
& = −E & / Z 画出 I & , (5)根据 I m 1 m m
' I2 ' U2 ' ' I2 r2
副边绕组经折算 后,原来的基本 方程组成为:
& = −E & +I & ( R + jX ) U 1 1 1 1 1 &′ = E &′ − I & ′ ( R ′ + jX ′ ) U
2 2 2 2 2
已没有变比k !
& =I & +I &′ I 0 1 2 & =E &′ E 1 2 & = −I & ( R + jX ) E m m 1 0 &′ = I &′ Z ′ U
& I 1
r1
& I m
x1
&' x' −I 2 2
r2'
&' −U 2
& U 1
rm xm
' ZL
20
简化的等效电路
负载运行时, Im在I1N中所占的比例很小。在工程实际计算 中,忽略Im ,将激磁回路去掉, 得到更简单的阻抗串联电路
& I 1
r1
x1
&' x' −I 2 p; U 1
第2-3讲单相变压器的负载运行
RL RL (I2 / I2)2 k2RL
综合次级边各阻抗的折合为次级电压量(包括 端电压,电压降等)也要折合,这和电势折合
xL
xL (I2 / I2)2
k2xL
规律相同。不难看出,次级边的电压、电流 及阻抗的折合是相关的,协调的。
x
2
k
2
x
2
U
2
kU
2
第2-1讲.变压器负载运行的等值电路 6
I 2W1 I0
I0W1
说明初级电流i1可分为两个分量: 一个为励磁电流分量i0,
I1
I0
(I
2
)
另一个为与次级电流折合值大小相等,
相位相反的负载电流分量i2’。
第2-1讲.变压器负载运行的等值电路 6
二、拆合后变压器的各平衡式
I1
I0
I
2
U1 E1 I1Z1
U 2
E2
I
2
(r2
jx 2 )
介绍内容
1.变压器负载运行时的电磁关系 2.变压器负载运行的等值电路 3.相对单位制一标幺值 4.变压器的试验和参数测定 5.变压器的外特性与效率
第2-1讲.变压器负载运行时的电磁关系 1 当次级绕组接通负载阻抗ZL后,有次级电流i2并建立
次级磁势i2W2。这时初级绕组有电流i1,相应的初级边磁 势为i1W1 。由于初,次级磁势都作用于主磁路上,因此由 它们共同激励而建立主磁通Фm。计算合成磁势为i1W1 +i2W2 =i0W1这里的i0W1就是建立Фm所需之励磁磁势。
第2-1讲-4变压器的试验和参数测定 4
二、空载试验
变压器空载试验的电路如图所示,将次级绕组开
路(故也称开路试验),初级绕组接电源额定电压UN1。 由于次级开路,次级电流为零,所以次级支路不起
变压器的负载运行解读
1 1 2 2
1 1 1 m
1
1
2
2
0
1
1
1
0
1
2
2
将磁动势平衡方程式表示成电流的形式,得 I ( N I ) I (3-26) N 由上式看出,变压器负载运行时的原边电 流 I1 是大于变压器空载运行时的原边电流 I0 的, 它由反映主磁通 大小的励磁电流分量 I 和反 I)组成。当 映负载大小的负载电流分量(- N N 负载增加时, I2 增加,副边磁动势 I N 增加,原 N 边电流的负载电流分量(- N I )也相应增加, I )N 得以抵消增加了 使其产生的磁动势(- N N l 的副边磁动势 I N ,以维持励磁电流分量 I0 不 变。可见,虽然变压器的原、副边没有直接的电 路联系,但负载电流的变化也会使原边电流相应 地改变。
变压器的负载运行(续6)
(1)副边电动势的折算值 折算的目的就是使折算后的副绕组匝数等于 N 1 ,有 原绕组的匝数,即 N 2 N E 1 (3-33) E N (2)副边电流的折算值 为保证折算前后副边磁动势的作用不变,有
2 2 1 1
N I N I 2 2 2 2
N2 N2 1 I2 I2 I2 I2 N2 N1 k
1 1 1 1 1 1 1 1
1
0
m
m
0
m
2
2
2
2
2
2
2
2
I ( r jx ) I Z U
2 2 L L 2
L
变压器的负载运行(续4)
1 1 1 m
1
1
2
2
0
1
1
1
0
1
2
2
将磁动势平衡方程式表示成电流的形式,得 I ( N I ) I (3-26) N 由上式看出,变压器负载运行时的原边电 流 I1 是大于变压器空载运行时的原边电流 I0 的, 它由反映主磁通 大小的励磁电流分量 I 和反 I)组成。当 映负载大小的负载电流分量(- N N 负载增加时, I2 增加,副边磁动势 I N 增加,原 N 边电流的负载电流分量(- N I )也相应增加, I )N 得以抵消增加了 使其产生的磁动势(- N N l 的副边磁动势 I N ,以维持励磁电流分量 I0 不 变。可见,虽然变压器的原、副边没有直接的电 路联系,但负载电流的变化也会使原边电流相应 地改变。
变压器的负载运行(续6)
(1)副边电动势的折算值 折算的目的就是使折算后的副绕组匝数等于 N 1 ,有 原绕组的匝数,即 N 2 N E 1 (3-33) E N (2)副边电流的折算值 为保证折算前后副边磁动势的作用不变,有
2 2 1 1
N I N I 2 2 2 2
N2 N2 1 I2 I2 I2 I2 N2 N1 k
1 1 1 1 1 1 1 1
1
0
m
m
0
m
2
2
2
2
2
2
2
2
I ( r jx ) I Z U
2 2 L L 2
L
变压器的负载运行(续4)
项目03_单相变压器的空载、短路及负载运行
功率。如图3-6所示。这时就有:
I0P=I0 sin I0Q=I0 cos 空载损耗则为:
(3-3)
P0=U1I0 cos1≈U1I0Q cos1
(3)空载相量图 如图3-6所示。
(3-4)
2020/9/30
单相变压器的空载、短路及负载运行
2.负载运行 (1)原理图及电压方程式 单相变压器负载运行原理图如图3-7所示,它的二 次侧可简化成图3-8所示的等效电路图,因一次侧等 效电路和空载时一样,这里只分析二次侧等效电路。 对照前面空载运行的分析,r2、XS2是二次侧绕组的电 阻和漏电抗,可以得到一次侧、二次侧电压方程式为 :
cos K= P K 。 U KIK
2020/9/30
单相变压器的空载、短路及负载运行
2020/9/30
单相变压器的空载、短路及负载运行
4.cos =0.8(感性)时的负载测定 (1)根据电路图(见图3-4)负载阻抗为可调的 ,为了保持功率因数不变,须接入功率因数表监视。 (2)先将负载阻抗调至最大,调节外加电压,使U1 =U1N,闭合负载端开关,使变压器带上负载,保持 原边电压不变,逐渐增加负载电流,在0~1.1IN范围内 读取I2 、U2共6~7点
单相变压器的空载、短路及负载运行
一、能力目标 二、使用的设备及仪器 调压器、单相变压器、电流表、电压表、功率因数 表、负载阻抗、开关、熔断器。 三、项目要求 1.变压器变压比的测定 (1)根据电路图(见图3-1)高压绕组接电源,低 压绕组开路。 (2)在调压器处于零位时合上电源开关,调节调 压器使高压绕组的电压约为高压边额定电压的50%, 测量一二次侧电压。
2020/9/30
单相变压器的空载、短路及负载运行
图3-1变比测定接线图
I0P=I0 sin I0Q=I0 cos 空载损耗则为:
(3-3)
P0=U1I0 cos1≈U1I0Q cos1
(3)空载相量图 如图3-6所示。
(3-4)
2020/9/30
单相变压器的空载、短路及负载运行
2.负载运行 (1)原理图及电压方程式 单相变压器负载运行原理图如图3-7所示,它的二 次侧可简化成图3-8所示的等效电路图,因一次侧等 效电路和空载时一样,这里只分析二次侧等效电路。 对照前面空载运行的分析,r2、XS2是二次侧绕组的电 阻和漏电抗,可以得到一次侧、二次侧电压方程式为 :
cos K= P K 。 U KIK
2020/9/30
单相变压器的空载、短路及负载运行
2020/9/30
单相变压器的空载、短路及负载运行
4.cos =0.8(感性)时的负载测定 (1)根据电路图(见图3-4)负载阻抗为可调的 ,为了保持功率因数不变,须接入功率因数表监视。 (2)先将负载阻抗调至最大,调节外加电压,使U1 =U1N,闭合负载端开关,使变压器带上负载,保持 原边电压不变,逐渐增加负载电流,在0~1.1IN范围内 读取I2 、U2共6~7点
单相变压器的空载、短路及负载运行
一、能力目标 二、使用的设备及仪器 调压器、单相变压器、电流表、电压表、功率因数 表、负载阻抗、开关、熔断器。 三、项目要求 1.变压器变压比的测定 (1)根据电路图(见图3-1)高压绕组接电源,低 压绕组开路。 (2)在调压器处于零位时合上电源开关,调节调 压器使高压绕组的电压约为高压边额定电压的50%, 测量一二次侧电压。
2020/9/30
单相变压器的空载、短路及负载运行
图3-1变比测定接线图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
& &′ & I1 + I 2 = I 0
& & &′ I1 = I 0 + ( − I 2 )
& & & & & U1 = − E1 + I1 (r1 + jxσ 1 ) = − E1 + I1Z1 & ′ & ′ &′ & ′ &′ ′ ′ U 2 = E2 − I 2 (r2′ + jxσ 2 ) = E2 − I 2 Z 2
′ ( I2 )
2
∗
∗
∗
′ xL = ( I 2 ) xL
2
折合算法其结果不改变变压器运行的物理本质, 折合算法其结果不改变变压器运行的物理本质, 既不改变功率,也不影响各矢量间的相位角度。 既不改变功率,也不影响各矢量间的相位角度。
2、折合后变压器的各平衡式
& &′ & I1W1 + I 2W1 = I 0W1
四、变压器的外特性与效率
1、外特性和电压调整率 (1)外特性: U2 = f (I2) U =C.,cosϕ =C.
1 2
& & & U 2 = E2 − I 2 (r2 + jxσ 2 )
(2)电压调整率:
UN2 −U2 ∆U = ×100% UN2
UN2 :次级额定电压
空载电压) (空载电压) U2 :变压器额定运行 时的次级 时的次级电压 ∆U ≈ 5~8%
其中
U1 z0 = I0
r0 = r1
2 x0 = z0 −r2 0
r << r 1 m
rm = r0 − r1 ≈ r0 xm = x0 − xσ 1 ≈ x0
x0 = xσ 1 + xm xσ1 << xm
Z m = rm + jxm
⋅
& & & 空载 U1 = − E1 + I 0 Z1 & & & 负载 U1 = − E1 + I1Z1
I0Z1 << U 1 I1 Z 1 < < U 1
E1 U1 Φm = ≈ 4.44 fW1 4.44 fW1
W1
W2
& & U1 ≈ − E1
变压器从空载到负载状态的电势
E1 和主磁通 Φm 应基本保持不变
& I1
& UK
xσ 1
& IK I&0
′x xσ 2 ′
σ2
r2′
r2′
& UK
& U1
& &′ E1 = E2
rm xm
&′ I2
&′ U2
′ ZL
初级电流达到额定值, 当初级电流达到额定值,此时所加初级电压称短路电压 Uk ,一般情况下, k ≈ ( 5~10) % N1 <<UN1 ,主磁通小,励磁 U U 一般情况下, 主磁通小, 不饱和,励磁电流极小,励磁支路的作用可忽略。 不饱和,励磁电流极小,励磁支路的作用可忽略。
2、空载试验 次级绕组开路, 次级绕组开路,初级绕组接电源额定电压 UN1 。
P0
r1
& I1
U 20
xσ 1
& U N1
r1
xσ 1
′ xσ 2
&′ rm I 2
xm
r2′
& I0
& U N1
& U1
& &′ E1 = E2
& I0 rm
xm
&′ U2
′ ZL
空载试验简化等值电路
P U 通过测量 U1 、 20 、 0 、I 0,可计算 z0 = r0 + jx0,
P η= 2 P 1
pFe = pcu = pcu1 + pcu 2
η
不变损耗= 不变损耗=可变损耗
ηmax
η ≈ 95 ~ 98%
五、标幺值
将变压器和电机的物理量或参数的实 1、相对单位制:将变压器和电机的物理量或参数的实 际值用相对于该量的基准值来表示的单位制。 际值用相对于该量的基准值来表示的单位制。 2、标幺值:相对单位制表达的量。 相对单位制表达的量。 相对单位制表达的量
2、电磁功率和效率
P = U1 I1 cos ϕ1 1 P = pcu1 + pFe + Pem 1
p cu 1 = I12 r1
p Fe = I 0 2 rm
′ Pem = E1 I 2 cosψ 2 = E 2 I 2 cosψ 2
P2 = Pem − pcu 2 pcu 2 = I 22 r2
α0
& I0 & Φm
ϕ2
&′ I2
ψ2
& & & U1 = − E1 + I1 ( r1 + jxσ 1 )
ϕ1 变压器输入端的
功率因数角
&′ U2 &′ I 2 r2′ &′ ′ jI 2 xσ 2
& & E1 = E 2
三、变压器的试验和参数测试
r1
xσ 1 & I1
& I0
′ xσ 2
&′ I2
第十二章 单相变压器的负载运行
1、变压器负载运行时的电磁关系 2、变压器负载运行的等值电路 3、变压器的试验和参数测试 4、变压器的外特性与效率 5、标幺值
一、变压器负载运行时的电磁关系
1、磁势平衡方程 & & & & F2 = I 2W2 F1 = I1W1
& & & F1 + F2 = F0 = I '0 W1
& & & U 2 = E2 − I 2 (r2 + jxσ 2 )
& & & & E2 = U 2 + I 2 Z 2 = I 2 ( Z L + Z 2 )
折合的原则:折合前后次级磁势的大小和相位不变。 折合前后次级磁势的大小和相位不变。 折合前后次级磁势的大小和相位不变
&′ & & E2 kE2 2 E2 ′ ′ ZL + Z2 = = =k = k 2 (Z L + Z 2 ) &′ & & I2 I2 k I2
& & & U1 = − E1 + I 0 ( r1 + jxσ 1 )
& & U 2 = I2ZL
3、变压器的电磁关系
& & U 1 = − E1 + I&1 (r1 + jxσ 1 ) ①
I&1r1 & U1 & I1
I&1W1
& I&1W1 + I 2W2 = I&0W1
④
I&0W1
& & = − E1 I0 Zm ⑤ & Φ
& I0
rm
&′ I2 &′ U2
′ ZL
& &′ E1 = E2
xm
r1
xσ 1
′ xσ 2
2
r2′
& I0
rm & U1
(− I&′ )
& (− U ′ )
2
′ ZL
xm
Г形等值电路 对于功率较大的变压器, (对于功率较大的变压器,Zm >> Z1)
4、折合后变压器的矢量图
′ I2 = ′ + R L )2 + ( xσ 2 + X L )2 ′ ′ (r2 ′ ′ E2
1、变压器的折合(统一电路图、统一矢量图) (统一电路图、统一矢量图)
r1
& I1 & U1 & E1 & E2
xσ 1
xσ 2
I&2
r2
W2′ = W1
& U2
ZL
& & & ′ E2 = (W W )E2 = kE2 = E1 1 2
&′ & & &′ & I 2W1 = I 2W2 I 2 = I 2 (W2 W1 ) = I 2 k
′ Zk = rk + jxk = (r +r2′) + j(xσ1 + xσ2) 1
I k 通过试验测得 Uk、P 、k ,可计算出
Uk zk = Ik
P r = k k 2 Ik
2 xk = zk −r2 k
一般情况下, 一般情况下,可近似认为 rk xk ′ ′ r ≈ r2 = xσ1 ≈ xσ2 = 1 2 2 注意事项: 一般在高压侧试验, 较大, (1) 一般在高压侧试验,使 UK 较大,保证测试相对精 度; (2)如需要低压边的参数,则应注意折合变换; (2)如需要低压边的参数,则应注意折合变换; 如需要低压边的参数 (3)若试验时的温度和变压器实际运行不同, (3)若试验时的温度和变压器实际运行不同,需要将测 若试验时的温度和变压器实际运行不同 出的电阻换算到工作温度时的数值。 出的电阻换算到工作温度时的数值。
m
& Φσ 1
& & Eσ 1 = − jI1 xσ 1
& E1
& & E1 E 2 = k ③
