17届高三理科数学11月19日同步测试(11.19周测试)答案
【高考数学】2017年全国卷(Ⅲ)(理)Word版含答案

绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣= A .12B .22C .2D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -=B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1311.已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP=λAB +μAD,则λ+μ的最大值为A .3B .22C .5D .2二、填空题:本题共4小题,每小题5分,共20分。
2017年全国卷3理科数学试题及参考答案(WORD版含部分选填详解)
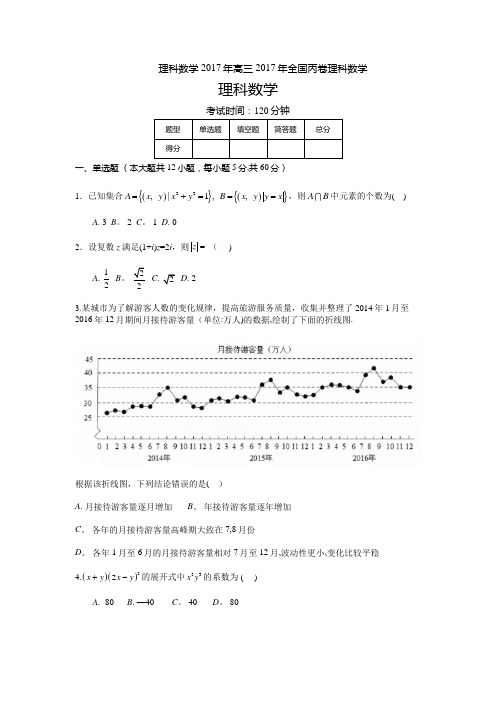
理科数学 2017年高三2017年全国丙卷理科数学理科数学考试时间:120分钟题型 单选题 填空题 简答题 总分 得分一、单选题 (本大题共12小题,每小题5分,共60分) 1.已知集合(){}(){}22,|1,,A x y x y B x y y x =+===,则AB 中元素的个数为( )A . 3B 。
2C 。
1D . 02.设复数z 满足(1+i )z =2i ,则z = ( )A .12 B 。
22C . 2D . 2 3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A . 月接待游客量逐月增加B 。
年接待游客量逐年增加C 。
各年的月接待游客量高峰期大致在7,8月份D 。
各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.()()52x y x y +-的展开式中33x y 的系数为 ( )A . -80B . —40C 。
40D 。
805.已知双曲线()2222:10,0x y C a b a b -=>>的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为( ) A . 221810x y -= B 。
22145x y -= C 。
22154x y -= D 。
22143x y -=6.设函数()cos 3f x x π⎛⎫=+ ⎪⎝⎭,则下列结论错误的是( )A . f (x )的一个周期为−2πB 。
y =f (x )的图像关于直线83x π=对称 C 。
f (x +π)的一个零点为6x π=D 。
f (x )在,2ππ⎛⎫⎪⎝⎭单调递减 7.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A 。
5B . 4C 。
一七年高考数学试卷

一、选择题(本大题共12小题,每小题5分,共60分) 1. 下列各数中,属于有理数的是( ) A. √2 B. π C. -3 D. 0.1010010001…… 2. 已知函数f(x) = x^2 - 4x + 3,则f(2)的值为( ) A. 1 B. 3 C. 5 D. 7 3. 下列函数中,在其定义域内单调递增的是( ) A. y = 2x + 1 B. y = -x^2 C. y = log2x D. y = e^x 4. 若复数z满足|z - 1| = |z + 1|,则复数z的实部为( ) A. 0 B. 1 C. -1 D. 不存在 5. 已知等差数列{an}的前三项分别为2, 5, 8,则该数列的公差为( ) A. 1 B. 2 C. 3 D. 4 6. 下列各点中,在直线3x + 4y - 12 = 0上的是( ) A. (0, 3) B. (2, 3) C. (3, 2) D. (4, 4) 7. 已知函数f(x) = |x - 1| + |x + 1|,则f(x)的最小值为( ) A. 0 B. 2 C. 4 D. 6 8. 若sinA + cosA = √2,则cosA的值为( ) A. √2/2 B. 1/2 C. -√2/2 D. -1/2 9. 在三角形ABC中,∠A = 60°,AB = 8,AC = 6,则BC的长度为( ) A. 10 B. 12 C. 14 D. 16 10. 已知函数f(x) = ax^2 + bx + c(a ≠ 0),若f(1) = 0,f(-1) = 0,则f(0)的值为( )
A. 0 B. a C. b D. c 11. 若等比数列{an}的首项a1 = 1,公比q = 2,则第n项an的表达式为( ) A. 2^n - 1 B. 2^n C. 2^n + 1 D. 2^n - 2 12. 已知函数f(x) = (x - 1)/(x + 1),则f(x)的值域为( ) A. (-∞, -1) ∪ (1, +∞) B. (-1, 1) C. (-∞, -1) ∪ [1, +∞) D. (-∞, 1) ∪ (1, +∞) 二、填空题(本大题共6小题,每小题5分,共30分) 13. 已知等差数列{an}的首项a1 = 3,公差d = 2,则第10项an = _______。 14. 若sin(α + β) = sinαcosβ + cosαsinβ,则cos(α - β)的值为 _______。
2017学年高考理科数学年全国卷3答案

时,
y
2
log2
1 16
2
4
2
.
5.【答案】 7 5
【解析】 tan
tan([
4
)
4
]
tan( ) tan
4
4
1 tan( )tan
1 1
6 1
1
7
.
5
44 6
6.【答案】 3 2
【解析】设球 O 的半径为 r ,则圆柱的底面半径为 r 、高为 2r ,所以 V1 r2 2r 3 . V2 4 r3 2 3
y0 ,即 x02
y02
1或 x02
y02
1.
又 P 在椭圆 E 上,故 x02 y02 1. 43
由
x02 x02 4
y02 1
y02
,解得
1
3
x0
47 7
,
y0
37 7
;
x02 x02 4
y02 y02 3
1
,无解.
6 / 10
(如果将没入水中部分冶理解为水面以上部分冶,则结果为 24 cm )
(2)如图, O,O1 是正棱台的两底面中心. 由正棱台的定义, OO1 平面EFGH ,所以 平面E1EGG1 平面EFGH , O1O EG .
同理, 平面E1EGG1 平面E1F1G1H1 , O1O E1G1 .
所以 MC
402 (10
7)2
30 ,从而 sin∠MAC
安徽省六安2024-2025学年高三上学期第四次月考(11月)数学试题含答案

六安2025届高三年级第四次月考数学试卷(答案在最后)命题人:时间:120分钟满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知,αβ是两个不同的平面,,m n 是两条不同的直线,下列命题不正确的是()A.若m ∥,n m α⊥,则n α⊥B.若,m m αβ⊥⊥,则α∥βC.若,m m αβ⊥⊂,则αβ⊥D.若m ∥,n ααβ⋂=,则m ∥n【答案】D 【解析】【分析】利用空间线面位置关系逐项分析判断即可.【详解】若m ∥,n m α⊥,则n α⊥,故A 选项正确;由m α⊥,m β⊥,可以推出//αβ,故B 选项正确;由平面与平面垂直的判定定理可知,若,m m αβ⊥⊂,则αβ⊥,故C 选项正确;//m α,n αβ= ,则//m n 或,m n 异面,故D 不正确.故选:D.2.在四棱锥P ABCD -中,底面ABCD 是正方形,E 为PD 的中点,若PA a = ,PB b = ,PC c =,则用基底{},,a b c 表示向量BE为()A.111222a b c →→→-+B.111222a b c →→→--C.131222a b c →→→-+ D.113222a b c →→→-+【答案】C【解析】【分析】根据空间向量的加法、减法、数乘运算求解即可.【详解】连接BD , E 为PD 的中点,111()()222BE BP BD PB BA BC =+=-++111111()()222222PB BA BC PB PA PB PC PB =-++=-+-+-311131222222PB PA PC a b c =-++=-+.故选:C .3.某学校高二年级选择“物化生”,“物化地”和“史地政”组合的同学人数分别为240,90和120.现采用分层抽样的方法选出30位同学进行某项调查研究,则“史地政”组合中选出的同学人数为()A.8B.12C.16D.6【答案】A 【解析】【分析】根据分层抽样的定义列出式子,进行求解.【详解】由题意得,史地政”组合中选出的同学人数为12030824090120⨯=++.故选:A4.已知数列{}n a 的首项110,1n n a a a +==++,则8a =()A.48B.80C.63D.65【答案】C 【解析】【分析】首先递推公式变形,结合等差数列的定义,即可求解.【详解】数列{}n a 的首项110,1n n a a a +==++,则:1111n n a a ++=++,整理得:)221=,所以:1=,1=(常数),所以数列是以1=为首项,1为公差的等差数列.()11n n=+-=,整理得:21na n=-(首项符合通项),则:21na n=-,所以:864163a=-=.故选:C5.已知等差数列{}n a满足131,3a a==,前n项和为nS,若12111nnTS S S=+⋯+,则与9T最接近的整数是()A.5B.4C.2D.1【答案】C【解析】【分析】求出等差数列的前n项,然后由裂项相消法求得n T即可得9T,从而得出结论.【详解】设{}n a的公差为d,则3131122a ad--===,所以()()1(1)11211112,22nnS n n nS n n n nnn-=⎪+⎛⎫=+==-++⎝⎭,则912111111111992121,222311105 nnT TS S S n n n⎛⎫⎛⎫=+⋯+=-+-+⋯+-=-=⨯=⎪ ⎪++⎝⎭⎝⎭,则与9T最接近的整数是2.故选:C.6.已知数列{}n a满足*712,8,N2,8nna n na na n-⎧⎛⎫-+>⎪ ⎪=∈⎝⎭⎨⎪≤⎩,若对于任意*n∈N都有1n na a+>,则实数a的取值范围是()A.1,12⎛⎫⎪⎝⎭B.113,220⎛⎫⎪⎝⎭C.13,120⎛⎫⎪⎝⎭D.31,2⎛⎫⎪⎝⎭【答案】C【解析】【分析】根据分段函数的单调性列出不等式组求解即可.【详解】由对于任意*n∈N都有1n na a+>知,数列{}n a为递减数列,所以只需满足89102011392a a a a a a⎧-<⎪⎪<<⎨⎪⎪=>=-⎩,解得13120a <<,故选:C7.在棱长为2的正方体1111ABCD A B C D -中,M 是线段11A C 上一个动点,则下列结论正确的有()A.不存在M 点使得异面直线BM 与AC 所成角为90B.存在M 点使得异面直线BM 与AC 所成角为30oC.存在M 点使得二面角M BD C --的平面角为45D.当1114A M AC =时,平面BDM 截正方体所得的截面面积为92【答案】D 【解析】【分析】异面直线BM 与AC 所成的角可转化为直线BM 与11A C 所成角,由当M 为11A C 的中点时判断选项A ;当M 与1A 或1C 重合时,直线BM 与AC 所成的角最小判断选项B ;当M 与1C 重合时,二面角M BD C --的平面角最小判断选项C ;对于D ,由1114A M AC =,过M 作EF ∥11D B ,得到四边形EFBD 即为平面BDM 截正方体所得的截面判断.【详解】解:异面直线BM 与AC 所成的角可转化为直线BM 与11A C 所成角,如图所示:当M 为11A C 的中点时,11BM AC ⊥,此时BM 与AC 所成的角为90,所以A 错误;如图所示;当M 与1A 或1C 重合时,直线BM 与AC 所成的角最小,为60o ,所以B 错误;当M 与1C 重合时,二面角M BD C --的平面角最小,1tan 21C OC ∠=>,所以145∠>C OC o ,所以C 错误;对于D ,如图所示:过M 作EF ∥11D B ,交11A B 于F ,交11A D 于E 点,因为1114A M AC =,所以E F 、分别是1111A D A B 、的中点,又11B D ∥BD ,所以EF ∥DB ,四边形EFBD 即为平面BDM 截正方体所得的截面,因为11122EF D B ==,且22115BF DE BB B F ==+=所以四边形EFBD 是等腰梯形,作FG DB ⊥交BD 于G 点,所以()1,222BG BD EF FG =-===,所以梯形的面积为()1922BD EF FG +⨯=,所以D 正确.故选:D8.已知一圆柱的轴截面为正方形,母线长为,在该圆柱内放置一个棱长为a 的正四面体,并且正四面体在该圆柱内可以任意转动,则a 的最大值为()A.1B.2C. D.4【答案】D 【解析】【分析】先通过圆柱的轴截面为正方形,可得该圆柱的内切球半径,再去研究球的内接正四面体,从而转化为研究正四面体的外接球问题即可.【详解】因为圆柱的轴截面为正方形,母线长为,若该圆柱内放置一个棱长为a 的正四面体,并且正四面体在该圆柱内可以任意转动,则该正四面体内接于该圆柱的内切球时,棱长a 最大,如图该正四面体P ABC -的棱长为a ,设点P 在面ABC 内的射影为H ,即PH ⊥面ABC ,则球心O 在PH 上,且OP OA ==,2cos3033AH AB a =⋅= ,所以3PH a ===,所以63OH PH OP a =-=在Rt OAH △中,222OA OH AH =+,即2226333a a ⎛⎛⎫=-+ ⎪ ⎪⎝⎝⎭,整理可得:240a a -=,解得4a =或0a =(舍),所以a 的最大值为4,故选:D【点睛】方法点睛:要让正四面体在圆柱内任意转动起来,转化为这个正四面体在圆柱的内切球内,从而问题得解.二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.如图的形状出现在南宋数学家杨辉所著的《详解九章算法-商功》中,后人称为“三角垛”.“三角垛”最上层有1个球,第二层有3个球,第三层有6个球,…,设第n 层有n a 个球,从上往下n 层球的总数为n S ,则()A.34S a =B.132n n n a a ++-=C.11n n a a n +-=+D.1055a =【答案】ACD 【解析】【分析】由已知题意,探索{}n a 递推规律,由规律得通项n a ,由此判断选项.【详解】由题意得,第n 层有n a 个球,121321,2,3,,a a a a a ==+=+ 11n n a a n +=++.即2123a =+=,31236a =++=,L ,()11232n n n a n +=+++⋅⋅⋅+=,因为3123413610,123410S a a a a =++=++==+++=,所以34S a =,A 正确;由11n n a a n +-=+,当2n =时,322332a a +-=≠,故B 错误,C 正确;由101011552a ⨯==,D 正确;故选:ACD.10.在边长为6的菱形ABCD 中,π3A ∠=,现将ABD △沿BD 折起到PBD △的位置,使得二面角P BD C --是锐角,则三棱锥P BCD -的外接球的表面积可以是()A.58πB.45πC.48πD.55π【答案】AD 【解析】【分析】作出二面角的平面角,利用球的性质确定外接球球心位置,求出球的半径,再由角的范围得出半径的范围,即可求出外接球表面积的范围.【详解】如图,由菱形边长为6,π3A ∠=,可知,PDB CDB △△是边长为6的正三角形,取BD 的中点为M ,连接,PM CM ,则,PM BD CM BD ⊥⊥,所以PMC ∠是二面角P BD C --的平面角,设π02PMC θθ⎛⎫∠=<< ⎪⎝⎭,外接球球心为O ,取,E F 分别为,PM CM 靠近M 的三等分点,连接,OE OF ,则EO ⊥平面PBD ,FO ⊥平面BCD ,连接,OC OM ,因为216233MC CF MC MF =⨯=====,所以在Rt OMF △中,tan2OF MF θ=,即tan 22OF MF θθ==,所以22222123tan 2R OC OF CF θ==+=+,由π02θ<<,可知π024θ<<,所以20tan 12θ<<,故21215R <<,所以()24πR 48π,60πS =∈.结合选项可知,AD 符合,BC 不符合.故选:AD11.对于棱长为1(单位:m )的正方体容器(容器壁厚度忽略不计),下列说法正确的是()A.底面半径为1m,高为1m 的圆锥形罩子(无底面)能够罩住水平放置的该正方体B.以该正方体同一顶点出发的三条棱作为圆锥的母线,则此圆锥的母线与底面所成角的正切值为2C.该正方体内能同时整体放入两个底面半径为0.5m,高为0.8m 的圆锥D.该正方体内能整体放入一个体积为33πm 17的圆锥【答案】BCD 【解析】【分析】选项A ,对照圆锥轴截面和正方体的表面,即可判断;选项B ,以1,,AB AA AD 三条棱作为圆锥母线,底面所在平面为平面1A BD ,等体积法求点A 到平面1A BD 的距离为,可求圆锥的母线与底面所成角的正切值;选项C ,过1AC 的中点P 作1AC 的垂线MN ,分别交11,AC A C 于点,M N ,计算,AP PM 的长度,判断能否放入两个圆锥;选项D ,计算以正方体的体对角线1AC 为圆锥的轴,1C 为圆锥顶点的最大圆锥体积即可,【详解】对于A ,圆锥和正方体高度相同,对照圆锥轴截面和正方体的表面,显然圆锥不可能罩住水平放置的该正方体,A不对;对于B ,如图,以1,,AB AA AD 三条棱作为圆锥母线,底面所在平面为平面1A BD ,等价于求AB 与平面1A BD 所成角的正切值,因为1,A A BD B AA D V V --=,所以1131111132232h ⎛⎫⎛⎫⨯=⨯⨯⨯⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭,所以点A 到平面1A BD的距离为h ,则此圆锥的母线AB 与底面1A BD232=,B 正确;对于C ,如图,平面11AA C C 内,过1AC 的中点P 作1AC 的垂线MN ,分别交11,AC A C 于点,M N ,13AC =,30.82AP =>,1326tan 0.5224PM AP C AC ∠=⋅=⨯=>,以正方体的体对角线1AC 作为圆锥的轴,正方体内能同时整体放入两个底面半径为0.5m,高为0.8m 的圆锥,C正确;对于D ,以正方体的体对角线1AC 作为圆锥的轴,1C 为圆锥顶点,MN 为圆锥底面圆的直径时,该圆锥的体积为221116333ππππ33421617V PM C P ⎛=⨯⨯=⨯⨯=> ⎝⎭,D 正确.事实上,以正方体的体对角线1AC 作为轴,1C 为顶点的圆锥的体积最大值,显然底面圆心在线段AP 上(不含P 点),设AG x =,当G I 与MN (M 为AC 的四等分点)重合时,MP NP =,因此3204x <≤,因为1AGH AC C ∽△△,所以11AG AH GH AC AC CC ==,则1636,,3333AH x GH x C H x ===,圆锥体积()22113232ππ1,03934V x GH C H x x x ⎛⎫⎛⎫=⨯⨯=-<≤ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,()()32209V x x x '=>在320,4⎛ ⎝⎦上恒成立,所以()V x 在0,4⎛ ⎝⎦上单调递增,体积的最大值为ππ41617V ⎛⎫=> ⎪ ⎪⎝⎭,D 正确.故选:BCD.【点睛】关键点点睛:判断CD 选项的关键是以矩形11AA C C 的中心为圆锥底面圆圆心,体对角线1AC 作为轴,算出圆锥的底面半径和最大高度,对结论时行判断.三、填空题:本题共3小题,每小题5分,共15分.12.已知一组数据1,2,0,1-,x ,1的平均数是1,则这组数据的中位数为______.【答案】1【解析】【分析】由平均数的公式求得x ,根据中位数的概念求出结果.【详解】这组数据的平均数为1,有()11201116x ++-++=,可求得3x =.将这组数据从小到大重新排列后,观察数据可知最中间的两个数是1与1,其平均数即中位数是(11)21+÷=.故答案为:1.13.已知四棱锥,A EBCD AE -⊥平面BCDE ,底面EBCD 是E ∠为直角,EB ∥DC 的直角梯形,如图所示,且224,CD EB AE DE ====,点F 为AD 的中点,则F 到直线BC 的距离为__________.【答案】2【解析】【分析】以E 为原点,建立空间直角坐标系,向量法求点到直线的距离.【详解】由题意知,AE ⊥平面BCDE ,,BE ED ⊂平面BCDE ,所以,AE BE AE ED ⊥⊥,又BE ED ⊥,故以E 为原点,,,EB ED EA 所在的直线分别为,,x y z 轴,建立如图空间直角坐标系,则()()()()0,0,2,2,0,0,4,3,0,0,3,0A B C D ,得()3,1F 所以()()2,23,0,2,3,1BC FB ==- ,记()13,,0,2,3,122BC c a FB BC ⎛⎫====- ⎪ ⎪⎝⎭ ,则4312a =++= ,31122a c ⋅=-=- ,所以F 到直线BC 的距离为22131||()842d a a c =-⋅=-= .故答案为:312.14.若在长方体1111ABCD A B C D -中,13,2,4AB BC AA ===.则四面体11ABB C 与四面体11A C BD 公共部分的体积为__________.【答案】43【解析】【分析】先判断出公共部分的位置,然后利用锥体体积公式来求得正确答案.【详解】记11111,,A D AD O A B AB E BO AC F ⋂=⋂=⋂=,由于1112OA AF BC FC ==,则F 为1AC 的第一个三等分点(靠近A ),连1EF EC 、,E 是1A B 的中点,由于B ∈平面11ABC D ,所以E 到平面11ABC D 的距离E d 是1A 到平面11ABC D 的独立1A d 的一半,则公共部分是三棱锥11111111,332E BFC BFC E BFC A E BFC V S d S d --=⨯=⨯ ,又112253BFC BAC S S == ,作11A H AD ⊥,垂足为H ,根据长方体的性质可知111111111,,,C D A H C D AD C D AD ⊥⋂⊂平面11ABC D ,所以1A H ⊥面11ABC D ,由等面积法可得111242522A H ⨯⨯=⨯⨯,所以1145A d A H ==,故14251143532E BFC V -⨯⨯==⨯.故答案为:43【点睛】方法点睛:几何图形的公共部分和体积计算:通过分析两个几何体公共部分的几何位置,逐步构造关键点,利用三角形面积和锥体体积公式,最终得出公共部分的体积,此方法清晰有效,能充分展示逻辑推理与代数运算等解题技巧.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.设三角形ABC 的内角A B C 、、的对边分别为,,a b c 且()2sin 23sin2A B C +=.(1)求角A 的大小;(2)若3,b BC =332ABC 的周长.【答案】(1)π3A =(2)9【解析】【分析】(1)利用三角形内角和的关系以及二倍角的余弦公式,并由辅助角计算可得结果;还可以根据二倍角的正弦公式求出正切值计算;(2)由三角形面积公式代入计算可得3a b c ===,求出周长.【小问1详解】因为,,A B C 为三角形ABC 的内角,所以()sin sin B C A +=,因为21cos sin 22A A -=,所以()2sin 2A B C +=可化为)sin 1cos A A =-,即sin A A +=πsin 32A ⎛⎫+= ⎪⎝⎭,又易知ππ4π,333A ⎛⎫+∈ ⎪⎝⎭,解得π2π33A +=,即π3A =.【小问2详解】由三角形面积公式得11sin ,322bc A b ==,代入得:1π13sin 232c ⨯=⨯,所以a c =,故ABC V 为正三角形,3a b c ===,周长等于9.16.已知无穷等比数列{}n a 的前n 项和为3nn S b =+.(1)求1,b a 的值;(2)设221,1,2,3,n n c a n n =+-= ,求数列{}n c 的前n 项和n T .【答案】(1)11,2b a =-=(2)()23914n n -+【解析】【分析】(1)根据等比数列中,n n a S 的关系可得解;(2)根据分组求和,利用等比数列、等差数列求和公式得解.【小问1详解】当2n ≥时,1123n n n n a S S --=-=⨯,因为{}n a 是等比数列,所以12a =,又因为113a S b ==+,所以1b =-.【小问2详解】由(1)知123n n a -=⨯,因为26a =,且222 9n na a +=,所以{}2n a 是以6为首项,9为公比的等比数列,()()2421321n n T a a a n ⎡⎤=+++++++-⎣⎦()29123691.9124n n n n n -⋅=⨯+=-+-17.如图所示,在三棱柱111ABC A B C -中,112,AC BC AB AB ===⊥平面ABC ,1,AC AC D ⊥点是AC 的中点(1)证明:11AC B C ⊥;(2)求1A D 与平面11BB C C 所成角的正弦值.【答案】(1)证明见解析(2)sin 34θ=【解析】【分析】(1)先根据线面垂直性质得出1AC AB ⊥,再应用线面垂直判定定理得出AC ⊥平面11AB C ,进而得出线线垂直;(2)建立空间直角坐标系,应用线面角求解即可;先根据等体积求出M 到平面11BB C C 距离,再应用线面角的定义进而得出线面角的正弦值.【小问1详解】由题意,1AB ⊥平面,ABC AC ⊂平面ABC ,所以1AC AB ⊥,又1AC AC ⊥,且11AB AC ⊂、平面1111,AB C AB AC A ⋂=,所以AC ⊥平面11AB C ,因为11B C ⊂平面11AB C ,所以11AC B C ⊥.【小问2详解】法一:由(1)知11AC B C ⊥,又BC //11B C ,所以AC BC ⊥,以C为原点建立如图所示的空间直角坐标系,则()()()()10,0,0,2,0,0,0,2,2,0,2,0C B B A ,0,1,0,所以()()()12,0,0,2,2,2,0,1,0CB BB DA ==-= ,()()()1110,1,02,2,22,3,2DA DA AA DA BB =+=+=+-=- ,设平面11BB C C 的法向量为 =s s ,则1202220n CB x n BB x y z ⎧⋅==⎪⎨⋅=-++=⎪⎩ ,所以 =0,1,−1,从而111cos ,34DA n DA n DA n⋅==⋅ ,故直线1A D 与平面11BB C C 所成角的正弦值为34.法二:取11C A 中点M ,则CM //1A D ,CM =1A D ,记CM 与平面11BB C C 所成角为θ,则1111112sin A CC B B M CC B Bd d CM CMθ--==,因为1,BC AC AB ⊥⊥平面ABC ,所以111,,,AB BC AC AB A AC AB ⊥⋂=⊂平面1AB C ,所以BC ⊥平面11,AB C CB ⊂平面1AB C ,所以1BC CB ⊥,1ACB中,1CB ==,所以111111*********,222B C C A B C S B C CB S =⨯=⨯⨯==⨯⨯=由111111A B C C C A B C V V --=,知1111111111133B C C A CC B B A B C S d S AB -⋅=⋅,即1112222A CC B B d -⋅=⨯解得1112A CC B B d -=,过M 做AC 垂线交C 的延长线垂足为H ,122,3MH C A CH ===又2223817CM CH MH =+=+=,所以34sin 34θ=18.如图1,在等腰梯形ABCD 中,AD ∥,8,4,60BC AD BC DAB ∠=== ,点,E F 在以AD 为直径的半圆上,且 AE EFFD ==,将半圆沿AD 翻折如图2.(1)求证:EF ∥平面ABCD ;(2)当多面体ABE DCF -的体积为32时,求平面ABE 与平面CDF 夹角的余弦值.【答案】(1)证明见解析(2)15【解析】【分析】(1)根据线面平行的判定定理来求得正确答案.(2)利用几何法,或建立空间直角坐标系,利用向量法来求得平面ABE 与平面CDF 夹角的余弦值.【小问1详解】设O 是AD 的中点,连,,,,,,OB OC OE OF AE EF FD ,依题意,在等腰梯形ABCD 中,AD ∥,8,4,60BC AD BC DAB ∠=== ,点,E F 在以AD 为直径的半圆上,且 AE EFFD ==,由等边三角形可知A B C D F E 、、、、、分布在同一个圆周上,且AE EF FD DC CB BA =====,则六边形ABCDFE 为正六边形,EF ∴//AD ∥,BC EF ⊄面,⊂ABCD BC 面,ABCD EF ∴∥ABCD .【小问2详解】在图1中连EB 交AD 于1O ,则AD EB ⊥,连FC 交AD 于2O ,则AD FC ⊥,故在图2中,1111111,,,,AD O E AD O B O E O B O O E O B ⊥⊥⋂=⊂平面1EOB ,所以AD ⊥平面1EO B ,同理可证得AD ⊥平面2FO C ,记面ABE 与面CDF 所成角为θ,则1212,6sin EO B FO C EO B FO C S S ∠∠θθ==== ,1221ABE DCF EO B FO C D FO CA EOB V V V V ----=++锥112121132sin 3233EO B EO B FO C S AO S EF S DO θ=⨯+⨯+⨯== ,故πsin 1,2θθ==,即面AEFD ⊥面ABCD .法一(几何法):延长AB DC 、交于,Q 延长AE DF 、交于,P 则PQ 为面ABE 与面CDF 交线且8,8AP AQ PD QD ====,取PQ 中点M ,连接AM DM 、,则,AM PQ DM PQ ⊥⊥,则AMD ∠即为面ABE 与面CDF 所成角.在AMD中,8AM DM AD ===,故281cos 5AMD +-∠==,故面ABE 与面CDF 所成角的余弦值为15.法二(坐标法):以1O 为坐标原点,111,,O B O D O E 所在的直线为,,x y z 轴,建立空间直角坐标系,则()()(()()(0,2,0,,0,0,,4,0,0,6,0,0,4,2A B E C D F-,()(2,0,0,2,AB AE ==,有2020AB n y AE n y ⎧⋅=+=⎪⎨⋅=+=⎪⎩,令1,x =得()1,n = ,同理可得面CDF 法向量()m = ,设面ABE 与面CDF 所成角为α,故1cos 5m n m n α⋅==⋅ .19.若存在非零常数t ,使得数列{}n a 满足()11231,n n a a a a a t n n +-=≥∈N ,则称数列{}n a 为“()H t 数列”.(1)判断数列:1,3,5,11,152是否为“()2H 数列”,并说明理由;(2)若数列{}n a 是首项为1的“()H t 数列”,数列{}n b 是等比数列,且{}n a 与{}n b 满足212321log n i n n i aa a a ab ==+∑ ,求t 的值和数列{}n b 的通项公式;(3)若数列{}n a 是“()H t 数列”,n S 为数列{}n a 的前n 项和,11,0a t >>,证明:1e nS n n n t S S -+>--【答案】(1)不是,理由见解析(2)1t =-,12n n b -=.(3)证明见解析【解析】【分析】(1)由“()H t 数列”定义验证即可;(2)由题可得212321111log n n n i n i aa a a a ab +=++=+∑ ,与212321log ni n n i a a a a a b ==+∑ 相减结合“()H t 数列”定义可得关于t 的方程,即可得答案;(3)要证1e n S n n n t S S -+>--等价于12e n S n n a a a -< ,即1212ln ln ln n n a a a a a a n +++<+++- ,构造函数()ln 1f x x x =-+,利用其单调性可证明结论.【小问1详解】根据“()H t 数列”的定义,则2t =,故11232n n a a a a a +-= ,因为212a a -=成立,3212a a a -=成立,43211113542a a a a -=-⨯⨯=-≠不成立,所以1,3,5,11,152不是“()2H 数列”.【小问2详解】由{}n a 是首项为1的“()H t 数列”,则231,21a t a t =+=+,由{}n b 是等比数列,设公比为q ,由212321log n i n n i aa a a ab ==+∑ ,则212321111log n n n i n i a a a a a a b +=++=+∑ .两式作差可得()2112312121log log n n n n n a a a a a a b b +++=-+- ,即()21123121log n n n a a a a a a q ++=-+ ,由{}n a 是“()H t 数列”,则1231n n a a a a t a +-= ,对于1,n n ≥∈N 恒成立,所以()()211121log n n n a a t a q +++=--+,即()12121log log n n n t a t b b +++=+-对于1,n n ≥∈N 恒成立,则()()22321log 1log t a t q t a t q ⎧+-=⎪⎨+-=⎪⎩,即()()222(1)log 121log t t q t t t q ⎧+-=⎪⎨++-=⎪⎩,因为0t ≠解得,1,2t q =-=,又由2111211,log a a a b ==+,则11b =,即12n n b -=,故所求的1t =-,数列{}n b 的通项公式12n n b -=.【小问3详解】设函数()ln 1f x x x =-+,则()11f x x'=-,令()0f x '=,解得1x =,当1x >时,()0f x '<,则()ln 1f x x x =-+在区间()1,∞+单调递减,且()1ln1110f =-+=,又由{}n a 是“()H t 数列”,即1231n n a a a a t a +-= ,对于1,n n ≥∈N 恒成立,因为11,0a t >>,则211a t a =+>,再结合121,0,1a t a >>>,反复利用1231n n a a a a t a +=+ ,可得对于任意的1,,1n n n a ≥∈>N ,则()()10n f a f <=,即ln 10n n a a -+<,则ln 1n n a a <-,即1122ln 1,ln 1,,ln 1n n a a a a a a <-<-⋯<-,相加可得1212ln ln ln n n a a a a a a n +++<+++- ,则()12ln n n a a a S n <- ,又因为ln y x =在()0,x ∞∈+上单调递增,所以12e n S n n a a a -< ,又1231n n a a a a t a +-= ,所以1e n S n n a t -+-<,即1e n S n n n S S t -+--<,故1e n S n n n t S S -+>--.【点睛】关键点点睛:本题第三问解题关键为理解“()H t 数列”的定义,通过构造函数()ln 1f x x x =-+利用单调性来证明ln 10n n a a -+<,进而得到()12ln n n a a a S n <- ,得证.。
2017年高考真题——理科数学(全国Ⅲ卷)+Word版含解析

2.设复数z满足 (1 + i) z = 2i ,则 z =
1 2 答案 C
A.
B.
2 2
C. 2
D.2
解析 由题, z =
2i (1 − i ) 2i 2i + 2 = = = i + 1 ,则 z = 12 + 12 = 2 ,故选C. 1 + i (1 + i )(1 − i ) 2
1 2016
7.执行右图的程序框图,为使输出 S 的值小于91,则输入的正整数 N 的最小值为 A.5 B .4 C .3 D.2 答案 D 解析 程序 行过程如 表所示 S M 0 100 1 初始状态 100 −10 2 第1次循环结束 90 1 3 第2次循环结束 时 S = 90 < 91 首次满足条 , 程序需在 t = 3 时跳出循环, 即 N = 2 为满足条 的最小值,故选D.
2017年普通高等学校招生全国统一考试 理科数学
试题及答案解析
一、选择题: 本题共12小题,每小题5分,共60分
全国
2 2 1.已知集合 A = ( x, y ) x + y = 1 , B = {( x, y ) y = x} ,则 A I B 中元素的个数为
{
}
B .2 C .1 D.0 A.3 答案 B 解析 A 表示圆 x 2 + y 2 = 1 所 点的集合, B 表示直线 y = x 所 点的集合, 故 A I B 表示两直线 圆的交点, 由图可知交点的个数为2, 即 A I B 元素的个数为2, 故选B.
3.某城 为了解游客人数的变化规律,提高旅游服 ,收集并整理了2014 12 期间 接 游客 单 万人 的数据,绘制了 面的折线图.
(完整版)2017年全国高考理科数学试题及答案-全国卷2,推荐文档
绝密★启用前理科数学注意事项:1. 答题前,考生先将自己的姓名、 准考证号填写清楚, 将条形码准确粘贴在条形码区域 内。
2. 选择题必须使用2B 铅笔填涂;非选择题必须使用 0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚3. 请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效; 在草稿纸、试卷上答题无效4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5•保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀项是符合题目要求的。
A. 1 2i灯三百八十一,请问尖头几盏灯?”意思是:一座 7层塔共挂了 381盏灯,且相邻两层中的下一层灯数是上一层灯数的 2倍,则塔的顶层共有灯() A. 1盏B. 3盏C. 5盏D. 9盏4. 如图,网格纸上小正方形的边长为 1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( ) A. 90B . 63C. 42D . 362x 3y 3 05.设x , y 满足约束条件 2x 3y 3 0,则z 2x y 的最小值是()y 3 02017年普通高等学校招生全国统一考试(全国卷2)、选择题:本题共12小题,每5分,共60分。
在每小题给出的四个选项中,只有 2.设集合A1,2,4 ,4x•若 AI B{1},则 B3. A.1, 3 1,01,31,5我国古代数学名着《算法统宗》中有如下问题:"远望巍巍塔七层,红光点点倍加增,共 2i26. 7. 8. 9. 10. 11. 12. A.15安排3名志愿者完成 排方式共有( )A. 12 种4项工作,每人至少完成.18种1项,每项工作由 .24种 1人完成,则不同的安.36种甲乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有位优秀,2位良好,我现在给甲看乙、 后甲对大家说:我还是不知道我的成绩. A.乙可以知道四人的成绩 C.乙、丁可以知道对方的成绩 执行右面的程序框图,如果输入的 A. B. C. D.若双曲线C: A. 2C. 2丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看 根据以上信息,则( .丁可以知道四人的成绩 2x~~2a已知直三棱柱 4所截得的弦长为2,.-.3.乙、丁可以知道自己的成绩DABC AB1G 中,C 120o ,C CC 1 1,则异面直线 1与G 所成角的余弦值为(15 5.10 5若x 2是函数f(x)(x 2axx 1'1)e 的极值点,则f(x)的极小值为A. 1B.2e 3C.5e 3D.1已知 ABC 是边长为2uun 的等边三角形, P 为平面ABC 内一点,贝U PA uuu uuu(PB PC)的最小值是( ) 3 4 A. 2B.C.D.123二、填空题:本题共 4小题,每小题5分,共20分。
浙江省稽阳联谊学校2024届高三上学期11月联考数学试题含解析
2023年11月稽阳高三联考数学试题卷(答案在最后)考生须知:1.本试题卷分选择题和非选择题两部分,满分150分,考试时间120分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号.3.所有答案必须写在答题卷上,写在试卷上无效.4.考试结束后,只需上交答题卷.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合01x A x x ⎧⎫=<⎨⎬-⎩⎭,112B x x ⎧⎫=->⎨⎩⎭,则A B ⋃=()A.1,12⎛⎫⎪⎝⎭B.()3,1,2⎛⎫-∞⋃+∞⎪⎝⎭C.13,,22⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭D.30,2⎛⎫ ⎪⎝⎭【答案】B 【解析】【分析】解出分式不等式和绝对值不等式,根据并集含义即可得到答案.【详解】(){}{}010011xA xx x x x x x ⎧⎫=<=-<=<<⎨⎬-⎩⎭,112x ->即112x ->或112x -<-,解得12x <或32x >,则1{|2B x x =<或3}2x >,则()3,1,2A B ⎛⎫-∞⋃+∞⋃ ⎝=⎪⎭,故选:B.2.已知复数z 满足()12i 3i z -=+,则z z ⋅=()A.175i+ B.45C.2D.1【答案】C 【解析】【分析】根据复数除法运算结合共轭复数的概念即可.【详解】由题意得3i (3i)(12i)17i12i (12i)(12i)5z ++++===--+,则17i 17i 5025525z z -+⋅=⋅==,故选:C.3.已知平面向量a ,b ,c 均为单位向量,则“3a b c +-= ”是“a 与b共线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】利用向量加法的三角形不等式,结合充分条件、必要条件的定义判断即得.【详解】平面向量a ,b ,c 均为单位向量,则||||||||3a b c a b c +-≤++= ,当且仅当,,a b c -同向共线时取等号,则当3a b c +-= 时,a 与b 共线,反之,a 与b共线并且方向相反时,1a b c +-= ,所以“3a b c +-= ”是“a 与b共线”的充分不必要条件,A 正确.故选:A4.我国魏晋时期的数学家刘徽创造性的提出了“割圆术”,刘徽认为圆的内接正n 边形随着边数n 的无限增大,圆的内接正n 边形的周长就无限接近圆的周长,并由此求得圆周率π的近似值.如图当6n =时,圆内接正六边形的周长为6r ,故6π2rr≈,即3π≈.运用“割圆术”的思想,下列估算正确的是()A.12n =时,π12sin15≈B.12n =时,π6sin15≈C.12n =时,π12cos15≈D.12n =时,π24cos15≈【答案】A 【解析】【分析】求出正十二边形的周长L ,可得出π2Lr≈,即可得解.【详解】设圆的内接正十二边形被分成12个如图所示的等腰三角形,其顶角为30 ,即30AOB ∠= ,作OH AB ⊥于点H ,则H 为AB 的中点,且15AOH ∠=,因为OA OB r ==,在Rt AOH △中,sin AH AOH OA∠=,即sin15AH r =,所以,sin15AH r = ,则22sin15AB AH r == ,所以,正十二边形的周长为122sin1524sin15L r r =⨯⨯=,所以,24sin15π12sin1522L r r r≈==.故选:A.5.已知等比数列{}n a 满足2342a a a +=,()()235111a a a ++=-,则1a 的值不可能...是()A.2-B.14C.1D.2【答案】D 【解析】【分析】根据题意求出首项和公比即可得解.【详解】设公比为()0q q ≠,由2342a a a +=,()()235111a a a ++=-,得()()23111241112111a q a q a qa q a q a q ⎧+=⎪⎨++=-⎪⎩,解得112q a =-⎧⎨=-⎩或111q a =-⎧⎨=⎩或121q a =⎧⎨=⎩或1214q a =⎧⎪⎨=⎪⎩.故选:D .6.第33届夏季奥运会预计在2024年7月26日至8月11日在法国巴黎举办,这届奥运会将新增电子竞技和冲浪两个竞赛项目以及滑板等5个表演项目.现有三个场地A ,B ,C 分别承担竞赛项目与表演项目比赛,其中电子竞技和冲浪两个项目仅能A ,B 两地承办,且各自承办其中一项.5个表演项目分别由A ,B ,C 三个场地承办,且每个场地至少承办其中一个项目,则不同的安排方法有()A.150种 B.300种C.720种D.1008种【答案】B【解析】【分析】根据组合数与排列数的计数方法,结合分类分步两个基本原理求解即可得的答案.【详解】首先电子竞技和冲浪两个项目仅能,A B 两地举办,且各自承办其中一项有22A 2=种安排;再次5个表演项目分别由,,A B C 三个场地承办,且每个场地至少承办其中一个项目则有3211253534C A C C C 150+=种,故总数为2150300⨯=种不同的安排方法.故选:B.7.已知()()221x x b f x b -=∈+R 是奇函数,实数m 、n 均小于1,e 2.71828= 为自然对数底数,且22log 2e 1e m b -+-=,22log 4e 14e n b -+-=,则()A.0m n <<B.0n m << C.01m n <<< D.01n m <<<【答案】B 【解析】【分析】利用函数奇偶性的性质可得出1b =,由已知可得出()22log 1e 1m -=-,()22log 12e 1n -=-,由()()22e 12e 1-<-结合对数函数的单调性可得出11m n -<-,可得出()()20m n m n -+-<,可得出n m <,并推导出1m <-、1n <-,即可得解.【详解】对任意的x ∈R ,210x+>,则函数()()221x x bf x b -=∈+R 的定义域为R ,因为函数()()221x x b f x b -=∈+R 为奇函数,则()1002b f -==,可得1b =,所以,()2121x x f x -=+,()()()()22121122112221x xx xx xx x f x f x --------====-+++,则函数()f x 为奇函数,合乎题意,因为22log 12e 1e m -+-=,22log 14e 14e n -+-=,则()222log 1e 2e 1e 1m -=-+=-,()222log 14e 4e 12e 1n -=+=--,因为()()22e 12e 1-<-,则22log 1log 1m n -<-,所以,11m n -<-,即()()2211m n -<-,即22220m m n n --+<,即()()20m n m n -+-<,因为1m <,1n <,则2m n +<,则20m n +-<,故0m n ->,即n m <,又因为()22log 1e 11m -=->,即12m ->,可得12m -<-或12m ->,则1m <-或3m >,即1m <-,同理可知,1n <-,故0n m <<.故选:B.8.椭圆2222Γ:1(0)x y a b a b+=>>的左焦点为F ,右顶点为A ,过点F 的倾斜角为45 的直线l 交椭圆Γ于点M ,N (点M 在x 轴的上方).若AMF 为等腰直角三角形,则椭圆Γ的离心率是()A.1- B.12C.2D.34【答案】C 【解析】【分析】求出,22a c a c M -+⎛⎫⎪⎝⎭,代入椭圆方程化简得到关于e 的方程,解出即可.【详解】显然90AMF ︒∠=,则由题意得2M a c x -=,则22M a c a cy a -+=-=,又因为点,22a c a c M -+⎛⎫ ⎪⎝⎭在椭圆Γ上,所以2222()()144a c a c a b -++=,即()22222()()144a c a c a a c -++=-,即()22()()144a c a c a a c -++=-,根据c e a=得2(1)1144(1)e e e -++=-,整理得323220e e e --+=.所以()2(1)420e e e +-+=,解得2e =,(其中21,10e e =+>=-<均舍去),故选:C.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知函数()()πsin 210,2f x A x A ϕϕ⎛⎫=++>< ⎪⎝⎭,()π3f x f ⎛⎫≤ ⎪⎝⎭对任意的x ∈R 恒成立,则()A.()f x 的一个周期为π2B.()f x 的图像关于直线2π3x =-对称C.()f x 在区间5ππ,4⎡⎤⎢⎥⎣⎦上有1个极值点 D.()f x 在区间5ππ,4⎡⎤⎢⎥⎣⎦上单调递增【答案】BD 【解析】【分析】对于A ,求得最小正周期即可判断;对于B ,由题意求得π6ϕ=-,检验2π3x =-πsin 26x ⎛⎫- ⎪⎝⎭是否为1±即可判断;对于CD ,由5ππ,4x ⎡⎤∈⎢⎥⎣⎦可得π11π7π2,366x ⎡⎤-∈⎢⎣⎦,从而可得()f x 在区间5ππ,4⎡⎤⎢⎥⎣⎦上单调递增,没有极值点,即可判断.【详解】对于A ,()f x 的最小正周期2ππ2T ==,A 错;对于B ,因为()π3f x f ⎛⎫≤ ⎪⎝⎭对任意的x ∈R 恒成立,所以当π3x =时,()f x 取得最大值,所以ππ22π,Z 32k k ϕ⨯+=+∈,解得π2π,Z 6k k ϕ=-+∈,又因为π2ϕ<,所以π6ϕ=-,所以()πsin 216f x A x ⎛⎫=-+ ⎪⎝⎭,所以当2π3x =-时,π4ππsin 2sin 1636x ⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭,所以()f x 的图像关于直线2π3x =-对称,B 对;对于CD ,因为5ππ,4x ⎡⎤∈⎢⎥⎣⎦,所以π11π7π2,366x ⎡⎤-∈⎢⎥⎣⎦,所以()f x 在区间5ππ,4⎡⎤⎢⎥⎣⎦上单调递增,没有极值点,C 错D 对.故选:BD.10.已知()()P A P A =,()()||P B A P B A >,则()A.()()P B P A >B.()()P A B P A B⋅>⋅C.()()||P A B P A B > D.()()P A B P A B⋅<⋅【答案】BD 【解析】【分析】根据对立事件的性质结合已知可得()()12P A P A ==,利用条件概率公式和全概率公式推导可判断ABD ;举特例可判断C.【详解】由对立事件性质知,()()1P A P A +=,又()()P A P A =,所以()()12P A P A ==,因为()()||P B A P B A >,所以()()()()P BA P BA P A P A >,所以()()P BA P BA >,B 正确;又因为()()()()()()P AB P AB P A P A P AB P AB +===+,所以()()()()0P AB P AB P AB P AB -=-<,得()()P AB P AB <,D 正确;由()()P BA P BA >,()()P AB P AB <得()()()()P AB P AB P AB P AB +>+,则()()P B P B >,又()()1P B P B +=,所以()()12P B P B >>,故()()P B P A <,A 错误;以掷一颗骰子为例,不妨记事件A :掷出的点数为奇数;事件B :掷出的点数为1点或3点.则A :掷出的点数为偶数;B :掷出的点数为2点或4点或5点或6点.易知,()()()()112,,233P A P A P B P B ====,()()()()111,0,,362P AB P AB P AB P AB ====,所以()()()()()()1|,|03P BA P BA P B A P B A P A P A ====满足题设()()P A P A =,()()||P B A P B A >,但()()()()()()1|0,|4P AB P AB P A B P A B P B P B ====,故C 错误.故选:BD11.在底面为菱形的直四棱柱1111ABCD A B C D -中,P 为1CC 中点,点Q 满足1DQ DB DD λμ=+,()0,1λ∈,()0,1μ∈()A.当1λμ+=时,1B Q AC ⊥B.当1λμ+=时,11B Q A C ⊥C.当12λμ+=时,//PQ 平面11AC D D.当12λμ+=时,//PQ 平面11AB D 【答案】AC 【解析】【分析】根据共面向量定理和共线向量定理结论结合线面垂直的判定、面面平行的判定和性质一一分析即可.【详解】由题意得三向量共面,当1λμ+=,根据共线向量定理的结论知1Q BD ∈(不与边界点重合),因为底面为菱形的直四棱柱,AC BD ⊥,1DD ⊥底面ABCD ,因为AC ⊂平面ABCD ,所以1DD AC ⊥,又因为1,BD DD ⊂平面11BDD B ,1BD DD D = ,所以AC ⊥平面11BDD B ,因为1B Q ⊂平面11BDD B ,所以1AC B Q ⊥,故A 正确;对B ,若11B Q A C ⊥,且由A 知1AC B Q ⊥,又因为1,AC AC ⊂平面11AA C C ,且1AC C AC ⋂=,所以1B Q ⊥平面11AA C C ,根据A 中的同样方法可证明11B D ⊥平面11AA C C ,则111//B Q D B ,显然不可能,故B 错误;对C ,当12λμ+=时,设BD 的中点为O ,1DD 的中点为M ,则22M DQ DO D λμ=+,则根据()21λμ+=可知Q OM ∈(不包含边界),根据中位线可知1//OP AC ,1AC ⊂平面11AC D ,OP ⊄平面11AC D ,所以//OP 平面11AC D ,同理根据11//PM C D 可得//PM 平面11AC D ,因为OP PM P = ,且,OP PM ⊂平面OPM ,所以平面//OPM 平面11AC D ,因为PQ ⊂平面OPM ,所以//PQ 平面11AC D ,故C 正确;对D ,由平面11AB D 与平面11AC D 相交,所以平面11AB D 与平面OPM 相交,则无法得到//PQ 平面11AB D ,故D 错误.故选:AC.12.已知定义在R 上的函数()f x ,()g x ,其导函数分别为()f x ',()g x ',()()6f x g x =-',()()161f x g x -=++',且()2g x -为奇函数,则()A.()02g =B.()()2f x f x +'='C.()()4g x g x +=D.()()()()113324f g f g +=【答案】ACD【解析】【分析】先根据条件分析出()g x '的周期性对称性,再得到()f x 的周期性的对称性,最后由求导得到()f x '和()g x 的周期性和对称性,代入求解即可.【详解】由题意得()()()()6161f x g x f x g x ⎧=-⎪⎨-=+'+'⎪⎩,所以()()()()161161f x g x f x g x ⎧-=--⎪⎨-+'=+'⎪⎩,两式相减可得()()11g x g x +=-'-'①,所以()g x '关于点()1,0中心对称,又因为()2g x -为奇函数,所以()()()222g x g x g x -=---=--+⎡⎤⎣⎦②,即()()4g x g x +-=,所以()g x 关于点()0,2中心对称,而()g x 定义域为R ,所以()g 02=,A 正确;②式两边对x 求导可得()()g x g x ''=-,所以()g x '是偶函数,以1x +替换①中的x 可得()()()2g x g x g x '''+=--=-,所以()()()42g x g x g x '''+=-+=,所以()g x '是最小正周期为4的周期函数,因为()()6f x g x =-',所以()f x 也是最小正周期为4的周期函数,即()()4f x f x +=,两边求导可得()()4f x f x ''+=,所以()f x '也是最小正周期为4的周期函数,所以()()2f x f x +'='不恒成立,B 错误;由①得()()11g x g x C +=-+,令0x =,解得0x =,所以()()11g x g x +=-③,即()g x 关于直线1x =对称,以1x +替换③中的x 可得()()2g x g x +=-,由②可知()()4g x g x -=-,所以()()24g x g x +=-④,所以()()()442g x g x g x +=-+=,所以C 正确;由上可知()g x '关于点()1,0中心对称,所以()10g '=又因为()g x '是偶函数,所以()()110g g ''-==又因为()g x '是最小正周期为4的周期函数,所以()()310g g ''=-=,由条件()()6f x g x =-'可得()()()()16163636f g f g ⎧=-=⎪⎨=='-'⎪⎩,所以()()()()()()()()()11336163613f g f g g g g g +=+=+,由④知()()134g g +=,所以()()()()11336424f g f g +=⨯=,D 正确,故选:ACD【点睛】关键点睛:解决这类题的关键是熟练掌握对称与周期的关系,若关于两点(纵坐标相同)或者两条直线(平行于y 轴)对称,则周期为这两点或者这两条直线的距离的两倍,若关于一点和一直线(平行于y 轴)对称,则周期为这点和这条直线的距离的四倍.三、填空题:本题共4小题,每小题5分,共20分.13.已知锐角θ满足1sin 3θ=;则ππsin(sin()44θθ+--=________.【答案】43##113【解析】【分析】根据给定条件,利用同角公式、和差角的正弦公式计算得解.【详解】锐角θ满足1sin 3θ=,则cos 3θ==,所以πππ4sin()sin(2cos sin 44433θθθ+--===.故答案为:4314.已知0a >,0b >,193a b -=,则128181ab a b++的最小值为________.【答案】29【解析】【分析】依题意得,21a b +=,则122181818181a b ab ab ab a b ab ab+++=+=+,由基本不等式求解即可.【详解】解:依题意得,2133a b -=,则21a b +=,故12212818181819a b ab ab ab a b ab ab +++=+=+≥=,当且仅当181ab ab=时等号成立,又21a b +=,解得1112,,或,3363a b a b ====,所以128181ab a b++的最小值为29.故答案为:29.15.已知抛物线2:4C x y =,圆222:(4)(0)M x y r r +-=>,若抛物线C 与圆M 有四个公共点,则r 的取值范围为________.【答案】()【解析】【分析】根据抛物线与圆的交点个数联立消元列不等式求解即可得r 的取值范围.【详解】联立方()222244x yx y r⎧=⎪⎨+-=⎪⎩消去x 整理得224160y y r -+-=因为抛物线C 与圆M 有四个公共点,所以()22Δ164164480rr=--=->,且2160r ->所以解得4r <<,则r的取值范围为().故答案为:().16.体积为111ABC A B C -中,2AB =,3AC =,则此三棱柱外接球的表面积的最小值为________.【答案】18π【解析】【分析】设直三棱柱111ABC A B C -的高为h ,ABC 外接圆的半径为r ,(),0,πBAC θθ∠=∈,直三棱柱111ABC A B C -外接球的的半径为R ,根据棱柱的体积可得7sin h θ=,利用正弦定理求出ABC 外接圆的半径,再利用勾股定理求出2R 的最小值,再根据球的表面积公式即可得解.【详解】设直三棱柱111ABC A B C -的高为h ,ABC 外接圆的半径为r ,(),0,πBAC θθ∠=∈,直三棱柱111ABC A B C -外接球的的半径为R ,则123sin 2h θ⨯⨯⋅=,所以sin h θ=,在ABC 中,由余弦定理可得49223cos 1312cos BC θθ=+-⨯⨯=-,则1312cos 2sin sin BC r θθθ-==,所以1312cos 2sin r θθ-=,所以22222221312cos 753cos 53cos 924sin 2sin sin 99cos h R r θθθθθθθ---⎛⎫=+=+==⋅ ⎪-⎝⎭,令()53cos ,2,8t t θ=-∈,则3cos 5t θ=-,则()222999916101629510t tR t t t t t ===≥=-+-⎛⎫---+ ⎪⎝⎭,当且仅当16t t =,即4t =,即1cos 3θ=时取等号,所以此三棱柱外接球的表面积的最小值为94π18π2⨯=.故答案为:18π.【点睛】方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.17.记ABC的内角A,B ,C 的对边分别为a ,b,c ,已知()223sin sin 2sin sin 8sin sin cos A C A C A C B +=+.(1)证明:2a c b +=;(2)若11cos 14B =,ABC ,求ABC 的周长.【答案】(1)证明见解析(2)15【解析】【分析】(1)根据正、余弦定理进行角换边即可证明;(2)首先求出sin B =,再结合三角形面积公式得21ac =,最后利用(1)中结论和余弦定理即可求出周长.【小问1详解】由正弦定理及余弦定理可得:()()22222222328242a c b a cac ac ac a c b ac+-+=+=++-化简得:22()42a c b a c b +=⇒+=.【小问2详解】因为11cos 14B =,且B 为三角形内角,sin B ∴==.11sin 22ABC S ac B ac ∴==⋅ ,所以21ac =.由余弦定理可得:2222cos a c b ac B =+-,所以22()2(cos 1)a c b ac B +-=+,112,cos ,2114a cb B ac +=== ,2211422117514b b ⎛⎫∴-=⨯⨯+= ⎪⎝⎭,即225,5b b ==,所以周长为315a c b b ++==.18.如图,在四棱锥S ABCD -中,底面ABCD 为矩形,平面SAB ⊥平面ABCD ,2AB AS ==,SB =1AD =,G 为ABC 的重心,(1)SB SE λλ=>.(1)当直线//GE 平面SDC 时,求λ的值;(2)当32λ=时,求平面CAE 与平面DAE 的夹角的大小.【答案】(1)32λ=;(2)π4.【解析】【分析】(1)利用线面平行的性质,结合三角形重心定理求解即得.(2)在平面SAB 内作Ax AB ⊥,以点A 为原点建立空间直角坐标系,利用面面角的向量求法求解即得.【小问1详解】连接DB AC O = ,由四边形ABCD 是矩形,得O 是AC 中点,而G 为ABC 的重心,则点G 在线段DB 上,有2133BG BO BD ==,于是2DGGB=,由//GE 平面SDC ,GE Ì平面SDB ,平面 SDB 平面SDC SD =,得//GE DS ,因此2SE DGEB GB==,所以32λ=.【小问2详解】在SAB △中,32,2AB AS SB ===,则132cos 2SBSBA AB ∠==,有30SBA ∠= ,在平面SAB 内作Ax AB ⊥,由平面SAB ⊥平面ABCD ,平面SAB 平面ABCD AB =,得Ax ⊥平面ABCD ,显然射线,,Ax AB AD 两两垂直,以点A 为坐标原点,射线,,Ax AB AD 分别为,,x y z 轴非负半轴,建立空间直角坐标系,由(1)知,33BE =,则3(0,0,0),(0,0,1),(0,2,0),(0,2,1),(,1,0)3A DBC E ,(0,0,1),(,1,0),(0,2,1)3AD AE AC === ,设平面DAE 的一个法向量为1(,,)n x y z = ,则11003n AD z n AE x y ⎧⋅==⎪⎨⋅=+=⎪⎩,令1y =,得1(n = ,设平面CAE 的一个法向量为2(,,)n a b c =,则222003n AC b c n AE a b ⎧⋅=+=⎪⎨⋅=+=⎪⎩,令a =,得21,2)n =- ,设平面CAE 与平面DAE 的夹角为θ,因此121212||cos |cos ,|2||||n n n n n n θ⋅=〈〉===,从而π4θ=,所以平面CAE 与平面DAE 的夹角的大小为π4.19.电网公司将调整电价,为此从某社区随机抽取100户用户进行月用电量调查,发现他们的月用电量都在50350kw h ~⋅之间,进行适当分组后(每组为左闭右开区间),画出如图所示的频率分布直方图.调价方案为:月用电量在kw h m ⋅以下(占总数的71%)的用户电价不变,月用电量在kw h m ⋅以上则电价将上浮10%.(1)求a 和m 的值;(2)若采用按比例分配的分层随机抽样的方法,从月用电量不低于250kw h ⋅的用户中抽9户用户,再从这9户用户中随机抽取3户,记月用电量在区间[)300,350内的户数为ξ,试求ξ的分布列和数学期望.【答案】(1)0.0044,225a m ==(2)分布列见解析,数学期望为1【解析】【分析】(1)根据频率分布直方图利用频率之和为1可求得a 的值,结合百分位数的估计可得m 的值;(2)利用分层抽样得两组各抽取样本数,结合超几何分布求解概率即可得分布列,从而可求数学期望.【小问1详解】因为()500.00240.00360.00600.00240.00121a ⨯+++++=所以0.0044a =第一到第六组的频率依次为:0.12,0.18,0.30,0.22,0.12,0.06前三组频率之和为0.120.180.300.60++=,前四组频率之和为0.120.180.300.220.82+++=,则第71百分位数m 在[)200,250区间内,所以()0.120.180.302000.00440.71m +++-⨯=,解得225m =;【小问2详解】月用电量在[)250,300,[)300,350的频率分别为:0.12,0.06,据按比例分配的分层随机抽样可知:用电量在[)250,300,[)300,350的分别有6人,3人,从而ξ可取的值为:0,1,2,3.()()()()32112366363333339999C C C C C C 515310,1,2,3C 21C 28C 14C 84P P P P ξξξξ============故ξ的分布列为:ξ123P5211528314181则()515310123121281484Eξ=⨯+⨯+⨯+⨯=20.已知各项非零的数列{}n a ,其前n 项的和为n S 2n a c =+.(1)若0c =,证明:221n n a a +>;(2)是否存在常数c ,使得{}n a 是等差数列?若存在,求出c 的所有可能值;若不存在,说明理由.【答案】(1)证明见解析;(2)存在,18c =.【解析】【分析】(1)利用给定的递推公式,结合已知可得0n a >,再借助11n n n S S a ++-=推理即得.(2)假定存在,利用等差数列的通项公式建立关于n 的恒等式,再分析计算判断即得.【小问1详解】由0c =2n a =12a =,又数列{}n a 的首项不为零,则114a =,由20,0n n a a =≥≠,于是0n a >,由21214,4n n n n S a a S ++==,得1112240()n n n n n S a a S a +++-=-=>,所以221n n a a +>.【小问2详解】2n a c =+,得22)(n n S a c =+,有2112)(n n S a c ++=+,两式相减并整理得:1114(())n n n n n a a a a a c +++=-++,假设存在常数c ,使得{}n a 是等差数列,设公差为d ,则有114[2(21)]a nd d a n d c +=⋅+-+,因此对任意*N n ∈,2211)(8448a dn a d cd d d n +=+-+恒成立,从而21128448a a d cd d d d ⎧=+-⎨=⎩,解得10a d ==(舍去)或18c d ==,1128a =+,解得1116a =,则2116n n a -=,所以存在c ,使得{}n a 是等差数列,此时121,816n n c a -==.21.双曲线2222:1(0,0)x y C a b a b-=>>的左顶点为A ,右焦点为F ,动点B 在C 上.当BF AF ⊥时,2AF BF =,且ABF △的面积为254.(1)求双曲线C 的方程;(2)若点B 在第一象限,且有3BFA BAF ∠=∠,求点B 的横坐标.【答案】(1)22145x y -=;(2)298+.【解析】【分析】(1)根据给定条件,求出点B 的坐标,进而求出|BF |,再结合三角形面积求出22,a b 即得.(2)设出点B 的坐标,利用斜率坐标公式及倍角的正切公式列式计算即得.【小问1详解】设双曲线的半焦距为c ,则(c,0)F ,由222222x c b x a y a b=⎧⎨-=⎩,得2(,)bB c a ±,由||2||AF BF =,得22b aa c =+,于是2()c a a -=,即35,22c a b a ==,由ABF △的面积为254,得2125()24b a c a ⋅+⋅=,解得224,5a b ==,所以双曲线C 的方程为22145x y -=.【小问2详解】设()00,B x y ,其中220000,0,145x y x a y >>-=,当0x c =时,有BF AF ⊥,||2||AF BF =,则1πtan 232BAF BFA ∠=≠∠=,此时3BFA BAF ∠≠∠,因此0x c ≠,设直线AB 、BF 的倾斜角分别为,αβ,则有,πBAF BFA αβ∠=∠=-,又00tan tan(π)tan 3y BFA x ββ∠=-=-=--,00tan tan 2y BAF x α∠==+,则22222tan tan tan tan 2tan (3tan )1tan tan 32tan 1tan tan 213tan 1tan 1tan αααααααααααααα++--===-⋅--⋅-20022220000000022222000000005[3()[3(2)(4)]22[3(2)]415(2)[(2)3](2)[(2)(4)]13()2]4y y y x x x x y x y y x x y x x x x ⋅-+--+++-===++-++---+0000020000(2)(734))734)(2)(3811(2)(381)1(y x x y x x x x x +++==+-+-,当3BFA BAF ∠=∠时,有000000734)tan 3tan (2)(33(8)11y x yBFA x x x α+==-=∠+--,所以0000(734)(3)(2)(38110)x x x x +-++-=,即200429260x x -+=,解得0298x ±=,而02x >,于是0298x +=,所以点B的横坐标为298+.【点睛】关键点睛:本题第2问,设出点B 的坐标,利用斜率坐标公式,结合倍角公式列出方程是求解问题的关系.22.已知函数()2ex f x a -=,()12ln g x x x x ⎛⎫=++ ⎪⎝⎭,e 2.71828= 为自然对数底数.(1)证明:当1x >时,1ln 22x x x<-;(2)若不等式()()f x g x >对任意的()0,x ∈+∞恒成立,求整数a 的最小值.【答案】(1)证明见解析;(2)4.【解析】【分析】(1)记()()1ln ,122x h x x x x=-->,利用导数研究单调性,结合()10h =可证;(2)构造函数()()()m x f x g x =-,根据()92ln 202m a =->确定4a ≥,再构造函数()211222e x x x x x x ϕ-⎛⎫⎛⎫++- ⎪⎪⎝⎭⎝⎭=,利用导数求函数()x ϕ的最大值,结合(1)中结论即可确定a 的最小值.【小问1详解】记()()1ln ,122x h x x x x=-->,则()222111112111102222h x x x x x x ⎛⎫⎛⎫=+-=-+=-> ⎪ ⎪⎝⎭⎝⎭',所以()h x 在()1,+∞上单调递增,又()111ln1022h =--=,所以,当1x >时,()1ln 022x h x x x =-->,即1ln 22x x x<-.【小问2详解】令()()()21e 2ln x m x f x g x a x x x -⎛⎫=-=-++ ⎪⎝⎭,由题可知,当()0,x ∈+∞时,()0m x >恒成立.因为()92ln 202m a =->,所以9ln 22a >,因为28e >,所以ln82>,即2ln 23>,所以992ln 23223a >>⨯=,因为a ∈Z ,所以4a ≥.当(]0,1x ∈时,ln 0x ≤,故()0m x >.当()1,x ∈+∞时,不等式()()f x g x >等价于212ln ex x x x a -⎛⎫++ ⎪⎝⎭>,设()222211212e 222e 2e x xx x x x x x x x x ϕ-⎛⎫⎛⎫⎛⎫++-+-- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭==,由(1)知,()212ln ex x x x x ϕ-⎛⎫++ ⎪⎝⎭>,()2223232e 22e xx x x x x ϕ⎛⎫-++++ ⎪⎝⎭'=,记()2232322n x x x x x=-++++,易知,()n x 在()1,+∞上单调递减,且()2232322220222n =-++++=,所以,当()1,2x ∈时,()0n x >,即()0x ϕ'>,()x ϕ单调递增;当()2,x ∈+∞时,()0n x <,即()0x ϕ'<,()x ϕ单调递减.故当2x =时,()x ϕ取得最大值()222221e 222272222e 8ϕ⎛⎫+⨯-- ⎪⎝⎭==.所以,()212ln 4e x x x x x ϕ-⎛⎫++ ⎪⎝⎭>>在区间()0,∞+上恒成立,所以,整数a 的最小值为4.【点睛】本题难点有二:一是通过取特值确定4a ≥,二是利用(1)中结论进行放缩,构造函数()211222e x x x x x x ϕ-⎛⎫⎛⎫++- ⎪⎪⎝⎭⎝⎭=,利用导数求最值即可.对于参变分离之后,函数复杂,不宜直接研究时经常采取适当放缩进行处理.。
陕西省十七校联考2024-2025学年高三上学期11月期中考试数学试题含答案
2025届高三第一学期期中考试检测卷数学(答案在最后)全卷满分150分,考试时间120分钟.注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将条形码粘贴在答题卡上的指定位置.2.请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷、草稿纸和答题卡上的非答题区域均无效.3.选择题用2B 铅笔在答题卡上把所选答案的标号涂黑;非选择题用黑色签字笔在答题卡上作答;字体工整,笔迹清楚.4.考试结束后,请将试卷和答题卡一并上交.5.本卷主要考查内容:高考范围.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数2i1i z -=-,则z 的虚部为()A.12-B.12C.1i2- D.1i 2【答案】A 【解析】【分析】利用复数的除法运算求出z ,再利用共轭复数及复数的意义即可得解.【详解】依题意,2i (2i)(1i)3i 31i 1i (1i)(1i)222--++====+--+z ,则31i 22z =-,所以z 的虚部为12-.故选:A2.已知集合{}13A x x =-<<,集合{}24B x x =≤<,集合{}14C x x =-<<,则()A.A B B =B.A B =∅C.C B =∅I D.A C C= 【答案】D 【解析】【分析】根据交集、并集的定义计算可得.【详解】因为集合{}13A x x =-<<,集合{}24B x x =≤<,集合{}14C x x =-<<,所以{}|14A B x x B ⋃=-<<≠,{}|23A B x x ⋂=≤<≠∅,{}24C B x x B ⋂=≤<=≠∅,{}14A C x x C ⋃=-<<=,故正确的只有D.故选:D 3.已知11tan ,tan()23ααβ=+=,则tan β=()A.16 B.17-C.17D.56【答案】B 【解析】【分析】利用角的变换()βαβα=+-,代入两角差的正切公式即可求解.【详解】11132tan tan[()]1716βαβα-=+-==-+.故选:B.【点睛】本题主要考查了角的变换,两角差的正切公式,属于基础题.4.已知23a =,ln 3b =,4πc =,则a ,b ,c 的大小关系为()A.a b c >>B.b a c>> C.a c b>> D.c b a>>【答案】A 【解析】【分析】本题根据指数函数、对数函数的性质借助中间值1比较可得.【详解】因为23a =,所以ln 2ln 3a =,即ln 3ln 2a =,又ln1ln 2ln e <<,即ln 210<<,又ln 3ln e=1>,所以ln 3ln 3ln 2a =>,所以1a b >>;因为4πc =,所以22πc =,所以22log πc =,所以2221log πlog log 12c ===所以a b c >>.故选:A.5.60C 是一种由60个碳原子构成的分子,形似足球,又名足球烯,其分子结构由12个正五边形和20个正六边形组成.如图,将足球烯上的一个正六边形和相邻正五边形展开放平,若正多边形的边长为1,,,A B C 为正多边形的顶点,则⋅=AB AC ()A.1B.2C.3D.4【答案】B 【解析】【分析】运用数量积定义计算即可.【详解】如图所示,连接BA ,BC ,由对称性可知,BA BC =,取AC 的中点H ,则AC BH ⊥,12AH AC =,又因为正六边形的边长为1,所以2AC =,所以cos 2AB AC AC AB BAC AC AH ⋅=⋅∠=⋅=,故选:B .6.已知某圆锥的侧面积为,轴截面面积为1,则该圆锥的母线与底面所成的角为()A.15︒B.30︒C.45︒D.60︒【答案】C 【解析】【分析】设相应长度,根据圆锥的侧面积和轴截面面积列式可得1l r h ⎧=⎪⎨==⎪⎩,再结合线面夹角运算求解.【详解】设圆锥的母线为0l >,底面半径为0r >,高为0h >,由题意可得:222π2π1212rl r h l r h ⎧=⎪⎪⨯⨯=⎨⎪=+⎪⎩,解得21l r h ⎧=⎪⎨==⎪⎩,设该圆锥的母线与底面所成的角为θ,则090θ︒<<︒,可得tan 1hrθ==,所以该圆锥的母线与底面所成的角为45θ=︒.故选:C.7.将函数()cos(2)(0)f x x ϕϕ=+>的图象向右平移6π个单位长度后得到函数()g x 的图象,若点,04π⎛⎫- ⎪⎝⎭是函数()y g x =图象的一个对称中心,则ϕ的最小值为()A.6π B.4π C.3π D.43π【答案】C 【解析】【分析】先求出平移后函数解析式,再由图象的对称中心,可得ϕ,从而得出结论.【详解】由已知得()cos 23g x x πϕ⎛⎫=-+ ⎪⎝⎭,所以232k πππϕπ--+=+,解得4()3k k Z πϕπ=+∈,又0ϕ>,当1k =-时,min 3πϕ=.故选:C.【点睛】本题考查三角函数的图象平移变换,考查函数的对称性,掌握诱导公式是解题关键.平移变换时要注意平移单位是对自变量x 而言,属于中档题.8.已知函数()()()22e 2e R xx f x x a a a =+-+∈的最小值为()g a ,则()g a 的最小值为()A.e -B.1e-C.0D.1【答案】B 【解析】【分析】由二次函数的性质可知()e xf x x ≥,令()e xP x x =,运用导数可求得()P x 的最小值,进而可得结果.【详解】因为()()()222e 2e e e e x x x x x f x x a a a x x =+-+=-+≥,令()e xP x x =,则()()e1xP x x ='+,当(),1x ∈-∞-时,()0P x '<,()P x 单调递减,当()1,x ∈-+∞时,()0P x '>,()P x 单调递增,()()11e P x P ∴≥-=-,()1e ex f x x ∴≥≥-,故选:B .二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.在62x⎛⎝的展开式中,下列命题正确的是()A.二项式系数之和为64B.所有项系数之和为1-C.常数项为60D.第3项的二项式系数最大【答案】AC 【解析】【分析】对于A :根据二项式系数之和为2n 分析判断;对于B :令1x =,可得所有项系数之和;对于C :结合二项展开式的通项分析求解;对于D :根据二项式系数的最值分析求解.【详解】对于选项A :因为6n =,可知二项式系数之和为6264=,故A 正确;对于选项B :令1x =,可得所有项系数之和为()6211-=,故B 错误;对于选项C :因为展开式的通项为()()36662166C 212C ,0,1,,6rr rr rr r r T x xr ---+⎛=⋅⋅=-⋅⋅⋅=⋅⋅⋅ ⎝,令3602r -=,可得4r =,所以常数项为()4245612C 60T =-⋅⋅=,故C 正确;对于选项D :因为6n =,可知二项式系数最大值为36C ,为第4项,故D 错误;故选:AC.10.已知a ,b 均为正实数,且2a b +=,则下列结论中正确的是()A.1ab ≤ B.22log log 0a b +≤C.228a b +≥D.191613a b ++≥【答案】ABD 【解析】【分析】根据基本不等式结合对数与指数的运算性质逐一分析即可得出答案.【详解】对于A ,2a b +=,∴212a b ab +⎛⎫≤= ⎪⎝⎭,故A 正确;对于B ,2222log log log log 10a b ab +==≤,故B 正确;对于C ,22224a b +===≥,故C 错误:对于D ,()191191131a b a b a b ⎛⎫+=+++ ⎪++⎝⎭11911610103133b a a b ⎛+⎛⎫=++≥+= ⎪ +⎝⎭⎝,故D 正确.故选:ABD.11.已知函数()21e 2xf x x x =--,则下列说法正确的是()A.函数()f x 在R 上单调递增B.0x =是函数()f x 的极值点C.过原点O 仅有一条直线与曲线()y f x =相切D.若0a b +>,则()()2f a f b +>【答案】ACD 【解析】【分析】求导根据导函数即可得出函数的单调性以及极值,进而判断A 、B 项;设出切点坐标,根据已知列出关系式,构造函数,根据导数研究函数的性质得出函数零点的个数,即可判断C 项;根据函数的单调性,得出()()()()f a f b f b f b +>+-,整理即可构造()2e exxh x x -=+-,利用导函数求出函数的最小值,即可得出D 项.【详解】对于A 项,由已知可得()e 1xf x x '=--,令()e 1xg x x =--,则()e 1xg x '=-.解()0g x '>可得,0x >,所以()g x 在()0,∞+上单调递增;解()0g x '<可得,0x <,所以()g x 在(),0-∞上单调递减.所以,()g x 在0x =处取得唯一极小值,也是最小值()00g =,所以,()0g x ≥恒成立,即()0f x '≥恒成立,所以函数()f x 在R 上单调递增,故选项A 正确;对于B 项,由A 可知,()f x 在R 上单调递增,故B 项错误;对于选项C ,设切点P 的坐标为21,e 2mm m m ⎛⎫-- ⎪⎝⎭,根据导数的几何意义可知,切线的斜率e 1m k m =--,所以过P 的切线方程为()21e (e 1)2mm y m m m x m ⎛⎫---=--- ⎪⎝⎭.又切线经过原点,所以有()()21e e 12mm m m m m ⎛⎫---=--- ⎪⎝⎭,整理为()211e 02mm m --=.令()()211e 2xh x x x =--,有()()e 1x h x x '=-,当0x ≥时,e 1x ≥,有()0h x '>;当0x <时,e 1x <,有()0h x '>.所以()0h x '≥恒成立,函数()h x 单调递增.又由()010h =-<,()22e 20h =->,根据零点存在定理可得函数()h x 在区间()0,2内有且仅有一个零点.故过原点O 仅有一条直线与曲线()y f x =相切,选项C 正确;对于D 选项,若0a b +>,有a b >-,由函数()f x 单调递增,有()()f a f b >-,()()()()22211e e e e 22bb b b f a f b f b f b b b b b b --+>+-=--+-+=+-.令()2e exxh x x -=+-,有()e e 2x x h x x -=--'.令()e e2xxx x ϕ-=--,有()e e 220x x x ϕ-=+-≥-='(当且仅当0x =时取等号),可得()0x ϕ'≥恒成立,所以函数()x ϕ单调递增.又由()00ϕ=,所以0x <时,()0x ϕ<,()0h x '<,所以()h x 在(),0-∞上单调递减;0x >时,()0x ϕ>,()0h x '>,所以()h x 在()0,∞+上单调递增.所以,()h x 在0x =处取得唯一极小值,也是最小值()02h =,所以()()02h x h ≥=,故()()2f a f b +>成立,选项D 正确.故选:ACD .三、填空题:本题共3小题,每小题5分,共15分.12.有一座六层高的商场,若每层所开灯的数量都是下面一层的两倍,一共开了1890盏,则底层所开灯的数量为______盏.【答案】30【解析】【分析】根据给定条件,构造等比数列,再利用等比数列列n 项和公式计算即得.【详解】依题意,从下往上每层灯的数据构成等比数列{}n a ,公比2q =,6n =,前6项和61890S =,于是66116(11218901)(12)a q a S q --===--,解得130a =,所以底层所开灯的数量为30盏.故答案为:3013.已知()ln f x x x =+,()e xg x x =+,若()()f a g b =,则2e 41b aa +++的最小值为_________.【答案】3【解析】【分析】合理分析题意,利用同构得到()()e bf a f =,再利用导数确定()f x 的单调性,消元后把目标式变为一元函数,利用基本不等式求解即可.【详解】因为()()f a g b =,所以ln e b b a a ++=,所以()()e bf a f =,易得()f x 定义域为(0,)x ∈+∞,而()110f x x'=+>,所以()f x 在(0,)+∞上单调递增,故e b a =,所以22e 444111b a a a a a a a ++++==++++,411131a a =++-≥-=+,当且仅当411a a +=+时取等,此时解得1a =.故答案为:3【点睛】关键点点睛:本题考查导数,解题关键是利用同构思想得到()()e bf a f =,然后化简目标式,由基本不等式得到所要求的最值即可.14.设A 为双曲线()2222Γ:10,0x y a b a b-=>>的一个实轴顶点,,B C 为Γ的渐近线上的两点,满足4BC AC =,AC a =,则Γ的渐近线方程是______.【答案】y =【解析】【分析】由角平分线定理,结合余弦定理,求得,OC OB ,再求AOC ∠的正切值,进而即可求得渐近线方程.【详解】根据题意,作图如下:依题意,OA 为COB ∠的角平分线,且444CB OA CA a ===,设OC m =,由角平分线定理可得:3OB AB OCAC==,则3OB m =;在OAC 中,由余弦定理2222cos 222AC CO OAm mOCA AC COam a+-∠===;在OBC △中,由余弦定理可得,2222cos OB OC BC OC BC OCA =+-⋅∠,即222916242m m m a m a a =+-⨯⨯⨯,解得3m a =.故cos cos 23m COA OCA a ∠=∠==,tan COA ∠=,所以Γ的渐近线方程是y =.故答案为:y =.【点睛】方法点睛:求双曲线的渐近线方程,常见有三种方法:①直接求出,a b ,从而得解;②只需要根据一个条件得到关于,,a b c 的齐次式,转化为,a b 的齐次式,从而得解;③求得其中一个渐近线的倾斜角(或斜率),从而得解.四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15.已知命题p :“x ∃∈R ,210x ax -+=”为假命题,设实数a 的所有取值构成的集合为A .(1)求集合A ;(2)设集合{}121B x m x m =+<<+,若t A ∈是t B ∈的必要不充分条件,求实数m 的取值范围.【答案】(1){}22A a a =-<<(2)12m m ⎧⎫≤⎨⎬⎩⎭【解析】【分析】(1)p 为假命题时,既可转化为关于x 的一元二次方程无解,然后利用判别式即可;(2)由t A ∈是t B ∈的必要不充分条件可得B A ,然后分B 为空集和非空集两种情况讨论即可.【小问1详解】因为命题p 为假命题,故关于x 的一元二次方程210x ax -+=无解,即()22440a a ∆=--=-<,解得22a -<<,故集合{}22A a a =-<<;【小问2详解】由t A ∈是t B ∈的必要不充分条件,可知B A ,当B =∅时,既121m m +≥+,解得0m ≤,此时满足B A ,当B ≠∅时,如图所示,故021212m m m >⎧⎪+≤⎨⎪+≥-⎩且等号不同时成立,解得102m <≤,综上所述,m 的取值范围是12m m ⎧⎫≤⎨⎬⎩⎭.16.在ABC V 中,A ,B ,C 分别为边a ,b ,c 所对的角,且满足()sin 20sin cos B C a C Bc++=⋅.(1)求B 的大小(2)若1a =,b =,求ABC V 的面积【答案】(1)2π3(2)4【解析】【分析】(1)利用正弦定理角化边,求解角度即可.(2)利用余弦定理求出边长,结合三角形面积公式求解面积即可.【小问1详解】因为()sin 20sin cos B C aC Bc++=⋅,且在ABC V 中,sin ,sin 0A C >,所以sin 20sin cos A a C B c +=⋅,由正弦定理得sin 2sin 0sin cos sin A AC B C +=⋅,所以sin 2sin sin cos sin A A C B C =-⋅,1cos 2B=-,故1cos 2B =-,()0,πB ∈,所以2π3B =.【小问2详解】在ABC V 中,由余弦定理得2113221c c+--=⨯⨯,解得1c =(负根舍去),所以111224ABC S =⨯⨯⨯=.17.如图,在直四棱柱1111ABCD A B C D -中,四边形ABCD 是矩形,11,2AC DB AA ⊥==,点P是棱1DD 上的一点,且12DP PD =.(1)求证:四边形ABCD 为正方形;(2)求直线1AD 与平面PAC 所成角的正弦值.【答案】(1)证明见解析(2)615【解析】【分析】(1)先证1BB AC ⊥,再由条件推导AC ⊥平面1BDB ,得到AC BD ⊥即可证得;(2)依题建系,写出相关点坐标,求得相关向量的坐标,利用空间向量的夹角公式计算即得.【小问1详解】如图,连接DB ,在直四棱柱1111ABCD A B C D -中,1BB ⊥平面ABCD ,AC ⊂平面ABCD ,所以1BB AC ⊥,又111111,,,AC DB BB DB B BB DB ⊥⋂=⊂平面1BDB ,所以AC ⊥平面1BDB ,又BD ⊂平面1BDB ,所以AC BD ⊥,又四边形ABCD 是矩形,所以四边形ABCD 为正方形;【小问2详解】如图,以D 为坐标原点,1,,DA DC DD 所在的直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,则)()()14,,0,0,2,0,0,3AC D P ⎛⎫ ⎪⎝⎭,所以()144,,233PA PC AD ⎫⎛⎫=-=-=⎪ ⎪⎭⎝⎭,设平面PAC 的一个法向量为(),,n x y z =,所以403403n PA z n PC z ⎧⋅=-=⎪⎪⎨⎪⋅=-=⎪⎩,故可取()n =,设直线1AD 与平面PAC 所成角的大小为θ,所以111sin cos ,,15n AD n AD n AD θ⋅====即直线1AD 与平面PAC 所成角的正弦值为615.18.驾驶员考试(机动车驾驶员考试)是由公安局车管所举办的资格考试,只有通过驾驶员考试才能取得驾照,才能合法的驾驶机动车辆.考试内容和合格标准全国统一,根据不同准驾车型规定相应的考试项目.机动车驾驶人考试内容分为道路交通安全法律、法规和相关知识考武科目(以下简称“科目一”)、场地驾驶技能考试科目(以下简称“科目二”)、道路驾驶技能和安全文明驾驶常识考试科目(以下简称“科目三”).申请人科目一、科目二、科目三考试均合格后,就可以领取驾驶证.某驾校经统计,驾驶员科目一考试平均通过的概率为1516,科目二:平均通过的概率为45,科目三平均通过的概率为45.该驾校王教练手下有4名学员参加驾驶员考试.(1)记这4名学员参加驾驶员考试,通过考试并领取驾驶证的人数为X ,求X 的分布列和数学期望及方差;(2)根据调查发现,学员在学完固定的学时后,每增加一天学习,没有通过考试拿到驾驶证的概率会降为原来的0.4,请问这4名学员至少要增加多少天的学习,才能保证这4名学员都能通过考试并领取驾驶证?(我们把概率超过0.99的事件称为必然事件,认为在一次试验中必然事件一定会发生)0.9975≈,lg 20.3010≈【答案】(1)分布列见解析,()125E X =,()2425D X =(2)6【解析】【分析】(1)根据题意可知34,5X B ⎛⎫~ ⎪⎝⎭,分步计算即可;(2)增加k (k 为正整数)天学习后,每位学员通过考试拿到驾驶证的概率为1215k +⎛⎫- ⎪⎝⎭,若这4名学员都能通过考试并领取驾驶证,有41210.995k +⎡⎤⎛⎫->⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,利用用对数运算求解不等式.【小问1详解】1名学员通过考试并领取驾驶证的概率为1544316555⨯⨯=,根据题意可知34,5X B ⎛⎫~ ⎪⎝⎭,X 的取值分别为0,1,2,3,4,()443160C 15625P X ⎛⎫==⨯-=⎪⎝⎭,()31433961C 155625P X ⎛⎫==⨯⨯-= ⎪⎝⎭,()2224332162C 155625P X ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭,()334332163C 155625P X ⎛⎫⎛⎫==⨯⨯-=⎪ ⎪⎝⎭⎝⎭,()44433814C 155625P X ⎛⎫⎛⎫==⨯⨯-=⎪ ⎪⎝⎭⎝⎭,故X 的分布列为:X 01234P166259662521662521662581625()312455E X =⨯=,()3324415525D X ⎛⎫=⨯⨯-= ⎪⎝⎭;【小问2详解】增加k (k 为正整数)天学习后,每位学员通过考试拿到驾驶证的概率为1322111555k k +⎛⎫⎛⎫--⨯=- ⎪ ⎪⎝⎭⎝⎭,若这4名学员都能通过考试并领取驾驶证,有41210.995k +⎡⎤⎛⎫->⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,有1210.99755k +⎛⎫-> ⎪⎝⎭,有120.00255k +⎛⎫< ⎪⎝⎭,有0.4log 0.00251k >-,又由0.4lg0.0025lg2542lg4422lg2220.3010log 0.0025 6.54lg0.4lg41lg4112lg2120.3010---++⨯====≈≈----⨯.可得 5.54k >,故这4名学员至少要增加6天的学习,才能保证这4名学员都能通过考试并领取驾驶证.19.已知函数()2ln 2x f x x ax =+-.(1)当1a =时,求曲线()y f x =在点()()1,1f 处的切线方程;(2)已知()f x 有两个极值点.(ⅰ)求a 的取值范围;(ⅱ)若()f x 的极小值小于ln23-,求()f x 的极大值的取值范围.【答案】(1)2230x y --=(2)(ⅰ)()2,+∞;(ⅱ)9,ln 28⎛⎫-∞-- ⎪⎝⎭【解析】【分析】(1)求导,结合导数的几何意义求切线方程;(2)(ⅰ)分析可知原题意等价于1x a x+=有两个不同的正实数根,结合基本不等式分析求解;(ⅱ)设1x a x+=有两个不同的正实数根1201x x <<<,根据单调性可知()f x 的极值点012,x x x =,结合零点代换可得()0002ln 12x f x x =--,构建()()()2ln 1,0,11,2x g x x x =--∈+∞U ,结合单调性分析可得22x >,则110x 2<<,即可得取值范围.【小问1详解】当1a =时,则()2ln 2x f x x x =+-,()11f x x x =+-',可得()112f =-,()11f '=,即切点坐标为11,2⎛⎫-⎪⎝⎭,切线斜率1k =,所以曲线()y f x =在()()1,1f 处的切线方程为112y x ⎛⎫--=- ⎪⎝⎭,即2230x y --=.【小问2详解】(ⅰ)由题意可知:()f x 的定义域为()0,∞+,()211x ax f x x a x x-+=+-=',令()10f x x a x=+-=',可得1x a x +=,原题意等价于1x a x+=有两个不同的正实数根,因为12x x+≥,当且仅当1x x =,即1x =时,等号成立,可知2a >,所以a 的取值范围()2,+∞;(ii )由(i )可知:1x a x+=有两个不同的正实数根1x ,2x ,不妨设1201x x <<<,可知121x x =,当12x x x <<时,()0f x '<;当10x x <<或2x x >时,()0f x '>;可知()f x 在()10,x ,()2,x +∞上单调递增,在()12,x x 上单调递减,所以2x 为()f x 的极小值点,1x 为()f x 的极大值点,对于()f x 的极值点012,x x x =,则()()0001,0,11,a x x x =+∈+∞U ,可得()000000022000201ln ln ln 1222x x x f x x ax x x x x x ⎛⎫=+-+-+=-- ⎪⎝⎭=,设()()()2ln 1,0,11,2x g x x x =--∈+∞U ,则()211x g x x x x-'=-=,当01x <<时,()0g x '>;当1x >时,()0g x '<;可知()g x 在()0,1内单调递增,在()1,+∞上单调递减,则()()2ln 1ln 2322x g x x g =--<-=,可知22x >,则110x 2<<,又因为()g x 在区间10,2⎛⎫ ⎪⎝⎭上单调递增,则()119ln 228f x g ⎛⎫<=--⎪⎝⎭,所以()f x 的极大值的取值范围是9,ln 28⎛⎫-∞--⎪⎝⎭.【点睛】方法点睛:利用导数研究函数极值、最值的方法(1)若求极值,则先求方程()0f x '=的根,再检查()f x '在方程根的左右函数值的符号;(2)若探究极值点个数,则探求方程()0f x '=在所给范围内实根的个数;(3)若已知极值大小或存在情况,则转化为已知方程()0f x '=根的大小或存在情况来求解;(4)求函数f (x )在闭区间[],a b 的最值时,在得到极值的基础上,结合区间端点的函数值()f a ,()f b 与()f x 的各极值进行比较,从而得到函数的最值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
(2 分) =3. (4 分)
因为 b= 所以 ( a
c)
2
3 ,b
a c 2 ac cos B
,所以 a 2
c ac
=3,即 ( a
=12,所以 a+c= 2
A sin C
3
.
1 2
(6 分)
s in C ) s in C
(2) 2 sin
= 2(
f ( x ) 0 x 1
或 x 0 ; f ( x ) 0 0 x 1 , 故 f ( x ) 在 ( , 0 ) 和 (1, ) 上
递增,在 ( 0 , 1) 上递减. 欲 f ( x ) 在 2 , t 上为单调函数,则 2 t 0 .(3 分) (2)因 f ( x ) 在 ( , 0 ) 及 (1, ) 上递增,在 ( 0 , 1) 上递减,所以 f ( x ) 在 x 1 处取得极 小值 e ,又 f ( 2 )
B (3, 2 3 ) ,故可得分布列:
(6 分)
由此分布列知 X 的期望 E ( X ) 3
3
2 3
2 .
(12 分)
18.解.(1)由条件, B= 因为 A B
BC
.
(1 分)
B)
=
2
3 2
,所以 a c co s(
2 2
=
3Hale Waihona Puke 2,所以21 2
ac
=
3 2
,即 ac=3.
x 2 cos α 1 y 2 sin α
,(3 分)
所以 C 1 为 ( x 1 ) 2 y 2 4 .(4 分) 又 C 2 为 4 sin ,即 x 2 y 2 4 y ,(5 分) 所以 C 1 和 C 2 公共弦所在直线为 2 x 4 y 3 0 (7 分) 所以 (1, 0 ) 到 2 x 4 y 3 0 距离为 23.解.(1)对于函数 当x
13 e
2
e ,所以 f ( x ) 在 2 , 上的最小值为 f ( 2 )
从而当 t 2 时,恒有 f ( 2 ) f ( t ) .(6 分) (3)证:因为
f ( x ) e
2
x
x x ,原方程即为 x x
2 3
2
2
2
2 3
( t 1) .
高三 11 月 19 日数学小练习(理科)
理科参考解答 一、选择题 DABB, ACCA, DCAC 二、填空题 13. 三、解答题 17.解.(1)
2
1 3
14. 2
15. 5 5
16. ( , 2 ) ( 0 , )
25 9
3 .8 4 1 ,
由此可知没有 95%以上的把握认为“生二胎与性别有关”. (2)由原条件, X
2 3 2 3
( t 1)
2
1 3
( t 2 ) ( t 1) ,故
当 t 4 或 2 t 1 时, g ( 2 ) g ( t ) 0 ,故 g ( x ) 0 在 ( 2 , t ) 上有唯一解. 当 1 t 4 时 , g ( 2 ) 0 且 g (t ) 0 , 但 g (0 )
f ( x ) | x 1 | | x 2 | ,则 | x 1 | | x 2 | 2
1 5 , ]. 2 2
…4 分 | f (x) .
,解得
1 2
x
5 2
. …10 分
故实数 x 的范围是 [
① E (1, 0 , 1) , B E ( 0 , 1,1) , B 1 E ( 0 , 1, 1) ,
C 1 E ( 1, 1, 1) .计算易得 B E B 1 E 0 , B E C 1 E 0 ,即 BE ⊥ B 1 E , BE ⊥ C 1 E ,
V 1 3 1 2
2
1
2 ,故所求的体积是
1 3
1 2
……2 分
(2)当 E 点为 A A1 的中点时,以 D 为原点, D A , D C , D D 1 所在直线分别为 x , y , z 轴建立直角坐标系如图,则易得
B (1,1, 0 ), B 1 (1,1, 2 ), C 1 ( 0 ,1, 2 ) ,
再设 E (1, 0 , m ) ,则 CE (1, 1, m ) , CD
( 0 , 1, 2 ) ,
设向量 n ( x , y , z ) 满足 n ⊥ CE ,且
1
n ⊥ CD
,故
x y mz 0 y 2 z 0
,解得
2
2
令 g (x) x x
( t 1) ,从而问题转化为讨论函数 g ( x ) x x
2 3
( t 1) 在区
2
间 ( 2 , t ) 内零点的个数.因
g (2) 6
2 3
( t 1)
2
2 3
( t 2 ) ( t 4 ) , g ( t ) t ( t 1)
x (2 m ) z y 2z
2 2
,取 z 1 ,则 n ( 2 m , 2 ,1 ) .……8 分
又 DC ( 0 ,1, 0 ) , c o s n , D C 解得 m 2
,故
2 2
m
m , 2 , 1 0 , 1, 0
) ,所以
3 2
cos C
=
3 cos C
.
(9 分)
因为 C ( 0 , 于是 2 sin
2 3
3 cos C (
3 2
3 2
, 3)
.
(11 分)
A sin C
的取值范围是 (
, 3)
.
(12 分)
19.解.(1)该三棱锥的直观图是有一条侧棱垂直于底面的三 棱锥,如图所示的三棱锥 D 1 ACD 其中底面 ACD 是直角边长 为 1 的直角三角形,高 DD
2 2
2
2 2
2 2
,
2 1
0 1 0
2
3 ,再由 m 2 ,得 m 2
3 .
0
即 AE 2
3 时,二面角 C E D 1 D 的大小为 4 5 .……12 分
21.解.(1)因为 f ( x ) ( x 2 3 x 3) e x ( 2 x 3) e x x ( x 1) e x .
故 B E 平面 B 1 C 1 E .……4 分 ②当 A 1 E PC 时,显然有 AD 1 ∥ BC 1 ,
BE ∥ PD 1 ,所以平面 B C 1 E ∥平面 P A D 1 ……6 分
③如前所述建坐标系,则 C ( 0 ,1, 0 ), D 1 ( 0 , 0 , 2 ) ,
1
(2, t)
( t 1) 0 , 故 g ( x ) 0 在
2
上有解,且只有两解.
当 t 1 时, g ( x ) x 2 x 0 x 0 或 x 1 ,故 g ( x ) 0 在 ( 2 , t ) 上有唯一解. 当 t 4 时, g ( x ) x 2 x 6 0 x 2 或 x 3 ,故 g ( x ) 0 在 ( 2 , 4 ) 上也有且 只有一解. 综上所述,当 t 4 或 2 t 1 时,原方程在 ( 2 , t ) 内有唯一解;当 1 t 4 时,有两个 不同解.(12 分) 22.解.曲线 y sin α
1或x 2
5 2
,所以公共弦长为 2 4 .
5 4
11 .
10 分
f 1 ( x ) | x 1 | | x 2 | ,当 x [1, 2 ] 时, f 1 ( x ) 1
时, f 1 ( x ) | ( x 1) ( x 2 ) | 1 恒成立,故 f 1 ( x ) 是“平底型”函数. (2)若 | t k | | t k | | k | f ( x ) 对一切 t R 恒成立,则 (| t k | | t k |) m in | k 因为 (| t k | | t k |) m in 2 | k | ,所以 2 | k | | k | f ( x ) .又 k 0 ,则 f ( x ) 2 . 因为
x 4 cos α
( 为参数)上的每一点纵坐标不变, 横坐标变为原来的一半
x 2 cos α 1 ,(2 分) y sin α
得到 y sin α
x 2 cos α
,然后整个图象向右平移 1 个单位得到
最后横坐标不变,纵坐标变为原来的 2 倍得到
