最小生成树
Boruvka算法求最小生成树
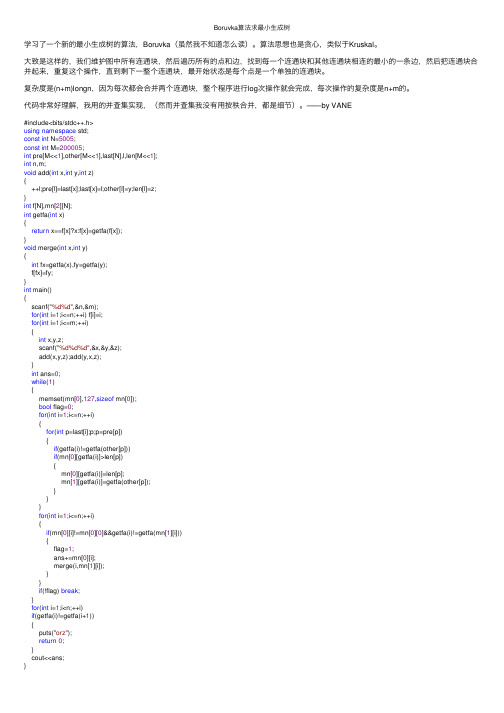
Boruvka算法求最⼩⽣成树学习了⼀个新的最⼩⽣成树的算法,Boruvka(虽然我不知道怎么读)。
算法思想也是贪⼼,类似于Kruskal。
⼤致是这样的,我们维护图中所有连通块,然后遍历所有的点和边,找到每⼀个连通块和其他连通块相连的最⼩的⼀条边,然后把连通块合并起来,重复这个操作,直到剩下⼀整个连通块,最开始状态是每个点是⼀个单独的连通块。
复杂度是(n+m)longn,因为每次都会合并两个连通块,整个程序进⾏log次操作就会完成,每次操作的复杂度是n+m的。
代码⾮常好理解,我⽤的并查集实现,(然⽽并查集我没有⽤按秩合并,都是细节)。
——by VANE#include<bits/stdc++.h>using namespace std;const int N=5005;const int M=200005;int pre[M<<1],other[M<<1],last[N],l,len[M<<1];int n,m;void add(int x,int y,int z){++l;pre[l]=last[x];last[x]=l;other[l]=y;len[l]=z;}int f[N],mn[2][N];int getfa(int x){return x==f[x]?x:f[x]=getfa(f[x]);}void merge(int x,int y){int fx=getfa(x),fy=getfa(y);f[fx]=fy;}int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;++i) f[i]=i;for(int i=1;i<=m;++i){int x,y,z;scanf("%d%d%d",&x,&y,&z);add(x,y,z);add(y,x,z);}int ans=0;while(1){memset(mn[0],127,sizeof mn[0]);bool flag=0;for(int i=1;i<=n;++i){for(int p=last[i];p;p=pre[p]){if(getfa(i)!=getfa(other[p]))if(mn[0][getfa(i)]>len[p]){mn[0][getfa(i)]=len[p];mn[1][getfa(i)]=getfa(other[p]);}}}for(int i=1;i<=n;++i){if(mn[0][i]!=mn[0][0]&&getfa(i)!=getfa(mn[1][i])){flag=1;ans+=mn[0][i];merge(i,mn[1][i]);}}if(!flag) break;}for(int i=1;i<n;++i)if(getfa(i)!=getfa(i+1)){puts("orz");return0;}cout<<ans;}。
最小生成树 课程思政

用最小生成树解决生态环境问题在当今社会,生态环境问题已成为一个日益严峻的问题,而最小生成树算法可以起到帮助优化生态环境的作用。
最小生成树算法是基于图论的,可以用来解决一系列的最小化问题,比如连接一组点的最小成本、电网建设的最小成本等等。
如果将环境问题看作一张图,图中的点表示生态环境的各个要素,如山水、空气、植被等等,而边则表示这些要素之间的关系和依存。
通过最小生成树算法的计算,可以得到连接这些要素所需要的最小成本。
比如,在国家级生态公园的建设中,应用最小生成树算法可以帮助规划出最佳的发展路径和公园布局,使生态环境能够得到最好地保护和发展。
同样地,在城市规划中,也可以应用最小生成树算法来确定最佳的路网建设方案,减少城市交通的拥堵和污染。
综上所述,最小生成树算法在生态环境问题的解决中可以发挥重要作用,为环保事业的发展提供有力支持。
PRIM算法求最小生成树

xx学院《数据结构与算法》课程设计报告书课程设计题目 PRIM算法求最小生成树院系名称计算机科学与技术系专业(班级)姓名(学号)指导教师完成时间一、问题分析和任务定义在该部分中主要包括两个方面:问题分析和任务定义;1 问题分析本次课程设计是通过PRIM(普里姆)算法,实现通过任意给定网和起点,将该网所对应的所有生成树求解出来。
在实现该本设计功能之前,必须弄清以下三个问题:1.1 关于图、网的一些基本概念1.1.1 图图G由两个集合V和E组成,记为G=(V,E),其中V是顶点的有穷非空集合,E是V中顶点偶对的有穷集,这些顶点偶对称为边。
通常,V(G)和E(G)分别表示图G的顶点集合和边集合。
E(G)也可以为空集。
则图G只有顶点而没有边。
1.1.2 无向图对于一个图G,若边集E(G)为无向边的集合,则称该图为无向图。
1.1.3 子图设有两个图G=(V,E)G’=(V’,),若V’是V的子集,即V’⊆V ,且E’是E的子集,即E’⊆E,称G’是G的子图。
1.1.4 连通图若图G中任意两个顶点都连通,则称G为连通图。
1.1.5 权和网在一个图中,每条边可以标上具有某种含义的数值,该数值称为该边的权。
把边上带权的图称为网。
如图1所示。
1.2 理解生成树和最小生成树之间的区别和联系1.2.1 生成树在一个连通图G中,如果取它的全部顶点和一部分边构成一个子图G’,即:V(G’)= V(G)和E(G’)⊆E(G),若边集E(G’)中的边既将图中的所有顶点连通又不形成回路,则称子图G’是原图G的一棵生成树。
1.2.2 最小生成树图的生成树不是唯一的,把具有权最小的生成树称为图G的最小生成树,即生成树中每条边上的权值之和达到最小。
如图1所示。
图1.网转化为最小生成树1.3 理解PRIM(普里姆)算法的基本思想1.3.1 PRIM算法(普里姆算法)的基本思想假设G =(V,E)是一个具有n个顶点的连通网,T=(U,TE)是G的最小生成树,其中U是T的顶点集,TE是T的边集,U和TE的初值均为空集。
曼哈顿距离最小生成树

曼哈顿距离最小生成树曼哈顿距离最小生成树(ManhattanMinimumSpanningTree)是一种在多维空间(N维空间)里寻找最小代价连接任何两个点的有效算法。
它使用曼哈顿距离作为代价并且能够在多维空间中解决最短路径问题。
曼哈顿距离是一种特殊的距离度量,用来测量在一个N维空间中任意两点之间的距离。
它能够很好地表达在有权重约束的多维空间中任意点之间的最短路径。
曼哈顿距离最小生成树以贪心算法的形式实现,能够有效地解决多维空间中的最短路径问题。
它的核心思想是从一个现有的最小生成树开始,不断的增加新的元素来加强和扩展树的结构。
曼哈顿距离最小生成树的基本步骤如下:(1)从空树开始,任意选取一个节点作为初始节点。
(2)以曼哈顿距离为标准,从剩余的n-1个节点中找出与初始节点距离较近的节点,从而构成一个最小生成树。
(3)重复步骤(2),直至最小生成树中包含所有节点,此时得到了一颗曼哈顿距离最小生成树。
曼哈顿距离最小生成树的一个重要特性是它有一个非常直接的应用:它能够帮助我们解决计算最短路径的问题,也就是计算从某个固定起点到任意终点的最短路径。
使用曼哈顿距离最小生成树来计算最短路径的过程如下:(1)先构造一颗曼哈顿距离最小生成树。
(2)对最小生成树中每条边计算曼哈顿距离,并保存到一个表中。
(3)对最小生成树中每个节点,根据曼哈顿距离计算出从起点到该节点的最短距离,并保存到一个表中。
(4)搜索表中最短路径,找到从起点到终点的最短路径,也就是从起点到终点的最短路径。
曼哈顿距离最小生成树在多维空间中解决最短路径问题时,具有非常强大的功能。
它能够快速、高效地找到任意两点之间的最短路径,而无需考虑权重的约束。
这样,它就成为了一种非常有效的最小代价连接算法,在多维空间中广泛应用。
总的来说,曼哈顿距离最小生成树是在多维空间中解决最短路径问题的一种经典算法。
它使用曼哈顿距离作为代价,能够快速、高效地找到任意两点之间的最短路径,而无需考虑权重的约束。
mst检测原理

mst检测原理
MST(最小生成树)是用于在一个带权无向连通图中找到一棵生成树,使得树的所有边的权重之和最小。
常用的MST算法有Prim算法和Kruskal算法,下面分别介绍它们的工作原理:
1. Prim算法:
- 选择一个起始节点作为生成树的根节点,并将其加入集合V(已访问节点集合)。
- 在集合V与剩余节点的边中选择一条权重最小的边,并将其对应的节点加入集合V。
- 重复上一步骤,每次选择与集合V中节点相连的权重最小的边,并将对应的节点加入集合V,直到集合V包含了图中的所有节点。
- 最终得到的生成树即为最小生成树。
2. Kruskal算法:
- 将图中的所有边按照权重从小到大进行排序。
- 依次选取权重最小的边,若将该边加入当前的生成树中不会形成回路,则将该边加入生成树。
- 重复上一步骤,直到生成树中包含了图中的所有节点。
- 最终得到的生成树即为最小生成树。
无论是Prim算法还是Kruskal算法,它们的目标都是选择权重最小的边,并构建一个连通的生成树,直到生成树包含了图中的所有节点。
不同之处在于Prim算法是基于节点的选择,而Kruskal算法是基于边的选择。
这两种算法的时间复杂度都与图中的边数E和节点数V相关。
Prim算法适用于稠密图,时间复杂度为O(V^2)或O(VlogV);Kruskal算法适用于稀疏图,时间复杂度为O(ElogE)或O(ElogV)。
MST算法在网络设计、电力传输网络、路径规划等领域有广泛的应用,通过构建最小生成树,可以实现高效的资源利用、减少成本和提升系统性能。
离散数学最小生成树例题

离散数学最小生成树例题
离散数学最小生成树例题是:
给定一个带权无向图G,其中顶点集V={1,2,3,4,5},边集E={(1,2),(1,3),(1,4),(2,5),(3,5)},权值集合W={1,2,3,4,5}。
用Kruskal算法求最小生成树。
首先对边集E和权值集合W按照边的权值从小到大进行排序;然后初始化一个空的并查集和一个空的森林;将并查集的根节点设置为第一个顶点,森林中添加这个顶点;对于每一条边,如果它的两个顶点不在同一个集合中,将这条边添加到森林中,并将这两个顶点合并到同一个集合中;最后森林中的边就是最小生成树。
最小生成树问题
2.1 最小生成树
树T(V,E)的性质:
E 树的边数等于其顶点数减“1”,即 V 1 ; 树的任意两个顶点之间恰有一条初级链相连接; 在树中任意去掉一条边后,便得到一个不连通的 图; 在树中任意两个顶点之间添加一条新边,所得新 图恰有一个初级圈。
例如,图 6.4.1 给出的 G1 和 G2 是树,但 G3 和 G4 则不是树。
44
44 69
结果显示于图
求最小生成树的 Prim 算法
Prim 算法的直观描述 假设 T0 是赋权图 G 的最小生成树。任选一 个顶点将其涂红,其余顶点为白点;在一个端 点为红色,另一个端点为白色的边中,找一条 权最小的边涂红,把该边的白端点也涂成红色; 如此,每次将一条边和一个顶点涂成红色,直 到所有顶点都成红色为止。最终的红色边便构 成最小生成树 T0 的边集合。
在求最小生成树的有效算法中,最著名的两个是 Kruskal(克罗斯克尔)算法和 Prim(普瑞姆)算法, 其迭代过程都是基于贪婪法来设计的。 1.求最小生成树的 Kruskal 算法
Kruskal 算法的直观描述 假设 T0 是赋权图 G 的最小生成树,T0 中的边和 顶点均涂成红色,初始时 G 中的边均为白色。 ① 将所有顶点涂成红色; ② 在白色边中挑选一条权值最小的边,使其与红 色边不形成圈,将该白色边涂红; ③ 重复②直到有 n1 条红色边,这 n1 条红色边 便构成最小生成树 T0 的边集合。
最小生成树算法
一个简单连通图只要不是树,其生成树就不唯 一,而且非常多。一般地,n 个顶点地完全图,其 不同地生成树个数为 nn2。因而,寻求一个给定赋 权图的最小生成树,一般是不能用穷举法的。例如, 30 个顶点的完全图有 3028个生成树,3028 有 42 位, 即使用最现代的计算机,在我们的有生之年也是无 法穷举的。所以,穷举法求最小生成树是无效的算 法,必须寻求有效的算法。
考研 计算机 数据结构 最小生成树的定义
考研计算机数据结构最小生成树的定义最小生成树是指在一个带权连通图中,找到一个生成树,使得所有边的权值之和最小。
也可以理解为在网络中连接所有节点的最小总成本。
算法实现方式有Prim算法和Kruskal算法。
Prim算法从一个起点开始,不断选取与当前生成树最近的节点,并加入生成树中。
Kruskal算法则是将所有边按权值从小到大排序,依次加入生成树中,若加入该边会形成环,则不加入。
最小生成树在计算机网络、航空航天、物流等领域中有广泛应用,能够有效降低运输成本,提高效率。
- 1 -。
《数据结构》课程设计 普里姆算法 最小生成树
[i].stop_vex,lge[i].weight); /*输出N-1条最小边的信息*/
for(i=0;i<12;i++)
{
line(vex[lge[i].start_vex][0],vex[lge[i].start_vex][1],vex[lge
lge[min]=lge[i];
lge[i]=edge;
vx=lge[i].stop_vex;
for(j=i+1; j<pgraph->n-1; j++)
{
vy=lge[j].stop_vex;
weight=pgraph->arcs[vx][vy];
if(weight<lge[j].weight)
{
{550,250},{520,330},{430,400},{350,450},{270,400},{200,330}};
/*初始化个顶点的坐标*/
int info[12][12];
char *text;
void initalGraph(int vec[][2]) /*画出顶点函数*/
{
int gd=DETECT,gm;
[i].stop_vex][0],vex[lge[i].stop_vex][1]);
}
/*根据生成的最小边数组连线*/
printf("---It is done!---");
getch();
exit(1);
}
此程序再TURBOC2.0环境中编译通过运行.TURBOC2.0下载的地址
最小生成树协议
最小生成树协议甲方(网络服务提供方):名称:_____________地址:_____________法定代表人:_____________联系电话:_____________乙方(用户方):名称:_____________地址:_____________法定代表人:_____________联系电话:_____________鉴于甲乙双方就最小生成树(MST)网络服务达成一致,经协商一致,订立本协议:一、服务内容1. 服务名称:最小生成树网络服务2. 服务范围:提供高效、稳定的网络连接3. 服务期限:_____________年_____________月_____________日至_____________年_____________月_____________日二、服务费用1. 服务费用:人民币_____________元/月2. 支付方式:银行转账现金3. 支付时间:每月_____________日前支付当月费用三、甲方责任1. 提供稳定可靠的最小生成树网络服务2. 定期维护和优化网络3. 确保网络连接的高效性和稳定性4. 及时处理乙方的咨询和投诉四、乙方责任1. 按时支付服务费用2. 配合甲方进行网络配置和优化3. 保持网络设备的正常运行4. 及时反馈网络故障和异常情况五、服务质量1. 甲方确保网络连接的高效性和稳定性2. 甲方定期进行网络性能测试六、数据管理1. 甲方负责管理和保护网络数据2. 乙方有权查询自己的网络使用情况3. 甲方保证数据的安全和隐私七、违约责任1. 甲方未按约定提供服务,需支付违约金2. 乙方未按时支付费用,需支付违约金3. 违约金为未支付金额的10%八、合同解除1. 双方协商一致可解除合同2. 任意一方严重违约,另一方有权解除合同九、争议解决协商不成,提交甲方所在地人民法院诉讼解决十、其他1. 本协议一式两份,甲乙双方各执一份2. 未尽事宜,按国家相关法律法规执行甲方签字/盖章:_________ 日期:______乙方签字/盖章:_________ 日期:______注:本协议仅为示例,具体条款依据实际情况调整。
