模糊控制器的查询表的实例计算过程
查询表法模糊控制器实验报告

查询表式模糊逻辑控制器设计实验报告
一、 实验目的
利用Matlab 软件实现模糊控制系统仿真实验,了解模糊控制的查询表方法的基本原理及实现过程,并找出参数Ke ,Kec ,和Ku 对模糊控制器性能影响的规律。
二、 实验要求 设计一个二维模糊控制器分别控制一一个一阶被控对象1
1)(11+=s T s G 。
先用模糊控制器进行控制,然后改变控制对象参数的大小,观察模糊控制的鲁棒性,找出参数Ke ,Kec ,和Ku 对模糊控制器性能影响的规律。
三、 实验步骤
叙述查询表式模糊控制系统仿真主要步骤。
四、实验内容
(一)查询表式模糊控制系统仿真实验
1、一阶对象1
1)(11+=s T s G 采用查询表式方法进行仿真实验,自己选定Ke ,Ku ,Kec 的值,按下表中给出的数值调整被控对象参数并观察输出响应曲线,观察模糊控制器对被控对象参数变化的适应性。
(其中T1称为被控对象参数,Ke ,Ku ,Kec 称为控制器参数)
2变其中的一个控制参数通过仿真实验观察它们各自对控制性能的影响。
将实验结果填入下表。
(1)Ke = Ku =
(二)实验讨论
1、通过对模糊控制器参数的设置及调整所获得的控制性能,得出关于控制
器参数对其性能影响的基本规律。
]
1、改变被控对象的参数,考察模糊控制器对被控对象参数变化的适应性,
并得出结论。
模糊控制程序实例

5.2.2 .6 模糊控制器设计实例1 、单输入模糊控制器的设计【例 5.12 】已知某汽温控制系统结构如图 5.10 所示,采用喷水减温进行控制。
设计单输入模糊控制器,观察定值扰动和内部扰动的控制效果。
图 5.10 单回路模糊控制系统按表 5-2 确定模糊变量 E 、 U 的隶属函数,按表 5-3 确定模糊控制规则,选择温度偏差 e 、控制量 u 的实际论域:,则可得到该系统的单输入模糊控制的仿真程序如 FC_SI_main.m 所示,仿真结果如图 5.11 所示。
设温度偏差 e 、控制量 u 的实际论域:,选择 e 、 u 的等级量论域为量化因子。
选择模糊词集为 { NB,NS,ZO,PS,PB } ,根据人的控制经验,确定等级量 E , U 的隶属函数曲线如图 5-8 所示。
根据隶属函数曲线可以得到模糊变量 E 、 U 的赋值表如表 5-3 所示。
图5-8 E ,U 的隶属函数曲线表 5-3 模糊变量 E 、 U 的赋值表( μ )-3 -2 -1 0 1 2 3 等级量μE 、 UPB 0 0 0 0 0 0.5 1 PS 0 0 0 0 1 0.5 0 ZO 0 0 0.5 1 0.5 0 0 NS 0 0.5 1 0 0 0 0 NB 1 0.5 0 0 0 0 0依据人手动控制的一般经验,可以总结出一些控制规则,例如:若误差 E 为 O ,说明温度接近希望值,喷水阀保持不动;若误差 E 为正,说明温度低于希望值,应该减少喷水;若误差 E 为负,说明温度高于希望值,应该增加喷水。
若采用数学符号描述,可总结如下模糊控制规则:若 E 负大,则 U 正大;若 E 负小,则 U 正小;若 E 为零,则 U 为零;若 E 正小,则 U 负小;若 E 正大,则 U 负大。
写成模糊推理句 :if E =NB then U =PBif E =NS then U =PSif E=ZO then U=ZOif E =PS then U =NSif E =PB then U =NB由上述的控制规则可得到模糊控制规则表,如表 5-4 所示。
模糊控制实例

x2 2 x5 A1 ( x ) 3 , 8 x 5 x 8 3
y 5 B1 ( y ) 3 11 y 3 z 1 C1 ( z ) 3 7 z 3 5 y 8 , 8 y 11
计算机控制算法
属函数 C ( z ) 为:
(1)以连续型重心法作为解模糊化机构:首先找出
因此
z 1 1 z 3 3 2 3 z 5 3 7 z C ( z ) 5 z 6 3 1 6 z 8 3 9 z 8 z9 3 3 z 1 52 67 z 81 99 z zdz zdz zdz zdz zdz 1 3 5 6 8 3 3 3 3 3 z 3 z 1 52 67 z 81 99 z dz dz dz dz 1 3 3 3 5 3 6 3 8 3 dz 28 16 49 28 25 18 3 18 6 18 2 4 1 2 1 3 3 2 3 6 4.7
{负大,负中,负小,负零,正零,正小,正中,正大}
{NB,NM,NS,NO,PO,PS,PM,PB}
第3章
计算机控制算法
2.变量的模糊化
基本论域:某个变量变化的实际范围 误差的基本论域为 [ xe , xe ] 误差变化的基本论域为[ xc , xc ] 输出变量的基本论域为[ yu , yu ]
变量的模糊子集论域 {n, n 1,
,0,
, n 1, n}
基本论域到模糊子集论域的转换公式
2n a b y x ba 2
模糊化就是将清晰的某个输入变量按隶属度转换到与 之相对应的模糊量的过程。
第3章
计算机控制算法
模糊控制器汇总
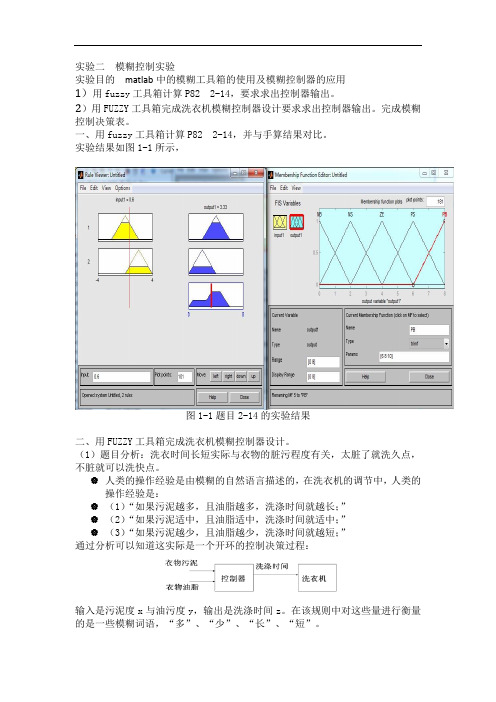
实验二模糊控制实验实验目的matlab中的模糊工具箱的使用及模糊控制器的应用1)用fuzzy工具箱计算P82 2-14,要求求出控制器输出。
2)用FUZZY工具箱完成洗衣机模糊控制器设计要求求出控制器输出。
完成模糊控制决策表。
一、用fuzzy工具箱计算P82 2-14,并与手算结果对比。
实验结果如图1-1所示,图1-1题目2-14的实验结果二、用FUZZY工具箱完成洗衣机模糊控制器设计。
(1)题目分析:洗衣时间长短实际与衣物的脏污程度有关,太脏了就洗久点,不脏就可以洗快点。
人类的操作经验是由模糊的自然语言描述的,在洗衣机的调节中,人类的操作经验是:(1)“如果污泥越多,且油脂越多,洗涤时间就越长;”(2)“如果污泥适中,且油脂适中,洗涤时间就适中;”(3)“如果污泥越少,且油脂越少,洗涤时间就越短;”通过分析可以知道这实际是一个开环的控制决策过程:输入是污泥度x与油污度y,输出是洗涤时间z。
在该规则中对这些量进行衡量的是一些模糊词语,“多”、“少”、“长”、“短”。
(2)定义输入、输出模糊集将污泥x 分为3个模糊集:{SD (污泥少),MD (污泥中),LD (污泥多)} 论域:{0,50,100}将油脂分为3个模糊集:{NG (油脂少),MG (油脂中),LG (油脂多)} 论域:{0,50,100} 输出模糊集:将洗涤时间分为5个模糊集:{VS (很短),S (短),M (中等),L (长),VL (很长)}。
论域:{0,10,25,40,60} 单位s 例如:(3)建立模糊控制器求:假设当前传感器测得信息为:x0(污泥)=90,y0(油脂)=90 观察控制器的输出。
(4)建立控制决策表 x0=10,20,30,40,50,60,70,80,90,y0=10,20,30,40,50,60,70,80,90,分别取值时,控制器的输出。
(5)改变输入输出变量的模糊值、隶属度函数的曲线、解模糊的方法等,观察控制器三维图以及控制器输出, Maltlab 提供5种反模糊化方法:1.centroid :面积重心法;2.bisector :面积等分法;3.mom :最大隶属度平均法;4.som :最大隶属度取小法;5.lom :最大隶属度取大法 三、按照上述要求完成洗衣机模糊控制器设计。
模糊控制应用示例讲解

0.4
0.2
0
-3
-2
NS
ZR
PS
-1
0
1
PB
2
u3
e de NB NS ZR PS PB
模糊推理规则
NB NS ZR PS PB
PB PB PS PS ZR PB PS PS ZR ZR PS PS ZR ZR NS PS ZR ZR NS NS ZR ZR NS NS NB
模糊控制系统设计
% Example 3.8 % 典型二阶系统的模糊控制 % %被控系统建模 num=20; den=[1.6,4.4,1]; [a1,b,c,d]=tf2ss(num,den); x=[0;0];
第5次课
例1:工业工程控制
例2:典型二阶环节 的模糊控 制
例1: 工业过程
例1: 某一工业过程要根据测量的温度 (t)和压力(p)来确定阀门开启的角
度: f (t, P) 这种关系很难用数
学模型精确描述。实际中由有经验的操 作员完成,因此通常可设计模糊控制器 取而代之。
输入输出变量的论域
0
0
0.5
1
1.5
2
2.5 压力 3
阀门开启角度的模糊隶属度 函数
“负” “零” “正”
1 0.8 0.6 0.4 0.2
0 -10 -8 -6 -4 -2 0 2 4 6 8 10
角度增量
隶属度函数
模糊推理规则库
模糊推理规则有3条:
If 温度“冷” and 压力“高”,则阀门角 度增量为“正”
If 温度“热” and 压力“高”,则阀门角 度增量为“负”
If 压力“正常”,则阀门角度增量为“零 ”
模糊控制算法PPT课件

-
1
一、概述
二、在汽车上的应用方面
三、举例说明在汽车空调当中的应用
四、简要介绍在其他方面的应用
-
2
一、概 述
1、什么叫模糊控制?
所谓模糊控制,就是对难以用已有规律描述的复 杂系统,采用自然语言(如大、中、小)加以叙 述,借助定性的、不精确的及模糊的条件语句来 表达,
模糊控制是一种基于语言的一种智能控制
正小PS(Positive Small)、
正中PM(Positive Medium),
正大PB(Positive Big),
则:
T(E)= {NB,NM,NS,- ZE,PS,PM,PB}
13
X
建立隶属函数:
各参数对相应子集的隶属函数分别由不同的函数族决定。参数的相应 子集指该参数被人为地划分成的等级所构成的一组模糊集合。相应子 集的多少,由控制精度决定。
-
8
3、模糊控制的特点
①适用于不易获得精确数学模型的被控 对象,
②是一种语言变量控制器 ③从属于智能控制的范畴。该系统尤其 适于非线性,时变,滞后系统的控制 ④抗干扰能力强,响应速度快,并对系 统参数的变化有较强的鲁棒性。
-
9
二、模糊控制在汽车的应用方面
1、ABS防抱死系统工况的多变及轮胎的非线性 2、汽车巡航系统外界负荷的扰动、汽车质量和传动系效率的不确
-
12
模糊控制是基于语言的控制 模糊语言集的组成: T(E)
T(E)={负大,负中,负小,零,正小,正中,正大}
用模糊语言变量E 来描述偏差,
或用符号表示
负大NB(Negative Big)、
负中NM(Negative Medium)、
模糊控制算法实例解析(含代码)

模糊控制算法实例解析(含代码)
首先来看一个实例,控制进水阀S1和出水阀S2,使水箱水位保持在目标水位O处。
按照日常操作经验,有以下规则:
1、若当前水位高于目标水位,则向外排水,差值越大,排水越快;
2、若当前水位低于目标水位,则向内注水,差值越大,注水越快;
3、若当前水位和目标水位相差很小,则保持排水速度和注水速度相等。
下面来设计一个模糊控制器
1、选择观测量和控制量
一般选择偏差e,即目标水位和当前水位的差值作为观察量,选取阀门开度u为控制量。
2、输入量和输出量的模糊化
将偏差e划分为5个模糊集,负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB),e为负表示当前水位低于目标水位,e 为正表示当前水位高于目标水位。
设定e的取值范围为[-3,3],隶属度函数如下。
偏差e对应的模糊表如下:隶属度
变化等级-3 -2
-1
1
2
3模糊集
PB 0 0 0 0 0 0.5
1PS 0
0 0.5 1 0.5 0ZO
0 0.5 1 0.5 0
0NS
0 0.5 1 0.5 0
0NB
0.5 0 0 0 0 0。
模糊控制器的典型例题概要

模糊控制器的典型例题中央电大理工部冼健生 2006年11月10日例题一、模糊控制算法已知:设x表示转速,y表示控制电压。
转速和控制电压的论域分别为X={100,200,300,400,500},Y={1,2,3,4,5}在X 、Y上的模糊子集为X×Y上的模糊关系为“若转速高,则控制电压高;否则控制电压不很高”。
求:现在转速不很高,控制电压如何?解:与模糊控制规则“若转速高,则控制电压高;否则控制电压不很高。
”对应的模糊关系矩阵为==由模糊推理合成规则可得讨论:本题所涉及的问题为典型的单输入-单输出模糊控制器的控制规则之一,其形式为,由模糊集合基础一节可知,这样的条件语句可表示为X×Y上的一个模糊关系。
结论由推理合成规则得到。
例题二、设计语言变量赋值表已知:某模糊控制系统的输入语言变量X的语言值为:VG、G、M、B、VB。
X的论域为X={0,1,2,3,4}。
以上论域中各元素对各语言变量值所确定的模糊子集的隶属函数曲线如下图所示。
求:试设计语言变量X的赋值表。
解:每个语言变量值,对应于其论域上的一个模糊集合,现论域中每个元素属于各模糊集合的隶属度已由图中的隶属度曲线给定。
根据给定的隶属度数值,可列出语言变量赋值表,表中的行表示论域中各元素对某个模糊集合的隶属度,表中的列表示论域中某个元素对各模糊集合的隶属度。
讨论:语言变量赋值表是语言变量论域上模糊集合的一种表示方法,其中的数值由模糊集合的隶属度给定。
需要明确的是语言变量赋值表中行与列所表示的不同含义。
例题三、设计模糊控制规则表已知:某液位控制系统的人工操作经验为若液位低于400cm 则增大流入阀阀门开度,低得越多开得越大;若液位等于400cm则保持流入阀阀门开度不变;若液位高于400cm则减小流入阀阀门开度,高得越多开得越小。
求:试写出该系统的模糊控制规则表。
解:设系统输入量为液位实测高度与给定值之误差,输出量为阀门开度的变化量;描述输入变量及输出变量的语言值和可取为NB、NS、O、PS、PB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用模糊控制实现水箱水温的恒温控制。
水箱由底部的电阻性电热元件加热,由电动搅拌器实现均温。
设控制的目标温度为25ºC,以实测温度T与目标温度R之差,即误差e=T-R,以及误差变化率ec为输入,以固态继电器通电时间的变化量u(以一个控制周期内的占空比表示,控制电加热器的功率)为输出。
设e的基本论域为[-5,5] ºC,其语言变量E 的论域为[-5,5];ec的基本论域为[-1,1] ºC/s,其语言变量EC的论域为[-5,5];控制量u的基本论域为[-5,5]单位,其语言变量U的论域为[-5,5]。
E、EC和U都选5个语言值{NB,NM,NS,Z,PS,PM,PB},各语言值的隶属函数采用三角函数,其分布可用表1和表2表示,控制规则如表3所示。
要求:1、画出模糊控制程序流程图;2、计算出模糊控制器的查询表,写出必要的计算步骤。
表
表
表3 模糊控制规则表(
解:步骤:
1)输入输出语言变量的选择。
输入变量选为实测温度T与目标温度R之差,即误差e,及误差变化率ec;输出语言变量选固态继电器通电时间的变化量u,故模糊控制系统为双输入—单输出的基本模糊控制器。
2)建立各语言变量的赋值表。
设误差e的基本论域为[-5,5]。
C,输入变量E的论域为[-5,-4,-3,-2,-1,0,1,2,3,4,5],误差的量化因子为ke=5/5=1。
语言变量E选取5个语言值:,,,,
PB PS ZE NS NB。
表1为语言变量E、EC的赋值表,表2为语言变量U的赋值表
3)建立模糊控制规则表,总结控制策略,得出一组由25条模糊条件语句构成的控制规 则,据此建立模糊控制规则表,如表3所示.表中行与列交叉处的每个元素及其所在列的第一行元素和所在行的第一列元素,对应于一个形式为”if E and EC then U”的模糊语句,根据该模糊语句可得相应的模糊关系i R ,则总控制规则的总模糊关系为25
1=i i R U R =。
表3 模糊控制规则表(内容为控制量U)
4)建立查询表。
根据推理合成原则,输出模糊集合2()T U E E R =⨯∆,利用判决结果可建立模糊控制器查询表。
通过查表得出U,乘以比例因子K u ,(K u =u max /n=5/5=1),即查表得出的结果U 即为控制量的值u 。
5)流程图如下图所示
流程图
6)在线查询表如表4所示
EC
E
-5 -4 -3 -2 -1 0 1 2 3 4 5 -5 5 5 5 5 5 5 5 3 3 3 0 -4 5 3 3 3 3 3 3 0 0 0 0 -3 5 3 3 3 3 3 3 0 0 0 0 -2 5 3 3 3 3 3 3 0 0 0 0 -1 3 3 3 3 0 0 0 -3 -3 -3 -3
0 3 3 3 3 0 0 0 -3 -3 -3 -3
1 3 3 3 3 0 0 0 -3 -3 -3 -3
2 3 0 0 0 -3 -3 -3 -3 -3 -3 -5
3 3 0 0 0 -3 -3 -3 -3 -3 -3 -5
4 3 0 0 0 -3 -3 -3 -3 -3 -3 -5
5 0 -3 -3 -3 -5 -5 -5 -5 -5 -5 -5
E=[1 0.4 0.1 0 0 0 0 0 0 0 0;
0 0.5 1 0.5 0 0 0 0 0 0 0;
0 0 0 0 0.3 1 0.3 0 0 0 0;
0 0 0 0 0 0 0 0.5 1 0.5 0;
0 0 0 0 0 0 0 0 0.1 0.4 1];%5*11 E的赋值表矩阵EC=E;
U=[1 0.6 0.2 0 0 0 0 0 0 0 0;
0 0.4 1 0.4 0 0 0 0 0 0 0;
0 0 0 0 0.5 1 0.5 0 0 0 0;
0 0 0 0 0 0 0 0.4 1 0.4 0;
0 0 0 0 0 0 0 0 0.2 0.6 1];
rule=[5 5 5 4 3;
5 4 4 3 3;
4 4 3 2 2;
4 3 2 2 1;
3 2 1 1 1];%5*5模糊控制规则表矩阵
R=zeros(121,11);%申请模糊控制的隶属度关系矩阵%计算模糊控制隶属度关系矩阵R? for ii=1:5
for jj=1:5
U_rule=rule(ii,jj);%按控制规则表找出语言变量对应的向量
A=E(ii,:);
B=EC(jj,:);
C=U(U_rule,:); %根据模糊算法,求(A'×B)对应按值取小
for i=1:11
for j = 1:11
if A(i)>B(j)
R_C(i,j)=B(j);
else
R_C(i,j)=A(i);
end
end
end
R_C1=reshape(R_C',11*11,1);%转置成121*1的列向量,形成单条控制语句的模糊关系的隶属度函数R1
for i=1:11*11
for j=1:11
if R_C1(i)>C(j)
R1(i,j)=C(j);%得到R1是121*11的矩阵
else
R1(i,j)=R_C1(i);
end
end
end %将R1合成为整个模糊关系的隶属度函数R,R是121*11的矩阵
for i=1:121
for j=1:11
if R(i,j)<R1(i,j)
R(i,j)=R1(i,j);
end
end
end
end
end
%计算控制量U1=(A1×B1)T2。
R,T2表示前面矩阵转化成行向量
for iii=1:11
for jjj=1:11 %求E的量化值对应的语言值的所对应的行向量
temp_maxA=E(1,iii);
line_no=ones(3,1);
for k=1:5
if(temp_maxA<E(k,iii))
temp_maxA=E(k,iii);
line_no(1)=k;
end
end
A1=E(line_no(1),:);%求EC的量化值对应的语言值的所对应的行向量
temp_maxB=EC(1,jjj);
for k=1:5
if(temp_maxB<EC(k,jjj))
temp_maxB=EC(k,jjj);
line_no(2)=k;
end
end
B1=EC(line_no(2),:);%求(A1×B1),并转置为行向量
for ii=1:11
for jj=1:11
if A1(ii)>B1(jj)
Temp(ii,jj)=B1(jj);
else
Temp(ii,jj)=A1(ii);
end
end
end
Temp_T=reshape(Temp',121,1)';%求出控制量
U1=zeros(1,11);
for ii=1:11
for jj=1:121 %将矩阵乘法中对应的项先取小,然后在取大,得到新的控制行向量U1(ii)=max(min(Temp_T(jj),R(jj,ii)),U1(ii));
end
end
temp_maxU1=U1(1);%用最大隶属度方法去模糊化,求得可量化的值
for k=1:11
if(temp_maxU1<U1(k))
temp_maxU1=U1(k);
line_no(3)=k;
end
end
U(iii,jjj)=line_no(3)-6;%将结果从(1,11)匹配到(-5,5)
end
end。
