2017年春季学期沪教版五四制九年级数学下册27.2、圆心角、弧、弦、弦心距之间的关系(1)教案
九年级数学下册27.2圆心角、弧、弦、弦心距之间的关系练习(无答案)沪教版五四制.doc
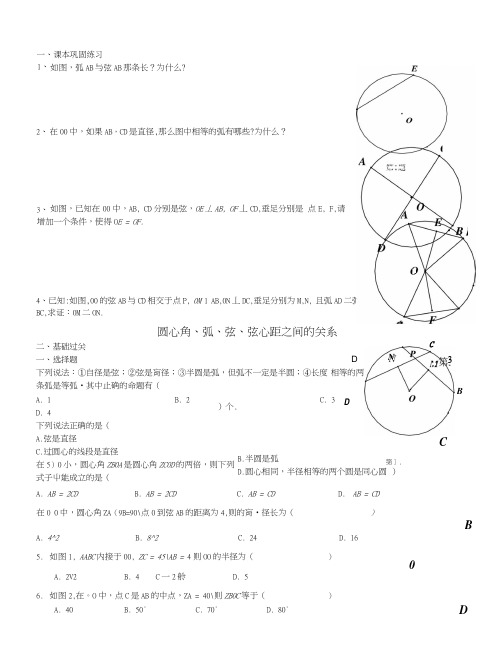
圆心角、弧、弦、弦心距之间的关系二、基础过关一、选择题D 下列说法:①自径是弦;②弦是肓径;③半圆是弧,但弧不一定是半圆;④长度 相等的两条弧是等弧•其中止确的命题有(A. 1B. 2D. 4下列说法正确的是(A.弦是直径C.过圆心的线段是直径在5)0小,圆心角ZB0A 是圆心角ZC0D 的两倍,则下列式子屮能成立的是(在0 0中,圆心角ZA (9B=90\点0到弦AB 的距离为4,则的肓•径长为()A. 4^2B. 8^2C. 24D. 165. 如图1, AABC 内接于00, ZC = 45\AB = 4则OO 的半径为()A. 2V2B. 4C 一2舲D. 56. 如图2,在。
O 中,点C 是AB 的中点,ZA = 40\则ZB0C 等于()A. 40B. 50°C. 70°D. 80°A. AB = 2CDB. AB = 2CDC. AB = CDD. AB = CD1、 2、 在00中,如果AB ,CD 是直径,那么图中相等的弧有哪些?为什么?如图,已知在00中,AB, CD 分别是弦,OE 丄AB, OF 丄CD,垂足分别是 点E, F,请增加一个条件,使得O E = OF.3、4、已知:如图,00的弦AB 与CD 相交于点P, 0M 1 AB,0N 丄DC,垂足分别为M,N, 且弧AD 二弧BC,求证:0M 二ON.)个.B.半圆是弧D.圆心相同,半径相等的两个圆是同心圆 )一、课本巩固练习如图,弧AB 与弦AB 那条长?为什么?C. 3 DC第].题 BDCB3题N二、填空题.(1) _______________________________________ 圆上任意两点Z 间的部分叫做 ;(2) _______________________________________ 连结圆上任意两点的线段叫做 ___ :过圆心的弦就是 ;(3) ____________________________________________________________________________ 圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做 _______________________________________________ ;(4) _____________ _________________________ 叫做优弧; 叫做劣弧.从圆心到弦的距离叫做 _____________ ,它和所对的弦的位置关系是 ________________ . 如图,在中,AD 为直径,ZAOB = ZBOC = ZCOD ,那么(1)所对的圆心角是 ________ 度;(2)与相等的弧有 __________________ ; (3) BD 与CO 的位置关系是 _________ .如图,已知AB 、CD 是的两条直径,弦CE 〃AB, ZEOC = 40°,贝ij ZBOC = _____________________________ . 如图,已知CD 是OO 的直径,E 是圆上一点,且ZEOD = 45°, A 是DC 延 <线上一点,AE 与交于点B,如度.如图4,已知AB 是OO 的直径,C 、D 是OO 上的两点,ZD = 130°,则ABAC 的度数是 ________________________ . 如图5, AB 是半圆O 的直径,E 是BC 的中点,0E 交弦BC 于点D,已知BC=8cm, DE=2cm,则AD 的长为 ________________如图,已知AB 是O0的眩,且AC 二BD,半径0E 、0F 分别过C 、D 两点.求证:AE = BF .果 AB 二0C,则 ZEAD 二 __________uB(用锐角三角比表示).第9题图第7题图第8题图如图 3,A 、B 、C 、D 是上四点,且D 是 AB 的中点,CD 交0B 于E, ZAOB = 100\ZOBC = 55°, ZOEC =_求证:AC = BC.如图,在0 0屮,AB是肓径,CO丄AB , D是CO的屮点,DE〃AB.求证:求证:AC = BD.18、如图所示,点0是ZEPF的平分线上一点,以0为圆心的圆和角的两边分别交于A. B和C・D, 求证:AB=CD.19、如图,EF为<30的肓径,过EF上一点P作弦AB. CD,且ZAPF二ZCPF.求证:PA二PC.如图,已知AB是OO的直径,队N分别是AO、B0的中点,20.如图, 00的弦CB. ED的延长线交于点A,且BC=DE. 求证:AC=AE. A。
2017春九年级数学下册276正多边形与圆(2)沪教版五四制!

2.顺次联结AC,CB,BD,DA.
新课探索四(2)
试一试2.已知⊙O,试用直尺和圆规作⊙O的内接正六边形.
作法:1.在⊙O上任取一点A,以A为圆心,OA为半径作弧,在上依次截得点B、C、D、E、F(即将圆六等分).
2.顺次联结AB、BC、CD、DE、EF、FA.
2.请画出下列各正多边形的一个中心角,并指出它的半径及边心距.
课前练习二
3.已知,如图,在△OAB中,OA=OB=R,∠O= .用R、的式子表示底角∠B,底边AB及底边上的高h及△OAB的面积S.
知识呈现:
新课探索一
如图,在正n边形中,分别经过各顶点的这些半径将这个正n边形分成n个______三角形.
每个等腰三角形的腰是正n边形的___,底边是正n边形的______,顶角是正n边形的_____,底边上的高是正n边形的_____圆的半径,它的长是正n边形的______.
设正n边形的半径长为R,中心角为n,边长为an,边心距为rn,由课前练习可知,利用等腰三角形OAB,通过解直角三角形,可由其中两个量求出其余的两个量.从而进一步求出这个正n边形的周长及面积.
课内练习三
3.已知圆的半径为R,分别求这个圆的内接正方形和正六边形的边长、边心距、周长和面积.
课内练习四
4.已知正三角形的边长为a,求它的半径,边心距及高.
课堂小结:
1.正多边形的计算(归纳为解直角三角形)2.正多边形的作法(等分圆周)
课外
作业
练习册
预习
要求
教学后记与反思
1、课堂时间消耗:教师活动分钟;学生活动分钟)
2、本课时实际教学效果自评(满分10分):分
3、本课成功与不足及其改进措施:
【最新】沪科版九年级数学下册第二十四章《圆心角、弧、弦、弦心距间关系》公开课课件.ppt

B. A︵D = B︵D
C. B︵C = A︵D
D.B︵D
,第 7 题图)
,第 8 题图)
8.(4 分)AB 是⊙O 的直径,BC,CD,DA 是⊙O 的弦,
且 BC=CD=DA,则∠BCD 的度数是__120°__.
9.(8 分)如图所示,M,N 分别是⊙O 的弦 AB,CD 的 中点,AB=CD.
• 10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 5:56:38 PM
求证:∠AMN=∠CNM.
解:证明:连接 OM,ON.∵O 为圆心,M,N 分别为弦 AB,CD 的中点,∴OM⊥AB,ON⊥CD,∵AB=CD,∴OM =ON,∴∠OMN=∠ONM,∵∠AMN=90°-∠OMN,∠ CNM=90°-∠ONM,∴∠AMN=∠CNM
一、选择题(每小题 6 分,共 12 分) 10.如图所示,⊙O 中 ,如果A︵B=2A︵C,那么( C )
C.四边形
二、填空题(每小题 6 分,共 12 分) 12.一条弦把圆周分成 2∶3 的两部分,那么这条弦所 对的圆心角的度数为__144°__.
13.如图,MN 是半径为 1 的⊙O 的直径,点 A 在⊙O 上,∠AMN=30°,点 B 为劣弧 AN 的中点.P 是直径 MN 上一动点,则 PA+PB 的最小值为__ 2__.
6.(4 分)如图,AB 是⊙O 的直径,B︵C=C︵D=D︵E,∠ COD=34°,则∠AEO 的度数是( A )
A.51° B.56° C.68° D.78°
7.(4 分)在⊙O 中,弦 AB 与 CD 相交于点 P,且 AB=
CD,则下列结论正确的是( D )
27.2 圆心角、弧、弦、弦心距之间的关系(课件)九年级数学下册(沪教版)

证明:连接OA,OB,OC,如图.
A
∵ AB=BC=CA,
∴∠AOB =∠BOC =∠COA
1
= 360 =120 .
3
O
B
C
【变式题】如图,在☉O 中,AB= AC,∠ACB = 60°, A
求证:∠AOB =∠BOC =∠AOC.
证明:∵ AB = AC ,
C.3个
D.4个
5.如图,已知⊙O 的半径为 5,弦 AB、CD 所对的圆心角分别是∠AOB、
∠COD,若∠AOB 与∠COD 互补,弦 CD=6,则弦 AB 的长为( B )
A.6
B.8
C.5 2
D.5 3
6.如图,AB、CE 是⊙O 的直径,∠COD=60°,且
=
,那么∠AOE
的度数是 60° ,与∠AOC 相等的角有 ∠BOD、∠BOE、∠DOE
⌒ ⌒
AB=CD
∠ = ∠
(2)如果 AB=CD,那么 ____________,_____________.
=
AB=CD .
(3)如果∠AOB=∠COD,那么 _____________,
_____________
E
A
B
O·
D
F
C
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
⌒
所对的弧为AB.
O·
B
判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
任意给圆心角,对应出现三个量:
A
圆心角
弧
O·
沪科版九年级下册数学 课时3 圆心角、弧、弦、弦心距间的关系 教学PPT课件

由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD, 那么,⌒AB=⌒CD,弦AB=弦CD,OE=OF
C
E
B
D
F
·
O
A
新课讲解
2.在等圆中探究
如图,在等圆中,如果∠AOB=∠CO ′ D,你 发现的等量关系是否依然成立?为什么?
C
F
B
E
D
新课导入
情境导入
熊宝宝要过生日了!要把蛋糕平均分成四块,你会分吗?
新课导入
把圆绕圆心旋转任意一个角度,仍与原来的圆重合吗?
·
新课讲解
典例分析
例 1 如图,在Rt△ABC中,∠C=90°,∠A=30°,
以点C为圆心,BC为半径的圆交AB于点D,交AC 于点E,则 BD 的度数为________. 解:连接CD,∵∠C=90°,
O·
A
O·'
新课讲解
圆心角、弧、弦与弦心距的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等, 所对的弦相等,所对弦的弦心距相等.
这个条件能去掉吗? 为什么?
①∠AOB=∠COD
②A⌒B=C⌒D ③AB=CD ④OE=OF
CB
DE
F
O
A
新课讲解
圆心角、弧、弦与Βιβλιοθήκη 心距间关系定理的推论在同圆或等圆中,如果两个圆心角以及这两个角
所对的弧、所对的弦、所对弦的弦心距中,有一组量相
等,那么其余各组量都分别相等.
圆心角 相等
弦 相等
弧 相等
弦心距 相等
新课讲解
典例分析
例 2 已知:如图,点O是∠ A平分线上的一点, ⊙O分别 交∠ A
沪教版(上海)数学九年级第二学期-27.2 (1)圆心角、弧、弦、弦心距之间的关系 教案

27.2(1)圆心角、弧、弦、弦心距之间的关系一、教学目标:理解圆心角、弧、弦、弦心距、等弧、等圆等概念,知道圆是一个旋转对称图形,理解圆的旋转不变性;经历探索同圆中圆心角、弧、弦、弦心距之间关系的过程,形成观察、归纳、总结数学问题的能力,掌握同圆或等圆中圆心角、弧、弦、弦心距之间关系的定理;能运用定理进行简单的几何论证和计算。
二、教学重点:理解圆心角、弧、弦、弦心距、等圆等概念,掌握同圆或等圆中圆心角、弧、弦、弦心距之间关系的定理。
三、教学难点:导出同圆或等圆中圆心角、弧、弦、弦心距之间的关系的定理及该定理的简单应用。
四、教学过程:三、探索定理1.提出问题:刚才我们在圆中画了两个相等的圆心角,再分别画出了它们所的弧、弦、弦的弦心距,在这4组量中,如果已知圆心角这组量相等了,那么这两个圆心角分别所对的弧、所对的弦、所对的弦的弦心距这3组量存在什么样的关系?为什么?2.学生4人一组进行讨论,写下结论并简要说明或证明。
3.学生交流,汇报结果;(教师视情况作相应的引导)4.归纳结论:在同圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
5.把文字语言转化为几何符号语言:在⊙O中,∵∠AOB=∠COD,∴⌒AB =⌒CD,AB=CD在⊙O中,∵∠AOB=∠COD,OE与OF分别是弦AB、CD的弦心距∴OE=OF6.思考:如果两个相等的圆心角不在同一个圆中,那么以上结论还成立吗?学生交流汇报:不一定成立。
可能情况一:在两个大小不等的圆中不成立;可能情况二:在两个大小相等的圆中成立。
教师视情况作引导。
7.完善结论,得到定理:圆心角、弧、弦、弦心距之间的关系的定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等. 直接抛出问题,让学生分组进行交流讨论,尽量让全体学生参与定理的产生过程。
复习回顾证明线段相等的方法。
锻炼学生综合归纳能力。
清楚定理应用的书写格式。
让学生对结论成立的前提产生思考,以加强记忆,同时加进等圆这个前提条件。
27-2圆心角、弧、弦、弦心距之间的关系(第3课时)(教学课件)-九年级数学下册精品课堂(沪教版)
*9.在⊙O中,点M、N分别为弦AB、CD的中点,如果OM ︵︵
= ON,那 么在结 论: ① AB=CD;②AB= CD; ③ ∠AOB=∠COD中,正确的是( ) A.①② B.①③ C.②③ D.①②③
【 点 拨 】 ∵ 点 M 、 N 分 别 是 弦 AB 、 CD 的 中 点 ,
∴OM⊥AB,ON⊥CD.
课堂小结
圆心角
弦、弧、圆心角 的关系定理
概念:顶点在圆心的角
在同圆或等圆中
圆心角 相等
弦 相等
应用提醒
①要注意前提条件; ②要灵活转化.
弧 相等
弦心距 相等ຫໍສະໝຸດ 4.如图,在△ABC中,∠C=90°,∠A=25°,以点C 为圆心,BC为半径的圆交AB于点D,交AC于点E,则 ︵ BD的度数为( C )
A.25° B.30° C.50° D.65°
5.如图,已知A、B、C、D是⊙O上的点,∠1=∠2,则 下列结论中正确的有( D ) ︵︵
①AB=CD; ︵︵
ON分别表示AB和CD的弦心距.
FB
•N
O
∵∠AFO=∠DFO,∴ OM=ON.
∴AB=CD.
D (2)∵AB=CD,∴ AC BD
.
典例2
例2: 已知,如图(4):⊙O是△ABC的外接圆,AE平分△ABC的外 角∠DAC,OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON 求证:(1)AE∥BC (2)AO⊥AE
∵OM=ON, ∴AB=CD,A︵B=C︵D,∠AOB=∠COD.
【答案】D
10.如图,在⊙O中,弦AB>CD,OM⊥AB,ON⊥CD, 点 M、 N 分 别 为 垂 足 , 那 么 OM、 ON 的 大 小 关 系 是 () A.OM>ON B.OM=ON C.OM<ON D.无法确定
九年级数学圆心角_弧_弦_弦心距的关系课件沪科版
___________,_________________.。推论
在同圆或等圆中,
。如果两个圆心角、两条弧、。两条弦或两条弦的弦心距中有。AC-BC=BD-
BC
共二十四页
11111111AC=BD,
,
求∠2的度数(dù shu)。
解: ∵ AC=BD (已知)
∴ AC-BC=BD-BC
(等式(děngshì)的性 质)
∴ AB=CD
∴ ∠1=∠2=45°
(在同圆中,相等(xiāngděng)的 弧所对的圆心角相等(xiāngděng))
共二十四页
判断下列(xiàliè)说法是否正确:
AB=AC.
∴ AB=AC.
A
O·
又∠ACB=60°,
B
C
∴ △ABC是等边三角形.
∴ AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
共二十四页
练习(liànxí)
1.如图,AB是⊙O 的直径(zhíjìng), ∠COD=35°,求∠AOE 的度数.
E
D
解:
∵
C
A
·
O
B
共二十四页
2.下列命题(mìng tí)中真命题(mìng tí)是( )
题设
结论
在
(
前 提
同 圆 或
) (qiántí)等圆中( 条 件 )
圆 心 角 相 等
圆心角所对的弧相等(xiāngděng), 圆心角所对的弦相等, 圆心 角所对弦的弦心距相等。
推论
在同圆或等圆中,
如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有
一组量相等,那么(nà me)它们所对应
《27.2圆心角、弧、弦、弦心距之间的关系》作业设计方案-初中数学沪教版上海九年级第二学期
《圆心角、弧、弦、弦心距之间的关系》作业设计方案(第一课时)一、作业目标本作业设计的目标是使学生通过练习和实践,加深对圆心角、弧、弦、弦心距之间关系的理解,并能够熟练运用这些知识解决实际问题。
同时,培养学生的空间想象能力和数学思维能力。
二、作业内容1. 基础知识巩固- 复习圆的基本概念,包括圆心、半径、弧、弦等。
- 掌握圆心角的概念及表示方法,熟悉弧与弦的定义及其对应关系。
- 练习并理解弦心距的概念,了解其与圆心角、弧的关系。
2. 理解关系式- 通过实例,让学生理解并熟记圆心角、弧、弦之间的关系公式。
- 练习通过给定的圆心角求对应的弧长或弦长。
- 探索不同情况下(如优弧、劣弧)的弧与弦的关系。
3. 实际应用练习- 设计一系列实际问题,如钟表指针与夹角的关系、圆的切线与弦的关系等。
- 要求学生运用所学知识,分析并解决这些问题。
- 通过实际问题的练习,培养学生的空间想象能力和应用能力。
4. 探究性任务- 提供一些具有挑战性的探究性问题,如圆的扇形面积与圆心角的关系等。
- 鼓励学生进行小组合作,共同探究问题,培养学生的合作能力和探究精神。
三、作业要求1. 基础题部分要求每个学生独立完成,并确保准确率。
2. 应用题部分要求学生能够结合所学知识,分析并解决问题,并鼓励一题多解。
3. 探究性任务部分要求学生小组合作完成,鼓励创新思维和批判性思维。
4. 作业需按时完成,并在下节课前上交。
四、作业评价1. 对学生的作业进行批改,重点评价学生对基础知识的掌握情况及对关系公式的运用能力。
2. 对学生的应用题解答进行评价,关注学生的问题分析能力和解题思路。
3. 对探究性任务的完成情况进行综合评价,鼓励创新和合作精神。
4. 将评价结果及时反馈给学生,指出不足之处并给予指导。
五、作业反馈1. 对学生的作业进行总结分析,找出共性问题及个别问题。
2. 在课堂上进行作业讲解,重点讲解共性问题及难点问题。
3. 针对学生的不足,布置相应的补充练习,帮助学生巩固提高。
沪教版(上海)九年级数学第二学期导学案设计:27.2圆心角-弧-弦-弦心距之间的关系(1)(无答案)
27.2 圆心角、弧、弦、弦心距之间的关系(1)[学习目标](1)理解圆心角、弧、弦、弦心距等概念.(2)掌握同圆或等圆中圆心角、弧、弦、弦心距之间关系的定理,能初步运用定理解决有关数学问题.一、课前预习1、知识回顾(1)⊙O 的半径5r cm =,圆心O 到直线的AB 距离3d OD cm ==. 在直线AB 上有P 、Q 、R 三点,且有4PD cm =,4QD cm >,4RD cm <. P 、Q 、R 三点对于⊙O 的位置各是怎么样的?(2)Rt ABC 中,90C ∠=︒,CD AB ⊥,13AB =,5AC =,对C 点为圆心,6013为半径的圆与点A 、B 、D 的位置关系是怎样的?2、概念学习弦:连结圆上任意两点的线段叫做弦. 直径:经过圆心的弦是直径.圆弧:圆上任意两点间的部分叫做圆弧,简称弧.弧的符号“”的表示.以A 、B 为端点的弧,记作 AB ,读作“圆弧AB ”或“弧AB ”.半圆:圆的任意一条直径的两个端点分圆成两条弧,每一条弧叫做半圆. 优弧:大于半圆的弧叫优弧. 劣弧:小于半圆的弧叫做劣弧.弓形:由弦及其所对的弧组成的图形叫做弓形. 同心圆:即圆心相同,半径不相等的两个圆叫做同心圆. 等弧:在同圆或等圆中,能够互相重合的弧叫做等弧. 圆心角:顶点在圆心的角叫圆心角.弦心距:从圆心到弦的距离叫做弦心距.问题:(1)指出图中⊙O 的弦、直径、半圆、优弧、劣弧、圆心角;(2)作出弦AB 的弦心距。
二、课堂学习在平面上,一个圆绕着它的圆心旋转任何一个角度(大于0°且小于360°) ,都能与原来图形重合. 所以,圆是以圆心为旋转对称中心的旋转对称图形,旋转角可为大于0°且小于360°的任何一个角.操作:自制两个圆形纸片(等圆),并且在两个圆中,画出两个相等的圆心角.探究:在⊙O 中,当圆心角∠AOB=∠A ′OB ′时,它们所对的弧AB 和A'B'、弦AB 和A ′B ′、弦心距OC 和OC ′是否也相等呢?把扇形OAB 绕圆心O 旋转,使OA 与OA'重合,那么OB 和 重合;点A 与点 重合,点B 与点 重合,这样AB 与 就一定重合. 两弦的垂线段OC 与 也重合(为什么?).于是,可以得到圆心角、弧、弦、弦心距之间关系的定理:定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.问题:这个命题不加“在同圆或等圆”这个前题条件是否是一个真命题呢?例题1 如图⊙0是△ABC 的外接圆,∠AOB=∠AOC=120°. (1)求证:△ABC 是等边三角形;(2)如果BC 的弦心距为3厘米,求AB 、AC 的弦心距.课堂小结三、课堂练习1、判断下列语句是否正确?为什么? (1)半圆是弧. (2)直径是弦; (3)弦是直径;(4)半圆是弧,但弧不一定是半圆; (5)半径相等的两个半圆是等弧; (6)长度相等的两条弧是等弧;OCBAC 'B ''O C BAOCBA2、如图,AB 与弦AB 哪条长?为什么?3、如图,在⊙0中,如果AB 、CD 是直径,那么图中相等的弧有哪些?为什么?4、如图,已知在⊙0中,AB 、CD 分别是弦.,OE AB OF CD ⊥⊥,垂足分别是点E 、F. 请添加一个条件,使得OE=OF.四、课后作业一、判断题(1)直径是弦,但弦不一定是直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课型
新授课
教
学
目
标
1、理解弧、弦、圆心角、弦心距、等圆等概念,通过操作、说理和证明,探索圆心角、弧、弦、弦心距之间的关系.
2、运用定理进行简单的几何论证和计算.
重点
圆心角、弧、弦、弦心距概念的理解.
难点
圆心角、弧、弦、弦心距之间的关系定理的论证及简单应用.
课堂小结:圆心角、弧、弦、弦心距之间的关系一.圆心角、弧、弦、弦心距的概念(圆具有旋转不变性)二.圆心角、弧、弦、弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
课外
作业
练习册习题27.2(1)
预习
要求
圆心角、弧、弦、弦心距之间的关系(2)
教学后记与反思
1、课堂时间消耗:教师活动分钟;学生活动分钟)
2、本课时实际教学效果自评(满分10分):分
3、本课成功与不足及其改进措施:
由此上述定理可补充为
新课探索五
例题如图,⊙O是△ABC的外接圆,∠AOB=∠AOC=120°.(1)求证:△ABC是等边三角形;(2)如果BC的弦心距为3厘米,求AB、AC的弦心距.
课内练习一
1.是非题:(1)在圆中相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等. ( )(2)半圆是弧,弧是半圆. ( )(3)如图,因为∠AEC=∠DEB,所以AC=DB. ( )
新课探索三
如图,∠AOB是圆心角,弦AB叫做圆心角∠AOB所对的弦,弧AB叫做圆心角∠AOB所对的弧.反之,∠AOB是AB(或.如图,过圆心O作弦AB的垂线,垂足为C,则垂线段OC的长是弦AB的弦心距.
如图,也可以说,
垂线段OC表示弦AB的弦心距
新课探索四(1)
圆心角、弧、弦、弦心距之间的关系
课题
27.2(1)圆心角、弧、弦、弦心距之间的关系
设计
依据
(注:只在开始新章节教学课必填)
教材章节分析:本课是研究圆中四组量圆心角、弧、弦、弦心距之间的关系的第一课时,学生将理解圆弧、弦、圆心角、优弧、劣弧、弦心距等概念及定理:同圆或等圆中,相等的圆心角所对的弧相等,所对的弦、弦心距相等.并能运用定理进行简单的论证及计算.
如图,若圆心角∠AOB=∠AOB,OC与OC分别是弦AB,AB的弦心距,则你能得到哪些量相等.
把扇形OAB绕圆心O旋转,使OA与OA重合.因为∠AOB=∠AOB,所以OB和OB重合;
新课探索四(2)
定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
半径长相等的两个圆一定能够重合,半径相等的两个圆称为等圆.
教学
准备
多媒体,尺,圆规
学生活动形式
预习,讲练结合
教学过程
设计意图
课题引入:
课前练习一
圆是一种和谐、美丽的图形,无论从哪个角度看,它都具有同一形状.十五的满月、圆圆的月饼都象征着圆满、团圆、和谐.
古希腊的数学家毕达哥拉斯认为:“一切立体图形中最美的是球,一切平面图形中最美的是圆”
没有特别说明的情况下,圆心角的范围在0到180度之间
课内练习二
3.如图,在⊙O中,如果AB、CD是直径,请说出图中相等的弧.
课内练习三
4.如图,已知在中,AB、CD分别是弦,OE⊥AB,OF⊥CD,垂足分别是点E、F.请添加一个条件,使得OE=OF.
所添加的条件是∠AOB=∠COD.
若添加的条件是AB=CD或AB=CD可以吗?
这就是我们下一课时要研究的课题.
知识呈现:
新课探索一
我们把图(3)中的∠AOB叫做圆心角.
根据图(3)中∠AOB的特点,你能讲一讲怎样的角叫做圆心角吗?
新课探索二
圆上任意两点之间的部分叫做圆弧,简称弧(如图).联结圆上任意两点的线段叫做弦(如图).过圆心的弦就是直径(如图).
圆的任意一条直径的两个端点将圆分成两条弧,每一条弧都叫做半圆.大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
