matlab多元函数极限与偏导数的符号运算及多元Taylor 公式
Matlab-详解导数及偏导数运算ppt课件

ppt课件.
20
du_dx=1/(x^2+y^2+z^2)^(1/2)*x du_dy =1/(x^2+y^2+z^2)^(1/2)*y du_dz = 1/(x^2+y^2+z^2)^(1/2)*z
u
x
x x2y2z2
u
z
z x2y2z2
u
y
y x2y2z2
ppt课件.
21
例 9 求下列函数的偏导数 z1 arctan( y / x);z2 x y。 解: 输入命令
3
1. 学习Matlab命令
建立符号变量命令 sym 和 syms 调用格式:
x=sym(‘x’) 建立符号变量 x;
syms x y z
建立多个符号变量 x,y,z;
ppt课件.
4
Matlab 求导命令 diff 调用格式:
diff(f(x)),
求 f (x)的一阶导数 f(x);
diff(f(x),n), 求 f(x)的 n阶导 f(n)(x 数 );
实验3 导数及偏导数运算
ppt课件.
1
实验目的:
1. 进一步理解导数概念及几何意义; 2. 学习Matlab的求导命令与求导法。
ppt课件.
2
实验内容:
学习 Matlab 命令 导数概念 求一元函数的导数 求多元函数的偏导数 求高阶导数或高阶偏导数 求隐函数所确定函数的导数与偏导数
ppt课件.
dy_dx = sin(t)/(1-cos(t))
ppt课件.
19
4. 求多元函数的偏导数
例8 设u x2y2z2,求 u的一阶偏导
解:输入命令
多元函数的Taylor公式

y
f
1, 2
1 2!
x
1
x
y
2
y
2
f
1, 2
f 1, 2 x 1 fx 1, 2 y 2 fy 1, 2
1 ( x 12
2!
f xx
1, 2 2 x 1 y 2
(4) 若函数z f (x, y)在区域D 上的两个一阶偏导数 恒为零, 由中值公式可知在该区域上 f (x, y) 常数.
n阶Taylor公式中关于h和k的n次多项式(或:除去函 数在点(x0+θh,y0+θk)(其中0<θ<1)处所有偏导数项以 后),称为n阶Taylor多项式.
在作近似计算时我们常用以下公式:
(h
x
k
y
)3
f
(0,
0)
3
C3p
p0
h
pk
3
p
x
3 p
f y3
p
(0,0)
2(h k)3
又 f (0, 0) 0,将h x , k y 代入三阶泰勒公式得
其中
R3
ln(1 x y)
(h
x
k
y
)
x
4
y
f ( h,
1 2
(x k)
h
y)2
x
1 3
1 4
(
x y)3
(x
(1 x
R3
y)4
y)4
ky
例2 写出在点(1,-2)附近函数 f x, y 2x2 xy y2
实验三 用matlab求极限和导数
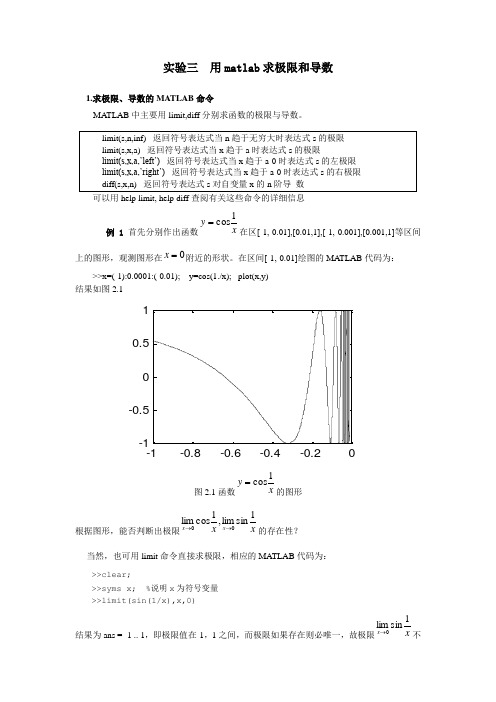
实验三 用matlab 求极限和导数1.求极限、导数的MATLAB 命令MATLAB 中主要用limit,diff 分别求函数的极限与导数。
可以用help limit, help diff 查阅有关这些命令的详细信息例1首先分别作出函数x y 1cos=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1图2.1函数x y 1cos=的图形根据图形,能否判断出极限x x x x 1sinlim ,1cos lim 00→→的存在性? 当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear;>>syms x; %说明x 为符号变量>>limit(sin(1/x),x,0)结果为ans = -1 .. 1,即极限值在-1,1之间,而极限如果存在则必唯一,故极限x x 1sinlim 0→不存在,同样,极限x x 1coslim 0→也不存在。
例2 首先分别作出函数x xy sin =在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2图2.2 函数x xy sin =的图形根据图形,能否判断出极限1sin lim0=→x xx 的正确性?当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear; >>syms x;>>limit(sin(x)/x,x,0) 结果为ans =1.例3 观测当n 趋于无穷大时,数列n n n a )11(+=和1)11(++=n n n A 的变化趋势。
MATLAB多元函数极值

多元函数的极值【实验目的】1. 多元函数偏导数的求法。
2. 多元函数自由极值的求法 3. 多元函数条件极值的求法.4. 学习掌握MATLAB 软件有关的命令。
【实验内容】求函数32824-+-=y xy x z 的极值点和极值【实验准备】1.计算多元函数的自由极值对于多元函数的自由极值问题,根据多元函数极值的必要和充分条件,可分为以下几个步骤:步骤1.定义多元函数),(y x f z =步骤2.求解正规方程0),(,0),(==y x f y x f y x ,得到驻点步骤3.对于每一个驻点),(00y x ,求出二阶偏导数,,,22222yzC y x z B x z A ∂∂=∂∂∂=∂∂=步骤4. 对于每一个驻点),(00y x ,计算判别式2B AC -,如果02>-B AC ,则该驻点是极值点,当0>A 为极小值, 0<A 为极大值;,如果02=-B AC ,判别法失效,需进一步判断;如果02<-BAC ,则该驻点不是极值点.2.计算二元函数在区域D 内的最大值和最小值 设函数),(y x f z =在有界区域D 上连续,则),(y x f 在D 上必定有最大值和最小值。
求),(y x f 在D 上的最大值和最小值的一般步骤为:步骤1. 计算),(y x f 在D 内所有驻点处的函数值;步骤2. 计算),(y x f 在D 的各个边界线上的最大值和最小值;步骤3. 将上述各函数值进行比较,最终确定出在D 内的最大值和最小值。
3.函数求偏导数的MATLAB 命令MATLAB 中主要用diff 求函数的偏导数,用jacobian 求Jacobian 矩阵。
可以用help diff, help jacobian 查阅有关这些命令的详细信息【实验方法与步骤】练习1 求函数32824-+-=y xy x z 的极值点和极值.首先用diff 命令求z 关于x,y的偏导数>>clear; syms x y; >>z=x^4-8*x*y+2*y^2-3; >>diff(z,x) >>diff(z,y)结果为ans =4*x^3-8*y ans =-8*x+4*y 即.48,843y x yzy x x z +-=∂∂-=∂∂再求解正规方程,求得各驻点的坐标。
matlab 偏导数

matlab 偏导数一、什么是偏导数偏导数是多元函数中的一个概念。
在多元函数中,每个自变量都可以独立地变化,而其他自变量保持不变。
对于一个函数$f(x_1,x_2,...,x_n)$,如果我们只考虑其中的一个自变量$x_i$的变化对$f$的影响,其他自变量保持不变,则称$f$关于$x_i$的偏导数为$\frac{\partial f}{\partial x_i}$。
二、matlab中的偏导数在matlab中,我们可以使用syms命令定义符号变量,然后使用diff 命令求解偏导数。
具体步骤如下:1. 使用syms命令定义符号变量:```syms x y```2. 定义多元函数:```f = x^2 + 2*x*y + y^2;```3. 使用diff命令求解偏导数:```df_dx = diff(f, x);df_dy = diff(f, y);```其中,diff命令第一个参数为要求解的函数,第二个参数为要对哪个自变量求解。
4. 输出结果:```df_dx =2*x + 2*ydf_dy =2*x + 2*y```三、示例下面以一个简单的示例来说明如何在matlab中求解偏导数。
问题:已知$f(x,y)=x^3+y^3-3xy$,求$\frac{\partial f}{\partial x}$和$\frac{\partial f}{\partial y}$。
解答:1. 使用syms命令定义符号变量:```syms x y```2. 定义多元函数:```f = x^3 + y^3 - 3*x*y;3. 使用diff命令求解偏导数:```df_dx = diff(f, x);df_dy = diff(f, y);```4. 输出结果:```df_dx =3*x^2 - 3*ydf_dy =3*y^2 - 3*x```因此,$\frac{\partial f}{\partial x}=3x^2-3y$,$\frac{\partial f}{\partial y}=3y^2-3x$。
多元函数的Taylor公式与极值

矩阵为: H f ( x0 )
f11 f21
f12
f
22
f1n
f
2n
设u f (P)在点
f
n1
f
n
2
f
nn
x0
P0 ( x01 , x02 , , x0n ) 的所有二阶偏导数
f11
f12
f1n
f 在点P0的 Hessian
H
f
(P0 )
f21
f
22
f
2n
矩阵为:
f
n1
f
x
, y)2
3 f
2! ,
x py3 p (1 x y)3
( p 0,1,2,3),
4 f 3! , ( p 0,1,2,3,4), x py4 p (1 x y)4
20
x x
y y
f
(0,0)
xfx (0,0)
yf y (0,0)
x
y,
x
y
2
f
(0,0)
x y
由假设, (t) 在 [0,1] 上满足一元函数泰勒公式的条件
于是有 (1) (0) (0) (0)
1!
2!
(n) (0) (n1) ( )
(0
1) .
n!
(n 1)!
(0) f ( x0 , y0 ) , (1) f ( x0 h , y0 k)
利用多元复合函数求导法则可得:
11
(4)在泰勒公式中,如果取 x0 0, y0 0,则 成为n阶麦克劳林(Maclaurin)公式.
f (x, y)
f
(0,0)
x
x
y
MATLAB的符号运算

MATLAB 的符号运算前面介绍的内容基本上是MATLAB 的数值计算功能,参与运算过程的变量都是被赋了值的数值变量.在MATLAB 环境下,符号运算是指参与运算的变量都是符号变量,即使是数字也认为是符号变量. 数值变量和符号变量是不同的.1 符号微积分下面着重介绍一些与微积分有关的指令,这些指令都需要符号表达式作为输入宗量. 求和symsum(S) 对通项S 求和,其中k 为变量且从0变到k-1.symsum(S,v) 对通项S 求和,指定其中v 为变量且v 从0变到v-1. symsum(S,a,b) 对通项S 求和,其中k 为变量且从a 变到b .symsum(S,v,a,b) 对通项S 求和,指定其中v 为变量且v 从a 变到b . 例:求∑-=10k i i ,键入k=sym('k') % k 是一个符号变量;symsum(k)得 ans = 1/2*k^2-1/2*k例:求∑=1002k k,键入:symsum(k^2,0,10)得 ans = 385 例:求∑+∞=0!k kk x 键入 symsum('x'^k/sym('k!'),k,0,inf),得 ans = exp(x)这最后的一个例子是无穷项求和.求极限limit(P) 表达式P 中自变量趋于零时的极限limit(P,a) 表达式P 中自变量趋于a 时的极限limit(P,x,a,'left') 表达式P 中自变量x 趋于a 时的左极限limit(P,x,a,'right') 表达式P 中自变量x 趋于a 时的右极限 例:求xx x sin lim 0→,键入 P=sym('sin(x)/x');limit(P)得 ans = 1例:求xx 1lim 0+→ 键入 P=sym('1/x');limit(P,'x',0,'right')得 ans = inf 例:求hx h x h sin )sin(lim 0-+→,键入: P=sym('(sin(x+h)-sin(x))/h');h=sym('h');limit(P,h,0)得ans = cos(x) 例:求)lim , )1(lim (-x x x x e xa -∞→-∞→+, 键入 v=sym('[(1+a/x)^x,exp(-x)]');limit(v,'x',inf,'left')得 ans = [ exp(a), 0]求导数diff(S,v) 求表达式S 对变量v 的一阶导数.diff(S,v,n) 求表达式S 对变量v 的n 阶导数.例如:设A=⎪⎪⎪⎭⎫ ⎝⎛++21cos 11x e x x b a ,求dx dA 键入命令: syms a b x; A= [1/(1+a),(b+x)/cos(x);1,exp(x^2)];diff(A,'x')得 ans = [0, 1/cos(x)+(b+x)/cos(x)^2*sin(x)][0, 2*x*exp(x^2)]例:求y=sinx+e x 的三阶导数,键入命令:diff('sin(x)+x*exp(x)',3)得 ans = -cos(x)+3*exp(x)+x*exp(x) 例:设⎪⎪⎪⎭⎫ ⎝⎛+=xyi n e xy y x y x A 1sin ,求A 的先对x 再对y 的混合偏导数.可键入命令: S=sym('[x*sin(y),x^n+y;1/x/y,exp(i*x*y)]');dsdxdy=diff(diff(S,'x'),'y')得: dsdxdy = [ cos(y), 0][ 1/x^2/y^2, i*exp(i*x*y)-y*x*exp(i*x*y)]例:求y=(lnx)x 的导数.可键入命令:p='(log(x))^x';p1=diff(p,'x')得:p1 = log(x)^x*(log(log(x))+1/log(x))例:求y=xf(x2)的导数.可键入命令:p='x*f(x^2)';p1=diff(p,'x')得:p1 = f(x^2)+2*x^2*D(f)(x^2)例:求xy=e x+y的导数.可键入命令:p='x*y(x)-exp(x+y(x))';p1=diff(p,'x')得:p1 = y(x)+x*diff(y(x),x)-(1+diff(y(x),x))*exp(x+y(x))再键入p2='y+x*dy-(1+dy)*exp(x+y)=0';dy=solve(p2,'dy')%把dy作为变量解方程得dy= -(y-exp(x+y))/(x-exp(x+y))求Taylor展开式taylor(f,v) f对v的五阶Maclaurin展开.taylor(f,v,n) f对v的n-1阶Maclaurin展开.例:求sinxe-x 的7阶Maclaurin展开.可键入f=sym('sin(x)*exp(-x)');F=taylor(f,8)得F = x-x^2+1/3*x^3-1/30*x^5+1/90*x^6-1/630*x^7例:求sinxe-x 在x=1 处的7阶Taylor展开.可键入f=sym('sin(x)*exp(-x)');F=taylor(f,8,1) 得F = sin(1)*exp(-1)+(-sin(1)*exp(-1)+cos(1)*exp(-1))*(x-1)-cos(1)*exp(-1)*(x-1)^2+(1/3*sin(1)*exp(-1)+1/3*cos(1)*exp(-1))*(x-1)^3-1/6*sin(1)*exp(-1)*(x-1)^4+(1/30*sin(1)*exp(-1)-1/30*cos(1)*exp(-1))*(x-1)^5+1/90*cos(1)*exp(-1)*(x-1)^6+(-1/630*cos(1)*exp(-1)-1/630*sin(1)*exp(-1))*(x-1)^7多元函数的Taylor展开MATLAB不能直接进行多元函数的Taylor展开.必须先调用MAPLE函数库中的mtaylor命令.方法为:在MATLAB的工作窗口中键入maple('readlib(mtaylor)')mtaylor的格式为mtaylor(f,v,n)f为欲展开的函数式v 为变量名.写成向量的形式:[var1=p1,var2=p2,…,varn=pn],展开式将在(p1,p2,…,pn )处进行.如只有变量名,将在0点处展开.n 为展开式的阶数(n -1阶).要完成Taylor 展开,只需键入maple('mtaylor (f,v,n )')即可.例:在(x0,y0,z0)处将F=sin xyz 进行2阶Taylor 展开.键入syms x0 y0 z0maple('readlib(mtaylor)');maple('mtaylor(sin(x*y*z),[x=x0,y=y0,z=z0],2)') 得:ans = sin(x0*y0*z0)+cos(x0*y0*z0)*y0*z0*(x-x0)+cos(x0*y0*z0)*x0*z0*(y-y0)+cos(x0*y0*z0)*x0*y0*(z-z0)求积分int(P) 对表达式P 进行不定积分.int(P,v) 以v 为积分变量对P 进行不定积分.int(P,v,a,b) 以v 为积分变量,以a 为下限,b 为上限对P 进行定积分. 例:求⎰+-dx x x 22)1(2,可键入int('-2*x/(1+x^2)^2')得 ans = 1/(1+x^2) 例:求⎰+dz z x )1(2,可键入键入int('x/(1+z^2)','z')得 ans = atan(z)*x例:求⎰+10)1ln(dx x x ,可键入 int('x*log(1+x)',0,1) 得ans = 1/4例:求⎰tt xdx ln sin 2可键入:int('2*x','sin(t)','log(t)') 得:ans = log(t)^2-sin(t)^2对(符号)矩阵积分例:求()⎰⎰dt e dt e att ,输入 int('[exp(t),exp(a*t)]'),得:ans = [ exp(t), 1/a*exp(a*t)]求符号方程的解ⅰ线性方程组的求解线性方程组的形式为A*X=B ;其中A 至少行满秩.X=linsolve(A,B) 输出方程的特解X .例:解方程组⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛11cos sin sin cos X t t t t .键入 A=sym('[cos(t),sin(t);sin(t),cos(t)]');B=sym('[1;1]');c=linsolve(A,B)c =[ 1/(sin(t)+cos(t))][ 1/(sin(t)+cos(t))]ⅱ 代数方程的求解solve(P,v)对方程P 中的指定变量v 求解.v 可省略.solve(p1,P2,…,Pn,v1,v2,…,vn)对方程P1,P2,…Pn 中的指定变量v1, v2…vn 求解.例:解r x p =+sin ,可输入solve('p+sin(x)=r') 得:ans =-asin(p-r)例:解⎩⎨⎧=+-=++034322x x y xy x ,可输入: P1='x^2+x*y+y=3';P2='x^2-4*x+3=0';[x,y]=solve(P1,P2) 得:x = [ 1][ 3]y = [ 1][ -3/2]解⎩⎨⎧=-=++1022v u v u a ,可输入: P1='a+u^2+v^2=0';P2='u-v=1';[u,v]=solve(P1,P2,'u','v') 得:u = [ 1/2+1/2*(-1-2*a)^(1/2)][ 1/2-1/2*(-1-2*a)^(1/2)]v = [ -1/2+1/2*(-1-2*a)^(1/2)][ -1/2-1/2*(-1-2*a)^(1/2)]对于有些无法求出解析解的非线性方程组,MATLAB 只给出一个数值解.这一点可以从表示解的数字不被方括号括住而确定.例:解⎪⎩⎪⎨⎧=-=-+20)sin(2y x ye y x x 键入:[x,y]=solve('sin(x+y)-exp(x)*y=0','x^2-y=2') 得:x = -6.0173272500593065641097297117905y = 34.208227234306296508646214438330由于这两个数字没有被[ ]括住,所以它们是数值解.另外,可利用solve 来解线性方程组的通解.例:解⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛246714922531372X 键入P1='2*x1+7*x2+3*x3+x4=6'; P2='3*x1+5*x2+2*x3+2*x4=4';P3='9*x1+4*x2+x3+7*x4=2';u=solve(P1,P2,P3,'x1','x2','x3','x4')Warning: 3 equations in 4 variables.u = x1: [1x1 sym]x2: [1x1 sym]x3: [1x1 sym]x4: [1x1 sym]可以看到:屏幕提示“有3个方程4个变量”,意为解不唯一(有时会提示解不唯一).且输出的是解的结构形式.为进一步得到解,可输入:u.x1,u.x2,u.x3,u.x4, 得:ans = x1ans = -5*x1-4*x4ans = 11*x1+9*x4+2ans = x4这样就得到了原方程组的通解.⑷ 解符号微分方程解符号微分方程的命令格式为: dsolve('eq1','eq2',…).其中eq 表示相互独立的常微分方程、初始条件或指定的自变量.默认的自变量为t .如果输入的初始条件少于方程的个数,则在输出结果中出现常数c1,c2等字符.关于微分方程的表达式有如下的约定:字母y 表式函数,Dy 表示y 对t 的一阶导数;Dny 表示y 对t 的n 阶导数. 例如:求⎪⎩⎪⎨⎧-==x dtdy ydt dx 的解可键入:[x,y]=dsolve('Dx=y','Dy=-x') 得x =cos(t)*C1+sin(t)*C2y =-sin(t)*C1+cos(t)*C2dsolve 中的输入宗量最多只能有12个,但这并不妨碍解具有多个方程的方程组,因为可以把多个方程或初始条件定义为一个符号变量进行输入.例如求 g f dt df 43+= ,g f dtdg 34+-= , f(0)=0 , g(0)=1 的解.可输入指令: P='Df=3*f+4*g,Dg=-4*f+3*g';v='f(0)=0,g(0)=1';[f,g]=dsolve(P,v)f = exp(3*t)*sin(4*t)g = exp(3*t)*cos(4*t)注意:微分方程表达式中字母D 必须大写. 例如求解微分方程⎪⎩⎪⎨⎧=''='=-=0(0)y 0,(0)y 1,y(0)33y dx y d 可输入y=dsolve('D3y=-y','y(0)=1,Dy(0)=0,D2y(0)=0','x') 得:y = (1/3+2/3*exp(1/2*x)*cos(1/2*3^(1/2)*x)*exp(x))/exp(x)最后看一个解非线性微分方程的例子:dsolve('(Dy)^2+y^2=1','y(0)=0','x')ans = [ sin(x)][ -sin(x)]对于无法求出解析解的非线性微分方程,屏幕将提示出错信息.微分方程的数值解及其它问题的数值解ⅰ 常微分方程的数值解MATLAB 提供了求微分方程数值解的指令:[t,x]=ode23('fname',[t0,tf],x0,tol,trace)[t,x]=ode45('fname',[t0,tf],x0,tol,trace)这两个格式中的输入参数意义完全一样.下面介绍这两个格式的有关内容及各参数的意义.这两个格式都采用Runge--Kutta 法求解微分方程的数值解.它们是针对一阶微分方程组设计的.因此,如果待解的是高阶微分方程,那么首先要化成形式为x'=f(t,x)的一阶微分方程组.称为“状态方程”.‘fname ’是f(t,x)的函数名.该函数以x'为输出,以t,x 为输入变量,注意次序不能颠倒. t0和tf 分别是积分的起始值和终止值.x0是初始值,以向量的形式输入.tol 是用来控制精度的参数,可缺省.缺省时ode23默认tol=1.e-3;ode45默认tol=1.e -6.trace 用来控制是否显示中间结果,可缺省.缺省时,默认trace=0,不显示.输出结果t 和x 分别是时间向量和相应的状态向量.虽然ode45比ode23的精度高,但它的运算速度更快.例:求著名的Van der pol 方程⎩⎨⎧=--=x yy x y x )1(2,并绘出其解的图形. 第一步:在编辑器中编写名为fname 的M 文件.function X=fname(t,x)X=zeros(2,1);X(1)=(1-x(2)^2)*x(1)-x(2);X(2)=x(1);第二步:将此文件存放于自己的文件夹中听候调用.第三步:在MATLAB 的命令窗口调用这个函数,即键入如下命令:[t,x]=ode45('fname',[0,20],[0,0.5]);plot(t,x)ⅱ 数值积分quad('fname',a,b,tol,trace) Simpson 法求数值积分.quad8('fname',a,b,tol,trace) Newton-Cotes 法求数值积分.fname 是被积函数文件名b,a 分别是积分上下限用tol 来控制积分精度.可缺省.缺省时默认tol=0.001.用trace 来控制是否用图形显示积分过程.可缺省.缺省时默认trace=0,不显示图形.例如:求 ⎰-302x e dx第一步:在编辑器中建立被积函数的M 文件.取名为fname 即在编辑器中输入: function y=fname(x)y=exp(-x^2);第二步:将此文件存放于自己的文件夹中.第三步:在MATLAB 环境下调用fname.即输入s=quad8('fname',0,3)就可以得到结果:s =8862。
MATLAB的微积分基本运算

MATLAB的微积分基本运算第六章 MATLAB 的微积分基本运算学习⽬标:1、熟悉符号对象和表达式的创建;2、熟悉计算结果的类型与精度控制和转换3、掌握MATLAB 中符号微积分运算:极限、导数、积分的命令及格式。
第⼀节极限⼀、极限概念演⽰:数列极限是指当n ⽆限增⼤时,n u 与某常数⽆限接近或n u 趋向于某⼀定值,就图形⽽⾔,其点列以某⼀平⾏y 轴的直线为渐近线。
函数极限也是如此。
例1:观察数列?+1n n ,当∞→n 时的变化趋势。
输⼊程序:>> n=1:100;xn=n./(n+1); >> for i=1:100;plot(n(i),xn(i),'r') % plot 是⼆维图形作图命令。
hold onend % for ……..end 语句是循环语句,循环体内的语句被执⾏100次由图可看出,随n 的增⼤,点列与直线y=1⽆限接近,所以11lim=+∞→n nn 例2:观察函数 xx f 1sin)(=,当0→x 时的变化趋势。
输⼊程序:>> x=-1:0.01:1;y=sin(1./x);plot(x,y)从图可看到,当0→x 时,x1sin 在-1和1之间⽆限次振荡,极限不存在。
例3:观察函数 xxx f )11()(+=,当∞→x 时的变化趋势输⼊程序:>> x=-1:10:1000;y=(1+1./x).^x;plot(x,y)从图可看到,当∞→x 时,函数值与某常数⽆限接近,这个常数就是e 。
⼆、极限计算:如果符号表达式F中只有⼀个变量x,x可以省略,当a=0时0也可以省略。
例:阅读理解下列程序>> syms x n>> limit(x^2*exp(x))ans =>> limit(exp(-1/x),x,0,'left')ans =inf>> limit((1+2/n)^(3*n),n,inf)ans =exp(6)三、符号对象与表达式的建⽴微积分运算的对象为函数,MATLAB称为符号表达式, MATLAB进⾏微积分运算⾸先要建⽴符号表达式,然后才可以利⽤MATLAB符号数学⼯具箱提供的函数进⾏运算。
