实验三_用matlab求极限和导数
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
MATLAB中极限与导数

(单位:元),
请你对该产品的长期价格作一预测。 >> syms t >> f=20-20*exp(-0.5*t); >> limit(f,t,inf)
ans =
20 结论:该产品的长期价格为20元. • Wang T.Y.
Matlab软件
计算二重极限 limit(limit(f,x,x0),y,y0)表示 ( x, y )lim 0, y 0) f ( x, y) ( x
例5 由方程xy sin z y 2 z确定的隐函数 z f ( x, y ), 求z x ' , z y ' Fy ' Fx ' dz dz zx ' , zy ' dx Fz ' dy Fz '
syms x y z F=2*z-x*y-sin(z)-y; pretty(-diff(F,x)/diff(F,z)) pretty(-diff(F,y)/diff(F,z))
例3 : 已知u e ,求
xyz
u
3
xyz
syms x y z u=exp(x*y*z); diff(diff(diff(u,x),y),z) pretty(diff(diff(diff(u,x),y),z))
ans=
2 2 2 exp(x y z) + 3 z x y exp(x y z) + y z x exp(x y z)
Matlab软件
教学内容
一、用Matlab软件求函数的极限;
二、用Matlab软件求函数的导数
• Wang T.Y.
Matlab软件
引例1 某储户将10万元的人民币以活期的形式存入银行, 年利率为5%,如果银行允许储户在一年内可任意次结算, 在不计利息税的情况下,若储户等间隔地结算n次,每次 结算后将本息全部存入银行,问一年后该储户的本息和 是多少?随着结算次数的无限增加,一年后该储户是否 会成为百万富翁?
matlab 《数学实验》报告9-matlab的极限和微分运算

matlab 《数学实验》报告9-matlab的极限和微分运算《数学实验》报告学号姓名成绩实验内容:Matlab的极限和微分运算。
一实验目的熟悉MATLAB软件中关于极限和微分运算的基本命令,掌握利用MATLAB软件求极限和微分运算的方法。
二预备知识(1)求函数的极限和微分的运算。
(2) Matlab基本命令limit,初等函数的表示方法。
三实验内容与要求1.求下列极限,将完成实验的程序写到文件sy31.m中xarctanF,(1); 1limxx,0Matlab命令结果clear%µÚ?þÖÖ???? =syms x atan(x)/xf=atan(x)/x ans =limit(f,'x',0) 1121,x,,F,(2) ,,2lim1,x,,x,0Matlab命令结果1clear F2 =syms x ((1+x)/(1-x))^(1/x) F2=((1+x)/(1-x))^(1/x) ans =limit(F2,'x',0) exp(2)xln(1x),F,(3) 3lim2x,0sinxMatlab命令结果 clear F3 =syms x x*log(1+x)/sin(x^2) F3=x*log(1+x)/sin(x^2) ans = limit(F3,'x',0) 1xarctanF,(4) 4limxx,,Matlab命令结果 clear F4 =syms x atan(x)/xF4=atan(x)/x ans =limit(F4,'x',inf) 011,,limF,,(5) ,,531x,1x,,,x1,Matlab命令结果 clear F5 =1/(1-x)-1/(1-x^3) syms xF5=1/(1-x)-1/(1-x^3) ans =limit(F5,'x',1) NaN2、求下列函数的倒数,将完成实验的程序写到文件sy32.m中3(1); y,cosx,cos3x1Matlab命令结果2clear%diyi y1 =syms x cos(x)^3-cos(3*x) y1=(cos(x))^3-cos(3*x) ans = diff(y1,x) -3*cos(x)^2*sin(x)+3*sin(3*x) (2) y,xsinxlnx2 Matlab命令结果 clear%dier y2 =syms xy2=x*sin(x)*log(x) x*sin(x)*log(x)diff(y2,x) ans =sin(x)*log(x)+x*cos(x)*log(x)+sin(x)xxe,1(3)y, 3sinxMatlab命令结果 clear%disan y3 =syms x (x*exp(x)-1)/sin(x) y3=(x*exp(x)-1)/sin(x) ans =diff(y3,x)(exp(x)+x*exp(x))/sin(x)-(x*exp(x)-1)/sin(x)^2*cos(x)x,,4(4),计算; y,ecosxy4Matlab命令结果 clear%disi y3 =exp(x)*cos(x) syms xans = y3=exp(x)*cos(x)diff(y3,x,4) -4*exp(x)*cos(x)2,,20y,xsin2x(5),计算 yMatlab命令结果 clear%diwu y5 =syms x x^2*sin(2*x)y5=x^2*sin(2*x) ans =-99614720*sin(2*x)-20971520*x*cos(2*x)+1048576*x^2*sindiff(y5,x,20) (2*x)3谣言:吃太咸了会得病,导语:“人体每日摄入食盐不应过多,否则易患多种疾病。
matlab求导和极值

数学实验二 用Matlab 软件求一元函数的导数和极(或最)值一、一元函数的导数1.调用格式一:diff(‘f(x)','x',n)式中,)(x f 为函数,x 为自变量,若未指明,按默认的自变量.n 为导数的阶数,缺省时,求一阶导数.例1 已知x x x f cos )(2=,求)(x f ′.解 在命令行中输入:dydx=diff('x^2*cos(x)') %未指明自变量,按默认的自变量输出导数结果结果如下:dydx =2*x*cos(x)-x^2*sin(x)即x x x x x f sin cos 2)(2−=′.例2 已知)arcsin(xt t y =(x 为常数),求22dty d . 解 在命令行中输入:d2ydt2=diff('t*asin(x*t)','t',2) %若不指明对t 求导,则默认对x 求导结果如下:d2ydt2 =2*x/(1-x^2*t^2)^(1/2)+t^2*x^3/(1-x^2*t^2)^(3/2)即3223222])(1[)(12xt t x xt x dt y d −+−=. 2.调用格式二:syms xdiff(f(x),x,n)例3 已知)arcsin(xt t y =(t 为常数),求2dx y d . 解 在命令行中输入:syms x td2ydx2=diff(t*asin(x*t),x,2)输出结果是:d2ydx2 =t^4/(1-x^2*t^2)^(3/2)*x即32422])(1[xt xt dx y d −=. 二、隐函数的导数在Matlab 中没有直接求隐函数导数的命令,但可调用Maple 中求隐函数导数的命令,调用格式如下:maple('implicitdiff(f(x,y)=0,y,x)')例4 求由方程05=−−+y x e xy 所确定的隐函数dxdy . 解 在命令行中输入:dydx=maple('implicitdiff(x*y-exp(x+y)-5=0,y,x)')运行结果是:dydx =-(y-exp(x+y))/(x-exp(x+y))即 yx yx e x e y dx dy ++−−−=. 三、一元函数的极(或最)值在Matlab 中只有求极(或最)小值命令的函数.若要求函数)(x f 在),(21x x 内的极(或最)大值,可转化为求)(x f −在),(21x x 内的极(或最)小值.求极(或最)小值点和极(或最)小值的调用格式是:[x,fual]=fminbnd(‘fun ’,x1,x2)式中,fun 为函数,x1,x2为x 的取值范围,x 为极(或最)小点,fual 为极(或最)小值.例5 求函数x e x f x sin 2)(−=在)5,2(的最小值点和最小值.解 在命令行中输入:[xmin,fmin]=fminbnd('2*exp(-x)*sin(x)',2,5)输出结果如下:x min=3.9270fmin =-0.0279例6 求函数231)(x x x f −−=在]9,10[−的最值点和最值.解 在命令行中输入:[xmin,fmin]=fminbnd('1-3*x-x^2',-10,9); %求)(x f 的最小值点和最小值[xmax,zmin]=fminbnd('-1+3*x+x^2',-10,9); %转化为求)(x f −的最小值点和最小值 fmax=-zmin; %))((x f −−的最大值xmin,fmin,xmax,fmax %输出最小值点、最小值和最大值点、最大值运行结果为:xmin =9fmin =-107xmax =-1.5000fmax =3.2500四、上机实验1.用help命令查看函数diff,fminbnd等的用法.2.上机验证上面各例.3.作相关小节练习中函数的导数和求函数的极(或最)值.。
MATLAB第三章

第三章微积分问题的计算机求解一、实验内容:题目1.试求出如下极限。
①limx→∞(3x +9x )1/ x,②lim x→∞[(x+2)x+2(x+3)x+3 ]/(x+5)2x+5【分析】:该题为单变量函数的极限。
极限问题可以用limit()函数直接求出。
要注意该函数的调用格式为:L=limit(fun,x,x0)(求极限),L=limit(fun,x,x0,’left’或’right’)(求极限)。
还需注意一开始要对函数的字符进行申明。
【解答】:(1)输入如下语句:>> syms x;f=(3^x+9^x)^(1/x);L=limit(f,x,inf)语句运行后显示如下:L =9(2)输入如下语句:>>syms x;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);>> L=limit(f,x,inf)语句运行后显示如下:L =exp(-5)题目2.试求下面的双重极限。
①lim x→−1y→2 (x2y+xy3)/(x+y) 3,②limx→0 y→0 xy /√(xy+1)−1,③limx→0y→0 [1−cos(x2+y2)]/(x2+y2)e x2+y2。
【分析】:该题为多变量函数的极限问题。
他可以用嵌套使用limit()函数来解决。
在MATLAB上可以用L=limit(limit(f,x,x0),y,y0)或者L=limit(f,y,y0),x,x0)来解决。
其思想是所有的先关于X求导,再所有的关于y求导。
【解答】:(1)输入如下语句:>> syms x y>> f=(x^2*y+x*y^3)/(x+y)^3;>> L=limit(limit(f,x,-1),y,2)语句运行后显示如下:L =-6(2)输入如下语句:>> syms x yf=(x*y)/(sqrt(x*y+1)-1);L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =2(3)输入如下语句:>> syms x yf=(1-cos(x^2+y^2))/(sqrt(x^2+y^2)*exp(x^2+y^2));L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =题目3.求出下面函数的导数。
实验三 用matlab求极限和导数
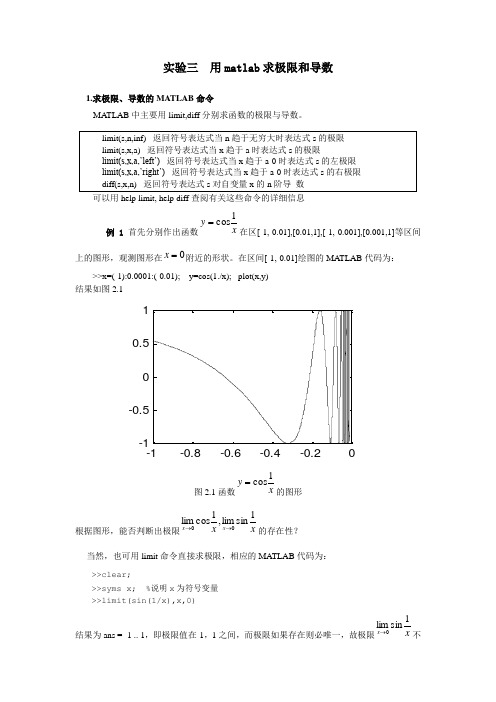
实验三 用matlab 求极限和导数1.求极限、导数的MATLAB 命令MATLAB 中主要用limit,diff 分别求函数的极限与导数。
可以用help limit, help diff 查阅有关这些命令的详细信息例1首先分别作出函数x y 1cos=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1图2.1函数x y 1cos=的图形根据图形,能否判断出极限x x x x 1sinlim ,1cos lim 00→→的存在性? 当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear;>>syms x; %说明x 为符号变量>>limit(sin(1/x),x,0)结果为ans = -1 .. 1,即极限值在-1,1之间,而极限如果存在则必唯一,故极限x x 1sinlim 0→不存在,同样,极限x x 1coslim 0→也不存在。
例2 首先分别作出函数x xy sin =在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2图2.2 函数x xy sin =的图形根据图形,能否判断出极限1sin lim0=→x xx 的正确性?当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear; >>syms x;>>limit(sin(x)/x,x,0) 结果为ans =1.例3 观测当n 趋于无穷大时,数列n n n a )11(+=和1)11(++=n n n A 的变化趋势。
实验3(极限、导数和积分)

符号方程求解
1. 符号代数方程求解 在MATLAB中,求解用符号表达式表示的代数 方程可由函数solve实现,其调用格式为: solve(s):求解符号表达式s的代数方程,求解变 量为默认变量。 solve(s,v):求解符号表达式s的代数方程,求解 变量为v。 例9-9 解关于x的方程x^2-3*x*y+2*y^2=0。 解 syms x y solve(x^2-3*x*y+2*y^2,x)
1.符号表达式的四则运算 符号表达式的加、减、乘、除运算可分别由函数 symadd、symsub、symmul和symdiv来实现,幂 运算可以由sympow来实现。 2.符号表达式的提取分子和分母运算 如果符号表达式是一个有理分式或可以展开为有理 分式,可利用numden函数来提取符号表达式中的 分子或分母。其一般调用格式为: [n,d]=numden(s) 该函数提取符号表达式s的分子和分母,分别将它们 存放在n与d中。
矩形公式和梯形公式
1、从矩形公式到梯形公式
辛普森公式
2、辛普森(Simpson)公式(抛物线公式)
辛普森公式
2、辛普森(Simpson)公式(抛物线公式)
牛顿-柯特斯公式
• 假设已知f(x0),f(x1),…,f(xn)的值。 • 以n + 1点进行插值,求得对应f(x)的拉格朗日多项 式。 • 对该n次的多项式求积。 • 梯形法则和辛卜生法则便是n = 1,2的情况。 n=1 n=2 n=3 n=4
% 第1问 syms x; AI1=int('x^3*exp(-x^2)',x) AI2=int('1/(x*sqrt(x^2+1))',x) %第2问 syms x; BI1=int('x/sin(x)^2',x,pi/4,pi/3) BI2=int('sin(x)^4*cos(x)^2',x,0,pi/2) %第3问 syms x y; CI=int(int('x*sin(x)',x,y,sqrt(y)),y,0,1) %第4问 syms x y z DI=int(int(int('x*y*z',z,0,x*y),y,0,x),x,0,1)
实验三 导数及偏导数的计算

3.用findsym来确认符号表达式中的符号
例:
4. 表达式化简
Matlab提供的对符号表达式化简的函数有:
simplify(S) 应用函数规则对S进行化简。 simple(S) 调用MATLAB的其他函数对 表达式进行综合化简,并显示化简过程。
例1 .(1)执行下面命令:
f=sym(‘cos(x)^2-sin(x)^2’); f=simple(f)
syms t a; dx_dt=diff(a*(t-sin(t)),t); dy_dt=diff(a*(1-cos(t))); dy_dx=dy_dt/dx_dt. 得结果: dy_dx=sin(t)/(1-cos(t)).
4.求多元函数的偏导数.
例 3.9 设u x 2 y 2 z 2 ,求 u 的一阶偏导数. 解: 输入命令: syms x y z; diff((x^2+y^2+z^2)^(1/2), x). 得结果: ans=1/(x^2+y^2+z^2)^(1/2)*x. 在命令中将末尾的x换成y将给出y的偏导数: ans=1/(x^2+y^2+z^2)^(1/2)*y. 也可以输入命令: jacobian((x^2+y^2+z^2)^(1/2),[x y]). 得结果: ans=[1/(x^2+y^2+z^2)^(1/2)*x, 1/(x^2+y^2+z^2)^(1/2)*y]
则h=3,2,1,0.1,0.01分别作出几条割线.
h=[3,2,1,0.1,0.01]; a=(exp(h)-1)./h; x=-1:0.1:3; plot(x,exp(x),’r’); hold on for i=1:5; plot(h(i),exp(h(i)),’r.’) plot(x,a(i)*x+1) end axis square
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 用matlab 求极限和导数
1.求极限、导数的MATLAB 命令
MATLAB 中主要用limit,diff 分别求函数的极限与导数。
可以用help limit, help diff 查阅有关这些命令的详细信息
例1首先分别作出函数
x y 1
cos
=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间
上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1
图2.1函数
x y 1
cos
=的图形
根据图形,能否判断出极限x x x x 1
sin
lim ,1cos lim 00
→→的存在性? 当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:
>>clear;
>>syms x; %说明x 为符号变量
>>limit(sin(1/x),x,0)
结果为ans = -1 .. 1,即极限值在-1,1之间,而极限如果存在则必唯一,故极限x x 1sin
lim 0
→不
存在,同样,极限x x 1
cos
lim 0
→也不存在。
例2 首先分别作出函数
x x
y sin =
在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上
的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2
图2.2 函数
x x
y sin =
的图形
根据图形,能否判断出极限1
sin lim
0=→x x
x 的正确性?
当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:
>>clear; >>syms x;
>>limit(sin(x)/x,x,0) 结果为ans =1.
例3 观测当n 趋于无穷大时,数列n n n a )11(+=和1
)1
1(++=n n n A 的变化趋势。
例如,
当100,,2,1 =n 时,计算
n
n A a ,的MATLAB 代码为:
>>for n=1:100, a(n)=(1+1/n)^n;,A(n)=(1+1/n)^n ;, end
在同一坐标系中,画出下面三个函数的图形:
e
y x
y x y x x =+=+=+,
)1
1(,
)1
1(1
观测当x 增大时图形的走向。
例如,在区间[10,400]绘制图形的MA TLAB 代码为
>>x=10:0.1:400;
>>y1=exp(x.*log(1+1./x)); y2=exp((x+2).*log(1+1./x)); y3=2.71828; >>plot(x,y1,'-.',x,y2,':',x,y3,'-'); %’-.’表示绘出的图形是点线,’-’是实
线
结果如图2.3,其中点线表示1)11(++=x x y 的图形,虚点线表示
x
x y )1
1(+=的图形。
图2.3
通过观测可以看到,当n 增大时,n n n a )11(+=递增,1
)11(++=n n n A 递减。
随着n 的
无穷增大,
n
a 和
n
A 无限接近,趋于共同的极限 71828.2=e .当然,也可用limit 命令直
接求极限,相应的MATLAB 代码为:
>>clear; >>syms n;
>>limit((1+1/n)^n,n,inf)
结果为ans =exp(1)。
例4已知
2
()f x ax bx c =++,求()f x 的微分. >> f=sym('a*x^2+b*x+c') %定义函数表达式
f =a*x^2+b*x+c
>> diff(f) %对默认变量x 求一阶微分 ans =2*a*x+b
>> diff(f,'a') %对符号变量a 求一阶微分 ans =x^2
>> diff(f,'x',2) %对符号变量x 求二阶微分 ans =2*a
>> diff(f,3) %对默认变量x 求三阶微分 ans =0
例5 先求函数363+-=x x y ,然后在同一坐标系里作出函数
363
+-=x x y 及
其导函数
6
3
'2-
=x
y的图形。
函数求导相应的MA TLAB代码为:
>>clear;
>>syms x;
>>diff(x^3-6*x+3,x,1)
结果为ans =3*x^2-6
函数绘图相应的MA TLAB代码为:
>>x=-4:0.1:4; y1=x.^3-6*x+3; y2=3*x.^2-6;
>>plot(x,y1,x,y2,’:’)
结果如图2.4,其中实线是
3
6
3+
-
=x
x
y的图形,点线是6
3
'2-
=x
y的图形。
图2.4 函数及其导数
这里画的是区间[-4,4]上的图形,也可以选别的区间试试。
习题16-3
1.求下列各极限
(1)
n
n n
)
1
1(
lim-
∞
→(2)
n n
n
n3
lim3+
∞
→(3)
)
1
2
2
(
lim n
n
n
n
+
+
-
+
∞
→
(4)
)
1
1
1
2
(
lim
2
1-
-
-
→x
x
x(5)
x
x
x
2
cot
lim
→(6
)
)
3
(
lim2x
x
x
x
-
+
∞
→
(7)
x
x x
m
)
(cos
lim
∞
→(
8)1
11
lim()
1
x
x x e
-
→
-
-(9)0
1
lim
x
x
+
→
2.求下列函数的导数
(1)
1)
y=
(2)
sin ln
y x x x
=
(3)
sin
x
y e x
-
=(4)
y=。
