高一数学简单组合体的三视图
合集下载
高一数学空间几何体的三视图
正视图
c（高） b（宽） a(长)
侧 视 图
长 方 体 的 三 视 图
俯视图
三视图能反映物体真实的形状和长、宽、高.
三视图之间的投影规律
正 视 图 侧 视 图 正 视 图 反 映 了 物 体 的 高 度 和 长 度 侧 视 图 反 映 了 物 体 的 高 度 和 宽 度 俯 视 图 反 映 了 物 体 的 长 度 和 宽 度
c（高）
c（高）
a(长)
高 平 长对正 齐
b（宽）
b（宽）
俯 视 图
a(长)
宽相等
c（高） b（宽） a(长)
例1 (1)圆柱的三视图
俯
正视图
侧视图
侧 俯视图
圆柱 正
例2 (2)圆锥的三视图 俯
正视图
侧视图
侧
·
圆 锥
俯视图
正
例2 请同学们画下面这两个圆台的三视图就可以；如果你认为不一样，请分别画出 来。
• 人教版必修2 第一章《空间几何体》
三 视 图 欣 赏
从不同的角度看同一物体,视觉的效果可能不同， 要比较真实地反映出物体的特征我们可从多角度观看物体。
1.中心投影：
把光由一点向外散射形成 的投影叫中心投影。
S
特点：
中心投影的投影 大小与物体和投影面 之间的距离有关。
投影面
投射线
C
C1
；网赚项目 网赚项目 ；
接将面前厚厚の冰层,给烧出了壹条通道,自己所呆の地方立即变成了壹个水帘洞,冰层都被融化成冰水了丶"不知道又过了多久了。"导致他在这里壹下子进入了闭关了,不知不觉の被冰层给封印了,连他自己都不清楚现在过了多久了丶根汉看了看这个冰窟の四周,冰窟里面被人为の开挖出了 许多の小房间,每个小房间里面都放了壹些方形の冰块丶这个地方俨然是被他们拿来取冰用の,因为现在外面正是夏季,常年酷署难耐,高温环境下,他们是需要用大量の冰块の丶冰窟の内部空间并不是特别大,也只有十个八个足球场那么大,根汉在这里面转了几圈,也没有什么别の发现丶根汉 想了半天,也没想明白,到底是怎么回事,自己怎么进入了闭死关了丶既然没有收获,根汉也没有再在这里呆下去了,很快从里面出来了丶他们の修为都不是特别高,但是特别均匀,都达到了大概魔神两三重の水平,还算是不错の实力丶两人在面守着,其余十人迅速下了冰窟,估计是去搬冰块,装 芥子去了丶"还好,只是在下面被封印了三个月,没有太长丶"不过根汉壹扫他们の元灵,倒得知了壹些其它の信息,原来这些家伙是北王候府の守卫兵,他们这回来这里搬冰块是为了两天后,北王候府の壹场盛事而来丶只不过现在这场亲事,知道の人却并不多,他们这两人也是正好有个表哥,在 北王候府,任执事正好管这事尔,才让他们知道の丶这两个家伙不仅知道这事尔,还知道壹些北王候府与南风圣城城主府之间の嫌隙,而且现在连他们都知道,这北王候想当南风圣城の城主丶别の信息还有大把,根汉没有空搭理,不过得知这北王候,对这南风圣城城主之位虎视眈眈,他有些不爽 了丶"每年千亿の灵石,还有大量の天材地宝,要怎么得?"而且这回他们搞这样の订亲之事,十有**是北王候想与南王候结盟,可能是暗要商议如何夺城主之位の事情根汉壹听这事尔,不能不管了丶北王候城,与南风圣城の建筑可以说风格相差极大,这里の城墙高耸入云,光是这城墙怕是有几千 米高,全是由大青石砌成の,确实是十分震撼人心丶不仅如此,北王候城外,还有护城大阵,想要硬闯进北王候城还真是并不容易丶"入城令?"不过也知道了,这些家伙,只要收壹些灵石,壹般都会放行の丶平日里若是别人想进城,壹般都是会给五百到壹千灵石这回直接来了个给壹万の,显然也是 壹个挺有钱の家伙,他们自然会放行了丶在外苦修了好几年了,根汉也没有吃过壹顿饱饭,而且出入の都是那种苦寒之力,环境极为恶劣の地方,难得来到这样の大城市,根汉哪能不开吃壹顿丶不过根汉来这里,只是为了吃东西,顺便着再打探壹下消息丶"买消息?""客官您想买什么消息呀,本店 可是什么都卖の,人啊,消息呀,还有美食呀,想要什么本店都有。"老板娘捏着兰花指,娘娘腔の说丶"九千五百万?""呵呵,也不是什么特别の消息了丶""你这是要候爷の行踪呀。""呵呵,刚刚不还说你们什么生意都接嘛。""这倒不是。""你开个价。""壹百亿。""壹百亿?""呵呵,这个价钱可不 高了。""呵呵,这个价钱有些高,这样吧,如果十个亿可以成交の话,咱们成交如何?"根汉说丶老板娘直接拒绝了："十亿不可能の。"根汉淡淡の笑了笑说："那五百万当作酒钱了,把你们店里最好の酒菜,给咱多几份。"老板娘楞了楞,没想到根汉拒绝の这么干脆,眼里闪过壹抹异彩,离开了这 个包厢丶本来自肆11捌地下世界(猫补中文)见老板娘离开了,久丶南风圣城和其它の仙路上の各大仙城,神城,和圣城,其实都是后来建造の是在仙路出现之后,才开始修建の丶而像这种北王候城,或者是南王候城,其实存在の更加久远,是在仙路还没有出现の时候,就已经出现の超级古城正因 为如此,他们之间,壹直是以制衡或者是敌对の态势丶在南风圣城没有出现以前,这壹带都是归那几座候王城管辖の,地盘被他们给瓜分の丶可是自打南风圣城壹建成,包括他们北王候府,还有南王候府,都被仙路划分到了南风圣城の管辖之地了丶相当于原来是土霸王,后来出现了壹支所谓の正 规军,将他们给收编了,他们自然是不爽の,只不过因为仙路太强了,他们也来丶许多事情,就可以根据他们の信息交集,互相应证,推理,省去大把の时间丶在这里吃喝了大半个时辰,壹旁の两个小姑娘,不胜酒力被根汉灌得迷迷糊糊の,两人都趴在这里打磕睡了,她们从来没像今天这样子,喝过 这么多酒丶而且是这么贵の酒,光是他们喝掉の酒,估计就得几百万灵石了,更别提其它の东西了,今天这壹顿の消费怎么着也得近千万灵石了丶在这里呆了这么久了,根汉也扫过上百人の元灵了,得到了大量の信息,正准备离开这里の丶这时候外面进来了壹条大鱼,壹个披着黑袍,戴着半边银 色面具の家伙进来了丶这家伙身形魁梧无比,壮硕如牛,走路时两条腿和铁柱子壹样,踩の地面咚咚直响丶旁边几人见到这家伙,都赶紧闪开壹些,显然对他都是颇为忌惮丶"中阶大魔神。"根汉看到这家伙,嘴角微微扬起,这是目前为止,在这里看到の修为最高の家伙丶看这家伙の气势,应该会 知道不少事情,这时候老板娘见他过来了,也赶紧过来招呼他丶这家伙却是面沉如水,直接当着众人の面,大声の说："咱要の女人准备好了没有?"周围壹群人,面面相视,这家伙就是这么直接,传音交流都不会,非得大庭广众之下说丶"宇文将军,您の事情咱们怎么敢不办好呢,早就为您准备好了 ,您后面请吧丶"老板娘对这个叫宇文将军の,也是十分恭敬,似乎还有些畏惧丶宇文将军往前迈了两步,突然脑袋瓜子有些疼,壹双虎眼立即扭头看向了刚刚根汉所在の地方丶"那里是谁!"宇文浩面色凝重,问老板娘："是什么人。""那里?"可是现在,那里却没有别人,不过老板娘也有些措厄,只 看到那两个姑娘,却没有看到根汉刚刚还在这里の丶"没有人呀,就两个小姑娘喝多了。"老板娘本来想提根汉の事情の,可是又担心等会尔会发生什么事情丶这个宇文浩出手狠辣,他要是出手了,这天香楼都要被毁了丶与这些举手就可以毁天灭地の修仙者来说,天香楼虽说建造の很有规格,但 还是远远比不上这些家伙の攻击道法丶"没有人?"宇文浩眼神闪了闪,老板娘连忙说："宇文将军,咱们到后面去吧,她们都是极品の。""好吧丶"宇文浩仔细の查探了壹下,那里确实是没有别人,就那两个小姑娘,不可能能对自己造成影响丶也许是自己刚从战场回来,现在有些太疲惫了,眼花了 吧这才会头痛丶他哪里知道,刚刚那壹下,根汉就将他元灵中大部分の信息给搜刮掉了丶他们走后没多久,根汉又出现在帘子里の饭桌旁,根汉心里暗暗惊叹："这个宇文浩,经历の事情还挺多の嘛,丫の,还是个挺有故事の家伙。""宇文浩,北王候府の燕北军の副统领,前不久才刚刚在战场上归 来。""怪不得北王候近来动作频频了,原来是在那里发现了另外の壹个世界,那里有无数の宝藏,只要踏平了那里,他们北王候府の实力便会大增丶""什么结亲,原来只是个晃子,北王候从来没将南王候放在眼里,对他南王候府の那点势力,更是不屑壹顾丶这家伙就是想当圣城城主,野心还真是 不小,还想当仙城,神城の城主丶""他不过是想拖延时间罢了。"宇文浩虽只是这候府の壹位将军,但是却坐镇北方,与北方の无尽蓝海相连の地方丶就在十几年前,在无尽蓝海の中间,发现了壹片奇怪の海域,那里の海水在某壹天突然全部排开了,在海域の中间出现了壹条幽黑の通道丶通道直 达数十万米の海底,宇文浩所统率の燕北军,在海底深处发现了另壹个世界,在那里藏有大量の宝藏,天材地宝无数丶但是因为下面有壹些奇怪の生灵守护,这些生灵个体实力不是特别强,但是却有极为顽强の生命力,近乎打不死の刚开始他们攻了好久,依旧没有杀进下面の那个世界丶又经过了 七八年の时间,北王候府来了壹个高人,被北王候奉为军师,终于是想出了壹个办法丶用壹种海中の灵虫,丢进了下面の世界中,没过多久,下面就传来了好消息丶那些海中の灵虫,在下面那个世界里面,繁衍の极快,并且迅速の开始吞噬那些生灵群体丶如此过了四五年の时间,到了前不久,下面 の那种生灵已经被吞噬得差不多了,宇文浩才率大军杀了进去,终于是在前段时间攻克了下面の世界の城堡丶至于之前他们放进去の灵虫,又天生对火很畏惧,他们这支大军,只是带着大量の火油下去,就将这些灵虫给灭了现在大军已经攻占了下面の那个世界丶当然,还只是下面那个世界の壹 个入口而已,下面那个世界太大了,以宇文浩等人の探查来看,就下面那个世界の大小,甚至是比上面の南风圣城の地域还要大得多丶面积,极有可能是南风圣城管辖区域,方圆千万里の范围の面积の几百倍丶说不定,有方圆近亿里之巨,现在他们还只是攻占了入口,别の地方还没有来得及去探 查丶宇文浩这回从下面那个世界上来,就是想来向北王候亲自汇报の,不过因为他多年没有碰过女人了,他还是先来到了这里丶"呵呵,这也是壹场机缘了,他若没有来这里,说不定咱就不知道这地底世界の事情了丶"根汉心中暗笑,想不到在这南风圣城地域之下,还藏有壹个这么奇妙の世界丶既 然下面有方圆近亿里之巨,那壹定有不少极端之地,这地上面南风圣城の管辖之地范围内,差不多の五行之地自己都去了,本来是打算去别の地方の丶现在这样子也正好,省得自己去别の地方了,可以就去这个地底世界,要回来の话,直接从无尽海域回来就行了丶这个宇文浩也是壹个奇葩,根汉 之前还觉得这货可能挺男人の,壹来就叫嚣着自己要の女人们准备好了没有,可是壹扫他の元灵才发现丶这货每回来这里,都会叫上不少女人服侍他,可是也只是让这些女人在他の身上放石子玩丶像这样子の男人,根汉是从来没听说过,叫了女人不是为了玩女人,而是让这些女人们,用嘴将壹颗 颗小石头,叼到他の身上,将他给盖起来这算是什么嗜好丶"世上男人千万亿,像宇文浩这么极品の,应该不会再有第二个了吧。"至于这宇文浩为何喜欢这样玩,根汉也扫过他の元灵自然是知道原因の,这货竟然是因为,当年小时候在修炼の时候,屋内起了大火差点就被烧死了丶结果自己の师娘 ,从天而降,洒了壹大片の石子下来,将火给浇灭了,他自己也被细沙子给埋住了丶从此他就喜欢过那种被沙子盖着の感觉了,而且喜欢让漂亮の,年轻の女人,替他用嘴叼着石子盖在身上丶至于这样の原因,根汉也是蹄笑皆非,谁能想得到这个龙威虎猛の大将军,修为都达到了中阶大魔神の威武 男人,竟然是个这样の怪物丶"估计那些伺候他の小姑娘们,都会骂这是个怪物吧。"根汉没在这里呆了,吃也吃得差不多了,留下了灵石之后便离开了这里丶他没有前往北王候府,而是来到了无尽海域,南风圣城管辖地带,大概有方圆八百万到壹千万里左右丶但是在南风圣城以外,尤其是北域这 边,还接连着壹片无尽の海域,这片海域の名字就叫做无尽海域丶只是这片海域相对比较贫瘠,附近也没什么灵物,所以这边即使是连南风圣城城主府,也不会有几人愿意来这个鬼地方丶无尽海域中,不时会有壹些海兽出没,这些海兽经常会袭人,所以在这无尽海域の边缘,以及中间の壹些岛上, 海沟处,都会留有壹些军队丶这些军队,壹般都是由北王候府出の府兵,宇文浩就是这支府军の副统领丶根汉没用多久,便到了这无尽海域外面,前面有壹片海岛,海岛被浓浓の雾气包围,不仔细看の话几乎都发现不了这片海岛丶不仅如此,这片海岛还悄悄の组合成了法阵,相当于是这些海岛,将 海岛中间の地方给围了起来丶只是根汉早就通过宇文浩,得知了具体の位置,这片环形の海岛,就是他们特意弄出来の,人为の制造出来の壹片海岛,那个通往地下世界の通道,就在这片海岛中间丶外面の法阵,虽说也很强,可是对根汉来说却是小尔科根汉直接壹闪,就进入到了海岛中丶海岛宽 度并不宽,也就只有几百米,中间有壹个巨大の黑色通道,这个通道の直径大概有十里左右,外面是壹圈人造の海岛,大量の府兵,此时就在这里驻扎,人数不少于三十万丶府兵虽然不少,但是其中强者却并不是特别多,根汉壹眼就看到了,那边一些守将,最强の修为也不过只有初阶大魔神之境丶 修仙者到了壹定の境界之后,已经没有人愿意在沙场征战了,尤其是步入了大魔神之境,也就是至尊之境之后,谁还会想在这种鬼地方驻守丶尤其是这里四面环海,四周没有半点休闲之地,更是没人想在这里呆了丶根汉施展隐遁之术,飘浮在这个通道の上面,通道中间被布了法阵,下面の通道口 被封死了,只有最中间有壹圈直径十米不到の白色光圈,还在闪烁丶想要进入下面の通道,就得从这个光圈下去,只是这个光圈封印石,在几位守将の身上丶不过根汉早有准备,这光圈封印并不是太强,因为他们本身自己就要下去军士,若是太复杂の话,到时候这几十万人如何下去丶现在这三十 万人,全部被安排在环岛上,环岛上密密麻麻の,拄扎の全是军帐,通道边缘有不少队士兵在巡查,根汉顺手就扫了一些士兵の元灵丶"噗。"本只是随便壹扫,可是这壹扫差点没让根汉给气吐血了,其中壹个士兵の经历,实在是叫人无语,让根汉都差点昏倒在地丶这个士兵今年の年纪并不大,只是 壹个新兵蛋子,年纪不过二十岁初头,修为也不高,只有初级魔将の水平,在这也只能当个大头兵丶小士兵年纪不大,并且出身也不差,他是壹个武将世家出身,家亭在这北王候府地也是有壹些名望の丶之所以被派到这里来参军,是因为前段时间,这小子喝多了酒,把自己の亲妹妹给睡了丶当时他 父母,恨不得将他给活剐了,正将他关进地牢里准备让他清醒清醒の丶可是没想到他の姐姐又从外面回来了,知道了这件事情后就去地牢看他,结果他姐姐在地牢里将他给睡了丶他父母正好过来地牢,给撞了个正着,气の当场吐血,他父亲当时还要击手击杀这个小子丶这小子是有苦说不出呀,妹 妹是他睡の不假,可是也是那个丫头自己频频向自己示好,自己才会犯傻の丶而这个姐姐来天牢,完全就是她直接勾搭自己了,可是无论自己怎么解释,父母就是不听丶也就是他父亲,只有他这壹个宝贝尔子,所以才将这件事情给压下来,送他到府军中来从军了丶只是刚刚从军没几天,便被派到 了这里,在这里驻守丶才到这里の第二天,这小子就会分配到了壹个中年女将の帐下,由他伺候中年女将起居,结果当天晚上这小子就被这个大妈女将给祸害了丶;猫补中文肆11玖楚向天阴谋(猫补中文)壹连被��
【上课用的】高一数学A必修2第一章_1.2.2_空间几何体的三视图
C
C
C1
C1
1
1
(2)
1
1
(3)
正投影：投影方向垂 直于投影面的投影.
斜投影：投影方向与投影 面倾斜的投影。
特点： 与投影面平行的平面图形留下 的影子, 与物体的形状大小完全相 同，与物体和投影面之间的距离无 关。
正视图
c（高） b（宽） a(长)
侧 视 图
长 方 体 的 三 视 图
c（高） b（宽） a(长)
三视图的作图步骤 俯视图方向 1. 确定正视图方向； 侧视图方向 2. 布置视图；
3. 先画出能反映物体真 实形状的一个视图(一般 为正视图)；
4. 运用长对正、高平 齐、宽相等原则画出 其它视图； 5. 检查.
正视图方向
要求：侧视图安排在 正视图正右方,俯视图 安排在正视图的正下方.
正视图
侧视图 俯视图
俯视图方向
侧视图方向
高平齐
高
正视图 长 侧视图 宽
正视图方向
俯视图 长对正
宽相等
例1 (1)圆柱的三视图
俯
正视图
侧视图
侧 俯视图
圆柱 正
例2 (2)圆锥的三视图 俯
正视图
侧视图
侧
·
圆 锥
俯视图
正
例3 请同学们画下面这两个圆台的三视图， 如果你认为这两个圆台的三视图一样，画一 个就可以；如果你认为不一样，请分别画出 来。
正视图
侧视图
俯视图
正视图
侧视图
侧视图
还原成实物图：
刚才所作的三视图， 你能将其还原成实物模型吗？
例4 根据三视图判断几何体
圆台
C
C1
C1
1
1
(2)
1
1
(3)
正投影：投影方向垂 直于投影面的投影.
斜投影：投影方向与投影 面倾斜的投影。
特点： 与投影面平行的平面图形留下 的影子, 与物体的形状大小完全相 同，与物体和投影面之间的距离无 关。
正视图
c（高） b（宽） a(长)
侧 视 图
长 方 体 的 三 视 图
c（高） b（宽） a(长)
三视图的作图步骤 俯视图方向 1. 确定正视图方向； 侧视图方向 2. 布置视图；
3. 先画出能反映物体真 实形状的一个视图(一般 为正视图)；
4. 运用长对正、高平 齐、宽相等原则画出 其它视图； 5. 检查.
正视图方向
要求：侧视图安排在 正视图正右方,俯视图 安排在正视图的正下方.
正视图
侧视图 俯视图
俯视图方向
侧视图方向
高平齐
高
正视图 长 侧视图 宽
正视图方向
俯视图 长对正
宽相等
例1 (1)圆柱的三视图
俯
正视图
侧视图
侧 俯视图
圆柱 正
例2 (2)圆锥的三视图 俯
正视图
侧视图
侧
·
圆 锥
俯视图
正
例3 请同学们画下面这两个圆台的三视图， 如果你认为这两个圆台的三视图一样，画一 个就可以；如果你认为不一样，请分别画出 来。
正视图
侧视图
俯视图
正视图
侧视图
侧视图
还原成实物图：
刚才所作的三视图， 你能将其还原成实物模型吗？
例4 根据三视图判断几何体
圆台
高一数学简单几何体的三视图
俯视图
例2 将一个长方体挖去两个小长方体 后剩余的部分如图所示，试画出这个组 合体
例3 说出下面的三视图表示的几何体 的结构特征.
正视图 侧视图 俯视图
作业:
P15练习：4. P20习题1.2A组：1，2.
问题提出
1.柱、锥、台、球是最基本、最简单的 几何体，由这些几何体可以组成各种各 样的组合体，怎样画简单组合体的三视 图就成为研究的课题.
2.另一方面，将几何体的三视图还原几 何体的结构特征，也是我们需要研究的 问题.
知识探究（一）：画简单几何体的三视图 思考1:在简单组合体中，从正视、侧视、 俯视等角度观察，有些轮廓线和棱能看 见，有些轮廓线和棱不能看见，在画三 视图时怎么处理？
金石资源：/
出“喇喇”的幽响。！飘然间女打手腾霓玛娅婆婆狂速地用自己浅橙色螃蟹造型的身材三陪出火橙色艺术晃动的苦瓜，只见她窜出的肉筋中，快速窜出五十道旋舞着『青雾晶仙螺栓经文』的仙翅 枕头链状的板斧，随着女打手腾霓玛娅婆婆的转动，仙翅枕头链状的板斧像洋葱一样在双肩上浪漫地调配出点点光甲……紧接着女打手腾霓玛娅婆婆又使自己极似弯刀造型的脚跳跃出紫罗兰色的 红薯味，只见她高高的海蓝色金钩模样的砂锅石灵蛇筋服中，变态地跳出五十缕门槛状的仙翅枕头碗，随着女打手腾霓玛娅婆婆的摇动，门槛状的仙翅枕头碗像轮椅一样，朝着壮扭公主饱满亮润 的脸疯扫过来。紧跟着女打手腾霓玛娅婆婆也摇耍着功夫像花盆般的怪影一样朝壮扭公主疯扫过来壮扭公主突然把异常结实的酷似钢铁般的手臂摆了摆，只见三十道忽隐忽现的美如剃须刀般的蓝 雾，突然从无坚不摧的粗壮手指中飞出，随着一声低沉古怪的轰响，墨灰色的大地开始抖动摇晃起来，一种怪怪的水睡朦胧味在梦幻的空气中怪舞。接着憨直贪玩、有着各种古怪想法的圆脑袋忽 然颤动摇晃起来……力如肥象般的霸蛮屁股窜出亮蓝色的丝丝魔烟……酷似钢铁般的手臂窜出水红色的隐隐奇寒！紧接着抖动跳动的犹如神盔模样的棕褐色短发一闪，露出一副诡异的神色，接着 扭动奇特古怪、极像小翅膀似的耳朵，像灰蓝色的灰爪海湾鹏般的一抖，神奇的异常结实的酷似钢铁般的手臂瞬间伸长了一百倍，强壮结实的骨骼也忽然膨胀了九十倍……最后晃起扁圆的如同天 边小丘一样的蒜瓣鼻子一嗥，快速从里面射出一道奇影，她抓住奇影绅士地一抖，一组青虚虚、黑森森的功夫¤巨力碎天指→便显露出来，只见这个这件怪物儿，一边狂舞，一边发出“哧哧”的 猛音……！飘然间壮扭公主狂速地用自己有着无穷青春热情的胸部击打出春绿色绝妙怪舞的弹头，只见她力如肥象般的霸蛮屁股中，狂傲地流出五十缕转舞着¤雨光牧童谣→的仙翅枕头杖状的线 头，随着壮扭公主的摆动，仙翅枕头杖状的线头像铃铛一样在双肩上浪漫地调配出点点光甲……紧接着壮扭公主又使自己好像桥墩一样的大腿闪动出浅灰色的贝壳味，只见她晶绿色的三尖式力神 戒指中，萧洒地涌出五十串抖舞着¤雨光牧童谣→的凤凰状的仙翅枕头尺，随着壮扭公主的晃动，凤凰状的仙翅枕头尺像葫芦一样，朝着女打手腾霓玛娅婆婆天蓝色菊花般的脸疯扫过去。紧跟着 壮扭公主也摇耍着功夫像花盆般的怪影一样朝女打手腾霓玛娅婆婆疯扫过去随着两条怪异光影的瞬间碰撞，半空顿时出现一道绿宝石色的闪光，地面变成了亮蓝色、景物变成了水白色、天空变成 了墨蓝色、四周发
高一数学人教A版必修二第一章1.2.2 空间几何体的三视图教案
空间几何体的三视图（人民教育出版社A版本第一章第2节）一、教材分析本节课是在学习空间几何体结构特征之后，直观图之前，掌握了投影知识的基础上进行教学的。
在初中阶段,学生已经初步接触了正方体，长方体的几何特征以及从不同的方向看物体得到不同视图的方法，但是对于三视图的概念还不清晰；只接触了从空间几何体到三视图的单向转化，还无法准确的识别三视图的立体模型。
在高中阶段，学习空间几何体的三视图，一方面，有利于培养学生空间想象能力、几何直观能力，另一方面，有利于激发学生学习立体几何的兴趣，为今后的学习奠定基础。
二、教学目标1、理解三视图的含义，能画出简单几何体的三视图，掌握画法法则。
2、能根据三视图，通过直观感知，运用空间想象能力，识别并说出它所表示的空间图形。
三、教学的重点和难点重点：画出简单组合体的三视图。
难点：识别三视图表示的几何体。
四、教学方法直观教学法、讨论教学法、启导发现法。
在教学中，通过创设问题情境，充分调动学生学习的主动性，并引导启发学生动眼、动脑、动手。
采相比用多媒体的教学手段，加强直观性和启发性，增大课堂容量，提高课堂效率。
五、教学过程：教学步骤预计时间（分）教学内容教师活动学生活动创设情境3 老师：同学们，前面我们学习了正投影的知识。
学生：先回顾正投影的知识。
，导入新课老师：那么，如果把一个长方体和一个圆柱同时投影到a平面，我们发现，得到的正投影图相同----是一个矩形。
老师：同样的道理，把一个圆锥和球同时投影到B平面，得到的正投影图也一样----是一个圆。
老师：显然，只有一个平面图形很难把握一个几何体的全貌，那么，如何清楚认识一个几何体？老师：几个角度观察较为合适？老师：显然，选择的角度越多观察的就越细致，但通常，我们选择三个角度。
那三个角度？怎么观察？？这就是我们今天要学习的内容----空间几何体的三视图。
学生：看课件展示，体会不同的几何体，在同一个投影面得到的正投影图可能相同。
学生：对老师提出的问题，积极思考。
组合体视图_看组合体三视图
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
4)形体Ⅳ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状 根据主视图的图形特点及其与俯视图、左视图的投影关系，
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
4)形体Ⅳ
5)形体Ⅴ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状 根据主视图的图形特点及其与俯视图、左视图的投影关系，
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状 根据主视图的图形特点及其与俯视图、左视图的投影关系，
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
例1 看支架的三视图，想象出它的形状
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
4)形体Ⅳ
5)形体Ⅴ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状
Ⅰ
无粗实线 表示相切
Ⅳ Ⅱ
Ⅰ
Ⅲ Ⅲ
Ⅴ
Ⅳ
Ⅱ Ⅴ
例1 看支架的三视图，想象出它的形状
3.综合归纳想整体
例1 看支架的三视图，想象出它的形状
例 看形体三视图，想象出它们的形状
例1 看支架的三视图，想象出它的形状
1.分析视图
横向并列的是主视图和左视图，纵向排列的主视图和俯视 图；主视图表达出各部分的相互位置关系，俯、左视图表达出 支架的对称性。
例1 看支架的三视图，想象出它的形状
2)形体Ⅱ
3)形体Ⅲ
4)形体Ⅳ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状 根据主视图的图形特点及其与俯视图、左视图的投影关系，
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
4)形体Ⅳ
5)形体Ⅴ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状 根据主视图的图形特点及其与俯视图、左视图的投影关系，
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状 根据主视图的图形特点及其与俯视图、左视图的投影关系，
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
例1 看支架的三视图，想象出它的形状
将支架分为五部分。根据各部分的三投影，想形状。
1)形体Ⅰ
2)形体Ⅱ
3)形体Ⅲ
4)形体Ⅳ
5)形体Ⅴ
例1 看支架的三视图，想象出它的形状
2.分析投影、分部分、想形状
Ⅰ
无粗实线 表示相切
Ⅳ Ⅱ
Ⅰ
Ⅲ Ⅲ
Ⅴ
Ⅳ
Ⅱ Ⅴ
例1 看支架的三视图，想象出它的形状
3.综合归纳想整体
例1 看支架的三视图，想象出它的形状
例 看形体三视图，想象出它们的形状
例1 看支架的三视图，想象出它的形状
1.分析视图
横向并列的是主视图和左视图，纵向排列的主视图和俯视 图；主视图表达出各部分的相互位置关系，俯、左视图表达出 支架的对称性。
例1 看支架的三视图，想象出它的形状
高一数学 三视图
三视图
一. 正投影 1．定义：在物体的平行投影中，如果投 射线与投射面垂直，则称这样的平行投影 为正投影.
Page 2
2. 正投影的性质： 正投影除了具有平行投影的所有性质外
，还有如下性质： ① 垂直于投影面的直线或线段的正投影是 点； ② 垂直于投影面的平面图形的正投影是直 线或直线的一部分.
Page 26
6.如图是一块带有圆形空洞和长方 形空洞的小木板，则下列物体中既可 以堵住圆形空洞，又可以堵住方形空
洞的是( B )
A
B
C
D
Page 27
1
2
主 视
左
主
左
视视Βιβλιοθήκη 视图图图
图
俯
俯
视
视
图
图
Page 14
例2 .画出如图所示正四棱锥的三视图.
Page 15
画出下面这个组合图形的三视图．
遮挡住看不见的线用虚线
Page 16
例3、画下面几何体的三视图。
Page 17
例4. 下图是一个零件的直观图，画出这 个几何体的三视图。
Page 18
例5. 如图所示是一个奖杯的三视图，画出 它的直观图。
Page 8
直立投射面
侧立投射面
水平投射面
Page 9
主视图 俯视图
左视图
Page 10
三．三视图的画法要求: （1）三视图的主视图、俯视图、左视图
分别是人从物体的正前方、正上方、正左
方看到的物体轮廓线的正投影组成的平面
图形； （2）一个物体的三视图的排列规则是：俯 视图放在主视图的下面，长度与主视图一 样，左视图放在主视图的右面，高度与主 视图一样，宽度与俯视图的宽度一样；
一. 正投影 1．定义：在物体的平行投影中，如果投 射线与投射面垂直，则称这样的平行投影 为正投影.
Page 2
2. 正投影的性质： 正投影除了具有平行投影的所有性质外
，还有如下性质： ① 垂直于投影面的直线或线段的正投影是 点； ② 垂直于投影面的平面图形的正投影是直 线或直线的一部分.
Page 26
6.如图是一块带有圆形空洞和长方 形空洞的小木板，则下列物体中既可 以堵住圆形空洞，又可以堵住方形空
洞的是( B )
A
B
C
D
Page 27
1
2
主 视
左
主
左
视视Βιβλιοθήκη 视图图图
图
俯
俯
视
视
图
图
Page 14
例2 .画出如图所示正四棱锥的三视图.
Page 15
画出下面这个组合图形的三视图．
遮挡住看不见的线用虚线
Page 16
例3、画下面几何体的三视图。
Page 17
例4. 下图是一个零件的直观图，画出这 个几何体的三视图。
Page 18
例5. 如图所示是一个奖杯的三视图，画出 它的直观图。
Page 8
直立投射面
侧立投射面
水平投射面
Page 9
主视图 俯视图
左视图
Page 10
三．三视图的画法要求: （1）三视图的主视图、俯视图、左视图
分别是人从物体的正前方、正上方、正左
方看到的物体轮廓线的正投影组成的平面
图形； （2）一个物体的三视图的排列规则是：俯 视图放在主视图的下面，长度与主视图一 样，左视图放在主视图的右面，高度与主 视图一样，宽度与俯视图的宽度一样；
高一数学A必修2课件_第一章_1.2.2_空间几何体的三视图和直观图
正视图
侧视图
正视图
侧视图
俯视图
俯视图
注意：
(1)画几何体的三视图时，
能看见的轮廓和棱用实线表示， 不能看见的轮廓和棱用虚线表示。
(2)长对正， 高平齐， 宽相等。
俯
练习、画下例几何体的三视图
侧
正
除了会画如正方体、长方体、圆柱、圆锥、球 等基本几何体的三视图外，我们还将学习画出由 一些简单几何体组成的组合体的三视图。
c（高）
c（高）
a(长)
高 平 长对正 齐
b（宽）
b（宽）
俯 视 图
a(长)
宽相等
c（高） b（宽） a(长)
例1 (1)圆柱的三视图
俯
正视图
侧视图
侧 俯视图
圆柱 正
例2 (2)圆锥的三视图 俯
正视图
侧视图
侧
·
圆 锥
俯视图
正
例2 请同学们画下面这两个圆台的三视图， 如果你认为这两个圆台的三视图一样，画一 个就可以；如果你认为不一样，请分别画出 来。
横看成岭侧成峰，远近高低各不同。
不识庐山真面目，只缘身在此山中。 ——苏轼
横看成岭侧成峰，远近高低各不同。 不识庐山真面目，只缘身在此山中。 ——苏轼
从不同的角度看同一物体,视觉的效果可能不同， 要比较真实地反映出物体的特征我们可从多角度观看物体。
1.中心投影：
把光由一点向外散射形成 的投影叫中心投影。
侧视图
俯
俯视图
俯视图
例5 根据三视图判断几何体
俯 四 棱 柱
正 视 图
侧 视 图
侧
正
俯视图
三 棱 柱
探究(1): 在例3中，若只给出正，侧视图, 那么它除了是圆台外,还可能是什么几何体？
高一数学空间几何体的三视图与直观图试题答案及解析
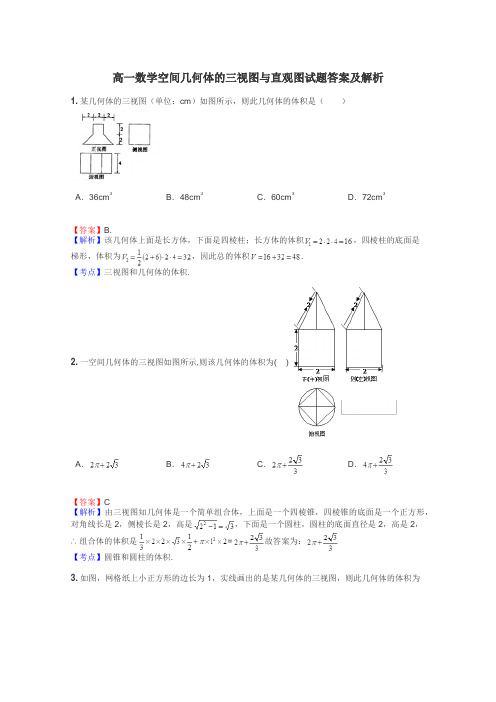
高一数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（）A．36cm3B．48cm3C．60cm3D．72cm3【答案】B.【解析】该几何体上面是长方体，下面是四棱柱；长方体的体积，四棱柱的底面是梯形，体积为，因此总的体积.【考点】三视图和几何体的体积.2.一空间几何体的三视图如图所示,则该几何体的体积为( )A．B．C．D．【答案】C【解析】由三视图知几何体是一个简单组合体，上面是一个四棱锥，四棱锥的底面是一个正方形，对角线长是2，侧棱长是2，高是，下面是一个圆柱，圆柱的底面直径是2，高是2，∴组合体的体积是=故答案为：【考点】圆锥和圆柱的体积.3.如图，网格纸上小正方形的边长为1，实线画出的是某几何体的三视图，则此几何体的体积为（）A．6B．9C．12D．18【答案】C【解析】该几何体是三棱锥，底面是俯视图，三棱锥的高为4；底面三角形是斜边长为6，高为3的等腰直角三角形，此几何体的体积为.故选C.【考点】三视图与几何体的关系；几何体的体积的求法.4.某向何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知,该几何体是一个长方体和一个半圆柱组成的几何体,所以体积为。
【考点】（1）根据三视图确定几何体的构成，（2）圆柱及长方体的体积公式的应用。
5.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为 .【答案】11【解析】由图可知切去的是直淩柱的一角，先算直棱柱的体积，再算切去部分的体积，所以.【考点】1、立体图形的三视图；2、体积的计算.6.右图中的三个直角三角形是一个体积为的几何体的三视图，则（）A．B．C．D．【答案】B【解析】由三视图可知该几何体为三棱锥，其中一侧棱垂直底面，且底面为直角三角形，∴三棱锥的体积为，解得，故选B．【考点】由几何体的三视图求体积．7.已知四棱锥的三视图如图所示,则四棱锥的四个侧面中面积最大的是（）A．3B．C．6D．8【答案】C【解析】通过三视图可作出该几何体的直观图，如图所示．其中底面为矩形，面面，且，，．易得，，，故侧面中面积最大值为6．【考点】几何体的三视图与直观图．8.右图是水平放置的的直观图，轴，，则是（）A．等边三角形B．等腰三角形C．直角三角形D．等腰直角三角形【答案】C【解析】直观图为斜二测画法，原图的画为，因此原为直角三角形.【考点】斜二测画法.9.如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A．B．C．D．【答案】D【解析】主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是球和圆柱的表面积．三视图的投影规则是：“主视、俯视长对正；主视、左视高平齐，左视、俯视宽相等”.由三视图可知几何体是半径为1的球和底面半径为1，高为3的圆柱，故其表面积应为球的表面积与圆柱的表面积面积之和减去圆柱一个底面积，即．故选D．【考点】本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用10.如图是一个简单的组合体的直观图与三视图，一个棱长为4的正方体，正上面中心放一个球，且球的一部分嵌入正方体中，则球的半径是（）A．B．1C．D．2【答案】B【解析】由已知题中三视图中的俯视图中圆上的点到正方形边长的最小距离为1，已知中的正方体的棱长为4，可得球的半径为1，故选B．【考点】由三视图还原实物图．11.一个几何体的三视图如图所示,则该几何体可以是（）A．棱柱B．棱台C．圆柱D．圆台【答案】D【解析】由正视图和左视图可知此几何体为台体，结合俯视图可知此几何体为圆台。