理科数学高考立体几何大题精选
历届高三数学(理)立体几何高考真题.docx

历届高三数学(理)立体儿何高考真题一、选择题:1.在一个几何体的三视图屮,正视图和俯视图如右图所示, 则相应的俯视图可以为2. 如图,网格纸上小正方形的边长为1,粗线画出的是某儿何体的三视图,则此儿何体的体积为( )(A) 6 (5) 9 (C)12 (0)183. 己知三棱锥S - ABC 的所有顶点都在球O 的求面上,MBC 是边长为 1的正三角形,SC 为球O 的直径,H.SC = 2;则此棱锥的体积为( )V2V3 V2 V2 (A)— (B) — (C) — (D) — 6 63 2 4. 某几何体的三视图如图所示,则该几何体的体积为力.16 + 8兀 B.8 + 8/TC.16 + 16龙 £).8 + 16龙5. 已知"为异面直线,刃丄 '卜面a , 〃丄平面P 。
直线丿满足/丄加,,丄刀,/ (Z a.l (Z P » 贝9()(A) a 〃 B 且/〃 a (B) a 丄 B 且/丄 B(O a 与0相交,且交线垂直于1 (D) a 与B 相交,且交线平行于/6. 一个四而体的顶点在空间总角处标系0-尤膨中的处标分 别是(1, 0, 1), (1, 1, 0),(0, 1, 1), (0, 0, 0),画该四而体三视图中的正视图时,以z 血平而为投影面,则得到正视图可以为(D)7. 如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长 的棱的长度为A.6^2 B .4近 C.6 D A&圆柱被一个平面截去一部分示与半球(半径为I*)组成一个几何体,该几何体三视图屮的正视图和俯视图如 图所示。
若该儿何体的衣面积为16 + 20龙,则u9.一个正方体被一个平血截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值 为10.已知A,B 是球0的球而上两点,ZAOB=90,C 为该球而上的动点,若三棱锥O-ABC 体积的最人值为36, 则球O 的表面积为A. 36HB.64RC.144RD.256TI二、填空题:11 •已知矩形肋CD 的顶点都在半径为4的球O 的球面上,llAB = 6i BC = 2^,则棱锥O-ABCD 的体积为(A) 1 (B) 2 (C) 4 (D) 8(A )i(D)6三、解答题:12(本小题满分12分)如图,四棱锥P—ABCD中,底面ABCD为平行四边形,ZDAB二60° ,AB二2AD,PD丄底面 ABCD.(I)证明:PA丄BD;(II)若PD=AD,求二面角A-PB-C的余弦值。
高考数学专题复习立体几何(理科)练习题

《立体几何》专题练习题1.如图正方体A BCD A1B C D 中,E、F 分别为D1C1 和B1C1 的中点,1C1 和B1C1 的中点,1 1 1P、Q分别为A1C1 与 EF、AC与 BD的交点,(1)求证: D、B、F、E 四点共面;ED1 C1(2)若 A1C与面 DBFE交于点R,求证: P、Q、R三点共线A1Q FB1D CPA B2.已知直线a、b 异面, 平面过a且平行于b , 平面过b 且平行于a , 求证: ∥.3.如图所示的多面体是由底面为ABCD 的长方体被截面AEFG 所截而得,其中AB 4, BC 1BE 3, CF 4 , 若如图所示建立空间直角坐标系.Z①求E F 和点G的坐标;②求异面直线EF 与 AD 所成的角;③求点C到截面AEFG 的距离.FGD E C yBAx4.如图,三棱锥P—ABC中, PC 平面 ABC,PC=AC=,2AB=BC,D是PB上一点,且CD 平面 PAB.(I) 求证:AB 平面 PCB;P(II) 求异面直线AP与 BC所成角的大小;(III )求二面角C-PA-B 的余弦值.DBC A5.如图,直二面角D—AB —E 中,四边形ABCD 是边长为 2 的正方形, AE=EB ,F 为 CE 上的点,且BF⊥平面ACE.(1)求证 AE⊥平面BCE;(2)求二面角B—AC—E 的余弦值.6.已知正三棱柱A BC A B C的底面边长为2,点 M在侧棱 BB1 上.1 1 1第 1 页共 3 页(Ⅰ)若P 为 AC的中点, M为 BB1 的中点,求证BP// 平面 AMC1;(Ⅱ)若AM与平面A A CC 所成角为30 ,试求BM的长.1 17.如图,在底面是矩形的四棱锥P—ABCD 中,PA⊥底面ABCD ,PA=AB =1,BC=2.(1)求证:平面PDC⊥平面PAD;P(2)若 E 是 PD 的中点,求异面直线AE E 与PC 所成角的余弦值;DAB C8.已知:在正三棱柱ABC—A1 B1C1中,AB = a ,AA1 = 2a . D 是侧棱BB1 的中点. 求证:(Ⅰ)求证:平面ADC1⊥平面ACC1A1;(Ⅱ)求平面ADC1 与平面ABC所成二面角的余弦值.9.已知直四棱柱A BCD ABC D 的底面是菱形,且DAB 60 ,A D AA1 F 为1 1 1 1棱B B1的中点,M 为线段 AC1 的中点.(Ⅰ)求证:直线MF // 平面 ABCD ;(Ⅱ)求证:直线MF 平面A CC A ;1 1(Ⅲ)求平面AFC1 与平面 ABCD 所成二面角的大小.AP CQ10.棱长是 1 的正方体,P、Q 分别是棱AB 、CC1 上的内分点,满足2PB QC1 第2 页共3 页(1)求证: A1P⊥平面AQD ;(2)求直线PQ 与平面AQD 所成角的正弦值.D1 C1A1 B1 QD CA BP11.如图,长方体ABCD -A1B1C1D1 中,E、F 分别是线段B1D1、A 1B 上的点,且D1E=2EB 1,BF=2FA 1.(1)求证 :EF∥AC1;(2)若 EF 是两异面直线B1D1、A 1B 的公垂线段,求证该长方体为正方体.D1 C1EA1 B 1FD CA B12.如图,在正四棱柱ABCD —A1B1C1D1 中,AA 1=B,M 三点的平面A1BMN 交C1D1 于点 N.(Ⅰ)求证:EM∥平面A1B1C1D1;12AB ,点 E、M 分别为 A 1B、C1C 的中点,过点A1,(Ⅱ)求二面角B—A1N—B1 的正切值 .第 3 页共 3 页。
高考数学立体几何大题汇总

故由三垂线定理知DE⊥AB.
所以∠DEF为二面角C—AB—D的平面角,由题设知∠DEF=60°
设
在
从而
因Rt△ADE≌Rt△BDE,故BD=AD=a,从而,在Rt△BDF中, ,
又 从而在△FGH中,因FG=FH,由余弦定理得
(Ⅱ)设E为BC的中点,求 与 夹角的余弦值。
解(Ⅰ)∵折起前AD是BC边上的高,
∴当ΔABD折起后,AD⊥DC,AD⊥DB,
又DB DC=D,
∴AD⊥平面BDC,
∵AD平面 平面BDC.
平面ABD 平面BDC。
(Ⅱ)由∠BDC= 及(Ⅰ)知DA,DB,DC两两垂直,不防设 =1,以D为坐标原点,以 所在直线 轴建立如图所示的空间直角坐标系,易得D(0,0,0),B(1,0,0),C(0,3,0),A(0,0, ),E( , ,0),
因此,异面直线AD与BC所成角的余弦值为
解法二:如答(19)图2,过F作FM⊥AC,交AB于M,已知AD=CD,
平面ABC⊥平面ACD,易知FC,FD,FM两两垂直,以F为原点,射线FM,FC,FD分别为x轴,y轴,z轴的正半轴,建立空间直角坐标系F—xyz.
不妨设AD=2,由CD=AD,∠CAD=30°,易知点A,C,D的坐标分别为
作 ,H为垂足,则 平面SBC。
,即F到平面SBC的距离为
由于ED//BC,所以ED//平面SBC,E到平面SBC的距离d也有
设AB与平面SBC所成的角为α,
则 ﻩﻩ…………12分
解法二:
以C为坐标原点,射线CD为x轴正半轴,建立如图所示的空间直角坐标系C—xyz。
近年高考理科立体几何大题汇编
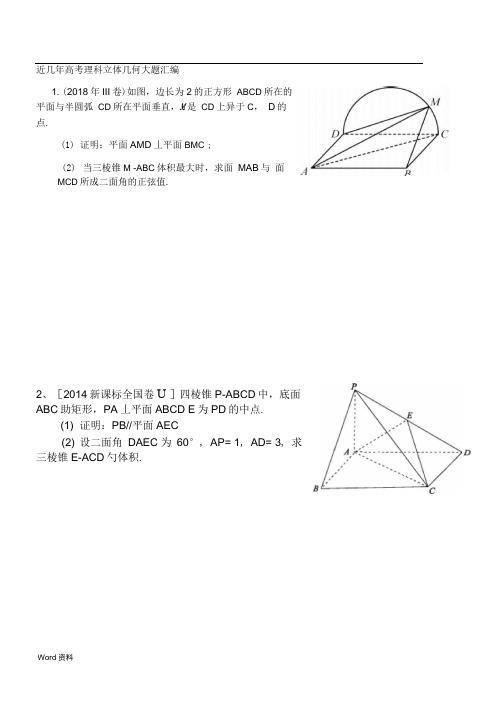
近几年高考理科立体几何大题汇编1. (2018年III卷)如图,边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD丄平面BMC ;(2)当三棱锥M -ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.2、[2014新课标全国卷U ]四棱锥P-ABCD中,底面ABC助矩形,PA丄平面ABCD E为PD的中点.(1) 证明:PB//平面AEC(2) 设二面角DAEC 为60°, AP= 1, AD= 3, 求三棱锥E-ACD勺体积.3. (2017?新课标I 卷)如图,在四棱锥P- ABCDh AB// CD 且/ BAP= CDP=90 . ⑴证明:平面PABL平面PAD(2)若PA=PD=AB=DC Z APD=90,求二面角A- PB- C 的余弦值.4. (菱形建系)[2014新课标全国卷I ]如图三棱柱ABC-AB i C中,侧面BBCC为菱形,AB 丄BC(1)证明:AOAB;⑵若AC丄AB,/ CBB= 60°, AB= BC,求二面角A -A i B i -G的余弦值.5. (菱形建系)【2015高考新课标1】如图,四边形ABCD为菱形,/ AB(=120°E, F是平面ABC阴一侧的两点,BE!平面ABCD DF丄平面ABCD BE=2DF, AE! EC (I)证明:平面AECL平面AFC(U)求直线AE与直线CF所成角的余弦值.6.(翻折)(2018年I卷)如图,四边形ABCD为正方形,E,F分别为AD, BC的中点,以DF为折痕把△ DFC折起,使点C到达点P的位置,且PF BF .(1) 证明:平面PEF —平面ABFD ;(2) 求DP与平面ABFD所成角的正弦值7.(翻折)(2016年全国II 高考)如图,菱形ABCD 的对角线AC 与BD 交于点O ,8.(动点问题)(2018年II 卷)如图,在三棱锥PA =PB = PC = AC =4, O 为 AC 的中点.(1) 证明:PO _平面ABC ;(2) 若点M 在棱BC 上,且二面角M -PA-C 为30,求PC 与平面PAM 所成角的正弦值.AB =5, AC =6,点 E,F 分别在 AD, CD 上,DEF 沿 EF 折到 D 'EF 位置,OD —10 .(I)证明:DH _平面ABCD ;(U)求二面角B —DA —C 的正弦值.5AE = CF , EF 交BD 于点H .将 4D fP-ABC 中,AB = BC=2“C近几年高考理科立体几何大题汇编1. (2018年III卷)如图,边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD丄平面BMC ;(2)当三棱锥M -ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.1.解:(1)由题设知,平面CM丄平面ABCD交线为CD因为BCLCDBC 平面ABCD所以BC丄平面CM[> BCL DM因为M为CD上异于C, D的点,且DC为直径,所以DM_ CM又BC1CIMC所以DM_平面BMC而DM 平面AMD故平面AM L平面BMC(2)以D为坐标原点,DA的方向为x轴正方向,建立如图所示的空间直角坐标系D- xyz.当三棱锥M ABC体积最大时,M为CD的中点.由题设得D(0,0,0), A(2,0,0), B(2,2,0), C(0,2,0), M (0,1,1),TFTAM =(—2,1,1),AB =(0,2,0), DA =(2,0,0)设n = (x, y, z)是平面MAB勺法向量,则可取 n = (1,0,2).DA 是平面MCD 勺法向量,因此n DA ; 5FnTDATT ,sin ,n,DA 二乎,所以面MA 南面MC 断成二面角的正弦值是乙5 .52、[2014新课标全国卷U ]如图1-3,四棱锥P-ABCD 中,底面ABCD 为矩形,PU 平 面ABCD E 为PD 的中点.PB// 平面 AEC如图,以A 为坐标原点,AB, AD ,AP 的方向为x 轴、y 轴、z 轴的正方向,|曲 (\~\1、为单位长,建立空间直角坐标系 Axyz ,贝U D (o ,百,0),Eo ,黔,1 琏=<2 2/ 0,n AM n AB =0.— 4°, 2y =0.cos n,(1)证明:PB//平面AECE-ACD 勺体积.因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO// PB 因为EO?平面AEC PB?平面AEC 所以 ⑵ 因为PAL 平面ABCD ABC 助矩形, 所以AB, AD ,AP 两两垂直.33+ 4m 2二2,解得论2.3. (2017?新课标I 卷)如图,在四棱锥 P- ABCDh AB ' II CD 且/ BAP=Z CDP=9° (1) 证明:平面PABL 平面PAD万江… (2) 若 PA=PD=AB=DC Z APD=90,求二面角 A - PB- C 的余 /、/弦值.3.【答案】(1)证明:I/ BAP=Z CDP=90 ,••• P 从 AB, PD ■- 丄CDAB// CD ,AB 丄 PD ,又PACPD=P , 且 PA ? 平面 PAD ,PD ? 平 面 PAD ,AB丄 平 面PAD ,又AB ?平 面PAB,平面PAB丄 平面PAD;(2) 解:• • • AB// CD AB=CD •' i 四边形ABCD 为平行四边形,由(1)知 AB 丄平面 PAD •- AB 丄Word 资料设 B (m °, °)( m>°),则 qm 心,°),辰(m \3 °) • 设 n 1 = (x , y , n 1 • AC = °, 则n 1 •辰 °,W 3 .m , °, z )为平面ACE 的法向量,m 灶 3y = 0,即312y + 2Z 二 °,可取n i = 由题设易知 -1, \I,°)为平面DAE 的法向量,1=2, |cos 〈 n i , n 2> | 因为E 为PD 的中点,所以三棱锥 西X |x 扌=甲.1 1 1E-ACD 勺高为2三棱锥E-ACD 的体积V = 心AD , 则在厶APD中, 腰边形ABCD 为矩形,/ APD=90 ,可得△ PAD为等三角PA=PD角PA=AB=2a AD=AD 中为坐标原点, 占八、、分别以, BCOA OE、中占I 八、、OP所在直线为x、y、z轴建立空间直角坐标系,则:D ((),P ( 0 , ),C.西二| 岳)PB =I -近a|50 = |-2^0,0'|PBCn-PB=Q[n BC^QAB 丄PD丄平面cosfy/2ax+2q\ -y/2az=0| -2y/2ax = 0 y=1PAD AD ? 平PAD AB 丄AD ,PD PA PA Q AB=APAB ,匚二为平面PAB的个法向量,PD = [-^laA-^/2a\ PBPB(菱形建系)AB丄B i C. [2014 新课标全国卷I]如图三棱柱ABC-ABC中,侧面BBCC为4.菱形,(1)证明:AC= AB;⑵ 若ACL AB,/ CB吐60°, A吐BC求二面角A-AB i -C的余弦值.4解:(1)证明:连接BC,交B1C于点O,连接AO因为侧面BBGC为菱形,所以BC L BC,且O为BC及BC的中点.又AB 丄B i C,所以BC 丄平面ABO 由于AO?平面ABO 故BC 丄AO 又 BO= CO 故 AC= AB.⑵ 因为ACL AB ,且O 为BC 的中点,所以Ad CO又因为AB= BC ,所以△ BOA2 △ BOC 故OAL OB 从而OA OB OB 两两垂直. 以O 为坐标原点,OB 的方向为x 轴正方向,| OB 为单位长,建立如图所示的空 间直角坐标系O xyz.设m 是平面ABC 的法向量, mA 1B i =0, -— 则同理可取(1 , —3, 3)m B i C =0,因为/ CBB =60 B(1 , 0, 0) , B 》,¥, °) CO ,- ¥,AB0, B C 1=BC = — 1,,所以△ CBB 为等边三角形,又 A 吐BC,贝U A0 , 0,3 3,A iB = AB= 3 3 ,设n = (x , y , z)是平面AA i B i 的法向量,则n AB = 0, n AB = 0,1所以结合图形知二面角A -A 1B 1 - C 的余弦值为75.(菱形建系)【2015高考新课标1】如图,四边形ABCD 为菱形,/ AB(=120° E , F 是平面ABCm —侧的两点,BE 丄平面ABCD DF 丄平面ABCQ BE=2DF, AE 丄EC(I)证明:平面 AECL 平面AFC【解析】试题分析;(I )连捲弭,设BDTOG,连接EG, 5G ; 通过计算可证乂丄FG 根据线面垂直判定定理可知轧一(II) LUG 为坐标原点,分别\^GB^GC 的方向为工轴,丁轴正方向,GB 淘单位长匡 建立空 直角坐标系 g 口利用向重法可求出异面直鏡三三与CF 所成角的余弦值试题解析’ 1 I )屋接33,设BD 'AC=G,连接EG, FG, EF,在觌 A3CD 中,不妨设33-1,由厶L HOI 二 可得JG=GC--j3 .由占三丄平面A3CD, A3=BC 可知*又••• AE1 EC ,二 E(=v3 , EGLAC, ••• A8 FG=G 二 E(L 平面 AFC ••• EG 面AEC 二平面 AFCL 平面AEC••…6分则 cos 〈n , m>I nil m = 7.(U)求直线AE 与直线CF 所成角的余弦值.5.,【答案】(I)见解析⑴33L MC-:■■■■ —I —在Rt △ EBO^,可得BE= 2 , 故 DF= 22在Rt △ FDG 中,可得FG= 6. 2在直角梯形BDFE 中,由 BD=2, BE= 2 , DF= 2 可得 EF=3 2 , 2 2••• EG 2 FG 2 二 EF 2 ,••• EG! FGDBWord资料y 轴正方向,|GB|为 单位长度,建立空间直角坐标系 G-xyz ,由(I)可得A (0,— 3 , 0), E(1,0,2) , F (— 1,0 , 2 ), C (0,3 , 0),A AE = (1, 3 , 2 ), CF2-屮3 ,).…10分2故cos C A E ,C F ・ A E "CF ) =|AE||CF| 36.(翻折)(2018年I 卷)如图,四边形ABCD 为正方形,E,F 分别为AD,BC 的中点,以DF 为折痕把△ DFC 折起,使点C 到达点P 的位置,且PF _ BF •(1) 证明:平面 PEF —平面ABFD ;(2) 求DP 与平面ABFD 所成角的正弦值6. 解:(1)由已知可得,BF 丄PF, BFL EF,所以 BF 丄平面PEF又BF 平面ABFD 所以平面 PEFL 平面ABFD(2)作PH 丄EF ,垂足为H.由(1)得,PH 丄平面ABFD=(-1,所以直线AE 与CF 所成的角的余弦值为12分以H 为坐标原点,HF 的方向为y 轴正方向,|BF|为单位长,建立如图所示的空间直 角坐标系H- xyz .由(1)可得,DEL PE 又 DF =2, DE =1,所以 PE= ..3.又 PF =1, EF =2,故 PEL PF 可得 PH 3,EH2 2则 H (0,0,0), P(0,0, 法向量•7 3)为平面ABFD 勺 2设DP 与平面ABFD 所成角为r,则si所以DP 与平面ABFD 所成角的正弦值为47. (翻折)(2016年全国II 高考)如图,菱形ABCD 的对角线AC 与BD 交于点0,5AB =5, AC =6,点 E,F 分别在 AD, CD 上, AE 二 CF , EF 交 BD 于点 H .将4DEF 沿 EF 折到 D 'EF 位置,OD = 一 10 .(I)证明:DH _平面ABCD ; (U)求二面角 B-DA-C 的正弦值.7.【解析】⑴证明:■/ AE =CF J ,4AE _CF AD CD ,• •• EF II AC .•••四边形 ABCD 为菱形,3),D ("20),|HP | | DP |3D f8.(动点问题)(2018年II 卷)如图,在三棱锥P-ABC 中,AB 二BC =2・2,PA =PB =PC =AC =4 , O 为 AC 的中点.(1)证明: PO _ 平面 ABC ;AC _ BD ,• •• EF _BD ,二 EF _DH ,二 EF _ D H .•/ AC =6 , • AO =3;又 AB =5 , AO _ OB , • OB =4 ,AEOH=AO OD 「,• DH4H=3,2 2 2OD'I =|OH| +|D'H |D'H _OH .又••• OH I EF =H ,• D'H _面 ABCD . ⑵建立如图坐标系H —xyz .B 5,0,0,C 1,3, 0,D' 0,0,3,A 1,- 3,0,AB 4,3,0,uuurAD'»1,3,3, uuuAC =[0,6,0 ,设面ABD'法向量n 1 = x ,y ,z , 由n1ABT 。
立体几何高考经典大题理科
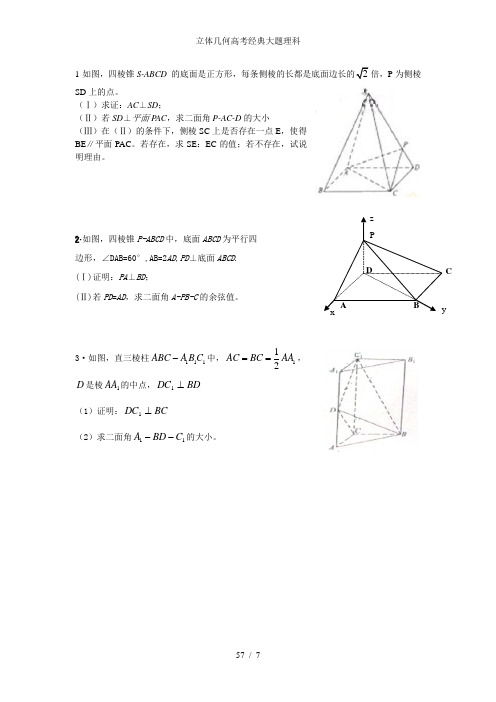
1·如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点。
(Ⅰ)求证:AC ⊥SD ;(Ⅱ)若SD ⊥平面P AC ,求二面角P-AC-D 的大小(Ⅲ)在(Ⅱ)的条件下,侧棱SC 上是否存在一点E ,使得BE ∥平面PAC 。
若存在,求SE :EC 的值;若不存在,试说明理由。
2·如图,四棱锥P-ABCD 中,底面ABCD 为平行四 边形,∠DAB=60°,AB=2AD ,PD ⊥底面ABCD . (Ⅰ)证明:PA ⊥BD ;(Ⅱ)若PD =AD ,求二面角A-PB-C 的余弦值。
3·如图,直三棱柱111ABC A B C -中,112AC BC AA ==, D 是棱1AA 的中点,BD DC ⊥1(1)证明:BC DC ⊥1(2)求二面角11C BD A --的大小。
z x PCBADy1·解法一:(Ⅰ)连BD ,设AC 交BD 于O ,由题意SO AC ⊥。
在正方形ABCD 中,AC BD ⊥,所以AC SBD ⊥平面,得AC SD ⊥.(Ⅱ)设正方形边长a ,则SD =。
又OD =,所以060SOD ∠=, 连OP ,由(Ⅰ)知AC SBD ⊥平面,所以AC OP ⊥, 且AC OD ⊥,所以POD ∠是二面角P AC D --的平面角。
由SD PAC ⊥平面,知SD OP ⊥,所以030POD ∠=, 即二面角P AC D --的大小为030。
(Ⅲ)在棱SC 上存在一点E ,使//BE PAC 平面由(Ⅱ)可得PD =,故可在SP 上取一点N ,使PN PD =,过N 作PC 的平行线与SC 的交点即为E 。
连BN 。
在BDN V 中知//BN PO ,又由于//NE PC ,故平面//BEN PAC 平面,得//BE PAC 平面,由于21SN NP =::,故21SE EC =::. 解法二:(Ⅰ);连BD ,设AC 交于BD 于O ,由题意知SO ABCD ⊥平面.以O 为坐标原点,OB OC OS ,,分别为x 轴、y 轴、z 轴正方向,建立坐标系O xyz -如图。
高考数学专题复习立体几何(理科)练习题

《立体几何》专题练习题1.如图正方体A BCD A1B C D 中,E、F 分别为D1C1 和B1C1 的中点,1C1 和B1C1 的中点,1 1 1P、Q分别为A1C1 与EF、AC与BD的交点,(1)求证:D、B、F、E 四点共面;ED1 C1(2)若A1C与面DBFE交于点R,求证:P、Q、R三点共线A1Q FB1D CPAB2.已知直线a、b 异面, 平面过a且平行于b , 平面过b 且平行于a , 求证: ∥.3. 如图所示的多面体是由底面为ABCD 的长方体被截面AEFG 所截而得,其中AB 4,BC 1BE 3, CF 4 , 若如图所示建立空间直角坐标系.Z①求EF 和点G的坐标;②求异面直线EF 与AD 所成的角;③求点C到截面AEFG 的距离.FGD E CyBAx4. 如图,三棱锥P—ABC中,PC 平面ABC,PC=AC=,2AB=BC,D是PB上一点,且CD 平面PAB.(I) 求证:AB 平面PCB;P(II) 求异面直线AP与BC所成角的大小;(III )求二面角C-PA-B 的余弦值.DBC A5. 如图,直二面角D—AB —E 中,四边形ABCD 是边长为 2 的正方形,AE=EB ,F 为CE 上的点,且BF⊥平面ACE.(1)求证AE⊥平面BCE;(2)求二面角B—AC—E 的余弦值.6. 已知正三棱柱A BC A B C的底面边长为2,点M在侧棱BB1上.1 1 1第 1 页共 3 页(Ⅰ)若P 为AC的中点,M为BB1 的中点,求证BP// 平面AMC1;(Ⅱ)若AM与平面A A CC 所成角为30 ,试求BM的长.1 17.如图,在底面是矩形的四棱锥P—ABCD 中,PA⊥底面ABCD ,PA=AB =1,BC=2.(1)求证:平面PDC⊥平面PAD;P(2)若E 是PD 的中点,求异面直线AE E与PC 所成角的余弦值;DAB C8.已知:在正三棱柱ABC—A1 B1C1中,AB = a ,AA1 = 2a . D 是侧棱BB1 的中点. 求证:(Ⅰ)求证:平面ADC1⊥平面ACC1A1;(Ⅱ)求平面ADC1 与平面ABC所成二面角的余弦值.9.已知直四棱柱A BCD ABC D 的底面是菱形,且DAB 60 ,AD AA1 F 为1 1 1 1棱B B1的中点,M 为线段AC1 的中点.(Ⅰ)求证:直线MF // 平面ABCD ;(Ⅱ)求证:直线MF 平面A CC A ;1 1(Ⅲ)求平面AFC1 与平面ABCD 所成二面角的大小.AP CQ10.棱长是 1 的正方体,P、Q 分别是棱AB 、CC1 上的内分点,满足 2PB QC1第 2 页共 3 页(1)求证:A1P⊥平面AQD ;(2)求直线PQ 与平面AQD 所成角的正弦值.D1 C1A1 B1 QD CA BP11.如图,长方体ABCD -A1B1C1D1 中,E、F 分别是线段B1D1、A 1B 上的点,且D1E=2EB 1,BF=2FA 1.(1)求证:EF∥AC1;(2)若EF 是两异面直线B1D1、A 1B 的公垂线段,求证该长方体为正方体.D1 C1EA1 B 1FD CA B12.如图,在正四棱柱ABCD —A1B1C1D1 中,AA 1=B,M 三点的平面A1BMN 交C1D1 于点N.(Ⅰ)求证:EM∥平面A1B1C1D1;12AB ,点E、M 分别为 A 1B、C1C 的中点,过点A1,(Ⅱ)求二面角B—A1N—B1 的正切值.第 3 页共 3 页。
2020年理科数学高考大题专项4 高考中的立体几何

高考大题专项四高考中的立体几何1.如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.(1)求证:EF∥平面ABD;(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD.2.在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证:(1)B1D⊥平面ABD;(2)平面EGF∥平面ABD.3.如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得⏜的中点.到的,G是DF⏜上的一点,且AP⊥BE,求∠CBP的大小;(1)设P是CE(2)当AB=3,AD=2时,求二面角E-AG-C的大小.(2018山西晋中调研,18)如图,已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD中,BC∥AD,AB⊥AD,且PA=AD=AB=2BC=2,M为AD的中点.(1)求证:平面PCM⊥平面PAD;(2)问在棱PD上是否存在点Q,使PD⊥平面CMQ,若存在,请求出二面角P-CM-Q的余弦值;若不存在,请说明理由.5.(2018河南郑州外国语学校调研,19)如图,在底面为等边三角形的斜三棱柱ABC-A1B1C1中,AA1=√3AB,四边形B1C1CB为矩形,过A1C作与直线BC1平行的平面A1CD交AB于点D.(1)证明:CD⊥AB;(2)若直线AA1与底面A1B1C1所成的角为60°,求二面角B-A1C-C1的余弦值.6.如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=√6,AB=4.(1)求证:M为PB的中点;(2)求二面角B-PD-A的大小;(3)求直线MC与平面BDP所成角的正弦值.(2018河北衡水中学适应性考试,18)如图,在三棱柱ABC-A1B1C1中,四边形A1C1CA为菱形,∠B1A1A=∠C1A1A=60°,AC=4,AB=2,平面ACC1A1⊥平面ABB1A1,Q在线段AC上移动,P为棱AA1的中点. (1)若Q为线段AC的中点,H为BQ中点,延长AH交BC于D,求证:AD∥平面B1PQ;,求点P到平面BQB1的距离.(2)若二面角B1-PQ-C1的平面角的余弦值为√13138.(2018山西大同一模,18)如图,在四棱锥P-ABCD中,AD∥BC,∠ABC=∠PAD=90°,PA=AB=BC=2,AD=1,M是棱PB中点且AM=√2.(1)求证:AM∥平面PCD;(2)设点N是线段CD上一动点,且DN=λDC,当直线MN与平面PAB所成的角最大时,求λ的值.9.(2018山西晋城一模,20)如图,在四棱锥P-ABCD中,PA=PD=AD=2CD=2BC=2,且∠ADC=∠BCD=90°.(1)当PB=2时,证明:平面PAD⊥平面ABCD;,且二面角P-AD-B为钝角时,求直线PA与平面PCD所成角的正弦值.(2)当四棱锥P-ABCD的体积为34高考大题专项四 高考中的立体几何1.证明 (1)∵BD ∥平面AEF ,BD ⊂平面BCD ,平面BCD ∩平面AEF=EF ,∴BD ∥EF.又BD ⊂平面ABD ,EF ⊄平面ABD , ∴EF ∥平面ABD.(2)∵AE ⊥平面BCD ,CD ⊂平面BCD ,∴AE ⊥CD.由(1)可知BD ∥EF ,又BD ⊥CD ,∴EF ⊥CD. 又AE ∩EF=E ,AE ⊂平面AEF ,EF ⊂平面AEF , ∴CD ⊥平面AEF ,又CD ⊂平面ACD , ∴平面AEF ⊥平面ACD.2.证明 (1)以B 为坐标原点,BA ,BC ,BB 1所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,如图所示,则B (0,0,0),D (0,2,2),B 1(0,0,4),C 1(0,2,4),设BA=a ,则A (a ,0,0),所以BA ⃗⃗⃗⃗⃗ =(a ,0,0),BD ⃗⃗⃗⃗⃗⃗ =(0,2,2),B 1D ⃗⃗⃗⃗⃗⃗⃗ =(0,2,-2),B 1D ⃗⃗⃗⃗⃗⃗⃗ ·BA ⃗⃗⃗⃗⃗ =0,B 1D ⃗⃗⃗⃗⃗⃗⃗ ·BD⃗⃗⃗⃗⃗⃗ =0+4-4=0,即B 1D ⊥BA ,B 1D ⊥BD.又BA ∩BD=B ,BA ⊂平面ABD ,BD ⊂平面ABD ,所以B 1D ⊥平面ABD.(2)由(1)知,E (0,0,3),G (a2,1,4),F (0,1,4),则EG ⃗⃗⃗⃗⃗ =(a 2,1,1),EF ⃗⃗⃗⃗⃗ =(0,1,1),B 1D ⃗⃗⃗⃗⃗⃗⃗ ·EG ⃗⃗⃗⃗⃗ =0+2-2=0,B 1D ⃗⃗⃗⃗⃗⃗⃗ ·EF⃗⃗⃗⃗⃗ =0+2-2=0,即B 1D ⊥EG ,B 1D ⊥EF. 又EG ∩EF=E ,EG ⊂平面EGF ,EF ⊂平面EGF ,所以B 1D ⊥平面EGF. 结合(1)可知平面EGF ∥平面ABD.3.解 (1)因为AP ⊥BE ,AB ⊥BE ,AB ,AP ⊂平面ABP ,AB ∩AP=A ,所以BE ⊥平面ABP ,又BP ⊂平面ABP ,所以BE ⊥BP ,又∠EBC=120°.因此∠CBP=30°.(2)(方法一)取EC⏜的中点H ,连接EH ,GH ,CH. 因为∠EBC=120°,所以四边形BEHC 为菱形,所以AE=GE=AC=GC=√32+22=√13. 取AG 中点M ,连接EM ,CM ,EC ,则EM ⊥AG ,CM ⊥AG , 所以∠EMC 为所求二面角的平面角.又AM=1,所以EM=CM=√13-1=2√3.在△BEC 中,由于∠EBC=120°,由余弦定理得EC 2=22+22-2×2×2×cos 120°=12,所以EC=2√3,因此△EMC 为等边三角形,故所求的角为60°.(方法二)以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.由题意得A (0,0,3),E (2,0,0),G (1,√3,3),C (-1,√3,0),故AE ⃗⃗⃗⃗⃗ =(2,0,-3),AG⃗⃗⃗⃗⃗ =(1,√3,0),CG ⃗⃗⃗⃗⃗ =(2,0,3),设m =(x 1,y 1,z 1)是平面AEG 的一个法向量.由{m ·AE ⃗⃗⃗⃗⃗ =0,m ·AG⃗⃗⃗⃗⃗ =0,可得{2x 1-3z 1=0,x 1+√3y 1=0.取z 1=2,可得平面AEG 的一个法向量m =(3,-√3,2). 设n =(x 2,y 2,z 2)是平面ACG 的一个法向量.由{n ·AG ⃗⃗⃗⃗⃗ =0,n ·CG ⃗⃗⃗⃗⃗ =0,可得{x 2+√3y 2=0,2x 2+3z 2=0.取z 2=-2,可得平面ACG 的一个法向量n =(3,-√3,-2).所以cos <m ,n >=m ·n |m ||n |=12.因此所求的角为60°.4.解 以A 为原点,射线AB ,AD ,AP 分别为x ,y ,z 轴的正半轴,建立空间直角坐标系如图.PA=AD=AB=2BC=2,A (0,0,0),B (2,0,0),C (2,1,0),D (0,2,0),P (0,0,2),AD ⃗⃗⃗⃗⃗ =(0,2,0),AP⃗⃗⃗⃗⃗ =(0,0,2), ∵M 为AD 的中点,∴M (0,1,0),MC⃗⃗⃗⃗⃗⃗ =(2,0,0). (1)∵MC⃗⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ =0,MC ⃗⃗⃗⃗⃗⃗ ·AP ⃗⃗⃗⃗⃗ =0, ∴CM ⊥PA ,CM ⊥AD.PA ⊂平面PAD ,AD ⊂平面PAD ,且PA ∩AD=A ,∴CM ⊥平面PAD. ∵CM ⊂平面PCM ,∴平面PCM ⊥平面PAD.(2)存在点Q 使PD ⊥平面CMQ ,在△PAD 内,过M 作MQ ⊥PD ,垂足为Q , 由(1)知CM ⊥平面PAD ,PD ⊂平面PAD ,∴CM ⊥PD , MQ ∩CM=M ,∴PD ⊥平面CMQ.设平面PCM 的一个法向量为n =(x ,y ,z ),则n ·MC⃗⃗⃗⃗⃗⃗ =2x=0⇒x=0, n ·PM ⃗⃗⃗⃗⃗⃗ =(x ,y ,z )·(0,1,-2)=y-2z=0⇒y=2z , 取n =(0,2,1).∵PD ⊥平面CMQ ,∴PD⃗⃗⃗⃗⃗ =(0,2,-2)是平面CMQ 的一个法向量. 由图形知二面角P-CM-Q 的平面角θ是锐角,故cos θ=n ·PD⃗⃗⃗⃗⃗⃗ |n |·|PD⃗⃗⃗⃗⃗⃗ |=√5·√8=√1010,所以二面角余弦值为√1010.5.(1)证明 如图,连接AC 1交A 1C 于点E ,连接DE.因为BC 1∥平面A 1CD ,BC 1⊂平面ABC 1,平面ABC 1∩平面A 1CD=DE , 所以BC 1∥DE.又四边形ACC 1A 1为平行四边形,所以E 为AC 1的中点,所以ED 为△AC 1B 的中位线,所以D 为AB 的中点. 又△ABC 为等边三角形,所以CD ⊥AB.(2)解 过A 作AO ⊥平面A 1B 1C 1,垂足为O ,连接A 1O ,设AB=2,则AA 1=2√3.因为直线AA 1与底面A 1B 1C 1所成的角为60°,所以∠AA 1O=60°. 在Rt △AA 1O 中,因为AA 1=2√3, 所以A 1O=√3,AO=3.因为AO ⊥平面A 1B 1C 1,B 1C 1⊂平面A 1B 1C 1,所以AO ⊥B 1C 1, 因为四边形B 1C 1CB 为矩形,所以BB 1⊥B 1C 1, 因为BB 1∥AA 1,所以B 1C 1⊥AA 1.因为AA 1∩AO=A ,AA 1⊂平面AA 1O ,AO ⊂平面AA 1O , 所以B 1C 1⊥平面AA 1O.因为A 1O ⊂平面AA 1O ,所以B 1C 1⊥A 1O.△A 1B 1C 1为等边三角形,边B 1C 1上的高为√3,又A 1O=√3,所以O 为B 1C 1的中点.以O 为坐标原点,分别以OA 1⃗⃗⃗⃗⃗⃗⃗⃗ ,OB 1⃗⃗⃗⃗⃗⃗⃗⃗ ,OA ⃗⃗⃗⃗⃗ 的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,如图.则A 1(√3,0,0),C 1(0,-1,0),A (0,0,3),B 1(0,1,0).因为AB ⃗⃗⃗⃗⃗ =A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(-√3,1,0),所以B (-√3,1,3),D -√32,12,3,因为AC ⃗⃗⃗⃗⃗ =A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(-√3,-1,0),所以C (-√3,-1,3),A 1B ⃗⃗⃗⃗⃗⃗⃗ =(-2√3,1,3),BC ⃗⃗⃗⃗⃗ =B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,-2,0),A 1C ⃗⃗⃗⃗⃗⃗⃗ =(-2√3,-1,3).设平面BA 1C 的法向量为n =(x ,y ,z ). 由{A 1B ⃗⃗⃗⃗⃗⃗⃗ ·n =0,BC ⃗⃗⃗⃗⃗ ·n =0,得{-2√3x +y +3z =0,y =0,令x=√3,得z=2,所以平面BA 1C 的一个法向量为n =(√3,0,2). 设平面A 1CC 1的法向量为m =(a ,b ,c ), 由{A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·m =0,A 1C ⃗⃗⃗⃗⃗⃗⃗ ·m =0, 得{√3a +b =0,2√3a +b -3c =0, 令a=√3,得b=-3,c=1,所以平面A 1CC 1的一个法向量为m =(√3,-3,1). 所以|cos <n ,m >|=|n ·m ||n ||m |=5√9191. 因为所求二面角为钝角,所以二面角B-A 1C-C 1的余弦值为-5√9191. 6.(1)证明 设AC ,BD 交点为E ,连接ME.因为PD ∥平面MAC ,平面MAC ∩平面PDB=ME ,所以PD ∥ME. 因为ABCD 是正方形,所以E 为BD 的中点.所以M 为PB 的中点. (2)解 取AD 的中点O ,连接OP ,OE.因为PA=PD ,所以OP ⊥AD.又因为平面PAD ⊥平面ABCD ,且OP ⊂平面PAD ,所以OP ⊥平面ABCD. 因为OE ⊂平面ABCD ,所以OP ⊥OE. 因为ABCD 是正方形,所以OE ⊥AD.如图建立空间直角坐标系O-xyz ,则P (0,0,√2),D (2,0,0),B (-2,4,0),BD⃗⃗⃗⃗⃗⃗ =(4,-4,0),PD ⃗⃗⃗⃗⃗ =(2,0,-√2).设平面BDP 的法向量为n =(x ,y ,z ),则{n ·BD ⃗⃗⃗⃗⃗⃗ =0,n ·PD ⃗⃗⃗⃗⃗ =0,即{4x -4y =0,2x -√2z =0.令x=1,则y=1,z=√2.于是n =(1,1,√2),平面PAD 的法向量为p =(0,1,0). 所以cos <n ,p >=n ·p |n ||p |=12.由题知二面角B-PD-A 为锐角,所以它的大小为π3. (3)解 由题意知M (-1,2,√22),C (2,4,0),MC ⃗⃗⃗⃗⃗⃗ =(3,2,-√22). 设直线MC 与平面BDP 所成角为α,则sin α=|cos <n ,MC ⃗⃗⃗⃗⃗⃗ >|=|n ·MC ⃗⃗⃗⃗⃗⃗⃗||n ||MC ⃗⃗⃗⃗⃗⃗⃗ |=2√69. 所以直线MC 与平面BDP 所成角的正弦值为2√69. 7.(1)证明 如图,取BB 1中点E ,连接AE ,EH.∵H 为BQ 中点,∴EH ∥B 1Q.在平行四边形AA 1B 1B 中,P ,E 分别为AA 1,BB 1的中点,∴AE ∥PB 1. 又EH ∩AE=E ,PB 1∩B 1Q=B 1, ∴平面EHA ∥平面B 1QP.∵AD ⊂平面EHA ,∴AD ∥平面B 1PQ.(2)解 连接PC 1,AC 1,∵四边形A 1C 1CA 为菱形, ∴AA 1=AC=A 1C 1=4. 又∠C 1A 1A=60°,∴△AC 1A 1为正三角形.∵P 为AA 1的中点,∴PC 1⊥AA 1.∵平面ACC 1A 1⊥平面ABB 1A 1,平面ACC 1A 1∩平面ABB 1A 1=AA 1,PC 1⊂平面ACC 1A 1,∴PC 1⊥平面ABB 1A 1,在平面ABB 1A 1内过点P 作PR ⊥AA 1交BB 1于点R.建立如图所示的空间直角坐标系P-xyz ,则P (0,0,0),A 1(0,2,0),A (0,-2,0),C 1(0,0,2√3),C (0,-4,2√3),设AQ⃗⃗⃗⃗⃗ =λAC ⃗⃗⃗⃗⃗ =λ(0,-2,2√3),λ∈[0,1], ∴Q (0,-2(λ+1),2√3λ), ∴PQ⃗⃗⃗⃗⃗ =(0,-2(λ+1),2√3λ). ∵A 1B 1=AB=2,∠B 1A 1A=60°, ∴B 1(√3,1,0),∴PB 1⃗⃗⃗⃗⃗⃗⃗ =(√3,1,0).设平面PQB 1的法向量为m =(x ,y ,z ),则{m ·PQ ⃗⃗⃗⃗⃗ =0,m ·PB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{-2(λ+1)y +2√3λz =0,√3x +y =0,令x=1,则y=-√3,z=-λ+1λ,∴平面PQB 1的一个法向量为m =1,-√3,-λ+1λ,设平面AA 1C 1C 的法向量为n =(1,0,0),二面角B 1-PQ-C 1的平面角为θ,则cos θ=m ·n|m ||n |=1√1+3+(-λ+1λ) =√1313.∴λ=12或λ=-14(舍),∴AQ⃗⃗⃗⃗⃗ =12AC ⃗⃗⃗⃗⃗ ,∴Q (0,-3,√3). 又B (√3,-3,0),∴QB ⃗⃗⃗⃗⃗ =(√3,0,-√3),∴|QB⃗⃗⃗⃗⃗ |=√3+3=√6. 连接BP ,设点P 到平面BQB 1的距离为h ,则13×12×4×√3×√3=13×12×4×√6×h , ∴h=√62,即点P 到平面BQB 1的距离为√62.8.(1)证明 如图,取PC 中点K ,连接MK ,KD ,因为M 为PB 的中点,所以MK ∥BC 且MK=12BC=AD , 所以四边形AMKD 为平行四边形, 所以AM ∥DK ,又DK ⊂平面PDC ,AM ⊄平面PDC , 所以AM ∥平面PCD.(2)解 因为M 为PB 的中点,设PM=MB=x ,在△PAB 中,∠PMA+∠AMB=π,设∠PMA=θ,则∠AMB=π-θ,所以cos ∠PMA+cos ∠AMB=0,由余弦定理得PM 2+AM 2-PA 22PM ·AM +BM 2+AM 2-AB 22BM ·AM =0,即x 2+2-42√2x x 2+2-42√2x=0, 解得x=√2,则PB=2√2,所以PA 2+AB 2=PB 2, 所以PA ⊥AB.又PA ⊥AD ,且AB ∩AD=A ,所以PA ⊥平面ABCD ,且∠BAD=∠ABC=90°.以点A 为坐标原点,建立如图所示的空间直角坐标系A-xyz ,则A (0,0,0),D (1,0,0),B (0,2,0),C (2,2,0),P (0,0,2),M (0,1,1),因为点N 是线段CD 上一点,可设DN⃗⃗⃗⃗⃗⃗ =λDC ⃗⃗⃗⃗⃗ =λ(1,2,0),故AN ⃗⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ +DN ⃗⃗⃗⃗⃗⃗ =(1,0,0)+λ(1,2,0)=(1+λ,2λ,0), 所以MN ⃗⃗⃗⃗⃗⃗⃗ =AN ⃗⃗⃗⃗⃗⃗ −AM ⃗⃗⃗⃗⃗⃗ =(1+λ,2λ,0)-(0,1,1)=(1+λ,2λ-1,-1).又面PAB 的法向量为(1,0,0),设MN 与平面PAB 所成角为θ,则sin θ=|√(1+λ)+(2λ-1)+1|=|√5λ-2λ+3|=|√5(1+λ)-12(1+λ)+10|=|√5-121+λ+10(11+λ) |=|1√10(11+λ-35) +75|,所以当11+λ=35时,即λ=23时,sin θ取得最大值.9.(1)证明 取AD 的中点O ,连接PO ,BO ,∵△PAD 为正三角形,∴OP ⊥AD , ∵∠ADC=∠BCD=90°,∴BC ∥AD ,∵BC=12AD=1,∴BC=OD ,∴四边形BCDO 为矩形,∴OB=CD=1,在△POB 中,PO=√3,OB=1,PB=2, ∴∠POB=90°,∴PO ⊥OB ,∵AD ∩OB=O ,∴PO ⊥平面ABCD ,∵PO ⊂平面PAD ,∴平面PAD ⊥平面ABCD. (2)解 ∵AD ⊥PO ,AD ⊥OB ,PO ∩BO=O ,PO ,BO ⊂平面POB ,∴AD ⊥平面POB ,∵AD ⊂平面ABCD ,∴平面POB ⊥平面ABCD ,∴过点P 作PE ⊥平面ABCD ,垂足E 一定落在平面POB 与平面ABCD 的交线BO 上.∵四棱锥P-ABCD 的体积为34,∴V P-ABCD =13×PE ×12×(AD+BC )×CD=13×PE ×12×(2+1)×1=12PE=34,∴PE=32, ∵PO=√3,∴OE=√PO 2-PE 2=√3-94=√32.如图,以O 为坐标原点,以OA ,OB 为x 轴,y 轴.在平面POB 内过点O 作垂直于平面AOB 的直线为z 轴,建立空间直角坐标系O-xyz ,由题意可知A (1,0,0),P 0,-√32,32,D (-1,0,0),C (-1,1,0),DP ⃗⃗⃗⃗⃗ =1,-√32,32,DC ⃗⃗⃗⃗⃗ =(0,1,0),设平面PCD 的一个法向量为n =(x ,y ,z ),则{n ·DP ⃗⃗⃗⃗⃗ =0,n ·DC ⃗⃗⃗⃗⃗ =0,得{x -√32y +32z =0,y =0,令x=1,则z=-23,∴n =1,0,-23,PA ⃗⃗⃗⃗⃗ =1,√32,-32,设直线PA 与平面PCD 所成的角为θ, 则sin θ=|cos <PA ⃗⃗⃗⃗⃗ ,n >|=|PA ⃗⃗⃗⃗⃗ ·n ||PA ⃗⃗⃗⃗⃗||n |=2×√133=3√1313. 则直线PA 与平面PCD 所成角的正弦值为3√1313.。
立体几何综合大题20道

立体几何综合大题(理科)40 道及答案1、四棱锥中 , ⊥底面 ,,,.( Ⅰ) 求证 : ⊥平面;( Ⅱ) 若侧棱上的点满足 , 求三棱锥的体积。
【答案】( Ⅰ) 证明 : 由于BC=CD,即BCD 为等腰三角形,又ACB ACD ,故 BD AC .由于PA底面ABCD ,因此PA BD ,从而BD与平面PAC 内两条订交直线PA, AC都垂直,故⊥平面。
( Ⅱ) 解:S BCD 1BC ? CD ? sin BCD1 2 2 sin23. 223由 PA1SBCD PA13 23 2 .底面 ABCD 知V P BDC33由 PF7FC , 得三棱锥F BDC 的高为1PA , 81113131故:V F BDC S BCD PA243838V P BDF V P BCD V F BCD17 2442、如图,四棱锥P ABCD 中,四边形ABCD 为矩形,PAD 为等腰三角形,APD 90 ,平面 PAD平面ABCD,且AB1, AD 2 ,E, F 分别为PC和 BD 的中点.(Ⅰ)证明: EF P 平面PAD;(Ⅱ)证明:平面PDC平面PAD;(Ⅲ)求四棱锥 P ABCD 的体积.O【答案】(Ⅰ)证明:如图,连接AC .∵四边形 ABCD 为矩形且F是BD的中点.∴F也是 AC 的中点.又E 是PC的中点, EF P AP∵ EF平面 PAD , PA 平面 PAD ,因此 EF P 平面PAD ;(Ⅱ)证明:∵平面 PAD平面 ABCD , CD AD ,平面 PAD I平面ABCD AD ,因此平面 CD平面 PAD ,又 PA 平面 PAD ,因此PA CD又 PA PD , PD , CD 是订交直线,因此 PA 面PCD又 PA平面 PAD ,平面 PDC平面 PAD ;(Ⅲ)取 AD 中点为 O .连接 PO , PAD 为等腰直角三角形,因此 PO AD ,由于面 PAD面 ABCD 且面 PAD I 面 ABCD AD ,因此, PO面 ABCD ,即 PO 为四棱锥 P ABCD 的高.由 AD 2 得PO 1.又 AB1.∴四棱锥 P ABCD 的体积V 1PO AB AD2 33考点:空间中线面的地址关系、空间几何体的体积.3、如图,在四棱锥P ABCD 中,PD平面 ABCD,CD PA ,DB均分ADC,E为PC的中点,DAC45o,AC 2 .(Ⅰ)证明: PA ∥平面 BDE ;(Ⅱ)若 PD 2, BD 2 2,求四棱锥 E ABCD 的体积【答案】(Ⅰ)设 AC BD F ,连接 EF,PD 平面 ABCD , CD平面ABCD,PD CD又CD PA, PD PA P, PD , PA平面PADCD 平面 PAD , AD平面PAD CD AD∵DAC 45 , ∴ DA DC ,∵ DB 均分ADC , F 为AC中点, E 为PC中点,∴EF 为 CPA 的中位线 .∵ EF ∥PA, EF平面BDE,PA平面BDE∴PA ∥平面 BDE .( Ⅱ) 底面四边形 ABCD 的面积记为 S;S S ADC S ABC1221232 2 .2222点 E为线段 PC的中点,VE ABCD1S1PD1212 2 .32323考点: 1. 线面平行的证明; 2. 空间几何体的体积计算 .4、如图,在四棱锥中,底面为菱形,其中,为的中点.,(1)求证: AD 平面 PQB ;(2)若平面平面ABCD ,且M为PC的中点,求四棱锥M ABCD 的体积.【答案】( 1)Q PA PD ,Q为中点,AD PQ连DB ,在ADB中,AD AB,,ABD 为等边三角形,为的中点,AD BQ ,PQ BQ Q , PQ平面PQB,BQ平面PQB, AD 平面 PQB .( 2)连接QC , 作MH QC 于 H .Q PQ AD , PQ平面PAD ,平面 PAD平面ABCD AD ,平面平面 ABCD,PQ 平面 ABCD , QC平面 ABCD , PQ QCPQ / / MH .MH平面 ABCD ,又 PM 12 PC ,MH1PQ132 3 .2222在菱形 ABCD 中,BD 2 ,SABD1AB AD sin 600 =122 3 = 3 ,222 S菱形ABCD 2SABD2 3 .V M ABCD 113.S菱形ABCD MH 2 31 3325 、如图,是矩形中边上的点,为边的中点,,现将沿边折至地址,且平面平面.⑴ 求证:平面平面;⑵求四棱锥的体积 .【答案】 (1)证明:由题可知,(2),则.6、已知四棱锥中,是正方形, E 是的中点,PEA BD C(1) 若PD AD ,求PC与面AC所成的角(2)求证:平面(3)求证:平面 PBC⊥平面 PCD【答案】平面,是直线在平面 ABCD 上的射影,是直线 PC 和平面 ABCD 所成的角。
