高考数学培优专题(1)——对数平均不等式的证明与应用(答安详解)
对数平均数
高考又见对数平均数在历年的高考压轴题中我们总是能见到对数平均数的影子。
2018年高考理科数学全国Ⅰ卷的压轴题最后一问,实际上就是对数平均数不等式的应用。
加强对对数平均数的理解,无疑能对我们解决压轴题有很大的帮助。
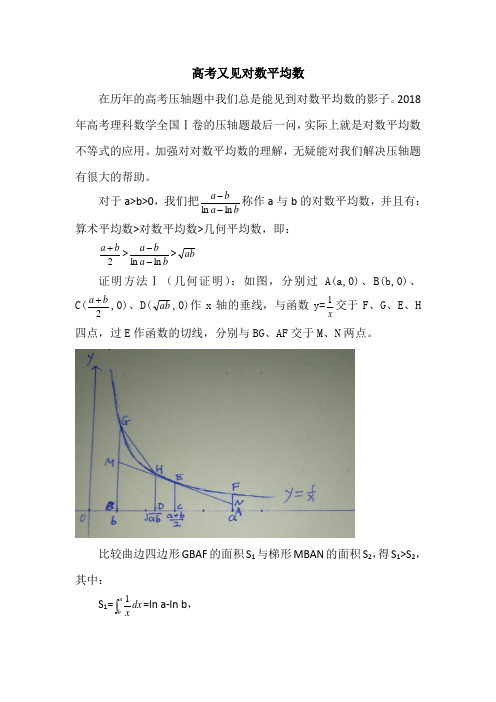
对于a>b>0,我们把ba ba ln ln --称作a 与b 的对数平均数,并且有:算术平均数>对数平均数>几何平均数,即:2b a +>ba ba ln ln -->ab 证明方法Ⅰ(几何证明):如图,分别过A(a,0)、B(b,0)、C(2b a +,0)、D(ab ,0)作x 轴的垂线,与函数y=x1交于F 、G 、E 、H 四点,过E 作函数的切线,分别与BG 、AF 交于M 、N 两点。
比较曲边四边形GBAF 的面积S 1与梯形MBAN 的面积S 2,得S 1>S 2,其中:S 1=⎰ab dx x1=ln a-ln b ,S 2=2AN BM +•AB=CE •AB=ba +2•(a-b) ∴ ln a-ln b>ba +2•(a-b)即:2b a +>ba b a ln ln --……①比较梯形GBDH 的面积S 3与曲边四边形GBDH 的面积S 4,得S 3>S 4,其中:S 3=21(GB+HD)•BD=21(b 1+ab 1)(ab -b)=abb a 2- S 4=⎰abb dx x 1=ln ab -ln b=2ln ln b a +-ln b=2ln ln ba - ∴abb a 2->2ln ln b a -即:ba ba ln ln -->ab ……②综合①②,得:2b a +>ba ba ln ln -->ab (a>b>0)证明方法Ⅱ(函数证明): 令f(x)=2ln x +12+x -1 (x>1),则有: f`(x)=x 21-2)1(1+x =22)1(24)1(+-+x x x x =22)1(2)1(+-x x x >0 ∴ f(x)>f(1)=0,即:2ln x +12+x -1>0, 令x=b a ,代入整理得: 2ln ln b a ->b a b a +-即:2b a +>ba b a ln ln --……①令g(x)=x-2•ln x-x1(x>1),则有:g`(x)=1-x 2+21x=22)1(x x ->0∴ g(x)>g(1)=0,即x-2•ln x-x1>0, 令x=b a ,代入整理得:abba ->ln a-ln b即:ba ba ln ln -->ab ……②综合①②,得:2b a +>ba ba ln ln -->ab (a>b>0)经过上述证明,我们对对数平均数有了一定的了解,接下来看一看2018年高考数学理科全国Ⅰ卷第21题:已知函数f(x)=x1-x+a •ln x (1) 讨论f(x)的单调性;(2) 若f(x)存在两个极值点x 1、x 2,求证:2121)()(x x x f x f --<a-2第一问略。
对数不等式证明

对数不等式证明
早些年,对数平均值不等式在导数大题里可谓风光一时,从2010年开始,很多年的高考题里总有一道两道导数大题可以利用对数均值不等式来解,但近些年这些题的具体应用已经渐渐淡化了。
具体的题目我们先不聊,今天只讲对数不等式的证明,以及从证明过程中我们可以得到哪些收获:
在学习不等式的时候,我们有过这个结论:对任意的正数a>b,均有:
即:平方平均值>算术平均值>几何平均值>调和平均值
如果我们引入了一个新的平均值-对数平均值:
则可以有以下对数平均值不等式链:
,
其中,标蓝部分即为著名的“A-L-G不等式”(Arithmetic-Logarithmic-Geometric mean inequalities),中文又称“对数均值不等式”,(在我们村,孩子们都叫它:“奥利给不等式”)
证明:(Ⅰ)
方法一:要证
,
只需证明
.
右侧上下同除b,即只要证明
,
令
,
只要证明
即可.
,
(Ⅱ)证明:。
对数平均不等式的证明及应用

2( a - b )
a
① L ( a, b ) ≤
⇔ lna - lnb>
⇔ ln >
b
2
a+b
a
2
-1
a
b
( ※ ). 令 x = > 1,则 ※ 式 等 价 于 lnx >
a
b
+1
b
2( x - 1 )
2( x - 1 )
. 构造函数 f ( x )= lnx ( x > 1 ),f '( x )=
所
a+b
以 L ( a,b ) ≥ ab 成立 . 因此, ab ≤ L ( a,b ) ≤
成立 .
2
二、对数平均不等式在高考解题中的应用
f ( x1 ) - f ( x2 )
对数平均不等式能有效解决含有
型
x1 - x2
不等式问题和极值点偏移问题 . 下面以近几年高考数学
试题为例,
给出对数平均不等式的应用 .
,要证
< a - 2,只需证
-2 +
x1 - x2
x1 - x2
a( lnx 1 - lnx 2 )
lnx 1 - lnx 2
明
< a,只需证明
< 1. 由对数平
x1 - x2
x1 - x2
lnx 1 - lnx 2
1
均不等式可知:
<
,又因为 x 1 x 2 = 1,所
x1 - x2
x1 x2
证明:
(Ⅱ)f '( x ) =
以
lnx 1 - lnx 2
f ( x1 ) - f ( x2 )
对数平均值不等式

题:研究性学习课题: 对数-平均值不等式(A-L-G 不等式)的证明及应用了解对数--平均值不等式并会证明,并探究其解决极值点偏移问题 对数--平均值不等式的证明及其在不等式证明中如何应用 .通过构造函数研究图象,探求对数--平均值不等式的证明和应用* 新授课*2课时.教学过程: 对数-平均值不等式(A-L-G 不等式)我们1^知+対位不普丸:2 .— a + h + 护-——-< VoL < ---------- <1丄12 -JH + SY即“调昶卡対歌”小于等于“儿何于均叢"小于等于"鼻求平妁tr 小于等于“半方卡幽僅”a = b.乱们还可尬引入《 —牛平*6值:时我+対僅:Ina 一 Inb那么上迟+対tt 不等光可td&:对戟千怜位不等丸JWL 站不零式的內咨昌a =* 6IPI主讲教师:刘大高河南省驻马店高级中学高二年级数学组 教学目的: 教学重点: 教学难点: 授课类型: 课时安排: 教具:多媒体、实物投影仪*证明如下: 先证明:a +b(I )—— 2a —b >导数证明不等式兵家大忌:盲目构造函数! In a Tn b a+b a-b 方法一:分析法:要证2In a-ln b 1 a — b,只需证明?(In a-l nb )》=7(不妨设a>"b>0)a 1 X — 1令丁沙1"^1.-—,只要证明X >1= f (X )>0,即可.右侧上下同除b,即只要证明a-1 a+1 b:f (x)T n x-汙(x f'(x) V—為0当 X A1 时,f (x)为增函数,「. f(X)〉f (1) = 0二 f(X)》0 a+b a-b 占亠2In a-lnb方法二:令a = bx,X A I,代人 A a~b即A bx —b两边约掉b即证明2 In a-1 nb 2 In bx—I nbx+1 X —1 In x X—1 七汁戸,--- >----- 二——>----- 万法同上.2 Inx 2 x+1(n )证明设a Ab >0,—a―b— A j ab= > In a-In b,左边上下同除以 bIn a—Inb J aba-1b >ln b>0,令x’b〉1则即证明X —1x -1>In X,令g(x) =1 nx-^^g'(x) J 仮Tx j)2^ _ -(仮-1)2X则x:>1,g(x)单调递减,g(x)<g(1) = 0在证明成立.A>L B G;F^式的内容星’J fl = ft <1 * bVfli t > 0 A o / b, < ■; :~~- < ==Lua - lo b 2以前我们给出了 Inx的一个不太精细的界、1 1(1)当 X 工1 时 In X <x—1 ,(2)令 X换成一时得 Inx >1 ——X X令a =bx代人A 0 A. fl # 力—==r < e * bb a - I D 6 2/曰r~~- bx — b bx+b得V bx b <----------- < ------In bxT nb 2亦+ -厂xT x+1约去 b,V x <------ <------Inx 2不等式的性质倒一下得丄二也A-2—T x x-1 x+1两边同除以(X—1)分两类得到In X还有一个更精细的界如下5,型二H心斗1*1 y/x证明记于(工)=L QH,射(M)N ---------- ,枇餾)=2 •工—!,贝I」有H + L/(!> = ^(1) = = 0,对三个函数分别求导得尸s==/ / V —工子丨449 + 2'于是有(0-炉2Xy/^ ‘所以79)-貳工)在(6 +8)上单调递确./(T)-血(巧在(0, +8)上单调递増.又因为/(I) - <K1) = /(!>-Ml) = 0*所氏有X € {□, l)li,5(x) < /(X)< h(z);茸€ (l,+(x>KA(j) < /(工)< 9(工)"证明S毕+ 由In龙的«细的?Mt们可叹估计出一些持殊数自然对戳的值,比如令H二珞2… d—< b2 <32刹用上面的不锋式容易证明5斗即可)A-JG不辱式(对》—¥均值不等式). r a —& o + bAZ祎式描述了我们在桁数中际導式關中常见的佈子的上下栗因此是外理轴问题的利器.证明不妨设住A b,令工=J •则St证不竽式等价于g-1尸 X乂(工十1■尸注意到当X =1时三者均为0 ,于是只需要证明以下略-注这个®数不等式比常用函数不等式Vz>0, Inz^z-l精细得多.说明:函数在某一点处交叉后,比一下导数的大小,可以看出函数图象上升的较快的图像在上 方.(—一 )两道咼考题2010天津高考理科(21)(本小题满分14分)已知函数f(x) =xed(x 亡R). .(I )求函数f(x)的单调区间和极值;(n )已知函数 y=g(x)的图象与函数 y=f(x)的图象关于直线 x=1对称.证明当 x>1时,f(x)>g(x);(川)如果 X i ^x 2,且= f (x 2),证明 X j +X 2 >2 .X(川)证明:f(x)=匚,f(X 1)= f(X 2),e由图象可知,0VX 1 <1,X 2 A1.代人函数得三1=¥ e X 2两边取对数得In x i —为 =1 n X 2 -X 2,目卩 x i —X 2 = In X j Tn x 2注意这里要给出公式的证明X 1~X2吒In x 1 Tn X 2 2X i —X2 x^ -x 2X 1 即八1八2=1,又;In 捲 Tn X2 ' In x , Tn x 2X 22X 1 〒X 22>1,即 X j +X 2 >222013高考陕西理科21.(本小题满分14分) 已知函数f(x)=e x,x 忘R .若直线y = kx + 1与f (x)的反函数的图像相切,求实数k 的值;2设x >0,讨论曲线y = f (x) 与曲线y=mx(m 〉0)公共点的个数.2g)va < b 拎 b-a = $ > 0二上式 K -------- 4—^ ----- = —• (r + 2>- + f-2 IIl2f L -令gW = 眉十r 一 2,则gU)=(『亠?)护十1 A 0恒成立-y二童(门>冒(0) = 0 而=沁—*11 (f + 2>e' +1-2 > 0 2f2/ - 」懐 2 —'占-口 •方法二对数平均值不等式法 令 X 1 = e a,贝y In X 1 = a,且为 > 0X 2 =e b ,贝y In X 2 =b,且x^0 X 1 A 0,X 2 A 0,设X 1 C X 2■r e +■卜-f (a) + f (b) ©a+e b二 X 1 +X 2f(b) -f(a)e b-e ab —aX 2In X 2 Tn X ,(川) 设a<b ,比较卫^严与晋2的大小,并说明理由.II I(E 十『3)佝一2 w* r 2 1 + e 1 -E■ * —=呂( ---------- 口 一口22b-a=3 — £3*)0 + G" — 2(1 — G" I =它" --------------------------- -由对数平均值不等式得为+X2 A X2 -X i 即f (a) + f (b) A f (b)-f(a)成立2 In X2 -In X j 2b -a(二).(例题分析)例题题目!已知函数/(X)= X - ae^有两个不同的零点叭,S 求证:衍+工2〉2【证明】容*判定两个不同的家点算2均大于6根据兀2为函数f(X)的零点可得:丸1 = ae^i => Znxi = Ina +X2 = => inx2 = Ina + 尤2以上两式相减可得:巧一疋2Znxi 一lnx2 = - X2 => ---- --- = 11?1尤1 —£71%2根据对数平均值不等式:工1 一兀2 兀1 +恋Inx^ —Inx^ ~ 2上式等号咸立的条件为尤1=兀2,因为巧,也为两个不同的零点,所以:例二、已知函数/ (工)=i-i? +(1 e 證)(1)若/'(X)存在极值点为1,求站的值;(2)若/(X)存在两个不同的零点£小,求证:工]+% > 2-解:(1)略(2)y *(.v)= (乂+ 1)( 1 \V /'(乂)存在两个不同的零点£ ,形则必有M > 0, 且f (rt)= …(1 ——V 仇进而可得《> 1化简可得丄=2兀+21□兀=2尤厂2111兀 a 2x^ + xf 2兀2 +尽;21.1^= 2 I 兀 -Vj + £ + 2 (工2 — £ )(兀 +玄2 +贝!I 有丄= --- --- + y ---- \ m ----a Xy + 工2 + 2 (兀上一£)(*] + + 2)2 4 2> ---------- + ---------------------- = -------Xy + 兀2 + 2 (兀1 + xj (xj + +2) X, + ,<2进而有斗+A\ > 2a > 2,证毕.(三).简单练习已知函 SSc/(A)= .vin X 与吃线F = m 交 y-A (A,|, rj, B (X,两总求证:/// * < A', < -—eflNkl: Rfttt f (X) = 2 lln T = + ax(a e /f) (yi fI 2,求X 1 的切线方科⑵若歯ft/BWWfltt 仃却92卜交点分剔为斗 <丹)・ 戒讪:八2作业2:设函数f(x)=(x +1)1 n X —ax,已知x ^ (1^),且函数f(x)的图像在点 (X 0, f(X 0))处的切线方程为y^^x —e.e(比例性质) 由对均不等式有山並-Iny並-壬h 宀 码> 2 £ 一 -V, X] + 2ln^(1)求a的值;(2)求证:函数f(x)在定义域内单调递增;1= ---- =lnn-ln(n-1) <n-1 n-1所以 In 2 -In1 <1,x=q ,= ln(七)V ——1 n-1 n —1 n —12 2 ⑶ 当n >1,n N 时,证明:-+-3 5 +…+ 2 <ln n v 1 + 1 2n-1 2 3 +…+ 1 n —1 证明由⑵知当X € (1,母)时,f(X)单调递增 故 f(x)〉f (1) = _2,= (x+1)ln x-2x A _2 故当 (1,址)时,lnx /(X-1) x+1 因此当山时,令"占,二ln(£1) 2占1) > — ,n 八 UV 1) n —1 2 —2n —1 2 即 ln n -ln(n -1) > ----- 2n -1 2 所以 ln2-1 n1 > —, 3 ln 3-1 n2>-, 5 2In n -ln(n -1) a ------ . 2n -1 2 2 2 相加得 In n A - +— +... + ----- 3 5 2n-1 由(1)知当 x €(l,+=c )时,g(x) =x +1—lnx 单调递增, 故 g(x)>g(1)=2,= In x<x —1,因此当 n>2 时,令1ln n Tn(n -1) < ----- ,n -11 1 相加得Inn ^+―+...+——2 n-1 2 2 2 1 1 13 5 2n -1 2 3 终上所述 第三问可以用数学归纳法函数的两个边界一个精细 左边用■2(x — C In X ,右边用In X V X -1n —1 ,一个常见的边界 x+1。
对数均值不等式公式

对数均值不等式公式对数均值不等式是数学中的一条重要不等式,它在许多领域中都有广泛的应用。
这条不等式可以用来证明其他数学问题,也可以用来解决实际问题。
对数均值不等式的表达形式是:对于任意正数a1、a2、......、an,有以下不等式成立:ln((a1+a2+......+an)/n) ≥ (ln(a1)+ln(a2)+......+ln(an))/n对数均值不等式在实际问题中有着广泛的应用。
例如,在概率论中,对数均值不等式被用来证明熵的性质。
在信息论中,对数均值不等式被用来证明信道容量的性质。
在经济学中,对数均值不等式被用来证明收入不平等性的性质。
除了在理论研究中的应用,对数均值不等式在实际问题中也有着重要的作用。
例如,在金融领域中,对数均值不等式被用来证明资产组合的风险。
在医学领域中,对数均值不等式被用来证明药物的疗效。
在工程领域中,对数均值不等式被用来证明信号的功率。
对数均值不等式的证明方法有很多种,其中最常用的是基于均值不等式的证明方法。
这种证明方法基于均值不等式的性质,通过适当选择函数,将原问题转化为均值不等式的形式,从而得到对数均值不等式。
除了均值不等式的证明方法,还有一种常用的证明方法是基于凸函数的证明方法。
这种证明方法利用凸函数的性质,通过适当选择凸函数,将原问题转化为凸函数的性质,从而得到对数均值不等式。
对数均值不等式是数学中的一条重要不等式,它在许多领域中都有广泛的应用。
这条不等式告诉我们,对于一组正数,取对数后再求平均值一定大于等于取对数后再求平均值。
这个不等式的证明方法有很多种,其中最常用的是基于均值不等式和凸函数的证明方法。
这条不等式在理论研究和实际问题中都有着重要的应用,可以帮助我们解决各种数学和实际问题。
指对数均值不等式

指对数均值不等式在数学中,不等式是一种重要的关系式,常被用于证明定理或解决问题。
其中最常用的一个不等式就是“对数均值不等式”。
对数均值不等式是在大量的数学领域中无处不在的一个不等式,它为我们提供了一种有效的方法来判断一组数据的大小关系。
它的推导过程相对简单,只需要利用对数函数的性质即可。
首先,假设有 n 个正数 a1, a2, ..., an,则它们的算术平均数为:A = (a1 + a2 + ... + an) / n它们的几何平均数为:G = a1 * a2 * ... * an 的 n 次方根自然对数函数 ln(x) 具有单调递增的性质,根据此性质,可得到:ln(A) = ln((a1 + a2 + ... + an) / n)= (ln a1 + ln a2 + ... + ln an) / n>= (n * ln G) / n= ln G进行指数运算,得到:A >= G这就是对数均值不等式。
对数均值不等式在数学中有广泛的应用,特别是在不等式证明中。
它可以用于证明调和平均数大于几何平均数、算术平均数大于等于几何平均数等形式多样的不等式。
但需要注意的是,对数均值不等式只适用于正数,不能应用于负数或零值。
此外,对数均值不等式还有一个重要的扩展形式——加权对数均值不等式。
它的形式为:(w1 * ln a1 + w2 * ln a2 + ... + wn * ln an) / (w1 + w2 + ... + wn) >= ln((a1的w1次方 * a2的w2次方 * ... * an的wn次方)^1/(w1+w2+...+wn))其中,w1, w2, ..., wn 为正数或零值,且 w1 + w2 + ... + wn 不为零。
对数均值不等式是一个简单而有用的数学工具,无论是在理论研究还是实际应用中,都有着重要的作用。
它的引入位置不仅局限于数学领域,同时也涉及到一些实际生活中的问题。
高考试题的探究(一)2对数平均数的不等关系的应用(定稿)
对数平均数的不等关系的应用安徽省太和县太和中学 岳 峻 236600中学数学教育专家安振平在剖析2013年陕西高考数学时指出,其压轴题的理论背景是: 当0ba时,2221122ln ln a b a bb ababa b aab. 其中ln ln a ba b--被称之为对数平均值.一、借助于对数平均数的不等关系巧妙放缩 对数平均数的不等式链,提供了多种巧妙放缩的途径,可以用来证明含自然对数的不等式问题.对数平均数的不等式链包含多个不等式,我们可以根据证题需要合理选取其中一个达到不等式证明的目的.例1 (2014年陕西)设函数)1ln()(x x f +=,()()g x xf x '=,其中()f x '是)(x f 的导函数.(1)(2)(略)(3)设+∈N n ,比较()()()12g g g n +++与()n f n -的大小,并加以证明.解析 (3)因为()1xg x x=+, 所以()()()1211112231231n g g g n n n n ⎛⎫+++=+++=-+++⎪++⎝⎭, 而()()ln 1n f n n n -=-+,因此,比较()()()12g g g n +++与()n f n -的大小,即只需比较113121++++n 与()ln 1n +的大小即可. 根据③式中,1ln ln ,b a b a b令,1,a n b n 则1ln 1ln ,1n n n所以1ln 2ln1ln 22<-=,1ln 3ln 23<-,1,ln(1)ln 1n n n <+-+, 将以上各不等式左右两边相加得:()111ln 1231n n +++<++,故()()()()12gg g n n f n +++>-.评注 本题是高考试题的压轴题,难度较大,为了降低试题的难度采取多步设问,层层递进,上问结论,用于下问,其第二问是为第三问做铺垫的“梯子”,尽管如此,步骤依然繁琐,求解过程复杂,但我们这里应用对数平均数不等式链来证明,思路简捷,别具新意,易于学生理解、掌握. 若根据③式中1ln ln ,bab a a令,1,a n b n 则1ln 1ln ,n nn可得:111ln 1123n n.若根据③式中111ln ln 2b a b a ab,又会得出怎样的结论呢?请看下例.例2 (2010年湖北)已知函数0b f x ax c a x的图象在点1,1f 处的切线方程为1yx .(1)用a 表示出,b c ;(2)(略) (3)证明:1111ln 11.2321nn n nn解析 (1)1,12b a c a ;(3)根据③式中,111ln ln ,2b ab a a b令,1,a n b n 则111ln 1ln ,21n nn n所以111ln 2ln1,212111ln 3ln 2,223,111ln 1ln ,21n nnn将以上各不等式左右两边分别相加得:111111ln 1,223421n n n即111111ln11,234212n n n故1111ln 1.2321nn nn例3 (2013年新课标Ⅰ)已知函数()()()1ln 11x x f x x xλ+=+-+.(1)若0x≥时, ()0,f x ≤求λ的最小值;(2)设数列{}n a 的通项111123n a n =++++,证明:21ln 24n na a n-+>. 解析 (1)易得()()()221200,(1)x x f f x x λλ--'==+.令()0,f x '=则120,,x x λλ-==若0λ<,则当0x >时,()()0,f x f x '>是增函数,()()00,f x f >=不符合题意;若102λ≤<,则当120x λλ-≤<时,()()0,f x f x '>是增函数,()()00,f x f >=不符合题意;若12λ≥,则当0x >时,()()0,f x f x '<是减函数,()()00,f x f ≤=符合题意;综上,λ的最小值是12.(2)根据③式中,111ln ln 2bab a a b,令,1,a n b n 则111ln 1ln ,21n nn n 所以111ln 1ln ,21n nnn 111ln 2ln 1,212n n n n111ln 3ln 2,223n n n n111ln 2ln 21,2212n n n n将以上各不等式左右两边分别相加得:1122221ln 2ln ,2123212n nn n n n n n即111111ln 2,2123214nn nn n n故1111ln 21224n n n n++++>++. 评注 本题提供标准答案是借助于第一问的λ的最小值12λ=时,()()()2ln 1022x x x x x++<≥+加以赋值,并进行变形,令1x k=,有()121111ln 12121k k k k k k +⎛⎫⎛⎫+<=+ ⎪ ⎪++⎝⎭⎝⎭,亦即()111ln 1ln 21k k k k ⎛⎫+-<+ ⎪+⎝⎭达到放缩的目的.两者相比较,自然是运用对数平均值的不等式链的方法简捷.例4 (2012年天津)已知函数()()()ln 0f x x x a a =-+>的最小值为0.(1)(2)(略)(3)证明:()()12ln 212*.21ni n n N i =-+<∈-∑ 解析 (3)易求1a =,待证不等式等价于()2222ln 2135721n n ++++<+-.根据③式中,1ln ln ,ba b a b令21,21,a n bn 则22ln 21ln 21,21121n n n n2ln 3ln1,32ln 5ln 3,52ln 7ln 5,,72ln 21ln 21,211n n n将以上各不等式左右两边分别相加得:()22222ln 213572121n n n +++++<+-+,()122ln 21222121ni n i n =-+<-<-+∑.得证. 例5 (2014福建预赛)已知1()ln(1)311f x a x x x =+++-+. (1)(略)(2)求证:()222223411ln 21411421431414n n n +++++>+⨯-⨯-⨯-⨯-对一切正整数n 均成立.解析 (2)根据 式中,ln ln ,b a ab令21,21,a n b n 则2ln 21ln 21,41n n n变形可得:222211142ln 21ln 21,444141n n n n n n n 则 212ln 3ln1,4411213ln 5ln 3,,4421211ln 21ln 21,441n n n n 将以上各不等式左右两边相加得:222223411ln(21)411421431414n n n +++++>+⨯-⨯-⨯-⨯-对一切正整数n 均成立.评注 本题提供标准答案是借助于第一问的a的最小值2a =-时,12ln(1)3101x x x -+++->+,即()1312ln 11x x x +->++,结合待证不等式的特征, 令()2*21x k N k =∈-,得122312ln(1)22121121k k k +⨯->+--+-,整理得:288212ln 4121k k k k ++>--,即()()211ln 21ln 21414k k k k +>+--⎡⎤⎣⎦-,借此作为放缩的途径达到证明的目的.你能注意到两种方法的区别吗?二、多变量问题蕴含的对数平均数的不等关系高考数学时常出现多变量的综合问题,且多出现在压轴题的位置,由于含有多个变量,使题目显得繁杂混乱,此类问题对学生的阅读能力、转化与划归的思维灵活性要求较高,许多学生面对此类问题往往一筹莫展,难以找到解决问题的突破口.如何从繁乱中理出头绪并顺利解决问题呢?例6 (2015合肥最后一卷)已知函数()ln .f x x kx =-(1)(略)(2)若函数()y f x =的有两个相异的零点12,,x x 求证:212.x x e > 分析 第(2)问属于多变量的综合问题,如何破解此类问题呢?因为函数()y f x =的有两个相异的零点12,,x x 显然0k >,不妨设120,x x <<则()()120f x f x ==,亦即1122ln ln 0x kx x kx -=-=,且()2121ln ln k x x x x -=-,要证212,x x e >即证12ln ln 2x x +>,只需证()122,k x x +>即212112ln ln 2,x x x x x x ->-+亦即()2121212ln ln x x x x x x -->+ 待证不等式()2121212ln ln x x x x x x -->+就是不等式2ln ln a b a ba b +->-的“化妆”而已, 破解此类问题,需运用转化与化归的思想,通过构造两个变量的比值(或差值)的函数,使之减少变量的个数,化归为我们所熟悉的一元函数,最后利用导数证明不等式.待证式()2121212ln ln x x x x x x -->+转化为21221121ln 1x x x x x x ⎛⎫- ⎪⎝⎭>+,令()211x t t x =>,则21221121ln 1x x x x x x ⎛⎫- ⎪⎝⎭>+等价于()21ln 1t t t ->+,令()()()21ln 11t g t t t t -=->+,则()()()()222114011t g t t t t t t -'=-=>++, 所以()g t 在区间()1,+∞单调递增,故()()10g t g >=,即()21ln 1t t t ->+成立,因此212x x e >得证.评注 以此为背景的两个变量的不等式的证明问题,其解题策略:先将待证不等式逆推分析,进行等价转化,使得其中的两个变量的特征显现出来,然后利用换元法将两个变量的比值(或差值)作为新的一元变量.这种解题策略是转化与化归、消元与换元、构造与求导等基本数学思想方法的有机整合,因此此类问题是高考考查的重点.对数平均数不等式链的证明方法与本例的证明方法是一样的.例7 (2014年绵阳三诊)已知函数()()()ln 0f x x a x a =+->有且只有一个零点.(1)(2)略(3)设()(),h x f x x =+对任意()()1212,1,x x x x ∈-+∞≠, 证明:不等式()()1212x x h x h x ->-恒成立.解析 (3)易求1a =,()()ln 1,h x x =+不妨设211x x >>-, 待证不等式等价于()()()()212111ln 1ln 1x x x x +-+>+-+根据④中的ln ln b a ab ba, 令211,1bx a x 即可.评注 本题原证的方法是令()21111x t t x +=>+,将待证不等式转化为()ln 1t t >>,()ln 1t t >>即可.想一想,若()1212,1,,x x x x ∈-+∞≠时,()()2112211ln 1ln 12x x x xx x -+<++-+是否恒成立呢?例8 (2015年江南十校联考)已知函数()ln .f x x ax =-(1)略;(2)若函数()y f x =的图像在1x =处的切线平行于x 轴,且()()()112212,,,A x y B x y x x <是函数()y f x =的图像上任意两个不同的点,设直线AB 的斜率为k ,证明:21111 1.k x x -<<- 解析 由题意可知()1,f x a x'=- ()110, 1.f a a '=-==()ln .f x x x =- ()()2211212121ln ln ln ln 1,x x x x x x k x x x x ----==---要证21111 1.k x x -<<-只需证21111,k x x <+<即212211ln ln 11,x x x x x x -<<-根据④中的ln ln b aba b a, 令21,bx a x 即可.对数平均数的不等式链的运用是近几年数学竞赛、名校模拟数学试题、高考数学真题的理论背景,正如罗增儒教授指出:通过有限的典型考题的学习去领悟那种解无限道题的数学机智。
对数均值不等式的应用典例
对数均值不等式的应用典例对数均值不等式是数学中一种常见的不等式,它在数学推导和证明中具有重要的应用价值。
在以下内容中,将介绍对数均值不等式的应用典例。
1. 应用于几何平均数和调和平均数的比较对数均值不等式可以用来比较几何平均数和调和平均数的大小关系。
几何平均数和调和平均数在统计学和概率论中经常用到,对于一组非负实数a1, a2, ..., an,它们的几何平均数定义为G = (a1 * a2 * ... * an)^(1/n),调和平均数定义为H = n / (1/a1 + 1/a2 + ... + 1/an)。
根据对数均值不等式,有ln(G) >= (ln(a1) + ln(a2) + ... + ln(an))/n >= ln(H),即G >= H。
这意味着,在一组非负实数中,几何平均数大于等于调和平均数。
2. 应用于证明不等式对数均值不等式在证明不等式时经常被使用。
例如,我们要证明对于任意正实数a, b,有a^2 + b^2 >= 2ab。
可以使用对数均值不等式来证明。
首先,我们可以将不等式化简为(a^2 + b^2)/2 >= ab,然后取对数得到ln((a^2 + b^2)/2) >= ln(ab)。
接下来,根据对数均值不等式,有ln((a^2 + b^2)/2) >= (ln(a) + ln(b))/2,ln(ab) = ln(a) + ln(b),所以ln((a^2 + b^2)/2) >= ln(ab)。
进一步化简得到(a^2 + b^2)/2 >= ab,即原不等式成立。
3. 应用于概率论中的熵和相对熵对数均值不等式在概率论中的熵和相对熵的推导中也有应用。
熵是一个度量随机变量的不确定性的概念,相对熵则是衡量两个概率分布之间差异的概念。
根据对数均值不等式,可以证明熵和相对熵是凸函数,这是由于对数函数是凸函数,而均值不等式保持凸性。
3直击高考之对数平均不等式
第三篇:对数平均数不等式高考相关:高考中很多题都是以对数平均不等式为背景,变形出题的,重要性毋庸置疑! 例(2018全国Ⅰ卷理21)(12分)已知函数1()ln f x x a x x=-+. (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点12,x x ,证明:()1212()2f x f x a x x -<--解:⑴函数的定义域为()0,+∞()22211'1a x ax f x x x x -+-=--+=24a ∆=-① 当22a -≤≤时,()'0f x ≤,()f x 在 ()0,+∞单调递减;② 当2a >时, ()'0f x =,1222a a x x +==,120x x << ()f x在0,2a ⎛⎫- ⎪ ⎪⎝⎭和2a ⎛⎫+∞ ⎪ ⎪⎝⎭上单调递减,在,22a a ⎡+⎢⎢⎥⎣⎦上单调递增;③ 当2a <-时,120x x <<,()f x 在 ()0,+∞单调递减. 综上所述:2a ≤时,()f x 在 ()0,+∞单调递减;2a >时,()f x在0,2a ⎛ ⎪⎝⎭和2a ⎛⎫++∞ ⎪ ⎪⎝⎭上单调递减,在,22a a ⎡+⎢⎢⎥⎣⎦上单调递增.⑵ ()f x 存在两个极值点12,x x ,由⑴知2a >12x x a +=,121x x =()()211122211212122112121211ln ln ln ln ()x x x a x x a x x x a x x f x f x x x x x x x x x x x --+-+-+-+--==---1212ln ln 2x x ax x -=--要证()1212()2f x f x a x x -<--,即证1212ln ln 1x x x x -<-方法一:1212ln ln 1x x x x -<=- 1212ln ln 1x x x x -<-得证.方法二:12x x a +=,121x x =,2a >,不妨设212ax >> 将121x x =代入1212ln ln 1x x x x -<-得, 2222ln 11x x x -<-, 22212ln x x x ->-,22212ln 0x x x +-< 证1212ln ln 1x x x x -<-,即证22212ln 0x x x +-< 令()()12ln ,1g x x x x x =-+>,那么()()2222212121'1x x x g x x x x x---+-=--== 0x >时,()'0g x <,()g x 在()+∞1,上单调递减, ()()21g x g <,()222212ln g x x x x =+-,()12ln1110g =+-= 22212ln 0x x x +-<得证.对数平均不等式2(0)11ln ln 2b a a ba ab b a b b a a b-+<<<<<<<-+3.典例剖析对数平均数的不等式链,提供了多种巧妙放缩的途径,可以用来证明含自然对数的不等式问题.对数平均数的不等式链包含多个不等式,我们可以根据证题需要合理选取其中一个达到不等式证明的目的. (一)0ln ln b a ba ab a的应用例1 (2014年陕西)设函数)1ln()(x x f +=,()()g x xf x '=,其中()f x '是)(x f 的导函数.(1)(2)(略) (3)设+∈N n ,比较()()()12g g g n +++与()n f n -的大小,并加以证明.解:()1'1f x x=+ ()()1x g x xf x x '==+()()()1211112...11...1231231n g g g n n n +++=+++=-+-++-++111...231n n ⎛⎫=-+++ ⎪+⎝⎭()()()2341231ln 1lnln ln ln 12312n n n f n n n n n n n ⨯⨯⨯⋅⋅⋅⨯++⎛⎫-=-+=-=-++⋅⋅⋅+ ⎪⨯⨯⨯⋅⋅⋅⨯⎝⎭令1n x n +=,那么1111n x=-+ 令()11ln 1ln 1g x x x x x⎛⎫=--=+- ⎪⎝⎭ ()22111'x g x x x x-=-= 1x >时,()'0g x >,()g x 在()1,+∞上单调递增,()()1g x g >11ln01n n n +->+ 11ln 1n n n +>+231111ln ln ln ...12231n n n n n +⎛⎫⎛⎫-++⋅⋅⋅+<-+++ ⎪ ⎪+⎝⎭⎝⎭()()()()12n f n g g g n -<+++(二)220ln ln b b aba b a的应用例 2 设数列{}n a 的通项(n a =,其前n 项的和为n S ,证明:()ln 1n S n <+.证:()231ln 1ln ln ln12n n n++=++⋅⋅⋅+比较1lnn n +()1ln 1ln n n n n +-<+-()ln 1ln n n ∴+->>1lnn n +∴>()ln 1n S n ∴<+(三)02ln ln a bb aba b a的应用例3. 设数列{}n a 的通项111123na n=++++,证明:()ln 21n a n <+. 证明:()3521ln 21ln ln ln 1321n n n ++=++⋅⋅⋅-方法一:比较1n 和21ln 21n n +- 令2121n x n +=-,那么1422n x =-+令4()ln 21f x x x =+-+ ()()()()()2222214114'()111x x x f x x x x x x x +--=-==+++ 1x >时,()'0f x >,()f x 在()1,+∞上单调递增,()()1f x f > 2144ln2ln1ln 2212111121n n n n ++->+-+-++- 211ln 21n n n+>- ()ln 21n a n <+方法二:()()()21214ln 21ln 212n n nn n +--<+-- ()()1ln 21ln 21n n n+--> 211ln21n n n+>- ()ln 21n a n <+(四)2011ln ln b ab a b aab的应用例 4. (2010年湖北)已知函数0b f x axc a x的图象在点1,1f 处的切线方程为1y x .(1)用a 表示出,b c ;(2)(略) (3)证明:1111ln 11.2321nn nnn(1)解:1yx ,1x =时,0y =,()10f a b c =++=()222'b ax bf x a x x-=-=,()'11f a b =-= 01a b c a b ++=⎧⎨-=⎩112b a c a=-⎧⎨=-⎩ (3)证明:()231ln 1ln ln ln12n n n ++=++⋅⋅⋅+ ()()1111111lnln 1ln 12+12+1n n n n n n n n n n +⎛⎫⎛⎫=+-<+-+=+ ⎪ ⎪⎝⎭⎝⎭()()()1111111ln 12121223121n nn n n n n ⎛⎫++<++++⋅⋅⋅+++ ⎪+++⎝⎭ ()()()()11111ln 1212232121n nn n n n n ++<+++⋅⋅⋅++++++()()111ln 112123n n n n++<+++⋅⋅⋅++(五)0ln ln b a ab b a b a的应用例5. (2014福建预赛)已知1()ln(1)311f x a x x x =+++-+. (1)(略) (2)求证:()222223411ln 21411421431414n n n +++++>+⨯-⨯-⨯-⨯-对一切正整数n 均成立.证明:()113521ln 21ln ln ln 441321n n n +⎛⎫+=++⋅⋅⋅+ ⎪-⎝⎭()()()()()()2121212121ln ln 21ln 212122121n n n n n n n n n n +--++-⎡⎤⎡⎤+⎣⎦⎣⎦=+--<-+-()2241214ln214141n n nn n n ++<<---21211ln 42141n n n n ++<-- ()222212341ln 21441142143141n n n ++<++++⨯-⨯-⨯-⨯-强化训练1. (2012年天津)已知函数()()()ln 0f x x x a a =-+>的最小值为0.(1)(2)(略)(3)证明:()()12ln 212*.21ni n n N i =-+<∈-∑ 证明:证明()12ln 21221ni n i =-+<-∑,即证明()1111ln 21212ni n i =-<+-∑ ()113521ln 21ln ln ln 221321n n n +⎛⎫+=++⋅⋅⋅+ ⎪-⎝⎭()()21ln ln 21ln 2121n n n n +=+---()()()2212121lnln 21ln 21212121n n n n n n n n +--⎡⎤+⎣⎦=+-->-++-211ln21n n n+>-()11111ln 212212n n ⎛⎫+>++⋅⋅⋅+ ⎪⎝⎭()111111111ln 2122422235212n n n n n +>++⋅⋅⋅+>++⋅⋅⋅++-- ()111111ln 2112135212n n n +>+++⋅⋅⋅++--()11111ln 211213521n n +>+++⋅⋅⋅+--()111ln 211221n i n i =+>--∑()12ln 21221ni n i =-+<-∑2.(2013年新课标Ⅰ)已知函数()()()1ln 11x x f x x xλ+=+-+.(1)若0x ≥时,()0,f x ≤求λ的最小值;(2)设数列{}n a 的通项111123n a n =++++,证明:21ln 24n n a a n-+>. 解:(1)()()()()()()()2222211211'111x x x x x x f x x x x λλλλ++-++-=-=-+++()2211x x x λλλ-⎛⎫+⎪⎝⎭=-+ ()'0f x =,12120,x x λλ-==① 当0λ<时,21x x <,0x ≥,()'0f x ≥,()f x 在[)0,+∞上单调递增,()(0)f x f ≥()0f x ≥;② 当0λ=时,()()ln 1f x x =+,0,()0x f x ≥≥; ③ 当102λ<<时,120x λλ-≤≤,()0f x ≥,()f x 单调递增,()(0)f x f ≥,()0f x ≥; ④ 当12λ≥时,0x ≥,()'0f x ≤,()f x 单调递减,()(0)f x f ≤, ()0f x ≤ 综上所述:λ的最小值为12(2)令12λ=,由(1)知当0x >时,()0f x <,即()()2ln 122x x x x +>++ 取1x k =,则()211ln 21k k k k k ++⎛⎫> ⎪+⎝⎭21111141224n n a a n n n n n -+=++⋅⋅⋅++++ ()()()()111111121212222444n n n n n n n=++++⋅⋅⋅+++++++()()()()1111112212122224n n n n n n=+++++⋅⋅⋅+++++ ()2111221n k n kk -=⎛⎫=+ ⎪ ⎪+⎝⎭∑ ()2121211ln ln 2ln 221n n k n k n k k n n k k k --==⎛⎫++=>=-= ⎪ ⎪+⎝⎭∑∑ 21ln 24n n a a n-+>。
对数平均数的不等式链的几何解释及应用——高中高考数学
对数平均数的不等式链的几何解释及应用——高中高考数学 1 / 8 对数平均数的不等式链的几何解释及应用
中学数学教育专家安振平先生在剖析2014年陕西高考数学试题时指出,其压轴题的理论背景是: 设,0,,abab则2lnlnabababab,其中lnlnabab被称之为对数平均数. 童永奇老师构造函数,借助于导数证明了对数平均数的上述不等式,难度较大,为此,我作了深入地探讨,给出对数平均数的不等关系的几何解释,形象直观,易于理解. 1 对数平均数的不等关系的几何解释
反比例函数10fxxx的图象,如图所示,APBCTUKV,MNCDx轴, ,0,Aa
1,,Paa1,0,,BbQbb,1,,Tabab作fx在点2,2abKab
处的切线分别与
,APBQ交于,EF,根据左图可知,
因为ABNMABQPABFESSS矩形曲边梯形梯形, 所以12lnln,badxbabaxab ① 又1lnlnabAUTPaSdxabax曲边梯形, 11lnln22ABQPbaS曲边梯形,
11111222AUTPABCDbaSabaS
aabab
梯形梯形
, 对数平均数的不等式链的几何解释及应用——高中高考数学 2 / 8 根据右图可知, AUTPAUTPSS曲边梯形梯形 ,所以lnlnbabaab, ② 另外,ABQXABYPABQPABQPSSSS矩形矩形曲边梯形梯形,可得: 11111lnln,2babababa
baba ③
综上,结合重要不等式可知: 211111lnln2baba
babababa
bababaab
,
即20112lnlnabbababababaab. ④ 2 不等式链的应用 对数平均数的不等式链,提供了多种巧妙放缩的途径,可以用来证明含自然对数的不等式问题.对数平均数的不等式链包含多个不等式,我们可以根据证题需要合理选取其中一个达到不等式证明的目的.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对数平均不等式:对于正数 a , b ,且 a b ,则有 ab a b a b ,即几何平均数<对 ln a ln b 2
数平均数<算术平均数,简记为 G a,b L a,b Aa,b .
(ⅱ)若 a 2 ,令 f (x) 0 得, x a a2 4 或 x a a2 4 .
2
2
当 x (0, a
a2 4 )
(a
a2 4 , ) 时, f (x) 0 ;
2
2
当 x(a
a2 4 a ,
a2 4 ) 时, f (x) 0 . 所以 f (x) 在 (0, a
2/6
高考数学培优专题(1)
例 3 (2014 年江苏南通二模)设函数 f (x) ex ax a ,其图像与 x 轴交于 A(x1, 0), B(x2, 0) 两点,且
x1 x2 . (Ⅰ)求实数 a 的取值范围; (Ⅱ)求证: f ( x1x2 ) 0 .
例 4(2011 年辽宁理科)已知函数 f (x) ln x ax2 (2 a)x .
a2 4 ) , (a
a2 4 , ) 单调递
2
2
2
2
减,在 (a
a2 4 a ,
a2 4 ) 单调递增.
2
2
(2)由(1)知, f (x) 存在两个极值点当且仅当 a 2 .
由于 f (x) 的两个极值点 x1 , x2 满足 x2 ax 1 0 ,所以 x1x2 1 ,不妨设 x1 x2 ,则 x2 1 . 由于
高考数学培优专题(1)
对数平均不等式的证明与应用
——由 2018 年全国 I 卷理科 21 题想到的
近年来以对数平均不等式为背景的试题经常活跃在各类考试中,2018 年全国 I 卷理科 21 题(见例
1)再次考了这个问题,值得大家引起高度重视。但很多同学,或年轻教师并不了解,为此介绍如下:
(一)对数平均数与对数平均不等式
f
(1)
0 ,因此当 t
1时,
f (t) 2 lnt t 1 0恒成立,即 ln a a b 成立.
t
bba
再证
ln
a a
b ln
b
a
2
b
,即证
ln
a b
2( a 1) b a 1
,
b
令 a t(t 1) , g(t) ln t 2(t 1) (t 1) ,
b
t 1
则 g(t) 1 4 (t 1)2 0 ,所以 g(t) 在 (1,) 递增,而 g(1) 0 ,因此当 t 1时, t (t 1)2 t(t 1)2
f (x1) f (x2 ) 1 1 a ln x1 ln x2 2 a ln x1 ln x2 ,
x1 x2
x1 x2
x1 x2
x1 x2
由对数平均不等式, x1 x2 > ln x1 ln x2
x1 x2
1
,所以
ln
x1 x1
ln x2 x2
1
所以 f (x1) f (x2 ) a 2 x1 x2
(1)讨论函数 f (x) 的单调性;
(2)设 a
0 ,证明:当 0
x
1 a
时
,
f (1 x) a
f
(
1 a
x)
;
(3)若函数 y f (x) 的图象与 x 轴交于 A、B 两点,线段 AB 中点的横坐标为 x0 ,证明:
f (x0 ) 0 .
3/6
高考数学培优专题(1)
答案
例 1(2018 年全国 I,21)已知函数 f (x) 1 x a ln x . x
.
例 2(2010 年天津高考理科 21 题)已知函数 f (x) xex (x R) .
(Ⅰ)求函数 f (x) 的单调区间和极值;
(Ⅱ)已知函数 y= g( x) 的图象与函数 y= f (x) 的图象关于直线 x 1 对称,证明:当 x 1 时,
f (x) g(x) ;
(Ⅲ)如果 x1 x2 ,且 f (x1) f (x2 ) ,证明: x1 x2 2 .
f
(x1) f (x2 ) x1 x2
a2.
例 2(2010 年天津高考理科 21 题)已知函数 f (x) xex (x R) . (Ⅰ)求函数 f (x) 的单调区间和极值; (Ⅱ)已知函数 y= g( x) 的图象与函数 y= f (x) 的图象关于直线 x 1 对称,证明:当 x 1 时, f (x) g(x) ; (Ⅲ)如果 x1 x2 ,且 f (x1) f (x2 ) ,证明: x1 x2 2 .
解(Ⅰ)、(Ⅱ)略.
(Ⅲ)将 x1ex1
x2e x2
两边取自然对数得, ln x1
x1
ln x2
x2 ,故 ln
x1 x1
x2 ln x2
1,
由对数平均数不等式知, x1 x2 ln x1 ln x2
1
x1
x2 2
,即 x1
x2
2.
4/6
高考数学培优专题(1)
例 3 (2014 年江苏南通二模)设函数 f (x) ex ax a ,其图像与 x 轴交于 A(x1, 0), B(x2, 0) 两点,且
ln t 2(t 1) 0恒成立,即 a b a b 成立.
t 1
ln a ln b 2
1/6
高考数学培优专题(1)
(三)对数平均不等式的应用
例 1(2018 年全国 I,21)已知函数 f (x) 1 x a ln x . x
(1)讨论 f (x) 的单调性;
(2)若
f
(x) 存在两个极值点 x1 , x2 ,证明:
(1)讨论 f (x) 的单调性;
(2)若
f
(x) 存在两个极值点 x1 , x2 ,证明:
f
(x1) f (x2 ) x1 x2
a2.
解:(1)
f
(x) 的定义域为 (0, ) ,
f (x)
1 x2
1
a xΒιβλιοθήκη x2ax x21
.
(ⅰ)若 a ≤2 ,则 f (x) ≤ 0 ,当且仅当 a 2 , x 1时 f (x) 0 ,所以 f (x) 在 (0, ) 单调递减.
(二)对数平均不等式的证明
不妨设 a b 0 .先证 ab a b ,即证 ln a a b ,
ln a ln b
bba
令 a t(t 1) ,设 f (t) 2ln t t 1(t 1) ,
b
t
则
f (t)
2 t
1 1 t2
(t 1)2 t2
0 ,所以
f
(t) 在 (1,) 递减,而
