Matlab遗传算法工具箱函数及应用实例_图文.
遗传算法详解(含MATLAB代码)

遗传算法详解(含MATLAB代码)Python遗传算法框架使用实例(一)使用Geatpy实现句子匹配在前面几篇文章中,我们已经介绍了高性能Python遗传和进化算法框架——Geatpy的使用。
本篇就一个案例进行展开讲述:pip install geatpy更新至Geatpy2的方法:pip install --upgrade --user geatpy查看版本号,在Python中执行:import geatpyprint(geatpy.__version__)我们都听过“无限猴子定理”,说的是有无限只猴子用无限的时间会产生特定的文章。
在无限猴子定理中,我们“假定”猴子们是没有像人类那样“智能”的,而且“假定”猴子不会自我学习。
因此,这些猴子需要“无限的时间"。
而在遗传算法中,由于采用的是启发式的进化搜索,因此不需要”无限的时间“就可以完成类似的工作。
当然,需要产生的文章篇幅越长,那么就需要越久的时间才能完成。
下面以产生"T om is a little boy, isn't he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much."的句子为例,讲述如何利用Geatpy实现句子的搜索。
之前的文章中我们已经讲述过如何使用Geatpy的进化算法框架实现遗传算法编程。
这里就直接用框架。
把自定义问题类和执行脚本编写在下面的"main.py”文件中:# -*- coding: utf-8 -*-import numpy as npimport geatpy as eaclass MyProblem(ea.Problem): # 继承Problem父类def __init__(self):name = 'MyProblem' # 初始化name(函数名称,可以随意设置) # 定义需要匹配的句子strs = 'Tom is a little boy, isn't he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much.'self.words = []for c in strs:self.words.append(ord(c)) # 把字符串转成ASCII码M = 1 # 初始化M(目标维数)maxormins = [1] # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)Dim = len(self.words) # 初始化Dim(决策变量维数)varTypes = [1] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)lb = [32] * Dim # 决策变量下界ub = [122] * Dim # 决策变量上界lbin = [1] * Dim # 决策变量下边界ubin = [1] * Dim # 决策变量上边界# 调用父类构造方法完成实例化ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)def aimFunc(self, pop): # 目标函数Vars = pop.Phen # 得到决策变量矩阵diff = np.sum((Vars - self.words)**2, 1)pop.ObjV = np.array([diff]).T # 把求得的目标函数值赋值给种群pop的ObjV执行脚本if __name__ == "__main__":"""================================实例化问题对象============================="""problem = MyProblem() # 生成问题对象"""==================================种群设置================================"""Encoding = 'RI' # 编码方式NIND = 50 # 种群规模Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,problem.borders) # 创建区域描述器population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被初始化,仅仅是完成种群对象的实例化)"""================================算法参数设置=============================="""myAlgorithm = ea.soea_DE_rand_1_L_templet(problem, population) # 实例化一个算法模板对象myAlgorithm.MAXGEN = 2000 # 最大进化代数"""===========================调用算法模板进行种群进化========================="""[population, obj_trace, var_trace] = myAlgorithm.run() # 执行算法模板population.save() # 把最后一代种群的信息保存到文件中# 输出结果best_gen = np.argmin(obj_trace[:, 1]) # 记录最优种群是在哪一代best_ObjV = obj_trace[best_gen, 1]print('最优的目标函数值为:%s'%(best_ObjV))print('有效进化代数:%s'%(obj_trace.shape[0]))print('最优的一代是第 %s 代'%(best_gen + 1))print('评价次数:%s'%(myAlgorithm.evalsNum))print('时间已过 %s 秒'%(myAlgorithm.passTime))for num in var_trace[best_gen, :]:print(chr(int(num)), end = '')上述代码中首先定义了一个问题类MyProblem,然后调用Geatpy内置的soea_DE_rand_1_L_templet算法模板,它实现的是差分进化算法DE-rand-1-L,详见源码:运行结果如下:种群信息导出完毕。
matlab遗传算法求解配送中心选址问题案例讲解

matlab遗传算法求解配送中心选址问题案例讲解遗传算法是一种基于生物进化原理的优化算法,可以用于求解各种复杂的问题,包括配送中心选址问题。
下面是一个使用MATLAB实现遗传算法求解配送中心选址问题的案例讲解。
一、问题描述假设有一组客户和一组候选的配送中心,每个客户都有一个需求量,配送中心有一个最大容量。
目标是选择一些配送中心,使得所有客户的需求量能够被满足,同时总成本最低。
二、算法实现1. 初始化种群在MATLAB中,可以使用rand函数随机生成一组候选配送中心,并使用二进制编码来表示每个配送中心是否被选中。
例如,如果候选配送中心有3个,则可以生成一个长度为3的二进制串来表示每个配送中心的状态,其中1表示被选中,0表示未被选中。
2. 计算适应度值适应度值是评估每个解的质量的指标,可以使用总成本来表示。
总成本包括建设成本、运输成本和库存成本等。
在MATLAB中,可以使用自定义函数来计算适应度值。
3. 选择操作选择操作是根据适应度值的大小选择解的过程。
可以使用轮盘赌选择、锦标赛选择等算法。
在MATLAB中,可以使用rand函数随机选择一些解,并保留适应度值较大的解。
4. 交叉操作交叉操作是将两个解的部分基因进行交换的过程。
可以使用单点交叉、多点交叉等算法。
在MATLAB中,可以使用自定义函数来实现交叉操作。
5. 变异操作变异操作是对解的基因进行随机修改的过程。
可以使用位反转、位变异等算法。
在MATLAB中,可以使用rand函数随机修改解的基因。
6. 终止条件终止条件是判断算法是否结束的条件。
可以使用迭代次数、最优解的变化范围等指标来判断终止条件。
在MATLAB中,可以使用自定义函数来实现终止条件的判断。
三、结果分析运行遗传算法后,可以得到一组最优解。
可以根据最优解的适应度值和总成本进行分析,并确定最终的配送中心选址方案。
同时,也可以使用其他评价指标来评估算法的性能,如收敛速度、鲁棒性等。
matlab 遗传算法 参数

Matlab 中可以使用遗传算法工具箱(Genetic Algorithm Toolbox)来实现遗传算法。
该工具箱提供了许多参数可以用于调整算法的行为。
以下是一些常用的参数:1. `PopulationSize`:种群大小,即染色体数量。
通常设置为一个相对较大的数值,以保证算法的搜索能力和多样性。
2. `MaxGenerations`:最大迭代次数。
算法将根据指定的迭代次数进行搜索,直到达到最大迭代次数或找到满足条件的解。
3. `CrossoverFraction`:交叉概率。
在每一代中,根据交叉概率对染色体进行交叉操作,以产生新的染色体。
4. `MutationFcn`:变异函数。
该函数将应用于染色体上的基因,以增加种群的多样性。
5. `Elitism`:精英策略。
该参数决定是否保留最佳个体,以避免算法陷入局部最优解。
6. `PopulationType`:种群类型。
可以选择二进制、实数或整数类型。
7. `ObjectiveFunction`:目标函数。
该函数将用于评估染色体的适应度,以确定哪些染色体更有可能产生优秀的后代。
8. `Variableargin`:变量参数。
可以将需要优化的变量作为参数传递给目标函数和变异函数。
9. `Display`:显示设置。
可以选择在算法运行过程中显示哪些信息,例如每个迭代的最佳个体、平均适应度等等。
以上是一些常用的参数,可以根据具体问题进行调整。
在Matlab 中使用遗传算法时,建议仔细阅读相关文档和示例代码,以便更好地理解算法的实现细节和如何调整参数来获得更好的结果。
用MATLAB实现遗传算法程序

用MATLAB实现遗传算法程序一、本文概述遗传算法(Genetic Algorithms,GA)是一种模拟自然界生物进化过程的优化搜索算法,它通过模拟自然选择和遗传学机制,如选择、交叉、变异等,来寻找问题的最优解。
由于其全局搜索能力强、鲁棒性好以及易于实现并行化等优点,遗传算法在多个领域得到了广泛的应用,包括函数优化、机器学习、神经网络训练、组合优化等。
本文旨在介绍如何使用MATLAB实现遗传算法程序。
MATLAB作为一种强大的数学计算和编程工具,具有直观易用的图形界面和丰富的函数库,非常适合用于遗传算法的实现。
我们将从基本的遗传算法原理出发,逐步介绍如何在MATLAB中编写遗传算法程序,包括如何定义问题、编码、初始化种群、选择操作、交叉操作和变异操作等。
通过本文的学习,读者将能够掌握遗传算法的基本原理和MATLAB编程技巧,学会如何使用MATLAB实现遗传算法程序,并能够在实际问题中应用遗传算法求解最优解。
二、遗传算法基础遗传算法(Genetic Algorithm,GA)是一种模拟自然选择和遗传学机制的优化搜索算法。
它借鉴了生物进化中的遗传、交叉、变异等机制,通过模拟这些自然过程来寻找问题的最优解。
遗传算法的核心思想是将问题的解表示为“染色体”,即一组编码,然后通过模拟自然选择、交叉和变异等过程,逐步迭代搜索出最优解。
在遗传算法中,通常将问题的解表示为一个二进制字符串,每个字符串代表一个个体(Individual)。
每个个体都有一定的适应度(Fitness),适应度越高的个体在下一代中生存下来的概率越大。
通过选择(Selection)、交叉(Crossover)和变异(Mutation)等操作,生成新一代的个体,并重复这一过程,直到找到满足条件的最优解或达到预定的迭代次数。
选择操作是根据个体的适应度,选择出适应度较高的个体作为父母,参与下一代的生成。
常见的选择算法有轮盘赌选择(Roulette Wheel Selection)、锦标赛选择(Tournament Selection)等。
matlab遗传算法 算例

下面是一个使用MATLAB实现的基本遗传算法算例。
本例用于解决简单的优化问题:寻找函数f(x) = x^2在[-10,10]范围内的最小值。
```matlab定义问题参数PopSize = 100; 种群数量Genes = -10:0.1:10; 基因范围FitnessFunc = @(x) -x.^2; 适应度函数(这里为了方便,使用了-x^2,即求最大值,实际应用中应改为-f(x))MaxGen = 50; 最大迭代次数初始化种群Pop = zeros(PopSize, length(Genes));for i = 1:PopSizePop(i,:) = rand(1,length(Genes))*2*Genes - Genes; 随机产生初始种群end开始迭代for gen = 1:MaxGen计算当前种群适应度Fitness = FitnessFunc(Pop);[BestFit, Index] = max(Fitness); 找到最佳适应度BestFitPos = Pop(Index,:); 找到最佳适应度对应的基因选择(轮盘赌选择)NewPop = zeros(PopSize, length(Genes));SumFitness = sum(Fitness);RandomFitness = rand(PopSize,1)*SumFitness; 随机生成每个个体的"随机适应度"for i = 1:PopSize[~, Index] = min(RandomFitness); 用随机适应度进行选择(越小被选中概率越大)NewPop(i,:) = Pop(Index,:); 将选择出的个体放入新种群RandomFitness(Index) = SumFitness; 将已选择的个体的随机适应度设为最大值,避免重复选择end交叉(杂交)for i = 1:PopSize/2随机选择两个父代个体Parent1 = NewPop(randi([1 PopSize]),:);Parent2 = NewPop(randi([1 PopSize]),:);生成新个体Child1 = (Parent1 + Parent2)/2; 中间值交叉Child2 = Parent1 + (Parent2 - Parent1)*rand; 一点交叉将新个体加入新种群NewPop((i-1)*2+1,:) = Child1;NewPop((i-1)*2+2,:) = Child2;end变异for i = 1:PopSizeif rand < 0.01 变异概率为0.01随机选择一个基因进行变异(取反)GeneIdx = randi(length(Genes));NewPop(i,GeneIdx) = ~NewPop(i,GeneIdx);endend更新种群Pop = NewPop;end输出结果BestFit = FitnessFunc(BestFitPos);fprintf('Best fitness: f\n', BestFit);fprintf('Best position: s\n', num2str(BestFitPos));```这个例子比较简单,只用了基本的遗传算法操作:选择、交叉和变异。
Matlab遗传算法工具箱简介
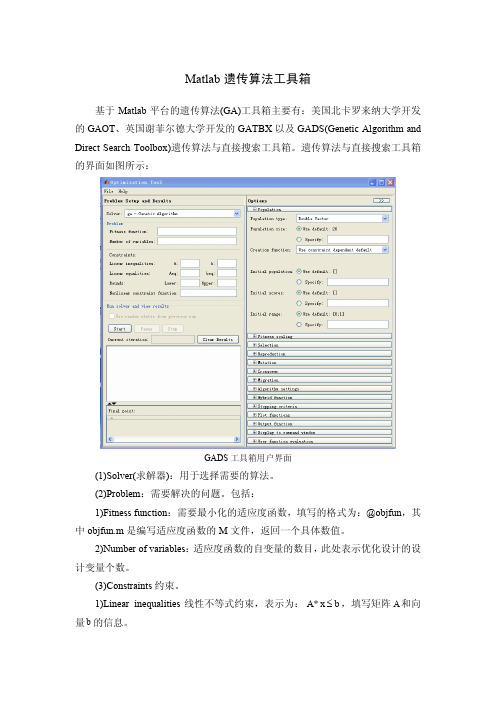
GADS 工具箱用户界面
(1)Solver(求解器):用于选择需要的算法。 (2)Problem:需要解决的问题。包括: 1)Fitness function:需要最小化的适应度函数,填写的格式为:@objfun,其 中 objfun.m 是编写适应度函数的 M 文件,返回一个具体数值。 2)Number of variables: 适应度函数的自变量的数目, 此处表示优化设计的设 计变量个数。 (3)Constraints 约束。 1)Linear inequalities 线性不等式约束,表示为: A * x b ,填写矩阵 A 和向 量 b 的信息。
2)Linear equalities 线性等式约束,表示为: Aeq * x beq ,填写矩阵 Aeq 和 向量 beq 的信息。 3)Bounds:填写独立变量的取值范围。在 Lower 中填写变量的取值下界, Upper 中填写变量的取值上界,均以向量形式表示。 4)Nonlinear constraint function 非线性约束函数,编写非线性约束函数的 M 文件 nonlcon.m,则在此处填写@nonlcon。 (4)Run solver and view results 运行求解器并观察结果。点击 Start 即 可开始运行。Current iteration 中将显示当前运行的代数。Final point 栏中 显示最优解对应的变量的取值。 (5)Option 部分是遗传算法参数的设定。 1)Population 种群参数设定。 Population type 种群类型,设定适应度函数的输入数据类型。工具箱提供了 两种输入类型:双精度、串位,用户还可以编写 M 文件自定义输入数据的类型。 Population size 种群规模,定义每一代种群的个体数量。种群规模越大,遗 传算法的运行速度越慢。 Creation function 创建函数,用于创建初始种群。 Initial population 初始种群,如果不指定初始种群,则系统将运用创建函数 创建初始种群。 Initial scores 初始得分,如果此处没有定义初始得分,则系统应用适应度函 数来计算初始得分。 Initial range 初始范围,用于指定初始种群中的各变量的上下限。初始范围 用一个矩阵表示,该矩阵行数为 2,列数为变量的个数。其中第一行描述初始种 群中变量的取值下限,第二行描述初始种群中变量的取值上限。 2)Fitness scaling 适应度测量,包括:Rank 排序尺度变换、Proportional 比例 尺度变换、Top 顶级尺度变换、Shift linear 线性转换尺度变换以及 Custom 用户 自定义。 3)Selection 选择,工具箱提供了以下几种选择函数:Stochastic uniform 随机 Remainder 剩余、 Uniform 均匀分布、 Roulette 轮盘赌选择、 Tournament 均匀分布、 锦标赛选项、Custom 用户自定义。 4)Reproduction 再生参数,需设定可生存到下一代的精英个数 Elite count, 以及下一代由交叉产生的部分所占比例 Crossover fraction。
matlab遗传算法实例

matlab遗传算法实例以MATLAB遗传算法实例为题,我们将介绍遗传算法的基本概念和在MATLAB中的实现方法。
遗传算法是一种基于进化思想的优化算法,通常用于求解最优化问题。
遗传算法的基本思想是通过模拟自然选择和遗传机制来搜索最优解。
它模拟了生物进化过程中的遗传、交叉和变异等过程,通过不断进化产生更好的解。
遗传算法包括三个基本操作:选择、交叉和变异。
选择操作根据个体适应度选择优秀个体,交叉操作通过交换基因信息产生新个体,变异操作在个体基因中引入随机扰动。
在MATLAB中,我们可以使用遗传算法工具箱来实现遗传算法。
首先,我们需要定义问题的目标函数和约束条件。
目标函数是我们要最小化或最大化的函数,约束条件是问题的限制条件。
然后,我们需要设置遗传算法的参数,包括种群大小、迭代次数、交叉概率和变异概率等。
接下来,我们可以使用遗传算法工具箱提供的函数来运行遗传算法,并获取最优解。
下面我们以一个简单的函数优化问题为例来演示如何使用MATLAB中的遗传算法工具箱。
假设我们要求解以下函数的最小值:f(x) = x^2 - 4x + 4我们需要定义目标函数和约束条件。
在MATLAB中,我们可以使用函数句柄来表示目标函数和约束条件。
对于上述函数,我们可以定义目标函数如下:objFunc = @(x) x^2 - 4*x + 4接下来,我们需要设置遗传算法的参数。
假设我们使用了50个个体,迭代100次,交叉概率为0.8,变异概率为0.1,可以使用以下代码设置参数:options = gaoptimset('PopulationSize', 50, 'Generations', 100, 'CrossoverFraction', 0.8, 'MutationFcn', {@mutationadaptfeasible, 0.1})我们可以使用MATLAB提供的遗传算法函数ga来运行遗传算法,并获取最优解。
遗传算法用matlab求函数极大值

遗传算法用matlab求函数极大值一、题目:寻找f(x)=x2,,当x在0~31区间的最大值。
二、源程序:%遗传算法求解函数最大值%本程序用到了英国谢菲尔德大学(Sheffield)开发的工具箱GATBX,该工具箱比matlab自带的GATOOL使用更加灵活,但在编写程序方面稍微复杂一些Close all;Clear all;figure(1);fplot('variable*variable',[0,31]); %画出函数曲线%以下定义遗传算法参数GTSM=40; %定义个体数目ZDYCDS=20; %定义最大遗传代数EJZWS=5; %定义变量的二进制位数DG=0.9; %定义代沟trace=zeros(2, ZDYCDS); %最优结果的初始值FieldD=[5;-1;2;1;0;1;1]; %定义区域描述器的各个参数%以下为遗传算法基本操作部分,包括创建初始种群、复制、交叉和变异Chrom=crtbp(GTSM, EJZWS); %创建初始种群,即生成给定规模的二进制种群和结构gen=0; %定义代数计数器初始值variable=bs2rv(Chrom, FieldD); %对生成的初始种群进行十进制转换ObjV=variable*variable; %计算目标函数值f(x)=x2 while gen<ZDYCDS %进行循环控制,当当前代数小于定义的最大遗传代数时,继续循环,直至代数等于最大遗传代数FitnV=ranking(-ObjV); %分配适应度值SelCh=select('sus', Chrom, FitnV, DG); %选择,即对个体按照他们的适配值进行复制SelCh=recombin('xovsp', SelCh, 0.7); %交叉,即首先将复制产生的匹配池中的成员随机两两匹配,再进行交叉繁殖SelCh=mut(SelCh); %变异,以一个很小的概率随机地改变一个个体串位的值variable=bs2rv(SelCh, FieldD); %子代个体的十进制转换ObjVSel=variable*variable; %计算子代的目标函数值[Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel);%再插入子代的新种群,其中Chrom为包含当前种群个体的矩阵,SelCh为包好当前种群后代的矩阵variable=bs2rv(Chrom, FieldD); %十进制转换gen=gen+1; %代数计数器增加%输出最优解及其序号,并在目标函数图像中标出,Y为最优解, I为种群的%序号[Y, I]=max(ObjV);hold on; %求出其最大目标函数值plot(variable(I), Y, 'bo');trace(1, gen)=max(ObjV); %遗传算法性能跟踪trace(2, gen)=sum(ObjV)/length(ObjV);end%以下为结果显示部分,通过上面计算出的数值进行绘图variable=bs2rv(Chrom, FieldD); %最优个体进行十进制转换hold on, grid;plot(variable,ObjV,'b*'); %将结果画出三、运行结果:由图可见该函数为单调递增函数,即当X=31时,该取得最大值f(x)max =961。
