MATLAB遗传算法工具箱及其应用

合集下载

MATLAB遗传算法工具箱在函数优化中的应用

[x, fval] = ga(fun, 1,,,,,,,, options);
%输出结果
disp(['x = ', num2str(x)]);
disp(['f(x) = ', num2str(fval)]);
在上述代码中，我们首先定义了目标函数，然后设置了遗传算法的参数，包括种群规模、最大迭代次数、交叉概率和变异概率。接下来，我们使用 optimoptions函数初始化遗传算法，并传入目标函数和参数设置。最后，我们使用ga函数求解最小值点，并输出结果。
在使用遗传算法工具箱进行函数优化时，需要注意以下问题：
1、适应度函数的设计：适应度函数是评价个体优劣程度的指标，必须合理设计以满足优化问题的需求。
2、种群规模和迭代次数的设定：种群规模和迭代次数是影响遗传算法性能的关键参数，需要根据问题规模和复杂度进行合理设定。
3、交叉和变异操作的控制：交叉和变异操作是遗传算法的核心操作，需要合理控制以保持算法的搜索能力和避免陷入局部最优解。
在定义了目标函数和约束条件之后，我们可以使用Matlab提供的ga函数来运行遗传算法。ga函数将根据指定的目标函数和约束条件，使用遗传算法搜索最优解。在运行过程中，我们可以使用Matlab提供的动画功能来实时查看遗传算法的迭代过程。
除了使用Matlab遗传算法优化工具箱来解决常规的优化问题外，还可以将其应用于其他领域。例如，在机器学习领域中，可以使用遗传算法来优化神经网络的连接权值和结构；在控制系统领域中，可以使用遗传算法优化控制系统的参数和结构；在图像处理领域中，可以使用遗传算法优化图像处理的算法和参数等。
通过本次演示的介绍，希望能使读者更好地理解和应用遗传算法工具箱解决实际优化问题。

MATLAB遗传算法工具箱及应用(第二版)图文 (1)

一旦计算了个体适应度值，种群中适应度高的个体将被选中并重组，产生下一代。遗传算子直接操作染色体的特征 (基因)，使用一般情况下个体的基因代码，产生更适合的个体。重组算子用在一对个体或一大组个体中交换基因信息。最简单的重组算子是单点交叉。
第一章遗传算法概述
考虑两个二进制父代串：
A=10010110 和 B=10111000 I是随机地在1到串长L减1之间（即［1，
在决策变量域中的染色体表现型已被编码，可以估计种群的个体成员的特性或适应度。通过特征目标函数来估计个体在问题域中的特性。在自然世界中，这就是个体在现行环境中的生存能力。因此，目标函数建立的基础是在整个繁殖过程中选择成对的个体进行交配。
第一章遗传算法概述
在再生(复制)期间，每个个体均被计算适应度值，它来自没有加工的原始特性度量，由目标函数给出。这个值用来在选择中偏向更加适合的个体。相对整个种群，适应度高的个体具有高的选中参加交配的概率，而适应度低的个体具有相对低的选中概率。
第一章遗传算法概述
1.2 遗传算法的特点
遗传算法具有如下优点：（1)对可行解表示的广泛性。遗传算法的处理对象不是参数本身，而是针对那些通过参数集进行编码得到的基因个体。此编码操作使得遗传算法可以直接对结构对象进行操作。所谓结构对象，泛指集合、序列、矩阵、树、图、链和表等各种一维或二维甚至多维结构形式的对象。这一特点使得遗传算法具有广泛的应用领域。比如： ①通过对连接矩阵的操作，遗传算法可用来对神经网络或自动机的结构或参数加以优化。 ②通过对集合的操作，遗传算法可实现对规则集合和知识库的精炼而达到高质量的机器学习目的。 ③通过对树结构的操作，用遗传算法可得到用于分类的最佳决策树。 ④通过对任务序列的操作，遗传算法可用于任务规划，而通过对操作序列的处理，可自动构造顺序控制系统。

使用MATLAB遗传算法工具实例详细

最新发布的MATLAB 7.0 Release 14已经包含了一个专门设计的遗传算法与直接搜索工具箱（Genetic Algorithm and Direct Search Toolbox，GADS）。

使用遗传算法与直接搜索工具箱，可以扩展MATLAB及其优化工具箱在处理优化问题方面的能力，可以处理传统的优化技术难以解决的问题，包括那些难以定义或不便于数学建模的问题，可以解决目标函数较复杂的问题，比如目标函数不连续、或具有高度非线性、随机性以及目标函数没有导数的情况。

本章8.1节首先介绍这个遗传算法与直接搜索工具箱，其余各节分别介绍该工具箱中的遗传算法工具及其使用方法。

8.1 遗传算法与直接搜索工具箱概述本节介绍MATLAB的GADS（遗传算法与直接搜索）工具箱的特点、图形用户界面及运行要求，解释如何编写待优化函数的M文件，且通过举例加以阐明。

8.1.1 工具箱的特点GADS工具箱是一系列函数的集合，它们扩展了优化工具箱和MATLAB数值计算环境的性能。

遗传算法与直接搜索工具箱包含了要使用遗传算法和直接搜索算法来求解优化问题的一些例程。

这些算法使我们能够求解那些标准优化工具箱范围之外的各种优化问题。

所有工具箱函数都是MATLAB的M文件，这些文件由实现特定优化算法的MATLAB语句所写成。

使用语句type function_name就可以看到这些函数的MATLAB代码。

我们也可以通过编写自己的M文件来实现来扩展遗传算法和直接搜索工具箱的性能，也可以将该工具箱与MATLAB的其他工具箱或Simulink结合使用，来求解优化问题。

工具箱函数可以通过图形界面或MATLAB命令行来访问，它们是用MATLAB语言编写的，对用户开放，因此可以查看算法、修改源代码或生成用户函数。

遗传算法与直接搜索工具箱可以帮助我们求解那些不易用传统方法解决的问题，譬如表查找问题等。

遗传算法与直接搜索工具箱有一个精心设计的图形用户界面，可以帮助我们直观、方便、快速地求解最优化问题。

Matlab遗传算法优化工具箱GAOT的研究与应用

M a tl ab遗传算法优化工具箱(GAO T)的研究与应用3周正武1,丁同梅1,2,田毅红2,3,王晓峰2,4(1.广东省技师学院,广东博罗　516100; 2.天津大学机械工程学院,天津　300072;3.承德技师学院,河北承德　067400;4.郑州职业技术学院,河南郑州　450121)摘　要:介绍遗传算法的基本原理和Matlab的遗传算法优化工具箱(G AOT),分析了优化工具函数。

探讨Matlab遗传算法工具箱在参数优化和非线性规划中的应用。

通过优化实例,说明遗传算法是一种具有良好的全局寻优性能的优化方法。

用Matlab语言及Matlab语言编制的优化工具箱进行优化设计具有语言简单、函数丰富、用法比较灵活、编程效率高等特点。

关键词:遗传算法;Matlab工具箱;优化中图分类号:T H164 文献标识码:A 文章编号:1007-4414(2006)06-0069-03The study and appli ca ti on of geneti c a lgor ith m opti m i za ti on toolbox i n M a tl abZhou Zheng-wu1,D ing T ong-mei1,2,Tian Yi-hong2,3,W ang Xiao-feng2,4(1.College of high-grade technician,B oluo Guangdong　516100,China;2.College of m echanical and engineering,Tianjin university,Tianjin　300072,China;3.Chengde college of high-grade technician,Chengde Hebei　067400,China;4.Zhengzhou vocational college of technology,Zhengzhou Henan　450121,China)Abstract:The paper intr oduces genetic algorith m(G A)and Matlab genetic algorith m op ti m izati on t oolbox and analyses the op ti m izati on t oolbox functi on.The functi on op ti m izati on p r oble m of para meter op ti m izati on and nonlinear has been given t o de monstrate that genetic algorith m is a better gl obal op ti m izati on method.The op ti m izati on design in M atlab and Matlab op ti m i2 zati on t oolbox have si m p le language、abundant functi ons、flexible method and high p r ogramm ing efficiency.Key words:genetic agolrith m;matlab t oolbox;op ti m izati on 遗传算法(G A)是一类借鉴生物界自然选择和遗传原理的随机优化搜索算法。

matlab工具箱遗传算法使用方法

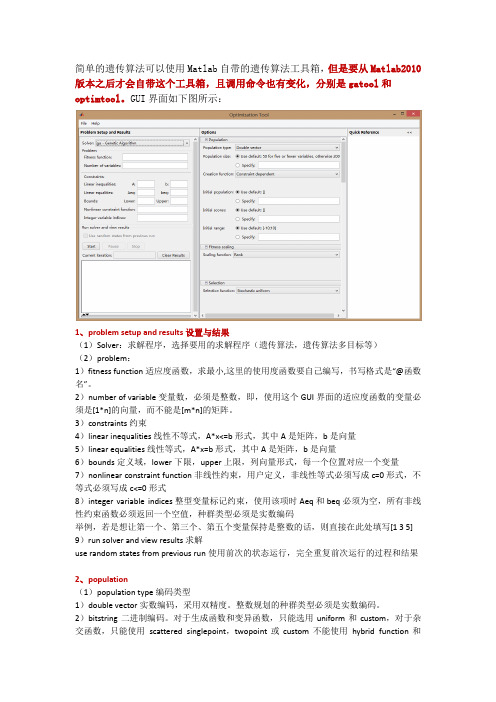
简单的遗传算法可以使用Matlab自带的遗传算法工具箱，但是要从Matlab2010版本之后才会自带这个工具箱，且调用命令也有变化，分别是gatool和optimtool。

GUI界面如下图所示：1、problem setup and results设置与结果（1）Solver：求解程序，选择要用的求解程序（遗传算法，遗传算法多目标等）（2）problem：1）fitness function适应度函数，求最小,这里的使用度函数要自己编写，书写格式是“@函数名”。

2）number of variable变量数，必须是整数，即，使用这个GUI界面的适应度函数的变量必须是[1*n]的向量，而不能是[m*n]的矩阵。

3）constraints约束4）linear inequalities线性不等式，A*x<=b形式，其中A是矩阵，b是向量5）linear equalities线性等式，A*x=b形式，其中A是矩阵，b是向量6）bounds定义域，lower下限，upper上限，列向量形式，每一个位置对应一个变量7）nonlinear constraint function非线性约束，用户定义，非线性等式必须写成c=0形式，不等式必须写成c<=0形式8）integer variable indices整型变量标记约束，使用该项时Aeq和beq必须为空，所有非线性约束函数必须返回一个空值，种群类型必须是实数编码举例，若是想让第一个、第三个、第五个变量保持是整数的话，则直接在此处填写[1 3 5] 9）run solver and view results求解use random states from previous run使用前次的状态运行，完全重复前次运行的过程和结果2、population（1）population type编码类型1）double vector实数编码，采用双精度。

整数规划的种群类型必须是实数编码。

Matlab遗传算法工具箱函数及应用实例

!"#$"%遗传算法工具箱函数及应用实例于玲!!贾春强""!#沈阳化工学院机械工程学院!辽宁沈阳!!$!%"#"&大连理工大学机械工程学院!辽宁大连!!’$"($摘要%基于!"#$"%语言的遗传算法工具箱支持二进制和浮点数编码方式!并且提供了多种选择&交叉&变异的方法’通过具体实例对!"#$"%的遗传算法工具箱的用法进行了说明介绍(关键词%)*+,*-#遗传算法#工具箱#优化中图分类号%./(0!&12文献标识码%3文章编号%!$$"4"(((""$$%)!!4$$"14$"&’()#*+(,"(-./"01$2,*(!"#$"%345++$%+/678*(9:!;<4=>’(?@*"(9A5!#67899,9:);78*<=7*,><?=<;;@=<?A68;<B*<?C<D+=+E+;9:F8;G=7*,.;78<9,9?BH68;<B*<?!!I!%"H F8=<*J"#67899,9:);78*<=7*,><?=<;;@=<?H K*,=*<L<=M;@D=+B9:.;78<9,9?BH K*,=*<!!’I"(H F8=<*N 4%,#B")#C.8;O;<;+=73,?9@=+8G.99,-9P-*D;Q9<)*+,*-DERR9@+D+8;-=<*@B*<Q:,9*+H*<Q+8;@;*@;+8;;P7;,,;<+ 9R;@*+9@D9:D;,;7+=9<H7@9DD9M;@*<Q GE+*+=9<=<+8;.99,-9PH+S9;P*GR,;D*-9E+89S+9ED;+8;.99,-9P*@;=<+@9QE7;Q =<+8=D R*R;@#C+=D+98;,R@;*Q;@D=GR@9M;+8;*-=,=+B+9*<*,BT;+8;UE;D+=9<*<Q D9,M;R@9-,;G ED=<?+8;.99,-9P# D2E F+B-,C G*+,*-J?;<;+=7*,?9@=+8GJ+99,-9PJ9R+=G=T*+=9<:遗传算法与!"#$"%语言!"#$"%是一种开放式软件!经过一定的程序可以将开发的优秀的应用程序集加入到!"#$"%工具的行列(这样!许多领域前沿的研究者和科学家都可以将自己的成果集成到!"#$"%之中!被全人类继承和利用(因此!!"#$"%中含有诸多的面向不同应用领域的工具箱!例如%信号处理工具箱&图像处理工具箱&通信工具箱&系统辨识工具箱&优化工具箱&鲁棒控制工具箱&非线性控制工具箱等!而且工具箱还在不断地扩展之中(A遗传算法工具箱的函数及其功能目前!国内图书市场上有关!"#$"%方面的书籍要么侧重于!"#$"%语言编程介绍!要么侧重于各种工具箱函数的解说!而对怎样用工具箱函数来解决实际问题鲜有涉及(本文将对遗传算法工具箱函数进行说明介绍(遗传算法工具箱&’()包括了许多实用的函数!这些函数按照功能可以分为以下几类%!"#主界面函数主程序*"+,提供了遗传算法工具箱与外部的接口(它的函数格式如下%-./012345/%345/#6"708194:;*"<%4=12>!0?"$@A!0?"$(5>!>#"6#345!45#>!#06,@A!#06,(5>!>0$07#@A!>0$07#(5>!.(?06@A>!.(?06(5>!,=#@A>!,=#(5>B输出参数输入参数!"!核心函数及其它函数具体见表C(G遗传算法工具箱应用实例$%&无约束优化问题利用遗传算法计算函数’<(B;(DEF*>G1<H(BDI*74><J(B/的最大值!其中(!-F!K:选择二进制编码!种群中的个体数目为EF!二进制编. 012345 %345#6"708194求得的最优解!包括染色体和适配度最终得到的种群最优种群的搜索轨迹每一代的最好适应度和平均适应度%4=12>0?"$@A0?"$(5>>#"6#34545#>#06,@A#06,(5>>0$07#@A>0$07#(5>.(?06@A.(?06(5>,=#@A,=#(5>变量上下界矩阵!矩阵的行数确定变量个数适应度函数传递给适应度函数的参数!默认值为+ALMM,初始种群选项(一个向量+05>G$41/564%N45>/2G>5$"O,!这里05>G$41表示两代之间的差距#564%N45>取F表示二进制编码!取E表示浮点数编码#2G>5$"O控制运行中是否输出当前群体和最好结果!取F表示运行中不输出!取E表示运行中输出(默认值为+E0P Q/E/F,终止函数的名称!默认值为+R,".&01)06,R,传递给终止函数的参数!默认值为+REFFR,选择函数的名称!默认值为+R146,&04,S0$07#R,传递给选择函数的参数!默认值为+RF+FTR,交叉函数名称表!以空格分开!浮点数编码默认值为+R/"6G#UV4?06/U0=6G>#G7V4?06/>G,5$0V4?06R,!二进制编码默认值为+R>G,5$0V4?06R,传递给交叉函数的参数表!浮点数编码默认值为+RW/F#W/C#W/FR,!二进制编码默认值为+F+Q,变异函数名称表!以空格分开!浮点数编码默认值为+R%4=12"6O!=#"#G41/,=$#GA41L1G9!=#"#G41141/L1G9!=#"#G41=P1G9!=#"#G41R,!二进制编码默认值为+R%G1"6O!=#"#G41R,传递给变异函数的参数表!浮点数编码默认值为+J/F#Q/EFF/C#J/EFF/C#J/F/F,!二进制编码默认值为+F+FH,表:表A码长度为!"!交叉概率为"#$%!变异概率为"#"&"采用’()*的程序清单如下#+编写目标函数文件,-.#/!文件存放在工作目录下"0123.4,256,7!89:7;<,-.=6,7!,-.4,26>?@<6,7=A>$89:7<@BA"C642=%C@>BDC 3,6=EC @>$F 生成初始种群!大小为A"?"424.G,-<424.4:74H8I:=A"!5"?$;!J,-.K>$L 调用遗传算法函数"5@?82MG ,-?NG ,-O.P:38;<I :=5"?$;!K,-.K !5;!424.G ,-!5A8Q R?A?A;!K/:@’82*8P/K !!%!K2,P/’8,/S 8783.K !5"#"&;!5K:P4.TU,98PK;!5!;!K2,2V240W1.:.4,2K !5!?!%?X;>?$经过!%次遗传迭代!运算结果为#!<D#&%RR "=!><!E#&%%E $即当!为D#&%RR 时!"=!>取最大值!E#&%%E "遗传算法一般用来取得近似最优解!另外!遗传算法的收敛性跟其初始值有关!大家运行上面的命令所得到的结果可能跟我的结果不同或是差别很大!但多执行几次上面的命令%随机取不同的初始群体&一定可以得到近似最优解"#$%有约束优化问题考虑如下问题#/42"=!><=!A Q !>!B=!!Q A>!6#.#&A =!><!A Q !!!BA !"&!=!><!!A EQ !!!BA !"本例中存在两个不等式约束!因此我们需要把有约束问题转换成无约束问题来求解"近年来提出了多种用遗传算法满足约束的技术!工程中常用的策略是惩罚策略!通过惩罚不可行解!将约束问题转换为无约束问题"惩罚项的适值函数一般有加法和乘法两种构造方式!本例采用加法形式的适值函数!惩罚函数由两部分构成!可变乘法因子和违反约束乘法"种群中的个体数目为A""!实数编码!交叉概率为"#$%!变异概率为"#"&"遗传算法求的是函数的极大值!因此在求极小值问题时!需将极大值问题转换为极小值问题求解"采用’()*的程序清单如下#Y 编写目标函数文件04.#/!文件存放在工作目录下"0123.4,256,7!89:7;<04.=6,7!,-.4,26>?@A<6,7=A>$@!<6,7=!>$PA<"#A $P!<"#&$Z 约束条件IA<@AQ !C @!BA $I!<@A#[!\EQ @!#[!BA $Z 加惩罚项的适值40?=IA]<">^=I!]<">89:7<=@AQ !>#[!B=@!Q A>#[!$876889:7<=@AQ !>#[!B=@!Q A>#[!BPAC I ABP!CI!$89:7<Q 89:7$82M_设置参数边界!本例边界为!O "N,12M6<,286%!!A &C5Q A !A;$‘调用遗传算法函数"5@O82MG,-ONG,-O.P:38;<I:=N,12M6!KW42K>O $a 性能跟踪"-7,.=.P:38=b !A>!.P:38=b !X>!KPQ K>$T,7MO,2-7,.=.P:38=b !A>!.P:38=b !!>!KNC K>$@7:N87=K’828P:.4,2K>cOd7:N87=Ke4..2866K>$f8I82M=K 解的变化K !K 种群平均值的变化K>$经过A""次遗传迭代!运算结果为#!<O5AOA;$此时极小值89:7=!><A $I A =!><"$I !!!><"#!%!显然最优解满足约束条件"!结论遗传算法工具箱功能强大!包括了大量的算子函数!提供各种类型的选择策略!交叉’变异的方式!适用于各类不同的实际问题"由于大多数实际问题都是有约束条件的!所以!用遗传算法处理约束条件的方法仍属于难点问题!需要进一步的研究和探讨"(参考文献)(")高尚#基于$%&’%(遗传算法优化工具箱的优化计算())*微型电脑应用!+,,+!"-.-/#0+102*(+)姜阳!孔峰*基于$%&’%(遗传算法工具箱的控制系统设计仿真())*广西工学院学报!+,,"!"+.23#41-*(5)飞思科技产品研发中心*$%&’%(4*0辅助优化计算与设计($)*北京#电子工业出版社!+,,5*%编辑阳光&作者简介#于玲%A$D$Q &!女!硕士!主要从事机电液一体化的教学及科研工作"收稿日期#!""EQ "DQ "R!!!!!!!!!!初始化函数424.4:74H8,I :#/P,178..8#/2,P/’8,/S 8783.#/.,1P2S 8783.#/64/-78U,98P#/3d3743U,98P#/7428PU,98P#/7428P,PM8PU,98P#/N,12M:PdW1.:.4,2#/2,2V240W1.:.4,2#//:@’82*8P/#/,-.W:@’82*8P/#/0!N#/N!0#/变异交叉二进制格式和浮点数格式的初始化函数有序数据的初始化函数常用的轮盘赌法基于归一化的优先选择法竞争选择法二进制格式或浮点数格式的交叉函数有序数据的交叉函数!可以将演化函数组合使用浮点数格式的变异函数主程序I :#/用来判断是否满足终止条件用来计算遗传算法满足精度要求时!染色体所需要的二进制位数用来完成二进制数和浮点数之间的相互转换选择函数终止函数二进制表示函数演化函数3:73N4.6#/424.4:74H8I :#/表"。

matlab遗传算法工具箱关于离散变量优化算例

1. 引言遗传算法是一种模拟自然选择与遗传机制的优化算法，被广泛应用于离散变量优化问题的求解。

在Matlab软件中，有专门的工具箱可以支持遗传算法的实现与应用，极大地方便了工程技术人员进行离散变量优化问题的研究与应用。

本文将介绍Matlab遗传算法工具箱在离散变量优化算例中的应用，并通过具体案例来展示其实际求解效果。

2. Matlab遗传算法工具箱介绍Matlab遗传算法工具箱是Matlab软件的一个重要工具箱，它提供了丰富的遗传算法函数和工具，方便用户进行遗传算法的实现和应用。

在离散变量优化问题的求解中，用户可以利用工具箱提供的函数对问题进行建模、参数设置、运行算法等操作，从而快速高效地求解问题。

3. 离散变量优化算例为了更好地展示Matlab遗传算法工具箱在离散变量优化中的应用效果，我们选取了一个经典的离散变量优化问题作为算例，具体问题描述如下：设有一组零件需要进行装配，零件的形状和尺寸有多种选择。

每种零件的装配工艺和成本不同，需要选择最佳的零件组合方案来满足装配要求并使总成本最低。

假设可供选择的零件种类有n种，每种零件有m个备选方案，且装配每种零件的成本已知。

问应选择哪些零件及其具体方案才能使得总装配成本最低？4. Matlab遗传算法工具箱的应用为了利用Matlab遗传算法工具箱求解上述离散变量优化问题，我们可以按照以下步骤进行操作：1) 利用Matlab的数据处理工具，将零件的备选方案数据以矩阵的形式导入Matlab环境；2) 利用工具箱提供的函数对遗传算法的参数进行设置，例如选择交叉方式、变异方式、群体大小、迭代次数等；3) 利用工具箱提供的函数对离散变量优化问题进行编码和解码，以便算法能够对离散变量进行操作；4) 利用工具箱提供的函数编写适应度函数，用于评价每个个体的适应度；5) 利用工具箱提供的主函数运行遗传算法，获取最优解及其对应的总装配成本。

5. 案例求解结果分析通过上述步骤，我们在Matlab环境中成功应用遗传算法工具箱求解了离散变量优化问题。

使用MATLAB遗传算法工具实例

使用MATLAB遗传算法工具实例MATLAB中提供了一种用于优化问题的遗传算法工具箱，可以帮助用户通过遗传算法来寻找最优解。

下面是一个示例，展示了如何使用MATLAB遗传算法工具箱解决一个简单的优化问题。

假设我们要求解以下函数的最大值：f(x)=x^2，其中x的取值范围在[-10,10]之间。

首先，我们需要定义适应度函数，即用来评估个体适应度的函数。

在本例中，适应度函数可以直接使用目标函数，即f(x)=x^2、在MATLAB中，我们可以使用函数句柄来定义适应度函数：```matlabfunction fitness = fitnessFunction(x)fitness = x^2;end```接下来，我们需要配置遗传算法的参数。

我们可以使用`gaoptimset`函数来创建一个参数结构体，并设置算法的各个参数：```matlaboptions = gaoptimset('PopulationSize', 50, 'Generations', 100, 'FitnessLimit', 1e-6, 'StallGenLimit', 10);```上述代码将设置种群大小为50，迭代次数为100，适应度极限为1e-6（即当适应度较小时停止迭代），最大迭代代数为10（即如果连续10代迭代没有改进，则停止迭代）。

接下来，我们需要调用`ga`函数来运行遗传算法并求解最优解。

我们可以使用以下代码来实现：```matlab```最后，我们可以打印出最优解及其目标函数值：```matlabdisp(['Optimal solution: x = ' num2str(x) ', f(x) = 'num2str(fval)]);```上述代码中，`num2str`函数用于将数字转换为字符串，然后使用`disp`函数打印出最优解和目标函数值。

基于Matlab遗传算法工具箱的优化计算实现

基于Matlab遗传算法工具箱的优化计算实现一、概述随着科技的发展和社会的进步，优化问题在众多领域，如工程设计、经济管理、生物科学、交通运输等中扮演着越来越重要的角色。

优化计算的目标是在给定的约束条件下，寻找一组变量，使得某个或某些目标函数达到最优。

许多优化问题具有高度的复杂性，传统的数学方法往往难以有效求解。

寻求新的、高效的优化算法成为了科研人员的重要任务。

遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传学机制的搜索算法，通过模拟自然界的进化过程，寻找问题的最优解。

自20世纪70年代初由美国密歇根大学的John Holland教授提出以来，遗传算法因其全局搜索能力强、鲁棒性好、易于与其他算法结合等优点，被广泛应用于各种优化问题中。

1. 遗传算法简介遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传学机制的优化搜索算法。

该算法起源于对生物进化过程中遗传机制的研究，通过模拟自然选择和遗传过程中的交叉、突变等操作，在搜索空间内寻找最优解。

自20世纪70年代初由John Holland教授提出以来，遗传算法已在多个领域取得了广泛的应用，包括函数优化、机器学习、模式识别、自适应控制等。

遗传算法的基本思想是将问题的解表示为“染色体”，这些染色体在算法中通过选择、交叉和突变等操作进行演化。

选择操作模仿了自然选择中“适者生存”的原则，根据适应度函数对染色体进行筛选交叉操作则模拟了生物进化中的基因重组过程，通过交换染色体中的部分基因，生成新的个体突变操作则是对染色体中的基因进行小概率的随机改变，以维持种群的多样性。

在遗传算法中，种群初始化是算法的起点，通过随机生成一组初始解作为初始种群。

根据适应度函数对种群中的个体进行评估，选择出适应度较高的个体进行交叉和突变操作，生成新的种群。

这个过程不断迭代进行，直到满足终止条件（如达到最大迭代次数或找到满足精度要求的最优解）为止。

遗传算法在matlab中的实现

遗传算法是一种模拟自然选择与遗传机制的优化算法，它模拟了生物进化的过程，通过优化个体的基因型来达到解决问题的目的。

在工程和科学领域，遗传算法被广泛应用于求解优化问题、寻找最优解、参数优化等领域。

而MATLAB作为一款强大的科学计算软件，拥有丰富的工具箱和编程接口，为实现遗传算法提供了便利。

下面将通过以下步骤介绍如何在MATLAB中实现遗传算法：1. 引入遗传算法工具箱需要在MATLAB环境中引入遗传算法工具箱。

在MATLAB命令窗口输入"ver"，可以查看当前已安装的工具箱。

如果遗传算法工具箱未安装，可以使用MATLAB提供的工具箱管理界面进行安装。

2. 定义优化问题在实现遗传算法前，需要清楚地定义优化问题：包括问题的目标函数、约束条件等。

在MATLAB中，可以通过定义一个函数来表示目标函数，并且可以采用匿名函数的形式来灵活定义。

对于约束条件，也需要进行明确定义，以便在遗传算法中进行约束处理。

3. 设置遗传算法参数在实现遗传算法时，需要对遗传算法的参数进行设置，包括种群大小、交叉概率、变异概率、迭代次数等。

这些参数的设置将会直接影响遗传算法的收敛速度和优化效果。

在MATLAB中，可以通过设置遗传算法工具箱中的相关函数来完成参数的设置。

4. 编写遗传算法主程序编写遗传算法的主程序，主要包括对适应度函数的计算、选择、交叉、变异等操作。

在MATLAB中，可以利用遗传算法工具箱提供的相关函数来实现这些操作，简化了遗传算法的实现过程。

5. 运行遗传算法将编写好的遗传算法主程序在MATLAB环境中运行，并观察优化结果。

在运行过程中，可以对结果进行实时监测和分析，以便对遗传算法的参数进行调整和优化。

通过以上步骤，可以在MATLAB中实现遗传算法，并应用于实际的优化问题与工程应用中。

遗传算法的实现将大大提高问题的求解效率与精度，为工程领域带来更多的便利与可能性。

总结：遗传算法在MATLAB中的实现涉及到了引入遗传算法工具箱、定义优化问题、设置算法参数、编写主程序和运行算法等步骤。

使用MATLAB遗传算法工具实例(详细)

使用MATLAB遗传算法工具实例(详细)最新发布的MATLAB Release 14已经包含了一个专门设计的遗传算法与直接搜索工具箱（Genetic Algorithm and Direct Search Toolbox，GADS）。

本章节首先介绍这个遗传算法与直接搜索工具箱，其余各节分别介绍该工具箱中的遗传算法工具及其使用方法。

遗传算法与直接搜索工具箱概述本节介绍MATLAB的GADS（遗传算法与直接搜索）工具箱的特点、图形用户界面及运行要求，解释如何编写待优化函数的M文件，且通过举例加以阐明。

8.1.1 工具箱的特点GADS工具箱是一系列函数的集合，它们扩展了优化工具箱和MATLAB数值计算环境的性能。

遗传算法与直接搜索工具箱包含了要使用遗传算法和直接搜索算法来求解优化问题的一些例程。

这些算法使我们能够求解那些标准优化工具箱范围之外的各种优化问题。

所有工具箱函数都是MATLAB的M文件，这些文件由实现特定优化算法的MATLAB语句所写成。

使用语句type function_name就可以看到这些函数的MATLAB代码。

工具箱函数可以通过图形界面或MATLAB命令行来访问，它们是用MATLAB语言编写的，对用户开放，因此可以查看算法、修改源代码或生成用户函数。

遗传算法与直接搜索工具箱可以帮助我们求解那些不易用传统方法解决的问题，譬如表查找问题等。

遗传算法与直接搜索工具箱有一个精心设计的图形用户界面，可以帮助我们直观、方便、快速地求解最优化问题。

【Matlab】自带遗传算法工具箱的介绍和使用注意事项

【Matlab】自带遗传算法工具箱的介绍和使用注意事项简单的遗传算法可以使用Matlab自带的遗传算法工具箱，但是要从Matlab2010版本之后才会自带这个工具箱，且调用命令也有变化，分别是gatool和optimtool。

GUI界面如下图所示：GUI界面使用注意事项：这里直接按从上到下，从左到右的顺序对Matlab自带的遗传算法工具箱的GUI界面进行介绍和使用注意事项的一些说明（宅主使用的是Matlab2013a，调用命令是optimtool）：1、problem setup and results设置与结果（1）Solver：求解程序，选择要用的求解程序（遗传算法，遗传算法多目标等）（2）problem：1）fitness function适应度函数，求最小,这里的使用度函数要自己编写，书写格式是“@函数名”。

2）number of variable变量数，必须是整数，即，使用这个GUI 界面的适应度函数的变量必须是[1*n]的向量，而不能是[m*n]的矩阵。

3）constraints约束4）linear inequalities线性不等式，A*x<=b形式，其中A是矩阵，b是向量5）linear equalities线性等式，A*x=b形式，其中A是矩阵，b 是向量6）bounds定义域，lower下限，upper上限，列向量形式，每一个位置对应一个变量7）nonlinear constraint function非线性约束，用户定义，非线性等式必须写成c=0形式，不等式必须写成c<=0形式8）integer variable indices整型变量标记约束，使用该项时Aeq 和beq必须为空，所有非线性约束函数必须返回一个空值，种群类型必须是实数编码举例，若是想让第一个、第三个、第五个变量保持是整数的话，则直接在此处填写[1 3 5]9）run solver and view results求解use random states from previous run使用前次的状态运行，完全重复前次运行的过程和结果2、population（1）population type编码类型1）double vector实数编码，采用双精度。

Matlab遗传算法工具箱的应用

文章编号：1006-1576（2005）06-0115-02Matlab遗传算法工具箱的应用曾日波（江西财经大学电子学院，江西南昌 330013）摘要：Matlab遗传算法（GA）优化工具箱是基于基本操作及终止条件、二进制和十进制相互转换等操作的综合函数库。

其实现步骤包括：通过输入及输出函数求出遗传算法主函数、初始种群的生成函数，采用选择、交叉、变异操作求得基本遗传操作函数。

以函数仿真为例，对该函数优化和GA改进，只需改写函数m文件形式即可。

关键词：遗传算法；Matlab；遗传算法工具箱；仿真中图分类号：TP391.9 文献标识码：AApplication of Genetic Algorithm Toolbox Based on MatlabZENG Ri-bo(College of Finance and Economics Electronics, Jiangxi University, Nanchang 330013, China) Abstract: The optimization toolbox of Matlab genetic algorithm (GA) is a excellent generalized function library is to bases on basic operation and terminate term, the inter-conversion between binary system and ten system the system etc. Its step includes: the main function of GA and the creation functions of initial population was calculated through inputting and outputting functions, and the basic functions of genetic operation was computed by choosing, interlacing, and aberrance functions to realize the system. Take the function simulation as an example, the optimization of function and improvement of GA were achieved by modification the file format of m function.Keywords: Genetic algorithm; Matlab; Optimization toolbox; Simulation1 引言遗传算法（GA：Genetic Algorithm）是对生物进化过程进行的数学方式仿真。

matlab遗传算法种群初始化

matlab遗传算法种群初始化摘要：一、遗传算法简介二、MATLAB 中的遗传算法工具箱三、种群初始化方法在遗传算法中的应用四、结论正文：一、遗传算法简介遗传算法（Genetic Algorithm，GA）是一种模拟自然界生物进化过程的优化算法。

其主要思想是将进化过程中的种群、适应度函数、选择、交叉和变异等生物学概念引入到算法中，通过模拟这些生物学过程来寻找问题的最优解。

遗传算法具有较强的全局搜索能力，适用于解决复杂、非线性、非凸优化问题。

二、MATLAB 中的遗传算法工具箱MATLAB 提供了遗传算法工具箱（GA Toolbox），用户可以在MATLAB 中直接调用这个工具箱中的函数来实现遗传算法。

这个工具箱中包含了两个主要的函数：ga 和gaoptimset。

其中，ga 函数用于执行遗传算法，其语法如下：```matlab[x,fval] = ga(fitnessfcn,nvars,a,b,aeq,beq,lb,ub,nonlcon,options)```其中，fitnessfcn 表示适应度函数，nvars 表示变量个数，a 和b 分别表示交叉概率和变异概率，aeq 和beq 表示交叉和变异的约束条件，lb 和ub 表示变量范围的下界和上界，nonlcon 表示非线性约束条件，options 表示算法参数。

gaoptimset 函数用于设置遗传算法的参数，其语法如下：```matlabgaoptimset("param1",value1,"param2",value2,...)```其中，param1、value1 等表示需要设置的参数及其值。

三、种群初始化方法在遗传算法中的应用在遗传算法中，种群初始化是一个重要的步骤。

合理的种群初始化方法可以提高算法的收敛速度和搜索能力。

MATLAB 中的遗传算法工具箱提供了两种种群初始化方法：随机初始化和均匀初始化。

利用MATLAB实现遗传算法和MATLAB神经网络工具箱的使用

实验一利用MATLA实现遗传算法一、实验目的1、熟悉MATLA语言编程环境2、掌握MATLA语言命令3、学会利用MATLA编程实现遗传算法二、实验原理MATLA是美国Math Works公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，MATLA可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计等领域。

通过学习遗传算法原理，使用 MATLA编写程序，实现其求解策略。

三、实验内容通过MATLA编程，利用遗传算法求解：f (x) 200exp( 0.05x)sin(x), 求maxf (x)，x [-2,2] .三、实验要求1 、程序设计2、调试3、实验结果4、撰写实验报告实验二MATLAB申经网络工具箱的使用一、实验目的1、掌握MATLA语言命令2、提高MATLA程序设计能力3、学会使用MATLA申经网络工具箱二、实验原理MATLA语言是Math Works公司推出的一套高性能计算机编程语言，集数学计算、图形显示、语言设计于一体，其强大的扩展功能为用户提供了广阔的应用空间。

它附带有 30多个工具箱，申经网络工具箱就是其中之一。

利用该工具箱可以方便的构建申经网络的结构模型、设计、训练等，实现申经网络算法。

三、实验内容通过MATLA编程，利用神经网络工具箱预测公路运量：公路运量主要包括公路客运量和公路货运量两个方面。

据研究，某地区的公路运量主要与该地区的人数、机动车数量和公路面积有关，上表给出了该地区20年的公路运量相关数据。

根据有关部门数据，该地区2010和2011 年的人数分别为73.39 和75.55 万人，机动车数量分别为3.9635 和4.0975 万辆，公路面积分别为0.9880和1.0268万平方千米。

请利用BP网络预测该地区2010和2011 年的公路客运量和公路货运量。

某地区20年公路运量数据三、实验要求1、程序设计2、调试3、实验结果4、撰写实验报告运用遗传算法求解函数最大值：所有的子程序为M文件%子程序：计算适应度函数，函数名称存储为fitnessfu.m function[Fitvalue,sumsump]=fitnessfun(population); global BitLengthglobal boundsbeginIfCroIfMut.mglobal boundsendpopsize=size(population,1); for i=1:popsizex=transform2to10(population(i,:));xx=boundsbegin+x*(boundsend-boundsbegin)/(power((boundsend),BitLength)-1); Fitvalue(i)=targetfun(xx); endFitvalue(i)=Fitvalue'+230; fsum=sum(Fitvalue);Pperpopulation=Fitvalue/fsum; cumsump(1)=Pperpopulation(1); for i=2:popsizecumsump(i)=cumsumo(i-1)+Pperpopulation(i); endcumsump=cumsump';%子程序：新种群交叉操作，函数名称存储为crossover.mfunction scro=crossover(population,seln,pc) BitLength=size(population,2); pcc=IfCroIfMut(pc); if pcc==1chb=round(rand*(BitLength-2))+1;scro(1,:)=[population(seln(1),1:chb),population(seln(2),chb+1:BitLength)]; scro(2,:)=[population(seln(2),1:chb),population(seln(1),chb+1:BitLength)]; else scro(1,:)=population(seln(1),:); scro(2,:)=population(seln(2),:); end% 子程序：新种群变异操作，函数名称存储为 mutation.m function snnew=mutation(snew,pmutation); BitLength=size(snew,2); snnew=snew;pmm=IfCroIfMut(pmutation); if pmm==1chb=round(rand*(BitLlength-1))+1; end%子程序：判断遗传运算是否需要进行交叉或变异，函数名称存储为 function pcc=IfCroIfMut(mutORcro); test(1:100)=0;1=round(100*mutORcro); test(1:1)=1; n=round(rand*99)+1; pcc=test(n);%子程序：新种群选择操作，函数名称存储为selection.mfunction seln=selection(population,cumsump);for i=1:2r=rand;prand=cumsump-r;j=1;whlie prand(j)<0j=j+1;end seln(i)=j; end%子程序：将二进制数转换为十进制数，函数名称存储为transform2to10.mfunction x=transform2to10(Population);BitLength=size(Population,2); x=Population(BitLength); for i=1:BitLength-1 x=x+Population(BitLength-i)*power(2,i);end%子程序：对于优化最大值或者极大值函数问题，目标函数可以作为适应度函数，%函数名称存储为targetfun.m function y=targetfun(x); y=200*exp(-0.05*x).*sin(x);涯程序：用遗传算法求解y=200*exp (-0.05*x ) .*sin (x)在[-2 2]区间上的最大值clc;clear all;close all;global BitLengthglobal boundsbeginglobal boundsendbounds=[-2 2];precision=0.0001;boundsbegin=bounds(:,1); boundsend=bounds(:,2);BitLength=cell(log2((boundsend-boundsbegin)'./precision));popsize=50;Generationnmax=12; pcrossover=0.90;pmutation=0.09; population=round(rand(popsize,BitLength));[Fitvalue,cumsump]=fitnessfun(population);cumsump Generation=1;while Generation<Generationnmax+1for j=1:2:popsize seln=selection(population,cumsump);scro=crossover(popuoation,seln,pcrossover);scnew(j,:)=scro(1,:); scnew(j+1,:)=scro(2,:);smnew(j,:)=mutation(scnew(j,:),pmutation); smnew(j+1,:)=mutation(scnew(j+1,:),pmutation); endpopulation=smnew; [Fitvalue,cumsump]=fitnessfun(population);[fmax,nmax]=max(Fitvalue); fmean=mean(Fitvalue);ymax(Generation)=fmax; ymean(Generation)=fmean;x=transform2to10(population(nmax,:));xx=boundsbegin+x*(boundsend-boundsbegin)/(power((boundsend),BitLength)-1);xmax(Generation)=xx;Generation=Generation+1;endGeneration=Generation-1;Bestpopulation=xx;Besttargetfunvalue=targetfun(xx);figure(1); hand1=plot(1:Generation,ymax);set(hand1,'linestyle','-','linewidth',1.8,'marker','*','markersize',6) hold on;hand2=polt(1:Generation,ymean);set(hand2,'color','linestyle','linewidth',1.8,'marker','h','mrkersize',6) xlabel;ylabel; xlim([1 Generationnmax]);legend;box off; hold off附件二(参考程序)利用神经网络工具箱预测公路运量：为了了解利用BP网络求解问题的过程，把问题分为六个模块处理： 1.原始数据的输入；2.数据归一化；3.网络训练；4.对原始数据进行仿真； 5.将原始数据仿真的结果与已知样本进行对比； 6. 对新数据进行仿真。

谢菲尔德大学Matlab遗传算法工具箱改进与应用

产生初始化种群个体适应值计算结束是满足结束条件否是迁移操作满足迁移条件否交叉（重组）操作变异操作选择操作产生下代种群谢菲尔德大学Matlab 遗传算法工具箱改进与应用王琦，陈发威，黄斌达（南昌航空大学飞行器工程学院，南昌330063）1引言遗传算法是一种借鉴生物界自然选择和进化机制发展起来的，具有并行、随机、自适应搜索算法［1］。

遗传算法从问题潜在的一个解群开始，种群是由每个个体通过某种方式的编码组成，初代种群随机产生，之后逐代地优胜劣汰，经过选择、交叉、变异等遗传操作产生比前代更加适应的下一代种群，末代种群中最优的个体为问题的近似最优解［2］。

与传统搜索和优化算法相比，搜索的点是并行的而不是单点，仅需要目标函数和相对的适应度函数，不需要辅助信息。

目前遗传算法已经广泛应用于函数优化、组合优化、生产调度、自动控制、图像处理等领域。

但在算法精度、可靠度等方面还没有有效的定量分析方法，另外也存在如编码表示的不准确性、容易出现过早收敛等不足［2］。

2工具箱简介Matlab 是一种集合了数值分析、矩阵运算、信号处理、图形显示于一体的高性能的数值计算和可视化软件，Matlab 具有良好的开放性和可扩充性，Matlab 还可以方便地与FORTRAN 、C 等语言接口。

另外用户可以根据自己具体的计算需求开发自己的工具箱［2］。

谢菲尔德大学遗传算法工具箱使用Matlab 将遗传操作的每一部分编写一个M 文件，通过函数间的相互调用来完成遗传计算，从而建立了能够完成遗传计算的一套通用工具。

2.1种群表示和初始化工具箱支持二进制、整数和浮点数编码。

其中二进制支持格雷码编码。

工具箱提供了二进制和实值之间的转化函数。

初始化种群由随机函数产生。

2.2适应度计算适应度函数用于转化目标函数值，给每个个体一个非负的价值数。

工具箱支持Goldberg 的偏移法和比率法以及贝克的线性评估法，另外支持非线性评估。

2.3选择函数选择函数有轮盘赌选择和随机遍历抽样选择，还有一个高级入口函数支持多种群遗传操作。

matlab遗传算法工具箱及其应用

5
函数crtbase
BaseVec = crtbase(Lind, Base) % This function creates a vector containing the base of the loci crtbase产生向量的元素对应染色体结构的基因座 BaseVec = crtbase([4,6],[8,5]) %创建一有4个基数为8的基本字符{0，1，2，3，4，5，6，7}和6个基数为5的基本字符 {0，1，2，3，4}的基本字符向量
6
函数crtbp
crtbp % 创建二进制串染色体 ① [Chrom,Lind,BaseV] = crtbp(Nind,Lind) %创建一大小为 Nind× Lind的随机二元矩阵，这里Nind指定种群中个体的数量，Lind指定个体的长度。此格式习惯于指定染色体的尺寸 (维度)。 ② [Chrom,Lind,BaseV] = crtbp(Nind,BaseV) %返回长度为 Lind 的染色体结构，染色体基因位的基本字符由向量BaseV 决定 ③ [Chrom,Lind,BaseV] = crtbp(Nind,Lind,Base) %用于产生基本字符为Base的染色体矩阵。如果Base是向量，Base的元素值指定了染色体的基因位的基本字符。在这种情况下，右边的第二个变元可省略，即为格式②。
ranking 常用的基于秩的适应度计算 scaling 比率适应度计算
11
函数 ranking
功能：基于排序的适应度分配。格式：① FitnV = ranking(ObjV) ② FitnV = ranking(ObjV,RFun) ③ FitnV = ranking(ObjV,RFun,SUBPOP) ranking按照个体的目标值ObjV由小到大的顺序对它们进行排序，并返回一包含对应个体适应度值FitnV的列向量。这个函数是从最小化方向对个体进行排序的. RFun是一任选向量，有1、2或length(ObjV)个参数。（1）如果省略RFun或为NaN，则采用线性排序，选择压差假设为2。

（实例）matlab遗传算法工具箱函数及实例讲解

（实例）matlab遗传算法工具箱函数及实例讲解matlab遗传算法工具箱函数及实例讲解核心函数：(1)function[pop]=initializega(num,bounds,eevalFN,eevalOps,options)--初始种群的生成函数【输出参数】pop--生成的初始种群【输入参数】num--种群中的个体数目bounds--代表变量的上下界的矩阵eevalFN--适应度函数eevalOps--传递给适应度函数的参数options--选择编码形式(浮点编码或是二进制编码)[precision F_or_B],如precision--变量进行二进制编码时指定的精度F_or_B--为1时选择浮点编码，否则为二进制编码,由precision指定精度)(2)function [x,endPop,bPop,traceInfo] =ga(bounds,evalFN,evalOps,startPop,opts,...termFN,termOps,selectFN,selectOps,xOverFNs,xOverO ps,mutFNs,mutOps)--遗传算法函数【输出参数】x--求得的最优解endPop--最终得到的种群bPop--最优种群的一个搜索轨迹【输入参数】bounds--代表变量上下界的矩阵evalFN--适应度函数evalOps--传递给适应度函数的参数startPop-初始种群opts[epsilon prob_ops display]--opts(1:2)等同于initializega 的options参数，第三个参数控制是否输出，一般为0。

如[1e-6 1 0] termFN--终止函数的名称,如['maxGenTerm']termOps--传递个终止函数的参数,如[100]selectFN--选择函数的名称,如['normGeomSelect']selectOps--传递个选择函数的参数,如[0.08]xOverFNs--交叉函数名称表，以空格分开，如['arithXover heuristicXover simpleXover']xOverOps--传递给交叉函数的参数表，如[2 0;2 3;2 0]mutFNs--变异函数表，如['boundaryMutation multiNonUnifMutation nonUnifMutation unifMutation'] mutOps--传递给交叉函数的参数表,如[4 0 0;6 100 3;4 100 3;4 0 0]matlab遗传算法工具箱附件【注意】matlab工具箱函数必须放在工作目录下【问题】求f(x)=x+10*sin(5x)+7*cos(4x)的最大值，其中0<=x<=9【分析】选择二进制编码，种群中的个体数目为10，二进制编码长度为20，交叉概率为0.95,变异概率为0.08【程序清单】%编写目标函数function[sol,eval]=fitness(sol,options)x=sol(1);eval=x+10*sin(5*x)+7*cos(4*x);%把上述函数存储为fitness.m文件并放在工作目录下initPop=initializega(10,[0 9],'fitness');%生成初始种群，大小为10[x endPop,bPop,trace]=ga([0 9],'fitness',[],initPop,[1e-6 1 1],'maxGenTerm',25,'normGeomSelect',...[0.08],['arithXover'],[2],'nonUnifMutation',[2 25 3]) %25次遗传迭代运算结果为：x =7.8562 24.8553(当x为7.8562时，f（x）取最大值24.8553)注：遗传算法一般用来取得近似最优解，而不是最优解。

matlab遗传算法工具箱函数及实例讲解3

matlab遗传算法工具箱函数及实例讲解1核心函数：(1)function [pop]=initializega(num,bounds,eevalFN,eevalOps,options)--初始种群的生成函数【输出参数】pop--生成的初始种群【输入参数】num--种群中的个体数目bounds--代表变量的上下界的矩阵eevalFN--适应度函数eevalOps--传递给适应度函数的参数options--选择编码形式(浮点编码或是二进制编码)[precision F_or_B],如precision--变量进行二进制编码时指定的精度F_or_B--为1时选择浮点编码，否则为二进制编码,由precision指定精度)(2)function [x,endPop,bPop,traceInfo] = ga(bounds,evalFN,evalOps,startPop,op ts,...termFN,termOps,selectFN,selectOps,xOverFNs,xOverOps,mutFNs,mu tOps)--遗传算法函数【输出参数】x--求得的最优解endPop--最终得到的种群bPop--最优种群的一个搜索轨迹【输入参数】bounds--代表变量上下界的矩阵evalFN--适应度函数evalOps--传递给适应度函数的参数startPop-初始种群opts[epsilon prob_ops display]--opts(1:2)等同于initializega的options 参数，第三个参数控制是否输出，一般为0。

如[1e-6 1 0]termFN--终止函数的名称,如['maxGenTerm']termOps--传递个终止函数的参数,如[100]selectFN--选择函数的名称,如['normGeomSelect']selectOps--传递个选择函数的参数,如[0.08]xOverFNs--交叉函数名称表，以空格分开，如['arithXover heuristicXover simpleXover']xOverOps--传递给交叉函数的参数表，如[2 0;2 3;2 0]mutFNs--变异函数表，如['boundaryMutation multiNonUnifMutation nonUnifMutation unifMutation'] mutOps--传递给交叉函数的参数表,如[4 0 0;6 100 3;4 100 3;4 0 0]注意】matlab工具箱函数必须放在工作目录下【问题】求f(x)=x+10*sin(5x)+7*cos(4x)的最大值，其中0<=x<=9【分析】选择二进制编码，种群中的个体数目为10，二进制编码长度为20，交叉概率为0.95,变异概率为0.08【程序清单】%编写目标函数function[sol,eval]=fitness(sol,options)x=sol(1);eval=x+10*sin(5*x)+7*cos(4*x);%把上述函数存储为fitness.m文件并放在工作目录下initPop=initializega(10,[0 9],'fitness');%生成初始种群，大小为10[x endPop,bPop,trace]=ga([0 9],'fitness',[],initPop,[1e-6 1 1],'maxGe nTerm',25,'normGeomSelect',...[0.08],['arithXover'],[2],'nonUnifMutation',[2 25 3]) %25次遗传迭代运算借过为：x =7.8562 24.8553(当x为7.8562时，f（x）取最大值24.8553)注：遗传算法一般用来取得近似最优解，而不是最优解。