高中数学必修 空间几何体的三视图和直观图
高考数学一轮复习-81-空间几何体的三视图-直观图-表面积与体积课件-新人教A

=172a2.所以 S 球=4πR2=4π×172a2=73πa2.
(2)这个几何体是一个圆台被轴截面割出来的一半.
根据图中数据可知圆台的上底面半径为 1,下底面半径为 2,高为 3,母线长为 2,几何体的表面积是两个半圆的面 积、圆台侧面积的一半和轴截面的面积之和,故这个几何 体的表面积为 S=12π×12+12π×22+12π×(1+2)×2+12 ×(2+4)× 3=112π+3 3. 答案 (1)B (2)112π+3 3
可能是圆柱,排除选项C;又由俯视图可知,该几何体
不可能是棱柱或棱台,排除选项A,B,故选D.
(2)如图,在原图形OABC中, 应有 OD=2O′D′=2×2 2 =4 2(cm), CD=C′D′=2 cm. ∴OC= OD2+CD2 = (4 2)2+22=6(cm), ∴OA=OC, 故四边形 OABC 是菱形. 答案 (1)D (2)C
诊断自测
1.判断正误(在括号内打“√”或“×”) 精彩PPT展示
(1)有两个面平行,其余各面都是平行四边形的几何体是
棱柱.
(×)
(2)有一个面是多边形,其余各面都是三角形的几何体是
棱锥.
( ×)
(3)正方体、球、圆锥各自的三视图中,三视图均相同.
(×)
(4)圆柱的侧面展开图是矩形.
(√)
2.(2014·福建卷)某空间几何体的正视图是三角形,则该几
(2)画出坐标系 x′O′y′,作出△OAB 的 直观图 O′A′B′(如图).D′为 O′A′的中 点.易知 D′B′=12DB(D 为 OA 的中点), ∴S△O′A′B′=12× 22S△OAB= 42× 43a2= 166a2.
高中数学人教版必修2课件:1.2空间几何体的三视图和直观图

(1)
(2)
(3)
图(1)的投影线交于一点 图(2)(3)的投影线平行
问题4 什么是中心投影?什么是平行投影?
光由一点向外散射形成的投影叫中心投影,其 投影线交于一点 把在一束平行光线照射下形成的投影叫平行投影, 其投影线互相平行
问题5 图(2)(3)同是平行投影,它们有什么区分呢?
图(2)的投影线与投影面垂直,称这种投影为正投影 图(3)的投影线与投影面不垂直,称这种投影为斜投 影
出来的空间图形。请视察一下中心投影下的直观图 与平行投影下有什么区分和联系?
立体几何中常用平行投影(斜投影)来画空间图 形的直观图,这种画法叫斜二测画法.
投影规律
1.平行性不变,但形状、长 度、夹角会改变; 2.平行直线段或同一直线上 的两条线段的比不变; 3.在太阳光下,平行于地面的 直线在地面上的投影长变
F A
B
y ME
O
D
x
NC
y'
O'
x'
y
F ME
A
O
Dx
B NC
y
x
y
F ME
A
O
Dx
B NC
y
F M E
A
O
D x
B N C
y
F ME
AБайду номын сангаас
O
Dx
B NC
A B
F
C
E
D
用斜二测画法画水平放置的平面图形的直观图 的关键步骤是
例2 用斜二测画法画水平放置的圆的直观图
例2
z
画法见课本P17页
问题1 阅读教材P11的内容,我们常用哪两种图
高中数学必修2空间几何体的三视图和直观图

俯视图
圆锥的三视图
正视图 侧视图
俯视图
思考:下列两组三视图分别是什么几何体?
正视图
侧视图
正视图
侧视图
俯视图
俯视图
圆台
三棱锥
一个几何体的三视图如下,则这个几 六棱锥 何体是______
正视图
主视图
左视图
俯视图
俯视图
画法说明
1、同一张图样中,同类图线的宽度应基本一致。 2、虚线、点划线相交时,应使两小段相交。
C
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
y
F
M
E D
A
B
O
x
N
C
斜二测画法的步骤:(平面图形)
(1)在已知图形中取互相垂直的x 轴和y 轴,两轴 相交于O点.画直观图时,把它画成对应的 x 轴、 轴,使 xOy=45 或135 ,它确定的平面表示水平 y 平面. (2)已知图形中平行于x轴或y轴的线段,在直观 图中分别画成平行于x′轴或y′轴的线段. (3)已知图形中平行于x 轴的线段,在直观图中保 持原长度不变;平行于y 轴的线段,长度为原来的一 半.
y
F
M
E D
A
y
F M E
N
A
B
O
x
N
B
O
D
C
x
C
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
y
F
M
E D
y
A
B
O
高一数学必修2《空间几何体的三视图和直观图》PPT课件

名 茶
&与同伴交流你的看法和具体做法.
(三)归纳总结
1、空间几何体的三视图:正视图、侧视图、俯视图; 2、三视图特点: 一个几何体的侧视图和正视图高度一样, 俯视图和正视图长度一样,侧视图和俯视图宽度一样; 3、三视图的应用及原实物图的相互转化.
(四)分层作业
层次1:教材习题1.2A组1、2
层次2:课外动手操作:
球的三视图
俯视图
还有哪种几何体的三种视图一样呢
比一比看一看
3、简单组合体的三视图
下图是一个蒙古包的照片.小明认为这个蒙古包可以看成如 图所示的几何体,请画出这个几何体的三种视图.你与小明的 做法相同吗? 正视图 侧视图
俯视图
4 、 三 视 图 与 几 何 体 之 间 的 相 互 转 化 . A
3.过程与方法: (1)主要通过学生自己的亲自实践,动手作图,体会三视图的作 用; (2)体会组合体与三视图之间转化关系在现实生活中的应用; (3)培养学生的空间概念,提高学生空间想象力,掌握画三视 图的基本技能. 4.情感目标: (1)提高空间想象能力,培养学生的动手实践能力,在实际 操作中培养学生分析问题、解决问题的能力,体会几何学在其 他学科方面的应用; (2)体会三视图的作用,引发学生学习和使用知识的兴趣, 发展创新精神,培养事实求是、理论与实际相结合的科学态度 和科学道德观.
2、柱、锥、台、球的三视图
(1)三视图的有关概念:
合作探究 用小正方体搭建一个几何体:
从 上 面俯 看视 到图 的 图
“三视图”
你还记得 三视图吗?
侧视图 从左面看到的图 驶向胜利 彼岸
能你能画出这个几何体的三视图
吗?
经过努力我会收获
“三视图”
高一数学A必修2课件_第一章_1.2.2_空间几何体的三视图和直观图

正视图
侧视图
正视图
侧视图
俯视图
俯视图
注意:
(1)画几何体的三视图时,
能看见的轮廓和棱用实线表示, 不能看见的轮廓和棱用虚线表示。
(2)长对正, 高平齐, 宽相等。
俯
练习、画下例几何体的三视图
侧
正
除了会画如正方体、长方体、圆柱、圆锥、球 等基本几何体的三视图外,我们还将学习画出由 一些简单几何体组成的组合体的三视图。
c(高)
c(高)
a(长)
高 平 长对正 齐
b(宽)
b(宽)
俯 视 图
a(长)
宽相等
c(高) b(宽) a(长)
例1 (1)圆柱的三视图
俯
正视图
侧视图
侧 俯视图
圆柱 正
例2 (2)圆锥的三视图 俯
正视图
侧视图
侧
·
圆 锥
俯视图
正
例2 请同学们画下面这两个圆台的三视图, 如果你认为这两个圆台的三视图一样,画一 个就可以;如果你认为不一样,请分别画出 来。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。 ——苏轼
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。 ——苏轼
从不同的角度看同一物体,视觉的效果可能不同, 要比较真实地反映出物体的特征我们可从多角度观看物体。
1.中心投影:
把光由一点向外散射形成 的投影叫中心投影。
侧视图
俯
俯视图
俯视图
例5 根据三视图判断几何体
俯 四 棱 柱
正 视 图
侧 视 图
侧
正
俯视图
三 棱 柱
探究(1): 在例3中,若只给出正,侧视图, 那么它除了是圆台外,还可能是什么几何体?
高一数学空间几何体的三视图与直观图试题答案及解析
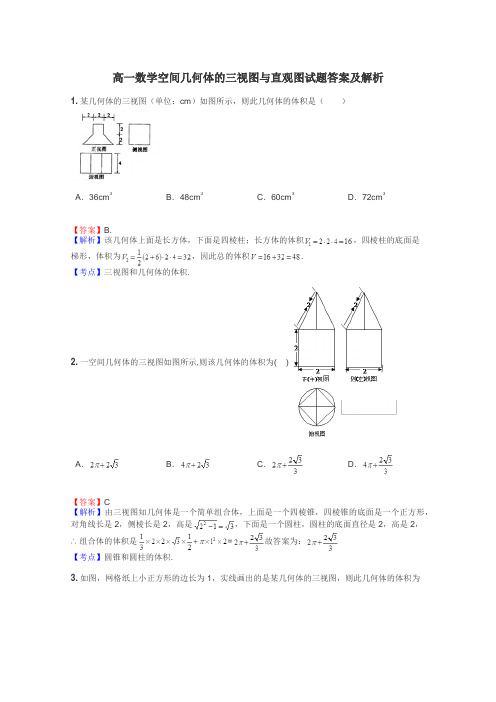
高一数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图(单位:cm)如图所示,则此几何体的体积是()A.36cm3B.48cm3C.60cm3D.72cm3【答案】B.【解析】该几何体上面是长方体,下面是四棱柱;长方体的体积,四棱柱的底面是梯形,体积为,因此总的体积.【考点】三视图和几何体的体积.2.一空间几何体的三视图如图所示,则该几何体的体积为( )A.B.C.D.【答案】C【解析】由三视图知几何体是一个简单组合体,上面是一个四棱锥,四棱锥的底面是一个正方形,对角线长是2,侧棱长是2,高是,下面是一个圆柱,圆柱的底面直径是2,高是2,∴组合体的体积是=故答案为:【考点】圆锥和圆柱的体积.3.如图,网格纸上小正方形的边长为1,实线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18【答案】C【解析】该几何体是三棱锥,底面是俯视图,三棱锥的高为4;底面三角形是斜边长为6,高为3的等腰直角三角形,此几何体的体积为.故选C.【考点】三视图与几何体的关系;几何体的体积的求法.4.某向何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是一个长方体和一个半圆柱组成的几何体,所以体积为。
【考点】(1)根据三视图确定几何体的构成,(2)圆柱及长方体的体积公式的应用。
5.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为 .【答案】11【解析】由图可知切去的是直淩柱的一角,先算直棱柱的体积,再算切去部分的体积,所以.【考点】1、立体图形的三视图;2、体积的计算.6.右图中的三个直角三角形是一个体积为的几何体的三视图,则()A.B.C.D.【答案】B【解析】由三视图可知该几何体为三棱锥,其中一侧棱垂直底面,且底面为直角三角形,∴三棱锥的体积为,解得,故选B.【考点】由几何体的三视图求体积.7.已知四棱锥的三视图如图所示,则四棱锥的四个侧面中面积最大的是()A.3B.C.6D.8【答案】C【解析】通过三视图可作出该几何体的直观图,如图所示.其中底面为矩形,面面,且,,.易得,,,故侧面中面积最大值为6.【考点】几何体的三视图与直观图.8.右图是水平放置的的直观图,轴,,则是()A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形【答案】C【解析】直观图为斜二测画法,原图的画为,因此原为直角三角形.【考点】斜二测画法.9.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A.B.C.D.【答案】D【解析】主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是球和圆柱的表面积.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.由三视图可知几何体是半径为1的球和底面半径为1,高为3的圆柱,故其表面积应为球的表面积与圆柱的表面积面积之和减去圆柱一个底面积,即.故选D.【考点】本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用10.如图是一个简单的组合体的直观图与三视图,一个棱长为4的正方体,正上面中心放一个球,且球的一部分嵌入正方体中,则球的半径是()A.B.1C.D.2【答案】B【解析】由已知题中三视图中的俯视图中圆上的点到正方形边长的最小距离为1,已知中的正方体的棱长为4,可得球的半径为1,故选B.【考点】由三视图还原实物图.11.一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台【答案】D【解析】由正视图和左视图可知此几何体为台体,结合俯视图可知此几何体为圆台。
三视图和直观图(含答案)

空间几何体的三视图和直观图一、探究 探究一:直观图1.如图,这是长方体、圆柱等四个几何体的直观图。
把空间图形(平面图形和立体图形的统称)画在平面内,使得既富有立体感,又能表达出主要部分的位置关系和度量关系的图形叫做直观图.空间几何体的直观图通常是在 投影下把空间图形展现在平面上,用平面的图形表示空间几何体。
探究二:斜二测画法 1.斜二测画法的方法步骤:①在已知图形中建立直角坐标系xOy ,画直观图时,把x 轴、y 轴画成对应的x '轴和y '轴,两轴交于点O ',使 ,它们确定的平面表示水平面.②已知图形中平行于x 轴或y轴的线段,在直观图中分别画成 于x '轴和y '轴的线段.③已知图形中平行于x 轴的线段,在直观图中 ,平行于y 轴的线段, . 2.空间几何体直观图的画法:立体图形与平面图形相比多了一个z 轴,90xoz ∠=o 。
其直观图中对应于z 轴的是z '轴,''90x oz ∠=o,平行于z 轴的线段,在直观图中画成 于z '轴,长度 . 二、自我检测1.下列结论正确的有 ①相等的线段在直观图中仍然相等。
②若两条线段平行,则在直观图中对应的两条线段仍然平行。
③矩形的直观图是矩形。
④圆的直观图一定是圆。
⑤角的水平放置的直观图一定是角。
2.直角坐标系中一个平面图形上的一条线段AB 的实际长度为4cm ,若AB//x 轴,则画出直观图后对应的线段=''B A ,若y AB //轴,则画出直观图后对应的线段B A ''= 。
3.根据斜二测画法的规则画直观图时,把Ox 、Oy 、Oz 轴画成对应的x O ''、y O ''、z O '',作y O x '''∠与z O x '''∠的度数分别为( )A .οο90,90 B .οο90,45 C .οο90,135D .ο45或οο90,1354.如图,A B C '''△是ABC △的直观图,那么ABC △是( ) A .等腰三角形 B .直角三角形C .等腰直角三角形D .锐角三角形 三、应用示例例1.用斜二测画法画水平放置的正六边形、任意三角形的直观图。
空间几何体的三视图和直观图

俯
侧
正三棱柱
正
注意:画几何体的三视图时,看见的 轮廓线和棱用实线表示,看不见的 轮廓线和棱用虚线表示。
正视图 俯视图
侧视图
现场考考你
下图是一个球体与一个圆台的 组合体,则此组合体的俯视 图可能是_(_2_) (_3)_(_5)_。
(1)
(2)
(3)
(4)
(5)
小组探究
1. 球体的三个视图形状大小一样吗? 2.正方体的三个视图形状大小一样吗? 3.总结画三视图的要领有哪些?
(蒙日的《画法几何》截图)
手影表演
中心投影与平行投影
平行投影
斜投影
中心 投影
A
正投影
三视图形成(一)
W V
H
三视图形成(二)
W V
•V 正视图 •H 俯视图 •W 侧视图
H
正投影与视图一样吗?
正投影
视图
三视图形成(三)—俯视图
三视图定义及其投影规律
考考你的想象力
掌握了画几何体三视图 的要领,你可以根据三视图 判断实物是由什么几何体组 成的吗?
由三视图还原几何体
正视图
侧视图
正视图
侧视图
俯
俯视图
左
长方体
俯
侧
俯视图
圆台
由三视图还原几何体
正视图
侧视图
正视图
侧视图
俯
左
俯视图
正四棱台
俯视图
正四棱锥
由三视图还原几何体
俯
正视图
侧视图 侧
俯视图
由三视图还原几何体
观察分析
想象猜测
还原验证
方法提炼与反思小结
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
D QC
MO N x
AP B
3画侧棱.过A,B,C,D,各点分别作z轴的平
行线,并在这些平行线上分别截取2cm长的线
段AA,BB,CC,DD.
Z
D
C y
A
D
BQ C
MO N x
AP B
4 成图.顺次连接A,B,C,D,并加以整理
去掉辅助线,将被遮挡住的部分改为虚线 ,
就可得到长方体的直观图.
y
F ME
A
OD
x
y
F M E
A
O
D x
B N C
B NC
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
y
F ME
A
O Dx
B NC
y
F M E
A
O
D x
B N C
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
斜投影
1.2.2 空间几何体的三视图
横看成岭侧成峰, 题
远近高低各不同.
西 林
不识庐山真面目, 壁
苏轼
只缘身在此山中
视图:将物体按正投影向投影面投 射所得到的图形.
光线自物体的前面向后面投射所得的 投影称为正视图 光线自上向下投射所得的投影称为俯 视图 光线自左向右所得的投影称为侧视图
几何体的正视图、侧视图、俯视图通称为 几何体的三视图
例3.已知几何体的三视图,用斜二测画法
画出它的直观图 正视图
侧视图
·Z
y
·O
·O
O y x
·
O
·
O
Ox
·
俯视图
例3.已知几何体的三视图,用斜二测画
法画出它的直观图 正视图
侧视图
·O
·O
·
·
O
O
·
俯视图
课堂小结:
1、水平放置的平面图形的直观图的画法 2、空间几何体的直观图的画法 作业:
课本P23第4、5题
持原长度不变;平行于y 轴的线段,长度为原来的一 半.
例2.用斜二测画法画长,宽,高分别是4cm, 3cm,2cm的长方体的直观图
1 画轴.画x轴,y轴,z轴,三轴交于点O,
使xO y=45 ,xO z 90 .
Z
y
O
x
2画底面.以O为中心,在x轴上取线段MN ,
使MN = 4 cm;在y轴上取线段PQ,使PQ=1.5cm; 分别过点M和N 作y轴的平行线,过点P和Q作 x轴的平行线,设它们的交点分别为A,B,C,D, 四边形ABCD就是长方形的底面ABCD
空间几何体的 三视图和直观图
➢中心投影和平行投影 ➢空间几何体的三视图 ➢空间几何体的直观图
1.2.1 平行投影和中心投影
概念
投影:光线通过物体,向选定的面 投射,并在该面上得到图形的方法.
概念
中心投影: 投射线交于一点的投影
Y
X
光光
概念
Y X
平行投影:投射线相互平行的投影 可以分为:
正投影(投影线正对投影面)
正视图
侧视图
正视图
侧视图
俯视图
圆台
俯视图
三棱锥
一个几何体的三视图如下,则这个几 何体是六__棱__锥__
正视图
主视图
左视图
俯视图
俯视图
画法说明
1、同一张图样中,同类图线的宽度应基本一致。 2、虚线、点划线相交时,应使两小段相交。
3、两直线相交处要避免间隙或线段出界。 4、两线相切的切点处,应画成一条线粗。
对称轴MN 所在直线为Y 轴,两轴交于点O。画相应
的X 轴和Y 轴,两轴相交于点O,使xOy=45
y
y
F ME
A
O Dx
O
x
B NC
2 以O为中心,在X上取AD=AD,在y轴上取
MN= 1 MN .以点N 为中心,画BC平行于x轴, 2
并且等于BC;再以M为中心,画EF平行于x轴,
并且等于EF.
坦 克 来 了 !
飞 机 来 了 !
三视图的投影
首先,观察从长方体的正前方的正投影
主视图
P
其次,观察从长方体的正左方的正投影
主视图
左视图
P
Q
再次,观察从长方体的正上方的正投影
主视图
左视图
V
俯视图
W
你能发现 这三个
视图之间 有什么 关系吗?
三视图的画法规则: (1)高平齐:正视图和 侧视图的高保持平齐
有一个正方体,在它的各个面上分别标上字 母A、B、C、D、E、F,甲、乙、丙三位同 学从不同的方向去观察其正方体,观察结果 如图所示.问这个正方体各个面上的字母对 面各是什么字母?
1.2.3 空间几何体的直观图
例1.用斜二测画法画水平放置的六边形的直观图
1 在六边形ABCDEF中,取AD所在的直线为X 轴,
简单组合体的三视图
例题讲解
例题讲解
口答:桌上放着一个圆柱和一个长方体, 请说出三幅图分别是从哪个方向看到的?
(1)
(2)
(3)
口答:一个几何体某一方向的视图是圆, 则它不可能是(D )
A球
B 圆锥
C 圆柱 D 长方体
从上面看俯视图ຫໍສະໝຸດ 从左面看 左视图从正面看 主视图
主视图
左视图
俯视图
y
F ME
A
O Dx
B NC
斜二测画法的步骤:(平面图形)
(1)在已知图形中取互相垂直的x 轴和y 轴,两轴
相交于O点.画直观图时,把它画成对应的 x 轴、
y轴,使 xOy=45 或135 ,它确定的平面表示水平
平面. (2)已知图形中平行于x轴或y轴的线段,在直观
图中分别画成平行于x′轴或y′轴的线段. (3)已知图形中平行于x 轴的线段,在直观图中保
下图中哪一幅是左视图?
左视图
俯视图
主视图
甲、乙、丙、丁四人分别面对面坐在一个四边形 桌子旁边,桌上一张纸上写着数字“9”,甲说他 看到的是“6”,乙说他看到的是“ ”,丙说他 看到的是“ ”,丁说他看到的是“9”,则下 列说法正确B的是( ) A.甲在丁的对面,乙在甲的左边,丙在丁的右边 B.甲在丁的对面,乙在甲的右边,丙在丁的右边 C.甲在乙的对面,甲的右边是丙,左边是丁 D.丙在乙的对面,丙的左边是甲,右边是乙
的 x轴、y轴、z 轴,使 xOy=45 ,xOz=90 ,它
确定的平面表示一个三维空间. (2)已知图形中平行于x轴, y轴,z轴的线段,在直
观图中分别画成平行于x轴,y 轴, z 轴的线段.
(3)已知图形中平行于x 轴或z 轴的线段,在直观 图中保持原长度不变;平行于y 轴的线段,长度为原 来的一半.
Z
D
C y
A
D
BQ C
MO N x
AP B
4 成图.顺次连接A,B,C,D,并加以整理
去掉辅助线,将被遮挡住的部分改为虚线 ,
就可得到长方体的直观图.
D
A
D
C B C
A
B
斜二测画法的步骤:(空间几何体)
(1)画轴.在已知图形中取两两垂直的x 轴, y 轴, z轴,三轴相交于O点.画直观图时,把它画成对应
(2)宽相等:侧视图的 宽和俯视图的宽相等
(3)长对正:正视图和 俯视图的长对正
(4)看不到的棱和轮廓 线用虚线表示,能看 到的则用实线表示
三个视图的位置
正视图
侧视图
画出下列几何体的三视图:
球的三视图
正视图 侧视图
俯视图
圆柱的三视图
正视图 侧视图
俯视图
圆锥的三视图
正视图 侧视图
俯视图
思考:下列两组三视图分别是什么几何体?
