各向同性材料的应力应变关系(广义胡克定律)
合集下载
弹性力学:04 应力和应变的关系

广义胡克定律
杨氏模量
单向应力状态时的胡克定律是
x E x
式中 E 称为弹性模量。对于一种材 料在一定温度下,E 是常数。
Chapter 5.1
广义胡克定律
泊松比
在单向拉伸时,在垂直于力作用线的方向发生收缩。
在弹性极限内,横向相对缩短 x 和纵向相对伸长 y
成正比,因缩短与伸长的符号相反,有:
ν
x y
Chapter 5.1
广义胡克定律
根据实验可知,xy只引起 xy 坐标面内的剪应变xy,
而不引起 xz、yz,于是可得
xy
xy
G
同理
yz
yz
G
zx
zx
G
Chapter 5.1
广义胡克定律
于是,得到各向同性材料的应变-应y
1 E
y
ν x
z
z
ij
1 2
ui, j u j.i
协调条件:
ij,kl kl,ij ik , jl jl,ik 0
对于一个假定位移场ui ,其相应的协调应变分量ij 可直接由应
变-位移关系得到。显然,这组协调的应变和位移,仅仅是许 多其他可能的应变和位移场中的一组。
几何可能的位移未必是真实的,真实位移在弹性体内部须满足 以位移表示的平衡微分方程。
应力和应变的关系
1. 本构关系的概念 2. 广义胡克定律 各向同性体 3. 各向异性弹性体 4. 热力学定律与应变能函数 5. 应变能和应变余能(自学) 6. 热弹耦合本构关系(自学) 7. 例题
应力和应变的关系
1. 本构关系的概念 2. 广义胡克定律 各向同性体 3. 各向异性弹性体 4. 热力学定律与应变能函数 5. 应变能和应变余能(自学) 6. 热弹耦合本构关系(自学) 7. 例题
材料学 胡克定律

l
b=50mm h=100mm
解: 梁为拉伸与弯曲的组合变形. A点有拉伸引起的正应力和弯曲 引起的切应力.
(拉伸) (负)
(1)A点处的主应变1, 2 , 3
A
x = 20
x = 30
(2)A点处的线应变 x , y , z
例题14 简支梁由18号工字钢制成. 其上作用有力F= 15kN, 已知
2.三向等值应力单元体的体积应变(The volumetric strain of triaxial-equal stress element body)
三个主应力为
m
单元体的体积应变
m
m
这两个单元体的体积应变相同 单元体的三个主应变为
2
1
dy
3
dz dx
m
m
m
如果变形前单元体的三个棱边成某种比例,由于三个棱边应 变相同,则变形后的三个棱边的长度仍保持这种比例. 所以在三向
因此,该圆筒变形后的厚度并无变化,仍然为 d =10mm .
例题13 已知矩形外伸梁受力F1,F2作用. 弹性模量E=200GPa,泊
松比m= 0.3, F1=100KN,F2=100KN. 求:(1)A点处的主应变 1,2 , 3 (2)A点处的线应变 x , y , z
F1
b
F2 A
F2 z
a
例题10 边长 a = 0.1m 的铜立方块,无间隙地放入体积较大,变形
可略去不计的钢凹槽中,如图所示. 已知铜的弹性模量E=100GPa,
泊松比μ=0.34,当受到F=300kN的均布压力作用时,求该铜块的主
应力,体积应变以及最大切应力.
解:铜块横截面上的压应力
Fa
应力和应变之间的关系
s2 0
即为平面应力状态,有
1
1 E
s 1 s 3
3
1 E
s 3 s 1
联立两式可解得:
s1
E 1
2
1 3
210 10 1 0 .3
2
9
240
0 . 3 160 10
6
s3
44 . 3 M Pa 9 E 210 10 3 1 160 0 . 3 240 10 2 2 1 1 0 .3
利用空间应力状态下最大切应力的计算式可得:
t max s1 s3
2 7.25MPa
§7-5 平面应力状态下的电测法
对各向同性材料图示平面应力状态,在线弹性、 小变形条件下,sx、sy与切应变无关,即有:
sy sx
x y
1 E 1 E
s s
E
x
s s s
y
y F a
sy sx sz
x
a
(a)
z
(b)
解:铜块应力状态如图b所示,横截面上的压应力为:
s
y
F A
30 MPa
受钢槽的限制,铜块在另两个方向的应变为零, 并产生压应力,即有:
x z
1 E 1 E
s s
x
s s
y
s s
z
0 0
所以,应变能密度为: v
d V dxdydz
1tx 2 G
而对纯剪应力状态,其主应力为:
s 1 tx
s2tx
s1 t
x
s
2
即为平面应力状态,有
1
1 E
s 1 s 3
3
1 E
s 3 s 1
联立两式可解得:
s1
E 1
2
1 3
210 10 1 0 .3
2
9
240
0 . 3 160 10
6
s3
44 . 3 M Pa 9 E 210 10 3 1 160 0 . 3 240 10 2 2 1 1 0 .3
利用空间应力状态下最大切应力的计算式可得:
t max s1 s3
2 7.25MPa
§7-5 平面应力状态下的电测法
对各向同性材料图示平面应力状态,在线弹性、 小变形条件下,sx、sy与切应变无关,即有:
sy sx
x y
1 E 1 E
s s
E
x
s s s
y
y F a
sy sx sz
x
a
(a)
z
(b)
解:铜块应力状态如图b所示,横截面上的压应力为:
s
y
F A
30 MPa
受钢槽的限制,铜块在另两个方向的应变为零, 并产生压应力,即有:
x z
1 E 1 E
s s
x
s s
y
s s
z
0 0
所以,应变能密度为: v
d V dxdydz
1tx 2 G
而对纯剪应力状态,其主应力为:
s 1 tx
s2tx
s1 t
x
s
2
应力与应变间的关系

22
例题7-7 边长 a = 0.1m 的铜立方块, 无间隙地放入体积较
大, 变形可略去不计的钢凹槽中, 如图 所示。 已知铜的弹 性模量 E=100GPa, 泊松比 =0.34, 当受到P=300kN 的均布 压力作用时, 求该铜块的主应力. 体积应变以及最大剪应力。
P a
y
z
x
23
y
解:铜块上截面上的压应力为
9
3、 特例
(1)平面应力状态下(假设 Z = 0 )
x
1 E
(
x
y)
y
1 E
(
y
x)
z E ( x y)
xy
xy
G
10
(2) 广义胡克定律用主应力和主应变表示时 三向应力状态下:
1
1
E [ 1
(
2
3)]
2
1 E
[
2
(
3
1)]
3
1 E
[
3
( 1
2)]
(7-7-6)
11
平面应力状态下 设 3 = 0, 则
x y z x y y z z x
y
σy
上面
x y z x y y z z x
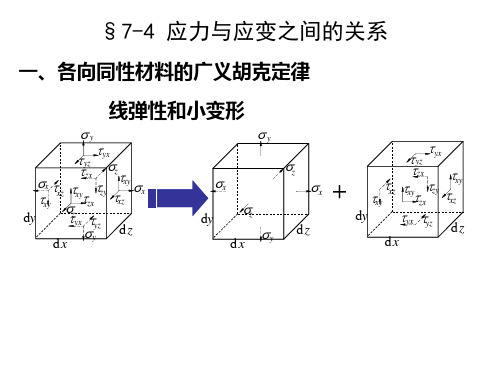
1、各向同性材料的广义胡克定律 (1)符号规定
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量:拉应力为正
σz
x
o
压应力为负。 z
前面
3
(b)三个剪应力分量: 若正面(外法线与坐标轴
dxdydz
dxdydz(1 1 2 3) dxdydz
dxdydz
第十七章 塑性应力应变关系(本构关系)

• 广义胡克定律的比例式:
x y y z z x xy yz zx 1 x y y z z x xy yz zx 2G
弹性应力应变关系的特点
• 应力与应变完全呈线性关系,应力主轴与应变主 轴重合。 • 弹性变形是可逆的,应力与应变单值对应。 • 弹性变形时,应力球张量使物体产生体积变化, 泊松比υ<0.5
' y
z
' z
xy
xy
yz
yz
zx
zx
d
d 3 2
x y
z x d x y y z z x 1 2 2 3 3 1 d 1 2 2 3 3 1
• 流动理论是描述材料处于塑性状态时,应 力与应变增量或应变速率之间关系的理论。 该理论针对是加载过程的任一瞬间,认为 应力状态确定的不是全量应变,而是该瞬 时的应变增量,从而撇开了加载路线和加 载历史的影响。
Levy—Mises方程
' ' ij ij d
x
' x
y
第五节 塑性应力应变关系(本构关系)
• 一、弹性应力应变关系———Hooke’s Law 对于各向同性材料,有广义虎克定律:
1 1 x y z ; xy xy E 2G 1 1 y y x z ; yz yz E 2G 1 1 z z x y ; zx zx E 2G
• 弹塑性
塑性应变
应力与应变之间的关系

因主应力和主应变相对应,则由题意可得: 解:因主应力和主应变相对应,则由题意可得:
σ2 = 0
即为平面应力状态, 即为平面应力状态,有
1 ε 1 = (σ 1 −νσ 3 ) E
1 ε 3 = (σ 3 −νσ 1 ) E
8
E 210 ×10 (ε1 +νε 3 ) = (240 − 0.3 ×160)×10 −6 σ1 = 1 −ν 2 1 − 0.32 = 44.3MPa E 210 ×109 (ε 3 +νε 1 ) = (− 160 + 0.3 × 240)×10−6 σ3 = 1 −ν 2 1 − 0. 3 2 = −20.3MPa 主应变ε2为: ν 0.3 (44.3 − 20.3)×106 ε 2 = − (σ 1 + σ 3 ) = − E 210 ×109 = −34.3 ×10 −6
§10-5 应力与应变之间的关系 101、各向同性材料的广义胡克定律 单向应力状态: 1)单向应力状态:
s
σ ≤ σ P 时, ε x =
横向线应变: 横向线应变:
σ
E
ε y = −ν
纯剪应力状态: 2)纯剪应力状态:
tx
σ
E
ε z = −ν
σ
E
τ ≤ τ P 时,
γ xy =
τx
G
1
gxy
空间应力状态: 3)空间应力状态:
1 ε x = (σ x −νσ y ) E 1 ε y = (σ y −νσ x ) E
εz = − γ xy
ν
E 1 = τ xy G
(σ
x
+σ y )
5
若用主应力和主应变来表示广义胡克定律, 若用主应力和主应变来表示广义胡克定律,有:
σ2 = 0
即为平面应力状态, 即为平面应力状态,有
1 ε 1 = (σ 1 −νσ 3 ) E
1 ε 3 = (σ 3 −νσ 1 ) E
8
E 210 ×10 (ε1 +νε 3 ) = (240 − 0.3 ×160)×10 −6 σ1 = 1 −ν 2 1 − 0.32 = 44.3MPa E 210 ×109 (ε 3 +νε 1 ) = (− 160 + 0.3 × 240)×10−6 σ3 = 1 −ν 2 1 − 0. 3 2 = −20.3MPa 主应变ε2为: ν 0.3 (44.3 − 20.3)×106 ε 2 = − (σ 1 + σ 3 ) = − E 210 ×109 = −34.3 ×10 −6
§10-5 应力与应变之间的关系 101、各向同性材料的广义胡克定律 单向应力状态: 1)单向应力状态:
s
σ ≤ σ P 时, ε x =
横向线应变: 横向线应变:
σ
E
ε y = −ν
纯剪应力状态: 2)纯剪应力状态:
tx
σ
E
ε z = −ν
σ
E
τ ≤ τ P 时,
γ xy =
τx
G
1
gxy
空间应力状态: 3)空间应力状态:
1 ε x = (σ x −νσ y ) E 1 ε y = (σ y −νσ x ) E
εz = − γ xy
ν
E 1 = τ xy G
(σ
x
+σ y )
5
若用主应力和主应变来表示广义胡克定律, 若用主应力和主应变来表示广义胡克定律,有:
第四章 应力和应变的关系

121112111211xyxyyzyzzxzx第三节各向同性体中的弹性常数c沿二轴转动任何角度后的方向弹性关系相121112121112121112xyxyyzyzzxzx第三节各向同性体中的弹性常数当绕z轴转一角度第三节各向同性体中的弹性常数利用ijsinxy1211121144变换后有因此有由原式第常数中只有2个独立
σ = c ε + c (ε + ε ) y 11 y 12 x z σ z = c11ε z + c12 (ε x + ε y )
σ x = c11ε x + c12 (ε y + ε z )
τ = c 44 γ xy xy τ =c γ 44 yz yz τ zx = c 44 γ zx
= c 44 γ
= c 44 γ
xy
yz
τ
zx
= c 44 γ
zx
第三节 各向同性体中的弹性常数 当绕Z轴转一角度 α 时,即 x y
m1 = sin α
z ( z ')
z
n1 = 0 n2 = 0 n3 = 1
x
x'
y'
α
y
x′
y′
l1 = cos α
α
l2 = − sin α m2 = cos α l3 = 0 m3 = 0
c41 = c42 = c43 = 0 c51 = c52 = c53 = 0 c61 = c62 = c63 = 0 只能证9个数为0
第三节 各向同性体中的弹性常数 (2)沿任意两个相反的方向,弹性关系相同。 如只改变z轴方向,w和z的方向改变,则
γ yz
∂w ∂v = + = −γ yz′ ∂y ∂z
σ = c ε + c (ε + ε ) y 11 y 12 x z σ z = c11ε z + c12 (ε x + ε y )
σ x = c11ε x + c12 (ε y + ε z )
τ = c 44 γ xy xy τ =c γ 44 yz yz τ zx = c 44 γ zx
= c 44 γ
= c 44 γ
xy
yz
τ
zx
= c 44 γ
zx
第三节 各向同性体中的弹性常数 当绕Z轴转一角度 α 时,即 x y
m1 = sin α
z ( z ')
z
n1 = 0 n2 = 0 n3 = 1
x
x'
y'
α
y
x′
y′
l1 = cos α
α
l2 = − sin α m2 = cos α l3 = 0 m3 = 0
c41 = c42 = c43 = 0 c51 = c52 = c53 = 0 c61 = c62 = c63 = 0 只能证9个数为0
第三节 各向同性体中的弹性常数 (2)沿任意两个相反的方向,弹性关系相同。 如只改变z轴方向,w和z的方向改变,则
γ yz
∂w ∂v = + = −γ yz′ ∂y ∂z
塑性应力应变关系

z
z
ϕLeabharlann ij m(7.2—13) (7.2—14)
ε = ϕ ⋅τ ,
xy
xy
ε = ϕ ⋅τ ,
yz
yz
ε zx = ϕ ⋅τ zx
如果认为在整个变形过程中材料不可压缩,泊松比ν = 0.5 ,则 K 0 = 0 ,式(7.2—13) 简化为:
ε ij = ϕ (σ ij − δ σij m ) = ϕ ⋅ sij
(7.1—10)
可见,服从广义胡克定律的各向同性线弹性材料,其应力莫尔圆与应变莫尔圆在几何
上是相似的,应力罗代参数 µ σ 等于应变罗代参数 µ ε 。等效应力与等效应变之间也有简 单关系。由等效应力定义式得:
σ= 1 2
(σ 1
−σ
)2
2
+ (σ
2
−σ 3)2
+ (σ
3
−σ1)2
= 2G 2
(ε 1 − ε 2 ) 2 + (ε 2 − ε 3 ) 2 + (ε 3 − ε 1 ) 2
+
eP ij
+ δ ij ε m
=
1 2G
s ij
+
φ 2G
s ij
+ 1− 2ν E
δσ ij m
=
1+φ 2G
s ij
+ 1− 2ν E
δ ijσ m
(7.2—12)
令 1+φ 2G
=ϕ
, 1− 2ν E
=
K 0 ,式(7.2—12)可改写成汉基理论的常用表达式:
ε ij = ϕs ij + K 0 δ ij σ m
求解小弹塑性变形问题,等同于求解某一非线性弹性力学问题,因此获得了广泛的应用。
