第三章 静态电磁场及其边值问题的解(课后题)
合集下载
谢处方《电磁场与电磁波》(第4版)课后习题-第3章 静态电磁场及其边值问题的解【圣才出品】
第3章 静态电磁场及其边值问题的解（一）思考题3.1 电位是如何定义的？中的负号的意义是什么？答：由静电场基本方程▽×E＝0和矢量恒等式可知，电场强度E 可表示为标量函数φ的梯度，即式中的标量函数φ称为静电场的电位函数，简称电位；式中负号表示场强方向与该点电位梯度的方向相反。
3.2“如果空间某一点的电位为零，则该点的电场强度也为零”，这种说法正确吗？为什么？答：不正确。
因为电场强度大小是该点电位的变化率。
3.3“如果空间某一点的电场强度为零，则该点的电位为零”，这种说法正确吗？为什么？答：不正确。
此时该点电位可能是任一个不为零的常数。
3.4 求解电位函数的泊松方程或拉普拉斯方程时，边界条件有何意义？答：边界条件起到给方程定解的作用。
3.5 电容是如何定义的？写出计算电容的基本步骤。
答：两导体系统的电容为任一导体上的总电荷与两导体之间的电位差之比，即其基本计算步骤：①根据导体的几何形状，选取合适坐标系；②假定两导体上分别带电荷＋q和－q；③根据假定电荷求出E；④由求得电位差；⑤求出比值3.6 多导体系统的部分电容是如何定义的？试以考虑地面影响时的平行双导线为例，说明部分电容与等效电容的含义。
答：多导体系统的部分电容是指多导体系统中一个导体在其余导体的影响下，与另一个导体构成的电容。
计及大地影响的平行双线传输线，如图3-1-1所示，它有三个部分电容C11、C12和C22，导线1、2间的等效电容为；导线1和大地间的等效电容为；导线2和大地间的等效电容为图3-1-13.7 计算静电场能量的公式和之间有何联系？在什么条件下二者是一致的？答：表示连续分布电荷系统的静电能量计算公式，虽然只有ρ≠0的区域才对积分有贡献，但不能认为静电场能量只存在于有电荷区域，它只适用静电场。
表示静电场能量存在于整个电场区域，所有E≠0区域对积分都有贡献，既适用于静电场，也用于时变电磁场，当电荷分布在有限区域内，闭合面S无限扩大时，有限区内的电荷可近似为点电荷时，二者是一致的。
3 静态电磁场及其边值问题全
2
边界条件
en E1 E2 0或者
en D1 D2 S 或者
3.1.2 电位函数
一、电位函数与电位差 电位函数 E 0 E 可由一标量函数表示。 ( ) 0 引入电位函数 ：E 关于电位函数的讨论
r
aU aU E dr 2 dr r r r
19
小结：求空间电场分布的方法
1、场源积分法 积分困难，对大多数问题不能得出解析解。 2、应用高斯定理求解 只能应用于电荷成对称分布的问题。 3、间接求解法 先求解空间电位分布，再求解空间电场。 在实际工程应用中，间接求解法应用最为广泛，适用于边值 问题的求解。
电位函数为电场的辅助函数，是一个标量函数； “－”表示电场指向电位减小最快的方向； 在直角坐标系中
E ex ey ez x y z
3
电位差（电压）
电位差反映了电场空间中不同位置处电位的变化量。 电位差的计算：
el l el 为 增加最快的方向 E el d E dl l B A AB B A Edl E dl
解法二：电荷均匀分布在导体球上，呈点对称。 设导体球带电总量为Q，则可由高斯定理求得，在球外空间，电场 强度为：
E
Q 4 0 r 2
er
Q 1 Q U E dr ( ) Q 4 0 aU a 4 0 r a 4 0 a aU E 2 er r
13
例题3.1.3两块无限大接地导体平板分别置于x=0和x=a 处，在两板之间x=b处有一面密度为SO的均匀电荷分 布。求两导体平板之间的电位和电场。 解：两板之间除x=b外电位函数方程：
边界条件
en E1 E2 0或者
en D1 D2 S 或者
3.1.2 电位函数
一、电位函数与电位差 电位函数 E 0 E 可由一标量函数表示。 ( ) 0 引入电位函数 ：E 关于电位函数的讨论
r
aU aU E dr 2 dr r r r
19
小结：求空间电场分布的方法
1、场源积分法 积分困难，对大多数问题不能得出解析解。 2、应用高斯定理求解 只能应用于电荷成对称分布的问题。 3、间接求解法 先求解空间电位分布，再求解空间电场。 在实际工程应用中，间接求解法应用最为广泛，适用于边值 问题的求解。
电位函数为电场的辅助函数，是一个标量函数； “－”表示电场指向电位减小最快的方向； 在直角坐标系中
E ex ey ez x y z
3
电位差（电压）
电位差反映了电场空间中不同位置处电位的变化量。 电位差的计算：
el l el 为 增加最快的方向 E el d E dl l B A AB B A Edl E dl
解法二：电荷均匀分布在导体球上，呈点对称。 设导体球带电总量为Q，则可由高斯定理求得，在球外空间，电场 强度为：
E
Q 4 0 r 2
er
Q 1 Q U E dr ( ) Q 4 0 aU a 4 0 r a 4 0 a aU E 2 er r
13
例题3.1.3两块无限大接地导体平板分别置于x=0和x=a 处，在两板之间x=b处有一面密度为SO的均匀电荷分 布。求两导体平板之间的电位和电场。 解：两板之间除x=b外电位函数方程：
第3章静态场的边值问题及解的唯一性定理
r
O
d
P(r, ) R q
处理方法：电位叠加原理：
1、先假设导体球面接地，则球面上存在电量为q' 的感应电荷， 镜像电荷可采用前面的方法确定q a q, d。 a2 2、为了满足电荷守恒原理。断开接地d线，将电d量为-q'的电荷加 到导体球面上，使这些电荷均匀分布在球面上，使导体球为等势 体，且表面总电荷为零。
l′
2 x2 (z h)2
均匀带电直线的电位分布
z 0，R R z0 0
l ln R C l ln R0
2
2 R
显然，满足边界条件。所以，原问题不变，所得的解是正确的。
11
第3 章
例3. 点电荷对相交半无限大接地导体平面的镜像 如图所示，两个相互垂直相连的半无限大接地导体平板，点
像把导体平面抽走一样，用两点电荷的场叠加计算。
7
第3 章
解：用一个处于镜像位置的点电荷代替导体边界的影响， 则z>0空间任一点 P 的电位由 q 及 q' 共同产生，即
q q 1 (
q
q
)
4π0 r 4π0 r 4π0 x2 y2 (z h)
x2 y2 (z h)2
l
2π
r r er
以r 0 为参考点，则电位
r r0
Edr
l 2π
ln
r0 r
l 2π
ln
1 r
C
1）长直线电荷与接地的长直圆柱导体平行，求圆柱外电位分布
在圆柱与线电荷之间，在圆柱内离轴线的距离b 处，平行放置一
根镜像线电荷 ， 代替圆柱导体上的感应电荷.
电磁场理论(柯亨玉)答案第三章静态电磁场.pdf
由B A
得： Az Ay 0 y z
Ax Az 0 z x
Ay x
Ax y
B0
可得一解为： Az Ay 0
还可得另一解为： Ax Az 0
还存在其它解。 两者之差的旋度：
Ax B0 y Ay B0 x
eˆx eˆy eˆz
( Ayeˆy Axeˆx ) (B0 xeˆy B0 yeˆx )
磁失势的引入及方程的推导过程我们以图解的方式表示其中引入的条件是无传导电流的单连通区域如电流是环形分布的磁标势适合的区域只能是挖去环形电流所围成的壳形之后剩下的区域
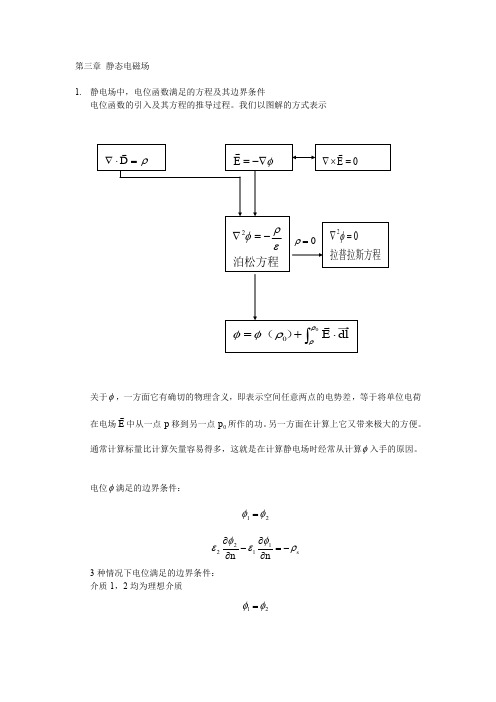
第三章 静态电磁场
1. 静电场中，电位函数满足的方程及其边界条件 电位函数的引入及其方程的推导过程。我们以图解的方式表示
D
E
x
0 y z
B0 y B0 x 0
3-10. 证明：设线圈中的电流分别为 I1, I 2
线圈 1 对线圈 2 的作用力为
f12
0 4
I
2
dl2
(I1
dl1r12 )
L1 L2
r132
0 I1I2
dl2
(dl1r12 )
4
L1 L2
r132
0 I1I 2
[(dl2 r12 )dl1 (dl1 dl2 )r12 ]
设介质被抽出的一段长为 x ， C 便等于无介质部分的电容 C1 与有介质部分的电容
C2 的迭加，即
C
C1
C2
2 0 x ln(b a)
2 (L x) ln(b a)
2 [L ln(b a)
(
0
)x]
则 W V2 C 2
V2 2
2 [L ( ln(b a)
静态电磁场及其边值问题的解chap3
ϕ ( P) = ∫
∞
P
v v E ⋅d l
（以无限远处为零电位做参考，任意点P的电位表示） 以无限远处为零电位做参考，任意点P的电位表示）
2、静电位的微分方程
v E = −∇ϕ ⇒ D = ε E = −ε∇ϕ
∇ ⋅ D = ρ ⇒ ∇⋅ ( −ε∇ϕ ) = ρ ⇒ ∇⋅ ( ∇ϕ ) = − ρ ⇒ ∇2ϕ = − ρ
ρS = 0
∂ϕ1 ∂ϕ2 ε1 =ε2 ∂n ∂n
导体
∂ϕ ε =−ρS ∂n
【例3.1.1】 求电偶极子 p = qdl 的电位 ϕ ( r ) 3.1.1】
当
z
+q d
r+ r− = r
P ( r,θ ,ϕ )
r >> d 1 1 1 ≈ + 2 d cosθ r+ r r
因此
ϕ=
θ
−q
解：取如图所示坐标系，场点 P ( r,θ ,ϕ ) 取如图所示坐标系， 的电位等于两个点电荷电位的叠加
a a
Cl =
ρl
U
=
D−a ln a
πε 0
≈
πε 0
ln( D / a)
ρl 1 ρl D − a 1 ( + )dx = ln 2πε 0 x D − x πε 0 a
F /m
【例3.1.5】同轴线的内导体的半径为a，外导 3.1.5】同轴线的内导体的半径为a 体的半径为b 体的半径为b，内外导体间填充介电常数为 ε 的均匀电介质，试求同轴线单位长度的电容。 的均匀电介质，试求同轴线单位长度的电容。
电 位 的 泊 松 方 程
ε
ε
若空间电荷分布为零， 若空间电荷分布为零，则有 ∇2ϕ = 0
《电磁场与电磁波》习题参考答案
况下，电场和磁场可以独立进行分析。（ √ ）
12、静电场和恒定磁场都是矢量场，在本质上也是相同的。（ × ）
13、静电场是有源无旋场，恒定磁场是有旋无源场。（ √ ） 14、位移电流是一种假设，因此它不能象真实电流一样产生磁效应。（
×）
15、法拉第电磁感应定律反映了变化的磁场可以产生变化的电场。（ √ ） 16、物质被磁化问题和磁化物质产生的宏观磁效应问题是不
D.有限差分法
6、对于静电场问题，仅满足给定的泊松方程和边界条件，
而形式上不同的两个解是不等价的。（ × ）
7、研究物质空间内的电场时，仅用电场强度一个场变量不能完全反映物 质内发生的静电现象。（ √ ）
8、泊松方程和拉普拉斯方程都适用于有源区域。（ × ）
9、静电场的边值问题，在每一类的边界条件下，泊松方程或拉普拉斯方 程的解都是唯一的。（ √ ）
是（ D ）。
A．镜像电荷是否对称
B．电位所满足的方程是否未改变
C．边界条件是否保持不变 D．同时选择B和C
5、静电场边值问题的求解，可归结为在给定边界条件下，对拉普拉斯
方程的求解，若边界形状为圆柱体，则宜适用( B )。
A.直角坐标中的分离变量法
B.圆柱坐标中的分离变量法
C.球坐标中的分离变量法
两个基本方程：
3、写出麦克斯韦方程组，并简述其物理意义。
答：麦克斯韦方程组的积分形式：
麦克斯韦方程组的微分形式：
每个方程的物理意义： (a) 安培环路定理，其物理意义为分布电流和时变电场均为磁
场的源。 (b) 法拉第电磁感应定律，表示时变磁场产生时变电场，即动
磁生电。 (c) 磁场高斯定理，表明磁场的无散性和磁通连续性。 (d)高斯定理，表示电荷为激发电场的源。
静态电磁场及其边值问题的解
E dl
A
P
定义点A电位： A
E dl
A
(P 为参考点，P 0 )
说明：
① 电位有明确的物理意义；
② 电位差与参考点的选择无关；
③ 同一问题中只能有一个参考点；
④ 选择电位参考点的原则是电位表达式要有意义，
应使电位表达式最简单：
电荷分布在有限区域时一般是无穷远为参考点，
, )
C
C
p cos 4 0r 2
中，p、0 为常数
故 等位面方程：r C1 cos (可画出 r 对 的曲线) ，而
dr Er
rd
E
r sind
E
dr
2 cos
rd sin
dr r
2d (sin sin
)
r
C2 sin2
第19页
[例] 求如图所示同轴电容器的电场和单位长度电容。
解：问题的边界条件是：
① a ， a ； b ， b
② 介质分界面上: E1t E2t，D1n D2n
用高斯定律试探解： E 1 , D 1
设
C
E1 E2 e
，C为常数，则
4 0r1r2 4 0r 2
定义电偶极矩矢量：
p qd
(单位 C m )
p cos 4 0r 2
p er
4 0r 2
p r
4 0r 3
p
4 0
1 r
第17页
电磁场与电磁波 第三章__静态电磁场及其边值问题的解
电磁场与波第3章 静态电磁场及其边值问题的解
第3章
静态电磁场及其边值 问题的解
时变情况下，电场和磁场相互关联，构成统一的电磁场 当场源不随时间变化时，激发不随时间变化的静态场 静态情况下，电场和磁场由各自的源激发，且相互独立
3.1 静电场分析
3.1.1 静电场的基本方程和边界条件
基本方程
D d S
S
dV
V
E d l 0
M P
E d l
rQ rPΒιβλιοθήκη Q ME d l
l
2 0 rQ rP
Q M
r r
2
d r
rQ
M
l
2 0
1 r
dr
l
2 0
ln
如果选择参考点在rQ=∞，得P=∞，显然不合理。 如果选择rQ=1，得 P
O
rP
P
l
2 0
ln
1 rP
，显然这种形式最简单。
,
D2
S 0b 0
最后得
1 ( x ) 2 ( x) 0a S 0b 0a
S 0 (a b)
(0 ≤ x ≤ b ) (b ≤ x ≤ a )
所以 D1 0
C 2 a D2 0 C1b D1 C 2 b D2 C 2 C1
d 1 ( x )
2
dx
2
2
0,
(0 x b)
y
S0
d 2 ( x) dx
2
1 ( x ) 2 ( x)
0,
(b x a )
o
b
a
x
方程的解为 1 ( x ) C1 x D1
静态电磁场及其边值 问题的解
时变情况下，电场和磁场相互关联，构成统一的电磁场 当场源不随时间变化时，激发不随时间变化的静态场 静态情况下，电场和磁场由各自的源激发，且相互独立
3.1 静电场分析
3.1.1 静电场的基本方程和边界条件
基本方程
D d S
S
dV
V
E d l 0
M P
E d l
rQ rPΒιβλιοθήκη Q ME d l
l
2 0 rQ rP
Q M
r r
2
d r
rQ
M
l
2 0
1 r
dr
l
2 0
ln
如果选择参考点在rQ=∞，得P=∞，显然不合理。 如果选择rQ=1，得 P
O
rP
P
l
2 0
ln
1 rP
，显然这种形式最简单。
,
D2
S 0b 0
最后得
1 ( x ) 2 ( x) 0a S 0b 0a
S 0 (a b)
(0 ≤ x ≤ b ) (b ≤ x ≤ a )
所以 D1 0
C 2 a D2 0 C1b D1 C 2 b D2 C 2 C1
d 1 ( x )
2
dx
2
2
0,
(0 x b)
y
S0
d 2 ( x) dx
2
1 ( x ) 2 ( x)
0,
(b x a )
o
b
a
x
方程的解为 1 ( x ) C1 x D1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
−1
由条件ϕ (a, φ ) = C，有 − E0 ρ cos φ + A1 ρ cos φ + C = C得A1 = a E0
−1 2
故圆柱外的电位为ϕ ( ρ , φ )＝(− ρ + a 2 ρ −1 ) E0 cos φ + C 若选择导体圆柱表面为电位参考点， 即ϕ (a, φ ) = C，故C = 0
2
µ0 I 2 b µ1µ 2 I 2 = + ln 16π 2π ( µ1 + µ 2 ) a
1 2 (2)由Wm = LI ，得到单位长度的自感为 2 µ1µ 2 2Wm µ 0 b L= 2 = + ln I 8π π ( µ1 + µ 2 ) a
3.22一个点电荷q放在60o的接地导体角域内的点(1,1,0)处，如图所示。 求：（ ）所有镜像电荷的位置和大小（2）P (2,1,0)处的电位 1
q
(2,1,0) x
q’3 q’4
q’5
' x4 = ' q4 = q , ' y4 = ' x5 = ' q5 = −q, ' y5 =
(2)点P (2,1,0)处的电位 ′ ′ ′ ′ ′ 1 q q1 q2 q3 q4 q5 ( + + + + + ) ϕ (2,1,0) = 4πε 0 R R1 R2 R3 R4 R5 0.321 = q = 2.89 × 109 qV 4πε 0
电位的边界条件为： 1.ϕ1 ( x,0) = ϕ1 ( x, a) = 0
y
ϕ 2 ( x,0) = ϕ 2 ( x, a ) = 0 2.ϕ1 ( x, y ) → 0, ( x → ∞) ϕ 2 ( x, y ) → 0, ( x → −∞)
d
qlห้องสมุดไป่ตู้
a x
∂ϕ 2 ∂ϕ1 qlδ ( y − y0 ) 3.ϕ1 (0, y ) = ϕ 2 (0, y ), ( − ) = ∂x ∂x x =0 ε0
同轴线中单位长度储存的磁场能量为
2 2 2
( a < ρ < b)
1 a B0 1 b B1 1 b B2 Wm = ∫ 2πρdρ + ∫ πρdρ + ∫ πρdρ 2 0 µ0 2 a µ1 2 a µ2 1 a 1 µ 0 Iρ 2 1 1 1 b µ1µ 2 I = ∫ ( ) 2πρdρ + ( + ) ∫ πρdρ 2 2 0 µ 0 2πa 2 µ1 µ 2 a π ( µ1 + µ 2 ) ρ
解：（ ）设沿厚度方向的两电极的电压为U1，则有 1 U1 σU1 E1 = ⇒ J1 = σE1 = d d σU1 α 2 2 I1 = J1S1 = ⋅ (r2 − r1 ) d 2 故得到沿厚度方向的电阻为 U1 2d R1 = = I1 ασ (r22 − r12 )
d
(2)设内外两圆弧面电极之间的电流为I 2 , 则 I2 I2 = J2 = S 2 αrd U2 = ∫
q’2
60 O
解：（1 ）这是一个多重镜像的问题，
2 cos 75o = 0.366 2 sin 75o = 1.366 2 cos165o = −1.366 2 sin 165o = 0.366 2 cos195o = −1.366 2 sin 195o = −0.366 2 cos 285o = 0.366 2 sin 285o = −1.366 2 cos 315o = 1 2 sin 315o = −1
解：同轴线的内外导体之间的磁场沿φ方向，在两种 磁介质的分界面上磁场只有法向分量。根据边界条件 可知，两种磁介质中的磁感应强度 B1 = B2 = B = eφ B (1)由安培环路定理，当ρ < a
µ2 µ1 a b
µ0 I 2 2πρB0 = 2 πρ πa
µ0 I ∴ B0 = ρ ( ρ < a) 2 2πa 当a < ρ < b区域内，有πρ ( H1 + H 2 ) = I B1 B2 µ1µ 2 I 即πρ（ + ） I , 故B = eφ = µ1 µ 2 π ( µ1 + µ 2 ) ρ
ql • 3.8证明：同轴线单位长度的静电储能 We = 2C
证明：由高斯定理可以求出同轴线内、外导体间的电场强度为 ql E(ρ ) = 2περ 内外导体间的电压为 U = ∫ Edρ = ∫ ql b ln a a 2περ 2πε a ql 2πε 则同轴线单位长度的电容为C = = U ln(b a )
在磁介质表面，磁化电流的面密度为 J mS = M × ez
z =0
(µ − µ0 ) I = eρ 2πµ0 ρ
• 3.19 同轴线的内导体是半径为a的圆柱，外导体是 半径为b的薄圆柱面，其厚度可以忽略不计。内、 外导体之间填充有磁导率分别为µ1、 µ2两种不同的 磁介质，设同轴线中通过的电流为I。试求（1）同 轴线中单位长度所储存的磁场能量（2）单位长度 的自感
∞
1 nπd nπx / a nπy ϕ 2 ( x, y ) = ∑ n sin( a )e sin ( a ), ( x < 0) πε 0 n =1 ql
∞
3.31在均匀电场中垂直于电场方向放置一根半径为a的 无限长导体圆柱。求导体圆柱外的电位和电场强度， 并求导体圆柱表面的感应电荷密度。 解：圆柱外的电场是外电场与感应电荷产生电场的叠 加，同时由于导体圆柱为无限长，电位与变量z无关。 在圆柱坐标系中，外电场的电位为
2 由条件1、，可以取位函数的通解为
ϕ1 ( x, y ) = ∑ An e
n =1 ∞
∞
− nπx / a
nπy sin ( ), ( x > 0) a
ϕ 2 ( x, y ) = ∑ Bn e
n =1 ∞
nπx / a
nπy sin ( ), ( x < 0) a
∞ nπy nπy 由条件3有： An sin ( ) = ∑ Bn sin ( ) ⇒ An = Bn ∑ a a n =1 n =1 ∞ qlδ ( y − d ) nπ nπy nπ nπy ∑ An a sin ( a ) + ∑ Bn a sin ( a ) = ε n =1 n =1 0 ∞
3.30两块平行无限大接地导体板，两板之间有一与z轴平行的 线电荷ql，其位置为(0，d )。求板间的电位分布。 解：由于在(0, d )处有一与z轴平行的线电荷ql，以x = 0为界将 场空间分割为x > 0, x < 0两个区域。这两个区域中的电位ϕ1、
ϕ 2都满足拉普拉斯方程。而在x = 0的分界面上, 可利用δ函数 将线电荷表示成电荷面密度ρ S ( y ) = qlδ ( y − y0 )
r2 r1
I2 ⇒ E2 = = σ σαrd
J2
I2 r2 ln E2 dr = σαd r1
故得到两圆弧面之间的电阻为 U2 1 r2 R2 = = ln I 2 σαd r1
(3)设沿α方向的两电极的电压为U 3，则有 U 3 = ∫ E3rdφ
0
α
U3 由于E3大小与φ无关，故得E3 = eφ αr σU 3 J 3 = σE3 = eφ αr
nπy 将上式两边同乘以 sin( )，并从0到a对y积分，有 a 2ql a 2ql nπy nπd An + Bn = ∫0 δ ( y − d ) sin( a )dy = nπε 0 sin( a ) nπε 0
nπd sin( ) 解得An = Bn = nπε 0 a ql 故： 1 nπd − nπx / a nπy ϕ1 ( x, y ) = ∑ n sin( a )e sin ( a ), ( x > 0) πε 0 n =1 ql
b b
2
ql
dρ =
则同轴线单位长度的静电储能为： 1 1 b ql 2 1 ql b ql 2 We = ∫ ε E dV = ∫ ε ( ) 2πρdρ = ln = 2 V 2 a 2περ 2 2πε a 2C
2 2
• 3.13 在一块厚度为d的导电板上，由两个半径分别为 r1和r2的圆弧和夹角为α的两半径割出的一块扇形体。 试求(1)沿厚度方向的电阻（2）两圆弧之间的电阻 （3）沿α方向的电阻。设导电板的电导率为σ
I 3 = ∫ J 3 ⋅ eφ dS
S3
σdU 3 σdU 3 r2 =∫ dr = ln r r1 αr α 故得到沿α方向的电阻为 U3 α R3 = = I 3 σd ln(r2 r1 )
r2
1
• 3.15无限长直线电流I垂直于两种磁介质的分界面， 试求（1）两种磁介质中的磁感应强度（2）磁化 电流的分布
0
ψ=0 ρ(x)
ψ=U0
ρ d3 故U 0 = － + Ad 6ε 0 d U ρ d 得A = + 6ε 0 d
0 0 0
0
d
ρ x3 U ρ d ∴ϕ = − +( + )x 6ε 0 d 6ε 0 d
0 0 0
ρ 0 x2 U 0 ρ 0 d ∂ϕ E = −∇ϕ = −ex = ex −( + ) ∂x d 6ε 0 2ε 0 d
第三章 静态电磁场及其边值问 题的解
课后练习题
• 3.2 一个点电荷q1=q位于点P1(-a,0,0)，另一点电荷 q2=－2q位于点P2(a,0,0)，求空间的零电位面。
解：两个点电荷在空间产生的电位 q 1 2q − ϕ ( x, y , z ) = 2 2 2 2 2 2 4πε 0 ( x + a ) + y + z ( x − a) + y + z q 2q 令ϕ ( x, y, z ) = 0，则有 − ＝0 2 2 2 2 2 2 ( x + a) + y + z ( x − a) + y + z 即 : 4 ( x + a) 2 + y 2 + z 2 = ( x − a) 2 + y 2 + z 2 5 5 故得： + a ) 2 + y 2 + z 2 = ( a ) 2 (x 3 3 5 4 ∴ 零电位面方程是一个以点（ − a,0,0）为球心，以 a为半径的球面 3 3
由条件ϕ (a, φ ) = C，有 − E0 ρ cos φ + A1 ρ cos φ + C = C得A1 = a E0
−1 2
故圆柱外的电位为ϕ ( ρ , φ )＝(− ρ + a 2 ρ −1 ) E0 cos φ + C 若选择导体圆柱表面为电位参考点， 即ϕ (a, φ ) = C，故C = 0
2
µ0 I 2 b µ1µ 2 I 2 = + ln 16π 2π ( µ1 + µ 2 ) a
1 2 (2)由Wm = LI ，得到单位长度的自感为 2 µ1µ 2 2Wm µ 0 b L= 2 = + ln I 8π π ( µ1 + µ 2 ) a
3.22一个点电荷q放在60o的接地导体角域内的点(1,1,0)处，如图所示。 求：（ ）所有镜像电荷的位置和大小（2）P (2,1,0)处的电位 1
q
(2,1,0) x
q’3 q’4
q’5
' x4 = ' q4 = q , ' y4 = ' x5 = ' q5 = −q, ' y5 =
(2)点P (2,1,0)处的电位 ′ ′ ′ ′ ′ 1 q q1 q2 q3 q4 q5 ( + + + + + ) ϕ (2,1,0) = 4πε 0 R R1 R2 R3 R4 R5 0.321 = q = 2.89 × 109 qV 4πε 0
电位的边界条件为： 1.ϕ1 ( x,0) = ϕ1 ( x, a) = 0
y
ϕ 2 ( x,0) = ϕ 2 ( x, a ) = 0 2.ϕ1 ( x, y ) → 0, ( x → ∞) ϕ 2 ( x, y ) → 0, ( x → −∞)
d
qlห้องสมุดไป่ตู้
a x
∂ϕ 2 ∂ϕ1 qlδ ( y − y0 ) 3.ϕ1 (0, y ) = ϕ 2 (0, y ), ( − ) = ∂x ∂x x =0 ε0
同轴线中单位长度储存的磁场能量为
2 2 2
( a < ρ < b)
1 a B0 1 b B1 1 b B2 Wm = ∫ 2πρdρ + ∫ πρdρ + ∫ πρdρ 2 0 µ0 2 a µ1 2 a µ2 1 a 1 µ 0 Iρ 2 1 1 1 b µ1µ 2 I = ∫ ( ) 2πρdρ + ( + ) ∫ πρdρ 2 2 0 µ 0 2πa 2 µ1 µ 2 a π ( µ1 + µ 2 ) ρ
解：（ ）设沿厚度方向的两电极的电压为U1，则有 1 U1 σU1 E1 = ⇒ J1 = σE1 = d d σU1 α 2 2 I1 = J1S1 = ⋅ (r2 − r1 ) d 2 故得到沿厚度方向的电阻为 U1 2d R1 = = I1 ασ (r22 − r12 )
d
(2)设内外两圆弧面电极之间的电流为I 2 , 则 I2 I2 = J2 = S 2 αrd U2 = ∫
q’2
60 O
解：（1 ）这是一个多重镜像的问题，
2 cos 75o = 0.366 2 sin 75o = 1.366 2 cos165o = −1.366 2 sin 165o = 0.366 2 cos195o = −1.366 2 sin 195o = −0.366 2 cos 285o = 0.366 2 sin 285o = −1.366 2 cos 315o = 1 2 sin 315o = −1
解：同轴线的内外导体之间的磁场沿φ方向，在两种 磁介质的分界面上磁场只有法向分量。根据边界条件 可知，两种磁介质中的磁感应强度 B1 = B2 = B = eφ B (1)由安培环路定理，当ρ < a
µ2 µ1 a b
µ0 I 2 2πρB0 = 2 πρ πa
µ0 I ∴ B0 = ρ ( ρ < a) 2 2πa 当a < ρ < b区域内，有πρ ( H1 + H 2 ) = I B1 B2 µ1µ 2 I 即πρ（ + ） I , 故B = eφ = µ1 µ 2 π ( µ1 + µ 2 ) ρ
ql • 3.8证明：同轴线单位长度的静电储能 We = 2C
证明：由高斯定理可以求出同轴线内、外导体间的电场强度为 ql E(ρ ) = 2περ 内外导体间的电压为 U = ∫ Edρ = ∫ ql b ln a a 2περ 2πε a ql 2πε 则同轴线单位长度的电容为C = = U ln(b a )
在磁介质表面，磁化电流的面密度为 J mS = M × ez
z =0
(µ − µ0 ) I = eρ 2πµ0 ρ
• 3.19 同轴线的内导体是半径为a的圆柱，外导体是 半径为b的薄圆柱面，其厚度可以忽略不计。内、 外导体之间填充有磁导率分别为µ1、 µ2两种不同的 磁介质，设同轴线中通过的电流为I。试求（1）同 轴线中单位长度所储存的磁场能量（2）单位长度 的自感
∞
1 nπd nπx / a nπy ϕ 2 ( x, y ) = ∑ n sin( a )e sin ( a ), ( x < 0) πε 0 n =1 ql
∞
3.31在均匀电场中垂直于电场方向放置一根半径为a的 无限长导体圆柱。求导体圆柱外的电位和电场强度， 并求导体圆柱表面的感应电荷密度。 解：圆柱外的电场是外电场与感应电荷产生电场的叠 加，同时由于导体圆柱为无限长，电位与变量z无关。 在圆柱坐标系中，外电场的电位为
2 由条件1、，可以取位函数的通解为
ϕ1 ( x, y ) = ∑ An e
n =1 ∞
∞
− nπx / a
nπy sin ( ), ( x > 0) a
ϕ 2 ( x, y ) = ∑ Bn e
n =1 ∞
nπx / a
nπy sin ( ), ( x < 0) a
∞ nπy nπy 由条件3有： An sin ( ) = ∑ Bn sin ( ) ⇒ An = Bn ∑ a a n =1 n =1 ∞ qlδ ( y − d ) nπ nπy nπ nπy ∑ An a sin ( a ) + ∑ Bn a sin ( a ) = ε n =1 n =1 0 ∞
3.30两块平行无限大接地导体板，两板之间有一与z轴平行的 线电荷ql，其位置为(0，d )。求板间的电位分布。 解：由于在(0, d )处有一与z轴平行的线电荷ql，以x = 0为界将 场空间分割为x > 0, x < 0两个区域。这两个区域中的电位ϕ1、
ϕ 2都满足拉普拉斯方程。而在x = 0的分界面上, 可利用δ函数 将线电荷表示成电荷面密度ρ S ( y ) = qlδ ( y − y0 )
r2 r1
I2 ⇒ E2 = = σ σαrd
J2
I2 r2 ln E2 dr = σαd r1
故得到两圆弧面之间的电阻为 U2 1 r2 R2 = = ln I 2 σαd r1
(3)设沿α方向的两电极的电压为U 3，则有 U 3 = ∫ E3rdφ
0
α
U3 由于E3大小与φ无关，故得E3 = eφ αr σU 3 J 3 = σE3 = eφ αr
nπy 将上式两边同乘以 sin( )，并从0到a对y积分，有 a 2ql a 2ql nπy nπd An + Bn = ∫0 δ ( y − d ) sin( a )dy = nπε 0 sin( a ) nπε 0
nπd sin( ) 解得An = Bn = nπε 0 a ql 故： 1 nπd − nπx / a nπy ϕ1 ( x, y ) = ∑ n sin( a )e sin ( a ), ( x > 0) πε 0 n =1 ql
b b
2
ql
dρ =
则同轴线单位长度的静电储能为： 1 1 b ql 2 1 ql b ql 2 We = ∫ ε E dV = ∫ ε ( ) 2πρdρ = ln = 2 V 2 a 2περ 2 2πε a 2C
2 2
• 3.13 在一块厚度为d的导电板上，由两个半径分别为 r1和r2的圆弧和夹角为α的两半径割出的一块扇形体。 试求(1)沿厚度方向的电阻（2）两圆弧之间的电阻 （3）沿α方向的电阻。设导电板的电导率为σ
I 3 = ∫ J 3 ⋅ eφ dS
S3
σdU 3 σdU 3 r2 =∫ dr = ln r r1 αr α 故得到沿α方向的电阻为 U3 α R3 = = I 3 σd ln(r2 r1 )
r2
1
• 3.15无限长直线电流I垂直于两种磁介质的分界面， 试求（1）两种磁介质中的磁感应强度（2）磁化 电流的分布
0
ψ=0 ρ(x)
ψ=U0
ρ d3 故U 0 = － + Ad 6ε 0 d U ρ d 得A = + 6ε 0 d
0 0 0
0
d
ρ x3 U ρ d ∴ϕ = − +( + )x 6ε 0 d 6ε 0 d
0 0 0
ρ 0 x2 U 0 ρ 0 d ∂ϕ E = −∇ϕ = −ex = ex −( + ) ∂x d 6ε 0 2ε 0 d
第三章 静态电磁场及其边值问 题的解
课后练习题
• 3.2 一个点电荷q1=q位于点P1(-a,0,0)，另一点电荷 q2=－2q位于点P2(a,0,0)，求空间的零电位面。
解：两个点电荷在空间产生的电位 q 1 2q − ϕ ( x, y , z ) = 2 2 2 2 2 2 4πε 0 ( x + a ) + y + z ( x − a) + y + z q 2q 令ϕ ( x, y, z ) = 0，则有 − ＝0 2 2 2 2 2 2 ( x + a) + y + z ( x − a) + y + z 即 : 4 ( x + a) 2 + y 2 + z 2 = ( x − a) 2 + y 2 + z 2 5 5 故得： + a ) 2 + y 2 + z 2 = ( a ) 2 (x 3 3 5 4 ∴ 零电位面方程是一个以点（ − a,0,0）为球心，以 a为半径的球面 3 3