第四讲一三章静态电磁场
第四章准静态电磁场

第四章 准静态电磁场4.1 准静态电磁场1.电准静态场由麦克斯韦方程组知,时变电场由时变电荷和时变磁场产生的感应电压产生。
时变电荷产生库仑电场,时变磁场产生感应电场。
在低频情况下,一般时变磁场产生的感应电场远小于时变电荷产生的库仑电场,可以忽略。
此时,时变电场满足ρ=∙∇≈⨯∇D 0E 称为电准静态场。
可见,电准静态场与静电场类似,可以定义时变电位函数ϕ ,即ϕ-∇=E且满足泊松方程ερϕ-=∇2 与电准静态场对应的时变磁场满足 0t =∙∇∂∂+=⨯∇B DE H γ 2.磁准静态场由麦克斯韦方程组知,时变磁场由时变传导电流和时变电场产生的位移电流产生。
在低频情况下,一般位移电流密度远小于时变传导电流密度,可以忽略。
此时,时变磁场满足0=∙∇≈⨯∇B J H c称为磁准静态场。
可见,磁准静态场与恒定磁场类似,可以定义时变矢量位函数A ,即A B ⨯∇=且满足矢量泊松方程c J A μ-=∇2与磁准静态场对应的时变电场满足ρ=∙∇∂∂-=⨯∇D B E t例1:图示圆形平板电容器,极板间距d = 0.5 cm ,电容器填充εr =5.4的云母介质。
忽略边缘效应,极板间外施电压t t u 314cos 2110)(=V ,求极板间的电场与磁场。
[解]:极板间的电场由极板上的电荷和时变磁场产生。
在工频情况下,忽略时变磁场的影响,即极板间的电场为电准静态场。
在如示坐标系下,得()()()V/m t 31410113t 31410501102d u z 4z 2z e e e E -⨯=-⨯⨯=-=-cos .cos . 由全电流定律得出,即由()z z 20r 4Sl t 31431410113d t H 2d e e S D l H ∙-π⨯⨯-=∙∂∂=π=∙⎰⎰ρεερφsin . 极板间磁场为φφφρe e H t 314103352H 4sin .-⨯== A/m也可以由麦克斯韦方程直接求解磁场强度,如下tt 0r ∂∂=∂∂=⨯∇E D H εε 展开,得t 314106694H 14sin .)(-⨯=∂∂φρρρ 解得φφφρe e H t 314103352H 4sin .-⨯== A/m 讨论:若考虑时变磁场产生的感应电场,则有tt ∂∂-=∂∂-=⨯∇H B E 0μ 展开,得t E z 314cos 103.231440ρμρ-⨯⨯-=∂∂- 解得 t E z 314cos 10537.428ρ-⨯= V/m可见,在工频情况下,由时变磁场产生的感应电场远小于库仑电场。
电磁场与电磁波第三章静态场及其边值问题的解PPT课件

解法的优缺点
分离变量法的优点是简单易行,适用于具有多个变量 的偏微分方程。但是,该方法要求边界条件和初始条
件相互独立,且解的形式较为复杂。
有限差分法的优点是简单直观,适用于各种形状的求 解区域。但是,该方法精度较低,且对于复杂边界条
件的处理较为困难。
有限元法的优点是精度较高,适用于各种形状的求解 区域和复杂的边界条件。但是,该方法计算量大,且
05 实例分析
实例一:简单电场的边值问题求解
总结词
通过一个简单的电场边值问题,介绍如 何运用数学方法求解静态场的边值问题 。
VS
详细描述
选取一个简单的电场模型,如平行板电容 器间的电场,通过建立微分方程和边界条 件,采用有限差分法或有限元法进行数值 求解,得出电场分布的解。
实例二:复杂电场的边值问题求解
恒定磁场与准静态场的定义与特性
恒定磁场
磁场强度不随时间变化的磁场。
准静态场
接近静态场的动态场,其特性随 时间缓慢变化。
特性
恒定磁场与准静态场均不产生电 磁波,具有空间稳定性和时间恒
定性。
恒定磁场与准静态场的边值问题
边值问题
描述场域边界上物理量(如电场强度、磁场强度)的约束条件。
解决边值问题的方法
静电屏蔽
在静电屏蔽现象中,静态 场用于解释金属屏蔽壳对 内部电荷或电场的隔离作 用。
高压输电
在高压输电线路中,静态 场用于分析电场分布和绝 缘性能。
02 边值问题的解法
定义与分类
定义
边值问题是指在一定的边界条件下,求解微分方程或积分方程的问题。在电磁场理论中,边值问题通常涉及到电 场、磁场和波的传播等物理量的边界条件。
特性
空间均匀性
第三章 静态电磁场
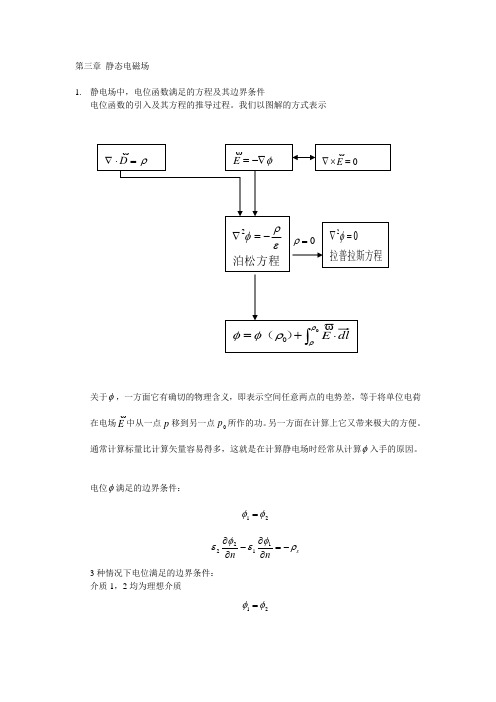
第三章 静态电磁场1. 静电场中,电位函数满足的方程及其边界条件电位函数的引入及其方程的推导过程。
我们以图解的方式表示关于φ,一方面它有确切的物理含义,即表示空间任意两点的电势差,等于将单位电荷在电场E中从一点p 移到另一点0p 所作的功。
另一方面在计算上它又带来极大的方便。
通常计算标量比计算矢量容易得多,这就是在计算静电场时经常从计算φ入手的原因。
电位φ满足的边界条件:21φφ=s nn ρφεφε-=∂∂-∂∂11223种情况下电位满足的边界条件: 介质1,2均为理想介质21φφ=s nn ρφεφε-=∂∂-∂∂1122介质1为导体,介质2为理想介质)(0常数φφ=s nρφε-=∂∂ 介质1,2均为导电介质,在恒定电流情况21φφ=01122=∂∂-∂∂nn φσφσ2. 静电场的能量,能密度;导体上的静电力与一个电荷分布相联系的势能可写成:⎰=v e dv W ρφ21或 ⎰⋅=ve dv E D W21其中第一个积分中的v 包含所有的电荷分布,第二式则包含所有E不为零的空间。
能量密度为:E D W e ⋅=21 当E D ε=时:221E W e ε=导体上的静电力分两种情况:常=∇=φe W F常=-∇=q eW F3. 恒定电场的方程和边界条件微分方程:0=⨯∇E0=⋅∇J)(K E J+=σ积分方程:0=⋅⎰E L0=⋅⎰sJ其中K表示电源作用在单位正电荷上的非静电力。
电位φ所满足的方程⎩⎨⎧⋅∇=∇)()(02电源内部电源外部K φ在两导体交界面上的边界条件:21φφ=nn ∂∂=∂∂2211φσφσ4. 恒定电流的磁场磁失势所满足的方程及边界条件磁失势的引入及方程的推导过程我们以图解的方式表示磁失势满足的边界条件:12A A =s A A nτμμ=⨯∇-⨯∇⨯)11(ˆ1122磁失势所满足的方程及边界条件:磁失势的引入及方程的推导过程我们以图解的方式表示其中m φ引入的条件是无传导电流的单连通区域如电流是环形分布的,磁标势适合的区域只能是挖去环形电流所围成的壳形之后剩下的区域。
静态电磁场I恒定电流的电场和磁场.pptx

5. 矢量磁位的泊松方程和拉普拉斯方程
1. 恒定磁场的矢量磁位 矢量磁位的定义
矢量磁位或称磁矢位
由 B 0
B A
即恒定磁场可以用一个矢量函数的旋度来表示。
3.利用矢量磁位A计算磁场
体电流分布:
A(r) 0 Jc (r' )dV '
4 V ' r r'
面电流分布:
A(r) 0 K (r' )dS '
4 S' r r'
线电流分布:
A(r) 0 I dl'
4 l' r r'
由于元电流矢量产生相同方向的元矢量磁位,故与基于B的分析计算相比,相 对较为简单,尤其在二维磁场(平行平面或轴对称磁场)。
dV
'
毕奥-萨伐尔定律(矢量积分关系式)
第21页/共59页
3.3.4 毕奥-萨法尔定律(矢量磁位)
根据导体中电流分布的不同形态:
体电流密度矢量 Jc v 面电流密度矢量 K v 线电流密度矢量 I v
元电流密度矢量 dqv
JcdV KdS Idl dq
因此,面、线电流分布情况下的磁感应强度为:
Jc dS 0
S
J1n J2n
E dl 0
l
E1t E2t
对线性各向同性媒质, J1 1E1 J2 2E2 (2) 良导体与不良导体分界面上的边界条件
tg1 1 tg2 2
1 2 1 90 o
2 0o
J2
n
例如,钢的电导率 1 = 5106 S/m,周围
2
土壤的电导率2 = 10-2 S/m,1 = 89, 可知,2 8。
sin2
e
第三章 静态电磁场剖析

代入
(r ) S (r) dS
S 4 0 | r r |
得
(
4 0 0 0 z2 2
S [ a2 z2 z ] 20
第三章 静态电磁场
【例2】 求偶极矩为 p = ez q l 的电偶极子引起的电场分布。 解:电偶极子由两个相距很近(l << r)的等值异号的点电 荷构成,电偶极子引起的电位就是此两个点电荷引起的电 位的叠加。
)
第三章 静态电磁场
【例3】 求真空中无限长均匀带电直线周围的电位分布,设
带电线的线电荷密度为 l 。
解:以带电直线为轴线建立圆柱坐标系。取距离轴线有限远
= 0 处为电位的零点。
该带电直线引起的电场为
E()
e
l 2 0
于是距带电线为处的电位为
0
0
(z) Edl
l
d l ln 0
2 0
位为 (r) E dl P
例如,点电荷 q 位于无限大介质中 r′处,其在场点 r 处引
起的电场为 则电位分布为
E
(r,
r)
q (r
4π |
r) r r|3
(r)
q
4π
(r r)dl
r
| r r|3
q
4π
r
dR R2
q
4π
R
4π
q |r
r|
第三章 静态电磁场
根据电位叠加原理,体积 V 中的电荷分布在场点 r 处
得
2 (r
)
1
4
V
(r )
|
r r r r |3 dV
因为
r r
|r
r |3
0
第三章 静态电磁场
第三章静态电磁场与..

y
dx2
dx2
方程的解为:1x C1x D1;2 x C2x D2
有题设边界条件:
o
b
ax
x 0处,10 0;1 x a处,2a 0 2.
x b处,1b 2 b.
3
2 x
x
1x
x xb
s0 0
4
解得:C1
s0 b
0a
a,
D1 0
; C2
s0b 0a
,
D2
s0b . 0
1
x
s
意义:电荷量为0的点电荷的电位。
格林定理 泊松方程的积分公式
格林恒等式是矢量分析中的重要恒等式。
由散度定理 gAd Ñ AgndS
S
设 A
而 gA g 2 g
Agn gn n
得格林第一恒等式
同理,若设 A
格林第一恒等式表示为
2
g
d
Ñ
S
n
dS
2
g
d
Ñ
S
n
dS
◇ 于是位于 r r ' 处的点电荷q 的体密度为 q r r '
◇ 单位点电荷产生的电位满足的泊松方程 2 r r ' /0
满足的方程:2G r, r ' r r '
◇
定义格林函数
Gr,r ' 0 r,r '
无界空间中的解:G
r,
r
'
0
r,
r
'
4
1 r
r
'
格林函数的对称性:G r, r ' G r ', r
◇ 极化体电荷 p P ◇ 极化面电荷 p en P (en 为介质表面外法线方向的单位矢量)
静态场分析

——静电场是有散(有源)无旋场,是保守场。
E D E V
() V 2 V ——泊松方程
无源区域
0
2 0 ——拉普拉斯方程
电磁场与电磁波
第4章 静态场分析
2. 恒定电场的拉普拉斯方程 恒定电场基本方程
l E dl 0 S Jc dS 0
电磁场与电磁波
第4章 静态场分析
2A Jc
分解
2 Ax J x 2 Ay J y
Jc 0
2 Az J z
2 A 0 ——矢量拉普拉斯方程
在没有电流分布的区域内,磁场也成了无旋场,具有位场 的性质,引入标量磁位 m来表示磁场强度。即 H m
– 恒定电场是指导电媒质中,由恒定电流产生的电场。
– 恒定磁场是指由恒定电流或永久磁体产生的磁场,亦称为静 磁场。
电磁场与电磁波
第4章 静态场分析
2. 静态场的麦克斯韦方程组 – 静态场与时变场的最本质区别: 静态场中的电场和磁场是彼此独立存在的。
H dl l
S
ห้องสมุดไป่ตู้
(
JC
D t
电磁场与电磁波
第4章 静态场分析
一、静态场特性
1. 静态场基本概念
– 静态场是指电磁场中的源量和场量都不随时间发生变化的场。
D 0, B 0, V 0
t
t
t
– 静态场包括静电场、恒定电场及恒定磁场,它们是时变电磁
场的特例。
– 静电场是指由静止的且其电荷量不随时间变化的电荷产生的 电场。
4π1R
D1
q 4πR2
aˆR
第三章 静态电磁场

D dS 0
由此即得
S
( 当 R )
1 We dV 2V
第三章
静态电磁场
对于面电荷分布,上式应改为 1 We S d S 2S 对若干导体构成的带电体系而言,注意到电荷只分布在表 面上,而导体表面是等位面,则可由上式得到体系的静电 能: 1 We i qi i 2 若保持各 i 和 qi 不变,令各导体的体积趋向于无限小, 则各导体成为点电荷,上式就成为点电荷系的静电能公式。
2 0
由上可见, 的微分方程包含了静电场的所有基本方 程和本构关系:
E 0
D
D E
因此,对静电场而言,电位的微分方程与场方程等价。
第三章
静态电磁场
在无界空间中,方程 2
的解为 ( r ) dV (r ) 4 | r r | V
于是得电位分布:
(r r ) d l (r ) E d l 4 0 | r r |3 r r q
q 4 0
r
dR q q R 2 4 0 R 4 0 | r r |
其中 R = r- r′。
第三章
静态电磁场
3.1.2
电荷体系引起的电位
为方便,对无界空间中电荷分布在有限区域的情形,通 常取无穷远处为电位零点。这样,电荷体系在空间任一场 点 P 引起的电位即为
(r ) E d l
P
第三章
静态电磁场
例:无限大真空中某点 r′ 处有一点电荷 q,其在场点 r 处 引起的电场为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2
s
E
导体表面
② 将上式应用于电位保持不变导体系: 导体系在改变过程中,电位保持不变,则导体 系电荷量将发生变化。外界(电源)对导体系 作功,其中一部分转变为静电场能,另外一部 分为导体系空间结构变化静电力所作的功。
F l=
iqi
1 2
iqi
电源对系统 静电场能
所做的总功 量改变量
| F W e 常量
第二个小电荷元自从无 穷远处移到r2点时,外 力克服电场力作功为:
r2
dW 2r2dV2E 1dLr2dV212
第三个小电荷元自从无穷远处移到r3点 时,外力克服电场力作功为:
d W 3r 3 d V 31 3 r 3 d V 32 3
第n个小电荷元自从无穷远处移到rn点时,外力 克服电场力作功为:
rq 4πcL 0o r2s4P πe0rr3
5 静电场的能量和能量密度
静电场对置于其中的电荷有力的作用,并对 电荷作功。这说明静电场具有能量。
根据能量守恒原理,静电场的能量等于电荷 体建立过程中,外力克服静电力做功的总和
第一个小电荷元自从无穷远处移 到r1,外界克服电场力做功为零
r1V1
r2V2
静电力作用下发生小的移 δl ,变
化后体系的静电能为We’, 静电 力作的虚功为:
δAFδl 该虚功等于电荷体系能量的减少
We WeWe
δl W e W e
F e ˆx W xee ˆy W yee ˆz W ze W e
① 将上式应用于电荷保持不变导体系: 结合导体系能量表达式,静电力为
将静电场能量公式应用到导体系,由于导体 的电位为常数,从而得到导体系的能量为
W e 1 2 V rrd V 1 2 siisd s 1 2 iq i
导体系相对于同一参考点的电位 导体系的电荷量
6 带电体系的静电作用力
虚功原理如下:设一定空间结构
的带电体系,静电能为 W e 。假
想该电荷体系的空间位形结构在
21
r
r
1
1 n S
2
2 n
S
- s
或
1
r
|S
2
r
| S
M
【例3-1】电偶极子由相距一
r1
小距离L的两个等值异号的
q
r2
点电荷所组成的电荷体系,
其方向由负电荷指向正电 荷,大小为:PqL 。求 电偶极子在远处的电场。
-q
r q
4π0
r11
1
r2
Er r 4π10r3eˆr2PecoseˆPesin
dWn rndVn1n rndVn2n
rndVn3n rn dVn n1,n
We r2dV212 r3dV313 r3dV323
n i1
lim n i1
j1
ri
dViji
另一方面:
dW2 r2dV212 12r2dV212 r1dV121
dW3 12r3dV313 r3dV323 r1dV131 r2dV232
dWn
1 2
rndVn1n rndVn2n rndVnn1,n
r1dV1n1 r2dV2n2 rn1 dVn1n,n1
n i1
WedW2dW3dW4dWnlni m i1
ri
j1
dViji
lim1n
2 n i1
n
ri dVi
j1ji
ji
lim1 n 2 n i1
ri idVi
r ε
S
n
引入电位函数r,令 E r r 得到 r 满足的方程
2rr (Poisson方程)
如果 r0 ,变为Lap lace方程 2r0
问题:静电场与电位函数是不是一一对应 关系,这是否意味着由电位函数决 定的静电场是多值的?
2 边界条件
电位函数方程的求解,必需知道位函数 在区域边界上的状态,即边界条件。所 谓边界条件即电场在介质交界面两侧所 满足的方程。
能否作为能
n
W elni m i 1
ri dV i i
V
1rrdV
2
量密度函数
利 D 用 和 E r r
We
1 2
V
rrdV
1 2
V
DrrdV
1 2
V
Dr
Er
dV
r
S
Dr
dS
两者都可 作为静电 场能量计 算公式但 意义不同
V
1 2
Dr
Er
dV
能量密度函数
静电场能量既可以通过电荷的分布计算,也可以通过 电场计算,但能量密度函数只能表示为电场的函数。
第四讲(一)
第三章 静态电磁场
主要内容:
静态电场的基本问题 带电导体系的作用力 静态电场的能量 静态磁场基本问题 静态磁场的能量
§3.1 静电场及其方程
1 电位函数及其方程
对于静电场,Maxwell方程为
Er0
D rr
这说明静电场是有散无旋矢 量场,可以表示为某个标量 场的梯度。
V
Er
| F We q常量
= 1
2
i sids E i
si
si
1 2
si Eds
si
f ds
单位导体表面积受到的静电力是:
| f
1 2
s
E
导体表面
|E 导体表面
为系统总电荷在导体表面处产生的电场
(含受力面元本身的电荷在内)
问题:根据库仑定律
f
| f sE 导体表面
按照虚功原理得到:
| f
另一方面:
Q 1 21
Q 212
dW2 r2dV212 12r2dV212 r1dV121
dW3 12r3dV313 r3dV323 r1dV131 r2dV232
1
dWn 2
rndVn1n rndVn2n rn dVn n1,n
r1dV1n1 r2dV2n2 rn1 dVn1n,n1
导体内部存在大量 可自由移动的电子 宏观上呈现电中性
附加场
+ +
+ + +
E
达到静电平衡状态 导体内部电场为零
电场中的导体: 导体内部电场为零,导体为等势体; 导体边界面上电场的切向分量为零; 电荷只分布在导体的表面
( 0n常数 ) s
sds
S
Q导体所带电荷 0 导体不带 电
4 静电场的定解问题 均匀介质空间Ω中的静 电场为确定边界条件下 Poisson方程的解,即
【例】 平行板电容器宽长度为l,宽度为b, 间距为d 。电容器两板极之间的部分区域充 满了电介质。如果将平行板电容器接入电压 为V0 的直流电源,求电容器的储能;求介质 板在拉出时受到的作用力。
E1 r
n
E2 r
DdsdV
s
V
(D2 D1 ) nˆ s
2 2 1 1 nˆ s
2
2
n
1
1
n
s
D2
2
D1
1
E dL 0
L
nˆ E 2 E 1 0
P2P 1P l1 iP m 2 P P 1 2Erdl 0
2r1rs0
3 导体的边界条件
没有外加电场
