Computing Boolean Functions Exact Quantum Query Algorithms and Low Degree Polynomials
数据挖掘原理与实践习题及参考答案

35 - 13 = 0.386 ; 70 - 13
(b)已知均值为 30,标准差为 12.94,则可将 35 规范化为: (c)使用小数定标规范化可将 35 规范化为:
35 - 30 = 0.386 ; 12.94
35 = 0.35 ; 100
(d)对于给定的数据,你愿意使用 min-max 规范化。理由是计算简单。 2.7 使用习题 2.5 给出的 age 数据 (a) 画一个宽度为 10 的等宽的直方图。 (b) 为以下每பைடு நூலகம்抽样技术勾画例子:有放回简单随机抽样,无放回简单随机抽样,聚类 抽样,分层抽样。使用大小为 5 的样本和层“青年”,“中年”和“老年”。 答:(a)如下为宽度为 10 的等宽的直方图:
1.2 给出一个例子,说明数据挖掘对商务的成功是至关重要的。该商务需要什么样的数据挖 掘功能?它们能够由数据查询处理或简单的统计分析来实现吗? 答:例如,数据挖掘在电子商务中的客户关系管理起到了非常重要的作用。随着各个电子商 务网站的建立,企业纷纷地从“产品导向”转向“客户导向” ,如何在保持现有的客户 同时吸引更多的客户、 如何在客户群中发现潜在价值, 一直都是电子商务企业重要任务。 但是,传统的数据分析处理,如数据查询处理或简单的统计分析,只能在数据库中进行 一些简单的数据查询和更新以及一些简单的数据计算操作,却无法从现有的大量数据中 挖掘潜在的价值。而数据挖掘技术却能使用如聚类、关联分析、决策树和神经网络等多 种方法,对数据库中庞大的数据进行挖掘分析,然后可以进行客户细分而提供个性化服 务、 可以利用挖掘到的历史流失客户的特征来防止客户流失、 可以进行产品捆绑推荐等, 从而使电子商务更好地进行客户关系管理,提高客户的忠诚度和满意度。 1.3 假定你是 Big-University 的软件工程师,任务是设计一个数据挖掘系统,分析学校课程 数据库。 该数据库包括如下信息: 每个学生的姓名、 地址和状态(例如, 本科生或研究生)、 所修课程,以及他们的 GPA。描述你要选取的结构,该结构的每个成分的作用是什么? 答: 任务目的是分析课程数据库, 那么首先需要有包含信息的关系型数据库系统, 以便查找、 提取每个属性的值;在取得数据后,需要有特征选择模块,通过特征选择,找出要分析 的属性;接下来需要一个数据挖掘算法,或者数据挖掘软件,它应该包含像分类、聚类、 关联分析这样的分析模块,对选择出来的特征值进行分析处理;在得到结果后,可以用 可视化软件进行显示。 1.4 假定你作为一个数据挖掘顾问, 受雇于一家因特网搜索引擎公司。 通过特定的例子说明, 数据挖掘可以为公司提供哪些帮助,如何使用聚类、分类、关联规则挖掘和离群点检测 等技术为企业服务。 答: (1) 使用聚类发现互联网中的不同群体,用于网络社区发现;
《人工智能》课程习题

《人工智能》课程习题第一章绪论1-1. 什么是人工智能?试从学科和能力两方面加以说明。
1-2. 在人工智能的发展过程中,有哪些思想和思潮起了重要作用?1-3. 为什么能够用机器(计算机)模仿人的智能?1-4. 现在人工智能有哪些学派?它们的认知观是什么?1-5. 你认为应从哪些层次对认知行为进行研究?1-6. 人工智能的主要研究和应用领域是什么?其中,哪些是新的研究热点?第二章知识表示方法2-1状态空间法、问题归约法、谓词逻辑法和语义网络法的要点是什么?它们有何本质上的联系及异同点?2-2设有3个传教士和3个野人来到河边,打算乘一只船从右岸渡到左岸去。
该船的负载能力为两人。
在任何时候,如果野人人数超过传教士人数,那么野人就会把传教士吃掉。
他们怎样才能用这条船安全地把所有人都渡过河去?再定义描述过河方案的谓词:L-R(x, x1, y, y1,S):x1个修道士和y1个野人渡船从河的左岸到河的右岸条件:Safety(L,x-x1,y-y1,S’)∧Safety(R,3-x+x1,3-y+y1,S’)∧Boat(L,S)动作:Safety(L,x-x1,y-y1,S’)∧Safety(R,3-x+x1,3-y+y1,S’)∧Boat(R,S’)R-L (x, x1, y, y1,S):x2个修道士和y2个野人渡船从河的左岸到河的右岸条件:Safety(R,3-x-x2,3-y-y2,S’)∧Safety(L,x+x2,y+y2,S’)∧Boat(R,S)动作:Safety(R,3-x-x2,3-y-y2,S’)∧Safety(L,x+x2,y+y2,S’)∧Boat(L,S’)(2) 过河方案Safety(L,3,3,S0)∧Safety(R,0,0,S0)∧Boat(L,S0)L-R(3, 1, 3, 1,S0) L-R(3, 0, 3, 2,S0)Safety(L,2,2,S1)∧Safety(R,1,1,S1)∧Boat(R,S1)Safety(L,3,1,S1’)∧Safety(R,0,2,S1’)∧Boat(R,S1’)R-L (2, 1, 2, 0,S1) R-L (3,0, 1, 1,S1’)Safety(L,3,2,S2)∧Safety(R,0,1,S2)∧Boat(L,S2)L-R(3, 0, 2, 2,S2)Safety(L,3,0,S3)∧Safety(R,0,3,S3)∧Boat(R,S3)R-L (3, 0, 0, 1,S3)Safety(L,3,1,S4)∧Safety(R,0,2,S1)∧Boat(L,S4)L-R(3, 2, 1, 0,S4)Safety(L,1,1,S5)∧Safety(R,2,2,S5)∧Boat(R,S5)R-L (1, 1, 1, 1,S5)Safety(L,2,2,S6)∧Safety(R,1,1,S6)∧Boat(L,S6)L-R(2, 2, 2, 0,S6)Safety(L,0,2,S7)∧Safety(R,3,1,S7)∧Boat(R,S7)R-L (0, 0, 2, 1,S7)Safety(L,0,3,S8)∧Safety(R,3,0,S8)∧Boat(L,S8)L-R(0, 0, 3, 2,S8)Safety(L,0,1,S9)∧Safety(R,3,2,S9)∧Boat(R,S9)R-L (0, 1, 1, 0,S9)Safety(L,1,1,S10)∧Safety(R,2,2,S10)∧Boat(L,S10)2-3利用图2.3,用状态空间法规划一个最短的旅行路程:此旅程从城市A开始,访问其他城市不多于一次,并返回A。
人工智能概论(新)
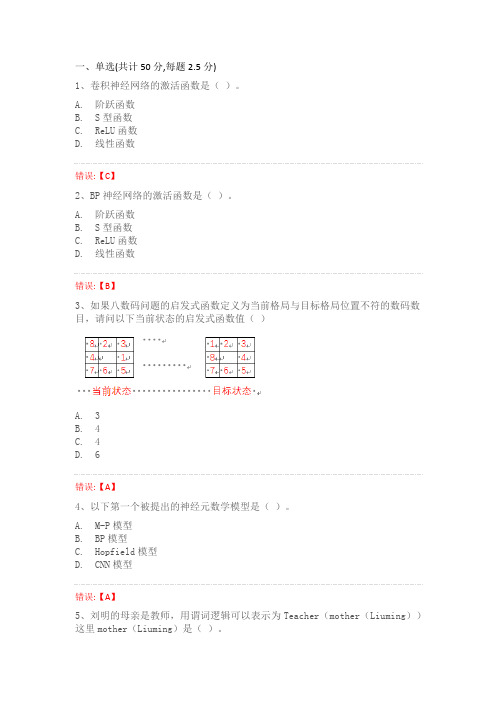
一、单选(共计50分,每题2.5分)1、卷积神经网络的激活函数是()。
A. 阶跃函数B. S型函数C. ReLU函数D. 线性函数错误:【C】2、BP神经网络的激活函数是()。
A. 阶跃函数B. S型函数C. ReLU函数D. 线性函数错误:【B】3、如果八数码问题的启发式函数定义为当前格局与目标格局位置不符的数码数目,请问以下当前状态的启发式函数值()A. 3B. 4C. 4D. 6错误:【A】4、以下第一个被提出的神经元数学模型是()。
A. M-P模型B. BP模型C. Hopfield模型D. CNN模型错误:【A】5、刘明的母亲是教师,用谓词逻辑可以表示为Teacher(mother(Liuming))这里mother(Liuming)是()。
A. 常量B. 变元C. 函数D. 一元谓词错误:【C】6、轮盘选择方法中,适应度函数与选择概率的关系是()。
A. 正比例相关B. 负比例相关C. 指数相关D. 不相关错误:【A】7、已知CF1(H)=-0.5 CF2(H)=0.3,请问结论H不确定性的合成CF1,,2(H)=?()。
A. -0.2B. -0.15C. -0.8D. -0.29错误:【D】8、MYCIN系统中使用不确定推理,规则E→H由专家指定其可信度CF(H,E),若E不支持结论H为真,那么可以得到以下结论?()。
A. CF(H,E)=0B. CF(H,E)>0C. CF(H,E)<0D. CF(H,E)=-1错误:【C】9、李明的父亲是教师,用谓词逻辑可以表示为Teacher(father(Liming))这里father(Liming)是()。
A. 常量B. 变元C. 函数D. 一元谓词错误:【C】10、在遗传算法中,将所有妨碍适应度值高的个体产生,从而影响遗传算法正常工作的问题统称为()。
A. 优化问题B. 迭代问题C. 功能问题D. 欺骗问题错误:【D】11、在当前人工智能领域主要使用的程序设计语言是()。
人工智能复习题及答案

一、填空:1.人工智能的研究途径有心理模拟、生理模拟和行为模拟。
2.任意列举人工智能的四个应用性领域智能控制、智能管理、智能决策、智能仿真。
3.人工智能的基本技术包括表示、运算、搜索归纳技术、联想技术。
4.谓词逻辑是一种表达能力很强的形式语言,其真值的特点和命题逻辑的区别是(10)。
5.谓词逻辑中,重言式(tautlogy)的值是(11)。
6.设P是谓词公式,对于P的任何论域,存在P为真的情况,则称P为(12)。
7.在著名的医疗专家系统MYCIN中规定,若证据A的可信度CF(A)=0,则意味着 13 ,CF(A)=-1,则意味着(14),CF(A)=1,则意味着(15)。
8.谓词公式G是不可满足的,当且仅当对所有的解释(16)。
9.谓词公式与其子句集的关系是(17)。
10.利用归结原理证明定理时,若得到的归结式为(18),则结论成立。
11.若C1=┐P∨Q,C2=P∨┐Q,则C1和C2的归结式R(C1,C2)= (19)。
12.若C1=P(x) ∨Q(x),C2=┐P(a) ∨R(y),则C1和C2的归结式R(C1,C2)= (20)。
13.有谓词公式G,置换δ,则G·ε= (21),δ·ε= (22)。
14.有子句集S={P(x),P(y)},其MGU= (23)。
15.在归结原理中,几种常见的归结策略并且具有完备性的是(24),(25),(26)。
16.状态图启发式搜索算法的特点是(27)。
17.广度优先搜索算法中,OPEN表的数据结构实际是一个(28),深度优先搜索算法中,OPEN表的数据结构实际是一个(29)。
18.产生式系统有三部分组成(30),(31)和推理机。
其中推理可分为(32)和(33)。
19.专家系统的结构包含人机界面、(34),(35),(36),(37)和解释模块。
20.在MYCIN推理中,对证据的可信度CF(A)、CF(A1)、CF(A2)之间,规定如下关系:CF(~A)= (38),CF(A1∧A2 )=(39),CF(A1∨A2 )= (40)。
2023年8月12日TACA清华大学丘成桐领军计划零试

2023年8月学科能力综合测试(TACA)丘成桐数学零试试题及解析题1.在如图所示的方格网中,每步只能从一个节点向右或向上走到相邻的节点,则从A 到Z的路径数为.解析:54如图所示,每个节点处的红色数字表示从A到该点的路径数.题2.对一个复方阵,定义cos A=I+∞∑n=1(−1)n(2n)!A2n.记矩阵cos(−5π3π−10π6π)的第二行第一列元素为x,则[|x|]=.解析:20令M=(−5π3π−10π6π),易知M的特征多项式为f(λ)=λ(λ−π),故其特征值为0,π.解出对应特征向量后,易知M=(3152)(π)(3152)−1于是cos M=(3152)(1−1)(3152)−1=(11−620−11)故所求答案为20.题3.I=limn→∞∫20231cos4(nx+n!)d x,则[100I]=.解析:758I=limn→∞∫20231cos4(nx+n!)d x,则[100I]=我们令I n=∫20231cos4(nx+n!)d x。
则I n=∫20231(1+cos(2nx+2·n!)2)2=∫20231(14+12cos(2nx+2·n!)+14cos2(2nx+2·n!))d x=20224+12∫20231cos(2nx+2·n!)d x+14∫202311+cos(4nx+4·n!)2d x=20224+12n∫20231d(sin(2nx+2·n!))+20228+18·4n∫20231d(sin(4nx+4·n!))显然∫20231d(sin(2nx+2·n!))和∫20231d(sin(4nx+4·n!))有界,故I=limn→∞I n=38×2022,故[I]=758.题4.设g(x)=∫πx(sin t)5td t,记S=∫πg(x)d x,则[100S]=.解析:106S=∫π0d x∫πx(sin t)5td t=∫π(sin t)5td t∫td x=∫π(sin t)5d t注意到令I n=∫πsin n t d t,则由熟知的结论,有I n=n−1nI n−2(n 2),所以S=I5=4×25×3I1=1615,于是[100S]=106.题5.n×n矩阵A n的主对角元素为n,其余元素为1.已知多项式f(x)满足f(A n)=O 对任意1 n 100均成立,则deg f的最小值为.解析:149n×n矩阵A的主对角元素为n,其余元素为1.已知复系数多项式f(x)满足f(A n)=O对任意1 n 100均成立,则deg f的最小值为.记f n(x)为A n的首相系数为1的最小多项式,则显然对任意1 n 100,均有f n(x)|f(x).接下来我们求f n(x).n=1时,显然f1(x)=x−1.n 2时,因为A n为实对称矩阵,所以A n可对角化.注意到rank(A n−(n−1)I n)=1,所以n−1为A n的特征值,其特征子空间维数为n−1.又因为A n全体特征值(计重数)之和为trace(A n)=n2,所以A n剩余特征值为n2−(n−1)2=2n−1.于是f n(x)=(x−(2n−1))(x−(n−1)).f1(x),f2(x),···,f n(x)包含的互不相同的一次式有x−1,x−2,···,x−98,x−99,x−101,x−103,···,x−199f(x)需且仅需被这些一次式整除即可,故deg f的最小值为149.题6.矩阵10−9−9−910−9−910−9−910−9−910−9−910−9−910−9−9−910的特征值为λ1 λ2 ··· λ8,则[λ6]=.解析:22显然该矩阵为循环矩阵,令J=1 1111111由熟知的结论,J的全部特征值即为全体8次单位根ϵi(i=0,1,···,7),令f(x)=−9x7−9x+10,则原矩阵为f(J),故该矩阵全部特征根为f(ϵi),注意到ϵi=ϵ7i(i= 0,1,···,7),所以f(ϵi)均为实数,且可能取值为10−18,10−9√2,10,10+9√2,10+18故λ6=10+9√2,[λ6]=22.题7.在透明的球袋中有1个黑球和2个白球.接下来从袋中摸球,每次摸出一个球,然后放回袋中,并继续往袋中再放入2个与摸出球同色的球.记S n为前n次中摸出黑球的次数.已知第2次摸出的球是黑球,记S100的期望为E,则[E]=.我们计算E(S n|S n−1).这时一共有1+2S n−1个黑球和2+2(n−1−S n−1)个白球.则第n次有1+2S n−13+2(n−1)的概率摸到黑球,故E(S n|S n−1)=S n−1+1+2S n−1 2n+1因为E(S n)=E(E(S n|S n−1)),所以E(S n)=E(S n−1)+E(1+2S n−1 2n+1)⇒E(S n)=12n+1+2n+32n+1E(S n−1)⇒12n+3E(S n)=1(2n+1)(2n+3)+12n+1E(S n−1)故E(S n) 2n+3=E(S2)7+114−14n+6因为已知第二次摸出的是黑球,所以E(S2)=1/3×3/51/3×3/5+2/3×1/5×2+2/3×1/51/3×3/5+2/3×1/5×1=85于是[E]=[E(S100)]=[203×85×17+20314−12]=60题8.对矩阵M(t),定义其微分dd t M(t)=B(t),其中dd tM ij(t)=B ij(t).矩阵微分方程dd tM(t)=AM(t),其中A=213132321,M(0)=321213132,令a=ln|det M(2)|,则[|a|]=.由常微分方程熟知结论,M (t )=M (0)e At .计算可得A 的特征多项式f (λ)=|λI −A |=(λ−6)(λ−√3)(λ+√3),于是A 的特征值为6,±√3,由于A 是实对称矩阵,所以存在正交矩阵T ,使得A =T6√3−√3T ′T DT ′于是|det M (2)|=|det M (0)||e 2D |=|−18e 12|=18e 12故[|a |]=[ln 18+12]=14.题9.5级方阵A 满足:第一行元素均为1,第二行元素从左至右依次为1,−1,1,−1,1,且trace (AA ′)=28.记det A 的最大值为M ,则[M ]=.解析:72我们记A =(α1,α2,···,α5)′,于是由trace (AA ′)=28,有5∑i =1|αi |2=28,注意到|α1|2=|α2|2=5,所以5∑i =3|αi |2=18.由熟知的结论,存在正交矩阵(变换)T ,使得AT =(β1,β2,···,β5)′为上三角矩阵.设该上三角矩阵的主对角元依次为a 1,a 2,···,a 5.则有正交变换的性质可知,|αi |=|βi |(i =1,2,···,5),且1=<α1,α2>=<β1,β2>于是5∑i =3|a i |2 5∑i =3|αi |2=181=<β1,β2>2 (5−a 21)×5⇒a 21245a 22 |β2|2=5于是|det A |=|a 1a 2a 3a 4a 5| (√6)3·…245·√5=72取得72时,AT=»245»15√5√6√6√6我们只需构造使得前两行可以对应的正交矩阵T即可得到满足条件的A.题10.对n=5,令L n=1n!d nd x n(x2−1)n,S=∫1−1|L n|2d x,则[|S|]=.解析:186令f n(x)=(x2−1)n.易知±1均为f n(x)的n重根,所以f(k) n (1)=f(k)n(−1)=0,0 k n−1.于是S=1(n!)2∫1−1(f(n)n(x))2d x=1(n!)2∫1−1d(f(n−1)n(x))f(n)n(x)=−1(n!)2∫1−1f(n+1)n(x)f(n−1)n(x)d x=−1(n!)2∫1−1f(n+1)n(x)d(f(n−2)n(x))=1(n!)2∫1−1f(n+2)n(x)f(n−2)n(x)d x······=1(n!)2∫1−1f(2n)n(x)f(0)n(x)d x=1(n!)2∫1−1(2n)!(1−x2)n d x=1(n!)2(2n)!∫1−1(1−x2)n d x=(2n)!(n!)2∫πsin2n+1d t=(2n)!(n!)22(2n)!!(2n+1)!!所以[S]=[10!(5!)2×2×10×8×···×211×9×···×1]=[204811]=186.题11.正方体旋转群元素最多的两个共轭类的元素个数之和为.解析:14由熟知的结论正方体旋转群同构于S4.所以两元素共轭等价于其分解成不叫的轮换和后,各个轮换和的长度对应相等.故元素最多的共轭类形如(abc)(d),有4×2!=8个元素,元素次多的共轭类形如(abcd),共有3!=6个元素,所求答案为8+6=14题12.A(x)=∞∑m=1∞∑n=0m!·x m·n!(m+n+1)!,则[100A(23)]=.解析:109令a m=∞∑n=0n!(n+m+1)!,则a m=∞∑n=0n!(n+m+1)!=∞∑n=01m(n!(n+m)!−(n+1)!(n+m+1)!)=1m1m!于是|x|<1时,A(x)=∞∑m=11mx m=−ln(1−x)所以[100A(23)]=[100ln3]=109题13.将方程(1+2+···+k)−3(1+2+···+t)=1的全体正整数解(k,t)按照从小到大的方式排列,得到序列{(k n,t n)},则k6=.解析:3196对原方程进行变形,有k(k+1)−3t(t+1)=2⇒(2k+1)2−3(2t+1)2=6令2k+1=u,2t+1=v.考虑虑方程u2−3v2=6的所有正整数解由小到大构成的序列{(u n,v n)}n 1,则由佩尔方程基本理论有u n+√3v n=(3+√3)(2+√3)n−1于是有u n+√3v n=(u n−1+√3v n−1)(2+√3)=2u n−1−3v n−1=(2u n−1+3v n−1)+√3(u n−1+2v n−1)即u n=2u n−1+3v n−1v n=u n−1+2v n−1,则我们依次写出{(u n,v n)}的前7项:(3,1),(9,5),(33,19),(123,71),(459,265),(1713,989),(6393,3691)注意到(3,1)对应的(k,t)不满足正整数的条件,所以k6=6393−12=3196.题14.I=∫π/4tan101x d x,则[13I].解析:67记I n=∫π/4tan n x d x,则I n=∫π/4sin n xcos n xd x=∫π/4sin n−1x d(−cos x)cos n xd x=−1+∫π/4((n−1)tan n−2x+n tan n x)d x =−1+(n−1)I n−2+nI n于是I n+I n−2=1n−1,n 2故I=1100−I99=1100−198+I97······=1100−198+196−···−12+I1=12(ln2+50∑k=1(−1)k1k)注意到50∑k=1(−1)k1k=∞∑k=1(−1)k1k−∞∑k=51(−1)k1k=−ln2−∞∑k=51(−1)k1k所以I=−∞∑k=51(−1)k1k=151−∞∑k=26(12k−12k+1)=151−14∞∑k=261k(k+1/2)>151−14∞∑k=26(1k−1/4−1k+3/4)=151−1103=525253且I=151−14∞∑k=261k(k+1/2)<151−14∞∑k=26(1k−1/8−1k+7/8)=151−1103.5=52.55278.5故67<5278.5×23×52.5<13I<5253×23×52<68于是[13I]=67.题15.M n={A|A是n级实对称矩阵,且元素取自0,±1,±2},记a n为所有trace(A6)(A∈M n)的平均值,a=limk→∞sup n k a nn4,则[a]=.解析:40令T={0,±1,±2},则S n=5n(n+1)/2a n=∑a ij∈T,i j∑0 t1,t2,···,t6 na t1t2a t2t3···a t6t1=∑0 t1,t2,···,t6 6∑a ij∈T,i ja t1t2a t2t3···a t6t1对a t1t2a t2t3···a t6t1项而言,我们关心a ij(i j)遍历所有T中元素后,这样的项得到的总和.我们称a ij和a ji为“同组”的元素.注意到x∈T⇔−x∈T,且a ij(i j)彼此的取值独立,所以若某组元素在a t1t2a t2t3···a t6t1中出现奇数次,则a t1t2a t2t3···a t6t1在和式中累加后为0.所以我们只需考虑以下三种情形:(1)情形1:a t1t2a t2t3···a t6t1由仅有同组元素构成,即形如a t1t1a t1t1···a t1t1或a t1t2a t2t1a t1t2···a t2t1易知这样的项在S n中的总和形如P n5n(n+1)/2+Qn(n−1)5n(n+1)/2,其中P,Q为常数.(2)情形2:a t1t2a t2t3···a t6t1由恰由两组元素构成,一组出现2次,一组出现4次.易知这样的项在S n中的总和形如Un(n−1)5n(n+1)/2,其中U为常数.(3)情形3:a t1t2a t2t3···a t6t1由恰由三组元素构成,每组出现2次.首先易知此时不存在t i=t i+1的情形,于是t1,t2,···,t6中同样的下标至多出现3次.我们下面按照t1,t2,···,t6中不同取值的个数分类,易知只有两种情况:(i)t1,t2,···,t6有三种不同取值此时这样的项在S n中的总和形如Rn(n−1)(n−2)5n(n+1)/2,其中R为常数.(ii)t1,t2,···,t6有四种不同取值,记为x,y,z,w.此时,t1,t2,···,t6可能的的排列只有xyxzxw,xyzywy,xyzyxw,xyxzwz,xyzwzy这五种情形,其在S n中总和形如V n(n−1)(n−2)(n−3)5n(n+1)/2,其中V为常数.于是S=5n(n+1)/2(P n+Qn(n−1)+Rn(n−1)(n−2)+V n(n−1)(n−2)(n−3))所以lim k→∞supn ka nn4=limk→∞supn kS nn45n(n+1)/2=V所以我们只需求出V即可.所有满足t1,t2,···,t6取值形如x,x,x,y,z,w的a t1t2a t2t3···a t6t1之和为5n(n−1)(n−2)(n−3)5n(n+1)/2−3∑p,q,r∈Tp2q2r2=2n(n−1)(n−2)(n−3)5n(n+1)/2−3(02+2×12+2×22)3=5×10353n(n−1)(n−2)(n−3)5n(n+1)/2故V=5×10353=40.。
哈工大人工智能原理习题homework-2

人工智能原理 练习题-2从习题中选择自己感兴趣的题目进行思考和解答,任何尝试都是有益的。
必要时,仔细阅读教科书当中的某些章节。
对于加星号的习题,应该编写程序来完成。
第3章 逻辑与推理1 对于下列每对原子语句,请给出最一般合一者,如果存在的话:a. (,,),(,,)P A B B P x y zb. (,(,)),((,),)Q y G A B Q G x y yc. ((),),((),)Older Father y y Older Father x Johnd. ((),),(,)Knows Father y y Knows x x2 写出下列语句的逻辑表示,使得它们适合应用一般化分离规则:a. 马、奶牛和猪都是哺乳动物。
b. 一匹马的后代是马。
c. Bluebeard 是一匹马。
d. Bluebeard 是Charlie 的父亲。
e. 后代和双亲是逆关系。
f. 每个哺乳动物都有一个双亲。
3 请根据第二章列出的任务环境特征描述wumpus 世界。
1,42,43,44,41,3 w !2,33,34,31,2 S OK 2,2OK3,24,21,1 V OK 2,1B V OK3,1 P !4,1A图7.4(a ) 智能体取得进展的两个后续函数。
(a )第三步移动之后,感知为[Stench,None,None,None];A = AgentB = BreezeG = Gllitter,GoldOK = Safe squareP = PitS = StenchV = Visited W= WumpusA4 假定智能体已经前进到图7.4(a)(如上图)所示的位置,感知到的情况为:[1,1]什么也没有,[2,1]有微风,[1,2]有臭气。
它现在想知道[1,3]、[2,2]和[3,1]的情况。
这3个位置中的每一个都可能包含陷阱,而最多只有一个可能有wumpus。
按照图7.5的实例,构造出可能世界的集合。
Grasshopper学习手册笔记(含英文注解)
Grasshopper学习手册笔记(含英文注解)一、Prams[n. 参数] 电池组(1).Geometry[ 美[d ?i' ɑ?m?tri],n. 几何,几何学] 电池组这一组都是对数据的抓取,电池都有左侧输入端和右侧输出端,都有两种输入数据的方法,一种是把相应数据连接到左侧输入端,另一种是电池上点右键Set one XXX ,新设置一个XXX。
Set multipleXXX ,[ 美['m ?lt ?pl],adj, 多种多样的,许多的,n. 倍数,关联] ,即设置多个。
但是Set one curve 只能选取Rhino 中创建好的,[ 美['ra ?no?],n. 犀牛]左侧输入端:任何相应属性数据。
右侧输出端:电池所包含的相应属性数据。
属性对应如下:Point: 输入点数据【美[p ??nt],n. 点】Vector :输入向量数据【美['vekt ?r ],n,向量,矢量】Circle :输入圆数据,这个电池只包含圆和椭圆相关曲线【美['s ??rkl] 】Curve:输入曲线数据【美[k ??rv] 】Plane:输入平面数据【美[ple ?n] 】Circular Arc :输入圆弧数据【美['s ??rkj ?l ?r ],adj, 圆形的,循环的,美[ ɑ?rk] ,n, 弧,弧形物】Line :输入直线数据【美[la ?n] 】Rectangle :输入网格数据【美['rekt? ?ɡl] ,n,矩形】Box:输入实体盒子数据【美[b ɑ?ks] 】Mesh:输入mesh面数据,即网格面数据【美[me?],n. 网状物】Surface: 输入曲面数据,为poly 曲面,不可输入mesh曲面【美['s ??rf ?s] n. 表面,外表】Brep: 输入任意实体或者曲面数据(这个很常用)【美[b'rep]n. 表面表示】Mesh Face:与mesh类似,这里更多的是提取规则的mesh面Twisted Box :输入北扭曲的实体【美['tw ?st ?d] ,adj ,扭曲的】Field ,输入磁场数据【美[fi ?ld] 】Group:输入成组的数据【美[ ɡru?p] 】Geometry:输入几何图形数据(包含点线面任何数据)Transform 输入三线性集合变换图形【美[tr?ns'f ??m],v, 改边,转换】Geometry Pipeline 从犀牛中输入集合管线到GH中【美['pa ?pla ?n] ,n, 管道,管线,渠道】Geometry Cache 物体缓存,【美[k? ?],n, 隐藏所,缓存】主要作用:1、快速烘培GH汇总的物体,2、快速选择已经烘培到Rhino 中的物体(2).Primitive 电池组【['pr ?m?t ?v] ,adj ,原始的,简陋的】Boolcean: 输入布尔值【['bu ?l i?n] n, 布尔布尔逻辑的】Integer :输入整数【[' ?n t ?d??r] n. [ 数] 整数;整体;】Number:输入一列双精度浮点数据Text: 输入任意文字Color :输入一列颜色参数的RGB值【['k ?l ?r] 】Culture :包含了一系列文化特征【[ ?k?lt ??] n. 文化,修养】Domain2: 输入任意二维区间数据或者UV范围【[do ?'me?n]N. 领地;领域;范围】Matrix: 包含了一系列的数据矩阵【['me ?t r?ks] n 矩阵】Complex:代表一个复核的集合。
微处理器系统结构与嵌入式系统设计答案
“微处理器系统结构与嵌入式系统设计”第一章习题解答1.2 以集成电路级别而言,计算机系统的三个主要组成部分是什么?中央处理器、存储器芯片、总线接口芯片1.3 阐述摩尔定律。
每18个月,芯片的晶体管密度提高一倍,运算性能提高一倍,而价格下降一半。
1.5 什么是SoC?什么是IP核,它有哪几种实现形式?SoC:系统级芯片、片上系统、系统芯片、系统集成芯片或系统芯片集等,从应用开发角度出发,其主要含义是指单芯片上集成微电子应用产品所需的所有功能系统。
IP核:满足特定的规范和要求,并且能够在设计中反复进行复用的功能模块。
它有软核、硬核和固核三种实现形式。
1.8 什么是嵌入式系统?嵌入式系统的主要特点有哪些?概念:以应用为中心,以计算机技术为基础,软硬件可裁剪,适应应用系统对功能、可靠性、成本、体积和功耗的严格要求的专用计算机系统,即“嵌入到应用对象体系中的专用计算机系统”。
特点:1、嵌入式系统通常是面向特定应用的。
2、嵌入式系统式将先进的计算机技术、半导体技术和电子技术与各个行业的具体应用相结合的产物。
3、嵌入式系统的硬件和软件都必须高效率地设计,量体裁衣、去除冗余,力争在同样的硅片面积上实现更高的性能。
4、嵌入式处理器的应用软件是实现嵌入式系统功能的关键,对嵌入式处理器系统软件和应用软件的要求也和通用计算机有以下不同点。
①软件要求固体化,大多数嵌入式系统的软件固化在只读存储器中;②要求高质量、高可靠性的软件代码;③许多应用中要求系统软件具有实时处理能力。
5、嵌入式系统和具体应用有机的结合在一起,它的升级换代也是和具体产品同步进行的,因此嵌入式系统产品一旦进入市场,就具有较长的生命周期。
6、嵌入式系统本身不具备自开发能力,设计完成以后用户通常也不能对其中的程序功能进行修改,必须有一套开发工具和环境才能进行开发。
第二章习题答案2.2 完成下列逻辑运算(1)101+1.01 = 110.01(2)1010.001-10.1 = 111.101(3)-1011.0110 1-1.1001 = -1100.1111 1(4)10.1101-1.1001 = 1.01(5)110011/11 = 10001(6)(-101.01)/(-0.1) = 1010.12.3 完成下列逻辑运算(1)1011 0101∨1111 0000 = 1111 0101(2)1101 0001∧1010 1011 = 1000 0001(3)1010 1011⊕0001 1100 = 1011 01112.4 选择题(1)下列无符号数中最小的数是( A )。
计算机系统结构(课后习题答案)
第一章计算机系统结构的基本概念1。
有一个计算机系统可按功能分成4级,每级的指令互不相同,每一级的指令都比其下一级的指令在效能上强M倍,即第i级的一条指令能完成第i-1级的M条指令的计算量。
现若需第i级的N 条指令解释第i+1级的一条指令,而有一段第1级的程序需要运行Ks,问在第2、3和4级上一段等效程序各需要运行多长时间?答:第2级上等效程序需运行:(N/M)*Ks.第3级上等效程序需运行:(N/M)*(N/M)*Ks。
第4级上等效程序需运行:(N/M)*(N/M)*(N/M)*Ks。
note: 由题意可知:第i级的一条指令能完成第i-1级的M条指令的计算量。
而现在第i 级有N条指令解释第i+1级的一条指令,那么,我们就可以用N/M来表示N/M 表示第i+1级需(N/M)条指令来完成第i级的计算量。
所以,当有一段第1级的程序需要运行Ks时,在第2级就需要(N/M)Ks,以此类推2.硬件和软件在什么意义上是等效的?在什么意义上又是不等效的?试举例说明。
答:软件和硬件在逻辑功能上是等效的,原理上,软件的功能可用硬件或固件完成,硬件的功能也可用软件模拟完成。
但是实现的性能价格比,实现的难易程序不同。
在DOS操作系统时代,汉字系统是一个重要问题,早期的汉字系统的字库和处理程序都固化在汉卡(硬件)上,而随着CPU、硬盘、内存技术的不断发展,UCDOS把汉字系统的所有组成部份做成一个软件.3.试以实例说明计算机系统结构、计算机组成与计算机实现之间的相互关系与影响。
答:计算机系统结构、计算机组成、计算机实现互不相同,但又相互影响。
(1)计算机的系统结构相同,但可采用不同的组成。
如IBM370系列有115、125、135、158、168等由低档到高档的多种型号机器。
从汇编语言、机器语言程序设计者看到的概念性结构相同,均是由中央处理机/主存,通道、设备控制器,外设4级构成。
其中,中央处理机都有相同的机器指令和汇编指令系统,只是指令的分析、执行在低档机上采用顺序进行,在高档机上采用重叠、流水或其它并行处理方式。
量子信息概论 by郭光灿
1⎤ − 1⎥⎦
业已证明,任意么正矩阵可做如下分解
物 委 其作用: 理 员 H 0 = 1 ( 0 + 1 )
U
=
eiα
⎡e−iβ /
⎢ ⎣
0
2
0⎤
eiβ
/
2
⎥ ⎦
⎢⎣⎡csions2r2r
−csoisn2r2r ⎥⎦⎤
⎡e−iδ /2
⎢ ⎣
0
0⎤
eiδ
/
2
⎥ ⎦
讲 会 2
式中为实数,注意:第二个矩阵为普
理讲 员 等效表示:ψ = cosθ 0 + eiϕ sin θ 1
会 2
2
习班 式中θ,ϕ为实数,θ和ϕ定义单位三维球面
上的一个点。Bloch球。
3
国
量子比特的物理载体:任意二态的量子体
数 家自 系,如光子、原子、电子、原子核等。 理学 然 一个量子比特表示多少信息? 部实科学 若对 ψ 进行一次测量,只能给出0或1,量子 验 基 比特的测量后的态为 0 或 1 。因此,从一次 物 金委 测量,人们只能获得关于量子比特态的一个 理讲 员 比特的信息。 习班会 X如若不进行测量,一个量子比特代表多少
班 业已证明:任意多量子比特门均可以由CNOT和单量
子比特门构成。
12
国 (3)基于非计算基的测量
家 量子比特 ψ = α 0 + β 1 数 自 采用基矢 0 , 1 进行测量,结果为 0 和 1 的几率分别为α 2 理学 然 和 β 2。
部 科 计算基并非是唯一的测量基,例如,可以选择另组正交基:
习 H 1 = 1 ( 0 − 1 )
通旋转矩阵,第一、三矩阵为绕围Z轴
