5.2 传递函数的频域辨识 [系统辨识理论及Matlab仿真]
系统辨识的Matlab实现方法(手把手)

最近在做一个项目的方案设计,应各位老总的要求,只有系统框图和器件选型可不行,为了凸显方案设计的高大上,必须上理论分析,炫一下“技术富”,至于具体有多大实际指导意义,那就不得而知了!本人也是网上一顿百度,再加几日探索,现在对用matlab 实现系统辨识有了一些初步的浅薄的经验,在此略做一小节。
必须要指出的是,本文研究对象是经典控制论理最简单最常用的线性时不变的siso 系统,而且是2阶的哦,也就是具有如下形式的传递函数:121)(22++=Ts s T s G ξ 本文要做的就是,对于有这样传递函数的一个系统,要辨识得到其中的未知数T , ξ!!这可是控制系统设计分析的基础哦,没有系统模型,啥理论、算法都是白扯,在实际工程中非常重要哦! 经过总结研究,在得到系统阶跃响应实验数据之后(当然如果是其他响应,也有办法可以辨识,在此还是只讨论最简单的阶跃响应实验曲线,谁让你我是菜鸟呢),利用matlab 至少可以有两种方法实现实现(目前我只会两种,呵呵)!一、函数法二、GUI 系统辨识工具箱下面分别作详细介绍!一、 函数法看官别着急,先来做一段分析(请看下面两排红*之间部分),这段分析是网上找来的,看看活跃一下脑细胞吧,如果不研读一下,对于下面matlab 程序,恐怕真的就是一头雾水咯!*******************************************************************************G(s)可以分解为:))((1)(212ωω++=s s T s G其中, [][]11112221--=-+=ξξωξξωTT1ω、2ω都是实数且均大于零。
则有:211ωω=T ,21212ωωωωξ+=传递函数进一步化为:))(()(2121ωωωω++=s s s G 因此,辨识传递函数就转化为求解1ω、2ω。
当输入为单位阶跃函数时,对上式进行拉普拉斯反变换,得系统时域下的单位阶跃响应为:tteet y 212111221)(ωωωωωωωω---+--=即 tteet y 21211122)(1ωωωωωωωω-----=-令1ω=2ωk )1(>k,得tk t ek e k k t y 22111)(1ωω-----=-⎥⎦⎤⎢⎣⎡--=---t k t e k e k k 2)1(2111ωω 对上式两边取以e 为底的对数得[]⎥⎦⎤⎢⎣⎡-+--=---t k e k t k k t y 2)1(211ln 1ln )(1ln ωω 当∞→t 时,⎥⎦⎤⎢⎣⎡---t k e k 2)1(11ln ω0→,则上式化简为[]t k k t y 21ln )(1ln ω--=-该式的形式满足直线方程b at t y +=)(*其中,)(*t y =[])(1ln t y -,1ln ,2-=-=k kb a ω)1(>k通过最小二乘算法实现直线的拟合,得到a ,b 的值,即可得到1ω、2ω的值,进而可得系统的传递函数。
matlab系统辨识的原理

matlab系统辨识的原理Matlab系统辨识的原理Matlab是一种强大的数学软件,可以用于各种科学计算和数据分析。
其中,系统辨识是Matlab的一个重要应用领域。
系统辨识是指通过对系统输入输出数据的分析,推断出系统的数学模型,从而实现对系统的预测、控制和优化。
本文将从Matlab系统辨识的原理、方法和应用三个方面进行介绍。
一、原理Matlab系统辨识的原理基于系统的输入输出数据,通过对数据进行处理和分析,推断出系统的数学模型。
具体来说,系统辨识的过程可以分为以下几个步骤:1. 数据采集:通过实验或仿真等方式,获取系统的输入输出数据。
2. 数据预处理:对采集到的数据进行滤波、降噪、去趋势等处理,以提高数据的质量和可靠性。
3. 模型结构选择:根据系统的特点和应用需求,选择合适的模型结构,如ARMA、ARIMA、ARMAX等。
4. 参数估计:利用最小二乘法、极大似然法等方法,对模型的参数进行估计。
5. 模型检验:通过残差分析、模型预测等方法,对模型的拟合程度和预测能力进行检验。
二、方法Matlab系统辨识的方法主要包括时间域方法、频域方法和时频域方法三种。
1. 时间域方法:时间域方法是指通过对系统的输入输出数据进行时域分析,推断出系统的数学模型。
常用的时间域方法包括ARMA、ARIMA、ARMAX等。
2. 频域方法:频域方法是指通过对系统的输入输出数据进行频域分析,推断出系统的数学模型。
常用的频域方法包括FFT、AR、ARMA等。
3. 时频域方法:时频域方法是指通过对系统的输入输出数据进行时频分析,推断出系统的数学模型。
常用的时频域方法包括小波变换、Wigner-Ville分布等。
三、应用Matlab系统辨识的应用广泛,主要包括以下几个方面:1. 预测:通过对系统的历史数据进行分析,预测未来的趋势和变化。
2. 控制:通过对系统的数学模型进行分析和优化,实现对系统的控制和调节。
3. 诊断:通过对系统的输入输出数据进行分析,诊断系统的故障和异常。
利用Matlab进行系统辨识的技术方法

利用Matlab进行系统辨识的技术方法在Matlab中进行系统辨识的技术方法主要有参数估计法和非参数估计法两种。
1.参数估计法:参数估计法是通过拟合已知输入和输出数据的数学模型来估计系统的参数。
常用的参数估计方法包括最小二乘法(OLS)、最小二乘法(LSE)、最小二乘法(MLE)和极大似然估计法(MLE)等。
a) 最小二乘法(OLS):OLS方法通过最小化实际输出与模型预测输出之间的误差平方和来估计系统参数。
在Matlab中,可以使用lsqcurvefit函数来实现最小二乘法的系统辨识。
b) 最小二乘法(LSE):LSE方法是通过最小化实际输出与模型预测输出之间的误差平方和来估计系统参数。
在Matlab中,可以使用lsqnonlin函数来实现最小二乘法的系统辨识。
c) 最小二乘法(MLE):MLE方法是通过最大化似然函数来估计系统参数。
在Matlab中,可以使用mle函数来实现最大似然估计法的系统辨识。
2.非参数估计法:非参数估计法不需要事先指定系统的数学模型,而是直接根据输入和输出数据的统计特性进行系统辨识。
常用的非参数估计方法包括频域方法、时域方法和时频域方法等。
a) 频域方法:频域方法通过对输入和输出数据进行频谱分析来估计系统的频率响应。
常用的频域方法包括傅里叶变换、功率谱密度估计和频率响应函数估计等。
在Matlab中,可以使用fft函数和pwelch函数来实现频域方法的系统辨识。
b) 时域方法:时域方法通过对输入和输出数据进行时间序列分析来估计系统的时域特性。
常用的时域方法包括自相关函数估计和互相关函数估计等。
在Matlab中,可以使用xcorr函数来实现时域方法的系统辨识。
c) 时频域方法:时频域方法结合了频域方法和时域方法的优势,可以同时估计系统的频率响应和时域特性。
常用的时频域方法包括短时傅里叶变换和小波变换等。
在Matlab中,可以使用spectrogram函数和cwt函数来实现时频域方法的系统辨识。
5.2 传递函数的频域辨识

• 其中logspace函数为: LOGSPACE Logarithmically spaced vector. • LOGSPACE(X1, X2) generates a row vector of 50 logarithmically equally spaced points between decades 10^X1 and 10^X2.
1 再求平均值得 , 1 2 n
k 'k k k , k 1, 2, k k
,nБайду номын сангаас
n
即可作为系统的纯延迟。
图1 对数频率特性曲线
例 设一个系统的实验频率响应曲线如图2所示,试确定系统 的传递函数。
• 图2 被测试系统的对数相频特性曲线
(1)根据近似对数幅频曲线低频下的斜率
20dB/dec. ,则由表1可知被测对象包含一 个积分环节 sn n 1 。
为 (2)近似对数幅频曲线有3个转折频率,即
0.1rad/sec,1 rad/sec和10 rad/sec,按转折频率
处的斜率变化和转折频率10rad/sec附近的谐振 峰值来确定传递函数的阻尼比和时间常数。
数的分子和分母的系数向量。
通过A和B可得到传递函数。
• 函数invfreqs()的Matlab解释:
• >> help invfreqs • • INVFREQS Analog filter least squares fit to frequency response
data.
[B,A] = INVFREQS(H,W,nb,na) gives real numerator and denominator coefficients B and A of orders nb and na respectively, where H is the desired complex frequency response of the system at frequency points W, and W contains the frequency values in radians/s. • INVFREQS yields a filter with real coefficients. This means that it
5.3开环系统频域测试及辨识
Phase (deg)
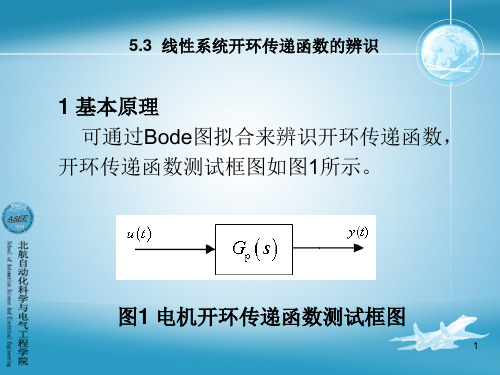
图4 实际对象与拟合传递函数的Bode图比较
12
开环系统辨识仿真程序
chap5_4a.m chap5_4b.m
13
ΨT
sin(w0) cos(w0)
sin(wh) cos(wh)
sin(wnh) cos(wnh)
c1 Af cos
c2 Af sin
,由式(1)和(2)得:
3
由式(1)和(2)得:
Y
Ψ
c1 c2
(3)
由式(3),根据最小二乘原理,可求出 c1 、 c2 的最小二乘解为:
cˆ1
cˆ2
ΨTΨ
1 ΨTY
(4)
对于角频率 ,开环系统输出信号的振幅和相移如下:
Af cˆ12 cˆ22
tg1
cˆ2 cˆ1
(5) (6)4
由于相频为输出信号与输入信号相位之差,幅频为稳态输出振幅
与输入振幅之比的分贝表示。由于输入信号 yd A msin(t) 的
相移为零,则开环系统的相频和幅频为:
1
0.5
0
-0.5
50
60
70
rad./s
Phase(Deg.)
图3 频率特性拟合误差曲线
11
Magnitude (dB)
Bode Diagram 40 20
0
-20 -40 -60
-80 0
-45
-90
-135
-180
-2
10
-1
10
0
10
1
10
2
10
3
10
Frequency (rad/sec)
记录采样区间为 10000 15000 的数据。
系统辨识理论及matlab仿真

系统辨识理论及matlab仿真系统辨识是一门评估和改进系统性能的研究领域,它利用外部观测数据对系统进行建模,使用这种模型来识别系统行为以及建议改进措施。
它结合了计算机科学、工程学、统计学和应用数学等多种学科的方法。
系统辨识的方法可以用于分析机器人系统、有限元素模型、分散系统和非线性系统等。
系统辨识理论是现代工程中最重要的技术,它能够有效地分析和模拟系统,以解决重大工程挑战。
系统辨识理论的基础可以回溯到20世纪40年代,当时大量研究的重点在于控制系统的设计与形成。
随着进步,它拓展到多种应用,其中包括一般系统建模和优化,以及系统健康监测,智能控制系统,复杂过程建模等等。
Matlab是一种基于矩阵的编程语言,它可以提供强大的工具来支持系统辨识理论的应用。
利用Matlab,可以非常方便地实现模型建模、数据处理、数值求解以及可视化等功能。
此外,它还提供了大量预定义函数,可以极大地简化系统辨识理论中所需要实现的功能,如参数估计、优化、数据验证等。
系统辨识理论和Matlab仿真在工程实践中应用十分广泛,其中最值得一提的有:(1)机器人控制:利用系统辨识理论和Matlab仿真,可以对机器人运动特性进行模型建模,并实现复杂的运动控制;(2)流体动力学:利用系统辨识理论和Matlab仿真,可以对流体动力学进行建模和模拟,以便改善和优化系统性能;(3)模糊控制:利用系统辨识理论和Matlab仿真,可以实现模糊控制系统的建模和仿真,用于实现智能控制等。
系统辨识理论和Matlab仿真的研究成果不仅可以改善系统性能,还可以用于展示系统原理及其实现。
以上是我关于系统辨识理论及Matlab仿真的研究结果及其应用。
经过以上介绍,可以看出系统辨识理论及Matlab仿真在工程应用中有重要的作用,它们为解决复杂工程问题提供了可行的解决方案。
然而,在实际应用过程中,系统辨识理论及Matlab仿真也存在一定的不足,比如误差控制方面的困难,这就要求我们不断改进和完善理论和技术,以提高系统的有效性和可靠性。
自动控制原理的MATLAB仿真与实践第5章 线性系统的频域分析

函数模型,如:tf(), zpk(), ss()。 bode(num,den):num,den分别为传递函数的分子与
margin(G);[Gm,Pm,Wcg,Wcp]= margin(G): 直接求出系统G的幅值裕度和相角裕度。 其中:Gm幅值裕度;Pm相位裕度;Wcg幅值裕度 处对应的频率ωc;Wcp相位裕度处对应的频率ωg。
nichols(G);nichols(G,w):绘制单位反馈系统开环传 递尼科尔斯曲线。
20
>>clear; num=[2, 3];den=[1, 2, 5, 7]; %G(s)的分子分母 多项式系数向量
p=roots(den) 求根结果:
%求系统的极点
p=
-0.1981 + 2.0797i
-0.1981 - 2.0797i
-1.6038 可见全为负根,则s右半平面极点数P=0。 绘制Nyquist曲线: >> nyquist(num,den) %绘制Nyquist曲线
本节分别介绍利用MATLAB进行频域绘图和频 率分析的基本方法。
6
5.2.1 Nyquist曲线和Bode图
MATLAB频率特性包括幅频特性和相频特性。 当用极坐标图描述系统的幅相频特性时,通常称为 奈奎斯特(Nyquist)曲线;用半对数坐标描述系 统的幅频特性和相频特性时,称为伯德(Bode) 图;在对数幅值-相角坐标系上绘制等闭环参数( M和N)轨迹图,称为尼克尔斯(Nichols)图。
基于MATLAB自动控制系统时域频域分析与仿真

基于MATLAB自动控制系统时域频域分析与仿真MATLAB是一款强大的数学软件,也是自动控制系统设计的常用工具。
它不仅可以进行时域分析和频域分析,还可以进行相关仿真实验。
本文将详细介绍MATLAB如何进行自动控制系统的时域和频域分析,以及如何进行仿真实验。
一、时域分析时域分析是指对系统的输入信号和输出信号进行时域上的观察和分析,以了解系统的动态特性和稳定性。
MATLAB提供了一系列的时域分析工具,如时域响应分析、稳态分析和步骤响应分析等。
1.时域响应分析通过时域响应分析,可以观察系统对于不同的输入信号的响应情况。
在MATLAB中,可以使用`lsim`函数进行系统的时域仿真。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
-定义输入信号。
- 使用`lsim`函数进行时域仿真,并绘制系统输出信号。
例如,假设我们有一个二阶传递函数模型,并且输入信号为一个单位阶跃函数,可以通过以下代码进行时域仿真:```num = [1];den = [1, 1, 1];sys = tf(num, den);t=0:0.1:10;u = ones(size(t));[y, t, x] = lsim(sys, u, t);plot(t, y)```上述代码中,`num`和`den`分别表示系统的分子和分母多项式系数,`sys`表示系统模型,`t`表示时间序列,`u`表示输入信号,`y`表示输出信号。
通过绘制输出信号与时间的关系,可以观察到系统的响应情况。
2.稳态分析稳态分析用于研究系统在稳态下的性能指标,如稳态误差和稳态标准差。
在MATLAB中,可以使用`step`函数进行稳态分析。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
- 使用`step`函数进行稳态分析,并绘制系统的阶跃响应曲线。
例如,假设我们有一个一阶传递函数模型,可以通过以下代码进行稳态分析:```num = [1];den = [1, 1];sys = tf(num, den);step(sys)```通过绘制系统的阶跃响应曲线,我们可以观察到系统的稳态特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线,虚线为拟合的传递函数 G's 所决定的对数相
频特性。如果虚线和实线很接近,则系统不含延
迟环节。如果虚线和实线相差较多,则系统存在
纯延迟。选取若干个频率 k k 1, 2, , n,对
应于每一个 k 可找出其实测曲线与拟合曲线的
相差角 k 'k ,k 于是
k
k k
• • H(s) = •
B(s) ------A(s)
• 仿真程序:chap5_2.m • close all; • w= logspace(-1,1) • num = [1] • den = [1,5] • H=freqs(num,den,w) • [num,den] = invfreqs(H,w,0,1); • G=tf(num,den)
• 仿真程序:chap5_3.m
• clear all;
• close all;
• w= logspace(-1,1)
• H = [ 0.9892 - 0.1073i 0.9870 - 0.1176i 0.9843 - 0.1289i 0.9812 0.1412i 0.9773 - 0.1545i 0.9728 - 0.1691i 0.9673 - 0.1848i 0.9608 - 0.2017i 0.9530 - 0.2200i 0.9437 - 0.2396i 0.9328 0.2605i 0.9198 - 0.2826i 0.9047 - 0.3058i 0.8869 - 0.3301i 0.8662 - 0.3551i 0.8424 - 0.3805i 0.8150 - 0.4060i 0.7840 0.4310i 0.7491 - 0.4549i 0.7103 - 0.4771i 0.6677 - 0.4968i 0.6216 - 0.5133i 0.5725 - 0.5258i 0.5210 - 0.5335i 0.4680 0.5361i 0.4144 - 0.5331i 0.3613 - 0.5242i 0.3099 - 0.5098i 0.2613 - 0.4900i 0.2164 - 0.4654i 0.1762 - 0.4370i 0.1413 0.4057i 0.1121 - 0.3728i 0.0886 - 0.3393i 0.0706 - 0.3064i 0.0577 - 0.2753i 0.0489 - 0.2466i 0.0436 - 0.2210i 0.0406 0.1987i 0.0391 - 0.1796i 0.0383 - 0.1635i 0.0377 - 0.1499i 0.0369 - 0.1385i 0.0356 - 0.1287i 0.0339 - 0.1201i 0.0318 0.1123i 0.0293 - 0.1051i 0.0266 - 0.0983i 0.0239 - 0.0919i 0.0212 - 0.0857i];
5.2 传递函数的频率辨识
5.2 传递函数的频率辨识
• 频率特性是描述动态系统的非参数模型,可通
过实验方法测取。本节讨论在频率特性的已经测 取的情况下,求系统传递函数的方法。
• 被控对象用频率特性描述时,一般表达式为
G
j
Y U
s s
Y U
j j
s j
式中Y s是辨识对象输出量的拉式变换,U s 是
个积分环节 sn n 1 。
(2)近似对数幅频曲线有3个转折频率,即 0.1rad/sec,1 rad/sec和10 rad/sec,按转折频率 处的斜率变化和转折频率10rad/sec附近的谐振 峰值来确定传递函数的阻尼比和时间常数。
对应标准形式
由于 1 0.1, 1, 2 10
• 仿真实例之二:假设在频率范围w上测出系统频率响应数值 为H,得到频率范围w及频率响应数值H如下:
• w= logspace(-1,1)
• H = [ 0.9892 - 0.1073i 0.9870 - 0.1176i 0.9843 - 0.1289i 0.9812 - 0.1412i 0.9773 - 0.1545i 0.9728 - 0.1691i 0.9673 - 0.1848i 0.9608 - 0.2017i 0.9530 - 0.2200i 0.9437 - 0.2396i 0.9328 - 0.2605i 0.9198 - 0.2826i 0.9047 - 0.3058i 0.8869 - 0.3301i 0.8662 - 0.3551i 0.8424 - 0.3805i 0.8150 - 0.4060i 0.7840 - 0.4310i 0.7491 - 0.4549i 0.7103 - 0.4771i 0.6677 - 0.4968i 0.6216 - 0.5133i 0.5725 - 0.5258i 0.5210 - 0.5335i 0.4680 - 0.5361i 0.4144 - 0.5331i 0.3613 - 0.5242i 0.3099 - 0.5098i 0.2613 - 0.4900i 0.2164 - 0.4654i 0.1762 - 0.4370i 0.1413 - 0.4057i 0.1121 - 0.3728i 0.0886 - 0.3393i 0.0706 - 0.3064i 0.0577 - 0.2753i 0.0489 - 0.2466i 0.0436 - 0.2210i 0.0406 - 0.1987i 0.0391 - 0.1796i 0.0383 - 0.1635i 0.0377 - 0.1499i 0.0369 - 0.1385i 0.0356 - 0.1287i 0.0339 - 0.1201i 0.0318 - 0.1123i 0.0293 - 0.1051i 0.0266 - 0.0983i 0.0239 - 0.0919i 0.0212 - 0.0857i];
节。若被控对象传递函数为 Gses ,则有
lim d G s e j
d
因此,根据频率 ω趋于无穷时实验所得 相频特性的相角变化率,即可确定延迟环 节的延迟时间τ 。但在高频时相频特性的实 验数据难以测量,所以工程上采用下列方 法确定系统的纯延迟。
如图1所示,图中实线为实验得到的对数相频曲
•
s
n
r i 1
T3is 1
l i 1
T42i s2 2T4i2is 1
其中 T1i 和 T3i是一阶微分环节和惯性环节的时间常数, 1i 和 2i 是二阶微分环节和振荡环节的阻尼比, T2i 和T4i 是二阶微分环节和振荡环节的时间常数。
通过实验测定系统的频率响应之后,就 可以利用表1 中各种基本环节频率特性的渐 进特性,获得相应的基本环节特性,从而 得到传递函数。具体方法是用一些斜率为 0, 20dB/dec,. 40dB/de…c. …的直线来逼 近幅频特性,并设法找到频率拐点,就可 以求式 的传递函数。
T1
1 1
10,T
1
1.0,T2
1 2
0.10
由图可以计算出超调量为16%,由公式% e/ 12 ,则
0.5
则可写出被测系统的传递函数为
Gs
K s 1
s
10s
1
s 10
2
s 10
1
(3)根据 0.01 时 ,幅频为 60dB,即 ,
辨识对象输入量的拉式变换。
5.2.1 利用Bode图特性求传递函数
• 如果实验测得了系统的频率响应数据,则可按
频率特性作出对数频率特性曲线,从而求得传递 函数。最小相位系统通常可以用以下式来描述:
G
s
K
p i 1
T1is 1
q i 1
T22i s2 2T2i1is 1
• 其中logspace函数为: LOGSPACE Logarithmically spaced vector.
• LOGSPACE(X1, X2) generates a row vector of 50 logarithmically equally spaced points between decades 10^X1 and 10^X2.
含延迟环节,考虑 Gses, 0.1 与实验曲线的相
频特性相符,则被测系统的传递函数可修正为
Gs
10 s 1 e0.1s
s
10s
1
s 10
2
s 10
1
5.2.2 利用MATLAB工具求系统传递函数
对连续系统传递函数
G(s)
以表1的第三行为例, 如果低频下幅频 和相频分别为0dB 和0度 ,高频下幅频和 相频分别为 20dB和90度 ,且相频为45度 时,幅频为 3dB,则说明基本环节为 Ts+1,
且T 可由 1/ T 求得。
表1 基本环节频率响应渐进特性
被测对象按最小相位系统处理,得到的 传递函数是 G(s),如果所求得G(s)的相角 与实验结果不符,且两者相差一个恒定的 角频变化率,则说明被控对象包含延迟环
'k k k
,
k 1, 2,
,n
再求平均值得 ,
1 n
1
2
n
即可作为系统的纯延迟。
图1 对数频率特性曲线
例 设一个系统的实验频率响应曲线如图2所示,试确定系统 的传递函数。
• 图2 被测试系统的对数相频特性曲线
(1)根据近似对数幅频曲线低频下的斜率
为 20dB/dec. ,则由表1可知被测对象包含一
0 1
1s 2s2 ... nsn 1s 2s2 ... msm
给定离散频率采样点 i,i 1, 2, , N
