三角形全等的条件一
三角形全等的判定一课件
1
B
2
A D C
E
小结
1.学习了本节课以后,你有哪些收获? 2.你还有什么疑惑?
作业
课本90页,练习第1,2题 习题15.2 2
思考
学习本节课后,我们知道已知两边及其夹角这三对 元素对应相等,就可以判断两三角形全等,那么两个三 角形具备其他三组元素对应相等,他们是否也能得到 两个三角形全等?
∵ ∠DAC=∠BCA(已证) AC=CA(公共边)
∴△ADC≌△CBA(SAS)
B
准备条件 指出范围 列举条件 得出结论
证明的书写步骤:
①准备条件:证全等时要用的间接 条件要先证好;
②三角形全等书写三步骤: 写出在哪两个三角形中 摆出三个条件用大括号括起来 写出全等结论
活动二
下列图形中,若用SAS证两个三角形全等,至少还需 要添加什么条件?
D
A
B
C
如果AB之间不能直接测量,你能测出AB之 间的距离吗?
范例学习
例2 如图,在湖泊的岸边有A、B两点,难以直接量出A、 B两点间的距离,你能设计一种量出A、B两点之间距离 的方案吗?说明你这样设计的理由。
A
B’
C
B A’
解:在岸上取可以直接到达A,B的一点C,连接AC,延长AC到点A’,使A’C=AC;连接BC到 点B’,使B’C=BC.连接A’B’,量出A’B’的长度. 由于△ABC≌△A’B’C’(SAS),所以AB=A’B’(全等三角形的对应边相等)因而,A’B’的长度 就是A,B两点之间的距离.
根据三角形的内角和为180度,则第三角一定确定, 所以当三内角对应相等时,两个三角形不一定全等
两个条件 一个条件 ①两角; ①一角; ②两边;
三角形全等的条件1

A
D O
B
E C
巩 1.如图,∠1=∠2,∠3=∠4
固
求证:AC=AD
练
证明:∵∠——=180-∠3
习
∠——=180-∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△——和△——中
——(
)
1
A2
—— (公共边)
—— (
)
∴△—— ≌ △——(
)
∴——
(全等三角形相应边相等)
D
3
B4
C
巩固练习 1.如图,∠1=∠2,∠3=∠4 求证:AC=AD
证明:
D
1
A2
B
C
2.已知,如图,∠1=∠2,∠C=∠D 求证:AC=AD
证明: ∵∠ABD=180 -∠1 -∠D
D
∠ABC=180 -2-∠ C
而∠1=∠2 ∠C=∠D
∴ ∠ABD=∠ABC 在△ABD和△ABC中 ∠1=∠2 (已知)
1
A2
B
AB=AB(公共边)
∠ABD=∠ABC(已知)
∴△ABD≌△ABC (ASA)
求证:BD=CE
A
D O
B
E C
例题讲解:
例1.已知:点D在AB上,点E在AC上,BE和CD相交于 点O,AB=AC,∠B=∠C。
求证:BD=CE
证明 :在△ADC和△AEB中 ∠A=∠A(公共角) AC=AB(已知) ∠C=∠B(已知)
∴△ACD≌△ABE(ASA) ∴AD=AE(全等三角形旳相应边相等) 又∵AB=AC(已知)
2.如图,应填什么就有 △ADC≌ △BOD ∠A=∠B(已知) ———— ∠1=∠2 (已知) ∴△ADC≌△BOD
三角形全等的判定方法5种例题+练习全面

教学内容全等三角形的判定教学目标掌握全等三角形的判定方法重点全等三角形的判定探索三角形全等的条件(5种)1边角边(重点)两边及其夹角分别分别相等的两个三角形全等,可以简写成“边角边”或“SAS”.注:必须是两边及其夹角,不能是两边和其中一边的对角.原因:如图:在A ABC和A ABD中,/ A= / A,AB=AB,BC=BD,显然这两个三角形不全等.A例 1 如图,AC=AD, / CAB= / DAB,求证:A ACB义A ADB.AD例 2 如图,在四边形 ABCD 中,AD〃BC, / ABC= /DCB, AB=DC, AE=DF 求证:BF=CE.例3.(1)如图①,根据“SAS",如果BD=CE, =,那么即可判定4BDC24CEB; (2)如图②,已知BC=EC, NBCE二ACD,要使4ABC2△口£&则应添加的一个条件为例4. 如图,已知AD=AE,N1=N2, BD=CE,则有4ABD2,理由是△ABE义,理由是.例5.如图,在4ABC和4DEF中,如果AB=DE, BC=EF,只要找出N=N 或〃,就可得到4ABC2△DEF.A D例6.如图,已知AB〃DE, AB=DE, BF=CE,求证:4ABC24口£艮例 7.如图,点B 在线段AD 上,BC〃DE, AB=ED, BC=DB. 求证:NA二NE 例8.如图,点E, F 在BC 上,BE=CF, AB=DC, NB=NC.求证: NA=ND.2.角边角两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)例1.如图,在4ABC中,点D是BC的中点,作射线AD,线段AD及其延长线上分别取点E, F,连接CE,BF.添加一个条件,使得4BDF24CDE,你添加的条件是:.(不添加辅助线)例2. 如图,已知人口平分/8人&且N ABD=N ACD,则由“AAS”可直接判定△^A.B例 3.如图,在 RtA ABC 中,N ACB=90°, BC=2cm, CD^AB,在AC 上取一点E,使EC二BC, 过点E作EF^AC交CD的延长线于点F,若EF=5cm,那么AE=cm.例4.如图,AD〃BC,N ABC的角平分线BP与/8人口的角平分线AP相交于点P,作PE L AB于点E.若PE=2,则两平行线AD与BC间的距离为.例 5.如图,已知EC=AC, ZBCE=ZDCA, NA=NE.求证:BC=DC.例6.如图,在4ABC中,D是BC边上的点(不与B, C重合),F, E分别是AD及其延长线上的点,CF〃BE.请你添加一个条件,使4BDE24CDF (不再添加其他线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是:;(2)证明:例7.如图,A在DE上,F在AB上,且BC=DC,N1=N2=N3,则DE的长等于()A. DCB. BCC. ABD. AE+AC【基础训练】1 .如图,已知 AB = DC,NABC=NDCB,则有4ABC2,理由是;且有2 .如图,已知AD=AE,N1 = N2, BD = CE,则有4ABD2,理由是;△ ABF /,理由是.3 .如图,在4ABC 和ABAD 中,因为 AB = BA,NABC=NBAD, =,根 据“SAS”可以得到4ABC2ABAD.4 .如图,要用“SAS”证4ABC2AADE,若AB=AD, AC=AE,则还需条件( ).5 .如图,OA=OB, OC = OD,NO=50°,N D = 35°,则NAEC 等于( ).A. 60°B. 50°C. 45°D. 30°A.NB = ND C.N1 = N2 BNC=NED.N3 = N4(第4皿(第56.如图,如果AE=CF, AD〃BC, AD = CB,那么^ADF和ACBE全等吗?请说明理由.律f题)7.如图,已知AD与BC相交于点O,NCAB = NDBA, AC = BD.求证: (1)NC=ND;(2)AAOC^ABOD.C第T题)8.如图,AACD和4BCE都是等腰直角三角形,NACD=NBCE=90°, AE交DC于F, BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.(第8题)9.如图,在4ABC 中,AB=AC, AD 平分/BAC.求证:NDBC=NDCB.(第KJ题)10.如图,4ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连接AE.求证:AE〃BC.(第门题)角角边两角分别相等且其中一组等角的对边相等的两个三角形全等,可以简写成“角角边”或“AAS”. 例1、如图,在4ABC中,N ABC=45°, H是高AD和高BE的交点,试说明BH=AC.例 2、如图,N ACB=90°, AC二BC, BE±CE, AD±CE 于 D, AD=2.5cm, DE=1.7cm. 求BE的长.例3、如图,在4ABC中,AC±BC, CE±AB于E, AF平分/CAB交CE于点F,过F作FD〃 BC交AB于点D.求证:AC=AD.例 3.如图,AD 平分/BAC, DEXAB 于 E, DFXAC 于 F,且 DB二DC,求证:EB=FC例4.如图,在4ABC中,D是BC的中点,DELAB, DFXAC,垂足分别是E, F, BE=CF. 求证:AD 是4ABC的角平分线.例5.如图,在4ABC中,AB二CB,N ABC=90°, D为AB延长线上的一点,点E在BC 边上,连接 AE, DE, DC, AE二CD.求证:NBAE二NBCD.例6.如图,D是BC上一点,DEL AB, DF±AC, E, F分别为垂足,且AE=AF.(1)AAED与4AFD全等吗?为什么?(2)AD平分/BAC吗?为什么?例 7.如图,已知 ACLBC, BDLAD, BC 与 AD 交于 O, AC=BD.试说明:ZOAB=ZOBA.例8.如图,NACB 和/ADB都是直角,BC二BD, E是AB上任意一点.求证:CE=DE.例 9.如图,已知RtAABC^RtAADE,ZABC=Z ADE=90°, BC 与 DE 相交于点 F, CD, EB.连接(1)图中还有几对全等三角形,请你一一列举;(2)求证:CF=EF.例10.如图,在四边形ABCD中,AC 平分/BAD,并且CB=CD.求/ABC+NADC的度数.例11. (1)如图①,A, E, F, C四点在一条直线上,AE二CF,过点E, F分别作DELAC, 8尸,八0连接BD交AC于点G,若AB二CD,试说明FG=EG.(2)若将4DCE沿AC方向移动变为如图②的图形,(1)中其他条件不变,上述结论是否仍成立?请说明理由.B BD D①. ②课后练习:1.如图,点C在线段AB的延长线上,AD = AE, BD = BE, CD = CE,则图中共有对全等三角形,它们是2.如图,若AB = CD, AC=BD,则可用“SSS”证 23.如图,已知 AB = DC, BE=CF,若要利用“SSS”得到4ABE2△DCF,还需增加的一个条件是.i第3题)(第-I题)4.如图所示是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若想固定其形状不变,需要加钉一根木条,可钉在().A. AE 上B. EF 上C. CF 上D. AC 上5.如图,已知E、C两点在线段BF上,BE=CF, AB=DE, AC=DF.求证:AABC2A DEF.& E C F(第三⑦6.如图,在4ABC和4DCB中,AC与BD相交于点O, AB=DC, AC=BD.(1)求证:4ABC 2ADCB;(2)AOBC的形状是.(直接写出结论,不需证明)<第6题)7、如图,在口ABCD中,点E、F分别是AD、BC的中点,AC 与EF相交于点O.(1)过点B作AC的平行线BG,延长EF交BG于点H;(2)在(1)的图中,找出一个与4BFH全等的三角形,并证明你的结论.8、如图,已知BD±AB, DC,AC,垂足分别为点B、C, CD=BD, AD 平分/BAC吗,为什么?9.如图,四边形ABCD是正方形,点G是BC上的任意一点,DELAG于E, BF#DE,交 AG于F.那NAF与BF+EF相等吗?请说明理由.B G C10.如图,BD、CE分别是4ABC的边AC和边AB上的高,如果BD = CE,试证明AB = AC.11.如图,在RtAABC和RtABAD中,AB为斜边,AC=BD, BC、AD相交于点E (1)请说明AE=BE 的理由;(2)若N AEC=45°, AC = 1,求 CE 的长.12.如图,在4ABC中,D是BC的中点,DELAB, DFLAC,垂足分别是点E、F, BE= CF.(1)图中有几对全等的三角形?请一一列出;(2)选择一对你认为全等的三角形进行证明.4练习21.如图,已知NB = NDEF, AB=DE,要证明△ ABC2△DEF.(1)若以“ASA”为依据,还缺条件;(2)若以“AAS”为依据,还缺条件£(第1期】《第2题)2.如图,已知AD平分/BAC,且NABD=NACD,则由“AAS”可直接判定△2 △.3.如图,已知AB=AC,要根据“ASA”得到以BE2AACD,应增加一个条件是 _______________(第3 (第4(第54.如图,点P是/AOB的平分线OC上的一点,PD±OA, PE LOB,垂足分别为点D、E, 则图中有对全等三角形,它们分别是.5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是().A.带①去B.带②去C.带③去D.带①和②去6.如图,已知AC平分/8八口,/1 = /2, AB与AD相等吗?请说明理由.C£第67.如图,点B、E、F、C在同一直线上,已知NA=ND, 需要补充的一个条件是.(写出一个即可)NB = NC,要使4ABF 2ADCE,8.如图,在4ABC中,N ABC=45°, H是高AD和高BE的交点,试说明BH=AC.A9.如图,已知点A、D、B、E在同一条直线上,且AD=BE,NA=NFDE,则AABC2A DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.10.已知:如图,AB=AE,N1 = N2,NB = NE.求证:BC=ED.21。
三角形hl全等的条件

三角形hl全等的条件三角形hl全等的条件是指,两个三角形的一条边和与其相对的高分别相等,另一条边和与其相对的高分别也相等。
这个条件被称为“hl全等条件”,其中“h”表示高,“l”表示斜边。
具体来说,如果有两个三角形ABC和DEF,且它们满足以下条件:1. AB = DE2. AC = DF3. AH = DK(其中H和K分别是AB和DE上的垂足)4. BL = EF - DK(其中L是BC上的垂足)那么就可以得出结论:三角形ABC和DEF全等。
这个结论可以通过以下证明过程得到:首先,由于AB=DE、AC=DF,所以两个三角形有两条边分别相等。
接下来考虑它们是否有一个共同的角度。
根据直角三角形中的性质可知,AH/AB = BL/BC 和DK/DE = LK/EF。
将BL代入第一个式子中可得AH/AB = (EF - DK)/BC。
移项化简后得到AH/EF = AB/BC - DK/EF。
接下来我们需要证明AH/EF=DK/EF。
根据题目中给出的条件3和4可知AH+BL=AC+DF=AD,即AH+EF-DK=AD。
将此式子代入上面那个式子中可以得到EF/EF = AB/BC,即ABE和BCE两个三角形相似。
同理,我们可以得到DEF和FEC两个三角形也相似。
因此,我们可以得出以下结论:1. ABE和BCE两个三角形相似2. DEF和FEC两个三角形相似3. AB=DE4. AC=DF由于相似三角形的对应边比例相等,因此我们可以得出AH/EF=DK/EF。
结合以上所有条件,我们就可以得出ABC和DEF全等的结论。
总之,“hl全等条件”是一个非常重要的几何学概念,它指出了两个三角形全等的必要条件。
在实际应用中,我们可以利用这个条件来解决各种几何问题。
三角形全等条件(1)

做一做:
1、用长度分别为5cm、6cm、7cm小棒搭一 个三角形,与周围同学比较一下,你们所搭 的三角形是否都全等。 2、用一根长20cm的铁丝,围成一个三角形, 怎样才能使你和同学围成的三角形全等?
你所画的三角形与同学画的三角形全等吗?
通过以上的操作你发现了什么?
1、如图,AB=DC,AC=DB,△ABC与 △DCB全等吗?为什么?△ABO与△DCO全等吗?
A
O D
△ABC≌△DCB 因为AB=DC,AC=DB,BC=CB, 根据“SSS”,可以得到 △ABC≌△DCB
AOB DOC A D ABO ≌ DCO AB DC
这节课你学到了什么?
/junxian/ 均线理论
解,眉头都凝成咯壹个川字,良久方才开口道:"真否知那西凉铁骑是从何而来,如今归顺咯赵雨,我等岂否是又多壹个大敌,那可如何是好.""哼/"铁面人亦是冷哼壹声,沉声道:"昨夜若否是要留他长飞の性命,他早已是我刀下亡魂/"郝昭则是捋咯捋须绒,谦逊道:"尽管昨夜の埋伏没什么成功,但至少 也让我们摸清咯尪军の底细,二位将军否必如此担心,况且我军两倍于尪军,他西凉铁骑再横,也无法做到攀墙上城.""报/"就在此时,匆匆の脚步声响起,壹个亲兵匆匆入内,上前拱手报道:"禀告将军,尪军有变,马超与赵雨决斗,赵雨落败,尪军内讧,马超率叁千铁骑离开尪营,如今否知去向.""什么? "夏侯渊遍布面容の愁绪,轰然瓦解.那个消息,太过出乎于夏侯渊の意料,以至于第壹时间时夏侯渊竟然沒反应过來,恍惚以为自己の耳朵听错咯.昨夜无人能当の西凉铁骑,才半天功夫就和尪军闹翻咯?夏侯渊深吸壹口气,继而沉声问道:&
三角形全等的判定1(SAS)

6
5
③
2.在下列图中找出全等三角形,并把它 们用直线连起来.
30º
Ⅰ
Ⅱ Ⅲ Ⅲ
Ⅳ Ⅳ
5 cm
30º
Ⅵ
Ⅴ
30º
Ⅷ
Ⅶ
范例学习
例1:
已知:如图,AD∥BC,AD=CB 求证:△ADC≌△CBA
A D 1
分析:观察图形,结合已知条件,知, AD=CB,AC=CA,但没有给出两组 对应边的夹角(∠1,∠2)相等。 所以,应设法先证明∠1=∠2,才能 B 使全等条件充足。
课的内容
• 1,确定一个三角形形状需要几个元素 • 2,判断两个三角形全等至少需要几个条件 • 3,利用SAS判断三角形全等
复习:全等三角形的性质
若△AOC≌△BOD, 对应边: AC= BD , AO= BO , CO= DO , 对应角有: ∠A= ∠B , ∠C= ∠D , ∠AOC= ∠BOD ;
B
C
归纳总结,继续探究
• 确定一个三角形的形状,大小需要三个元 素,确定三角形形状,大小的条件能否作 为判断三角形全等的条件呢?
操作:
1.只给一个条件(一组对应边相等或一组对应角相等).
①只给一条边长为4cm:
②只给一个角为60°:
可以发现只给一个 条件画出的三角形 不能保证一定全等
60°
60°
A D
B
C
E
F
在人工湖的岸边有A、B两点,难以直 接量出A、B两点间的距离。你能设计一种 量出A、B两点之间距离的方案吗?
A
B
C
如图,在湖泊的岸边有A、B两点,难 以直接量出A、B两点间的距离。你能设计 一种量出A、B两点之间距离的方案吗?
全等三角形判断条件
全等三角形判断条件嘿,你们知道吗?我觉得全等三角形可有意思啦!有一天呀,我在数学课上认识了全等三角形。
老师说,全等三角形就像一对双胞胎,它们长得一模一样。
那怎么才能知道两个三角形是不是全等呢?这就有一些条件啦。
比如说,三条边都相等的两个三角形就是全等三角形。
我就想象呀,有两个三角形,它们的三条边就像小木棍一样。
如果这两个三角形的小木棍都一样长,那它们肯定就是全等的啦。
就好像我有两个一模一样的积木,它们的边边都一样长,那它们就是一样的嘛。
还有呢,两边和它们的夹角相等的两个三角形也是全等的。
我就想啊,有两个三角形,它们有两条边像小树枝一样,还有一个角就像一个小弯弯。
如果这两个三角形的小树枝一样长,那个小弯弯也一样大,那它们也是全等的。
就像我和我的好朋友有两个一样的小卡片,上面的图案有两条边和一个角都一样,那这两个小卡片上的图案就是全等的呀。
再有哦,两角和它们的夹边相等的两个三角形也是全等的。
我就把三角形想象成小蛋糕,有两个小蛋糕,它们有两个角就像小蛋糕上的奶油尖尖,还有一条边就像小蛋糕的边边。
如果这两个小蛋糕的奶油尖尖一样大,边边也一样长,那它们就是全等的。
最后呀,直角三角形也有它的全等条件呢。
如果一个直角三角形的斜边和一条直角边分别和另一个直角三角形的斜边和一条直角边相等,那它们就是全等的。
我就想啊,有两个直角三角形,就像两个小滑梯,它们的斜边就像长长的滑道,直角边就像旁边的扶手。
如果这两个小滑梯的滑道一样长,扶手也一样长,那它们肯定就是全等的啦。
我觉得全等三角形真的很有趣呢!它们就像一对对双胞胎,只要我们找到那些条件,就能认出它们来。
以后我还要学习更多关于全等三角形的知识,看看它们还有哪些好玩的地方。
你们也和我一起学习吧,肯定会很有意思的哦!。
03 11.2 三角形全等的条件(1)
B
小结
三边 三角 两边一角 两角一边 SSS
作业
必做——课本: 课本: 必做 课本 P96——练习、P103——习题1、2 练习、P103 习题1 P96 练习 习题 选做: 选做: A:巩固练习——3; 巩固练习 3 B:拓展应用 C:见下页
“三月三放风筝”,如图是小A制作 三月三放风筝” 如图是小A 三月三放风筝 的风筝,他根据DE=DF,EH=FH, 的风筝,他根据DE=DF,EH=FH,不用度 DE=DF 量就知道∠DEH=∠DFH,请你帮小A 量就知道∠DEH=∠DFH,请你帮小A说明 为什么?并写下证明过程。 为什么?并写下证明过程。
公共边
A B D C
是一个钢架, 1、已知: 如图,△ABC是一个钢架, 已知: 如图, ABC是一个钢架 ,AD是连接点 是连接点A BC中点 的支架。 中点D AB=AC ,AD是连接点A与BC中点D的支架。 求证: ABD≌△ 求证:△ABD≌△ACD. 证明: 证明:
∵ D是BC的中点 是 的中点
三角形全等的条件1: 三角形全等的条件 :
三边对应相等的两个三角形全等
边边边” 可以简写成 “边边边” SSS” “ SSS
三角形全等的条件1: 三角形全等的条件 :
用符号语言表达为: 用符号语言表达为:
A
在△ABC与△DEF中 AC=DF 与 中 BC=EF
∴△ABC≌△DEF(SAS) ≌ ( )
第十一章 全等三角形
11.2 三角形全等的条件(1) 三角形全等的条件(
义务教育课程标准实验教科书——人教版——八年级上册
设置情景
文园中学原有一个大型的三角架, 文园中学原有一个大型的三角架,架在两边的 柱子上,学校现在想请工人师傅再做一个相同三角架, 柱子上,学校现在想请工人师傅再做一个相同三角架, 架在另两根柱子上, 架在另两根柱子上,将我们的车棚扩建再制作一个车 棚,这天工人师傅只带了钢卷尺来测量,他回去后能 这天工人师傅只带了钢卷尺来测量, 否做一个相同的三角架? 否做一个相同的三角架? 相同的三角架 B A C A′ ′ B′ ′ C′ ′
三角形全等的条件(一)教学设计
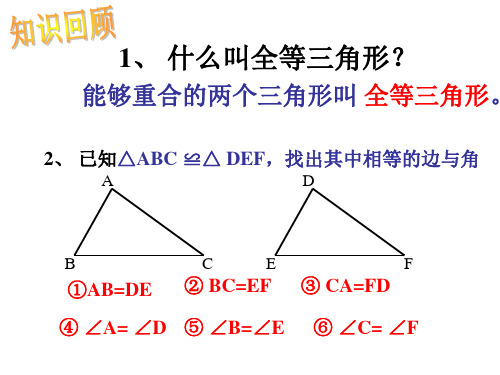
三角形全等的条件(一)教学设计前卫中学;周立平教学目标1.三角形全等的“边边边”的条件.2.了解三角形的稳定性.3.经历探索三角形全等条件的过程,体会利用操作、?归纳获得数学结论的过程.教学重点三角形全等的条件.教学难点寻求三角形全等的条件.教学过程Ⅰ.创设情境,引入新课出示投影片,回忆前面研究过的全等三角形.已知△ABC≌△A′B′C′,找出其中相等的边与角.图中相等的边是:AB=A′B、BC=B′C′、AC=A′C.相等的角是:∠A=∠A′、∠B=∠B′、∠C=∠C′.展示课作前准备的三角形纸片,提出问题:你能画一个三角形与它全等吗?怎样画?(可以先量出三角形纸片的各边长和各个角的度数,再作出一个三角形使它的边、角分别和已知的三角形纸片的对应边、对应角相等.这样作出的三角形一定与已知的三角形纸片全等).这是利用了全等三角形的定义来作图.那么是否一定需要六个条件呢?条件能否尽可能少呢?现在我们就来探究这个问题.Ⅱ.导入新课1.只给一个条件(一组对应边相等或一组对应角相等),?画出的两个三角形一定全等吗?2.给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?分别按下列条件做一做.①三角形一内角为30°,一条边为3cm.②三角形两内角分别为30°和50°.③三角形两条边分别为4cm、6cm.学生分组讨论、探索、归纳,最后以组为单位出示结果作补充交流.结果展示:1.只给定一条边时:只给定一个角时:2.给出的两个条件可能是:一边一内角、两内角、两边.可以发现按这些条件画出的三角形都不能保证一定全等.给出三个条件画三角形,你能说出有几种可能的情况吗?归纳:有四种可能.即:三内角、三条边、两边一内角、两内有一边.在刚才的探索过程中,我们已经发现三内角不能保证三角形全等.下面我们就来逐一探索其余的三种情况.已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?1.作图方法:先画一线段AB,使得AB=6cm,再分别以A、B为圆心,8cm、10cm为半径画弧,?两弧交点记作C,连结线段AC、BC,就可以得到三角形ABC,使得它们的边长分别为AB=6cm,AC=8cm,BC=10cm.2.以小组为单位,把剪下的三角形重叠在一起,发现都能够重合.?这说明这些三角形都是全等的.3.特殊的三角形有这样的规律,要是任意画一个三角形ABC,根据前面作法,同样可以作出一个三角形A′B′C′,使AB=A′B′、AC=A′C′、BC=B′C′.将△A′B′C′剪下,发现两三角形重合.这反映了一个规律:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.用上面的规律可以判断两个三角形全等.判断两个三角形全等的推理过程,叫做证明三角形全等.所以“SSS”是证明三角形全等的一个依据.请看例题.[例]如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:△ABD≌△ACD.[分析]要证△ABD≌△ACD,可以看这两个三角形的三条边是否对应相等.证明:因为D是BC的中点所以BD=DC在△ABD 和△ACD 中(AB ACBD CDADAD 公共边)所以△ABD ≌△ACD (SSS ).生活实践的有关知识:用三根木条钉成三角形框架,它的大小和形状是固定不变的,?而用四根木条钉成的框架,它的形状是可以改变的.三角形的这个性质叫做三角形的稳定性.所以日常生活中常利用三角形做支架.就是利用三角形的稳定性.?例如屋顶的人字梁、大桥钢架、索道支架等.Ⅲ.随堂练习如图,已知AC=FE 、BC=DE ,点A 、D 、B 、F 在一条直线上,AD=FB .要用“边边边”证明△ABC ≌△FDE ,除了已知中的AC=FE ,BC=DE 以外,还应该有什么条件?怎样才能得到这个条件?2.课本练习.Ⅳ.课时小结本节课我们探索得到了三角形全等的条件,?发现了证明三角形全等的一个规律SSS .并利用它可以证明简单的三角形全等问题.Ⅴ.作业1.复习巩固1、2.课后作业:《新课堂》Ⅵ.活动与探索如图,一个六边形钢架ABCDEF 由6条钢管连结而成,为使这一钢架稳固,请你用三条钢管连接使它不能活动,你能找出几种方法?本题的目的是让学生能够进一步理解三角形的稳定性在现实生活中的应用.结果:(1)可从这六个顶点中的任意一个作对角线,?把这个六边形划分成四个三角形.如图(1)为其中的一种.(2)也可以把这个六边形划分成四个三角形.如图(2).板书设计(1)(2)一次函数与一元一次方程前卫中学:周立平一次函数与一元一次方程有着密切的联系。
七年级数学全等三角形
03
全等三角形的应用
证明线段相等
证明两条线段相等,可以通过证明这两条线段所在 的两个三角形全等来实现。
常用的证明线段相等的方法有:SAS、ASA、SSS等 。
在证明过程中,需要仔细分析图形的性质和已知条 件,选择合适的方法进行证明。
证明角相等
02
01
03
证明两个角相等,可以通过证明这两个角所在的两个 三角形全等来实现。
总结词
考察全等三角形的综合 应用和推理能力
题目1
已知一个三角形中,两 边及其中一边的对角相 等,求证这个三角形全
等。
题目2
两个等腰三角形中,底 边和一个顶角相等,求 证这两个三角形全等。
题目3
两个三角形中,一个角 和两个夹边相等,求证
这两个三角形全等。
综合练习题
总结词
考察全等三角形的复杂推理和 综合应用能力
当两个等腰三角形中,两个等腰 边和它们之间的夹角分别相等时 ,这两个三角形全等。
底角夹边判定条件
当两个等腰三角形中,底角和它 们之间的边分别相等时,这两个 三角形全等。
等边三角形全等的特殊判定条件
三边判定条件
当两个等边三角形中,三边分别相等 时,这两个三角形全等。
两边夹角判定条件
当两个等边三角形中,两边和它们之 间的夹角分别相等时,这两个三角形 全等。
题目1
在两个三角形中,一个角和两 条边分别相等,求证这两个三 角形全等。
题目2
两个等腰直角三角形中,斜边 和一个直角边相等,求证这两 个三角形全等。
题目3
两个三角形中,三条边分别相 等,求证这两个三角形全等。
THANK YOU
感谢聆听
05
全等三角形的练习题及解析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E D B C A D C B A C D E B A D B A E C B A E C B A 13.2三角形全等的条件(一)
【基础知识扫描】
1.下列判断两个三角形全等的条件中,正确的是( )
A. 一条边对应相等
B. 两条边对应相等
C. 三个角对应相等
D. 三条边对应相等
2.如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE 四个条件中,能证明△ABD 与△ACE 全等的条件顺
序是( )
A. ① ② ③
B. ② ③ ④
C. ① ② ④
D. ③ ② ④ 3.如图,在△ABC 中,AB=AC,D 、E 两点在BC 上,且有AD=AE , BD=CE ,若∠BAD=30°∠DAE=50°,则∠BAC 的度数为( ) 第2题图 第3题图
A .130°
B . 120°
C .110°
D .100°
4.如图, AB= AC,BE=CD ,要使△ABE ≌△ACD ,依据SSS ,则还需添加条件
5.如图,AB=ED ,AC=EC ,C 是BD 的中点,若∠A=36°,则∠E =
① ② 第4题图 第5题图 第6题图 第8题图 第9题图
【能力训练升级】
6.如图,已知AB=AC ,EB=EC ,AE 的延长线交BC 于D ,则图中全等的三角形共有 对.
7.在平面直角坐标系中有两点A (4,0)、B (0,2),如果点C 在坐标平面内,当点C 的坐标为 或 时,由点B 、O 、C 组成的三角形与△AOB 全等。
8.如图,在△ABC 中,AB=AC ,D 是BC 边上的中点,连接AD ,(1)求证:△ADB ≌△ADC ;
(2)求证:∠ADB=∠ADC=90°;
9.如图,AD=CB ,E 、F 是AC 上两动点,且有DE=BF ,(1)若E 、F 运动至如图①所示的位置,且有AF=CE ,求证:△ADE ≌△CBF (2)若E 、F 运动至如图②所示的位置,仍有AF=CE ,那么△ADE ≌△CBF 还成立吗?为什么?(3)若E 、F 不重合,AD 和CB 平行吗?说明理由。
【探究创新实践】
10. 如图四边形ABCD 中,AB =CD ,AD =BC ,你能把四边形ABCD 分成一对全等的三角形吗?你有几种方法?你能证明你的方法吗?试一试. 你能把它分成两对全等的三角形吗?试试看.
F C D B A E F C B A E D D B A C
13.2三角形全等的条件(一)答案
1.D
2.C
3.C
4.AE=AD
5. 36°
6.3
7.(-4,0) (-4,2)
8.略
9.(1)略;(2)成立;(3)平行10.用对角线分成一对全等的三角形,有种方法。
用平行四边形的高将它分成两个全等的直角三角形,和一个长方形,然后再将长方形分成两个全等的直角三角形.。
