《通信原理》课后习题答案及每章总结(樊昌信,国防工业出版社,第五版)第五章
《通信原理》课后习题答案及每章总结(樊昌信,国防工业出版社,第五版)第七章

《通信原理》习题参考答案第七章7-7. 设输入抽样器的信号为门函数)(t G τ,宽度ms 20=τ,若忽略其频谱第10个零点以外的频率分量,试求最小抽样速率。
解:ff f Sa f G t G πτπτπτττsin )()()(==⇔ 在第十个零点处有:10=τf 即最高频率为:Hz f m 500102010103=⨯==-τ根据抽样定理可知:最小抽样频率要大于m f 2,即最小抽样频率为1000KHz7-8. 设信号t A t m ωcos 9)(+=,其中A ≤10V 。
若m(t)被均匀量化为40个电平,试确定所需的二进制码组的位数N 和量化间隔υ∆。
解: 402≥N ,所以N =6时满足条件信号m(t)的最大电压为V max =19V ,最小电压为V min =-1V即信号m(t)的电压差ΔV =20V∴V V 5.0402040==∆=∆υ7-10. 采用13折线A 律编码电路,设最小量化间隔为1个单位,已知抽样脉冲值为+653单位: (1) 试求此时编码器输出码组,并计算量化误差; (2) 写出对应于该7位码(不包括极性码)的均匀量化11位码。
(采用自然二进制码。
) 解:(1)极性码为正,即C 7=1即段落码C 6C 5C 4=110抽样脉冲值在段内的位置为:653-512=123个量化单位 由于段内采用均匀量化,第7段内量化间隔为:32251210244=- 而32×3≤123≤32×4,所以可以确定抽样脉冲值在段内的位置在第3段,即C 3C 2C 1C 0=0011所以编码器输出码组为:C 7C 6C 5C 4C 3C 2C 1C 0=11100011 量化误差:11)232332512(635=+⨯+- (2)635对应的量化值为:624232332512=+⨯+ 对应的11位自然二进制码元为:010********7-11. 采用13折线A 律编码电路,设接收端收到的码组为“01010011”、最小量化间隔为1个量化单位,并已知段内码改用折叠二进制码:(1)试问译码器输出为多少量化单位;(2)写出对应于该7位码(不包括极性码)的均匀量化11位自然二进码。
现代通信原理课后答案樊昌信

现代通信原理课后答案樊昌信【篇一:《现代通信原理》教学日历(2015)】>(2014 ~2015 学年第二学期) (第 1 页,共 2 页)任课教师在每学期开课以前根据教学大纲编写教学日历,一式三份,经教研室讨论,一份交系(院),一份存教研室,一份教师保留【篇二:通信原理考核大纲及样卷(含答案)】考核对象通信工程专业本科生。
二、命题依据本课程的教学大纲、教材及参考文献。
三、考核形式及试卷结构1、试卷总分:100分2、考核时限:120分钟3、考核方式:闭卷4、学生携带文具要求:笔等常规文具、计算器5、试卷题型比例:选择题:20%填空题:20% 判断题:10%简答题:20%计算题:30%6、试卷内容比例:通信系统概论5%~10%随机过程 5%~10%信道和噪声 5%~10%模拟调制系统15%~25%数字基带传输系统 15%~20%数字调制系统10%~20%模拟信号的数字传输10%~20%数字信号的最佳接收5%~10%同步原理 2%~5%四、课程考核内容和要求1、通信系统概论考核内容:通信系统的模型;通信系统的分类及通信方式;通信系统的主要性能指标;信息的度量。
考核要求:掌握通信系统的模型,通信系统的分类及通信方式,通信系统的主要性能指标,信息的度量。
2、信道和噪声考核内容:信道定义、分类和模型;恒参信道特性;随参信道特性;信道的加性噪声;信道容量的概念。
考核要求:掌握信道定义、分类和模型;理解信道特性,随参信道特性,信道的加性噪声;信道容量的概念,信道容量的计算。
3、模拟调制系统考核内容:幅度调制(am、dsb、ssb)的原理及抗噪声性能;角度调制(fm、pm)的原理及抗噪声性能;各种模拟调制系统的比较;频分复用;复合调制及多级调制。
考核要求:掌握幅度调制的工作原理,am、dsb、ssb调幅系统的调制与解调的方法,各种调幅系统的性能分析与比较,角度调制系统的基本原理,窄带角度调制产生及解调方法,宽带调频和调相产生及解调方法;理解频分多路复用机理,复合调制及多级调制。
《通信原理》课后习题答案及每章总结(樊昌信,国防工业出版社,第五版)第六章

《通信原理》习题参考答案第六章6-1. 设发送数字信息为011011100010,试分别画出OOK 、2FSK 、2PSK 及2DPSK 信号的波形示意图。
解:6-4. 假设在某2DPSK 系统中,载波频率为2400Hz ,码元速率为1200B ,已知相对码序列为1100010111:(1)试画出2DPSK 信号波形(注:相位偏移ϕ∆可自行假设); (2)若采用差分相干解调法接收该信号时,试画出解调系统的各点波形; (3)若发送信息符号0和1的概率分别为0.6和0.4,试求2DPSK 信号的功率谱密度。
解:(1)载波频率为码元速率的2倍0 1 1 0 1 1 1 0 0 0 1 0 OOK 2FSK 2PSK2DPSK 2DPSK 1 1 0 0 0 1 0 1 1 1(2)相干解调系统的原理框图如下:1 1 0 0 0 1 0 1 1 1abcdef(3) )]2400()2400([41)]()([41-++=-++=f P f P f f P f f P P s s c s c s E ,其中:∑+∞∞---++--=)()(])1([)()()1(2212221s s ss s mf f mf G a P Paf f G a a P P f P δ∑+∞∞--+=)()(04.0)1(196.022s s s mf f m Sa f f Sa f δππ)(04.0)()1200/(sin 115222f f f δππ+= ∴⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+=2222)2400()2400(1200sin )2400()2400(1200sin 2.29f f f f P E ππ )]2400()2400([01.0-+++f f δδ6-5. 设载频为1800Hz ,码元速率为1200B ,发送数字信息为011010: (1) 若相位偏差︒=∆0ϕ代表“0”、︒=∆180ϕ代表“1”,试画出这时的2DPSK 信号波形; (2) 又若︒=∆270ϕ代表“0”、︒=∆90ϕ代表“1”,则这时的2DPSK 信号的波形又如何?(注:在画以上波形时,幅度可自行假设。
《通信原理》樊昌信第五版3 4 5 6 8 9 10习题答案【khdaw_lxywyl】

D: sD(t) = Acm(t) cos(2π fct) sin(2π fct) + Acmˆ (t) sin(2π fct) sin(2π fct)
=
1 [ Acm(t) sin(4π
fct )
+
∧
Ac m(t)
−
∧
Ac m(t) cos(4π
fct )]
通过低通滤波器抑制载频的二倍频分量,得到解调信号为 y0(t) = Ac m(t) 2
4.2 已知某调幅波的展开式为:
s(t) = cos(2π ×104t) + 4 cos(2π ×1.1×104t) + cos(2π ×1.2×104t)
(1)求调幅系数和调制信号频率; (2)写出该信号的傅式频谱式,画出它的振幅频谱图; (3)画出该信号的解调框图。
解:解调框图:
题图 4.7
理想低通滤波器
输出 y 0( t)
Cos(Wct) 与发端相干解调
R( f ) = A [M ( f + fc) + M ( f − fc)] 2
Y1( f ) = A [M ( f + fc) + M ( f − fc)]* 1 [δ ( f + fc) + δ ( f − fc)]
S下( f ) = 50[1 δ ( f + 79900) + 1 δ ( f − 79900) − jδ ( f + 79900)
2
2
+ jδ ( f − 79900)]
= 50[(1 − j)δ ( f + 79900) + (1 + j)δ ( f − 79900)]
《通信原理》课后习题答案及每章总结(樊昌信,国防工业出版社,第五版)第一章

《通信原理》习题参考答案第一章1-1. 设英文字母E 出现的概率为0.105,x 出现的概率为0.002。
试求E 及x 的信息量。
解: )(25.3105.01)(log 2bit E I ==)(97.8002.01)(log 2bit X I == 题解:这里用的是信息量的定义公式)(1log x P I a =注:1、a 的取值:a =2时,信息量的单位为bita =e 时,信息量的单位为nita =10时,信息量的单位为哈特莱2、在一般的情况下,信息量都用bit 为单位,所以a =21-2. 某信息源的符号集由A ,B ,C ,D 和E 组成,设每一符号独立出现,其出现概率分别为1/4,1/8,1/8,3/16和5/16。
试求该信息源符号的平均信息量。
解:方法一:直接代入信源熵公式:)()()()()(E H D H C H B H A H H ++++=516165316163881881441log log log log log 22222++++=524.0453.083835.0++++= 符号)/(227.2bit =方法二:先求总的信息量I)()()()()(E I D I C I B I A I I ++++= 516316884log log log log log 22222++++= 678.1415.2332++++= )(093.12bit =所以平均信息量为:I/5=12.093/5=2.419 bit/符号题解:1、方法一中直接采用信源熵的形式求出,这种方法属于数理统计的方法求得平均值,得出结果的精度比较高,建议采用这种方法去计算2、方法二种采用先求总的信息量,在取平均值的方法求得,属于算术平均法求平均值,得出结果比较粗糙,精度不高,所以尽量不采取这种方法计算注:做题时请注意区分平均信息量和信息量的单位:平均信息量单位是bit/符号,表示平均每个符号所含的信息量,而信息量的单位是bit ,表示整个信息所含的信息量。
樊昌信《通信原理》笔记和课后习题(含考研真题)详解模拟调制系统【圣才出品】

第5章模拟调制系统5.1复习笔记一、幅度调制SU(线性调制)原理幅度调制是由调制信号去控制高频载波的幅度,使之随调制信号作线性变化的过程。
1.调幅(AM)(1)调制模型图5-1AM调制模型(2)时域表达式调幅信号时域表达式为式中,A0为外加的直流分量;m(t)可以是确知信号,或随机信号。
(3)AM调制波形和频谱图图5-2AM调制波形和频谱(4)频谱①频谱表达式若m(t)为确知信号,则AM信号的频谱为②频谱特性a.AM信号的频谱由载频分量、上边带、下边带三部分组成。
b.频谱的带宽是基带信号带宽f H的2倍,即B AM=2f H(5)调制特性①调制功率a.调制总功率AM信号的总功率包括载波功率和边带功率两部分。
b.载波功率载波分量并不携带信息,载波功率表达式为c.边带功率边带功率与调制信号有关,边带功率表达式为②调制效率a.调制效率的定义调制效率是有用功率(用于传输有用信息的边带功率)占信号总功率的比例。
b.调制效率的一般表达式c.调制效率的特殊表达式单音余弦调制信号调制效率为/在“满调幅”(时,又称100%调制)条件下,调制效率的最大值为。
AM信号的功率利用率比较低。
2.双边带调制(DSB)(1)时域表达式将AM调制中的直流A0去掉,得到一种高调制效率的调制方式双边带调制(DSB)。
其时域表达式为(2)DSB调制波形和频谱图图5-3DSB信号的波形和频谱图(3)频谱①频谱表达式②频谱特性a.频谱中不存在载波分量;b.所需的传输带宽是调制信号带宽f H 的2倍,即2DSB HB f (4)调制特性①DSB 信号的调制效率是100%,即全部功率都用于信息传输。
②DSB 信号的包络不与调制信号的变化规律一致,不能采用简单的包络检波来恢复调制信号,需采用相干解调,又称同步检测。
3.单边带调制(SSB)(1)滤波法①滤波法原理先产生一个双边带信号,然后让其通过一个边带滤波器,滤除不要的边带,即可得到单边带信号。
通信原理教程樊昌信习题答案第五章
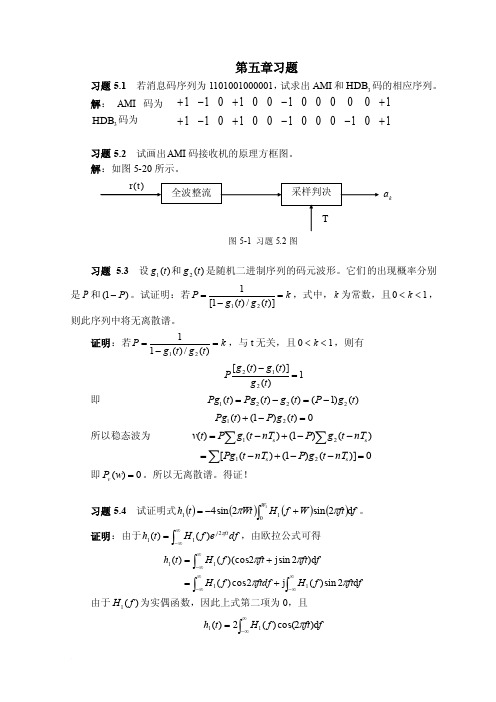
第五章习题习题5.1 若消息码序列为1101001000001,试求出AMI 和3HDB 码的相应序列。
解: AMI 码为 3HDB 码为习题5.2 试画出AMI 码接收机的原理方框图。
解:如图5-20所示。
图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。
它们的出现概率分别是P 和)1(P -。
试证明:若k t g t g P =-=)](/)(1[121,式中,k 为常数,且10<<k ,则此序列中将无离散谱。
证明:若k t g t g P =-=)(/)(1121,与t 无关,且10<<k ,则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。
所以无离散谱。
得证!习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。
证明:由于⎰∞∞-=df e f H t h ft j π211)()(,由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数,因此上式第二项为0,且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a《通信原理》习题第五章令,'d d ,'f f W f f =+=,代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称,故上式第一项为0,因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示,并且它们出现的概率相等,码元持续时间等于T 。
通信原理教程+樊昌信+课后习题答案第一章至第八章

第一章习题习题1.1 在英文字母中E 出现的概率最大,等于0.105,试求其信息量。
解:E 的信息量:()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题1.2 某信息源由A ,B ,C ,D 四个符号组成,设每个符号独立出现,其出现的概率分别为1/4,1/4,3/16,5/16。
试求该信息源中每个符号的信息量。
解:b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-=b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题1.3 某信息源由A ,B ,C ,D 四个符号组成,这些符号分别用二进制码组00,01,10,11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这四个符号等概率出现; (2)这四个符号出现概率如习题1.2所示。
解:(1)一个字母对应两个二进制脉冲,属于四进制符号,故一个字母的持续时间为2×5ms 。
传送字母的符号速率为Bd 100105213B =⨯⨯=-R 等概时的平均信息速率为b 2004log log 2B 2B b ===R M R R(2)平均信息量为符号比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 b 7.197977.1100B b =⨯==H R R习题1.4 试问上题中的码元速率是多少?解:311200 Bd 5*10B B R T -===习题1.5 设一个信息源由64个不同的符号组成,其中16个符号的出现概率均为1/32,其余48个符号出现的概率为1/96,若此信息源每秒发出1000个独立的符号,试求该信息源的平均信息速率。
解:该信息源的熵为96log 961*4832log 321*16)(log )()(log )()(22264121+=-=-=∑∑==i i i i Mi i x P x P x P x P X H=5.79比特/符号因此,该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《通信原理》习题参考答案第五章5-3. 设随机二进制序列中的0和1分别由g(t)和-g(t)组成,它们的出现概率分别为P 和(1-P);(1)求其功率谱密度及功率;(2)若g(t)为图P5-2(a)所示,T s 为码元宽度,问该序列存在离散分量f s =1/T s 否?(3)若g(t)改为图P5-2(b),回答题(2)所问。
解:(1)随机二进制的功率谱密度是由稳态波)(t v T 的功率谱密度和交流波)(t u T 的功率谱密度之和,即: )()()(ωωωu v s P P P +=()[]sm s s s s T f G f G P P mf f mf G P mf PG f 1)()()1()()(1)(221221--+-⋅-+=∑∞-∞=δ ()sm s s s T f G P P mf fmf G P f1)()1(4)()(12222-+-⋅-=∑∞-∞=δ s m s s s T f G P P mf f mf G P f 1)()1(4)()()12(2222-+-⋅-=∑∞-∞=δ∴⎰∞∞-=ωωπd P S s )(21df T f G P P mf f mf G P f s m s s s ⎰∑∞∞-∞-∞=⎥⎦⎤⎢⎣⎡-+-⋅-=1)()1(4)()()12(2222δ df T f G P P df mf f mf G P f s m s s s ⎰⎰∑∞∞-∞∞-∞-∞=-+-⋅-=1)()1(4)()()12(2222δtt(a) (b) 图P5-2df f G P P T df mf f mf G P f s s m s s⎰⎰∑∞∞-∞∞-∞-∞=-+--=2222)()1(41)()()12(δ (2) 若g(t)为图P5-2(a),则g(t)经过傅立叶变化可得到它的频谱,即:)2()(ss T Sa T G ωω=将ω换为f 得: ffT f T f T T f T Sa T f G s s s ss s πππππsin sin )()(=== 判断频域中是否存在s T f 1=,就是将sT f 1=代入)(f G 中,得:0sin sin )(===ππππss T f f T f G说明sT f 1=时g(t)的功率为0,所以不存在该分量。
(3) 若g(t)为图P5-2(b),它的频谱为:)4(2)(s s TSa T G ωω=将ω换为f 得: 2s i n 1)2(2)(f T f f T Sa T f G s s s πππ==将sT f 1=代入)(f G 中,得:02sin 2sin 1)(≠===πππππs s s TT f T f f G说明sT f 1=时g(t)的功率为πs T ,所以存在该分量。
5-8. 已知信息代码为1010000011000011,试确定相应的AMI 码及HDB 3码,分别画出它们的波形图。
解:波形土如下:信息码:AMI 码:HDB3码: (0码参考)5-11. 设基带传输系统的发送滤波器、信道及接收滤波器组成总特性为H(ω),若要求以2/T s 波特的速率进行数据传输,试检验图P5-7各种H(ω)满足消除抽样点上码间干扰的条件否?解:当码元速率为2/T s 时,它的频谱周期为:sT T πω4=,即在频谱上将H(ω)左右平移一个T ω,若在s T π2-和sT π2范围内为常数,则无码间干扰,否则就存在码间干扰,现分别对上图进行分析:对图(a)有:在虚线范围内叠加不为常数,所以存在码间干扰;(a) (b) 图P5-7(c) (d)(a)(b)在虚线范围内叠加不为常数,所以存在码间干扰;对图(c)有:(c)在虚线范围内叠加为常数1,所以无码间干扰;对图(d)有:(d)在虚线范围内叠加不为常数,所以存在码间干扰。
5-13. 为了传送码元速率R B =103(B)的数字基带信号,试问系统采用图P5-9中所画的哪一种传输特性较好?并简要说明其理由。
解:分析各个传输特性有无码间干扰,由于码元传输速率为R B =103,即频谱的周期为:3102⨯=πωT , 对于图(a)有:在〔-103π,103π〕区间内叠加为常数2,所以不存在码间干扰;该系统的频带利用率为:Hz B /2110410233=⨯⨯=ππη 对于图(b)有:图 P5-9在〔-103π,103π〕区间内叠加为常数2,所以不存在码间干扰;该系统的频带利用率为:Hz B /110210233=⨯⨯=ππη 对于图(c)有:在〔-103π,103π〕区间内叠加为常数1,所以不存在码间干扰;该系统的频带利用率为:Hz B /110210233=⨯⨯=ππη综上所述,从系统的可靠性方面看:三个系统都不存在码间干扰,都可以进行可靠的通信;从系统的有效性方面看:(b)和(c)的频带利用率比较高;从系统的可实性方面看:(a)和(c)比较容易实现,(b)比较难实现。
所以从以上三个方面考虑,(c)是较好的系统。
5-14. 设二进制基带系统的分析模型如图P5-7所示,现已知⎪⎩⎪⎨⎧≤+= 其它ω 0,τπω ),cos ωτ(1τ000)(ωH试确定该系统最高的码元传输速率R B 及相应码元间隔T s发 送 传输 接 收n(t)图5-7 基带系统模型解:因为⎪⎩⎪⎨⎧≤+= 其它ω 0,τπω ),cos ωτ(1τ000)(ωH ,它是1=α的升余弦特性,它的频谱宽度为:00τπωτπ≤≤- ,频率范围:002121ττ≤≤-f 即)(f H 左右平移021τ后,在002121ττ≤≤-f 内可以叠加为一个常数,所以它允许的最高码元传输速率为:021τ=B R ,码元宽度:021τ==Bs R T5-16. 设一相关编码系统如图P5-10所示。
图中,理想低通滤波器的截止频率为1/2T s ,通带增益为T s 。
试求该系统的单位冲激相应和频率特性。
解:已知⎪⎩⎪⎨⎧≤= 其它f 0,T ,s s πωωT H )(',它的冲激相响应为:)()('t T Sa t h sπ=所以系统的冲击函数为:[])(*)2()()('t h T t t t h s --=δδ[])(*)2()(t T Sa T t t ss πδδ--=()⎥⎦⎤⎢⎣⎡--=s s s T t T Sa t T Sa 2)(ππ⎪⎪⎭⎫ ⎝⎛--=πππ2)(t T Sa t T Sa s s图 P5-10系统的传输函数为:)()1()('2ωωωH e H s T j --= )()1('2ωωH e s T j --=⎪⎩⎪⎨⎧≤-=- 其它 0,T πω ,)T e (1s s jω2T s5-17. 若上题中输入数据为二进制的,则相关编码电平数为何值?若数据为四进制的,则相关电平数为何值? 解:若数据为二进制,则码元中的电平有0和1,它们相减的组合有: 0-0=0 0-1=-1 1-0=1 1-1=0所以相关编码电平数有3个,分别为-1、0、1若数据为四进制,则码元中的电平有0、1、2和3,它们相减的组合有: 0-0=0 0-1=-1 0-2=-2 0-3=-3 1-0=1 1-1=0 1-2=-1 1-3=-2 2-0=2 1-1=1 2-2=0 2-3=-1 3-0=3 3-1=2 3-2=1 3-3=0 所以相关编码电平数有7个,分别为-3、-2、-1、0、1、2、35-21. 若二进制基带系统如图5-7所示,并设1)(=ωC , )()()(ωωωH G G R T ==。
现已知⎪⎩⎪⎨⎧≤+= 其它ω 0,τπω ),cos ωτ(1τ000)(ωH(1)若)(t n 的双边功率谱密度为)/(2/0Hz W n ,试确定)(ωR G 的输出噪声功率;(2)若在取样时刻KT(K 为任意正整数)上,接收滤波器的输出信号以相同概率取0、A 电平,而输出噪声取值V 服从下述概率密度分布的随机变量0(常数)λ e 2λ1f(V)λV>=- 试求系统最小误码率P e 。
解:(1)已知)()(ωωH G R =,所以输出噪声的功率谱密度为:[])cos 1(2)(2)(2)(000020ωττωωω+===n H n G n P R o ,0τπω≤ 输出的功率为:[]⎰⎰--+==0000//000//0)cos 1(221)(21τπτπτπτπωωττπωωπd n d P N ⎥⎦⎤⎢⎣⎡+=⎰⎰--0000////00000cos 2221τπτπτπτπωωττωτπd n d n 20n =(2)已知 21)()0(==A P P ,最佳判决电平2A V d =所以:)(21)()0(00eA e eA e e P P P A P P P P +=+= 其中0e P 为0电平产生的误码概率:()e e A v v V ve d ddv edv e P λλλλλλλ2021212121--∞-∞-==⋅-⋅==⎰eA P 为A 电平产生的误码概率: e e e e e A A v v A vAv vA eA d d ddv e dv eP λλλλλλλλλλ22121212121---∞--∞---==⋅=⋅⋅⋅==⎰∴e AeA e eA e e P P P A P P P P λ20021)(21)()0(-=+=+=5-22. 某二进制数字基带系统所传送的是单极性基带信号,且数字信息“0”和“1”的出现概率相等。
(1)若数字信息为“1”时,接收滤波器输出信号在抽样判决时刻的值为A=1(V),且接收滤波器输出噪声是均值为0、均方根值为0.2(V)的高斯噪声,试求这时的误码率P e ;(2)若要求误码率P e 不大于10-5,试确定A 至少应该是多少?解:(1)在均值为0高斯白噪声、单极性基带信号条件下:⎥⎥⎦⎤⎢⎢⎣⎡=n e A erfc P σ2221现已知:2.0=n σ ∴⎥⎦⎤⎢⎣⎡=24.0121erfc P e 根据Q 函数与误差函数之间的关系:⎥⎦⎤⎢⎣⎡=221)(a erfc a Q 可得:5.2=a即:31021.6)5.2(-⨯==Q P e(2)若要求510-≤e P ,即510)2(2221-≤=⎥⎥⎦⎤⎢⎢⎣⎡=n n e AQ A erfc P σσ 查表可得:3.42≥nAσ,即n A σ6.8≥5-22. 设有一个三抽头的时域均衡器,如图P5-11所示。
x(t)在各抽样点的值依次为x -2=1/8,x -1=1/3,x 0=1,x +1=1/4,x +2=1/16(在其他抽样点均为零)。
试求输入波形x(t)峰值的畸变值及时域均衡器输出波形y(t)峰值的畸变值。
