三角形的中位线专题复习
三角形的中位线专题复习

7.如图, 在4ABC 中,AB=AC , AD ±BC 于点 D ,求DE 的长.word 格式-可编辑-感谢下载支持三角形的中位线1 .已知A ABC 各边长分别为3、4、5,则连接各边中点的三角形的周长为2 .如图,A ABC 中,D 、E 分别是 AB 、AC 的中点,NA=50°,NADE=60°,则NC 二—3 .如图,在DABCD 中,对角线AC, BD 相交于。
点,E 为CD 的中点,若OE=3,则求AD 二□ABCD 的对角线AC 、BD 交于点O ,点E 是AD 的中点,C A BCD =8,求C A DEQ .D 、E 、F 分别是^ABC 的边AB 、AC 、BC 的中点,求证:AF 与DE 互相平6.如图,口ABCD 周长为m ,延长AB 至E 使BE=BC , BN ±EC 于N , M 为AC 、BD 的交点,连接MN ,求MN 的长度.4.如图,5.如图, 分.8.如图,E 为D ABCD 中DC 边的延长线上一点,CE=CD , AE 交BC 于F , AC 交BD 于 O ,连接OF.(1)求证:△ABF 04ECF ; (2)探究OF 与DE 的数量关系.A【连接两点构造三角形中位线】1.如图,E 、F 、G 、H 分别是四边形ABCD 的边AB 、BC 、CD 、DA 的中点,连接EF 、FG 、GH 、HE ,证明:四边形EFGH 是平行四边形.3.如图,点P 是四边形ABCD 的对角线BD 的中点,E , F 分别是AB , CD 的中点,AD=BC ,NCBD=45°,NADB=105°,探究EF 与PF 之间的数量关系,并证明。
常规辅助线【利用角平分线+垂直】1 .点 M 为4ABC 的边 BC 的中点,AB=12, AC=18, BD ±AD 于 D ,连接 DM.(1)如图,若AD 为N BAC 的角平分线,求MD 的长.2. 如图 于N, 在DABCD 中,E,F 分别是AD, BC 上的点,且AE=BF, 求证:MN 平行且等于2 AD 。
专题11 三角形中位线定理(原卷版)

专题11 三角形中位线定理【考点归纳】(1)三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.(2)几何语言:【好题必练】一、选择题1.(2020秋•罗湖区期末)如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2.其中正确结论的个数是()A.1B.2C.3D.42.(2020秋•安丘市期末)如图,面积为2的等边三角形ABC中,D,E,F分别是AB,BC,CA的中点,则△DEF的面积是()A.1B.C.D.3.(2020秋•长春期末)如图,在边长为4的等边三角形ABC中,DE为△ABC的中位线,则四边形BCED 的面积为()A.2B.3C.4D.64.(2020秋•长春期末)△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF 的周长为()A.4.5B.9C.10D.125.(2020秋•绿园区期末)如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=10m,则A,B之间的距离是()A.5m B.10m C.20m D.40m6.(2020秋•内江期末)如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是()A.50°B.40°C.30°D.20°二、填空题7.(2020春•兴化市期中)如图,D、E分别是△ABC的边AB、AC的中点.若BC=6,则DE的长为.8.(2020春•姜堰区期中)已知以三角形各边中点为顶点的三角形的周长为6cm,则原三角形的周长为cm.9.(2020春•建湖县期中)如图,AB∥CD,AB=7,CD=3,M、N分别是AC和BD的中点,则MN的长度.10.(2020春•常熟市期中)如图,在△ABC中,BC=14,D、E分别是AB、AC的中点,F是DE延长线上一点,连接AF、CF,若DF=12,∠AFC=90°,则AC=.11.(2020•凤山县一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点.若BC=2,则EF的长度为.三、解答题12.(2020•房山区二模)如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,F是BD中点.求证:EF平分∠BED.13.如图,四边形ABCD中,AB=AD,对角线BD平分∠ABC,E,F分别是BD,CD的中点.求证:AD∥EF.14.如图,在△ABC中,D为BC的中点,E为AC的中点,AB=6,求DE的长.15.如图,在△Rt△ABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD,求证:CD=EF.16.如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为10,求△ABC的周长。
专题--三角形的中位线(含提示答案)
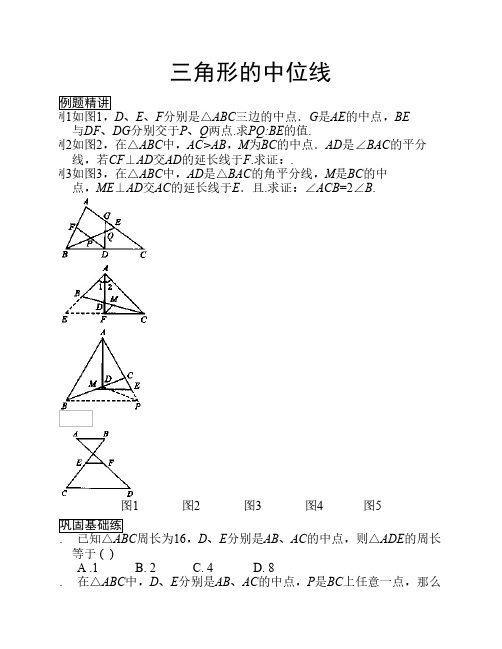
三角形的中位线例题精讲例1如图1,D、E、F分别是△ABC三边的中点.G是AE的中点,BE 与DF、DG分别交于P、Q两点.求PQ:BE的值.例2如图2,在△ABC中,AC>AB,M为BC的中点.AD是∠BAC的平分线,若CF⊥AD交AD的延长线于F.求证:.例3如图3,在△ABC中,AD是△BAC的角平分线,M是BC的中点,ME⊥AD交AC的延长线于E.且.求证:∠ACB=2∠B.图1 图2 图3 图4 图5巩固基础练1. 已知△ABC周长为16,D、E分别是AB、AC的中点,则△ADE的周长等于 ( )A .1 B. 2 C. 4 D. 82. 在△ABC中,D、E分别是AB、AC的中点,P是BC上任意一点,那么△PDE面积是△ABC'面积的 ( ) A . B. C. D.3. 如图4,在四边形ABCD中,E、F分别为AC、BD的中点,则EF与AB+CD的关系是 ( )A . B. C. D. 不确定4. 如图5,AB∥CD,E、F分别是BC、AD的中点,且AB=a,CD=b,则EF的长为 .图6 图7 图8 图9 图105. 如图6,四边形ABCD中,AD=BC,F、E、G分别是AB、CD、AC的中点,若∠DAC=200,∠ACB=600,则∠FEG= .6.如图7,△ABC的周长为1,连接△ABC三边的中点构成第二个三角,再连接第二个三角形三边中点构成第三个三角形,依此类推,第2003个三角形的周长为 .7. 已知三角形三条中位线的比为3:5:6,三角形的周长是112cm,求三条中位线长.8. 如图8,△ABC中,AD是高,BE是中线,∠EBC=300,求证:AD=BE.(过E点向BC作垂线)9. 如图9,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB中点,连接CE、CD.求证:CD=2EC.(延长AC到F,使AC=CF,则CD=BF)10.如图10,AD是△ABC的外角平分线,CD⊥AD于D,E是BC的中点.求证:(1)DE∥AB; (2).(延长DC交BA的延长线于G)提高过渡练1. 如图11,M、P分别为△ABC的AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N,已知PN=1,则PB的长为 ( ) A. 2 B. 3 C .4 D. 52. 如图12,△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,AB=10,则MD的长为 ( )A. 10B. 8 C .6 D. 53. 如图13,△ABC是等边三角形,D、E、F分别是AB、BC、AC的中点,P为不同于B、E、C的BC上的任意一点,△DPH为等边三角形.连接FH,则EP与FH的大小关系是 ( )A. E P>FHB. EP=FHC. EP<FHD.不确定4. 如图14,在△ABC中,AD平分∠BAC,BD⊥AD,DE∥AC,交AB于E,若AB=5,则DE的长为 .5. 如图15,△ABC中,AB=4,AC=7,M为BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于 . (1、延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E)(2、设点N是AC的中点,连接MN,则MN∥AB)图11 图12 图13 图14 图156. 已知在△ABC中,∠B=600,CD、AE分别为AB、BC边上的高,DE=5,则AC的长为 .7. 如图16,在△ABC中,D、E是AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点,直线MN分别交AB、AC于P、Q.求证:AP=AQ (过M、N两点连接BC的中点G)8. 如图17,BE、CF是△ABC的角平分线,AN⊥BE于N,AM⊥CF于M.求证:MN∥BC. (延长AM、AN交BC于H、G)9. 如图18,在△ABC中,AD平分∠BAC,AD=AB,CM⊥AD于M.求证:AB+AC=2AM (延长AM至E 使得AE=AC,连结EC)10.如图19,四边形ABCD中,G、H分别是AD、BC的中点,AB=CD.BA、CD的延长线交HG的延长线于E、F.求证:∠BEH=∠CFH. (连接BD,取中点I,连接IG,IH)图16 图17 图18 图19 图20顶级超强练1. 如图20,在△ABC中,∠ABC=2∠C,AD平分∠BAC,过BC的中点M作ME⊥AD,交BA的延长线于E,交AD的延长线于F.求证:.(过B点作AC的平行线交EF于H,在AC截取AG,使AG=AB,延长EF交AC于K)2. 如图21,在△ABC中,AB<AC,P为AC上的点,CP=AB,K为AP的中点,M为BC的中点,MK的延长线交BA的长线于N.求证:AN=AK. (连接BP,取BP中点O,连接OK,OM)3. 如图22,分别以△ABC的边AC、BC为腰,A、B为直角顶点,作等腰直角△ACE和等腰直角△BCD,M为ED的中点.求证:AM⊥BM.4. 如图23,点O是四边形ABCD内一点,∠AOB=∠COD=1200,AO=BO,CO=DO,E、F、G分别为AB、CD、BC的中点.求证:△EFG为等边三角形. (连接AC、BD,则AC=BD,EF=BD)5. 如图24,△ABC中,M是AB的中点,P是AC的中点,D是MB的中点,N是CD的中点,Q是MN的中点,直线PQ交MB于K.求证:K是DB的中点.6. 如图25,P为△ABC内一点,∠PAC=∠PBC,PM⊥AC于M,PN⊥BC于N.D是AB的中点.求证:DM=DN (取PA、PB的中点E、F,连接ME、DE、NF、DF,△MED≌△NFD)图21 图22 图23 图24 图257. 如图26,AP是△ABC的角平分线,D、E分别是AB、AC上的点,且BD=CE.又G、H分别为BC、DE的中点.求证:HG∥AP.8. 如图27,已知△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=900,如图(a),连接DE,设M为DE的中点.(1)求证:MB=MC; (△MCE≌MBD)(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图(b)的位置,试问MB=MC是否成立?并证明其结论.(取AD、AE 的中点F、G,连接BF、MF、MG、CG,∴△BFM≌△MGC)9. 已知△ABC面积为S,作直线l∥BC,交AB于D,交AC于E,若△BED的积为K.求证:S≥4K.10.如图28,在△ABC中,AB=AC,D是BC边上的一点,E是线段AD上的一点.且∠BED=2∠CED=∠BAC.求证:BD=2CD.图26 图27 图28。
专题05 三角形中位线(知识点串讲)(解析版)

专题05 三角形中位线重难突破三角形中位线1.三角形中位线:连接三角形两边中点的线段叫做三角形的中位线.2.三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.3.相关结论:顺次连接任意四边形中点所得到的四边形是平行四边形.(连接原四边形一条对角线,由中位线定理可证)4.拓展:①梯形的中位线等于上底加下底和的一半. (连接梯形一条对角线,由中位线定理可证)②过三角形一边的中点作另一边的平行线,与第三边交于一点,则这两点之间的线段为三角形的中位线. 如图,过△ABC的边AB的中点作平行于边BC的直线,交边AC于点E,则DE为△ABC的中位线.典例1.(2018春•定兴县期末)如图所示,已知P、R分别是四边形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么EF的长()A.逐渐增大B.逐渐变小C.不变D.先增大,后变小【答案】C【解析】解:∵E、F分别是PA、PR的中点,∴EF AR,∴EF的长不变,故选:C.【点睛】根据三角形中位线定理得到EF AR,判断即可.本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.典例2.(2018春•柳州期末)在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN ⊥AE于N,若AC=6,BC=8,则MN=___.【答案】2【解析】解:延长CM交AB于G,延长CN交AB于H,∵∠ACB=90°,AC=6,BC=8,∴AB=10,在△BMC和△BMG中,,∴△BMC≌△BMG,∴BG=BC=8,CM=MG,∴AG=2,同理,AH=AC=6,CN=NH,∴GH=4,∴MN GH=2,故答案为:2.【点睛】延长CM交AB于G,延长CN交AB于H,证明△BMC≌△BMG,得到BG=BC=8,CM=MG,同理得到AH=AC=6,CN=NH,根据三角形中位线定理计算即可.典例3.(2018春•成都期末)已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE =2,则AC的长等于______.【答案】见解析【解析】解:过D点作DF∥BE,∵AD是△ABC的中线,AD⊥BE,∴F为EC中点,AD⊥DF,∵AD=BE=2,则DF=1,AF,∵BE是△ABC的角平分线,AD⊥BE,∴△ABG≌△DBG,∴G为AD中点,∴E为AF中点,∴AE=EF=CF,∴AC AF.故答案为:.【点睛】过D点作DF∥BE,则DF BE=1,F为EC中点,在Rt△ADF中求出AF的长度,根据已知条件易知G为AD中点,因此E为AF中点,则AC AF.典例4.(2018春•吉州区期末)如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.【答案】见解析【解析】解:如图,延长BD与AC相交于点F,∵AD平分∠BAC,BD⊥AD,∴∠DAB=∠DAF,AD=AD,∠ADB=∠ADF,∴△ADB≌△ADF,∴AF=AB,BD=DF,∵AB=6,AC=10,∴CF=AC﹣AF=AC﹣AB=10﹣6=4,∵E为BC中点,∴DE是△BCF的中位线,∴DE CF4=2.【点睛】延长BD与AC相交于点F,根据等腰三角形的性质可得BD=DF,再利用三角形的中位线平行于第三边并且等于第三边的一半可得DE CF,然后求解即可.典例5.(2018春•濮阳期末)已知等边三角形ABC的边长为a分别以这个三角形的三边中点为顶点作一个三角形,记为△A1B1C1,再以△A1B1C1各边中点为顶点做三角形记为△A2B2C2,…依次做下去,求△A5B5C5的周长.【答案】见解析【解析】解:等边△ABC的边长为a,∴等边△ABC的周长为3a.∵A2、B2分别是边A1B1、B1C1的中点,∴A2B2是△A1B1C1的中位线,∴A2B2A1B1.同理,A2C2A1C1,C2B2C1B1.∴△A2B2C2的周长等边△A1B1C1的周长.同理,△A3B3C3的周长△A2B2C2的周长等边△A1B1C1的周长.…,∴△A n B n∁n的周长△A1B1C1的周长.∴△A5B5C5的周长.【点睛】据三角形中位线定理知,△A2B2C2的各边的边长是△A1B1C1的各边边长的,△A3B3C3是△A2B2C2的各边的边长的,找出规律即可得出结论.本题考查了等边三角形的性质、三角形中位线定理.三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.典例6.(2018春•南山区期末)如图,△ABC中,AB>AC,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则①EF∥AB;②∠BCG(∠ACB﹣∠ABC);③EF (AB﹣AC);④(AB﹣AC)<AE(AB+AC).其中正确的是()A.①②③④B.①②C.②③④D.①③④【答案】A【解析】解:∵AD平分∠BAC,∴∠GAF=∠CAF,∵CG⊥AD,∴∠AFG=∠AFC=90°,在△AFG和△AFC中∴△AFG≌△AFC(ASA),∴GF=CF,∵AE为△ABC的中线,∴BE=CE,∴EF∥AB,故①正确;∵△AFG≌△AFC,∴∠AGC=∠ACB,∵∠AGC=∠B+∠BCG,∴∠ACG=∠B+∠BCG,∴∠BCG=∠ACB﹣∠ACG=∠ACB﹣(∠B+∠BCG),∴2∠BCG=∠ACB﹣∠B,∴∠BCG(∠ACB﹣∠B),故②正确;∵△AFG≌△AFC,∴AC=AG,∴BG=AB﹣AG=AB﹣AC,∵F、E分别是CG、BC的中点,∴EF BG,∴EF(AB﹣AC),故③正确;∵∠AFG=90°,∴∠EAF<90°,∵∠AFE=∠AFG+∠EFG>90°,∴∠AFE>∠EAF,∴AE>EF,∵EF(AB﹣AC),∴(AB﹣AC)<AE,延长AE到M,使AE=EM,连接BM,∵在△ACE和△MBE中∴△ACE≌△MBE(SAS),∴AC=BM,在△ABM中,AM<AB+AC,∵AE=EM,∴2AE<AB+AC,∴AE(AB+AC),即(AB﹣AC)<AE(AB+AC),故④正确;故选:A.【点睛】求出F为CG中点,根据三角形的中位线性质即可判断①,求出∠ACG=∠AGC=∠B+∠BCG,即可判断②;根据三角形中位线性质即可判断③,求出2AE<AB+BC和AE>EF,即可判断④.巩固练习1.(2018春•坪山区期末)如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为()A.12 B.11 C.10 D.9【答案】D【解析】解:∵点D,E分别AB、BC的中点,∴DE AC=3.5,同理,DF BC=3,EF AB=2.5,∴△DEF的周长=DE+EF+DF=9,故选:D.2.(2018春•抚顺期末)如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=25°,则∠EPF的度数是()A.100°B.120°C.130°D.150°【答案】C【解析】解:∵P是对角线BD的中点,E,F分别是AB,CD的中点,∴PE AD,PF BC,∵AD=BC,∴PE=PF,∴∠PFE=∠PEF=25°,∴∠EPF=130°,故选:C.3.(2018春•颍东区期末)如图在△ABC中,M是BC中点,AP是∠A平分线,BP⊥AP于P,AB=12,AC=22,则MP长为()A.3 B.4 C.5 D.6【答案】C【解析】解:延长BP交AC于N.∵AP是∠BAC的角平分线,BP⊥AP于P,∴∠BAP=∠NAP,∠APB=∠APN=90°,∴△ABP≌△ANP(ASA),∴AN=AB=12,BP=PN,∴CN=AC﹣AN=22﹣12=10,∵BP=PN,BM=CM,∴PM是△BNC的中位线,∴PM CN=5.故选:C.4.(2018春•开江县期末)如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形,……如此操作下去,那么第5个三角形直角顶点的坐标为()A.(,)B.()C.()D.()【答案】B【解析】解:由题意:第1个三角形的直角顶点坐标:(﹣2,2);第2个三角形的直角顶点坐标:(﹣1,1);第3个三角形的第1个三角形的直角顶点坐标:(,);第4个三角形的直角顶点坐标:(,);第5个三角形的直角顶点坐标:(,);故选:B.5.(2017秋•洪雅县期末)如图,在△ABC中,AB=5,AC=3,AD是角平分线,AE是中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为___.【答案】1【解析】解:∵AD是其角平分线,CG⊥AD于F,∴△AGC是等腰三角形,∴AG=AC=3,GF=CF,∵AB=5,AC=3,∴BG=2,∵AE是中线,∴BE=CE,∴EF为△CBG的中位线,∴EF BG=1 故答案为:1.。
中考数学复习微专题:《三角形的中位线》突破与提升专题练习(无答案)

中考数学复习微专题:《三角形的中位线》突破与提升专题练习一.选择题.1.如图,在△ABC中,AB=10,AC=8,BC=12,AD⊥BC于点D,点E,F分别在AB,AC边上,把△ABC沿EF折叠,使点A与点D恰好重合,则△DEF的周长是( )A.14B.15C.16D. 172.如图,在△ABC中,AC=8,BC=12,AF交BC于F,E为AB的中点,CD平分∠ACB,且CD⊥AF,垂足为D.连接DE,则DE的长为( )A.2B.C.3D.43.任意三角形两边的中点的连线与第三边上的中线( )A.互相平分B.互相垂直C.相等D.互相垂直平分4. 如图,在△ABC中,E,D,F分别是AB,BC,CA的中点,AB=6,AC=4,则四边形AEDF的周长是 ( )A.10B.20C.30D.405. 如图,▱ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB·AC;③OB=AB;④OE=BC,成立的个数有()A.1个B.2个C.3个D.4个6.如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第2014个正△A2014B2014C2014的面积是( )A.×B.×C.×D.×二.填空题.7.如图,一张三角形纸片ABC,AB=AC=5.折叠该纸片,使点A落在BC的中点上,折痕经过AC 上的点E,则AE的长为_________.8.如图,▱ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE 的周长为_________.9. 如图,在▱ABCD中,对角线AC,BD相交于点O,点E是AB的中点,OE=5 cm,则AD的长是_________cm.10. 如图,在△ABC中,D,E分别是边AB,AC的中点,连接DE,若DE=3,则线段BC的长等于_________.11. 如图所示,在四边形ABCD中,P为对角线BD的中点,E,F分别为AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是_________.12.如图,在△ABC中,CD是高,CE是中线,CE=CB,点A,D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为_________.13.如图,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB=10,AC=6,则DF的长为_________.三.解答题.14.如图,BM,CN分别平分△ABC的外角∠ABD,∠ACE,过A分别作BM,CN的垂线,垂足分别为M,N,交CB,BC的延长线于D,E,连接MN.求证:MN=(AB+BC+AC).15.已知:如图,在△ABC中,∠ACB=90°,点D,E分别是AC,AB的中点,点F在BC的延长线上,且∠CDF=∠A,求证:四边形DECF是平行四边形.16如图,在△ABC中,AD是高,E,F分别是AB,AC的中点.(1)若四边形AEDF的周长为24,AB=15,求AC的长.(2)求证:EF垂直平分AD.17.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形.(2)求证:∠DHF=∠DEF.18.我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH.(1)这个中点四边形EFGH的形状是________.(2)请证明你的结论.。
专题 三角形中位线定理的运用(原卷版)

八年级下册数学《第十八章 平行四边形》专题 三角形中位线定理的运用【例题1】(2022秋•长沙期中)如图,在△ABC 中,D ,E 分别是AB ,AC 的中点,F ,G 分别是AD ,AE 的中点,且FG =2cm ,则BC 的长度是( )A .4cmB .6cmC .8cmD .10cm【变式1-1】(2022秋•海淀区期中)如图,BD 是△ABC 的中线,E ,F 分别是BD ,BC 的中点,连接EF .若AD =4,则EF 的长为( )A .32B .2C .52D .4【变式1-2】(2022秋•莲池区校级期末)如图,在△ABC 中,∠B =45°,∠C =60°,AD ⊥BC 于点D ,BD =E ,F 分别为AB ,BC 的中点,则EF 的长为( )A B C D 【变式1-3】(2022春•巨野县校级月考)如图,在△ABC 中,D 是AB 上一点,AE 平分∠CAD ,AE ⊥CD 于点E ,点F 是BC 的中点,若AB =10,AC =6,则EF 的长为( )A .4B .3C .2D .1【变式1-4】(2022秋•南关区校级期末)如图,四边形ABCD 中,∠A =90°,AB =12,AD =5,点M 、N 分别为线段BC 、AB 上的动点,点E 、F 分别为DM 、MN 的中点,则EF 长度的可能为( )A .2B .2.3C .4D .7【变式1-5】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.若AB=8,AD=12,则四边形ENFM的周长为 .【变式1-6】(2022春•海淀区校级期中)如图,在Rt△ABC中,∠BAC=90°,点D和点E分别是AB,AC的中点,点F和点G分别在BA和CA的延长线上,若BC=10,GF=6,EF=4,则GD的长为 .【变式1-7】(2022春•本溪期末)如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,顺次连接EM,MF,FN,NE,若AB=CD=2,则四边形ENFM 的周长是 .过点C 作CF ∥BE ,交DE 的延长线于点F ,若EF =3,求DE 的长.【变式1-9】如图,在△ABC 中,AB =12cm ,AC =8cm ,AD 、AE 分别是其角平分线和中线,过点C 作CG ⊥AD 于点F ,交AB 于点G ,连接EF ,求线段EF 的长.【例题2】(2022秋•安岳县期末)如图,在△ABC 中,D 、E 、F 分别是AB 、AC 、BC 的中点,若∠CFE =55°,则∠ADE 的度数为( )A .65°B .60°C .55°D .50°60°,∠B=75°,则∠ANM= .【变式2-2】(2022•永安市模拟)如图,DE是△ABC的中位线,∠ABC的平分线交DE于点F,若∠DFB =32°,∠A=75°,则∠AED= .【变式2-3】(2022春•顺德区校级期中)如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,求∠ADC的度数.【变式2-4】(2022•九江二模)如图,在四边形ABCD中,点E,F,G分别是AD,BC,AC的中点,AB =CD,∠EGF=144°,则∠GEF的度数为 .【变式2-5】(2022秋•新泰市期末)如图,四边形ABCD 中,AD =BC ,E ,F ,G 分别是AB ,DC ,AC 的中点.若∠ACB =64°,∠DAC =22°,则∠EFG 的度数为 .【变式2-6】(2022春•鼓楼区期中)如图所示,在△ABC 中,∠A =40°,D ,E 分别在AB ,AC 上,BD =CE ,BE ,CD 的中点分别是M ,N ,直线MN 分别交AB ,AC 于P ,Q .求∠APQ 的度数.【例题3】(2021秋•杜尔伯特县期末)如图,已知△ABC 中,D 是AB 上一点,AD =AC ,AE ⊥CD ,垂足是E ,F 是BC 的中点.求证:BD =2EF.【变式3-1】(2021春•秦都区期末)如图,在△ABC中,AB=AC,点D、E分别是边AB、AC上的点,连接BE、DE,∠ADE=∠AED,点F、G、H分别为BE、DE、BC的中点.求证:FG=FH.【变式3-2】(2021秋•互助县期中)如图,已知AB=AC,BD=CD,DB⊥AB,DC⊥AC,且E、F、G、H分别为AB、AC、CD、BD的中点,求证:EH=FG.【变式3-3】已知:如图,E为▱ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于O,连接OF.求证:AB=2OF.【变式3-4】(2021春•崇川区校级月考)已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.求证:(1)DE∥FG;(2)DG和EF互相平分.【变式3-5】(2022春•富平县期末)如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别是AB、CD的中点,E、F分别交BD、AC于点G、H,取BC边的中点M,连接EM、FM.求证:(1)△MEF是等腰三角形;(2)OG=OH.【变式3-6】(2022春•瑶海区期末)已知:如图,在△ABC中,点D、E分别是AB、AC的中点(1)若DE=2,则BC= ;若∠ACB=70°,则∠AED= °;(2)连接CD和BE交于点O,求证:CO=2DO.【变式3-7】(2022春•虎丘区校级期中)如图,线段AM是∠CAB的角平分线,取BC中点N,连接AN,过点C作AM的垂线段CE垂足为E.(1)求证:EN∥AB.(2)若AC=13,AB=37,求EN的长度.【例题4】(2021春•莆田期末)如图,在四边形ABCD 中,AD =BC ,E 、F 分别是边DC 、AB 的中点,FE 的延长线分别AD 、BC 的延长线交于点H 、G ,求证:∠AHF =∠BGF .【变式4-1】(2022春•西峰区校级月考)如图,四边形ABCD 中,AD =BC ,P 是对角线BD 的中点,N 、M 分别是AB 、CD 的中点,求证:∠PMN =∠PNM .【变式4-2】(2021春•歙县期中)如图,CD 是△ABC 的角平分线,AE ⊥CD 于E ,F 是AC 的中点,(1)求证:EF ∥BC ;(2)猜想:∠B 、∠DAE 、∠EAC三个角之间的关系,并加以证明.【变式4-3】如图,△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q,求证:∠QPA=∠PQA.【变式4-4】一个对角线相等的四边形ABCD,E、F分别为AB,CD的中点,EF分别交对角线BD,AC 于M,N,求证:∠OMN=∠ONM.【变式4-5】(2022春•船营区校级月考)如图是华师版九年级上册数学教材第80页的第3题.如图①,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM(1)在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F,如图②,请先完成图①的证明,再继续证明∠AEN=∠F.(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为 .【例题5】(2022秋•任城区期末)如图,在△ABC 中,AE 平分∠BAC ,BE ⊥AE 于点E ,点F 是BC 的中点,若AB =10,AC =6,则EF 的长为( )A .2B .3C .4D .5【变式5-1】(2022春•綦江区校级月考)如图,在四边形ABCD 中,AC ⊥BD ,BD =16,AC =30,E ,F 分别为AB ,CD 的中点,则EF =( )A .15B ..16C .17D .8【变式5-2】(2021春•沈北新区期末)如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=12 CF.【变式5-3】如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P 为AE的中点,连接PG,则PG的长为 .【变式5-4】(2021•罗湖区校级模拟)如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN = .【变式5-5】(2022春•香坊区校级期中)如图所示,在四边形ABCD中,点E、F分别是AD、BC的中点,连接EF,AB=20,CD=12,∠B+∠C=120°,则EF的长为 .【变式5-6】(2022秋•张店区校级期末)已知:如图,在△ABC中,点D在AB上,BD=AC,E、F、G 分别是BC、AD、CD的中点,EF、CA的延长线相交于点H.求证:(1)∠CGE=∠ACD+∠CAD;(2)AH=AF.【变式5-7】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.(1)如图1,BE的延长线与AC边相交于点D,求证:EF=12(AC﹣AB);(2)如图2,请直接写出线段AB、AC、EF的数量关系.【变式5-8】(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.求证:FG=12(AB+BC+AC).[提示:分别延长AF、AG与直线BC相交](2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.【变式5-9】如图,在四边形ABCD中,AB=CD,E.F分别是BC.AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M,N,则∠BME=∠CNE(不必证明)(温馨提示:在图(1)中,连接BD,取BD的中点H,连接HE.HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线的性质,可证明∠BME=∠CNE)(1)如图(2),在四边形ADBC中,AB与CD相交于点O,AB=CD,E.F分别是BC.AD的中点,连接EF,分别交CD.BA于点M.N,判断△OMN的形状,请直接写出结论.(2)如图(3)中,在△ABC中,AC>AB,D点在AC上,AB=CD,E.F分别是BC.AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD形状并证明.。
复习中位线定理

B
C
经典题型 如图,在梯形ABCD中 如图,在梯形ABCD中,AD∥BC ,E是 ABCD AB中点 中点, 腰AB中点,若CE⊥DE. 求证: AD+BC=CD。 求证: AD+BC=CD。
A E D
F
B
C
本节课你有什么收获?
小结: 1、三角形中位线定义及定理。 、三角形中位线定义及定理。 2、中点四边形的重要特征。 、中点四边形的重要特征。 3、梯形中位线定义及定理。 、梯形中位线定义及定理。 4、梯形腰上中点的常见辅助线作法。 、梯形腰上中点的常见辅助线作法。
我能行
如图,在四边形ABCD中 如图,在四边形ABCD中,E、F、G、H分别 ABCD 是边AB BC、CD、DA的中点 AB、 的中点, 是边AB、BC、CD、DA的中点,请添加一个 条件,使四边形EFGH为菱形。 条件,使四边形EFGH为菱形。 EFGH为菱形 A 解:添加的条件 H AC=BD =
2 3
……
A
n
A1
C
2
C1 B2
1 2 1 4
a
s
1 4 1 16
a
s
1 8 1 64
a
……
s
……
1 n 2 1 n 4
a
s
B
A2 B1
C
二、中点四边形
已知:如图,在四边形 已知:如图,在四边形ABCD中,E、F、G、H分别是 中 、 、 、 分别是 AB、BC、CD、DA的中点 的中点. 、 、 、 的中点 求证:四边形 是平行四边形. 求证:四边形EFGH是平行四边形 是平行四边形 A E B F H D G C
复习中位线定理
一、三角形中位线
三角形的中位线

4
,.若∠ = ∠, = ,则的长为___.
知识点2 中点四边形
例2 如图,四边形各边的中点分别是,,,,若对角线
42
= , = ,则四边形的周长是____.
第六章 平行四边形
3 三角形的中位线
复习回顾
底边上的高线、顶角的平分线
1.等腰三角形底边上的中线与____________________________重合.
预习效果检测
两边中点
1.(1)连接三角形__________的线段叫做三角形的中位线.一个三角形
三
有____条中位线.
平行
一半
(2)三角形的中位线______于第三边,且等于第三边的______.
2.如图,在△中,,分别为和的中点,若 = ,则
6
的长为___.
(第2题)
3.如图,△中,∠ = ∘ ,∠ = ∘ ,点是的中点,点是
62 ∘ .
的中点,则∠ =____
(第3题)
4.如图,,,,分别是四边形四条边的中点,四边形
由(1)知,△≌△, =
∴ = =
,即
= .
,
课堂导学
左讲Байду номын сангаас
知识点1 三角形中位线定理及应用
例1 [2024无锡] 在△中, = , = , = ,,,分
9
别是,,的中点,则△的周长为___.
右练
平行四边形
的形状一定是____________.
(第4题)
5.如图,点,分别是△的边,的中
点,则下列说法不正确的是( C )
A.是△的中位线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O
E D
C
B A E D
C B
A
三角形的中位线
1.已知∆ABC 各边长分别为3、4、5,则连接各边中点的三角形的周长为
2.如图,∆ABC 中,D 、E 分别是AB 、AC 的中点,∠A=50°,∠ADE=60°,则∠C=
3.如图,在□ABCD 中,对角线AC ,BD 相交于O 点,E 为CD 的中点,若OE=3,则求AD=
4.如图,□ABCD 的对角线AC 、BD 交于点O ,点E 是AD 的中点,C △BCD =8,求C △DEO .
5.如图,D 、E 、F 分别是△ABC 的边AB 、AC 、BC 的中点,求证:AF 与DE 互相平分.
6.如图,□ABCD 周长为m ,延长AB 至E 使BE=BC ,BN ⊥EC 于N ,M 为AC 、BD 的交点,连接MN ,求MN 的长度.
7.如图,在△ABC 中,AB=AC ,AD ⊥BC 于点D ,E 是AC 的中点,BC=2,AD=22,求DE
的长.
8.如图,E 为□ABCD 中DC 边的延长线上一点,CE=CD ,AE 交BC 于F ,AC 交BD 于O ,连
B
A B C
D
E
B
F N
M E
D
C B A
P F E D
C B
A
接OF.(1)求证:△ABF ≌△ECF ;(2)探究OF 与DE 的数量关系.
【连接两点构造三角形中位线】
1. 如图,E 、F 、G 、H 分别是四边形ABCD 的边AB 、BC 、CD 、DA 的中点,连接EF 、FG 、
GH 、HE ,证明:四边形EFGH 是平行四边形.
2. 如图,在□ABCD 中,E,F 分别是AD ,BC 上的点,且AE=BF ,BE 交AF 于M ,CE 交DF 于N ,
求证:MN 平行且等于
1
2
AD 。
3. 如图,点P 是四边形ABCD 的对角线BD 的中点,E ,F 分别是AB ,CD 的中点,AD=BC ,
∠CBD=45°,∠ADB=105°,探究EF 与PF 之间的数量关系,并证明。
常规辅助线
【利用角平分线+垂直】
1.点M 为△ABC 的边BC 的中点,AB=12,AC=18,BD ⊥AD 于D ,连接DM.
(1) 如图,若AD 为∠BAC 的角平分线,求MD 的长.
(2) 如图,若AD 为∠BAC 的外角平分线,求MD 的长.
B
B C
M
D C B A
F M
E C B A
变式:如图,△ABC 中,CD 平分∠ACB ,AD ⊥CD ,垂足为D 点,点E 为AB 的中点.
(1) 求证:DE ∥BC ;
(2) 若AC=10,BC=16,求DE 的长.
2.如图,在△ABC 中,AB=10,BC=7,BE 平分∠ABC ,AE ⊥BE ,点F 为AC 的中点,连接EF ,求EF 的长度.
3.如图,在∆ABC 中,点M 为BC 的中点,AD 为∆ABC 的外角的平分线,且AD ⊥BD ,若AB=12,AC=18,求MD 的长。
4.如图,在∆ABC 中,AB=BC ,∠ABC=90°,F 为BC 上一点,M 为AF 的中点,BE 平分∠ABC ,且EF ⊥BE ,求证:CF=2ME 。
【取中点构造中位线】
A
B
A
N
M
D C B A
F
N
M E C
B
A 1.如图,在四边形ABCD 中,AB=CD ,∠ABD=20°,∠BDC=110°,E 、F 、M 分别为AD 、BD 、BC 的中点,探索EM 与EF 的数量关系.
2.如图,AD ∥BC ,∠B+∠BCD=90°,连接AC ,M 、N 、P 分别为AD 、BC 、AC 的中点.
(1) 求证:MP ⊥NP ;(2)若AB=2,CD=3,求MN 的长.
3.如图,四边形ABCD 中,M ,N 分别为AD ,BC 的中点,边BD ,若AB=10,CD=8,求MN 的取值范围。
4.如图,在∆ABC 中,∠C=90°,CA=CB ,E ,F 分别为CA ,CB 上一点,CE=CF ,M ,N 分别为AF ,BE 的中点,求证:
MN
变式:如图,梯形ABCD 中,E 、F 分别为对角线BD 、AC 的中点.
求证:(1)EF ∥CD ;(2)CD -AB=2EF.
5.如图,在∆ABC 中,∠B=2∠A ,CD ⊥AB 于D ,E ,F 分别为AB ,BC 的中点,求证:DE=DF 。
B
B
5.如图,在□ABCD 中,E 是CD 的中点,F 是AE 的中点,FC 交BE 于G .
(1) 求证:GF=GC ;(2)求证:BG=3EG.
6.如图,△ABC 的两条中线BE 、CD 交于点O ,连接AO ,探究OE 与OB 的数量关系.
【借助平行四边形的性质】
1. 如图,在平行四边形BCFD 的对角线CD 的延长线上取一点E ,连接FE 并延长至A 点,使
EA=EF ,连接AB ,求证:CE ∥AB.
2. 如图,AE ⊥AB ,BF ⊥AB ,AB 的垂直平分线交AB 于N ,交EF 于M ,求证:BF -AE=2MN.
A
A B。
