轨道交通站点选址模型及实例
基于GIS的城市轨道选线、车辆段选址方法和实践

基于GIS的城市轨道选线、车辆段选址方法和实践发表时间:2016-06-12T15:22:28.577Z 来源:《基层建设》2016年4期作者:庞乃敬[导读] 城市轨道交通选线、车辆段选址是涉及众多学科、大量信息分析的综合性问题。
深圳市规划国土发展研究中心摘要:本文通过整合现状与规划的各类数据资料,利用GIS强大的空间分析和可视化表达功能,建立城市轨道选线、车辆段选址的GIS 平台,探讨城市轨道选线、车辆段选址的新方法,并以实例分析验证该方法的可靠性和先进性。
关键词:GIS;平台;城市轨道选线;选址;方法引言城市轨道交通选线、车辆段选址是涉及众多学科、大量信息分析的综合性问题,现在主要利用计算机辅助设计CAD处理该问题,但由于CAD本身的局限性,基于CAD的城市轨道选线、车辆段选址方法缺乏对信息的管理和分析能力,且难以反应人口分布、经济发展、土地利用等社会经济指标对选线、选址的影响,使城市轨道选线、车辆段选址缺乏系统性和完整性。
图1 基于GIS的城市轨道选线、车辆段选址方法示意图地理信息系统GIS具有强大的信息管理和空间分析功能,利用GIS进行城市轨道选线、车辆段选址,不仅可以提高工作效率,也使得选线、选址方法更具系统性和完整性。
本文将基于美国环境系统研究所公司(ESRI)的ArcGiS软件建立城市轨道交通选线、车辆段选址的平台,并在实践应用中对基于GIS的城市轨道选线、车辆段选址新方法进行探讨。
GIS选线、选址方法介绍 GIS是一个强大的图形管理系统,可对大量空间数据信息进行录入、编辑和管理;同时GIS具有强大的空间分析与可视化表达功能,可非常方便地对GIS数据进行定性、定量、定位分析,分析过程和结果可以多样化直观表达。
图2 GIS轨道选线、车辆段选址平台数据库资料图由于GIS本身的功能特点,基于GIS的选线方法与基于CAD选线方法不同,基于GIS选线首先要建立整合各种现状、规划信息的数据库平台,再通过轨道选线、车辆段选址方案与各类信息的空间叠置关系,对涉及的各种数据信息进行定性、定量分析,并直观地评价选线、选址方案。
某轻轨车站的设计方案

某轻轨车站的设计方案近年来,随着城市化进程的加快和交通拥堵问题的日益突出,轨道交通成为解决城市交通问题的重要选择。
设计一座合理、高效的轻轨车站,不仅可以缓解城市交通压力,还能提升城市形象和居民出行体验。
本文将从站点选址、建筑设计和功能布局等方面,探讨某轻轨车站的设计方案。
一、站点选址站点选址是轻轨车站设计的首要问题。
它的位置应考虑到市区人流聚集的地方和交通换乘的便利性。
某轻轨车站的选址位于市中心繁华地区,与多条公交线路和地铁线路相接,方便市民从各个方向到达。
同时,站点旁边没有大型建筑物遮挡,站台可以充分接受自然光线,提供良好的观光视野,减少乘客的不安感。
二、建筑设计轻轨车站建筑设计要兼顾实用性和美观性。
某轻轨车站的建筑设计以简约、现代化为主线,结合当地的地方特色,力求打造一个人性化、舒适的候车空间。
1. 外观设计:车站外观采用现代风格的钢结构和玻璃幕墙,在保证建筑牢固的同时,还能很好地与周围环境相融合。
精心设计的外墙艺术装饰,通过图案和抽象造型的应用,展现城市的独特魅力。
2. 站厅设计:站厅是乘客进出车站的主要区域,因此在设计上应注重通风、采光和便利性。
某轻轨车站的站厅设有高大开敞的天窗,借助自然光线,减少照明能源的消耗。
站厅内设置有咨询台、自助售票机和便利店等服务设施,方便乘客获取信息和购买日常用品。
3. 站台设计:站台是乘客乘坐轻轨的主要区域,因此在设计上应考虑到乘客的舒适感和安全性。
某轻轨车站的站台宽敞明亮,设置有舒适的座椅和休息区域,供乘客休憩使用。
同时,为了增加安全性,站台设有防护栏和紧急疏散通道,保障乘客的安全出行。
三、功能布局某轻轨车站的功能布局合理,充分利用空间,提供多种服务,满足乘客的不同需求。
1. 车站出入口设置合理:为了方便市民的进出和换乘,某轻轨车站设置了多个出入口,分布在不同方向,减少拥堵和混乱。
每个出入口都配备自动扶梯和无障碍通道,方便残疾人和行李携带者的进出。
2. 车站内部设施完善:某轻轨车站内部设施齐全,包括洗手间、电动扶梯、自动售货机等,方便乘客的日常使用。
地铁线路设计规划模型-数学建模
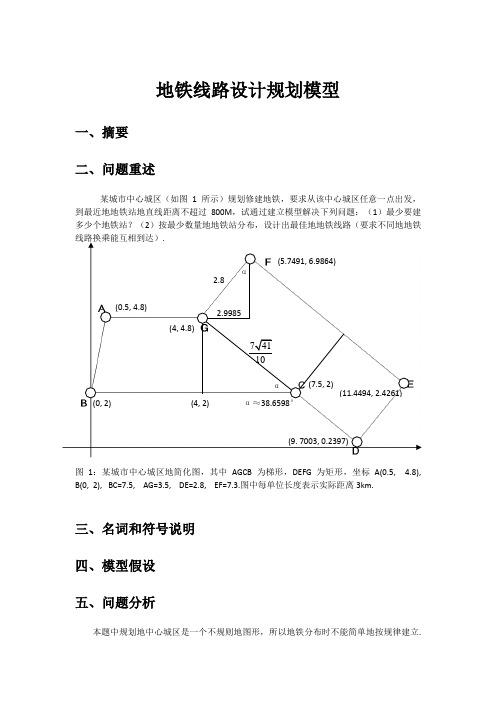
地铁线路设计规划模型一、摘要二、问题重述某城市中心城区(如图1所示)规划修建地铁,要求从该中心城区任意一点出发,到最近地地铁站地直线距离不超过800M,试通过建立模型解决下列问题:(1)最少要建多少个地铁站?(2)按最少数量地地铁站分布,设计出最佳地地铁线路(要求不同地地铁图1:某城市中心城区地简化图,其中AGCB为梯形,DEFG为矩形,坐标A(0.5, 4.8), B(0, 2), BC=7.5, AG=3.5, DE=2.8, EF=7.3.图中每单位长度表示实际距离3km.三、名词和符号说明四、模型假设五、问题分析本题中规划地中心城区是一个不规则地图形,所以地铁分布时不能简单地按规律建立.我们设想地是先建造一种拥有最佳有效面积地地铁站点.首先,我们利用微分地思想,以地铁站为圆心,800m为半径画圆再在圆内画内接多边形,希望最后能将两个圆内内接多边形重叠之后重叠地面积尽量少.之后,我们又从化学原子排列规律中得到了另一种模型,从中我们再比较选出最佳地模型.之后,我们利用CAD按比例画出题目地图与地铁站点阵进行比较,为了获取地铁站间地距离,我们用C语言编了一个程序计算出每个地铁站地距离矩阵,最后再利用Matlab画出地铁站点图地最小生成树,从中得出最佳路线.思路一:我们抛开这个城市地图形,以地铁站为圆心,800m为半径画圆,如图5-1.图 5-1然后,为了使所有两个地铁站能无缝地接在一起,我们把这个图尽可能多地划分成内接多边形.如图(b)~(e).....图5-2图5-3 图 5-4 图 5-5这里,我们又出现一个新地问题,要使内接多边形能接在一起,内接多边形地角度必须能整除360,n边形内角和为(2)180n-⨯,每个内角为(2)180n n-⨯÷.满足整除360,只有n=3,4,6.现在,我们先假设n=3(图5-3),则每个点有效面积2433rSa=;n=4(图5-4),则这个点有效面积22rSa=;n=6(图5-5),则这个点有效面积2233rSa=.所以可得,取n=6时,有效面积aS最大,即将地铁站看成内接六边形时,两个地铁站之间衔接起来有效面积最大.思路二:考虑到每个地铁站建成后都会覆盖附近面积为S 地区域.但由思路一可知,a S S <,所以思路二地基本想法就是允许S 有适当重叠,并得到重叠时地状态,然后算出重叠状态下对于每个站点与其他站点交盖地面积'a S ,通过比较各种重合状态下地'a S ,选得最小地,就是我们要得到地最优设计.具体实现:1. 考虑四个圆地圆心组成矩形地情况图 5-6 图 5-7 图 5-8可以看到,中间地A 区域没有被覆盖,此时有两种解决方案,方案一是在A 区域地中心在建一个站,覆盖掉空白地部分,如图5-7;方案二是直接使四个圆重叠,覆盖空白部分,如图5-8.很容易发现,对于上面两种情况,每一个圆与其他圆共同交盖地面积都是2224 2.2832r r π-≈,即阴影所示区域.2.考虑四个圆地圆心组成菱形地情况:如果组成普通菱形(锐角不是60度),和正方形相比,每一个圆地交盖面积'a S 增加.3.考虑锐角为60度地菱形:图 5-9 图5-10方案三:如图5-9是正六边形,其中正六边形边长为r ,对每一个圆来说交盖面积'a S 为222 1.0870r π-≈;方案四:如图5-10,对每一个圆来说交盖面积'a S 为222 3.68512r π-≈.比较四种情况地'a S ,方案三地'a S 是最小地,从而有效面积2'2a a S S S =-=.综合上述两种思路,最后得出地最佳有效面积皆为2a S =,因此,接下来我们就选择将每个地铁站地覆盖面积视作正六边形.六、模型建立与优化问题一:最少要建多少个地铁站?以一个地铁站地有效面积为内接六边形2a S =,在Auto CAD 中将边长为800单位地正六边形用阵列方法排出20×20地矩阵.将原题地城市图中各端点地坐标求出并放大比例按坐标画进地铁站六边形矩阵阵中,然后将城市图平移,旋转,比较不同情况下,城市图所含盖地正六边形数目最少地情况.由于使用枚举法列举城市图与六边形之间关系地各种情况并清点城市图覆盖地六边形数目过于繁琐,我们考虑了一种优化方法.先让城市图地某一条边覆盖地正六边形数目最少,再考虑其他边覆盖地数目最少地情况,再通过平移等方法尽量减少七个边覆盖地正六边形地数目,以此逼近最优解.数六边形数目地时候为防止人工数数出错,我们采用将范围内地六边形载入选区并由电脑技术地方法保证了数据地真实性和准确性.如下图6-1至图6-10列出了我们枚举地八种特殊情况.图 6-1矩形短边横排233图 6-2矩形短边斜排左对齐226图 6-3矩形长边斜排左对齐226图 6-4矩形长边斜排右对齐227图 6-5矩形长边横排左对齐226图 6-6矩形长边横排右对齐231图 6-7梯形长边横排233图 6-8梯形长边斜排230由以上八张截图可发现,图6-2,图6-3,图6-5地六边形数目均为226,因此可以得出最小覆盖正六边形地数目为226个地结论,即最少要建226个地铁站才能完全铺满这个城市.经过多方比较,我们选取了最易于生成最小树地图6-5作为我们第二问地地铁线路设计目标.问题二:按最少数量地地铁站分布,设计出最佳地地铁线路(要求不同地地铁线路换乘能互相到达)我们在Auto CAD 中将图6-5情况下地226个正六边形替换为800半径地圆并按一定地顺序编号(图6-9),并且利用Auto CAD 地查询—列表显示功能将226个圆地圆心坐标全部输出(输出内容见附件8.1),通过Word 、Excel 等一系列Office 软件对数据地编辑操作,得到了226个点地有序坐标地txt 格式文件(数据见附件8.2).用Visual C++编程软件将txt 文件中地所有数据依次导入并编程(C++文件见附件8.3)计算每一个点到其他225个点地距离导出至新地txt 文件(数据量过大不适合在附件中呈现).用Matlab 软件将距离值全部导入,并利用Primf 最小生成树算法求出生成地最小树结果(结果与Primf 代码见附件8.4).最后在Auto CAD 中绘出最小树(图6-10),并归纳了31条地铁线路(不拐弯地一条直线视为一条线路)共62组坐标点(见表6-1),在Visual C++中求出地铁线路总长度为311769m (编程代码见附件8.5).图 6-9 226个地铁站按顺序编号3 6 8 12 4 5 7 9 10 11 12 13 1415 16 17 18 19 20 2122 23 2425262728 29 35 343332 31 30 36 42 41 40 39 38 37 4948 47 46 454443 5655 54 53 52 51 50 576463 6261 60 59 58 73 72 71 70 69 68 67 66 6582818079787776 75 7492 91 90 89 88 87 86 85 84 83 102 101 100 99 98 97 96 95 94 93 114 113 112 111 110 109 108 107 106 105 104 103 126 125 124 123 122 121 120 119 118 117 116 115 139 138 137 136 135 134 133 132 131 130 129 128 127 152 151 150 149 148 147 146 145 144 143 142 141 140 166165164163162161160159158157156155154153181 180 179 178 177 176 175 174 173 172 171 170 169 168 167 190 189 188 187 186 185 184 183 182 208207 206 205 204 203 202 201 200 216215214213 212 211 210 209 222 221 220 219 218 217 199198 197 196 195 194 193 192 191 225 224 223 226图 6-10 最小生成树地铁线路图七、模型地评价与推广八、附录附录8.1:Auto CAD输出地226个圆地圆心坐标及其他命令: _list 找到 226 个圆图层: 0空间: 模型空间句柄 = 188e圆心点, X=30400.0000 Y=15242.0471 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1880圆心点, X=28000.0000 Y=19398.9690 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 187f圆心点, X=28000.0000 Y=18013.3284 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 187e圆心点, X=28000.0000 Y=16627.6878 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 187d圆心点, X=28000.0000 Y=15242.0471 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 187c圆心点, X=28000.0000 Y=13856.4065 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 187b圆心点, X=28000.0000 Y=12470.7658 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1871圆心点, X=25600.0000 Y=22170.2503 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1870圆心点, X=25600.0000 Y=20784.6097 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 186f圆心点, X=25600.0000 Y=19398.9690 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 186e圆心点, X=25600.0000 Y=18013.3284 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 186d圆心点, X=25600.0000 Y=16627.6878 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 186c圆心点, X=25600.0000 Y=15242.0471 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 186b圆心点, X=25600.0000 Y=13856.4065 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 186a圆心点, X=25600.0000 Y=12470.7658 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1869圆心点, X=25600.0000 Y=11085.1252 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 185f圆心点, X=23200.0000 Y=20784.6097 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 185e圆心点, X=23200.0000 Y=19398.9690 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 185d圆心点, X=23200.0000 Y=18013.3284 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 185c圆心点, X=23200.0000 Y=16627.6878 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 185b圆心点, X=23200.0000 Y=15242.0471 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 185a圆心点, X=23200.0000 Y=13856.4065 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1859圆心点, X=23200.0000 Y=12470.7658 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1858圆心点, X=23200.0000 Y=11085.1252 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1857圆心点, X=23200.0000 Y=9699.4845 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 184c圆心点, X=20800.0000 Y=18013.3284 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 184b圆心点, X=20800.0000 Y=16627.6878 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 184a圆心点, X=20800.0000 Y=15242.0471 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1849圆心点, X=20800.0000 Y=13856.4065 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1848圆心点, X=20800.0000 Y=12470.7658 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1847圆心点, X=20800.0000 Y=11085.1252 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1846圆心点, X=20800.0000 Y=9699.4845 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1845圆心点, X=20800.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1844圆心点, X=20800.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1843圆心点, X=20800.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1842圆心点, X=20800.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1841圆心点, X=20800.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1840圆心点, X=20800.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 183f圆心点, X=20800.0000 Y= 0.0000 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 183a圆心点, X=18400.0000 Y=16627.6878 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1839圆心点, X=18400.0000 Y=15242.0471 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1838圆心点, X=18400.0000 Y=13856.4065 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1837圆心点, X=18400.0000 Y=12470.7658 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1836圆心点, X=18400.0000 Y=11085.1252 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1835圆心点, X=18400.0000 Y=9699.4845 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1834圆心点, X=18400.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1833圆心点, X=18400.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1832圆心点, X=18400.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1831圆心点, X=18400.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1830圆心点, X=18400.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 182f圆心点, X=18400.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 182e圆心点, X=18400.0000 Y= 0.0000 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1828圆心点, X=16000.0000 Y=15242.0471 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1827圆心点, X=16000.0000 Y=13856.4065 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1826圆心点, X=16000.0000 Y=12470.7658 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1825圆心点, X=16000.0000 Y=11085.1252 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1824圆心点, X=16000.0000 Y=9699.4845 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1823圆心点, X=16000.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1822圆心点, X=16000.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1821圆心点, X=16000.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1820圆心点, X=16000.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 181f圆心点, X=16000.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 181e圆心点, X=16000.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 181d圆心点, X=16000.0000 Y= 0.0000 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1815圆心点, X=13600.0000 Y=12470.7658 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1814圆心点, X=13600.0000 Y=11085.1252 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1813圆心点, X=13600.0000 Y=9699.4845 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1812圆心点, X=13600.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1811圆心点, X=13600.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1810圆心点, X=13600.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 180f圆心点, X=13600.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 180e圆心点, X=13600.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 180d圆心点, X=13600.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 180c圆心点, X=13600.0000 Y= 0.0000 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1803圆心点, X=11200.0000 Y=11085.1252 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1802圆心点, X=11200.0000 Y=9699.4845 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1801圆心点, X=11200.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1800圆心点, X=11200.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ff圆心点, X=11200.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17fe圆心点, X=11200.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17fd圆心点, X=11200.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17fc圆心点, X=11200.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17fb圆心点, X=11200.0000 Y= 0.0000 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17f0圆心点, X=8800.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ef圆心点, X=8800.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ee圆心点, X=8800.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ed圆心点, X=8800.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ec圆心点, X=8800.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17eb圆心点, X=8800.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ea圆心点, X=8800.0000 Y= 0.0000 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17df圆心点, X=6400.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17de圆心点, X=6400.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17dd圆心点, X=6400.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17dc圆心点, X=6400.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17db圆心点, X=6400.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17da圆心点, X=6400.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17d9圆心点, X=6400.0000 Y= 0.0000 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ce圆心点, X=4000.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17cd圆心点, X=4000.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17cc圆心点, X=4000.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17cb圆心点, X=4000.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ca圆心点, X=4000.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17c9圆心点, X=4000.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17c8圆心点, X=4000.0000 Y= 0.0000 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17bd圆心点, X=1600.0000 Y=8313.8439 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17bc圆心点, X=1600.0000 Y=6928.2032 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17bb圆心点, X=1600.0000 Y=5542.5626 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17ba圆心点, X=1600.0000 Y=4156.9219 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17b9圆心点, X=1600.0000 Y=2771.2813 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17b8圆心点, X=1600.0000 Y=1385.6406 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 17b7圆心点, X=1600.0000 Y= 0.0000 Z= 0.0000半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 176e圆心点, X=29200.0000 Y=17320.5081 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 176d圆心点, X=29200.0000 Y=15934.8674 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 176c圆心点, X=29200.0000 Y=14549.2268 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1760圆心点, X=26800.0000 Y=21477.4300 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 175f圆心点, X=26800.0000 Y=20091.7893 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 175e圆心点, X=26800.0000 Y=18706.1487 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 175d圆心点, X=26800.0000 Y=17320.5081 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 175c圆心点, X=26800.0000 Y=15934.8674 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 175b圆心点, X=26800.0000 Y=14549.2268 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 175a圆心点, X=26800.0000 Y=13163.5861 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1759圆心点, X=26800.0000 Y=11777.9455 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 174f圆心点, X=24400.0000 Y=21477.4300 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 174e圆心点, X=24400.0000 Y=20091.7893 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 174d圆心点, X=24400.0000 Y=18706.1487 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 174c圆心点, X=24400.0000 Y=17320.5081 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 174b圆心点, X=24400.0000 Y=15934.8674 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 174a圆心点, X=24400.0000 Y=14549.2268 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1749圆心点, X=24400.0000 Y=13163.5861 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1748圆心点, X=24400.0000 Y=11777.9455 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1747圆心点, X=24400.0000 Y=10392.3048 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 173d圆心点, X=22000.0000 Y=20091.7893 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 173c圆心点, X=22000.0000 Y=18706.1487 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 173b圆心点, X=22000.0000 Y=17320.5081 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 173a圆心点, X=22000.0000 Y=15934.8674 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1739圆心点, X=22000.0000 Y=14549.2268 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1738圆心点, X=22000.0000 Y=13163.5861 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1737圆心点, X=22000.0000 Y=11777.9455 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1736圆心点, X=22000.0000 Y=10392.3048 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1735圆心点, X=22000.0000 Y=9006.6642 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1734圆心点, X=22000.0000 Y=7621.0235 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1733圆心点, X=22000.0000 Y=6235.3829 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1732圆心点, X=22000.0000 Y=4849.7422 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1731圆心点, X=22000.0000 Y=3464.1016 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1730圆心点, X=22000.0000 Y=2078.4609 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 172f圆心点, X=22000.0000 Y= 692.8203 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 172a圆心点, X=19600.0000 Y=17320.5081 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1729圆心点, X=19600.0000 Y=15934.8674 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1728圆心点, X=19600.0000 Y=14549.2268 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1727圆心点, X=19600.0000 Y=13163.5861 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1726圆心点, X=19600.0000 Y=11777.9455 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1725圆心点, X=19600.0000 Y=10392.3048 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1724圆心点, X=19600.0000 Y=9006.6642 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1723圆心点, X=19600.0000 Y=7621.0235 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1722圆心点, X=19600.0000 Y=6235.3829 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1721圆心点, X=19600.0000 Y=4849.7422 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1720圆心点, X=19600.0000 Y=3464.1016 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 171f圆心点, X=19600.0000 Y=2078.4609 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 171e圆心点, X=19600.0000 Y= 692.8203 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1718圆心点, X=17200.0000 Y=15934.8674 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1717圆心点, X=17200.0000 Y=14549.2268 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1716圆心点, X=17200.0000 Y=13163.5861 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1715圆心点, X=17200.0000 Y=11777.9455 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1714圆心点, X=17200.0000 Y=10392.3048 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1713圆心点, X=17200.0000 Y=9006.6642 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1712圆心点, X=17200.0000 Y=7621.0235 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1711圆心点, X=17200.0000 Y=6235.3829 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1710圆心点, X=17200.0000 Y=4849.7422 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 170f圆心点, X=17200.0000 Y=3464.1016 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 170e圆心点, X=17200.0000 Y=2078.4609 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 170d圆心点, X=17200.0000 Y= 692.8203 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1705圆心点, X=14800.0000 Y=13163.5861 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1704圆心点, X=14800.0000 Y=11777.9455 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1703圆心点, X=14800.0000 Y=10392.3048 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1702圆心点, X=14800.0000 Y=9006.6642 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1701圆心点, X=14800.0000 Y=7621.0235 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 1700圆心点, X=14800.0000 Y=6235.3829 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16ff圆心点, X=14800.0000 Y=4849.7422 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16fe圆心点, X=14800.0000 Y=3464.1016 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16fd圆心点, X=14800.0000 Y=2078.4609 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16fc圆心点, X=14800.0000 Y= 692.8203 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16f3圆心点, X=12400.0000 Y=11777.9455 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16f2圆心点, X=12400.0000 Y=10392.3048 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16f1圆心点, X=12400.0000 Y=9006.6642 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16f0圆心点, X=12400.0000 Y=7621.0235 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16ef圆心点, X=12400.0000 Y=6235.3829 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16ee圆心点, X=12400.0000 Y=4849.7422 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16ed圆心点, X=12400.0000 Y=3464.1016 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16ec圆心点, X=12400.0000 Y=2078.4609 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16eb圆心点, X=12400.0000 Y= 692.8203 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16e1圆心点, X=10000.0000 Y=10392.3048 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16e0圆心点, X=10000.0000 Y=9006.6642 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16df圆心点, X=10000.0000 Y=7621.0235 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16de圆心点, X=10000.0000 Y=6235.3829 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16dd圆心点, X=10000.0000 Y=4849.7422 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983圆图层: 0空间: 模型空间句柄 = 16dc圆心点, X=10000.0000 Y=3464.1016 Z= 0.0000 半径 800.0000周长 5026.5482面积 2010619.2983。
城市轨道交通站点选址分析

城市轨道交通站点选址分析摘要:随着经济快速的发展,城市化进程不断加快,大量的人口向城市聚集。
因此,不可避免的给城市带来了拥堵、噪音、尾气等污染。
而轨道交通具有大运量、方便快捷、乘坐舒适、安全准时、环境污染少等优点,因此加快轨道交通建设成为了各个国家应对城市化进程加快、城市交通日益拥堵的首选措施。
木文以城市轨道交通站点分布优化为课题,旨在为轨道交通站点选取及线路选择提供一种新思路,使得选择的方案能够在最短的路径上服务更多的区域、节省更多的费用成本,真正符合“以人为本、按需设置、技术可行、经济合理”的城市轨道交通建设基木理念。
关键词:城市轨道交通;站点分布优化;站间距引言:城市轨道交通是指:使用车辆固定在轨道上运行且主要用于城市客运交通的系统。
主要以电力为牵引动力,路权形式为基本隔离。
城市轨道交通按照其技术特性、运量以及服务区域可分为地铁、轻轨以及市域快线。
1.轨道交通站点分布相关影响因素分析1.1站点分布对相关因素的影响1.1.1对吸引客流影响根据苏州轨道交通一号线乘客出行调查反馈的抽样问询调查表可以看出:从出发点到地铁站的乘客中,步行到站乘客占60.71%,骑自行车到站的乘客占20.41%,乘公交到站乘客占16.31%,乘坐出租车到站乘客占2.57%,乘客下车后到达目的地情况与之类似。
1.1.2对乘客出行时间影响乘坐轨道交通完成一次出行的总时间一般由三个部分组成:乘客从出发地到达轨道交通站厅时间以及乘客到站下车后达到目的地的时间;车站候车时间;乘车时间;(1)站点分布对候车时间影响。
对乘客而言,在站候车时间主要与其到达车站的时刻有关,若到达时刚好有一列车发出,则候车时间最长,为一个发车间隔时间。
由于乘客到达具有一定随机性,因此平均候车时间一般为发车间隔的一半。
对轨道交通来说,其发车间隔一般都很短,一般都是3—8分钟不等。
因此站点分布对候车时间影响不大。
(2)站点分布对乘车时间的影响。
若采用大站间距,一方面可以充分发挥列车性能提高列车旅行速度,另一方面由于减少了站点密度,还能避免因列车频繁加减速以及停车带来的时间损失,从而缩短乘车时间。
关于青岛市黄岛区地铁站选址的分析评价模型

三、符号的说明
C1 :站点建设成本 C2 :带动经济效益 C3 :站址周边环境
C4 :环境保护 C5 :产业布局 C6 :施工风险 C7 :舒缓客流度 C8 :提高出行时间率 P 1 :瓦屋庄站 P2 :薛家港湾站 P3 :安子东站 P4 :安子站 P5 :天目山路站 P6 :矿大西路站 P7 :人民广场站 P8 :井冈山路站 P9 :黄岛汽车站总站站 P 10 :江山路站
0.4938,0.2354,0.0906,0.0750,0.0992,0.2757,0.6996,0.3340T
归一化后得到向 0.2144,0.1022,0.0393,0.0326,0.0431,0.119 7,0.3037,0.1450 下一步我们考虑矩阵 A 一致性检验,结合
根据我们在建造地铁站固定投资及地皮价格对建设成本的影响, 不同地点的房价如图二 所示:
图二: 站址周围房价水平
计算出不同选址的建站成本(房价仍是估算的,并非准确的) :
P 1 : 7000 8000 1.5 1 / 3 =11000(万) P 2 : 7000 8000 1.5 1 / 3 =11000(万) P3 : 7000 8000 1.5 1 / 3 =11000(万) P4 : 7000 8200 1.5 1 / 3 =11500(万) P5 : 7000 9000 1.5 1 / 3 =11500(万) P6 : 7000 10000 1.5 1 / 3 =12000(万) P7 : 7000 9000 1.5 1 / 3 =11500(万) P8 : 7000 10000 1.5 1 / 3 =12000(万) P9 : 7000 12000 1.5 1 / 3 =13000(万) P 10 : 7000 10000 1.5 1 / 3 =12000(万)
轨道交通走廊的TOD项目选址与开发模型

址方法,建立了一个均衡模型来表示居住地点的选择,以社
会福利最大化为定量指标;其次,提出了 2种序列优化算法,
与拟牛顿方法对比求解效果;最后,分析了模型中地价、租 金、供给敏感度参数对结果产生的影响&
作者简介:张'鹏(1981-),男,硕士,教授级高工,研究方向:交通规划与管理& 谢秉磊(1975-),男,博士,教授,研究方向:交通规划与管理&
Microcomputer Applications Vol. 37,No. 7,2021
开发应用
微型电$%用2021年第37)第7期
文章编号!007-757X(2021)07-0182-04
轨道交通走廊的TOD项目选址与开发模型
张鸥鹏12,谢秉磊1 (1哈尔滨工业大学(深圳)建筑学院,广东深圳518000; 2.深圳市综合交通设计研究院有限公司,广东深圳518000)
选择行为&与之前的TOD项目开发相关策略研究不同(例 如,Cervero和Day】8* ;Loo[9]),在前人的研究基础上,研究轨 道交通走廊中TOD项目的最优设计问题,考虑TOD位置和 开发量的确定&但是以往研究没有考虑到:(1)TOD项目的 最佳位置和大小如何确定,开发的TOD项目投资回报率有 多高? 土地价格对最佳TOD项目的位置具有哪方面的影 响?(2)考虑开发多个TOD项目,如何进行最佳设计,确定 每个TOD项目的最佳尺寸&
通沿线TOD项目2开发地点和时间顺序;序列算法可以简化计算2同时得到与以往算法相同2结果;远离CBD 2 TOD项目
能够创造更多2社会福利°
关键词:出行者&交通走廊;社会效益
中图分类号:U491
轨道交通站场与枢纽城市轨道交通车站站位规划方案

❖中国站间距的规定
《城市快速轨道交通工程项目建设标准(试行本)》 中提出”车站间距应参照城市道路布局和客流吸 引范围而定。在市中心区宜为1km左右,在市区 外围宜为2km左右。”
而在地下铁道设计规范中又规定“车站间的距离 应根据实际需要确定,在市区宜为1km左右,在 郊区不宜大于2km”。
分布 原则
4.换乘点最好为两 线交叉,以利于 分散换乘客流, 合理控制换乘站 规模,简化换乘 站客流组织,降 低工程施工难度, 节省工程造价,
5.换乘点应主要分 布于城市重点区 域,如中心区或 外围特大型客流 集散点。
14
改善换乘效果的途径及实例
改善换乘效果的途径及实例
路网规划 创造同站台换乘、结点换乘的机会
换乘方式的选择
任何换乘点的换乘方式都应以满足换乘客流功能需要为 第一位,同时还要考虑其他相关因素: 1. 换乘点上两条线的修建顺序; 2. 换乘点上两条线路的交织形式和车站位置; 3.换乘点的换乘客流量和客流组织方式; 4.换乘点的线路和车站的结构形式、施工方法; 5.换乘点的周围地形条件、地质条件以及城市规划的地 面和地下空间开发要求等。
44
❖ 2)站台层布置需以车站上下行远期超高峰小时设计客流 量来计算站台宽度,根据线路走向及换乘要求确定站台 型式。根据车站需要布置设备或管理用房区。
❖ 3)车站出入口应设置于道路两边红线以外或城市广场周边, 需具有标志性或可识别性,以利于吸引客流、方便乘客。 有条件的出入口考虑地面人行过街的功能。出入口规模应 满足远期预测客流量的通过能力,并考虑与其他交通的换 乘和接驳大型公共建筑所引起的客流量。
19
通过改变换乘站布置改善换乘 -两条线路站台在不同垂直面上平行布置
项目一城市轨道交通线路车站位置设计

项目任务
• 1) 掌握城市轨道交通规划设计的基本知识, 能够初步运用相关知识进行简单的项目设 计。 2) 分析福州的轨道交通线路位置。 3) 分析福州城市轨道交通车站的位置。 4) 练习思考线路车站位置与客流的关系。
项目准备
• 单轨铁路是铁路的一种,特点是使用的轨 道只有一条,而非传统铁路的两条平衡路 轨。单轨铁路主要分成两类:悬挂式单轨 铁路和跨座式单轨铁路。
• 3.城市轨道交通线路与市郊铁路线的衔接与 换乘 (1) 市郊铁路深入市区,在市区内形成贯通 线向外辐射。 • (2) 利用原有铁路开行市郊列车,市郊列车 一般不深入市区,起点站在市区边沿,在 起点站车站与城市轨道交通及地面常规公 共交通工具进行换乘衔接。
• 4.城市轨道交通线路与地面铁路车站的衔接 与换乘 5.城市轨道交通线路与私人交通工具的衔接 与换乘 (1) 与机动车的衔接与换乘。 (2) 与自行车的衔接与换乘。
车站选址
车站设计
• (1) 车站站位应尽可能地靠近人口密集区和商业 区,最大限度地方便乘客出行。 (2) 车站的设计应尽可能地与物业开发相结合, 使土地的使用效益最大化。 (3) 车站具体位置大部分应设在地面交通道路的 交叉路口,如图1-6所示,同时还应考虑沿线居 民方便乘车、购物、上下班等,因此在居民集中 的社区、大型购物休闲地点附近、单位集中的地 带等也应多设置车站。 (4) 车站总体设计要注意与周围环境的协调,如 与城市景观、地面建筑规划相协调。
世界上著名的单轨铁路
• ☆日本有六个城市有单轨铁路。当中东京 的单轨铁路年载客量超过一亿人次。 • ☆美国加州迪士尼乐园及佛罗里达州和路 迪士尼世界都建有单轨。每年载客量超过 五百万人次。 • ☆美国拉斯维加斯于2004年建成连接各赌 场及会议中心的单轨铁路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
城市轨道交通规划与设计轨道交通站点选址模型学院:公路学院专业:交通运输工程******学号:**********指导教师:***完成时间:2015年3月24日二〇一五年三月轨道交通站点选址模型1 研究背景随着世界经济的迅猛发展,城市化进程的不断加快,大量的人口向城市聚集,因此,不可避免的带来了城市交通拥堵不堪、汽车尾气污染、噪音污染、能源浪费等一系列难以解决的难题。
而轨道交通作为一种能够有效疏散客流量、运量大、方便快捷、乘坐舒适、安全准时、环境污染少等优点的交通运输体系,现已为国内外许多城市所认同,而且有利于解决交通拥堵、优化交通结构,所以发展城市轨道交通系统已经成为解决我国很多大中城市出行难问题的必经之路。
城市轨道交通作为大城市公共客运体系的骨干,既能解决我国大城市交通问题,又能促进大城市发展、引导大城市布局调整。
而发挥其客流集散功能首先是通过站点实现的。
绝大多数出行者是把到达轨道交通站点的方便性作为选择轨道交通出行的首要因素。
也就是说,轨道交通站点的布设方案将会对乘客的吸引范围、服务水平、系统的运营效率甚至城市的形态布局、路网结构等产生影响。
虽然我国城市轨道交通建设正处于蒸蒸日上的高潮时期,并且取得了一些成绩,掌握了一些技术水平。
但从总体上看还没有形成与轨道交通建设相配套的规划设计、科研开发、运营管理、人才培养等一系列体系。
具体来说,存在以下几点不足:1、对轨道交通线网规划重视程度不够、认识不足。
有些城市把线路规划放在线网规划之前,这忽略了轨道交通与城市布局、土地利用的适配关系,不利于处理轨道交通与其他方式间的关系。
2、对轨道交通线网规划理论体系、规划方法等缺乏深入研究。
通常轨道交通的线网规划主要采用了“四阶段法”,而此方法主要用于道路交通规划,因此并未形成一套适合自身的体系。
3、对轨道交通线网规划的一些研究并不到位,且大多数时候采用定性分析居多,而忽略了定量分析的重要性。
一些参数标定如:吸引区域、站点选址、站间距合理范围、线路比选等缺乏理论支撑,大多受人为因素影响较深。
4、对线路中站点布局方法及线路方案的选择过于简单化,对线路指标的评价研究不深,受人为因素影响较大,给站点布设带来一定的困难。
2 研究意义针对以上在城市轨道交通系统规划和建设中出现的问题,将关注点放在轨道交通站点的选址上。
因为,轨道交通站点作为区间线路之间的连接点,将线路与线路之间有效的连接起来,其在整个轨道交通系统的建设和运营中发挥着举足轻重的作用,只有将站点设置合理了,才能有效的疏散客流,优化城市的交通结构,发挥一个轨道交通系统所应该具有的作用,从而增加城市居民的满意程度,提升他们的生活品质。
城市轨道交通站点有一个十分重要的特性,那就是能够吸引大量的客流,形成“廊道效应”,从而带动周边地区经济的转型与发展,并吸引各种商业形式朝其聚集,容易形成新的商业中心;反过来,商业中心的形成也能够增加客流量,为轨道交通事业的进一步发展提供了可能。
站点选址是线路规划中一个重要的环节,需要认真分析轨道交通站点选址的核心因素,通过系统的分析研究,做到理论研究与实际建设相结合,具有重要的意义。
3 城市轨道车站分布影响因素分析城市轨道交通车站的布设受很多因素的影响,为了能更加合理对轨道车站进行规划布局,有必要轨道车站选址的相关影响因素进行分析。
(1)城市规模、形态和土地使用布局城市规模包括城市人口规模、城市用地规模、城市经济发展水平三个方面。
人口规模决定了城市交通出行的总量,城市用地规模(面积)影响了居民出行时间和距离,即城市规模决定了城市的交通需求,也就影响到轨道交通的规模与车站分布。
城市形态和土地利用也是影响到轨道车站分布的因素。
不同的城市形态和用地布局决定了居民出行的空间分布,也就决定了轨道线路的几何空间形态。
(2)城市道路网络结构和其他交通方式的站点布局城市轨道交通是城市公共交通骨干,但要成为城市大运量的通道还要与各种城市设施和交通工具紧密衔接,密切配合,并真正体现方便乘客、以人为本的原则。
轨道线路一般沿城市道路进行布设,道路网的格局将影响轨道线路的走向,而其他交通工具的站点作为轨道车站集散客流的场所,其布局也影响着轨道车站分布的规划。
同时,轨道交通和常规公交之间又具有竞争性,要使各种交通方式协调发展,这也要求轨道交通车站的车站间距要大于常规共交的站点间距。
(3)客流特性和列车特性轨道交通的客流是动态流。
它在空间上表现为各条线路客流不均衡、上下行方向客流不均衡、线路断面客流分布不均衡、各车站乘降人数不均衡;在时间上表现为一日内、一周内客流不均衡,进出车站高峰小时出现时间与断面客流高峰小时时间通常不相同。
客流空间分布不均衡主要影响着轨道车站分布,时间的不均衡主要影响着轨道交通的运力安排,高峰小时客流则是车站设备容量确定的基本依据。
列车特性主要包括车辆的长度、载客能力,列车的正常运行速度及加减速能力。
车辆的长度、载客能力决定车站长度和规模。
从列车特性发挥角度来说,站间距应使列车可以在车站间运行时发挥出速度优势,并且尽可能少的刹车。
(4)城市人文地理轨道车站的分布必须与国家的名胜古迹、自然保护区等协调,避免与其发生冲突。
城市水文地质等自然条件限制轨道线路的走向、车站的选址和车站的建筑布局。
由于轨道交通采用的是全封闭设计,这样它对城市社会经济活动的分隔作用非常强。
在确定轨道车站布局时,要充分结合城市的自然地理条件,充分利用那些天然分隔物(河流、山脉等),将轨道的走向、车站的选址与这些天然障碍物结合起来,最大程度的减少轨道交通对城市经济活动的分隔,这样才能使轨道交通建设的社会效益才能实现最大化。
4 基于 Voronoi 图的城市轨道交通站点选址模型V oronoi 图表述了自然界中宏观及微观物体之间通过距离的大小进行相互作用的普遍结构,很好的描述了平面上离散点集(相邻但不相连)之间的邻近关系以及其各自的影响区域等信息。
由于轨道交通线路相互交叉呈放射性网状结构,这时线路上所有的站点可达性基本相同,因此,居民在出行过程中倾向于选择距离最近的轨道站点。
根据这一原则,结合 V oronoi 图的特点,将其引入轨道站点来构建选址模型,争取采用最少的站点使站点的合理吸引覆盖范围达到最大。
4.1 Voronoi 图的特性分析V oronoi 图是由给定数量的数据样本(P i )点将给定平面(P )划分成几个相邻但不相交的子区域i 组成的,其中每个区域内都仅仅包含一个给定的数据样本点。
V oronoi 图上的样本数据点集{}()12P=P P P ,2m n R n ⊂≤<∞,,有以下特性:1、其中的任意两个样本数据点都不重叠,即()()P P ,1,i j i j i j n ≠≠≤≤2、其中任意四个样本数据点都不共圆3、子区域i 内的任意一点到其对应的样本数据点P i 的距离小于到P 中其他任何数据样本点的距离,即(){()()},,P <,P ,P ,P P i i j i j i j V x d x d x P i j =∈≠≠。
V oronoi 图通常是对每个样本数据点进行区域插值,采用边界内插法画出样本数据点中每两个相邻点连线之间的垂直平分线,此时线与线相互交叉会形成多个凸多边形,从而将大区域分割成若干个子区域,每个子区域中均包含一个样本数据点,具体形状如图1所示。
图1 V oronoi 图在V oronoi 图的多种数学特性中间与轨道交通站点选址相关的特性主要有以下三个方面:1、空心圆特性由V oronoi 图的基本形状,我们可以看出每个V oronoi 顶点都是由三条V oronoi 边相交所形成的交点,若以任意一个顶点为圆心、以顶点与其对应的一个样本数据点的距离为半径做圆,则这个V oronoi 顶点所对应的所有样本数据点(3个或更多)都在这个圆上,而在这个圆的内部却不包含任何给定的样本数据点,这时我们称这个圆是一个空心圆,在建立新的站点时,半径越大的空心圆顶点最易产生新的样本数据点,这就是V oronoi 的空心圆特性,如图2所示。
在城市轨道交通路网规划中,空心圆的区域没有站点说明在该区域的旅客运送能力较差,在设计规划中应该优先考虑加强这些地区的轨道交通站点的设置。
图2 最大空心圆特性2、与D 三角网对偶将V oronoi 图中有公共边的凸多边形内的样本数据点一一连接,会形成一组三角网,如图3所示,这个三角网被称作Delaunay 三角网,其中每一个V oronoi 顶点qi都是Delaunay 三角网中三角形的外接圆圆心,每个V oronoi 图都唯一对应一个Delaunay 三角网,而且三角网的外边界构成了点集P 的凸多边形的外壳。
如果将其中具有公共V oronoi边的样本数据点相连,可以得到一种新的规划图,这也为轨道交通选线的研究提供了新的思路。
图3 V oronoi 图及其对偶D 三角网3、最邻近特性V oronoi 图中每一个样本数据点都对应着唯一的一个凸多边形,落在这个凸多边形内的任一点与其对应的样本数据点的距离值相对于其他样本数据点来说都是最小的。
应用 V oronoi 多边形的这一性质,在进行轨道交通站点选址的时候,每一个站点的吸引范围都唯一的对应一个 V oronoi 多边形,凡是在这个多边形内的所有乘客到该站点的距离都是最近的。
4.2 基于Voronoi 图的选址分析4.2.1根据未有站建立新的站点(1)构建选址模型确定初始站点当一座城市的轨道交通系统需要整体规划时,将整个城市根据地理坐标划定范围作为规划的区域,在根据该城市城区的划分选定初始区域后,以整个区域内最下边与最左边两个点的切线的交点为坐标原点,以此为基准建立平面坐标系,从而可以得到所有数据样本点的坐标。
由于在轨道交通大力发展的现阶段,政府为了鼓励大众采用轨道交通的方式出行,降低对环境的污染,一般对其的支持力度较大,对轨道交通的收益回收期要求较低,来推动轨道事业的发展。
所以轨道交通站点的选址模型从城市居民的角度出发,以居民到达轨道交通站点的时间最短为目标建立相关的数学模型。
具体模型如下所示:目标函数:()()122211min m nj i j i i ij j i s x p y q z η==⎡⎤=-+-⨯⨯⎢⎥⎣⎦∑∑ (1) 约束条件:min max i x p x ≤≤ (2) min max i y q y ≤≤ (3) min max j x x x ≤≤ (4) min max j y y y ≤≤ (5)10ij z ⎧=⎨⎩居民由第i 个居民集散点前往第j 个轨道交通站点居民不由第i 个居民集散点去第j 个轨道交通站点 (6)11m ij j z ==∑ (7)其中: s ——居民由集散点到达轨道交通站点的距离。
