高等数学下二课堂10-2
高等数学下二课堂10-3(1)
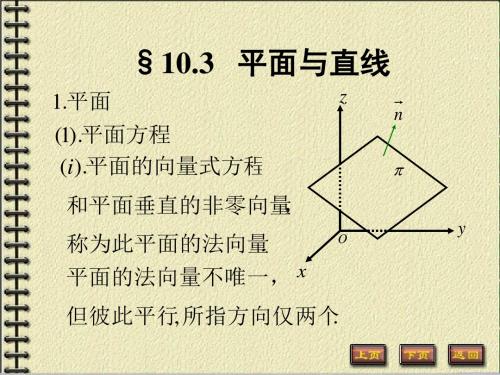
1.平面
z
(1).平面方程 (i).平面的向量式方程
n
和平面垂直的非零向量 , 称为此平面的法向量 .
O
y
平面的法向量不唯一, x 但彼此平行, 所指方向仅两个 .
已知平面 上的一个定点M 0 , 平面的法向量n , 建立平面方程.
设 M 是 上的任一点, 有 M0 M n ,
4
2
.
| n1 n2 | 2 | | 证 : cos | n1 || n2 | 2 2 2
2 0 cos , 2
4
2
(3).点到平面的距离
求平面 Ax By Cz D 0 ( A, B, C 不全为零 ) 外点 M 0 ( x0 , y0 , z0 ) 到平面的距离d . n
2 2 2
Ax0 By0 Cz0 D A B C
2 2 2
例: 求平行于平面 x y z 5 0的平面方程,
使点M 0 (1,1,2)到所求平面的距离为 2.
解 : 设所求为 x y z D 0 ,
则点 M 0 到平面的距离 d 11 2 D 3
0
M 0到该平面的距离为 d p n r0 ,
0
其中M 0的位置向量r0 OM 0 . 证 : 平面上任一点 M 1满足n 0 r1 p, 其中r1是M 1 ( x1 , y1 , z1 )的位置向量 ,
故d prj 0 M 0 M1 n ( r1 r0 ) p n r0
得 M0M n 0 , 或 (r r0 ) n 0 ,
高等数学A10-2二重积分的计算(1)

10-2 二重积分的计算
(宋)苏轼
寄蜉蝣于天地,
渺沧海之一粟.
哀吾生之须臾,
羡长江之无穷.
10-2 二重积分的计算
第二节 二重积分的计算
一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、小结与思考
10-2 二重积分的计算
一、利用直角坐标系计算二重积分
(1) 在直角坐标系下用平行于 y
坐标轴的直线网来划分区域 D,
则面积元素为
d dxdy
o
D
x
故二重积分可写为
f ( x, y)d f ( x, y)dxdy
D
D
10-2 二重积分的计算
(2) 如果积分区域 D如图所示,那么可用不等式表示为
a x b, 1( x) y 2( x). [X-型]
其中ri 为 ri与 ri ri 的平均值.由此当 ri , i 充分小 时,极坐标系下的面积元素 d rdrd.
10-2 二重积分的计算
其次, 直角坐标系与极坐标系有如下变换关系
x r cos
y
r
sin
最后, 两坐标系下积分区域 D 形状不变,因此有
f ( x, y)d f (r cos , r sin )rdrd .
D
o
10-2 二重积分的计算
D
D
以下我们讨论极坐标下的二重积分的计算.
r 1( ) r 2( )
DD
r 1( )
r 2( ) D
r 2( )
D
o
Ao
Ao
A
r 1( ) 0
同济六版 高等数学下10-2

y
D
x yd 1 d y
2 y2 y2
2
y2
y
2
xyd x
O 1
4 x y x2
D
1 2 x y 1 2
1 2 d y [ y ( y 2) 2 y 5 ] d y 2 1
10
例3
求 x e
D
2 y2
dxdy ,其中 D 是以(0,0), (1,1),
c
d
2 ( y)
1( y)
f ( x , y ) d x (先x后y)
[Y-型] c y d, 1 ( y ) x 2 ( y ).
d
[X-型] a x b, 1 ( x ) y 2 ( x ).
y 2 ( x )
D
y 1 ( x )
0 0 2 x2 2 2 2 2
dx
8 x 2
0
f ( x , y )d y
y
2 2 x y 8 1 2 2 0 y 8 x 0 y x D1 : 2 2 , D2 : 1 2 2 x 2 2 y 2 x 0 x2 D2
解: 积分域由两部分组成:
x a a y
a
a a
a a y
f的方法吗?
16
将积分换序 解 D:
y
I dx
a
ax ax x
f ( x, y)dy
0 x 2a
ax x y ax
2a
y ax
I
D
7
dy y
y
《高数下》讲义笔记【高斯课堂】

练习
1.3:设
x z
ln
z y
,求
2z x2
练习
1.4:设
zx,
y由方程 sinxyz
z
1 xy
1 所确定,求 dz
(0,1)
。
4
微信扫一扫
4 小时速成课程
高斯课堂系列课程
官方公众号:蜂考
蜂考——大学生备考集训营
课时二 多元函数(二)
考点 1.复合函数求偏导 2.偏导,连续,可微关系
重要程度 必考 ★★
3 3 3 27
2 确定条件函数 gx, y, z
3 构造拉格朗日函数
L f x, y, z gx, y, z
Lx 0
Ly
Lz
0 0
( x0
,
y0 ,
z0
)
L 0
即为所求极值点。
8
微信扫一扫
4 小时速成课程
高斯课堂系列课程
官方公众号:蜂考
蜂考——大学生备考集训营
练习 3.1: f (x, y, z) x 2yz 3 ,求在 ( 1 , 1 , 1 , ) 的梯度
2
y
(1,0)
Pk 1,1
el
1 2
,1 2
gradf (1,2)
f l
gradf el (1, 2) (
1,0
1, 2
1 )3 2 22
方向导数解题方法:
1.求在 P 点梯度
2.求 pk 的单位向量 el
f 3. l
gradf
el
(梯度点乘 l 的单位向量)
二、多元函数的极值
分值 6 ~ 10 0~3
常见题型 大题
选择、填空
高数第十单元无穷级数

第十单元 无穷级数10-1 常数项级数的概念与审敛法[教学基本要求]高等数学 1. 理解无穷级数收敛、发散以及收敛级数和的概念,了解无穷级数的基本性质及收敛的必要条件;2.了解正项级数的比较审敛法以及几何级数与p -级数的敛散性,掌握正项级数的比较审敛法;3.了解交错级数的莱布尼茨定理;4.了解绝对收敛与条件收敛的概念及二者的关系.微积分 1。
理解无穷级数收敛、发散以及收敛级数和的概念,了解无穷级数的基本性质及收敛的必要条件;2.了解正项级数的比较审敛法,掌握几何级数与p -级数的敛散性结果,掌握正项级数的比较审敛法;3.了解交错级数的莱布尼茨定理;4.了解绝对收敛与条件收敛的概念及二者的关系.[知识要点]一、常数项级数的敛散性判别法及其说明除开因lim n n u →∞≠0,而判定n n u ∞=1∑发散外,常用以下方法判别级数的收敛性.),(2)limn≤,其且其和S u1几何级数(等比级数)n n aq ∞=1∑:当|q |<1时级数收敛;当|q |≥1时级数发散。
p -级数p n n ∞=11∑:当p >1时级数收敛,当p 0<≤1时级数发散。
级数ln pn n n∞=21∑,当p >1时级数收敛,当p 0<≤1时级数发散. 二、正项级数判敛的一般程序:nu∞=1∑ ρ=1 n u n n u ∞=1∑发散 n n u ∞=1∑发散,n n u ∞=1∑收敛三、任意项级数的判敛程序:收敛 n n u ∞=1∑条件收敛nn u∞=1∑发散nn u∞=1∑绝对收敛nn u∞=1∑发散[错误诊断]例1 判别下列级数的敛散性:(1)n ∞=1 (2)()nn n ∞=14+-12∑. (1)[错解]因为n =0,故该级数收敛.[错误分析] lim n n u →∞=0是级数n n u ∞=1∑收敛的必要条件,不是充分条件.因此不能用一般项的极限为零判别级数收敛,但如果lim n n u →∞≠0,级数n n u ∞=1∑一定发散.[正确解法]因n n ==1,由n n ∞=11∑发散,知该级数发散. (2)[错解]因为()()()lim lim lim[()]n n n n n nn n n n nu u +1+1+1+1→∞→∞→∞4+-14+-14+-1==2224+-1不存在,所以该级数发散. [错误分析]正项级数的比值判别法只是正项级数收敛的充分条件,不是必要条件.也就是说,正项级数n n u ∞=1∑收敛,并不一定有limn n nu u ρ+1→∞=<1.[正确解法]因为该级数是正项级数,且当n ≥1时,()n n n n u 4+-15=≤22.由于等比级数nn ∞=152∑收敛,由比较判别法知所给级数收敛.例2 若n n u ∞=1∑与n n v ∞=1∑皆收敛,且对于一切自然数n 有n n n u c v ≤≤,证明n n c ∞=1∑也收敛.[错误证明]由于n n c v ≤,且n n v ∞=1∑收敛,故由比较判别法可知n n c ∞=1∑收敛.[错误分析]上述证明的依据是级数的比较判别法,但是这个判别法只适用于正项级数.而题中并没有指明n n u ∞=1∑与n n v ∞=1∑为正项级数,因此上述证明方法不正确.[正确证法]由于n n n u c v ≤≤,因此n n n n c u v u 0≤-≤-,即()n n n c u ∞=1-∑与()n n n v u ∞=1-∑皆为正项级数.由于n n u ∞=1∑与n n v ∞=1∑都收敛,因此()n n n v u ∞=1-∑收敛.由正项级数的比较判别法可知()n n n c u ∞=1-∑收敛.又()n n n n c u c u =+-,由级数的性质可知n n c ∞=1∑收敛.[典型例题补充]例1 选择题 下列命题中正确的是( ).A . 若nn u∞=1∑与n n v ∞=1∑都收敛,则()n n n u v ∞=1+∑可能发散.B . 若nn u∞=1∑收敛,n n v ∞=1∑发散,则()n n n u v ∞=1+∑必定发散.C . 若nn u∞=1∑与n n v ∞=1∑都发散,则()n n n u v ∞=1+∑必定发散.D . 若()nn n uv ∞=1+∑收敛,则n n u ∞=1∑与n n v ∞=1∑必定收敛.解 正确答案是B .由级数的性质知命题A 错误.由反正法知命题B 正确.事实上,假设()n n n u v ∞=1+∑收敛,由n n u ∞=1∑收敛及()n n n n v u v u =+-知,n n v ∞=1∑也收敛,这与已知矛盾.故()n n n u v ∞=1+∑必定发散.若设n n n u ∞∞=1=1=1∑∑发散,()n n n v ∞∞=1=1=-1∑∑也发散,但是()()n n n n u v ∞∞=1=1+=1-1=0∑∑收敛.可知命题C 与D 都不正确.说明 若n n u ∞=1∑收敛,n n v ∞=1∑发散,则()n n n u v ∞=1±∑必定发散可以作为判定级数()n n n u v ∞=1±∑发散的充分条件使用.例1表明有限项相加的性质不能随意使用到无穷多项相加之中. 例2 判别下列级数的敛散性:(1)()n nn n n ∞=131+∑;(2) (cos )n n ∞=111-∑;(3)nn n n ∞=1⎛⎫⎪2+1⎝⎭∑;(4) !()n n n a n a n ∞=1>0∑. 解 (1)因为lim lim()n n n n u e n→∞→∞13=3=≠011+,所以n n u ∞=1∑发散. (2)分析:由于lim(cos )n n →∞11-=0,而cos sin n u n n211=1-=2>02 注意:sin ()lim lim lim ()sinn n n n nu n u n n n222+1→∞→∞→∞212⎡⎤112+1⎛⎫===1 ⎪⎢⎥12+12⎝⎭⎣⎦22 可知所给级数不能利用比值判别法判定.解法1 注意 cossin n u n n211=1-=2>02 由于当x >0时,sin x x <,可知sin n n 11<22,sin n n 2211<24 正项级数n n ∞2=114∑为收敛级数,由比较判别法可知(cos )n n ∞=111-∑收敛.解法2 由于当x →0时,sin x ~x .可知当n →∞时sin n u n 21=22~n v n21=2则 sin lim lim n n n nu n u n 2+1→∞→∞2122==112,由于n n ∞2=11∑收敛,可知(cos )n n ∞=111-∑收敛. (3)因为n n 1==<12,所以nn n n ∞=1⎛⎫ ⎪2+1⎝⎭∑收敛. (4)分析:题中的a 没有限制其值,因此应该对a 加以讨论.解 因为()!!lim limlim ()n n n n n n n n n nu a n a n a au e n n n +1+1+1→∞→∞→∞+1===+11⎛⎫1+ ⎪⎝⎭故当a e >时,原级数发散;当a e <时,原级数收敛;当a e =时,不能用比值判别法判定所给级数的收敛性.但注意到数列nn ⎧⎫1⎪⎪⎛⎫1+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭为单调增加且有上界,由于n n u u +1≥,又lim n n nu u +1→∞=1,由极限的性质可知当n 充分大时,必有n n u u +1>>0,因此lim n n u →∞≠0.故!n n n a n n ∞=1∑发散.例3 讨论级数ln ()pn np n∞=3>1∑的敛散性. 分析:通项中有ln n 因子,可考虑用积分判别法.解 令ln ()p x f x x =,当x ≥3时()f x ≥0,又ln ()()p p xf x p x +11-'=<0>1,故()f x 在[,)3+∞是正的单调递减函数,且ln ()p nf n n=,ln ()ln pp px x x f x dx dx xdx p p xx +∞1-1-+∞+∞+∞33331==-⋅1-1-⎰⎰⎰ln ()p ppp 1-1-233=-3<+∞1-1- 故由积分判别法知级数收敛.例4 设()ln nn n u n +1=-1,试判定n n u ∞=1∑与n n u ∞2=1∑的收敛性,并指出是绝对收敛,还是条件收敛?分析:n n u ∞=1∑是交错级数,n n u ∞2=1∑是正项级数.由于||ln ln()n n u n n+11==1+,注意到x →0时,ln()x x1+等价.解 因为ln()()n nn 111+→∞,所以lim ln ()n n n →∞111+=1,由于n n∞=11∑为发散的调和级数,因此lnn n n∞=1+1∑为发散级数. 因为ln()ln()n n 111+>1++1,且lim ln()lim n n n n →∞→∞111+==0,则由莱布尼兹定理知()ln n n n n ∞=1+1-1∑收敛.从而知其条件收敛.因ln ()nu n 221=1+,且lim ln ()lim()n n n n nn 2222→∞→∞11111+==1 由于级数n n ∞2=11∑为收敛级数,故由极限形式的比较判别法可知n n u ∞2=1∑收敛.[课堂练习]一、填空题1.若正项级数n n u ∞=1∑收敛,则n ∞=1是 级数.2.已知lim ()n n nu k →∞=≠0,则n n u ∞=1∑是 级数.3.已知lim n n a a b →∞=>>0,则nn n b a ∞=1⎛⎫⎪⎝⎭∑是 级数.4.级数(ln )nnn ∞=153∑的和为 . 5.级数()()()n n n n n n 3∞=1-2+52-12+12+3∑是 级数.二、选择题1.下列命题中正确的是( ).A .若n n u ∞=1∑收敛,则必有lim n n u →∞=0; B.若n n u ∞=1∑发散,则必有lim n n u →∞≠0;C.若lim n n u →∞=0,则n n u ∞=1∑必定收敛; D.若lim n n u →∞=0,则n n u ∞=1∑必定发散.2.下列命题中正确的是( ).A .若||n n u ∞=1∑收敛,则n n u ∞=1∑必条件收敛;B.若n n u ∞=1∑发散,则||n n u ∞=1∑必定发散;C.若||n n u ∞=1∑发散,则n n u ∞=1∑必定发散; D.若n n u ∞=1∑收敛,则||n n u ∞=1∑必定收敛.3.若级数n n u ∞=1∑收敛于S ,则级数()n n n u u ∞+1=1+∑( ).A .收敛于S 2; B.收敛于S u 12+; C.收敛于S u 12-; D.发散.4.若级数nn a ∞2=1∑和nn b ∞2=1∑都收敛,则级数n n n a b ∞=1∑( )A .一定条件收敛;B.一定绝对收敛;C.一定发散;D.可能收敛可能发散. 5.设a为常数,则sin ()n na n ∞2=1-∑为( ). A .绝对收敛; B.条件收敛; C.发散;D.收敛性与a 有关.三、判别下列级数的敛散性1.n n 1∞3=11⎛⎫ ⎪⎝⎭∑; 2.nn n 1∞=11⎛⎫⎪⎝⎭∑; 3.n ∞=1.四、判别下列级数的敛散性,若收敛,是绝对收敛,还是条件收敛? 1.ln()()nn n n ∞=11+-11+∑; 2. ()(cos )n n n α∞=1-11-∑ (α>0为常数).答案 一、1.收敛;2.发散;3.收敛;4.ln 33-5;5.发散.二、1.A ; 2.B ; 3.C; 4.B; 5.C三、1.发散,p 级数;→1; 3.收敛. 四、1.条件收敛; 2.绝对收敛.10-2 幂级数[教学基本要求]高等数学 1。
D10_2二重积分的计算 高等数学高数

2
说明: 计算二重积分选择积分次序是重要的。既要考
虑区域D的形状,又要注意被积函数的特点。
机动 目录 上页 下页 返回 结束
例4. 交换下列积分顺序
2
x2
22
8 x 2
I
0
dx 2 0
f (x, y)dy 2
dx0
f (x, y)dy
解: 积分域由两部分组成:
y
D1
:
0
y
1 2
x2,
0x2
D2
累次积好算为妙
图示法
• 写出积分限
( 先穿刺,后扫描 )
不等式
充分利用对称性 • 计算要简便
应用换元公式
机动 目录 上页 下页 返回 结束
例1. 计算 I xyd , 其中D 是直线 y=1, x=2, 及 D
y=x 所围的闭区域. 解法1. 将D看作X–型区域,
则D
:
11
y x
x 2
y
I
上面讨论的累次积分法仍然有效 .
(2) 若积分区域既是X–型区域又是Y –型区域 ,
则有 D f (x, y) dx dy
b
dx
a
2 (x) 1( x)
f (x, y) dy
d
dy
2(y)
f (x, y) dx
c
1(y)
y d
y 2(x)
x
y
c
1(
y) y
x
D
1(x)
2
(
y)
o a x bx
2
dx
1
x
xyd y 1
2 1
1 2
xy2
xd
高等数学 下册 (殷锡铭 许树声 著) 华东理工出版社 课后答案 第10章解答
即
2 2 2 cos , 则 cos
2 , 2
0 ,所以
3 3 ,即 a 与 b 的夹角为 。 4 4
** 9.在 yz 平面内求模为 10 的向量 b,使它和向量 a 8i 4 j 3k 垂直。 解:∵ 向量 b 在 yz 平面内, ∵ b a,
即: a1b1 a2b2 a3b3
a1 a2 a3 b1 b2 b3 ,
2
2
2
2
2
2
33
ቤተ መጻሕፍቲ ባይዱ ∴
ai
2 i 1
3
bi
2 i 1
3
a b
i 1
3
i i
。
第 10 章(之 3)
教学内容:§10.3 平面与直线[10.3.1] 1.填空题 *(1) 平行于 x 轴,且过点 P (3,1,2) 及 Q(0,1,0) 的平面方程是______ 。 答: y z 1 **(2) 与 xoy 坐标平面垂直的平面的一般方程为______ 。 答: Ax By d 0
29
1 ,求: 3
(2) 5a 2b 与 a b 的夹角。 解: (1) a b
2
a b
a b
∴ a b
2 2 a b 2a b 4 2 5 2 2 4 5 cos 21 , 3
2
2
a b a b a b ,
2
2 2 2 b 2a b a b 2a b ,
高等数学(II)(第十章、重积分)
27
Z
A ( x )
(x)
z f ( x, y)
2
1
(x)
f ( x , y ) dy
y
1( x )
所以:
2(x)
2 (x)
D
f(x,y)dxdy
b
A(x)dx
a
[
a
b
f(x .y ) dy ]dx
1 (x)
3-12
28
注意: 1)上式说明: 二重积分可化为二次定 积分计算;
2)积分次序: X-型域 3)积分限确定法: 先Y后X;
域中一线穿—定内限, 域边两线夹—定外限
为方便,上式也常记为:
b
dx
a
2 (x)
f(x .y ) dy
1 (x)
29
3、Y-型域下二重积分的计算:
同理:
d
x 1( y)
D
x 2( y)
c
D
f ( x, y )d
6
得 (3) 求和. 将这 n 个小平顶柱体的体积相加,
到原曲顶柱体体积的近似值,即
V
i1
n
V i f ( i , i ) i .
i1
n
(4) 取极限. 将区域 D 无限细分且每一个子域趋 向于缩成一点, 这个近似值就趋向于曲顶柱体的体
积, 即
V lim
0
将区域 D 任意分成 n 个小区域
任取一点 若存在一个常数 I , 使 记作
则称 f ( x , y )
可积 , 称 I 为 f ( x , y ) 在D上的二重积分.
高等数学下册第十章课件.ppt
(2) 若D为Y -型区域
则
说明:
即先对y后对x积分
即先对x后对y积分
第二节 直角坐标系中二重积分的计算
为计算方便,可选择积分序, 必要时还可以交换积分序.
则有
(4) 若积分域较复杂,可将它分成若干
X-型域或Y-型域 ,
则
(3) 若积分区域既是X-型区域又是Y -型区域
第二节 直角坐标系中二重积分的计算
记作
第五节 三重积分(一)
利用直角坐标计算三重积分
方法1 投影法 (“先一后二” )
如图,
第五节 三重积分(一)
划分:
记作
第五节 三重积分(一)
化为三次积分
区域
方法2 截面法 (“先二后一”)
第五节 三重积分(一)
记作
于是
注:方法一和方法二的可看作由上下两个曲面所围成.即平行于z轴且穿过内部的直线与的边界曲面相交不多于两点.
直角坐标系
柱面坐标系
球面坐标系
说明:
三重积分类似于二重积分也可以利用对称性计算.
变量可分离.
围成 ;
第六节 三重积分(二)
例 求
解 原式
第六节 三重积分(二)
几种的图形
第六节 三重积分(二)
三重积分的应用 1.物体的质心
设物体占有空间域 ,
有连续密度函数
则
设空间有n个质点,
其质量分别
例 计算
其中D 是直线 y=1, x=2, 及
y=x 所围的闭区域.
解法1 将D看作X-型区域, 则
解法2 将D看作Y-型区域, 则
第二节 直角坐标系中二重积分的计算
例 计算
其中D 是抛物线
高等数学同济六版第十章10-2
取 F (ξ i ,η i ) = P (ξ i ,η i ) i + Q (ξ i ,η i ) j ,
∆Wi ≈ F (ξ i ,η i ) ⋅ M i −1 M i ,
y
F(ξi ,ηi )
B
L
A
M2 M1
Mi−1 x i ∆
一、对坐标的曲线积分的概念与性质
y
变力沿曲线所作的功
L : A → B,
F ( x , y) = P ( x , y)i + Q ( x, y) j
B
L
A
M2 M1
Mi−1 xi ∆
∆yi
Mi Mn−1
常力所作的功 W = F ⋅ AB . o
x
分割 A = M 0 , M 1 ( x1 , y1 ),⋯ , M n−1 ( x n−1 , y n−1 ), M n = B .
n
n
性质 (1) 如α 与β 是 常数 则 常数,则
∫L [α F 1 ( x , y ) + β F 2 ( x , y )] ⋅ d r = α ∫ F 1 ( x , y )d r + β ∫ F 2 ( x , y )d r L L
( 2) 若有向曲线弧 L可分成两段光滑的有向 曲线弧 L1和 L2 , 则
i =1
n
精确值
定义
设L为 xoy面内从点 A到点 B的一条有
向光滑曲线弧 , 函数 P ( x , y ), Q ( x , y )在 L 上有界 . 用 L上的点 M 1 ( x1 , y1 ), M 2 ( x2 , y2 ), ⋯ , M n−1 ( xn−1 , yn−1 )把 L分成 n个有向小弧段 M i −1 M i ( i = 1,2,⋯, n; M 0 = A, M n = B ). 设∆xi = xi − xi −1 , ∆yi = yi − yi −1 , 点( ξ i , ηi )为 M i −1 M i 上任意取定的点 . 如果当各小弧段 长度的最大值 λ → 0时 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例: 设a 5,2,5, b 2,1,2, 求(a)b 及(a , b).
^
10 2 10 解: ) b (a 6 9 |b|
a b
18 6 cos( a , b) 3 54 9 | a || b |
^
a b
6 (a , b) arccos 3
x, y, z 是 OP 在 i , j , k 上的投影, 有 x OP i , y OP j , z OP k , OP (OP i ) i (OP j ) j (OP k ) k 通常记为 OP x, y, z , 向量的坐标表示式 . i 1, 0, 0 , j 0, 1, 0 , k 0, 0, 1
有 cos2 cos2 cos2 1.
例: 求方向角
0
3
,
4
, 模为3的向量 a.
1 1 1 解 : a cos , cos , cos , , 2 2 2 3 3 3 , a 3a , 2 2 2
三坐标面把整个空间 分为八个卦限 z 0 ( z 0) .
O
x
Ⅲ (Ⅶ) Ⅳ(Ⅷ)
过空间任一点 分别作 P 与各坐标面平行的平面 , 平面与x轴, y轴, z轴的交点在 对应轴上的坐标分别是 , y, z, x
点 P 坐标 ( x, y, z )
x
z
z
P
o
y
y
x
点P 三元有序实数组( x, y, z )
a1 b1 a2 b2 a3 b3 , , 1, AB中点P 2 2 2
(2).向量的内积运算
a a1, a2 , a3 , b b1, b2 , b3 a b (a1 i a2 j a3 k ) (b1 i b2 j b3 k )
§10.2 空间直角坐标系与向量代数
1.空间直角坐标系 过空间定点O, 作三条互相垂直的数轴 , 称为 x轴, y轴, z轴 ( 坐标轴, 横轴, 纵轴, 竖轴 ) , 常用的是按右手法则排 称点O为坐标原点 列, . y 坐标面,
xoy坐标面, yoz坐标面, zox坐标面. Ⅱ(Ⅵ) Ⅰ (Ⅴ)
a i a1 0 cos cos(a , i ) a i 2 2 2 | a || i | a1 a2 a3 a2 0 cos a j 2 2 2 a1 a2 a3 a3 0 cos a k 2 2 2 a1 a2 a3
^
a0 cos , cos , cos
a11a22 a12 a21
a11a22 a33 a12 a23 a31 a13 a21a32 a13 a22 a31 a12 a21a33 a11a23 a32
a11 a21 a31
a12 a22 a32
a13
a11 a12
a23 a21 a22 a33 a31 a32
[ AB, AC, AD] 0 x2 x1 y2 y1 z 2 z1 x3 x1 y3 y1 z3 z1 0 x4 x1 y4 y1 z 4 z1
例: 求以A (2,2,0), B (0,1,1), C (2,3,1),
D (1,4,3)为顶点的四面体的体积 . V
两点距离公式
A1 ( x1 , y1 , z1 ), A2 ( x2 , y2 , z2 ),
A1 A2 x2 x1, y2 y1, z2 z1
d | A1 A2 | ( x2 x1 ) ( y2 y1 ) ( z2 z1 )
2 2 2
投影量
设a a1 , a2 , a3 , b b1 , b2 , b3 ,
解 : s AB 2, 5, 2
W F S 3,4,8 2,5,2 10
向量的模
设a a1 , a2 , a3 ,
2 2 则由| a |2 a a a12 a2 a3 及 | a | 0,
2 2 得 | a | a12 a2 a3 .
i j a1 a2 b1 b2
k a2 a3 b 2 b3
a3 b3
i
a1 a3 b1 b3
j
a1 a2 b1 b2
kቤተ መጻሕፍቲ ባይዱ
(3).向量的外积运算
a a1, a2 , a3 , b b1, b2 , b3 a b (a1 i a2 j a3 k ) (b1 i b2 j b3 k )
解 : AB 2,3,1, AC 4,5,1, AD ,2,3 1
1 V [ AB , AC , AD ] 6 2 3 1 1 7 |4 5 1 | 3 6 1 2 3
横坐标, 纵坐标, 竖坐标
2. 向量沿坐标轴的分解
在 x, y, z 轴上分别取与轴 同向的单位向量 i , j ,k ,
i
M
z
Q
P
k
基本单位向量,
o
j
N
y
有i j ,j k ,k i , x | i || j || k | 1 ,
OP OM ON OQ x i y j z k
a1b1 i i a2b1 j i a3b1 k i a1b2 i j a2b2 j j a3b2 k j a1b3 i k a2b3 j k a3b3 k k
由于 i j , j k , k i , | i || j || k | 1 ,
则a
0
a |a|
1
2 a12 a2 a3
a1 , a2 , a3 2
称非零向量a a1 , a2 , a3 与三坐标轴正向的 夹角 , , ( 0 , , )为 a 的方向角,
称方向角的余弦cos , cos , cos 为 a 的方向余弦.
^
例: 求与向量 a 2 i j 2 k 平行
且满足 a x 18的向量 x .
解 : 设x a,
则 a x | a | 9 18
2
得 2
x 2a 4 i 2 j 4 k
二阶行列式
a11
a12
a21 a22 三阶行列式 a11 a12 a13 a21 a22 a23 a31 a32 a33
[a, b, c] (a b) c
a2 b2 a3 a3 , b3 b3 a1 a1 , b1 b1 a2 c1 , c2 , c3 b2 a1 a2 a3 a1 a2 b1 b2 c3 b3 b1 b2 c1 c2
c1
a2 b2
a3 b3
故a b (a1b2 a2b1 ) k (a2b3 a3b2 ) i (a3b1 a1b3 ) j
a1 a2 b1
i b1
b2
j b2
k
k a3 b3
a2 b2
a3 b3
i
a3 a1 b3 b1
j
a1 a2
例: A (1,1,2), B (5,6,2), C (1,3,1), 设
(1).求同时垂直于AB, AC 的单位向量;
(2).计算 ABC的边 AC 上的高 BD的长度.
解 : AB 4, 5, 0 , AC 0, 4, 3
i
(1).n AB AC 4 0
2 2
5 0 15, 12, 16 4 3
2
j
k
| n | 15 12 16 25
a1b1 i i a2b1 j i a3b1 k i a1b2 i j a2b2 j j a3b2 k j a1b3 i k a2b3 j k a3b3 k k
由于 i j k , j k i , k i j , i i j j k k 0,
点 P ( x, y, z ) OP x, y, z
3. 向量代数
(1). 向量的线性运算
a a1, a2 , a3 , b b1, b2 , b3 , , R
a b
(a1 i a2 j a3 k ) (b1 i b2 j b3 k )
c2
a1 b1
a3 b3 c3
a1
a2
a3
三向量a, b, c共面 b1 b2 b3 0 c1 c2 c3 四点A ( x1 , y1 , z1 ), B ( x2 , y2 , z2 ),
C ( x3 , y3 , z3 ), D ( x4 , y4 , z4 )共面
设a a1 , a2 , a3 , b b1 , b2 , b3 ,
则a // b a b a b 0 a1 a2 a3 b1 b2 b3
a b a b 0 a1b1 a2b2 a3b3 0
设a a1 , a2 , a3 0,
故 i j j k k i 0, i i j j k k 1,
因此 a b a1b1 a2b2 a3b3
例: 一质点在力F 3 i 4 j 8 k 的作用下,
从点 A ( 2, 2, 0 ) 沿直线运动到 点 B ( 4,, ), 求力 F 所作的功. 32
(a1 b1) i (a2 b2 ) j (a3 b3 )k
a1 b1 , a2 b2 , a3 b3
