数学竞赛线性规划训练讲义(含详细答案)2
数学线性规划试题答案及解析

数学线性规划试题答案及解析1.在平面直角坐标系中,为不等式组所表示的区域上一动点,则直线斜率的最小值为 .【答案】【解析】不等式组表示的区域如图,当取得点时,直线斜率取得最小,最小值为.故选C.2.若实数满足其中,若使得取得最小值的解有无穷多个,则等于.【答案】2.【解析】表达式可看成是定点与动点连线斜率(点在所给不等式组表示的平面区域内),如图,动直线过定点,为使满足题意的点有无穷多个,此时直线应过,从而【考点】本题考查含参数的二元一次不等式组表示平面区域等知识,意在考查画图、用图及计算能力.3.设实数满足条件,则的最大值是()A.B.C.D.【答案】A【解析】画出可行域,如图所示,目标函数变形为,直线经过可行域,尽可能地向下平移经过点时取到最大值,即的最大值为.【考点】本题考查线性规划等基础知识,意在考查学生数形结合思想的运用能力和基本运算能力.4.已知实数满足:,则的最小值为 .【答案】【解析】画出可行域及直线..,如图所示.平移直线,当经过点时,直线的纵截距最大,所以,.【考点】本题考查简单线性规划的应用等知识,意在考查作图、识图、用图的能力及数形结合思想.5.某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需送往A地至少72吨的货物,派用的每辆车需满载且只运送一次,派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元.该公司合理计划当天派用两类卡车的车辆数,可得最大利润z= () A.4 650元B.4 700元C.4 900元D.5 000元【答案】C【解析】设派用甲型卡车x辆,乙型卡车y辆,则,目标函数z=450x+350y,画出可行域如图,当目标函数经过A(7,5)时,利润z最大,为4 900元6.若x,y满足约束条件则z=3x-y的最小值为________.【答案】-1【解析】本小题主要考查线性规划最优解的应用,解题的突破口是正确作出可行域和平移目标函数曲线.利用不等式组,作出可行域,则目标函数直线过(0,1)时,z取最小值-1.7.已知变量满足约束条件,若的最大值为,则实数 .【答案】或(对1个得3分,对2个得5分)【解析】利用线性规划的知识画出不等式组表示的可行域如下图所示:其中点,根据线性规划的知识可得目标函数的最优解在只能是,当目标函数在点A处取得最优解时,有符合题意,当目标函数在点B处取得最优解时, 符合题意,当目标函数在C点取得最优解时, 无解,所以或,故填或.8.已知点满足约束条件,为坐标原点,则的最大值为.【答案】5【解析】作出可行域,得到当位于时,最大,其值为5.9.浙江理)设,其中实数满足,若的最大值为12,则实数________。
线性规划专题含答案

线性规划专题1.已知变量满足约束条件,则的最大值为A. B. C. D.2.设实数满足约束条件则的取值范围是A. B. C. D.3.已知求的范围A. B. C. D.4.已知,若的最小值是2,则a=A.1B.2C.3D.45.设不等式组其中a>0,若z=2x+y的最小值为,则a=().A. B. C. D.6.在平面直角坐标系中,不等式组,表示的平面区域的面积是A. B.4 C. D.27.已知不等式组所表示的平面区域为,若直线与平面区域有公共点,则的取值范围是A. B.C. D.8.已知实数x,y满足约束条件,则使恒成立的的取值范围是A.[0,2]B.C.[2,D.[-,1)9.已知不等式组所表示的平面区域为若直线与平面区域有公共点,则的取值范围为A. B.C. D.10.已知正数,满足,则的最小值为A.1B.C.D.11.已知点和在直线的同侧,则取值范围A. B.C. D.12.已知函数处取得极大值,在处取得极小值,满足的取值范围是A. B. C. D.13.若点满足,则的取值范围是A. B.C. D.14.设x,y满足约束条件,若目标函数的值是最大值为12,则的最小值为A. B. C. D.415.设非负实数满足:,(2,1)是目标函数取最大值的最优解,则的取值范围是A. B. C. D.16.定义在R上的函数满足,为的导函数,已知y=的图象如图所示,且有且只有一个零点,若非负实数a,b满足,则的取值范围是A. B. C. D.17.满足约束条件,若取得最大值的最优解不唯一.则实数的值为A.或B.或C.或D.或18.已知点在由不等式组确定的平面区域内,则点所在平面区域的面积是A.1B.2C.4D.819.已知满足约束条件若对于满足约束条件的所有,总有不等式成立,则实数的最小值为A. B. C. D.020.设满足约束条件,若目标函数的最大值为,则的最小值为A. B. C. D.21.x,y满足约束条件,若z=y-ax取得最大值的最优解不唯一,则实数a的值为A.或-1B.2或C.2或1D.2或-122.设实数满足则的取值范围为A. B. C. D.23.已知实数满足,则的取值范围是_____.24.已知方程,其一根在区间(0,1)内,另一根在区间(1,2)内,则的取值范围为________. 25.已知满足满足约束条件,那么的最大值为___.26.已知m>0,实数x,y满足若z=x+2y的最大值为2,则实数m=_________.27.已知实数,满足则的最大值为 .28.若满足约束条件,若目标函数仅在点(1,0)处取得最小值,则a的取值范围为_________.29.设变量x,y满足约束条件:,则目标函数的最小值为.30.已知是方程的两根,且则的范围是31.若满足约束条件则的最小值为 .32.不等式组所表示的平面区域面积为 .33.已知实数满足约束条件则的最大值等于___ .34.若实数满足不等式组则的取值范围是35.在平面直角坐标系中,满足不等式组的整点个数是 .36.已知,求:(1)的取值范围;(2)的最小值.37.变量x、y满足.(1)设z=,求z最大值.(2)设z=x2+y2,求z的取值范围.1.C2.A3.A4.B5.D6.B7.C8.B9.C10.C 11.C12.B13.A14.A15.C 16.D17.B18.C19.B20.D 21.D22.D 23.[0,9] 24. 25.58 26.1 27. 28.29.1 30. 31. 32. 33.8 34. 35.2 551参考答案1.C【解析】本题主要考查线性规划等基础知识,意在考查考生数形结合的思想及运算求解能力.:如图【备注】无2.A【解析】本题主要考查线性规划的应用,考查两点间的距离公式和点到直线的距离公式.根据所求式子的几何意义,利用数形结合即可得结论.作出不等式组对应的平面区域,如图:的几何意义是可行域内的点与点两点间距离的平方.由图可知,D 到距离最大,=17;D 到直线,.A.故选3.A7【解析】本题主要考查线性规划、直线的斜率公式.作出不等式组所表示的平面区域,如图所示的阴影部分,易求A(1,3),B(3,1),将化为,则表示过点P ()与阴影区域内任意一点(x,y)的直线的斜率,k PA =,k PB =,则,即的范围【备注】无4.B【解析】本题考查线性规划问题,意在考查考生的分析理解能力.作出可行域,依题意,若的最小值是2,当时,则为其最小值最优解,此时.当时,则为最小值最优解,即得,不合题意.故本题正确答案为B.5.D【解析】本题考查线性规划,意在考查考生的分析理解能力.作出可行域,显然函数z=2x+y过(1,﹣2a)时,z取到最小值,得2﹣2a =,得a =.故本题正确答案为D.89【备注】无 6.B【解析】本题主要考查线性规划问题.作出不等式组所表示的平面区域,如图所示,不等式组所表示的平面区域是斜边为4、高为2的等腰直角三角形,所以面积为4.【备注】无 7.C【解析】本题考查简单的线性规划问题.作出不等式组所表示的平面区域M 如图中阴影部分所示,因为直线恒过点,则,,由图象知,要使直线与平面区域M 有公共点,须或.故选C.10【备注】无 8.B【解析】本题主要考查线性规划的应用及恒成立问题,利用式子的几何意义解题. 由约束条件作出可行域,如图中阴影部分:的几何意义是可行域内的点P (x ,y )与定点A (两点连线的斜率.由图像可知,当P越靠近可行域的右上方,斜率越大,显然.. 若使恒成立,只需.故选B 【备注】无 9.CyxO1. A(-1,1).P(x,y )【解析】本题考查线性规划问题.画出可行域(如图三角形ABC所示);而直线过定点;,;因为直线与平面区域有公共点,所以或;即的取值范围为.选C.【备注】体会数形结合思想.10.C【解析】本题考查简单线性规划.由题意知,图中阴影部分为满足的正数,由可得,在处取得最小值.选C.【备注】体会数形结合思想.11.C【解析】本题考查简单线性规划.由题意知,,解得, 或,所以取值范围.选C.【备注】无12.B【解析】本题考查函数的极值与导函数相应方程的根的关系、简单的线性规划问题;因为函数处取得极大值,在处取得极小值,所以是方程的两个不等实根,且,则,作出可行域(如图所示),因为,而表示过点与可行域内的点的直线的斜率,由图象,得,即;故选B.【备注】无13.A【解析】本题考查简单线性规划问题.如图阴影部分表示的可行域,表示可行域内任一点与图中点的斜率,因为,,所以的取值范围是.选A.【备注】体会数形结合思想.14.A【解析】本题主要考查线性规划问题、基本不等式.作出约束条件所表示的平面区域,如图所示阴影部分,当目标函数过点A(4,6)时取得最大值,则有,则,当且仅当,即a=b=时,等号成立.【备注】无15.C【解析】本题考查线性规划问题,意在考查考生的分析理解能力.作出可行域,依题意,(2,1)是目标函数取最大值的最优解,则直线的斜率,得.故本题正确答案为C.【备注】无16.D【解析】本题考查函数的图像与性质,导数在研究函数中的应用,线性规划问题.由y=的图象可得:当时,,单减,当时,,单增;而非负实数a,b满足,所以,;画出可行域(如图四边形所示);;当过点时,取得最小值;当过点时,取得最大值;即的取值范围是.选D.【备注】体会化归与转化思想、数形结合思想.17.B【解析】本题主要考查线性规划问题以及求目标函数的最值.作出约束条件所表示的可行域,如图所示阴影部分(包括边界),因为目标函数取得最大值的最优解不唯一,且点A(0,2),B(2,0),C(-2,-2),所以,观察图象可知,当目标函数与直线或重合时,满足题意,则有或,则实数的值为或.【备注】无18.C【解析】本题主要考查二元一次不等式组表示的平面区域,意在考查考生的化归与转化的思想及计算求解能力.要求所在平面区域的面积,一定要得到关于的横纵坐标不等式组;由已知得:,令,解得:,即:,它表示的平面区域如下:xyO22-2所以,区域的面积.应选C.【备注】无19.B【解析】本题考查线性规划,意在考查考生的分析理解能力.作出可行域,由恒过定点,直线过点时,最大,此时.故本题正确答案为B.【备注】无20.D【解析】本题考查线性规划问题,基本不等式.画出可行域(如图四边形OABC所示);当过点时,目标函数取得最大值,即;所以(当且仅当时等号成立).即的最小值为4.选D.【备注】体会数形结合思想.21.D【解析】本题考查线性规划问题.画出可行域(如图所示);当y=ax+z与或平行时,z取得最大值的最优解不唯一,所以.选D.【备注】体会数形结合思想.22.D【解析】本题主要考查线性规划以及换元法、函数的单调性求最值.作出不等式组所表示的平面区域,如图所示(),令,由图可得,则在.显然是增函数,所以,当时,,当时,,因此,的取值范围为23.[0,9]【解析】本题主要考查了线性规划问题.首先根据不等式组作出可行域如图,为△ABC及其内部,由目标函数的几何意义可知的最小值为0,当过点A时取得最大值9,故填[0,9].【备注】无24. .【解析】本题主要考查一元二次方程根的分布、线性规划等基础知识,意在考查考生对基础知识的灵活运用能力.设,要使方程一根在区间(0,1)内,另一根在区间(1,2)内,必有,可得:,令,可以将看作过点和的直线斜率;画图如下:可得:;解得:;故:;应填:.【备注】无25.58【解析】无26.1【解析】主要考查简单的线性规划问题.由已知约束条件可知,目标函数在点处取最大值,即故答案为1.【备注】无27.【解析】主要考查简单的线性规划问题和基本不等式的应用.采用数形结合的思想.首先画出实数所满足的可行域如图所示,设由图像可知,是线段上所有的点,而由基本不等式可知:当且仅当时等号成立,即的最大值在线段的中点处取得),所以故答案为.【备注】无28.【解析】本题考查简单的线性规划问题及最优解的个数问题;将化为,作出可行域(如图所示),若目标函数仅在点(1,0)处取得最小值,即取得最小值,则,解得;故填.【备注】无29.1【解析】本题主要考查线性规划问题、二元一次方程的求解及直线的斜率问题,从中体会数形结合的思想.依题可画图如下,目标函数表示可行域内的点到固定点的斜率,其最小值为过的直线的斜率,由解得:,∴,故填1.【备注】无30.【解析】本题主要考查线性规划、一元二次方程根的分布等基础知识,意在考查考生对概念和基本公式的灵活运用能力.=,不妨令,可得:=;下面求的取值范围;由方程的两根,可得:;画可行域如下图:可得:,,故:;即:,令,该函数在区间单调递减,在区间单调递增;故:;应填:.【备注】无31.【解析】本题考查线性规划问题.画出可行域(如图所示);;当过点时,取得最小值.【备注】体会数形结合思想,一般在所围区域的端点处取得最值.32.【解析】本题考查简单的线性规划问题.画出可行域(如图所示);,,所以.【备注】画出图形是解决问题的关键.33.8【解析】本题主要考查线性规划问题的最优解.由题意,作出满足约束条件易知可行域为一个三角形,验证知在点A(﹣2,1)时,z1=x+y﹣2取得最小值﹣3,∴z最大值是8,故答案为:8.【备注】无34.【解析】本题考查简单的线性规划问题以及分类讨论思想的应用;当时,可化为,当时,可化为;作出可行域和目标函数基准直线(如图所示),由图象得:当时,直线过点时,;当时,直线过点时,;故填.【备注】无35.2 551【解析】作出不等式组表示的平面区域,如图中△OAB内部及边界上的整点.由两轴及x+y=100围成区域(包括边界)内的整点数=1+2+3+…+101=5 151(个).由得其交点为A(75,25).当y=0时,有101-1=100个整点(不包括△AOB边界上的点);当y=1时,y=1与y=(不包括)及x+y=100交点的横坐标分别为x=3,x=99,所以3<x≤99,共有96个整点;当y=2时,6<x≤98,有92个整点;当y=3时,9<x≤97,有88个整点.故整点数构成了以100为首项,-4为公差的正项等差数列,从而y=0与y=(不包括)及x+y=100所围成的区域共有×25=1 300(个)整点.由对称性可知x=0与y=3x(不包括)及x+y=100所围成的区域也有1 300个整点.故△AOB内(包括边界)共有5 151-2 600=2 551(个)整点.故填2 551.【备注】思路点拨:要研究整点,必须作出图形,根据图形特征结合对称性进行研究. 名师点评: 解决格点(即横、纵坐标均为整数的点)问题,一般采取数形结合的思想,即根据区域特征进行逐一讨论,很多时候运用对称思想可以极大地降低问题的难度.36.(1)三条直线的交点分别是,表示点与两点斜率的取值范围.的取值范围是(2)表示可行域中的点与点(0,5)的距离的平方最小值.到直线的距离的平方为是最小的.【解析】本题主要考查的是简单的线性规划,两点间的距离公式,直线的斜率等知识点,意在考查考生的数形结合能力.(1)分析题意可得,表示点与两点斜率的取值范围,据此计算即可得到答案.(2)表示可行域中的点与点(0,5)的距离的平方,结合两点间的距离公式不难得到最小值..【备注】无37.由约束条件,作出可行域如图所示.由,解得由,解得;由,解得.(1)z=的几何意义是过原点直线的斜率,从图上可知直线过A点时候,斜率最大,所以(2)的几何意义是可行域上的点到原点的距离的平方,结合图形可知,可行域上的点到原点的距离中,,所以所求的取值范围为.【解析】本题主要考查线性规划问题的运用.能准确的作图,表示可行域以及平移法求解线性目标函数的最值是解题的关键,同时能利用两点的距离的几何意义求解目标函数的最值问题.【备注】无。
数学讲义:第3章 3.5 3.5.2 简单线性规划 Word版含答案
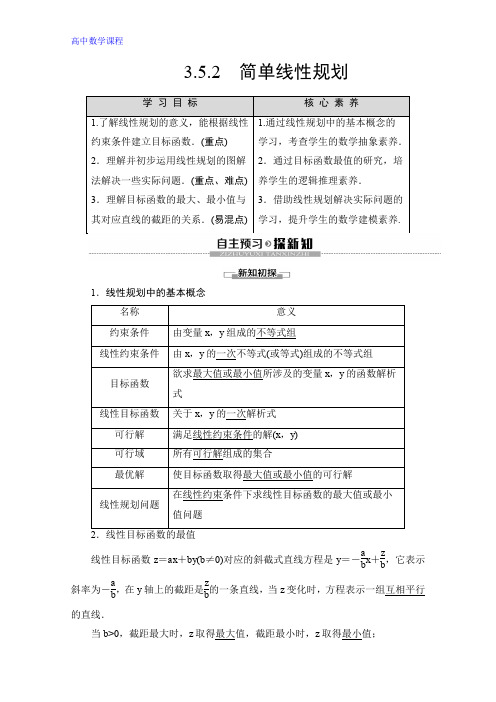
1.线性规划中的基本概念
名称
意义
约束条件
由变量x,y组成的不等式组
线性约束条件
由x,y的一次不等式(或等式)组成的不等式组
目标函数
欲求最大值或最小值所涉及的变量x,y的函数解析式
线性目标函数
关于x,y的一次解析式
可行解
满足线性约束条件的解(x,y)
[解]由不等式组 作出可行域,如图所示.
∵目标函数为z=3x+5y,
∴作直线l:3x+5y=0.
平移直线l,在可行域内以经过点A 的直线l1所对应的z最大.
类似地,在可行域内,以经过点B(-2,-1)的直线l2所对应的z最小.
∴zmax=3× +5× =17,zmin=3×(-2)+5×(-1)=-11.
本题即求满足不等式组 且使z=160x+252y取得最小值的非负整数x与y的值.
不等式组表示的平面区域即可行域如图所示,其可行域为四边形ABCD区域(含边界线段),它的顶点是A ,B ,C(7,2),D(5,4).结合图形可知,在四边形区域上,横坐标与纵坐标都是非负整数的点只有P1(3,4),P2(4,4),P3(4,3),P4(5,2),P5(5,3),D(5,4),P6(6,2),P7(6,3),P8(7,1),C(7,2)10个点.
作直线l:160x+252y=0.
使l向上方平行移动,可发现它与上述的10个点最先接触到的点是P4(5,2),得到的z的值最小,zmin=160×5+252×2=1 304.
即当公司每天出动A型卡车5辆,B型卡车2辆时,公司的成本费用最低.
解答线性规划应用题的一般步骤:
(1)审题——仔细阅读,对关键部分进行“精读”,准确理解题意,明确有哪些限制条件,起关键作用的变量有哪些.由于线性规划应用题中的变量比较多,为了理顺题目中量与量之间的关系,有时可借助表格来理顺.
线性规划题及答案

线性规划题及答案线性规划是一种数学优化方法,用于解决线性约束条件下的最优化问题。
在线性规划中,我们需要确定一组决策变量的取值,以使得目标函数达到最大或最小值,同时满足一组线性约束条件。
下面我将为您提供一个线性规划题目及其答案,以便更好地理解线性规划的应用。
题目:某公司生产两种产品A和B,每单位产品A的利润为5元,每单位产品B的利润为8元。
公司有两个车间可供生产,车间1每天生产产品A需要2小时,产品B需要1小时;车间2每天生产产品A需要1小时,产品B需要3小时。
车间1每天可工作8小时,车间2每天可工作10小时。
公司希望确定每个车间生产的产品数量,以使得利润最大化。
解答:首先,我们需要定义决策变量。
设x1为车间1生产的产品A的数量,x2为车间1生产的产品B的数量,x3为车间2生产的产品A的数量,x4为车间2生产的产品B的数量。
其次,我们需要建立目标函数。
公司的利润可以表示为:Profit = 5x1 + 8x2 +5x3 + 8x4。
然后,我们需要建立约束条件。
根据车间1和车间2的工作时间限制,我们可以得到以下两个约束条件:2x1 + x2 ≤ 8 (车间1的工作时间限制)x3 + 3x4 ≤ 10 (车间2的工作时间限制)另外,由于产品数量不能为负数,我们还需要添加非负约束条件:x1, x2, x3, x4 ≥ 0综上所述,我们得到了以下线性规划模型:Maximize Profit = 5x1 + 8x2 + 5x3 + 8x4Subject to:2x1 + x2 ≤ 8x3 + 3x4 ≤ 10x1, x2, x3, x4 ≥ 0接下来,我们可以使用线性规划求解方法来求解该问题。
通过求解器或手动计算,我们可以得到最优解:x1 = 2,x2 = 4,x3 = 1,x4 = 2利润最大化为:Profit = 5(2) + 8(4) + 5(1) + 8(2) = 58元。
通过以上求解过程,我们可以得出结论:为了使公司的利润最大化,车间1应该生产2个单位的产品A和4个单位的产品B,车间2应该生产1个单位的产品A和2个单位的产品B,此时公司的利润为58元。
线性规划题及答案

线性规划题及答案线性规划是一种数学优化方法,用于解决在给定约束条件下求解线性目标函数的最优解的问题。
本文将介绍一个线性规划题及其答案,以帮助您更好地理解和应用线性规划。
题目描述:某工厂生产两种产品A和B。
每单位产品A需要3个工时和2个材料单位,每单位产品B需要4个工时和1个材料单位。
工厂每天有总共24个工时和10个材料单位可用。
产品A的利润为100元/单位,产品B的利润为80元/单位。
问工厂每天应该生产多少单位的产品A和产品B,以最大化利润?解答步骤:1. 确定决策变量:设工厂每天生产的产品A的单位数为x,产品B的单位数为y。
2. 建立目标函数:目标是最大化利润,因此目标函数为:Z = 100x + 80y。
3. 建立约束条件:根据题目描述,工厂每天可用的工时为24个,每单位产品A需要3个工时,每单位产品B需要4个工时,因此工时的约束条件为:3x + 4y ≤ 24。
工厂每天可用的材料单位为10个,每单位产品A需要2个材料单位,每单位产品B需要1个材料单位,因此材料单位的约束条件为:2x + y ≤ 10。
另外,生产的产品数量不能为负数,即:x ≥ 0,y ≥ 0。
4. 构建线性规划模型:综合考虑目标函数和约束条件,可以得到线性规划模型如下:Maximize Z = 100x + 80ySubject to:3x + 4y ≤ 242x + y ≤ 10x ≥ 0y ≥ 05. 解答最优解:通过线性规划求解器或图形法等方法,可以求解出最优解。
假设最优解为x*和y*,则工厂每天应该生产x*单位的产品A和y*单位的产品B,以最大化利润。
答案解析:通过线性规划求解器求解上述线性规划模型,得到最优解为x* = 4,y* = 4。
即工厂每天应该生产4个单位的产品A和4个单位的产品B,以最大化利润。
利润最大化时的最优解下,工厂每天使用的工时为3x* + 4y* = 3*4 + 4*4 = 24个,使用的材料单位为2x* + y* = 2*4 + 4 = 12个。
线性规划题及答案

线性规划题及答案引言概述:线性规划是运筹学中的一种数学方法,用于寻觅最优解决方案。
在实际生活和工作中,线性规划问题时常浮现,通过对问题进行建模和求解,可以得到最优的决策方案。
本文将介绍一些常见的线性规划题目,并给出详细的答案解析。
一、生产规划问题1.1 生产规划问题描述:某工厂生产两种产品A和B,产品A每单位利润为100元,产品B每单位利润为150元。
每天工厂有8小时的生产时间,产品A每单位需要2小时,产品B每单位需要3小时。
问工厂每天应该生产多少单位的产品A 和产品B,才干使利润最大化?1.2 生产规划问题答案:设产品A的生产单位为x,产品B的生产单位为y,则目标函数为Max Z=100x+150y,约束条件为2x+3y≤8,x≥0,y≥0。
通过线性规划方法求解,得出最优解为x=2,y=2,最大利润为400元。
二、资源分配问题2.1 资源分配问题描述:某公司有两个项目需要投资,项目A每万元投资可获得利润2万元,项目B每万元投资可获得利润3万元。
公司总共有100万元的投资额度,问如何分配投资额度才干使利润最大化?2.2 资源分配问题答案:设投资项目A的金额为x万元,投资项目B的金额为y万元,则目标函数为Max Z=2x+3y,约束条件为x+y≤100,x≥0,y≥0。
通过线性规划方法求解,得出最优解为x=40,y=60,最大利润为240万元。
三、运输问题3.1 运输问题描述:某公司有两个仓库和三个销售点,每一个销售点的需求量分别为100、150、200,每一个仓库的库存量分别为80、120。
仓库到销售点的运输成本如下表所示,问如何安排运输方案使得总成本最小?3.2 运输问题答案:设从仓库i到销售点j的运输量为xij,则目标函数为Min Z=∑(i,j) cij*xij,约束条件为每一个销售点的需求量得到满足,每一个仓库的库存量不超出。
通过线性规划方法求解,得出最优的运输方案,使得总成本最小。
四、投资组合问题4.1 投资组合问题描述:某投资者有三种投资标的可选择,预期收益率和风险如下表所示。
2 线性规划习题解答
2 线性规划习题答案1、试述线性规划数学模型的组成部分及其特性答:线性规划数学模型由决策变量、约束条件和目标函数三个部分组成。
线性规划数学模型特征:(1) 用一组决策变量表示某一方案,这组决策变量均为非负的连续变量;(2) 存在一定数量(m )的约束条件,这些约束条件可以用关于决策变量的一组线性等式或者不等式来加以表示;(3) 有一个可以用决策变量加以表示的目标函数,而该函数是一个线性函数。
2、一家餐厅24小时全天候营业,在各时间段中所需要的服务员数量分别为:2:00~6:00 3人 6:00~10:00 9人 10:00~14:00 12人 14:00~18:00 5人 18:00~22:00 18人 22:00~ 2:00 4人设服务员在各时间段的开始时点上上班并连续工作八小时,问该餐厅至少配备多少服务员,才能满足各个时间段对人员的需要。
试构造此问题的数学模型。
解:用决策变量1x ,2x ,3x ,4x ,5x ,6x 分别表示2:00~6:00, 6:00~10:00 ,10:00~14:00 ,14:00~18:00,18:00~22:00, 22:00~ 2:00 时间段的服务员人数。
其数学模型可以表述为:123456m in Z x x x x x x =+++++16122334455612345639125184,,,,,0x x x x x x x x x x x x x x x x x x +>=+>=+>=+>=+>=+>=≥3、现要截取2.9米、2.1米和1.5米的元钢各100根,已知原材料的长度是7.4米,问应如何下料,才能使所消耗的原材料最省。
试构造此问题的数学模型。
方法一解:圆钢的截取有不同的方案,用θ表示每种切割方案的剩余材料。
其切割方案如下所示: 2.9 2.1 1.5 θ 1' 1 1 1 0.9 2' 2 0 0 0.1 3' 1 2 0 0.3 4' 1 0 3 0 5' 0 1 3 0.8 6' 0 0 4 1.4 7' 0 2 2 0.2 8'31.1目标函数为求所剩余的材料最少,即12345678min 0.90.10.300.8 1.40.2 1.1Z x x x x x x x x =+++++++1234135781245671234567821002231003342100,,,,,,,0x x x x x x x x x x x x x x x x x x x x x x x +++>=++++>=+++++>=≥方法二解:由题意,因为所有套裁方案有21种,全部写出需考虑因素太多,故需先做简化。
线性规划题及答案
线性规划题及答案引言概述:线性规划是一种常见的数学建模方法,用于解决优化问题。
它在工程、经济学、运筹学等领域中得到了广泛应用。
本文将介绍线性规划题的基本概念和解题方法,并给出相应的答案。
一、线性规划的基本概念1.1 目标函数:线性规划的目标是最大化或者最小化一个线性函数,称为目标函数。
目标函数通常表示为Z = c1x1 + c2x2 + ... + cnxn,其中ci为系数,xi为决策变量。
1.2 约束条件:线性规划的决策变量必须满足一系列约束条件,这些条件通常表示为一组线性不等式或者等式。
例如,Ax ≤ b,其中A为系数矩阵,x为决策变量向量,b为常数向量。
1.3 可行解:满足所有约束条件的决策变量取值称为可行解。
可行解的集合称为可行域。
二、线性规划问题的解题方法2.1 图形法:对于二维线性规划问题,可以使用图形法求解。
首先绘制可行域的图形,然后通过挪移目标函数的等高线来确定最优解。
最优解通常浮现在可行域的顶点处。
2.2 单纯形法:对于高维线性规划问题,可以使用单纯形法求解。
该方法通过迭代计算,逐步接近最优解。
单纯形法的基本思想是通过交换基本变量和非基本变量来改变目标函数值,直到找到最优解。
2.3 整数规划法:当决策变量需要取整数值时,可以使用整数规划法求解。
整数规划问题通常比线性规划问题更难解决,因为整数解的集合通常是离散的。
三、线性规划题的实例分析3.1 生产计划问题:某工厂生产两种产品A和B,每单位产品A需要3小时的生产时间,每单位产品B需要2小时的生产时间。
工厂每天有8小时的生产时间,且产品A和B的利润分别为10元和8元。
求工厂每天应生产多少单位的产品A和B,才干最大化利润。
3.2 运输问题:某物流公司有3个仓库和4个配送点,每一个仓库的库存和每一个配送点的需求如下表所示。
每单位产品的运输成本如下表所示。
求如何安排运输,使得总运输成本最低。
仓库 | 库存----|----A | 50B | 80C | 70配送点 | 需求------|-----D | 30E | 40F | 50G | 60运输成本 | 仓库A | 仓库B | 仓库C--------|------|------|------配送点D | 10 | 12 | 15配送点E | 14 | 8 | 11配送点F | 7 | 16 | 9配送点G | 13 | 10 | 63.3 资源分配问题:某公司有3个项目需要分配资源,每一个项目的利润和资源需求如下表所示。
第二章 线性规划习题(附答案)
x1
x2
x3
x4
x5
x6
RHS
z
1
0
5/2
0
5/3
0
1/3
8
x1
2
1
1/2
0
1/2
0
1/2
2
x4
0
0
5/2
0
1/2
1
1/2
6
x3
1
0
1/2
1
1/2
0
-1/2
1
新的最优解为(x1,x2,x3,x4,x5,x6)T=(2,0,1,6,0,0)T,maxz=8。
2-10某厂生产A,B,C三种产品,其所需劳动力、材料等有关数据见表2-46。要求:(1)确定利润最大的产品生产计划;(2)产品A的利润在什么范围内变动时,上述最优计划不变;(3)如果设计一种新产品D,单件劳动力消耗为8单位,材料消耗为2单位,每件可获利3元,问该种产品是否值得生产?(4)如果劳动力数量不增,材料不足时可从市场购买,每单位0.4元。问该厂要不要购进原材料扩大生产,以购多少为宜。(5)由于某种原因该厂决定暂停A产品的生产,试重新确定该厂的最优生产计划。
-2/5
0
x3
-3
6/5
3/5
1
0
-1/5
2
当前基既是原始可行基,又是对偶可行基,因而是最优基。最优解为
x1=0,x2=0,x3=2,maxz,=-6,即min z=6
2-8已知2-45表为求解某线性规划问题的最终单纯形表,表中x4, x5为松弛变量,问题的约束为≤形式。
表2-45最终单纯形表
z
x1
(1)
(2)
解:(1)原问题的对偶问题为:
线性规划专题 含答案
线性规划专题(含答案)1. 设,满足约束条件则的最大值是.2. 设,满足约束条件则的最大值是.3. 设,满足约束条件则的最大值为.4. 在约束条件下,目标函数的最大值为.5. 已知实数,满足约束条件,则的最小值为.6. 若,则目标函数的取值范围是.7. 已知实数,满足不等式组那么目标函数的最大值是.8. 已知满足条件则目标函数的最大值为.9. 若实数,满足不等式组则的最小值是.10. 已知,满足约束条件则的最小值为.11. 若,满足约束条件则的最大值为.12. 已知,满足则的最大值为.13. 设、满足约束条件则的最小值为.14. 在约束条件下,目标函数的最小值是.15. 设变量、满足约束条件:则的最小值为.16. 已知实数,满足则的最大值为.17. 若,满足约束条件,则的最小值为.18. 若实数,满足条件则的最大值为.19. 已知实数,满足条件则的取值范围是.20. 设变量,满足约束条件则目标函数的最大值为.21. 已知是坐标原点,点,若点为平面区域上的一个动点,则的取值范围是.22. 若圆关于直线对称,动点在不等式组表示的平面区域内部及边界上运动,则的取值范围是.23. 若,满足约束条件则的最大值为.24. 设实数,满足,,且,则的最大值为.25. 实数,满足不等式组则的取值范围是.26. 在平面直角坐标系中,已知点,,,点为边界及内部的任意一点,则的最大值为.27. 已知实数,满足且的最大值为.28. 已知实数,满足则的取值范围是.29. 若实数,满足不等式组则目标函数的最大值为.30. 设,满足约束条件则目标函数的最大值为.31. 若变量,满足约束条件,则的最大值是.32. 已知,满足若目标函数的最大值为,则展开式的常数项为.33. 若,满足约束条件则的最小值为.34. 设,满足约束条件则的取值范围是.35. 已知实数,满足约束条件则的最大值为.36. 已知变量,满足约束条件若使取得最小值的最优解有无穷多个,则实数.37. 已知,,满足约束条件若的最大值为,则.38. 若实数,满足约束条件则的最大值为.39. 若,满足约束条件则的最大值为.40. 设实数,满足则的最大值为.41. 如果实数,满足约束条件则的最大值为.42. 已知实数满足条件则的最小值为.43. 若,满足约束条件则的最大值为.44. 已知实数,满足则的最小值为.45. 设实数,满足则的取值范围是.46. 记不等式组所表示的平面区域为,若直线与有公共点,则的取值范围是.47. 已知变量,满足约束条件则的最小值是.48. 若实数,满足条件则的最小值为.49. 设,满足约束条件,则的最大值为,则的值为.50. 若,满足约束条件则的最小值是.51. 如果实数,满足条件则的最大值为.52. 设实数,满足向量,.若,则实数的最大值为.53. 如果实数,满足约束条件那么目标函数的最小值为.54. 设,满足约束条件向量,,且,则的最小值为.55. 设,满足约束条件若目标函数的最大值为,则的最小值为.56. 设为坐标原点,点,点满足则的取值范围为.57. 若实数满足且的最小值为,则.58. 已知,满足约束条件则的最大值.59. 已知点的坐标满足条件那么点到直线的距离的最小值为.60. 已知,满足则的最小值为.61. 已知点的坐标满足条件那么的取值范围为.62. 若变量,满足约束条件则的最大值为.63. 设实数,满足则的最小值为.64. 若,满足约束条件则的取值范围是.65. 已知点,是坐标原点,点的坐标满足,则的取值范围是.66. 已知平面区域夹在两条斜率为的平行直线之间,且这两条平行直线间的最短距离为,若点,且的最小值为,的最大值为,则等于.67. 已知整数,满足不等式,则的最大值是;的最小值是.68. 设实数,满足则动点所形成区域的面积为,的取值范围是.69. 若点满足线性约束条件则的最小值是;的取值范围是.70. 已知,满足约束条件则的最小值为.71. 已知实数,满足则的最小值为.72. 若,满足且的最大值为,则.73. 已知,满足若有最大值,则实数的值为.74. 若直线上存在点满足约束条件则实数的取值范围是.75. 已知变量,满足约束条件则目标函数的取值范围是.76. 已知实数,满足则的最小值为.77. 设,满足则的最大值为.78. 若点位于曲线与所围成的封闭区域内(包含边界),则的最小值为.79. 若实数,满足则的取值范围是,的取值范围是.80. 已知,满足约束条件若的最大值为,则.81. 已知实数,满足则的最大值为.82. 已知实数,满足不等式组则的最大值为.83. 若实数,满足且的最小值为,则.84. 若,满足约束条件则的最大值为.85. 设,满足约束条件则的最大值是.86. 设实数,满足约束条件若目标函数的最大值为,则的最小值为.87. 设,满足约束条件则的最小值是.88. 若,满足条件则的最大值是.89. 设变量,满足约束条件则目标函数的最小值为.90. 已知实数,满足则的取值范围为.91. 不等式组的解集记作,实数,满足如下两个条件:①,;②,.则实数的取值范围为.92. 设为不等式表示的平面区域,直线与区域有公共点,则的取值范围是.93. 若,满足约束条件则的最小值是.94. 已知实数,满足则的最大值是.95. 设,满足不等式组若的最大值为,最小值为,则实数的取值范围为.96. 在等差数列中,已知首项,公差.若,,则的最大值为.97. 设实数,满足约束条件若目标函数的最大值为,则的最小值为.98. 已知实数,满足则的取值范围为.99. 若,满足若的最大值为,则实数.100. 已知正数满足:,,则的取值范围是.答案第一部分1.2.3.4.5.6.7.8.9.10.11.【解析】先作出不等式对应的区域,由图形可知直线过时,目标函数取得最大值,由解得即,.12.13.【解析】画出可行域:由图可知,当直线过点时,取得最小值为.14.15.【解析】不等式组对应的平面区域如图所示.平移直线,当直线经过点时,直线的截距最大,此时最小为.16.17.【解析】由图知最小值在点处取到,最小值为.18.【解析】满足约束条件的可行域如下图所示:令,由可得,直线经过时,取得最大值:;此时的最大值为.19.【解析】由约束条件作出可行域如图,联立解得.的几何意义为可行域内的动点与定点连线的斜率,因为.所以则的取值范围是.20.【解析】,画出可行域如图中阴影部分所示,的最小值为,所以.21.【解析】作出可行域,如图所示,由题意.设,作,易知,过点时有最小值,;过点时有最大值,,所以的取值范围是.22.【解析】圆关于直线对称,所以圆心在直线上,,表示的平面区域如图,表示区域内点与点连线的斜率.,,所以的取值范围是.23.【解析】由变形为,纵截距为,当直线过点时最大,所以.24.【解析】,即为,所以顶点坐标为,设目标函数,则当目标函数经过点,的值最大,即,故的最大值为.25.【解析】的取值范围是可行域中的点与点连线的斜率的取值范围.平面区域如图:所以斜率最小值为,无最大值,当区域中的点的横纵坐标都趋于无穷大时,斜率趋近于.26.27.【解析】由约束条件作出可行域如图,设,可行域内的动点,则..其几何意义为向量与向量夹角的余弦值的倍,所以当与重合时,有最大值为.28.29.【解析】画出约束条件所表示的平面区域,如图中阴影部分所示.由图可知:当直线经过点时最大,由解得,所以的最大值为.30.【解析】作出不等式组表示的平面区域,得到如图的四边形,其中,,,为原点.设为区域内一个动点,则表示点到原点的距离,所以,可得当到原点距离最远时达到最大值,因此,运动点使它与点重合时,达到最大值,.所以最大值31.【解析】变量,满足的约束条件对应的平面区域是以点,和为顶点的三角形区域(包括边界),当经过点时,取得最大值.32.【解析】由约束条件,满足作出可行域如图,联立解得,化目标函数为,由图可知,当直线过时,直线在轴上的截距最大,有最大值为.则.由.令得.所以则展开式的常数项为.33.【解析】因为线性约束条件所决定的可行域为非封闭区域且目标函数为线性的,最值一定在边界点处取得.分别将点,代入目标函数,求得:,,所以最小值为.34.35.36.37.【解析】先作出不等式组对应的区域,若的最大值为,则,直线过定点,则直线与相交于,得,同时也在直线上,即,得.38.【解析】作出所对应可行域(如图),变形目标函数可得,平移直线可得当直线经过点时,直线的截距最小,取最大值,代值计算可得最大值为:.39.【解析】画出表示的平面区域如图所示,由,得,画出,并平移经过时,.40.【解析】不等式组对应的平面区域如图,设,当此直线经过图中时,在轴的截距最小,即最大,所以的最大值为.41.【解析】由约束条件作出可行域如图联立解得,化目标函数为,由图可知,当直线过时,直线在轴上的截距最大,有最大值为.42.【解析】画出的可行域如图阴影区域:由得,目标函数可看做斜率为的动直线,由图数形结合可知:当过点时,最小为.43.【解析】44.【解析】由约束条件作出可行域如图,化目标函数为,由解得,由图可知,当直线过时直线在轴上的截距最大,有最小值,等于.45.【解析】由约束条件作出可行域如图,,联立解得.的几何意义为可行域内的动点与定点连线的斜率,因为,.所以的取值范围是.46.【解析】画出可行域,如图中区域.又直线恒过定点,是直线的斜率,当直线经过点与点这两个边界点时,对应的分别为与,故的范围为.47.【解析】画出约束条件表示的平面区域如图中阴影部分所示,则直线经过点时最小,由得,所以.48.【解析】根据约束条件画出可行域,如图中阴影部分所示,则当,时,取得最小值.49.【解析】由得,作出不等式组对应的平面区域如图(阴影部分):平移直线由图象可知当直线经过点时,直线的截距最大,此时也最大,由,解得,即,将代入目标函数,得.解得.50.【解析】作出不等式组对应的平面区域如图:的几何意义是平面区域内的点到原点的距离,由图象得到直线的距离最小,此时最小值,则的最小值是.51.【解析】,根据约束条件画出可行域,可判断当,时,取得最小值,则的最大值为.52.【解析】因为,所以,即.由已知,画出可行域如下图阴影部分.所以当直线过点时取到最大值.53.【解析】由已知画图如下.当目标函数经过点时,截距取到最大值,也就是取到最小值.54.【解析】由向量,,且,得,根据约束条件画出可行域,设,将最小值转化为轴上的截距的最大值,当直线经过点时,最小,最小值是:.55.【解析】由题,可行域图象如下:结合目标函数中,,可知其经过时,取得最大值,故有,即,又,所以.56.【解析】设.画出可行域,如图所示:当直线过点时,取最大值;当直线过点时,取最小值.所以的取值范围为.57.【解析】画出可行域,当目标函数表示的直线平移到经过点时,取得最小值,然后将坐标代入即可.58.【解析】由约束条件得到可行域如图:直线经过图中点时,直线在轴的截距最小,此时最大,且,所以的最大值为;59.【解析】依题意画图如下.为图中三角形(包括边界)中的点,显然点到直线的距离最小,为.60.【解析】作出不等式组对应的平面区域,如下图中三角形,将直线进行平移,可得当直线经过点时,取得最小值,由解得时,取得最小值,所以.61.【解析】表示的平面区域如图,表示区域内点与点的距离的平方,由图知:最大;到直线的距离的平方最小.由于不取等号,所以不是最小值.62.【解析】由约束条件作出可行域如图,联立解得,化目标函数为,由图可知,当直线过点时,直线在轴上的截距最小,有最大值为.63.【解析】不等式组对应的平面区域如图,设,当此直线经过图中时,在轴的截距最大,即最小,所以的最小值为.64.65.【解析】不等式组所表示的平面区域如图所示:为阴影部分中的点,其中,,所以与平面的夹角的范围为..所以的取值范围是.66.67. ,68. ,69. ,【解析】画出满足条件的平面区域,如图所示:,表示过平面区域的点由得:,当直线过时,最小,最小值与的直线的斜率,显然直线过时,,直线过时,.70.71.【解析】作出不等式组对应的平面区域如图:(阴影部分).由得,平移直线,由图象可知当直线过点时,直线的截距最大,此时最小.由解得即,代入目标函数得,即的最小值为.72.73.74.【解析】由题意,由可求得交点坐标为,要使直线上存在点满足约束条件如图所示.可得,则实数的取值范围.75.76.【解析】如图阴影部分为的可行域,平行移动直线,过点时取得最小值,.77.78.79. ,80.【解析】作出不等式组表示的平面区域如图中阴影部分所示,则,.显然直线过时不能取得最大值,若直线过点时取得最大值,则,解得,此时,目标函数为,作出直线,平移该直线,当直线经过点时,截距最小,此时,的最大值为,满足条件.81.82.【解析】作出不等式组所对应的可行域(如图阴影),变形目标函数可得,由可得平移直线可知,当直线经过点时,取最大值,代值计算可得的最大值为.83.【解析】实数,满足约束条件的可行域如图所示,的最小值为,可知目标函数的最优解过点,由解得,所以,解得.84.【解析】作出不等式组约束条件表示的平面区域,得到如图的及其内部,其中,,,设,将直线进行平移,当经过点时,目标函数达到最大值,.所以最大值85.86.【解析】由得,作出可行域如图:因为,,所以直线的斜率为负,且截距最大时,也最大.平移直线,由图象可知当经过点时,直线的截距最大,此时也最大.由解得即.此时,即,即在直线上,的几何意义为直线上点到原点的距离的平方,则原点到直线的距离,则的最小值为.87.88.89.90.【解析】作出不等式组对应的平面区域如图,的几何意义是区域内的点与原点连线的斜率,由图象知的斜率最小,的斜率最大,由得即,此时斜率,由得即,此时斜率,则的取值范围为.91.【解析】作出不等式组对应的平面区域如图,即,由图象可得,.因为①,,当时,恒成立,当时,过点时斜率最小,即,所以,综上所述的范围为.因为②,,所以直线一定在点的下方或过点,所以,综上所述的范围为.92.93.【解析】,满足约束条件的可行域如图:则的几何意义是可行域的点到坐标原点距离,由图形可知的距离最小,直线的斜率为,所以.94.【解析】实数,满足作图:易知可行域为一个三角形,平移,可知,当直线经过时,目标函数取得最大值,由解得,最大值为.95.【解析】由得,直线是斜率为,轴上的截距为的直线,作出不等式组对应的平面区域如图:则,,因为的最大值为,最小值为,所以直线过点时,取得最大值为,经过点时取得最小值为,若,则,此时满足条件,若,则目标函数斜率,要使目标函数在处取得最小值,在处取得最大值,则目标函数的斜率满足,即,若,则目标函数斜率,要使目标函数在处取得最小值,在处取得最大值,则目标函数的斜率满足,即,综上.96.【解析】由,得,将看作自变量,看作因变量,可得可行域如图所示:由图象知,在取得最大值,此最大值为.97.【解析】根据不等式组,画出平面区域如图所示.所以由平移基准线的位置可知,在处,目标函数,即.又由,,解得:,所以的最小值为.98.99.【解析】提示:如图,画出可行域.分别将、、代入验证知,只有当直线经过点时,符合题意,此时.100.【解析】根据条件得到不等式组和目标函数,利用线性规划求解.由已知,得令则问题转化为:求的取值范围.画出可行域,如图,由于,则的最大值为.设曲线在点处的切线方程为,将原点的坐标代入,解得,从而切点为.而切点在曲线上的点、之间,所以的最小值为.故的取值范围是.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学竞赛训练讲义一、选择题1、若点P (x ,y )在直线x+3y=3上移动,则函数f (x ,y )=yx93+的最小值等于( )(A )51)427(5 (B )71)927(7 (C )71)916(7 (D )31)25(32、满足20073+++=x x y 的正整数数对(x ,y )( ) (A )只有一对 (B )恰有有两对 (C )至少有三对 (D )不存在3、设集合M={-2,0,1},N={1,2,3,4,5},映射f :M →N 使对任意的x ∈M ,都有)()(x xf x f x ++是奇数,则这样的映射f 的个数是( )(A )45 (B )27 (C )15 (D )114、设方程1)19cos()19sin(2007220072=+y x 所表示的曲线是( ) (A )双曲线 (B )焦点在x 轴上的椭圆 (C )焦点在y 轴上的椭圆 (D )以上答案都不正确5、将一个三位数的三个数字顺序颠倒,将所得到的数与原数相加,若和中没有一个数字是偶数,则称这个数为“奇和数”。
那么,所有的三位数中,奇和数有( )个。
(A )100 (B )120 (C )160 (D )2006、函数)(x f y =与)(x g y =有相同的定义域,且对定义域中的任何x ,有1)()(,0)()(=-⋅=+-x g x g x f x f 。
若1)(=x g 的解集是}0|{=x x ,则函数)(1)()(2)(x f x g x f x F +-=是( )A 、奇函数B 、偶函数C 、既是奇函数又是偶函数D 、既不是奇函数又不是偶函数二、填空题7、边长均为整数且成等差数列,周长为60的钝角三角形共有 个。
8、已知三个正整数x ,y ,z 的最小公倍数是300,并且⎩⎨⎧=+-=-+032023222z y x z y x ,则方程组的解(x ,y ,z )= 。
9、已知关于x 的实系数方程0222=+-x x 和0122=++mx x 的四个不同的根在复平面上对应的点共圆,则m 的取值范围是 。
10、设平面上的向量→→→→y x b a ,,,满足关系→→→→→→+=-=y x b y x a 2,,又设→a 与→b 的模为1,且互相垂直,则→x 与→y 的夹角为 。
11、设函数|2)(|)(|,1)(|)(|,|)(12010-=-==x f x f x f x f x x f ,则函数)(2x f 的图象与x 轴所围成图形中的封闭部分的面积是 。
12、若正整数n 恰有4个正约数,则称n 为奇异数,例如6,8,10都是奇异数,那么在27,42,69,111,125,137,343,899,3599,7999这10个正整数中奇异数有 个。
三、解答题13、已知△ABC 的三边长分别为a 、b 、c ,且满足abc=).1)(1)(1(2---c b a(1)是否存在边长均为整数的△ABC ?若存在,求出三边长;若不存在,说明理由。
(2)若a >1,b >1,c >1,求出△ABC 周长的最小值。
14、已知椭圆12222=+by a x 过定点A (1,0),且焦点在x 轴上,椭圆与曲线|y|=x 的交点为B 、C 。
现有以A 为焦点,过点B 、C 且开口向左的抛物线,抛物线的顶点坐标为M (m ,0)。
当椭圆的离心率e 满足1322<<e 时,求实数m 的取值范围。
数学竞赛训练讲义参考答案1.(A )解:5321321321321321321322)31(233333321321533332132133339393)(x x x x x x x x x x x xx xxxy x x f ---------⋅⋅⋅⋅⋅⋅⋅≥+++⋅+⋅=+=+=+=+==5153)427(53415⋅=⋅⋅,等号当且仅当x x 3213321-=⋅,即)2l o g 1(533+=x 时成立,故f (x ,y )的最小值是51)427(5⋅2、(B )解:设2007,322+=+=x b x a ,其中a ,b 均为自然数,则y=a+b ,167322004))((222⨯⨯==+-=-a b a b a b 。
因为b+a 与b-a 有相同的奇偶性,且b+a>b-a,所以⎩⎨⎧=-=+21002a b a b 或⎩⎨⎧=-=+6334a b a b 解得⎩⎨⎧==502500b a 或⎩⎨⎧==170164b a3、(A )解:当x=-2时,x+f (x )+xf (x )=-2-f (-2)为奇数,则f (-2)可取1,3,5,有三种取法;当x=0时,x+f (x )+xf (x )=f (0)为奇数,则f (0)可取1,3,5,有3种取法;当x=1时,x+f (x )+xf (x )=1+2f (1)为奇数,则f (1)可取1,2,3,4,5,有5种取法。
由乘法原理知,共有3×3×5=45个映射。
4、(C ) 解:))(1360(19)1360(19)19(19191003100322007+∈+=+⨯=⨯=N n n于是,19sin )1919360sin()19sin(2007=+⨯=n ,同理 19cos )19cos(2007=。
因为019sin 19cos >>,故应选(C ) 5、(A )解:设三位数是321a a a ,则321a a a +)()(10)(100312231123a a a a a a a a a +++++=。
若31a a +不进位,则和数的十位数必为偶数,不符合题意,所以31a a +=11,13,15,17。
因11=9+2=8+3=7+4=6+5,所以3,1a a 取值有224A 种可能; 因13=9+4=8+5=7+6,所以3,1a a 取值有223A 种可能;因15=9+6=8+7,所以3,1a a 取值有222A 种可能; 因17=9+8,所以3,1a a 取值有22A 种可能;由于22a a +不能进位,所以2a 只能取0,1,2,3,4。
因此,满足条件的数共有:5(224A +223A +222A +22A )=100(个)6、(B )解:由,,12511,1256122111⋅⋅⋅+⨯==+⨯==--a a 猜想:1251+⨯=-n n a 。
由已知递推关系式,易用数学归纳法给予证明(略) 于是,当n>1时,).10(mod 1≡n a故)10(mod 220066200721≡+=+⋅⋅⋅++a a a 因此,应选(B) 7.(20,60,100)解:记方程组中的两个方程为(1),(2),消去x 得 038522=+-z yz y ,即0))(35(=--z y z y 所以035=-z y , (3) 或 0=-z y , (4)由(1)、(3)得x z x y 5,3==,即x :y :z=1:3:5,于是,由已知条件,必有x=20,y=60,z=100; 由(1)(4),得x=-y=-z ,与已知条件矛盾。
8.{m|-1<m<1或m=-3/2}解:易知方程0222=+-x x 的两根为.1,121i x i x -=+=当0442<-=∆m ,即11<<-m 时,方程0122=++mx x 有两个共轭的虚根4,3x x ,且4,3x x 的实部为1≠-m ,这时4321,,,x x x x 在复平面内对应的点构成等腰梯形或矩形,它们共圆。
当0442>-=∆m ,即1-<m 或0>m 时,方程0122=++mx x 有两个不等的实根4,3x x ,则21,x x 对应的点在以4,3x x 对应的点为直径端点的圆上,该圆的方程为0))((243=+--y x x x x ,即0)(434322=++-+x x x x x y x ,将1,24343=-=+x x m x x及21,x x 对应点的坐标(1,±1)代入方程,即得23-=m 。
故m 的取值范围是{m|-1<m<1或m=-3/2} 9、)1010arccos(-π 解:由已知,得32,3-=+=,设→x 与→y 的夹角为θ,则1010||||cos -=⋅⋅=→→→→y x yx θ,所以θ=)1010arccos(-π10、 7解:函数)(2x f y =的图象如图的实线部分所示。
所求的封闭部分的面积为712212)62(21=⨯⨯-⨯+=-∆CDE ABCD S S 梯形 11、xy --=3626 解:当AQ=x 时,设GQ 与面BDE 交于点N ,作NM ⊥BD 于点M ,联结QM 线BC 于点'P ,取点'P 为点P ,知此时y=|MN|最小。
建立如图1的空间直角坐标系,则Q(0足x+y=z ,故可令),,(0000y x y x N +。
由点N 在QG 上,知在(0,1)内存在λ使QN=λQG 。
代入消去λ得.)1(,120000x y x x y x =-=+从而,x xy x x x -+=--=31,3100 于是,).32,31,31(xx x x x N --+--= 而点M 在BD 上,故可令).1,1,(11x x M - 由0=⋅BD MN ,知).31(231xx x --= 于是,.3626)31(26||xx x MN y --=--== 12、20074012解:设i i a x +=22,则i i i x x a -⋅=12,且120071=∑=i i x ,所以)()()(122006212007312007322007212007200721x x x x x x x x x x x x a a a +⋅⋅⋅++⋅⋅⋅+⋅⋅⋅++⋅+⋅⋅⋅++⋅⋅⋅⋅⋅=⋅⋅⋅200620062120062007312006200732200721200720062006200612x x x x x x x x x x x x ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅≥=200720072007401220062=⋅13解:(1)不妨设整数a ≥b ≥c ,显然c ≥2。
若c ≥5,这时.51111≤≤≤c b a 由)1)(1)(1(2---=c b a abc ,可得3)54()11)(11)(11(21≥---=c b a 。
矛盾。
故c 只可能取2,3,4。
当c=2时,)1)(1(--=b a ab ,有.1=+b a 又a ≥b ≥2,故无解。
当c=3时,)1-)(1(43b a ab -=,即12)4)(4(=--b a又a ≥b ≥3,故⎩⎨⎧=-=-14124b a 或⎩⎨⎧=-=-2464b a 或⎩⎨⎧=-=-3444b a 解得⎩⎨⎧==516b a 或⎩⎨⎧==610b a 或⎩⎨⎧==78b a 能构成三角形的只有a=8,b=7,c=3。
