线路逐桩坐标计算原理讲解
线路逐桩坐标法放样曲线..

RTK测量系统一般由以下三部分组成:GPS接收设备、 数据传输设备、软件系统。 1.GPS接收机 RTK测量系统中至少包含两台GPS接收机,其中一台 安置在基准站上,另一台或若干台分别安置在不同 的流动站上。
2.数据传输系统
数据传输设备是由调制解调器和无线电台组成。在 基准站上,利用调制解调器将有关数据进行编码和 调制,然后由无线电发射台发射出去。在流动站上 利用无线电接收台将其接收,并由解调器将数据解 调还原,送入流动站上的GPS接收机中进行数据处 理。
四、 GPS RTK技术在中线放样中的应用
1.根据现有的各种线形中桩坐标计算软件,计 算出公路中线上各桩点的坐标,然后将中桩 点坐标传输到GPS控制手簿中,建立以桩号 为标识符的公路放样文件,个别加桩点的坐 标以手工输入法输入电子手簿。另外现场调 用RTK系统中的实时放样功能,放样出中桩 点的点位。 2.利用RTK系统中自带的道路放样模块进行操 作。
五、应用GPS RTK技术进行线路定测的优点
(1)基准站GPS天线周围无高度超过15°的障碍物阻挡 卫星信号,周围无信号反射物。并要尽量避开交通要道、 过往行人的干扰。 (2)基准站要远离微波塔、通信塔等大型电磁发射源200 米外,要远离高压输电线路、通讯线路50米外。 (3)基准站应选在地势相对高的地方,以利于GPS电台 的作用距离。 (4)基准站连结必须正确,注意电池的正负极。RTK作 业期间,基准站不允许移动或关机又重新启动,若重启 动后必须重新校正。 (5)确认输入正确的控制点三维坐标。
X x
y
Y
三、YHi 点到HZi点之间的中桩点坐标计算
此段为第二缓和曲线段,先算出其参数方程,再进行坐标旋转 平移,其旋转平移公式如下。
X
当曲线为由转角时 ,应以yi=- yi代入
路线中桩坐标计算

路线逐桩坐标计算高等级公路路线设计中,必须计算各点位的逐桩坐标,以作为路线施工放样的依据,也是公路交工和峻工验收时检测中线偏位的依据,故坐标计算能力,已是道路桥梁工程技术专业学生的必备技能。
1、 路线交点偏角、交点间距、曲线要素及主点桩计算如图所示,设路线起点坐标),,(000YJ XJ JD 任一交点i 的坐标为,,...3,2,1),,(n i YJ XJ JD i i i =则相邻两交点之间的坐标增量:1,11,1-----=∆-=∆i i i i i i i i YJD YJD Y XJD XJD X路线交点坐标计算:ii i i i i i i Y Y J D Y J D X X J D X J D ,11,11----∆+=∆+=交点间距:2,12,1,1)()(i i i i i i Y X S ---∆+∆=象限角i,1i i ,1i ,1X Y arctan---∆∆=i i θ象限角与方位角A 之间关系i i i i i i i i i i A Y X ,1,1,1,1,1,0,0-----=>∆>∆θθ位于第一象限,时,i i i i i i i i i i A Y X ,1,1,1,1,1180,0,0-----=>∆<∆θθ-位于第二象限,时, i i i i i i i i i i A Y X ,1,1,1,1,1180,0,0-----+=<∆<∆θθ 位于第三象限,时, i i i i i i i i i i A Y X ,1,1,1,1,1360,0,0-----=<∆>∆θθ-位于第四象限,时,路线偏角i α 等于后方位角减前方位角: 12θθα-=一般情况下,i α为正时,曲线右偏;i α为负时,曲线左偏。
2、 直线段上中桩坐标计算图中,设交点i 的坐标为Jdi(Xji,YJi),交点i 前后相邻直线的方位角分别为A i-1,i 和A i,i+1.则ZH(或ZY)点的坐标: )180sin()180cos(,1,1++=++=--i i i i ZHi i i i i ZHi A T YJD Y A T XJD XHZ(或YZ)点的坐标:1,1,sin cos +++=+=i i i i HZi i i i i HZi A T YJD Y A T XJD X设直线上加桩里程为L ,ZHi 、Hzi 表示曲线i 的起、终点里程,则交点i 前直线上任意点坐标(i ZH L ≤)。
公路逐桩坐标计算程序

2 )sinαAB +(
P 点为顺时针方向时,其方位角为 αAB+900 P 点为逆时针方向时,其方位角为 αAB−900
第一段缓和曲线时:以直缓点(ZH)为起点计算,αAB 为 ZH 点的坐标方位角,L 为 P 点距 ZH 点的距离。 第二段缓和曲线时:以缓直点(HZ)为起点计算,αAB 为 HZ 点坐标方位角的反 方向即 HZ 点方位角加 180 度,L 为 P 点距 HZ 点的距离,加减 90 度刚好与第一 段缓和曲线相反。图如下:
缓和曲线转角公式:β
=
L2
2RLs
(2) 边桩坐标计算公式
左侧
XA=XP+T1cos(αAB± β-900) YA=YP+T1sin(αAB± β-900)
右侧
XB=XP+T2cos(αAB± β+900) YB=YP+T2sin(αAB± β+900)
*第二段缓和曲线计算边桩坐标时, 注意加减 90 度时, 与第一段缓和曲线相反。
2、 缓和曲线段 (1) 中桩坐标计算公式
Xp=X1+(L − Yp=Y1+(L −
L5 40R 2 Ls L5 40R 2 Ls
2 )cosαAB+(
L3 6RLs L3 6RLs
− −
L7 336R 3 ������s 3 L7 336R 3 ������s 3
)sin(αAB±900) )sin(αAB±900)
右侧
XB=XP+T2cos(αAB± β+900) YB=YP+T2sin(αAB± β+900)
第二章
公路导线测量计算
1
公路导线测量为附合导线测量,按路线前进方向测量右角。β
路线中线桩点的坐标计算
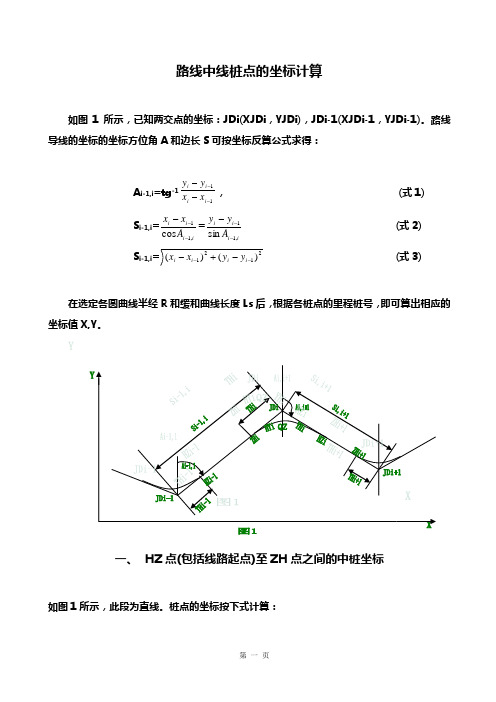
路线中线桩点的坐标计算如图1所示,已知两交点的坐标:JDi(XJDi ,YJDi),JDi-1(XJDi-1,YJDi-1)。
路线导线的坐标的坐标方位角A 和边长S 可按坐标反算公式求得:A i-1,i =tg -111----i i i i x x y y , (式1)S i-1,i =i i i i A x x ,11cos ---=ii i i A y y ,11sin --- (式2)S i-1,i =2121)()(---+-i i i i y y x x (式3)在选定各圆曲线半经R 和缓和曲线长度Ls 后,根据各桩点的里程桩号,即可算出相应的坐标值X,Y 。
一、 HZ 点(包括线路起点)至ZH 点之间的中桩坐标如图1所示,此段为直线。
桩点的坐标按下式计算:X JDi =X HZi-1+D i cosA i-1,iY JDi =Y HZi-1+D i sinA i-1,I (式4)式中A i-1,i 为线路导线JDi-1到JDi 的坐标方位角;Di 为桩点到HZi-1的距离(Si-1,i –THi-1),即桩点里程与HZi-1点里程之差;X HZi-1、Y HZi-1为HZi-1点的坐标,由下式计算:XHZi-1=X JDi-1+T Hi-1cosA i-1,iY HZi-1=X JDi-1+T Hi-1sinA i-1,i (式5)同理计算出直线终点ZHi 点的坐标 X ZHi =X JDi-1+(Si-1,i –THi)cosA i-1,iY ZHi =X JDi-1+(Si-1,i –THi)sinA i-1-I (式6)二、 ZH 点至YH 点之间的中桩坐标如图1所示,此段包括第一缓和曲线及圆曲线,先计算桩点的切线支距法坐标x 、y :1、缓和曲线上桩点的切线支距法坐标x 、y :X=()L -22540SL R L Y=SRL L 63(式7)L 为桩点(测点)到缓和曲线起点ZH 的曲线长,即测长;R 为圆曲线半径;L S 为缓和曲线总长2、圆曲线上桩点的切线支距法坐标x 、y :以ZH 为起点:(带有缓和曲线的圆曲线,)X=Rsin ϕ+q=Rsin )2(1800S L L R +π+2S L –23240RL SY=R(1-cos ϕ)+p=R …1–cos )2(1800S L L R +π‟+RL S 242 (式8) ○1L 为桩点到HY(缓圆点,既圆曲线的起点)的曲线长,仅为圆曲线部分的长度,则: 式中ϕ=α+βo =R L π180⨯+βo =RL π0180⨯+πR L S 21800⨯=)2(1800S L L R +π, ○2若L 为桩点到ZH(直缓点)的曲线长,则:式中ϕ=α-βo =R L π180⨯-βo =RL π0180⨯-πR L S 21800⨯=)2(1800S L L R -π。
线路中桩坐标计算

线路中桩坐标计算
首先是测量过程。
在进行线路中桩坐标计算之前,需要进行一系列的测量工作,包括线路的起点和终点位置,以及其他关键位置的测量。
这些测量通常使用全站仪或其他测量设备进行,可以确定各个位置的水平和垂直坐标。
接下来是计算过程。
在测量数据获取之后,需要进行一些计算以确定各个桩的坐标。
这个过程通常涉及直线或曲线的计算,以及测量数据的加工和处理。
通过使用适当的计算方法和公式,可以确定线路上各个位置的坐标。
最后是标记过程。
一旦确定线路上各个桩的坐标,需要将这些坐标标记在实际的线路上。
这可以通过在地面上设置标志、使用喷漆等方法来实现。
标记过程通常需要注意标记的准确性和可读性,以确保后续的工程施工和测量工作的顺利进行。
线路中桩坐标计算有很多应用。
例如,在公路、铁路和输电线路等工程项目中,需要确定每个桩的位置,以便安装和施工。
此外,线路中桩坐标计算还可以用于监测工程项目的变形和位移,以及进行地理信息系统(GIS)数据的管理和分析。
线路中桩坐标计算的精度要求通常比较高,因为它直接关系到后续工程项目的质量和安全。
因此,在进行线路中桩坐标计算之前,需要仔细规划和准备,确保测量和计算的准确性和可靠性。
此外,使用高质量的测量设备和适当的计算方法也是确保计算结果正确的关键。
总的来说,线路中桩坐标计算是一种重要的工程技术方法,它可以用于确定线路上各个位置的具体坐标。
通过测量、计算和标记的过程,可以确定线路中桩的位置,并为后续工程项目的施工和监测提供准确的参考。
(以上内容仅为参考,具体情况还需根据实际需要进行调整和解决。
公路平面线形要素及逐庄坐标计算原理
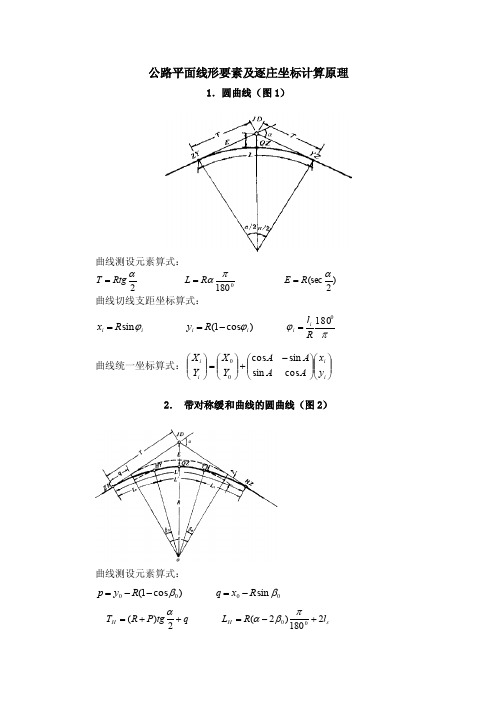
公路平面线形要素及逐庄坐标计算原理1.圆曲线(图1)曲线测设元素算式:2αRtg T = 0180παR L = )2(sec αR E = 曲线切线支距坐标算式:i i R x ϕsin = )cos 1(i i R y ϕ-= πϕ0180R l i i =曲线统一坐标算式:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i i i y x A A A A Y X Y X cos sin sin cos 002. 带对称缓和曲线的圆曲线(图2)曲线测设元素算式:)cos 1(00β--=R y p 00sin βR x q -=q tgP R T H ++=2)(αs H l R L 2180)2(00+-=πβαR p R E H -+=2sec)(αH H H L T D -=2 缓和曲线段切线支距坐标算式:(两段缓和曲线分别以ZH 、HZ 点为坐标原点)6613449225599040345640si s i s i i i l R l l R l l R l l x -+-= 7715551133739676800422403366s i s i s i s i i l R l l R l l R l Rl l y -+-= 缓和曲线段统一坐标算式:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i i y x A AA A Y X Y X cos sin sin cos 00 圆曲线段切线支距坐标算式:q R x i i +=ϕs i n p R y i i +-=)c o s 1(ϕ 00180βπϕ+=R l i i 圆曲线段统一坐标算式:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i i y x A AA A Y X Y X cos sin sin cos 003.带不对称缓和曲线的圆曲线曲线测设元素算式:)cos 1(0101β--=R y p 0101sin βR x q -= )cos 1(0202β--=R y p 0202sin βR x q -=ααsin 2)(21111p p q tgP R T H --++= ααsin 2)(21222p p q tg P R T H -+++= 2100201180)(s s H l l R L ++--=πββα1111q T p R arctg H -+=γ 2222q T p R arctg H -+=γR p R E H -+=11sin γ 1s l 缓和曲线段切线支距坐标算式:(ZH 点为坐标原点) 6161341492125599040345640s i s i s i i i l R l l R l l R l l x -+-=71715515113137139676800422403366s i s i s i s i i l R l l R l l R l Rl l y -+-=2s l 缓和曲线段切线支距坐标算式:(HZ 点为坐标原点) 6261342492225599040345640s i s i s i i i l R l l R l l R l l x -+-= 72715525113237239676800422403366s i s i s i s i i l R l l R l l R l Rl l y -+-= 缓和曲线段统一坐标算式: ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i i y x A AA A Y X Y X cos sin sin cos 00 圆曲线段切线支距坐标算式:(ZH 点为坐标原点)1s i n q R x i i +=ϕ 1)c o s 1(p R y i i +-=ϕ100180βπϕ+=R l i i 圆曲线段统一坐标算式:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛i i j jj jj j i i y x A A A A Y X Y X cos sin sin cos 004.复曲线曲线测设元素算式:21121αtg R T T == 243T D T T JD B JD A -==-2232αtg TR = 02211180)(πααR R L += 1R 曲线切线支距坐标算式:(以ZY 点为坐标原点)i i R x ϕsin 1= )cos 1(1i i R y ϕ-= πϕ01180R l i i =2R 曲线切线支距坐标算式:(以GQ 点为坐标原点) i i R x ϕsin 2= )cos 1(2i i R y ϕ-= πϕ02180R l i i =曲线统一坐标算式:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i i y x A AA A Y X Y X cos sin sin cos 005.带缓和曲线的复曲线曲线测设元素算式:)cos 1(01101β--=R y p j 01101sin βR x q j -=111112)(q tgP R T ++=α 2)(1112αtgP R T +=23T D T JD B JD A -=- 12322p tgT R -=α 1122s s l R R l =)cos 1(02202β--=R y p 02202sin βR x q -=222242)(q tgP R T ++=α210022200111180)(180)(s s H l l R R L ++-+-=πβαπβα1111q T p R arctg H -+=γ 2222q T p R arctg H -+=γR p R E H -+=11sin γ 1s l 缓和曲线段切线支距坐标算式:(ZH 点为坐标原点) 6161134141921215599040345640s i s i s i i i l R l l R l l R l l x -+-= 717115515111313171139676800422403366s i s i s i s i i l R l l R l l R l l R l y -+-= 2s l 缓和曲线段切线支距坐标算式:(HZ 点为坐标原点) 6262134242922225599040345640s i s i s i i i l R l l R l l R l l x -+-= 727215525211323272239676800422403366s i s i s i s i i l R l l R l l R l l R l y -+-= 缓和曲线段统一坐标算式: ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i i y x A AA A Y X Y X cos sin sin cos 00 1R 圆曲线段切线支距坐标算式:(ZH 点为坐标原点)11s i n q R x i i +=ϕ 11)c o s 1(p R y i i +-=ϕ 1001180βπϕ+=R l i i2R 圆曲线段切线支距坐标算式:(HZ 点为坐标原点)22s i n q R x i i +=ϕ 22)c o s 1(p R y i i +-=ϕ 1002180βπϕ+=R l i i圆曲线段统一坐标算式: ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i iy x A AA A Y X Y X cos sin sin cos 006.带过渡缓和曲线的复曲线(卵形线,如图3)曲线测设元素算式:)cos 1(01101β--=R y p j 01101sin βR x q j -=111112)(q tgP R T H ++=α 2)(1112αtgP R T +=23T D T JD B JD A -=- 22322p tgT R -=α)cos 1(02202β--=R y p j 02202sin βR x q j -=222242)(q tgP R T H ++=α12p p p -=∆ 21R R R -=∆R R R p l s ∆⋅⋅⋅∆=124213; 332124R R R p l F ∆∆=; 323124RR R p l M ∆∆= 321000222000111180)(180)(s s s M F H l l l R R L +++--+--=πββαπββα1s l 缓和曲线段切线支距坐标算式:(ZH 点为坐标原点) 6161134141921215599040345640s i s i s i i i l R l l R l l R l l x -+-= 717115515111313171139676800422403366s i s i s i s i i l R l l R l l R l l R l y -+-= 2s l 缓和曲线段切线支距坐标算式:(HZ 点为坐标原点)6262134242922225599040345640s i s i s i i i l R l l R l l R l l x -+-= 727215525211323272239676800422403366s i s i s i s i i l R l l R l l R l l R l y -+-= 缓和曲线段统一坐标算式:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i i y x A AA A Y X Y X cos sin sin cos 00 1R 圆曲线段切线支距坐标算式:(ZH 点为坐标原点)11sin q R x i i +=ϕ 11)cos 1(p R y i i +-=ϕ 1001180βπϕ+=R l i i2R 圆曲线段切线支距坐标算式:(HZ 点为坐标原点)22sin q R x i i +=ϕ 22)cos 1(p R y i i +-=ϕ 1002180βπϕ+=R l i i圆曲线段统一坐标算式: ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛i i j j j jj j i i y x A AA A Y X Y X cos sin sin cos 00 过渡缓和曲线切线支距坐标计算(如图4所示):⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛3327232225''336640M i Mi M i i i i l R l l R l l R l l y x ; ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛''00cos sin sin cos i i i i y x y x y x αααα;图3.带过渡缓和曲线的复曲线坐标计算示意图图4.过渡缓和曲线坐标计算示意图⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛''00cos sin sin cos F F F F y x y x y x αααα; ⎪⎪⎭⎫ ⎝⎛-++=⎪⎪⎭⎫ ⎝⎛0111111cos sin F F F R R p R q y x αα; ⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛3327232225''336640M F M F M F F F F l R l l R l l R l l y x ; F F βαα-=01 ; 0110101180πβαR l y F +=;0110190πβR l s =;22180310111s s y l l R l --=πα ;22180320222s s y l l R l --=πα 过渡缓和曲线的几个特性:(1)缓和曲线两端点的曲率半径分别与两圆曲线的半径相等; (2)较小半径圆曲线对应于较大半径圆曲线内移一定距离; (3)缓和曲线的二分之一分别插入两圆曲线; (4)缓和曲线段中点通过内移距离的中点。
公路逐桩及对应边桩坐标的设计计算方法

位 角的计 算 如图 2 ,当 给定 P点里 程 满 足 Z i< e H() L<
Z i ,HY() Z i ,Y i ,HZ i H() i ,Q () H() ()等 。
( )平 曲线主 点坐标 计 算 2 Z 点 坐标 : H()
丑,
HY() ,则 P点 落 在 J i的 第一 缓 和 曲线 段 i时 O() 上 ,在 坐标 系 中 ,P点局 部坐 标为 :
线 三 种 基 本 线 形 ,不 论 何 种 平 曲 线 组 合 ,均 可
以图 1中所 示 基 本 型 曲线 的 计算 单 元 为 例 ,
在 这 个 计 算 单 元 ,通 常 包 括 第 一 缓 和 曲线 、圆 曲线 、第 二 缓 和 曲线 和 直 线 段 四个 部 分 。计 算 时 .给 出里 程 或 桩 距 , 即可 求 得 逐 桩 坐 标 。 同
时 各种 曲线 主点 需作 为加 桩 按 序 插 入相 应 位 置 ,
归 结 为 这 三 种 平 面 线 形 要 素 的逐 桩 坐 标 和 切 线
方 位 角 的 计 算 。为 简 化 计 算 ,一 般 对 平 曲线 的
各 个 要 素 单 元 建 立 相 对 坐 标 系 ,求 出 在 该 相 对 坐 标 系 下 的 逐 桩 坐 标 ,然 后 归 化 到 统 一 的 坐标
摘Leabharlann 要公路 逐 桩 坐标 是 设 计 单 位 在 设 计 阶 段 要 做 的 工 作 ,逐 桩 对应 边 桩 坐标 的计 算是 施 工 单
位 为 方便 施 工 及 编 制 竣 3 图要 做 的 工 作 。 传 统 的 坐标 计 算 方 法 比较 繁 琐 ,本 文 根 据 实 际 经 验 ,总 结 -
提 出了 简便 实 用 的逐 桩 及 对 应 边 桩 坐标 计 算 方 法 。 关 键 词 公 路 设 计 逐 桩 坐标 边 桩 坐标 计 算 方 法
演示文稿:第二节中线逐桩坐标表计算方法讲解

在缓和曲线的终点处,l=l0,β用β0表示,则上式可写 l0 为:
0
2R
工作任务4
一、回旋型缓和曲线基本公式
2、缓和曲线的参数方程
缓和曲线及其测设
以缓和曲线的起点为坐标原点,过该点的切线为x轴,过原点的半径为y轴,任 取一点P的坐标为(x,y),则微分弧长dl在坐标轴上的投影为: dx dl cos dy dl sin l2 将 cosβ、 sinβ按级数展开,将 代人后积分得: 2 Rl 0 l5 xl 40R2l02
l3 y 6 Rl0
圆曲线段:
x R sin q y R(1 cos ) p
l l0 180 0 R 其测设方法与圆曲线切线支距法相同。
工作任务4
四、带有缓和曲线的平曲线的详细测设
2、偏角法 缓和曲线上各点测设:
y y sin 以弧代弦,则 或 l l
ls2 p 24 R ls ls3 q 2 240 R 2
工作任务4
二、曲线要素计算
2、测设元素的计算
切线长 曲线长
TH ( R p) tan / 2 q
缓和曲线及其测设
LH R ( 2 0 )
180
2l0
其中圆曲线长 L R ( 2 0 ) 外距
道路纵横断面测量
工作任务4
相关知识
缓和曲线及其测设
缓和曲线——连接直线和圆曲线的过渡曲线。缓和曲线的曲率半径是由无穷大逐渐变化为 圆曲线的半径。 在缓和曲线上任一点的曲率半径与该点至起点的曲线长度成反比。 缓和曲线的线型有回旋曲线(亦称辐射螺旋线)、三次抛物线、双纽线等,目前多采用回旋 曲线作为缓和曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线路逐桩坐标计算原理讲解
线路逐桩坐标计算是通过一系列的桩号,计算出线路上每个桩点的坐标,从而得到线路的几何形状。
它是土木工程中常用的计算方法,用于设计和施工过程中的位置确认以及标高确定。
本文将详细讲解线路逐桩坐标计算的原理,以及其应用。
一、线路逐桩坐标计算原理
1.起点坐标确定:首先需要确定线路的起点坐标,可以通过GPS定位或者大地测量等方法来获取。
2.桩号确定:根据设计或者施工要求,确定线路上需要计算坐标的桩号范围。
3.桩点间距确定:根据线路的几何形状参数,确定桩点之间的间距。
通常情况下,间距是固定的,也可以根据实际需要来调整。
4.桩点坐标计算:根据起点坐标、桩号和桩点间距,按照线路的几何形状参数进行计算,得到每个桩点的坐标。
5.标高计算:根据设计或者施工要求,使用地形图、高程测量等方法来确定每个桩点的标高。
二、线路逐桩坐标计算的应用
1.道路和铁路线路设计:在线路的设计过程中,需要准确计算出每个桩点的坐标和标高,以便确定线路的几何形状和纵断面。
2.隧道和桥梁设计:隧道和桥梁的设计需要确定每个桩点的坐标和标高,以便确定结构的形状和尺寸。
3.施工坐标确定:在线路的施工过程中,需要按照设计要求和坐标计
算结果来确定施工点的位置和标高。
4.管道工程设计:管道工程中,需要计算出管道的中心线坐标和标高,以便确定管道的走向和高程。
5.环境影响评价:在环境影响评价过程中,需要对线路的几何形状和
标高进行计算和分析,以评估其对周边环境的影响。
三、线路逐桩坐标计算的优势
1.精确性:线路逐桩坐标计算可以根据实际的桩号和线路的几何形状
参数,精确计算出每个桩点的坐标和标高,保证了设计和施工的准确性。
2.高效性:线路逐桩坐标计算可以通过计算机和专业的软件工具来完成,大大提高了计算的效率,并减少了人为错误的发生。
3.便捷性:线路逐桩坐标计算的原理简单明了,运算过程极为简便,
适用于各类工程中的位置确认和标高确定。
总结:线路逐桩坐标计算是土木工程中常用的计算方法,通过已知的
桩号和起点坐标,计算出线路上每个桩点的坐标和标高。
其应用广泛,包
括道路和铁路线路设计、隧道和桥梁设计、施工坐标确定、管道工程设计
以及环境影响评价等。
线路逐桩坐标计算具有精确性、高效性和便捷性等
优势,是土木工程设计和施工过程中不可或缺的重要工具。
