通过逐桩坐标计算曲线要素
道路勘测设计 第二章道路平面设计3
R
0
]
y P R {1 cos[( LP LS 2) 180 R]}
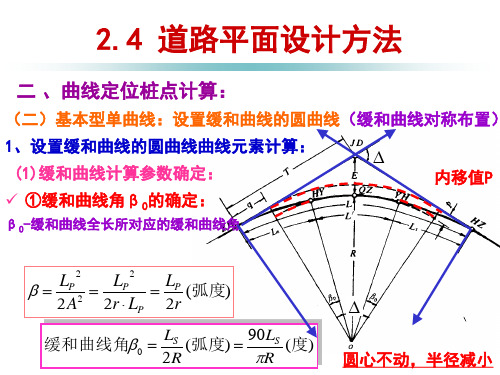
基本形单曲线回旋线要素计算
(二)设置缓和曲线的圆曲线:基本型单曲线 3、加密桩点坐标计算: (1)缓和曲线段内坐标计算: 切线支距法:
LP x LP 2 40 R 2 LS
L y P 6 RLS
2.4 道路平面设计方法
三、平面设计一般规定与基本步骤
道路平面布置设计的步骤:
(1)根据道路的技术等级,根据《标准》JTG B01-2003和《规范》 JTG D20-2006查出设计速度、最小半径、缓和曲线最小长度、直线 段的最大最小长度等主要技术标准的规定值
(2)根据地形、地物条件确定控制因素
(三)复曲线设计:
3、卵形复曲线:
实际工程中,应尽量避免采用这种曲线
(三)复曲线设计:
3、卵形复曲线:
①复中设置缓和曲线的特点: 缓和曲线段两端点的 曲率半径分别与相应 圆的圆曲线半径一致
曲线定位桩点计算
FZ
较小半径圆曲线相对 于大半径圆曲线内移 一段距离
即复曲线中间缓和曲 线段被原公切点中分 缓和曲线段中点(FZ 点)通过内移距离(内 移值之差PF)的中心
Eh B
切线支距法: x q R sin
Lh
y P R (1 cos )
LP LS 180 [
LS 90 LS 0 (弧度) (度) 2R R
θ
LP LS / 2180
R
x q R sin[( LP LS 2) 180 R]
Eh ( R P) sec R(m) 2
Lh ( 2 0 )
复曲线逐桩坐标计算公式的推导及应用

复曲线逐桩坐标计算公式的推导及应用曾过生林桂銮(广东冠粤路桥有限公司广州 510630)摘要: 利用广湛高速一复曲线坐标测设过程中的实例数据,通过数学分析和推导,得出求复曲线逐桩坐标的公式,此推导公式可作为我们道路测设中的一个范例来运用,有很强的指导意义。
关键词: 推导复曲线逐桩坐标公式1.引言现代高等级公路的连接线、互通立交、匝道和城市道路的线型设计很多都采用了复曲线形式。
复曲线在设计中的复核、校正和在施工放样中都要通过一种可行的计算方法才能实现,本文利用广湛高速一复曲线的实例数据,推导得出了求复曲线逐桩坐标的实用计算公式,由于在审图、施工放样过程中,可以用该公式求出复曲线内任意一点的坐标,具有很好的可操作性,方便了核对图纸和现场施工作业,审图和测量精度、质量得到了保证,因此该方法可作为我们道路测设中的一个范例来运用。
2.复曲线逐桩坐标计算公式的推导2.1 实例数据广湛高速公路一复曲线(如图),图纸中已知R1=150米,R2=60米,AB段为复曲线(回旋线组合型式);A点坐标为x=68881.232,y=42197.281;B点坐标为x=68889.467,y=42236.967;θA=66。
37′59.7′′,θB=93。
58′51.6″;A点里程为TZK0+866.402;B点里程为TZK0+907.315,导求其它里程点坐标。
2.2 几个参数的计算设新坐标系为x′o′y′,o′x′为横轴,o′y′为纵轴,A点上的切线与o′x′的夹角为βA,B点上的切线与o′x′的夹角为βB。
因AB段长度为907.315-866.402=40.913(米)根据回旋线方程1/R=CL,C=1/A2(其中L为AO′长度,A为回旋参数),则:1/150=CL (1)1/60=C(L+40.913) (2)求解上述(1)、(2)方程组得:A=63.96,L=27.275。
因βA=L/2R1×180/π=5。
带有缓和曲线圆曲线逐桩坐标计算例题
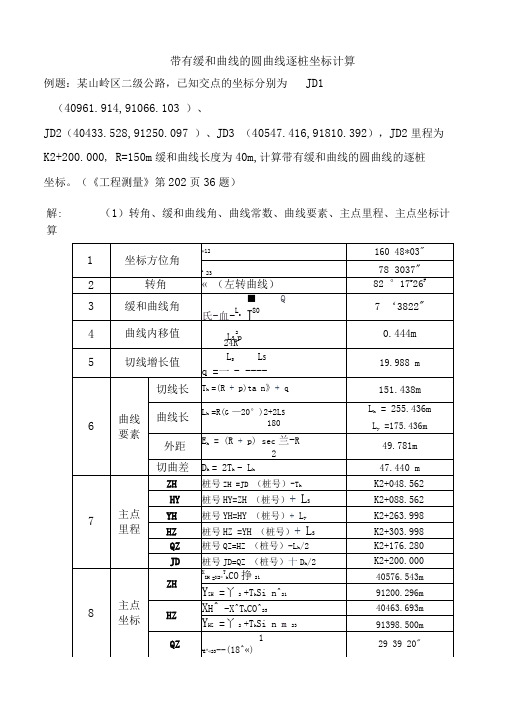
带有缓和曲线的圆曲线逐桩坐标计算
例题:某山岭区二级公路,已知交点的坐标分别为 JD1
(40961.914,91066.103 )、
JD2(40433.528,91250.097 )、JD3 (40547.416,91810.392),JD2里程为 K2+200.000, R=150m 缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩
坐标。
(《工程测量》第202页36题) (1)转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计
解: 算
方法一:偏角法(坐标正算)(2)第一缓和段坐标计算% =73822 :12 = 160 48 03
K2+088.562
(4)第二缓和段坐标计算.0 = 7 38 22
方法二:切线支距法(坐标系转换)
(2)第一缓和段坐标计算
:-12 =160 48 03
X i 二X ZH• xcos〉12 ysi n〉12Y 二Y ZH xsi n〉12 - ycos〉12(本题为左转曲线)
(3)圆曲线段坐标计算
:o =7 3822 p=0.444mq=19.988m
12 =160 48 03 ZH(40576.543,91200.296
X i = X ZH xcos:12 ysin :12Y =Y ZH xsin:12-ycos:12
(4)第二缓和段坐标计算
F =78 30 37
X i =X HZ—xcos:23 - ysi n〉23 Y =Y HZ - xs in 乜—ycos:23 (本题为左转曲线)。
曲线道路坐标计算(Excel)

曲线道路坐标计算§1 曲线要素计算缓和曲线是在不改变直线段方向和保持圆曲线半径不变的条件下,插入到直线段和圆曲线之间的。
其曲率半径ρ从直线的曲率半径∞(无穷大)逐渐变化到圆曲线的半径R ,在缓和曲线上任意一点的曲率半径ρ与缓和曲线的长度l 成反比,以公式表示为:l1∝ρ 或 C l =⋅ρ(C 为常数,称曲线半径变更率)。
当o l l =时,R =ρ,应有o l R l C ⋅=⋅=ρ以上几式是缓和曲线必要的前提条件。
在实际应用中,可采取符合这一前提条件的曲线作为缓和曲线。
常用的有辐射螺旋线及三次抛物线,我国采用辐射螺旋线。
为了在圆曲线与直线之间加入一段缓和曲线o l ,原来的圆曲线需要在垂直于其切线的方向移动一段距离p ,因而圆心就由'O 移到O ,而原来的半径R 保持不变,如图。
由图中可看出,缓和曲线约有一半的长度是靠近原来的直线部分,而另一半是靠近原来的圆曲线部分,原来圆曲线的两端其圆心角o β相对应的那部分圆弧,现在由缓和曲线所代替,因而圆曲线只剩下缓圆点(HY )到圆缓点(YH )这段长度即y l 。
o β为缓和曲线的切线角,即缓圆点或圆缓点切线与直缓点或缓直点切线的交角,亦即圆曲线HY→YH 两端各延长2ol 部分所对应的圆心角。
γ为缓和曲线总偏角,即从直缓点(ZH )测设缓圆点(HY )或从缓直点(HZ )测设圆缓点(YH )的偏角。
q 为切线增量(切垂距),即ZH (或HZ )到从圆心O 向ZH (或HZ )的切线作垂线垂足的距离。
p 为圆曲线内移值,即垂线(从圆心O 向ZH (或HZ )的切线作垂线)长与圆曲线半径R 之差。
§1.1 不等长缓和曲线要素计算:在铁路曲线测设中,线路曲线一般是由相等的两条缓和曲线中间加一个圆曲线构成,有时还会出现由两个不等长的缓和曲线中间加一个圆曲线构成的特殊情况,如图:缓和曲线长分别为1o l 、2o l , 切线长分别为1T 、2T ,曲线偏角(线路转角)为α,圆曲线半径为R ,圆曲线长为y l ,曲线长为L ,外矢距为E ,切曲差为J ,(缓和曲线后)圆曲线内移值分别为1p 、2p ,(缓和曲线)切线增量分别为1q 、2q ,缓和曲线偏角分别为1o β、2o β , 回旋线参数分别为121o Rl A =、222o Rl A =各曲线要素计算公式如下:231112402R ll q o o -=232222402Rll q o o -=341211268824R lR l p o o -=342222268824RlR l p o o -=ααsin )(2)(12111p p tgp R q T -+++=ααsin )(2)(21222p p tgp R q T -+++=Rl R l o o o ππβ111901802=⋅=Rl R l o o o ππβ222901802=⋅=︒--++=180)(2121Rl l L o o o o πββα从以上公式可以看出,当21o o l l =时,就是等长(对称)缓和曲线的情况。
曲线要素坐标计算
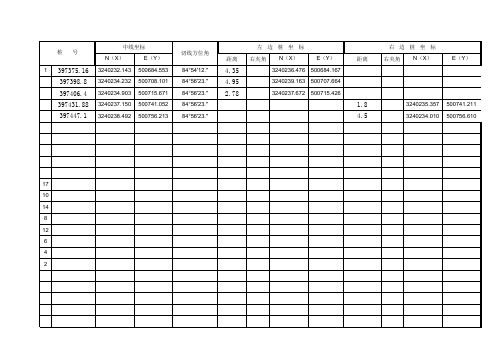
中线坐标
N(X)
E(Y)
切线方位角
距离
左边桩坐标 右夹角 N(X)
E(Y)
距离
右边桩坐标 右夹角 N(X)
E(Y)
1 397375.16 3240232.143 500684.553 84°54′12.″
4.35
3240236.476 500684.167
397398.8 3240234.232 500708.101 84°56′23.″
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号中Leabharlann 坐标切线方位角左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
道路逐桩坐标计算

道路逐桩坐标计算[可读数据库文件(.mdb),或读文本文件(.txt或.dat)附件(点击下载):;;; by yshf;;;道路逐桩坐标计算[可读数据库文件(.mdb),或读文本文件(.txt或.dat)];;;1. 根据“道路设计参数文件”[.txt或.dat(文本文件),;;; 或者.mdb(Access 2000 数据库)] ”中的平面曲线线元参数、;;; 道路纵断面参数成批地计算所求点坐标和相应中线点的设计高程,;;; 并在Auto CAD中绘制出逐桩坐标表。
;;;;;;2. 必须将下载的文件“zbjgchjsb1.fas”存到“E:\\算例文件夹”中,;;; 如存入其它地方,则程序不会进行计算。
;;;;;;3. 运行环境为:Auto CAD 2000以上版,Access 2000以上版数据库。
;;;;;;4. 计算前,先准备数据:;;; (一)平面曲线;;; 平面曲线按线元法将各线元要素录入到Access 2000以上版数据;;; 库的“道路平面曲线线元参数表”中,或者录入到文本文件(.txt或;;; .dat)。
当曲线左偏时,其线元长度输入负值;右偏及直线时其线元;;; 长度输入正值。
;;; 起点切线方位是以度.分分秒秒的形式录入的,例如57°09′13.32″;;; 录入为57.091332。
;;;;;; (二)平曲线曲率半径约定如下:;;; (1).当线元为直线时,其起点、止点的曲率半径为无穷大,以10的45次;;; 代替。
;;; (2).当线元为圆曲线时,无论其起点、止点与什么线元相接,其曲率半;;; 径均等于圆弧的半径。
;;; (3).当线元为完整缓和曲线时,起点与直线相接时,曲率半径为无穷大,;;; 以10的45次代替;与圆曲线相接时,曲率半径等于圆曲线的半径。
止点与直;;; 线相接时,曲率半径为无穷大,以10的45次代替;与圆曲线相接时,曲率半;;; 径等于圆曲线的半径。
线路逐桩坐标计算原理讲解
线路逐桩坐标计算原理讲解线路逐桩坐标计算是通过一系列的桩号,计算出线路上每个桩点的坐标,从而得到线路的几何形状。
它是土木工程中常用的计算方法,用于设计和施工过程中的位置确认以及标高确定。
本文将详细讲解线路逐桩坐标计算的原理,以及其应用。
一、线路逐桩坐标计算原理1.起点坐标确定:首先需要确定线路的起点坐标,可以通过GPS定位或者大地测量等方法来获取。
2.桩号确定:根据设计或者施工要求,确定线路上需要计算坐标的桩号范围。
3.桩点间距确定:根据线路的几何形状参数,确定桩点之间的间距。
通常情况下,间距是固定的,也可以根据实际需要来调整。
4.桩点坐标计算:根据起点坐标、桩号和桩点间距,按照线路的几何形状参数进行计算,得到每个桩点的坐标。
5.标高计算:根据设计或者施工要求,使用地形图、高程测量等方法来确定每个桩点的标高。
二、线路逐桩坐标计算的应用1.道路和铁路线路设计:在线路的设计过程中,需要准确计算出每个桩点的坐标和标高,以便确定线路的几何形状和纵断面。
2.隧道和桥梁设计:隧道和桥梁的设计需要确定每个桩点的坐标和标高,以便确定结构的形状和尺寸。
3.施工坐标确定:在线路的施工过程中,需要按照设计要求和坐标计算结果来确定施工点的位置和标高。
4.管道工程设计:管道工程中,需要计算出管道的中心线坐标和标高,以便确定管道的走向和高程。
5.环境影响评价:在环境影响评价过程中,需要对线路的几何形状和标高进行计算和分析,以评估其对周边环境的影响。
三、线路逐桩坐标计算的优势1.精确性:线路逐桩坐标计算可以根据实际的桩号和线路的几何形状参数,精确计算出每个桩点的坐标和标高,保证了设计和施工的准确性。
2.高效性:线路逐桩坐标计算可以通过计算机和专业的软件工具来完成,大大提高了计算的效率,并减少了人为错误的发生。
3.便捷性:线路逐桩坐标计算的原理简单明了,运算过程极为简便,适用于各类工程中的位置确认和标高确定。
总结:线路逐桩坐标计算是土木工程中常用的计算方法,通过已知的桩号和起点坐标,计算出线路上每个桩点的坐标和标高。
卡西欧5800道路施工逐桩坐标计算程序
卡西欧5800道路施工逐桩坐标计算程序说明:本程序包括了一个完整复合曲线的所有计算,其中需要输入的要素也是对应的完整复合曲线的要素,对不完整的曲线需要将要素进行必要的计算,转换后方能使用该程序,本程序已经包括了边桩几斜交边桩坐标的计算,参见要素说明.本程序是通过4800,4850程序的改编而来,详细程序如下:?D:?A:?R:?C:?N:?E:?F (输入计算要素,见后)C2÷6÷R-C4÷336÷R3+C6÷42240÷R5-R(1-COS(90C÷R÷∏))→XC-C3÷40÷R2+C5÷3456÷R4-RSin(90C÷R÷∏)-C7÷599040÷R6→Y90C÷∏÷R→B(R+X)tan(Abs(A))÷2)+Y→T(Abs(A)-2B) ∏R÷180+2C→LD-T→GG+C→HG+L÷2→IG+L-C→KG+L→MA÷Abs(A) →SF+A÷2+90S→U(R+X)÷cos(A÷2)→VN+V cos(U)→BE+V sin(U)→OLbl 1?Z 输入待求点桩号If Z≤GThenT+G-Z→LF+180→VF→UGoto 2IfEndIf Z≤HThenZ-G→LGoto 7IfEendThenF+A÷2+180+90S+(Z-I)×180S÷R÷∏→LL+90S→UGoto 5IfEendIf Z≤MThenM-Z→LGoto 7IfEndIf Z>MThenZ-M+T→LF+A→VV→UGoto 2IfEndLbl 2“X=”:N+Lcos(V)→X ▲“Y=”:E+Lsin(V)→Y ▲Goto 6Lbl 3“X=”:X+Abs(J)cos(V)→X ▲“Y=”:Y+Abs(J)sin(V)→Y ▲Goto 1Lbl 4“X=”:N+Tcos(J)+Vcos(Y)→X ▲“Y=”:E+Tsin(J)+Vsin(Y)→Y ▲Goto 6Lbl 5“X=”:B+Rcos(L)→X ▲“Y=”:O+Rsin(L)→Y ▲Goto 6Lbl 7L-L5÷(40 R2 C2)+L9÷3456÷R4÷C4-L13÷599040÷(C6R6)→VL3÷(6RC)-L7÷336÷(C3R3)+L11÷42240÷(C5R5)→JStan-1(J÷V) →U√(V2+J2)→VIf Z≤G+CThenGoto 8If Z≤MThenGoto 9IfEendLbl 8F+180→JF+U→YF+90SL2÷(RC∏)→UGoto 4Lbl 9F+A→JJ+180-U→YJ-90SL2÷(RC∏) →UGoto 4Lbl 6“BZ=”:?→J 开始计算边桩坐标,J为斜距,左侧输负,右侧输正90→V 斜交角度,如果不是正交改为:?→VIf J=0 如果不计算边桩坐标J输0直接返回到桩号输入ThenGoto 1IfEndIf J<0ThenU-180+V→VGoto 3IfEndIf J>0ThenU+V→VGoto 3IfEnd要素说明:D—交点桩号,该交点为完整复合曲线的大交点,如果不满足条件需要转换A—转角值,路线右偏输正,左偏输负。
公路逐桩坐标计算
紫色为已知数据,需输入,黑色为计算结果。 序号 ZH HY QZ YH HZ 起点桩号 2 3 4 5 6 7 8 9 桩号 695.181 745.181 769.225 793.269 843.269 700 720 740 760 780 800 820 840 860 左侧坐标X 4872.150 4915.883 4934.840 4952.210 4985.446 4876.523 4894.410 4911.610 4927.744 4942.922 4956.793 4970.079 4983.259 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 左侧坐标Y 71785.194 71809.396 71824.305 71841.036 71878.464 71787.218 71796.176 71806.435 71818.361 71831.473 71845.993 71860.985 71876.035 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 中桩坐标X 4853.963 4898.660 4918.719 4937.354 4972.064 4858.344 4876.442 4894.171 4911.181 4927.258 4942.293 4956.365 4969.876 中桩坐标Y 71776.874 71799.230 71812.468 71827.645 71863.601 71778.880 71787.392 71796.643 71807.152 71819.038 71832.218 71846.427 71861.173 右侧坐标 X 4872.150 4915.883 4934.840 4952.210 4985.446 4876.523 4894.410 4911.610 4927.744 4942.922 4956.793 4970.079 4983.259 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 右侧坐标Y 71785.194 71809.396 71824.305 71841.036 71878.464 71787.218 71796.176 71806.435 71818.361 71831.473 71845.993 71860.985 71876.035 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VA9095775 E 5.543 加桩间距 20 终点桩号 843.024 方位角(弧度) 0.429060108 0.533226774 0.633409074 0.733591374 0.837758041 0.430027676 0.454725813 0.511638785 0.594972118 0.670969772 0.759750807 0.81519851 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041 0.837758041
坐标计算实例(缓和曲线)(1)
缓和曲线逐桩坐标计算(转载)摘要:利用一缓和曲线算例,通过数学分析,推导出缓和曲线逐桩坐标计算公式,此公式可作为道路测设中的范例来运用,有很强的指导意义。
关键词:缓和曲线、公式、逐桩坐标一、引言道路建设中,由于受地形或地质影响,经常需要改变线路方向,为满足行车要求,往往要用曲线把两条直线连接起来。
曲线的构成形式无外乎圆曲线和缓和曲线,本文以河北省沿海高速某曲线段为例推导出缓和曲线的逐桩坐标计算公式,以方便图纸的审核,满足施工放样的需求。
本公式具有良好的操作性,方便施工、提高精度,可作为道路测设中的范例运用。
二、公式推导1 、实例数据河北省沿海高速公路一缓和曲线(如图):AB 段为缓和曲线段,A 为ZH 点,B 为HY 点,R B=800m ;A 点里程为NK0+080 ,切线方位角为θA=100 ° 00 ′ 24.1 ″,坐标为X A=4355189.493,Y A=476976.267 ;B 点里程为NK0+158.125 ,切线方位角为θB=102 ° 48 ′ 15.6 ″,坐标为X B=4355174.669 ,Y B=477052.964 ,推求此曲线段内任意点坐标。
2 、公式推导及实例计算方法一:弦线偏角法1 )公式推导由坐标增量的计算方法我们不难理解,求一点坐标可以根据其所在直线的方位角以及直线上另一点的坐标和距待求点的距离。
所以我们可以利用ZH 点,只要知道待求点距ZH 点的距离(弦长S )和此弦与ZH 点切线方位角的夹角(转角a ),即可求出该点坐标。
根据回旋线方程C=RL ,用B 点数据推导出回旋线参数:C=RL S=800*78.125=62500 (L S为B 点至ZH 点的距离)设待求点距ZH 点距离为L因回旋线上任意点的偏角β0=L2/2RL S, 且转角a=β0/3 ,可得该点转角a 。
(曲线左转时a 代负值)。
根据缓和曲线上的弧弦关系S=L-L5/90R2L S2,可以求出待求点至ZH 点的弦长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通过逐桩坐标表推算曲线要素(CAD篇)摘要:现在从事工程行业的都流行使用AutoCAD进行绘制图形,为了更好的利用这个绘图工具来绘制线路曲线要素,本文将讲解如何通过设计院提供的逐桩坐标表推算未知曲线要素。
关键词:AutoCAD 技巧曲线要素说明:AutoCAD已经成为国际上广为流行的绘图工具。
具有良好的用户界面,通过交互菜单或命令行方式便可以进行各种操作。
它的多文档设计环境,让非计算机专业人员也能很快地学会使用。
在不断实践的过程中更好地掌握它的各种应用和开发技巧,从而不断提高工作效率。
如何提高CAD速率?通常在开始绘图的时候一些人由于对工具命令不熟悉直接使用工具栏等查找命令,这样对制图的效率会大打折扣从而导致绘图的速率缓慢,提高制图的方法需要掌握CAD的快捷命令,孰能生巧的记住,然后择优选用其中的一些常用的绘图命令,把繁琐的长命令转化为简单的命令使用,其次需要多练习绘图的方式与方法才会提高绘图水平。
推算原理:通过逐桩坐标表(含曲线五大桩)然后利用Excel生成展点命令在AutoCAD中进行坐标展点,再通过工具或命令绘制进行查询曲线长、切线长、外失距、交点坐标、交点里程、曲线半径、方位角、转角等。
准备工作:1、逐桩坐标表X、Y(含曲线五大桩)2、AutoCAD绘图软件演示版本为:AutoCAD 2007示例文件:某高速铁路逐桩坐标表演示范围:DK07+586.707~DK12+126.03(由于该交点属于大转角则演示明显)操作流程:坐标展点→绘制半径→绘制切线长→查询方位角→查询转角→查询交点坐标→查询交点里程→查询外失距→绘制缓和曲线。
(请注意逐桩坐标表中所提供的ZH、HY、QZ、YH、HZ等说明)准备操作如下:1、打开“逐桩坐标表”并复制(里程桩号、坐标X、坐标Y)数据到“曲线坐标计算程序VBA 4.6”的“交点法正算”表格中,效果图如下:逐桩坐标表见(本文附件)下载地址附后!2、在“曲线坐标计算程序VBA 4.6”的“交点法正算”表中“点击生成展点”然后点击“复制数据”按钮,再打开AutoCAD在命令行中输入pline按回车键,并在命令行上点击鼠标右键选择“粘贴”,图示如下:3、展点完毕后删除起始点那根长线段(该线段属于展点命令的起始端位置,该线段无用可以直接删除),然后在命令行中输入zoom按回车键再选择E按回车键,图示如下:绘图操作准备:1、基本设置:点击AutoCAD顶部工具栏中的“格式”→“标注样式”(或输入命令d)→“修改”→主单位精度选择“0.000”→角度标注:单位格式选择“度/分/秒”,精度选择“0d’00.00””→确定→设为当前。
2、在命令行中输入:se按回车键,然后弹出草图设置面板→选择“全部清除”→在“圆心”上面打勾→确定。
绘制曲线半径:半径:在圆中,连接圆心和圆上任意一点的线段叫做圆的半径。
先找到HY 7946.707位置,点击顶部工具栏中的“绘图”→“圆弧”→“三点”然后在HY 7946.707圆心位置单击鼠标左键,图示如下:通过同样的方法用工具栏中的“实时平移”工具找到QZ 9856.369和YH 11766.03位置并在所对应的圆心位置单击鼠标左键,然后通过标注查询绘制的曲线半径,图示如下:如图所示,曲线半径R为:4500绘制切线长T:切线长:指的是路线交点至曲线起点或止点的直线距离。
同绘制曲线半径方式找到ZH 7586.707位置然后在命令行中输入画线命令pline按回车键→单击7586.707圆心位置,图示如下:再找到直线段7160位置,这时将鼠标指针放在7160所对应的圆心位置中心(不可单击鼠标),然后在命令行中输入-2500按回车键,图示如下:通过以上方式绘制完毕的图形如下:解疑:为什么选择7160位置和-2500这个数值?1、通过逐桩坐标表了解7152.556~7586.707属于两交点夹直线段,选择7160刚好处于上个交点的HZ缓直位置,也是本段直线的起点位置,画出来的长直线就会更精确(如果选择短距离画直线会出现误差)。
2、选择-2500是因为画的线段需要大于真实切线长,画出来才会使两段切线相交,由于我们并不知道真实切线长是多少,所以我们需要从曲线五大桩进行分析,由于需要画的直线属于ZH 7586.707向大里程方向,但是ZH 7586.707向大里程方向又属于曲线段而无法获取直线方向,那么则需要通过向小里程获取反向正确方向从而找到直线方向输入负数就是为了该线段反方向画线。
当我们不知道真实的切线长时,现在需要通过交点桩号所处于的位置进行判断,交点桩号处于QZ 9856.368曲中点所对应的外失距法线方向,那么用9856.368-7586.707=2269.661由于外失距大所以真实切线长大于曲线段长,而且这个交点属于大转角,那么外失距就会变得更大,之所以还需要加上该值的10%,(9856.368-7586.707)+2269.661*0.1=2496.627(≈2500)。
通过以上同样的方法绘制第二段切线长,用“实时平移”工具找到HZ12126.03在命令行中输入pline并在HZ 12126.03圆心位置单击鼠标左键,再找到15150的位置用鼠标指针指向该圆心位置(不可单击鼠标),在命令行中输入-2500按回车键,绘制完毕后得到了两段切线长所交的位置为交点,通过该点还可以查询本交点坐标,图示如下:查询直线方位角F:方位角:是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角。
通过“实时平移”工具找到直缓起点位置ZH 7586.707,打开状态栏下的“正交”然后在命令行中输入pline按回车键,再点击7586.707圆心位置,将鼠标垂直向上移动并在命令行中输入50按回车键,图示如下:现在对画好的直线进行查询方位角,点击顶部“标注”→“角度”(或输入命令dimangular)→选择刚画好的垂线,再选择切线,标注完毕会显示图示如下:为什么会显示98?6’55.66”而不是正常显示度分秒呢?其实这是标注当时没有设置字体所造成的原因,现在我们选中标注的角度98?6’55.66”在命令行中输入ddedit按回车键→弹出一个文字格式提示框,按Ctrl+A把标注内容全选,再点击更换字体型号,选择“宋体”点击确定即可正常显示,图示如下:查询结果直线方位角F为:98°56ˊ55.66″为什么这样查询?是因为在测量坐标系中正北方向N属于天顶方向正好是向上,所以垂直向上标注则是为了找方位角起始0度,然后顺时针旋转到某方向的夹角则为真方位角。
查询直线方位角F方法之二:我们还可以通过坐标反算原理进行求得两点间的水平距离和直线方位角,找到直线段任意两个点坐标,示例如下:起端DK 07+160.000 3378671.820 453227.191止端DK 07+580.000 3378606.488 453642.079通过CASIO fx-5800P 方位角计算程序进行求解,程序名称“FWJ”,运行程序提示输入如下:Z(X)? 输入3378671.820Z(Y)? 输入453227.191Q(X)? 输入3378606.488Q(Y)? 输入453642.079显示结果:F=98°56ˊ55.77″S=420.000解疑:98°56ˊ55.77″和98°56ˊ55.66″为什么相差0.11″?是因为我们两种方法找到的起止点不同,从而导致方向差异,不过0.11″我们可以完全忽略,因为这么小的差值对坐标计算完全没有影响。
所以直线段两点间距越近差值会越大,直线段两点间距越大差值会越小,提醒大家需要找远距离进行标注方位角才会更精准。
查询转角α:转角:即前段道路交点线的延长线与后段道路交点线的夹角。
转角正负:交点线向右偏转时转角为正,向左偏转时角度为负。
找到绘制完毕的两条切线交叉位置,然后通过查询方位角标注方法对转角进行标注,图示如下:通过以上方法查询转角α结果为:53°12ˊ46″,还可以通过第二切线方位角减去第一切线方位角得到的水平夹角即为转角。
提示:如何判断转角±?根据第二切线的走向判断,由于本交点的第二切线属于顺时针旋转所以转角为正(右),同理逆时针旋转为负(左)。
查询交点坐标:交点坐标位于两切线段交叉位置,通过查询坐标命令即可正确获取。
同样先找到两切线交叉位置,在命令行中输入id按回车键然后在交点的交叉位置单击鼠标左键,即会在命令行中出现坐标数值,图示如下:查询结果:交点坐标X:3378226.7307、交点坐标Y:456053.7207还可以按F2打开AutoCAD文本窗口查看坐标,由于测量坐标系和数学坐标系相反之所以这里的X、Y顺序相反。
查询交点里程JD:方法非常简单,我们只需把刚才画好的切线长度标注好即可获得直缓到交点的长度,找到ZH 7586.707位置用标注工具标注好长度后,用ZH 7586.707加上第一切线长即等于交点里程,标注结果图示如下:直缓7586.707+切线长2434.652=交点里程10021.359查询外失距E:外失距:是曲线的曲中点(QZ)到切线交点的距离。
方法也是运用到标注工具获取,点击顶部“标注”→“对齐”(或输入命令dimaligned)→点击QZ 9856.369圆心位置,下一点单击两切线交点位置确定即可得到外失距E长度,图示如下:标注结果外失距E长为:534.312绘制缓和曲线:缓和曲线:指的是平面线形中,在直线与圆曲线,圆曲线与圆曲线之间设置的曲率连续变化的曲线。
关于上次发表的文章中提到“在AutoCAD中绘制缓和曲线圆曲线的方法”讲述如何绘制缓和曲线,可运用此方法进行绘制!我们先找到ZH 7586.707位置在命令行中输入qxhz当提示:请获取(或输入)曲线起点坐标时请用鼠标左键单击“ZH 7586.707”圆心位置,起点方位角输入:98d56’55.66”(字符为英文状态),曲线长度输入360,起点半径输入0,止点半径输入4500,计算间距输入1,提示曲线绘制完毕,通过同样的方法绘制第二缓和曲线,图示如下:说明:绘制曲线长度360则是HY 7946.707-ZH 7586.707=360数据核对:通过本文讲解的方法与成果现在将查询的数据与设计院提供的原始数据做个对比。
从以上数据对比成果可以看出差值几乎完全符合要求,对比表如下:数据对比表名称设计提供查询结果差值交点坐标X3378226.7313378226.7307-0.3mm交点坐标Y456053.721456053.7207-0.3mm 转角α53.1246153.1246-0.1″曲线半径R450045000切线长T2434.6522434.6520曲线长L4539.3234539.3230结论:利用国际上最为广泛的绘图工具AutoCAD进行查询曲线相关要素,操作方式简便、获取数据轻松,在实际工作中使用相关的计算软件操作不仅仅繁琐,还会让工作效率降低,所以运用此方法可得以提高。
