总结高考数学复习三角函数公式
新高考数学复习三角函数

以实现角α的弦切互化. 2.sin α,cos α的齐次式的应用 1)已知tan α的值,求关于sin α与cos α的齐n次分式的值:分子、分母同除以 cosnα,转化为关于tan α的式子求解. 2)“1”的代换问题:含有sin2α,cos2α及sin α·cos α的整式求值问题,可将所 求式子的分母看作“1”,利用“sin2α+cos2α=1”代换后转化为“切”,然 后求解. 3.同角三角函数基本关系式的常用变形 1)sin2α=1-cos2α,cos2α=1-sin2α.
专题五 三角函数与解三角形
5.1 三角函数的概念、 同角三角函数的基本关系及诱导公式
高考 数学
基础篇
考点 三角函数的概念、同角三角函数的基本关系及诱导公式 一、三角函数的概念 1.象限角
第一象限角 的集合
第二象限角 的集合
第三象限角 的集合
第四象限角 的集合
|
2kπ
π 22kπ,kZ α |2k
0,
2
,tan
2α=
2
cos α sin
α
,则tan
α=
()
A. 15
15
B. 5
5
C. 5
3
D. 15
3
解析
∵tan
2α=
2
cos α sin
α
,且α∈
0,
2
,∴
sin 2α cos 2α
=
2
cos α sin
α
,∴2sin
2α=cos
α
cos 2α+sin αsin 2α,即4sin αcos α=cos(2α-α)=cos α,又cos α≠0,∴4sin α=1,
高考数学三角函数公式总结

高考数学三角函数公式总结三角函数是中学数学的七类基本初等函数之一,具有比较完备的函数性质,又因系统的三角公式及其变换,使三角函数问题丰富多彩、层次分明、变化多端,常与函数、三角、数列、解析几何等结合考查.因此三角函数解答题备受命题者青睐,是历届高考的命题热点,以下是本人为大家精心准备的高考数学三角函数公式的总结,内容仅供参考,欢迎阅读!高考数学三角函数公式总结如下:同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1 sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα sin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosα tan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)三角函数的和差化积公式三角函数的积化和差公式sinα+sinβ=2sin(2/(α+βα-β))·cos(2/(α+βα-β))sinα-sinβ=2cos(2/(α+βα-β))·sin(2/(α+βα-β))cosα+cosβ=2cos(2/(α+βα-β))·cos(2/(α+βα-β))cosα-cosβ=-2sin(2/(α+βα-β))·sin(2/(α+βα-β))sinα ·cosβ=-[sin(α+β)+sin(α-β)]/21cosα ·sinβ=-[sin(α+β)-sin(α-β)]/21cosα ·cosβ=-[cos(α+β)+cos(α-β)]/21sinα ·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α+β)=(tanα+tanβ)/(1-tanα ·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα ·tanβ)sinα=2tan(α/2)/(1+tan2(α/2))cosα=(1-tan2(α/2))/(1+tan2(α/2))tanα=(2tan(α/2))/(1-tan2(α/2))半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2αtan2α=2tanα/(1-tan2α)sin3α=3sinα-4sin3αcos3α=4cos3α-3cosαtan3α=(3tanα-tan3α)/(1-3tan2α);。
超实用高考数学专题复习:第五章三角函数解三角形 第3节两角和与差的正弦余弦和正切公式

答案
3 2
5.(2020·南京、盐城一模)已知锐角α,β满足(tan α-1)·(tan β-1)=2,则α+β的值为
________.
解析 因为(tan α-1)(tan β-1)=2,所以 tan α+tan β=tan αtan β-1,因此 tan(α+β)
=1t-antαan+αttaannββ=-1,因为 α+β∈(0,π),∴α+β=34π.
因为 tanα-54π=15,所以1t+antαan-αttaann5544ππ=15,即t1a+n αta-n α1=15,
解得 tan α=32.
法二
因为 tanα-54π=15,所以 tan α=tanα-54π+54π=t1a-ntαa-nα54π-+54πtatnan5π 454π
=1-15+15×1 1=32.
可以变形为 β
tan α+tan
β=tan(α+β)(1-tan
αtan β),
且对任意角 α,β 都成立.( )
解析 (4)变形可以,但不是对任意的 α,β 都成立,α,β,α+β≠π2+kπ,k∈Z. 答案 (1)√ (2)√ (3)√ (4)×
2.(2019·全国Ⅰ卷)tan 255°=( )
即tan 70°-tan 10°+tan 120°=tan 60°tan 70°tan 10°,
所以 tan
tan 10°tan 70° 70°-tan 10°+tan
120°=tan
t7a0n°t1a0n°t1a0n°t7a0n°60°=
33.
规律方法 (1)两角和、差正切公式的变形 tan α±tan β
70°-2cos
40°
=cos
20°(cos 10°+ sin 20°
高考数学三角函数知识点总结及练习

高考数学三角函数知识点总结及练习集团标准化小组:[VVOPPT-JOPP28-JPPTL98-LOPPNN]三角函数总结及统练一. 教学内容:三角函数总结及统练 (一)基础知识1. 与角α终边相同的角的集合},2{Z k k S ∈+==απβ2. 三角函数的定义(六种)——三角函数是x 、y 、r 三个量的比值3. 三角函数的符号——口诀:一正二弦,三切四余弦。
4. 三角函数线 正弦线MP=αsin 余弦线OM=αcos 正切线AT=αtan5. 同角三角函数的关系平方关系:商数关系:倒数关系:1cot tan =⋅αα 1csc sin =⋅αα 1sec cos =⋅αα 口诀:凑一拆一;切割化弦;化异为同。
6.正弦余弦正切 余切7. 8. 二倍角公式——代换:令αβ=降幂公式⎪⎪⎩⎪⎪⎨⎧+=-=22cos 1cos 22cos 1sin 22αααα半角公式:2cos 12sinαα-±=;2cos 12cos αα+±=;αααcos 1cos 12tan +-±= 函数图10. 函数)sin(ϕω+=x A y 的图象变换 0,0>>ωA函数)sin(ϕω+=x A y 的图象可以通过下列两种方式得到:(1)−−−−−−−−−→−+=−−−−→−=倍横坐标缩短到原来的图象左移ωϕϕ1)sin(sin x y x y(2)−−−−→−=−−−−−−−−−→−=ωϕωω图象左移倍横坐标缩短到原来的)sin(sin 1x y x y(二)数学思想与基本解题方法1. 式子变形原则:凑一拆一;切割化弦;化异为同。
2. 诱导公式原则:奇变偶不变,符号看象限。
3. 估用公式原则:一看角度,二看名称,三看特点。
4. 角的和与差的相对性如:)(βαβ+=-α 角的倍角与半角的相对性 如:422,22αααα==5. 升幂与降幂:升幂角减半,降幂角加倍。
6. 数形结合:心中有图,观图解题。
高中高考数学三角函数公式集合

锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边 / ∠α的邻边cot α=∠α的邻边 / ∠α的对边倍角公式Sin2A=2SinACosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B 降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a)cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tan γ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0。
高三数学三角函数公式

高三数学三角函数公式高三数学三角函数公式大全进入高三,我们必须对自己所学的各科知识的有个全面的把握。
高三数学复习从基础复习到慢慢深入,高三学生学习高中数学,要掌握好高三数学公式。
以下是关于高三数学三角函数公式的相关内容,供大家参考!高三数学三角函数公式大全sinα=∠α的对边/斜边cosα=∠α的邻边/斜边tanα=∠α的对边/∠α的邻边cotα=∠α的邻边/∠α的对边倍角公式Sin2A=2SinA?CosACos2A=CosA?-SinA?=1-2SinA?=2CosA?-1tan2A=(2tanA)/(1-tanA?)(注:SinA?是sinA的平方sin2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a=tana·tan(π/3+a)·tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina三角函数辅助角公式Asinα+Bcosα=(A?+B?)’(1/2)sin(α+t),其中sint=B/(A?+B?)’(1/2)cost=A/(A?+B?)’(1/2)tant=B/AAsinα+Bcosα=(A?+B?)’(1/2)cos(α-t),tant=A/B降幂公式sin?(α)=(1-cos(2α))/2=versin(2α)/2cos?(α)=(1+cos(2α))/2=covers(2α)/2tan?(α)=(1-cos(2α))/(1+cos(2α))三角函数推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos?α1-cos2α=2sin?α1+sinα=(sinα/2+cosα/2)?=2sina(1-sin?a)+(1-2sin?a)sina=3sina-4sin?acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos?a-1)cosa-2(1-sin?a)cosa=4cos?a-3cosasin3a=3sina-4sin?a=4sina(3/4-sin?a)=4sina[(√3/2)?-sin?a]=4sina(sin?60°-sin?a)=4sina(sin60°+sina)(sin60°-sina)=4sina__2sin[(60+a)/2]cos[(60°-a)/2]__2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos?a-3cosa=4cosa(cos?a-3/4)=4cosa[cos?a-(√3/2)?]=4cosa(cos?a-cos?30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa__2cos[(a+30°)/2]cos[(a-30°)/2]__{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)三角函数半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin?(a/2)=(1-cos(a))/2cos?(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角函数三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)三角函数两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)三角函数和差化积sinθ+sinφ=2sin[(θ+φ)/2]cos[(θ-φ)/2]sinθ-sinφ=2cos[(θ+φ)/2]sin[(θ-φ)/2]cosθ+cosφ=2cos[(θ+φ)/2]cos[(θ-φ)/2]cosθ-cosφ=-2sin[(θ+φ)/2]sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)三角函数积化和差sinαsinβ=[cos(α-β)-cos(α+β)]/2cosαcosβ=[cos(α+β)+cos(α-β)]/2sinαcosβ=[sin(α+β)+sin(α-β)]/2cosαsinβ=[sin(α+β)-sin(α-β)]/2三角函数诱导公式sin(-α)=-sinαcos(-α)=cosαtan(—a)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαsin(π/2+α)=cosαcos(π/2+α)=-sinαsin(π-α)=sinαcos(π-α)=-cosαsin(π+α)=-sinαcos(π+α)=-cosαtanA=sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan’(α/2)]cosα=[1-tan’(α/2)]/1+tan’(α/2)]tanα=2tan(α/2)/[1-tan’(α/2)]其它公式(1)(sinα)?+(cosα)?=1(2)1+(tanα)?=(secα)?(3)1+(cotα)?=(cscα)?证明下面两式,只需将一式,左右同除(sinα)?,第二个除(cosα)?即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)?+(cosB)?+(cosC)?=1-2cosAcosBcosC(8)(sinA)?+(sinB)?+(sinC)?=2+2cosAcosBcosC(9)si nα+sin(α+2π/n)+sin(α+2π__2/n)+sin(α+2π__3/n)+……+sin[α+2π__(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π__2/n)+cos(α+2π__3/n)+……+cos[α+2π__(n-1)/n]=0以及sin?(α)+sin?(α-2π/3)+sin?(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0高三数学学习技巧一、用好课本:侧重以下几个方面1.对数学概念重新认识,深刻理解其内涵与外延,区分容易混淆的概念。
高考数学总复习 第四章 三角函数 第22讲 两角和与差的正弦、余弦和正切公式、二倍角公式课件 理

第九页,共四十四页。
考点 1 三角函数公式的基本应用 例1(1)若 α∈π2 ,π,tanα+π4 =17,则 sin α 等于( ) A.35 B.45 C. -35 D. -45
第十页,共四十四页。
【解析】(1)∵tanα+π4 =t1a-n taαn+α1=17,
∴tan
α=-34=csions
α α,
∴cos α=-43sin α. 又∵sin2α+cos2α=1,
∴sin2α=295. 又∵α∈π2 ,π,∴sin α=35.
【答案】A
第十一页,共四十四页。
(2)
计
算
sin
47°-sin 17°cos 30° cos 17°
的
值
等
于
__________.
cos 2α=2cos2α-1=35,
∴f(α)=12sin
2α+
3 2 cos
2α=3
3-4 10 .
第十九页,共四十四页。
1. 对于任意一个三角公式,应从“顺、逆”两个 方面去认识,尽力熟悉它的变式,以及能灵活运用.
2. 公式应用要讲究“灵活、恰当”,关键是观察、 分析题设“已知”和“未知”中角之间的“和、差、 倍、半”以及“互补、互余”关系,同时分析归纳题 设中三角函数式的结构特征,探究化简变换目标.
第二十五页,共四十四页。
2. 已知 α∈π2 ,π,cos α=-45,则 tanα+π4
=( )
1 A.7
B. 7
C. -17
D. -7
【解析】∵α∈π2 ,π,cos α=-45,∴sin α=35,
∴tan α=-34,∴tanα+π4 =t1a-n taαn+α1=-1+ 34+341=17.
2023年高考数学一轮复习讲义——同角三角函数基本关系式及诱导公式
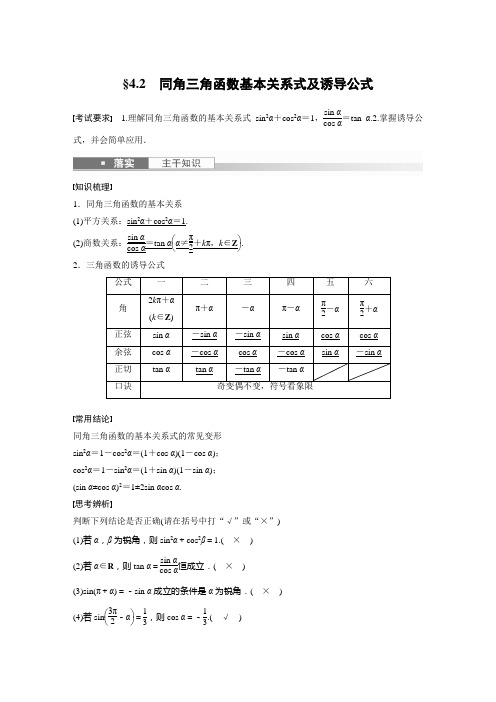
§4.2 同角三角函数基本关系式及诱导公式考试要求 1.理解同角三角函数的基本关系式sin 2α+cos 2α=1,sin αcos α=tan α.2.掌握诱导公式,并会简单应用.知识梳理1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1.(2)商数关系:sin αcos α=tan α⎝⎛⎭⎫α≠π2+k π,k ∈Z . 2.三角函数的诱导公式公式 一 二 三 四 五 六 角 2k π+α (k ∈Z ) π+α -α π-α π2-α π2+α 正弦 sin α -sin α -sin α sin α cos α cos α 余弦 cos α -cos α cos α -cos α sin α -sin α 正切 tan αtan α-tan α-tan α口诀奇变偶不变,符号看象限常用结论同角三角函数的基本关系式的常见变形 sin 2α=1-cos 2α=(1+cos α)(1-cos α); cos 2α=1-sin 2α=(1+sin α)(1-sin α); (sin α±cos α)2=1±2sin αcos α. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.( × ) (2)若α∈R ,则tan α=sin αcos α恒成立.( × )(3)sin(π+α)=-sin α成立的条件是α为锐角.( × ) (4)若sin ⎝⎛⎭⎫3π2-α=13,则cos α=-13.( √ )教材改编题1.已知α是第二象限角,sin α=55,则cos α的值为 . 答案 -255解析 ∵sin α=55,α是第二象限角, ∴cos α=-1-sin 2α=-255.2.已知sin α-2cos α3sin α+5cos α=-5,那么tan α的值为 .答案 -2316解析 由sin α-2cos α3sin α+5cos α=-5,知cos α≠0,等式左边分子、分母同时除以cos α,可得tan α-23tan α+5=-5,解得tan α=-2316.3.化简cos ⎝⎛⎭⎫α-π2sin ⎝⎛⎭⎫5π2+α·sin(α-π)·cos(2π-α)的结果为 . 答案 -sin 2α解析 原式=sin αcos α·(-sin α)·cos α=-sin 2α.题型一 同角三角函数基本关系例1 (1)已知cos α=-513,则13sin α+5tan α= .答案 0解析 ∵cos α=-513<0且cos α≠-1,∴α是第二或第三象限角. ①若α是第二象限角,则sin α=1-cos 2α=1-⎝⎛⎭⎫-5132=1213, ∴tan α=sin αcos α=1213-513=-125.此时13sin α+5tan α=13×1213+5×⎝⎛⎭⎫-125=0. ②若α是第三象限角, 则sin α=-1-cos 2α=-1-⎝⎛⎭⎫-5132 =-1213,∴tan α=sin αcos α=-1213-513=125,此时,13sin α+5tan α=13×⎝⎛⎭⎫-1213+5×125=0. 综上,13sin α+5tan α=0.(2)已知tan α=12,则sin α-3cos αsin α+cos α= ;sin 2α+sin αcos α+2= .答案 -53 135解析 已知tan α=12,所以sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.sin 2α+sin αcos α+2 =sin 2α+sin αcos αsin 2α+cos 2α+2=tan 2α+tan αtan 2α+1+2=⎝⎛⎭⎫122+12⎝⎛⎭⎫122+1+2=135.(3)已知sin θ+cos θ=713,θ∈(0,π),则tan θ= .答案 -125解析 由sin θ+cos θ=713,得sin θcos θ=-60169,因为θ∈(0,π),所以sin θ>0,cos θ<0, 所以sin θ-cos θ=1-2sin θcos θ=1713, 联立⎩⎨⎧sin θ+cos θ=713,sin θ-cos θ=1713,解得⎩⎨⎧sin θ=1213,cos θ=-513,所以tan θ=-125.教师备选1.(2022·锦州联考)已知sin α+3cos α3cos α-sin α=5,则cos 2α+12sin 2α等于( )A.35 B .-35C .-3D .3答案 A解析 由sin α+3cos α3cos α-sin α=5,得tan α+33-tan α=5,可得tan α=2,则cos 2α+12sin 2α=cos 2α+sin αcos α=cos 2α+sin αcos αcos 2α+sin 2α=1+tan α1+tan 2α=35. 2.若α∈(0,π),sin(π-α)+cos α=23,则sin α-cos α的值为( ) A.23B .-23 C.43 D .-43答案 C解析 由诱导公式得sin(π-α)+cos α=sin α+cos α=23, 所以(sin α+cos α)2=1+2sin αcos α=29,则2sin αcos α=-79<0,因为α∈(0,π),所以sin α>0, 所以cos α<0,所以sin α-cos α>0, 因为(sin α-cos α)2=1-2sin αcos α=169,所以sin α-cos α=43.思维升华 (1)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.(2)注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α. 跟踪训练1 (1)(2021·新高考全国Ⅰ)若tan θ=-2,则sin θ(1+sin 2θ)sin θ+cos θ等于( )A .-65B .-25 C.25 D.65答案 C解析 方法一 因为tan θ=-2, 所以角θ的终边在第二或第四象限,所以⎩⎨⎧sin θ=25,cos θ=-15或⎩⎨⎧sin θ=-25,cos θ=15,所以sin θ(1+sin 2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θ =45-25=25.方法二 (弦化切法)因为tan θ=-2, 所以sin θ(1+sin 2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θsin 2θ+cos 2θ=tan 2θ+tan θ1+tan 2θ=4-21+4=25.(2)已知α是三角形的内角,且tan α=-13,则sin α+cos α的值为 .答案 -105解析 由tan α=-13,得sin α=-13cos α,将其代入sin 2α+cos 2α=1,得109cos 2α=1,所以cos 2α=910,易知cos α<0,所以cos α=-31010,sin α=1010,故sin α+cos α=-105. 题型二 诱导公式例2 (1)已知sin ⎝⎛⎭⎫α-π4=13,则cos ⎝⎛⎭⎫π4+α的值为( ) A.223B .-223C.13 D .-13答案 D解析 cos ⎝⎛⎭⎫π4+α=cos ⎣⎡⎦⎤π2+⎝⎛⎭⎫α-π4 =-sin ⎝⎛⎭⎫α-π4=-13.延伸探究 本例(1)改为已知θ是第二象限角,且sin ⎝⎛⎭⎫θ+π4=45,则tan ⎝⎛⎭⎫θ-π4= . 答案 34解析 ∵θ是第二象限角,且sin ⎝⎛⎭⎫θ+π4=45, ∴θ+π4为第二象限角,∴cos ⎝⎛⎭⎫θ+π4=-35, ∴tan ⎝⎛⎭⎫θ-π4=sin ⎝⎛⎭⎫θ-π4cos ⎝⎛⎭⎫θ-π4 =sin ⎣⎡⎦⎤⎝⎛⎭⎫θ+π4-π2cos ⎣⎡⎦⎤⎝⎛⎭⎫θ+π4-π2 =-cos ⎝⎛⎭⎫θ+π4sin ⎝⎛⎭⎫θ+π4=-⎝⎛⎭⎫-3545=34. (2)tan (π-α)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-α-π)sin (-π-α)的值为( )A .-2B .-1C .1D .2 答案 B解析 原式=-tan α·cos α·(-cos α)cos (π+α)·[-sin (π+α)]=tan α·cos 2α-cos α·sin α =-sin αcos α·cos αsin α=-1.教师备选1.已知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P ,且角α的始边与x 轴的正半轴重合,终边过点P ,则cos ⎝⎛⎭⎫11π2-αsin ⎝⎛⎭⎫9π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin (-π-α)等于( )A.23 B .-23C.32 D .-32答案 B解析 易知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P (2,3), 故tan α=32,则cos ⎝⎛⎭⎫11π2-αsin ⎝⎛⎭⎫9π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin (-π-α)=cos ⎝⎛⎭⎫3π2-αsin ⎝⎛⎭⎫π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin α=-sin αcos α+2sin αcos α-sin αsin α=-cos αsin α=-1tan α=-23.2.若sin x =3sin ⎝⎛⎭⎫x -π2,则cos x ·cos ⎝⎛⎭⎫x +π2等于( ) A.310 B .-310C.34 D .-34答案 A解析 易知sin x =3sin ⎝⎛⎭⎫x -π2=-3cos x , 所以tan x =-3, 所以cos x cos ⎝⎛⎭⎫x +π2 =-sin x cos x =-sin x cos xsin 2x +cos 2xtan 2x +110思维升华 (1)诱导公式的两个应用①求值:负化正,大化小,化到锐角为终了; ②化简:统一角,统一名,同角名少为终了. (2)诱导公式的应用步骤任意负角的三角函数――――――→利用诱导公式三或一任意正角的三角函数――――――→利用诱导公式一0~2π内的角的三角函数――――――→利用诱导公式二或四或五或六锐角三角函数. 跟踪训练2 (1)已知cos(75°+α)=13,求cos(105°-α)+sin(15°-α)= .答案 0解析 因为(105°-α)+(75°+α)=180°, (15°-α)+(α+75°)=90°,所以cos(105°-α)=cos[180°-(75°+α)] =-cos(75°+α)=-13,sin(15°-α)=sin[90°-(α+75°)] =cos(75°+α)=13.所以cos(105°-α)+sin(15°-α)=-13+13=0.(2)(2022·盐城南阳中学月考)设tan(5π+α)=2,则sin (-3π+α)+cos (α-π)cos ⎝⎛⎭⎫α-112π+sin ⎝⎛⎭⎫9π2+α= .答案 3解析 由已知tan(5π+α)=tan α=2, sin (-3π+α)+cos (α-π)cos ⎝⎛⎭⎫α-112π+sin ⎝⎛⎭⎫9π2+α=sin (π+α)+cos (π-α)cos ⎝⎛⎭⎫α+π2+sin ⎝⎛⎭⎫π2+α-sin α+cos α=sin α+cos αsin α-cos α=tan α+1tan α-1=3. 题型三 同角三角函数基本关系式和诱导公式的综合应用 例3 已知f (α)=sin (α-3π)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-π-α)sin (-π-α).(1)化简f (α);(2)若α=-31π3,求f (α)的值;(3)若cos ⎝⎛⎭⎫-α-π2=15,α∈⎣⎡⎦⎤π,3π2,求f (α)的值. 解 (1)f (α)=sin (α-3π)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-π-α)sin (-π-α)=-sin α×cos α×(-cos α)-cos α×sin α=-cos α. (2)若α=-31π3,则f (α)=-cos ⎝⎛⎭⎫-31π3=-cos π3=-12. (3)由cos ⎝⎛⎭⎫-α-π2=15, 可得sin α=-15,因为α∈⎣⎡⎦⎤π,3π2, 所以cos α=-265,所以f (α)=-cos α=265.教师备选设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos ⎝⎛⎭⎫3π2+α-sin 2⎝⎛⎭⎫π2+α(1+2sin α≠0). (1)化简f (α);(2)若α=-23π6,求f (α)的值. 解 (1)f (α)=(-2sin α)·(-cos α)-(-cos α)1+sin 2α+sin α-cos 2α=2sin αcos α+cos α2sin 2α+sin α=cos α(2sin α+1)sin α(2sin α+1)=cos αsin α=1tan α. (2)当α=-23π6时, f (α)=f ⎝⎛⎭⎫-23π6=1tan ⎝⎛⎭⎫-23π6 =1tan ⎝⎛⎭⎫-4π+π6 =1tan π6=133= 3. 思维升华 (1)利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.(2)注意角的范围对三角函数符号的影响.跟踪训练3 (1)(2022·聊城模拟)已知α为锐角,且2tan(π-α)-3cos ⎝⎛⎭⎫π2+β+5=0,tan(π+α)+6sin(π+β)-1=0,则sin α的值是( )A.355B.377C.31010D.13答案 C解析 由已知得⎩⎪⎨⎪⎧3sin β-2tan α+5=0,tan α-6sin β-1=0. 消去sin β,得tan α=3,∴sin α=3cos α,代入sin 2α+cos 2α=1,化简得sin 2α=910,则sin α=31010(α为锐角). (2)已知-π<x <0,sin(π+x )-cos x =-15,则sin 2x +2sin 2x 1-tan x= . 答案 -24175解析 由已知,得sin x +cos x =15, 两边平方得sin 2x +2sin x cos x +cos 2x =125, 整理得2sin x cos x =-2425. ∴(sin x -cos x )2=1-2sin x cos x =4925, 由-π<x <0知,sin x <0,又sin x cos x =-1225<0, ∴cos x >0,∴sin x -cos x <0,故sin x -cos x =-75. ∴sin 2x +2sin 2x 1-tan x =2sin x (cos x +sin x )1-sin x cos x=2sin x cos x (cos x +sin x )cos x -sin x=-2425×1575=-24175.课时精练1.cos ⎝⎛⎭⎫-19π3等于( ) A .-32 B .-12 C.12D.32 答案 C解析 cos ⎝⎛⎭⎫-19π3=cos 19π3=cos ⎝⎛⎭⎫6π+π3=cos π3=12. 2.若cos 165°=a ,则tan 195°等于( )A.1-a 2B.1-a 2aC .-1-a 2aD .-a 1-a 2 答案 C解析 若cos 165°=a ,则cos 15°=cos(180°-165°)=-cos 165°=-a ,sin 15°=1-a 2,所以tan 195°=tan(180°+15°)=tan 15°=sin 15°cos 15°=-1-a 2a. 3.若cos ⎝⎛⎭⎫α-π5=513,则sin ⎝⎛⎭⎫7π10-α等于( ) A .-513B .-1213 C.1213 D.513答案 D解析 因为7π10-α+⎝⎛⎭⎫α-π5=π2,所以7π10-α=π2-⎝⎛⎭⎫α-π5,所以sin ⎝⎛⎭⎫7π10-α=cos ⎝⎛⎭⎫α-π5=513.4.(2022·天津西青区模拟)已知sin α+cos α=-2,则tan α+1tan α等于() A .2 B.12 C .-2 D .-12答案 A解析 由已知得1+2sin αcos α=2,∴sin αcos α=12,∴tan α+1tan α=sin αcos α+cos αsin α=sin 2α+cos 2αsin αcos α=112=2.5.(多选)在△ABC 中,下列结论正确的是( )A .sin(A +B )=sin CB .sin B +C 2=cos A 2C .tan(A +B )=-tan C ⎝⎛⎭⎫C ≠π2D .cos(A +B )=cos C答案 ABC解析 在△ABC 中,有A +B +C =π,则sin(A +B )=sin(π-C )=sin C ,A 正确.sin B +C 2=sin ⎝⎛⎭⎫π2-A 2=cos A 2,B 正确.tan(A +B )=tan(π-C )=-tan C ⎝⎛⎭⎫C ≠π2,C 正确.cos(A +B )=cos(π-C )=-cos C ,D 错误.6.(多选)已知α∈(0,π),且sin α+cos α=15,则( ) A.π2<α<π B .sin αcos α=-1225C .cos α-sin α=75D .cos α-sin α=-75答案 ABD解析 ∵sin α+cos α=15, 等式两边平方得(sin α+cos α)2=1+2sin αcos α=125, 解得sin αcos α=-1225,故B 正确; ∵α∈(0,π),sin αcos α=-1225<0, ∴α∈⎝⎛⎭⎫π2,π,故A 正确;cos α-sin α<0,且(cos α-sin α)2=1-2sin αcos α=1-2×⎝⎛⎭⎫-1225=4925, 解得cos α-sin α=-75,故D 正确. 7.cos 1°+cos 2°+cos 3°+…+cos 177°+cos 178°+cos 179°= .答案 0解析 因为cos(180°-α)=-cos α,于是得cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°+cos 91°+…+cos 177°+cos 178°+cos 179° =cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°-cos 89°-…-cos 3°-cos 2°-cos 1° =cos 90°=0.8.设f (θ)=2cos 2θ+sin 2(2π-θ)+sin ⎝⎛⎭⎫π2+θ-32+2cos 2(π+θ)+cos (-θ),则f ⎝⎛⎭⎫17π3= . 答案 -512解析 ∵f (θ)=2cos 2θ+sin 2θ+cos θ-32+2cos 2θ+cos θ=cos 2θ+cos θ-22cos 2θ+cos θ+2,又cos 17π3=cos ⎝⎛⎭⎫6π-π3=cos π3=12,∴f ⎝⎛⎭⎫17π3=14+12-212+12+2=-512.9.(1)已知cos α是方程3x 2-x -2=0的根,且α是第三象限角,求sin ⎝⎛⎭⎫-α+3π2cos ⎝⎛⎭⎫3π2+αtan 2(π-α)cos ⎝⎛⎭⎫π2+αsin ⎝⎛⎭⎫π2-α的值;(2)已知sin x +cos x =-713(0<x <π),求cos x -2sin x 的值.解 (1)因为方程3x 2-x -2=0的根为x 1=1,x 2=-23,又α是第三象限角,所以cos α=-23,所以sin α=-53,tan α=52.所以原式=-cos αsin αtan 2α-sin αcos α=tan 2α=54.(2)∵sin x +cos x =-713(0<x <π),∴cos x <0,sin x >0,即sin x -cos x >0,把sin x +cos x =-713,两边平方得1+2sin x cos x =49169, 即2sin x cos x =-120169, ∴(sin x -cos x )2=1-2sin x cos x =289169, 即sin x -cos x =1713, 联立⎩⎨⎧ sin x +cos x =-713,sin x -cos x =1713,解得sin x =513,cos x =-1213, ∴cos x -2sin x =-2213. 10.(2022·衡水模拟)已知角α的终边经过点P (3m ,-6m )(m ≠0).(1)求sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2的值; (2)若α是第二象限角,求sin 2⎝⎛⎭⎫α+3π2+sin(π-α)cos α-cos ⎝⎛⎭⎫π2+α的值. 解 (1)∵m ≠0,∴cos α≠0,即sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2 =-sin α-cos αcos α+2sin α=-tan α-11+2tan α. 又∵角α的终边经过点P (3m ,-6m )(m ≠0),∴tan α=-6m 3m=-2, 故sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2=-tan α-11+2tan α =2-11+2×(-2)=-13. (2)∵α是第二象限角,∴m <0,则sin α=-6m (3m )2+(-6m )2 =-6m 35|m | =255, cos α=3m(3m )2+(-6m )2 =3m 35|m | =-55, ∴sin 2⎝⎛⎭⎫α+3π2+sin(π-α)cos α-cos ⎝⎛⎭⎫π2+α =cos 2α+sin αcos α+sin α=⎝⎛⎭⎫-552+255×⎝⎛⎭⎫-55+255=-1+255.11.(多选)已知角α满足sin α·cos α≠0,则表达式sin (α+k π)sin α+cos (α+k π)cos α(k ∈Z )的取值可能为( )A .-2B .-1或1C .2D .-2或2或0答案 AC解析 当k 为奇数时,原式=-sin αsin α+-cos αcos α=(-1)+(-1)=-2;当k 为偶数时,原式=sin αsin α+cos αcos α=1+1=2. ∴原表达式的取值可能为-2或2.12.(2022·河北六校联考)若sin α是方程5x 2-7x -6=0的根,则sin ⎝⎛⎭⎫-α-3π2sin ⎝⎛⎭⎫3π2-αtan 2(2π-α)cos ⎝⎛⎭⎫π2-αcos ⎝⎛⎭⎫π2+αsin (π+α)等于( )A.35B.53C.45D.54答案 B解析 方程5x 2-7x -6=0的两根为x 1=-35,x 2=2,则sin α=-35. 原式=cos α(-cos α)tan 2αsin α(-sin α)(-sin α)=-1sin α=53. 13.曲线y =e x +x 2-23x 在x =0处的切线的倾斜角为α,则sin ⎝⎛⎭⎫2α+π2= . 答案 45解析 由题意得y ′=f ′(x )=e x +2x -23, 所以f ′(0)=e 0-23=13, 所以tan α=13, 所以α∈⎝⎛⎭⎫0,π2, 所以cos α=310, 所以sin ⎝⎛⎭⎫2α+π2 =cos 2α=2cos 2α-1=2×910-1=45. 14.函数y =log a (x -3)+2(a >0且a ≠1)的图象过定点Q ,且角α的终边也过点Q ,则3sin 2α+2sin αcos α= .答案 75解析 由题意可知点Q (4,2),所以tan α=12, 所以3sin 2α+2sin αcos α=3sin 2α+2sin αcos αsin 2α+cos 2α =3tan 2α+2tan α1+tan 2α=3×14+2×121+14=75.15.(多选)已知f (α)=2sin αcos α-2sin α+cos α+1⎝⎛⎭⎫0≤α≤π2,则下列说法正确的是() A .f (α)的最小值为- 2B .f (α)的最小值为-1C .f (α)的最大值为2-1D .f (α)的最大值为1- 2答案 BD解析 设t =sin α+cos α=2sin ⎝⎛⎭⎫α+π4,由0≤α≤π2,得π4≤α+π4≤3π4,则1≤t ≤2,又由(sin α+cos α)2=t 2,得2sin αcos α=t 2-1,所以f (α)=g (t )=t 2-1-2t +1=t -1-2t +1,又因为函数y =t -1和y =-2t +1在[1,2]上单调递增,所以g (t )=t -1-2t +1在[1,2]上单调递增, g (t )min =g (1)=-1,g (t )max =g (2)=1- 2.16.已知关于x 的方程2x 2-(3+1)x +m =0的两根分别是sin θ和cos θ,θ∈(0,2π),求:(1)sin 2θsin θ-cos θ+cos θ1-tan θ的值; (2)m 的值;(3)方程的两根及此时θ的值.解 (1)原式=sin 2θsin θ-cos θ+cos θ1-sin θcos θ=sin 2θsin θ-cos θ+cos 2θcos θ-sin θ=sin 2θ-cos 2θsin θ-cos θ=sin θ+cos θ.由已知得sin θ+cos θ=3+12, 所以sin 2θsin θ-cos θ+cos θ1-tan θ=3+12. (2)由已知得sin θcos θ=m 2, 因为1+2sin θcos θ=(sin θ+cos θ)2,所以1+m =⎝⎛⎭⎪⎫3+122, 解得m =32. (3)联立⎩⎪⎨⎪⎧ sin θ+cos θ=3+12,sin θcos θ=34,解得⎩⎨⎧ sin θ=32,cos θ=12 或⎩⎨⎧ sin θ=12,cos θ=32.因为θ∈(0,2π),所以θ=π3或π6.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总结高考数学复习三角函数公式
三角函数一样用于运算三角形中未知长度的边和未知的角度。以
下是三角函数公式,期望考生能够好好经历。
同角三角函数的差不多关系式
倒数关系: 商的关系: 平方关系:
tan cot=1
sin csc=1
cos sec=1 sin/cos=tan=sec/csc
cos/sin=cot=csc/sec sin2+cos2=1
1+tan2=sec2
1+cot2=csc2
(六边形经历法:图形结构上弦中切下割,左正右余中间1经历方法对
角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于
下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的
三角函数值的乘积。)
诱导公式(口诀:奇变偶不变,符号看象限。)
sin(-)=-sin
cos(-)=cos tan(-)=-tan
cot(-)=-cot
sin(/2-)=cos
cos(/2-)=sin
tan(/2-)=cot
cot(/2-)=tan
sin(/2+)=cos
cos(/2+)=-sin
tan(/2+)=-cot
cot(/2+)=-tan
sin()=sin
cos()=-cos
tan()=-tan
cot()=-cot
sin()=-sin
cos()=-cos
tan()=tan
cot()=cot
sin(3/2-)=-cos
cos(3/2-)=-sin
tan(3/2-)=cot
cot(3/2-)=tan
sin(3/2+)=-cos
cos(3/2+)=sin
tan(3/2+)=-cot
cot(3/2+)=-tan
sin(2)=-sin
cos(2)=cos
tan(2)=-tan
cot(2)=-cot
sin(2k)=sin
cos(2k)=cos
tan(2k)=tan
cot(2k)=cot
(其中kZ)
两角和与差的三角函数公式 万能公式
sin(+)=sincos+cossin
sin(-)=sincos-cossin
cos(+)=coscos-sinsin
cos(-)=coscos+sinsin
tan(+)=(tan+tan)/(1-tan tan)
tan(-)=(tan-tan)/(1+tan tan)
sin=2tan(/2)/(1+tan2(/2))
cos=(1-tan2(/2))/(1+tan2(/2))
tan=(2tan(/2))/(1-tan2(/2))
半角的正弦、余弦和正切公式 三角函数的降幂公式
二倍角的正弦、余弦和正切公式 三倍角的正弦、余弦和正切公式
sin2=2sincos
cos2=cos2-sin2=2cos2-1=1-2sin2
tan2=2tan/(1-tan2)
sin3=3sin-4sin3
cos3=4cos3-3cos
tan3=(3tan-tan3)/(1-3tan2)
三角函数的和差化积公式 三角函数的积化和差公式
sin+sin=2sin(2/(+ -))cos(2/(+ -))
sin-sin=2cos(2/(+ -))sin(2/(+ -))
cos+cos=2cos(2/(+ -))cos(2/(+ -))
cos-cos=-2sin(2/(+ -))sin(2/(+ -))
sin cos=-[sin(+)+sin(-)]/2
1cos sin=-[sin(+)-sin(-)]/2
1cos cos=-[cos(+)+cos(-)]/2
1sin sin= -[cos(+)-cos(-)]
2化asin bcos为一个角的一个三角函数的形式(辅助角的三角函数的公
式)
事实上,任何一门学科都离不开死记硬背,关键是经历有技巧,“死记”之
后会“活用”。不记住那些基础知识,如何会向高层次进军?专门是语文学科
涉猎的范畴专门广,要真正提高学生的写作水平,单靠分析文章的写作技巧
是远远不够的,必须从基础知识抓起,每天挤一点时刻让学生“死记”名篇佳
句、名言警句,以及丰富的词语、新颖的材料等。如此,就会在有限的时刻、
空间里给学生的脑海里注入无限的内容。日积月累,积少成多,从而收到水滴
石穿,绳锯木断的功效。三角函数公式的内容确实是这些,查字典数学网预
祝考生能够金榜题名。
家庭是幼儿语言活动的重要环境,为了与家长配合做好幼儿阅读训练
工作,小孩一入园就召开家长会,给家长提出早期抓好幼儿阅读的要求。
我把幼儿在园里的阅读活动及阅读情形及时传递给家长,要求小孩回家向
家长朗诵儿歌,表演故事。我和家长共同配合,一道训练,幼儿的阅读能
力提高专门快。2021年高考第一轮复习备考专题差不多新奇出炉了,专题
包含高考各科第一轮复习要点、复习方法、复习打算、复习试题,大伙儿
来一起看看吧~
我国古代的读书人,从上学之日起,就日诵不辍,一样在几年内就能识记
几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹
经纶的文人。什么缘故在现代化教学的今天,我们念了十几年书的高中毕业
生甚至大学生,竟提起作文就头疼,写不出像样的文章呢?吕叔湘先生早在19
78年就尖锐地提出:“中小学语文教学成效差,中学语文毕业生语文水平
低,……十几年上课总时数是9160课时,语文是2749课时,恰好是30%,十年
的时刻,二千七百多课时,用来学本国语文,却是大多数只是关,岂非咄咄怪
事!”寻根究底,其要紧缘故确实是腹中无物。专门是写议论文,初中水平以上
的学生都明白议论文的“三要素”是论点、论据、论证,也通晓议论文的差
不多结构:提出问题――分析问题――解决问题,但真正动起笔来就犯难了。
明白“是如此”,确实是讲不出“什么缘故”。全然缘故依旧无“米”下“锅”。
因此便翻开作文集锦之类的书大段抄起来,抄人家的名言警句,抄人家的事
例,不参考作文书就专门难写出像样的文章。因此,词汇贫乏、内容空泛、千
篇一律便成了中学生作文的通病。要解决那个问题,不能单在布局谋篇等写
作技方面下功夫,必须认识到“死记硬背”的重要性,让学生积存足够的“米”。
