第一课浙大自控原理习题课
第一章自动控制原理绪论例题 ppt课件

PPT课件
26
• 画出图示电加热系统的结构图,简述结构 特点和调节过程,并说明受控对象,被控 量、给定量、偏差、内扰、外扰都指的是 哪些设备和物理量。
PPT课件
27
• 结构图:结构特点为闭环,具备抗干扰能 力。
• 被控量:电阻炉温度;受控对象:电阻炉; 给定量:电阻炉的温度希望值;外扰:炉门 开关频度变化;内扰:电源电压波动。
PPT课件
29
判别下列动态方程所描述的系统的性质:线性或非线 性,定常或时变,动态或静态。
t ; (1)C( t ) 5 r ( t ) t r ( t ) 6C ( t ) 8C( t ) r ( t ); t 3C (2)r
2
( t ) C( t ) r ( t ) 3r t ; (3)tC (4)C( t ) r t cost 5; ( t ) 5 r d ; (5)C( t ) 3rt 6r (6)C( t ) r t ;
PPT课件
18
• 系统的被控对象是电炉,被控量是电炉炉温; 电动机、减速器、调压器是执行机构,热电偶 是检测元件。 • 电炉温度控制系统的方块图如图1-16所示。
PPT课件
19
1-7 在按扰动控制的开环控制系统中,为什么说一 种补偿装置只能补偿一种与之相应的扰动因素? 对于图1-19中的按扰动控制的速度控制系统,当 电动机的激磁电压变化时,转速如何变化?该补 偿装置能否补偿这个转速的变化?
PPT课件
12
1-4 图1-13为水温控制系统示意图。冷水在热交换器 中由通入的蒸汽加热,从而得到一定温度的热水。 冷水流量变化用流量计测量。试绘制系统方块图, 并说明为了保持热水温度期望值,系统是如何工作 的?系统的被控对象和控制装置各是什么?
浙大自控原理习题课

K 10
T
T 1
11. 系统的开环频率特性为:
G( j)H ( j) K ( j 1) j( j 1)
0
K 1
G( j)H ( j) K 1 2 K
0
12
G( j)H ( j) 180 arctan 90 arctan
G(s)H (s) K (s 1) , K 0 s(s 1)
应用奈氏判据判断闭环系统的稳定性。
1. (1)系统的传递函数为
G(s)
K (2s 1)
s(4s 1)(0.5s 1)(0.2s 1)
由于 L(1) 20 lg K 20 lg1 20 lg 1 22 20 lg 1 42 20 lg 1 0.52 20 lg 1 0.22 0
4.47 0.56
系统开环传递函数为:
G(s) 20 s(s 5)
KV 4 稳态误差 e() 0.25
2.(2)加入微分反馈时的系统闭环传递函数为:
Φ(s)
s2
(5
20 2Kd
)s
20
2 n
2 n
5
20 2
K
d
由于 0.8
Kd 1.08
得 K 2.1,所以传递函数为
G(s)
2.1(2s 1)
s(4s 1)(0.5s 1)(0.2s 1)
() 90 arctan 2 arctan 4 arctan 0.5 arctan 0.2
(c ) 140 .43 相位裕量: 180 (c ) 39.57
2
T 0.2
自动控制原理课后习题答案第一章

1-1 图1-2是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c 维持不变,试说明系统工作原理并画出系统方块图。
图1-2 液位自动控制系统解:被控对象:水箱;被控量:水箱的实际水位;给定量电位器设定水位r u (表征液位的希望值r c );比较元件:电位器;执行元件:电动机;控制任务:保持水箱液位高度不变。
工作原理:当电位电刷位于中点(对应r u )时,电动机静止不动,控制阀门有一定的开度,流入水量与流出水量相等,从而使液面保持给定高度r c ,一旦流入水量或流出水量发生变化时,液面高度就会偏离给定高度r c 。
当液面升高时,浮子也相应升高,通过杠杆作用,使电位器电刷由中点位置下移,从而给电动机提供一定的控制电压,驱动电动机,通过减速器带动进水阀门向减小开度的方向转动,从而减少流入的水量,使液面逐渐降低,浮子位置也相应下降,直到电位器电刷回到中点位置,电动机的控制电压为零,系统重新处于平衡状态,液面恢复给定高度r c 。
反之,若液面降低,则通过自动控制作用,增大进水阀门开度,加大流入水量,使液面升高到给定高度r c。
系统方块图如图所示:1-10 下列各式是描述系统的微分方程,其中c(t)为输出量,r (t)为输入量,试判断哪些是线性定常或时变系统,哪些是非线性系统? (1)222)()(5)(dt t r d t t r t c ++=;(2))()(8)(6)(3)(2233t r t c dt t dc dt t c d dt t c d =+++; (3)dt t dr t r t c dt t dc t )(3)()()(+=+; (4)5cos )()(+=t t r t c ω; (5)⎰∞-++=t d r dt t dr t r t c ττ)(5)(6)(3)(;(6))()(2t r t c =;(7)⎪⎩⎪⎨⎧≥<=.6),(6,0)(t t r t t c解:(1)因为c(t)的表达式中包含变量的二次项2()r t ,所以该系统为非线性系统。
自动控制原理_第一章课后习题解答

第一章1.1 图1.18是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c 维持不变,试说明系统工作原理并画出系统方块图。
c+-SM___1Q 浮浮浮浮浮浮2Q 浮浮浮浮浮浮浮浮浮浮浮浮fi -+解:系统的控制任务是保持液面高度不变。
水箱是被控对象,水箱液位是被控变量。
电位器用来设置期望液位高度*c (通常点位器的上下位移来实现) 。
当电位器电刷位于中点位置时,电动机不动,控制阀门有一定的开度,使水箱的流入水量与流出水量相等,从而使液面保持在希望高度*c 上。
一旦流出水量发生变化(相当于扰动),例如当流出水量减小时,液面升高,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一定的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液体流量减少。
这时,水箱液位下降.浮子位置相应下降,直到电位器电刷回到中点位置为止,系统重新处于平衡状态,液位恢复给定高度。
反之,当流出水量在平衡状态基础上增大时,水箱液位下降,系统会自动增大阀门开度,加大流入水量,使液位升到给定高度*c 。
系统方框图如图解1. 4.1所示。
1.2恒温箱的温度自动控制系统如图1.19所示。
(1) 画出系统的方框图;(2) 简述保持恒温箱温度恒定的工作原理;(3) 指出该控制系统的被控对象和被控变量分别是什么。
M放大器电机减速器调压器 220~热电偶电阻丝- +- +图1.19 恒温箱的温度自动控制系统解:恒温箱采用电加热的方式运行,电阻丝产生的热量与调压器电压平方成正比,电压增高,炉温就上升。
调压器电压由其滑动触点位置所控制,滑臂则由伺服电动机驱动.炉子的实际温度用热电偶测量,输出电压作为反馈电压与给定电压进行比较,得出的偏差电压经放大器放大后,驱动电动机经减速器调节调压器的电压。
在正常情况下,炉温等于期望温度T ,热电偶的输出电压等于给定电压。
此时偏差为零,电动机不动,调压器的滑动触点停留在某个合适的位置上。
自控原理课件及习题解答

s→0
s
1+
k sν
G0H0
r(t)=R·1(t) R(s)=R/s
ess=
1+
R lim k s→0 sν
r(t)=R·t R(s)=R/s2
ess=
R
lim s
s→0
k sν
·
r(t)=Rt2/2 R(s)=R/s3
ess=
R
lim
s→0
s2·skν
取不同的ν
R·1(t) R·t Rt2/2 R·1(t) R·t Rt2/2
用正无穷小量ε代替。
劳斯判据
系统稳定的必要条件: s6 1 3 5 7
特征方程各项系数 s5 2 44 6
均大于零!
有正有负一定不稳定!
s4 1 2 77
s3 0ε --88
缺项一定不稳定!
s2 2ε+8 7ε
-s2-5s-6=0稳定吗? s1 -8(2ε+8) -7ε2
系统稳定的充分条件: s0 7ε
引出点移动
G1
G1
H2 G2
H1
H2 G2
H1
G3
G4
H3
1 G4
G3 a G4 b
H3
综合点移动
G3 G1
向同类移动
G3
G1
G2
H1
G2 G1 H1
G4
G1
G2
H1
G4
G1
G2
H1 H1
作用分解
G3 H3
G3 H3 H3
梅逊公式介绍 R-C : △称为系统特征式
C(s) R(s)
=
∑Pk△k △
. EEˊ(rsν()=s=)C1=希-CRH实称((=ss))为RH-(C(ssⅠ))(s-型)C(系s) 统
六年级下册第一课《自动控制系统》 课件 浙教版2023

21:0543210987654321
计算机具有哪些优点呢? 其他自动控制技术有哪些不足?
10:0543210987654321
计算机具有哪些优点呢? 其他自动控制技术有哪些不足?
新知建构
计算机是自动控制系统的关键组成部分,它可以实现 快速、精准、可靠的控制功能。
问题驱动
计算机在自动控 制系统中的作用
手机屏幕亮度 自动控制
新知建构
水位球
感应器
新知建构
计算机参与的自动控制系统
小组讨论
计算机参与的自动控制系统有哪 些优点呢?
要求:小组合作,用时三分钟以内。
计算机具有哪些优点呢? 其他自动控制技术有哪些不足?
32:0543210987654321
计算机具有哪些优点呢? 其他自动控制技术有哪些不足?
观看视频,试着用自己的话说说
计算机在自动控制系统当中发挥的 作用有哪些方面。
问题驱动
计算机在自动控 制系统中的作用
01
利用计算机指Βιβλιοθήκη ,实现更 精准、更复杂的控制。02
利用计算机指令,实现智 能的控制方式,使系统参 数的调整更加方便。
延伸拓展
两种不同的农场灌溉系统
总结回顾
1、常见的控制系统 2、计算机在自动控制系统中的作用
课后练习
制作一份电子小报,介绍一个 生活中常见的自动控制系统, 说一说它的特点,并简单说明 计算机在其中的作用。
第一课、自动控制系统
2023浙教版信息科技六年级下 册
新知导入
开着空调的教室为什么能实现恒 温?能保持在设定的温度呢?
1、根据生活经验,谈谈看你的想法。 2、这样的功能你知道其他哪些领域也运用了吗?
新知导入
浙江大学自动控制原理第一章课件.

自动控制理论
零阶保持器( ZOH )是把kT时刻的采样值恒值地保持到下一采样时 刻(K+1)T。
由图7-13(b)得
脉冲响应
g h (t ) l (t ) l (t T )
1 e TS Gh ( S ) S
传递函数
Tj sin(T ) jT 1 e 2 e 2 频率特性 Gh ( j ) T T j 2 2 T 把 代入上式,得 S sin( ) j ( ) S 2 Gh ( j ) e S
PT (t )
k sin jk st 1 T 1 1 T ak 2T ee dt T 2 T k T
2018/10/19 第七章 离散化控制系统
k
jks t a e k
(7-4)
(7-5)
9
自动控制理论
其中, a k
1 T
若令 T 10
1
则 a0
1 T
a1
0.984 T
பைடு நூலகம்
a2
0.935 T
…
图7-8
2018/10/19
第七章 离散化控制系统
10
自动控制理论
图7-9
f s* (t ) f (t )T (t ) f (t ) ak e jkst
k
1 [ 2
2018/10/19
F ( j )e jt d ] ak e jkst
自动控制理论
图7-8可知,相邻两频谱不重叠交叉的条件是
s 2max
香农采样定理
s 2max
s
图7-12
f s* (t ) 就含有连续信号f(t)的全部信息,通过图7-11所示的理想滤
自动控制原理习题及答案.doc.
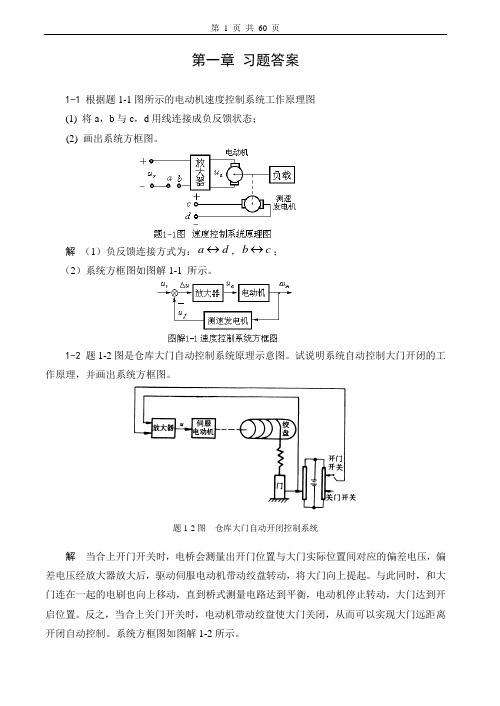
第一章 习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a ,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1-1 所示。
1-2 题1-2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。
与此同时,和大门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开启位置。
反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离开闭自动控制。
系统方框图如图解1-2所示。
1-3 题1-3图为工业炉温自动控制系统的工作原理图。
分析系统的工作原理,指出被控对象、被控量和给定量,画出系统方框图。
题1-3图 炉温自动控制系统原理图解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比,c u 增高,炉温就上升,c u 的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量,输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较,得出偏差电压e u ,经电压放大器、功率放大器放大成a u 后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T °C ,热电偶的输出电压f u 正好等于给定电压r u 。
此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值。
这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下的控制过程:控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.47 0.56
系统开环传递函数为:
G(s) 20 s(s 5)
KV 4 稳态误差 e() 0.25
2.(2)加入微分反馈时的系统闭环传递函数为:
Φ(s)
s2
(5
20 2Kd
)s
20
2 n
2 n
5
20 2
K
d
由于 0.8
Kd 1.08
K 10
T
T 1
11. 系统的开环频率特性为:
G( j)H ( j) K ( j 1) j( j 1)
0
K 1
G( j)H ( j) K 1 2 K
0
12
G( j)H ( j) 180 arctan 90 arctan
线s=-1的左侧,试确定开环增益 K 的取值范围。
8. 一单位负反馈系统的开环传递函数为
G(s) K (s2 2s 5) (s 2)(s 0.5)
试绘制根轨迹图,并在根轨迹上确定该闭环系统无超调
响应时的开环增益 K 的取值范围。
9. 某一阶环节的 为正值的幅相特性曲线如图所示,
Kds
3. 已知一单位负反馈系统控制系统的开环传递函数为 G(s) K (s 2 5s 6) s(s 1)
试以 K 为变量证明部分根轨迹为圆,并求分离点和会合点。
4. 试求系统的传递函数C(s) / R(s) 、E(s) / R(s)。
R(s)
G1
G5
G2
G4
C(s) G3 G6
G(s)H (s) K (s 1) , K 0 s(s 1)
应用奈氏判据判断闭环系统的稳定性。
1. (1)系统的传递函数为
G(s)
K (2s 1)
s(4s 1)(0.5s 1)(0.2s 1)
由于 L(1) 20 lg K 20 lg1 20 lg 1 22 20 lg 1 42 20 lg 1 0.52 20 lg 1 0.22 0
C() lim sC(s) K 10 s0
单位脉冲响应:g(t) L1[(s)]
Ks2 Kas
Ks 2
lim
t0
g (t )
lim s(s)
s
lim
s
Ts
N
1
sN
s
a
lim
s
Ts
N
1
lim c(t) 10
t0
为满足上式,必须有:N 1
Kd d 1 j2 d 1 j2
0.24
d 0.41
由劳斯判据,当 0.2 K 0.75,系统稳定。
当 0.2 K 0.24,
系统无超调响应。
9. 设一阶环节的传递函数为:
G(s) K Ts 1
则由图可知:
K 4
4 2T 2
1
4 25T 2
1
5. 若某二阶环节的 为正值的幅相特性如图所示,图a中A
点频率 2rad/s , 0 时幅相特性的实部为-2a,a为大
于零的常数。求:
(1)开环传递函数;
(2)若 a 1,试求 1 、 2 、 3 。
Im a
Re
L( ) 20
A
a
1 2
3
2
T 0.2
所以,G(s) 4 0.2s 1
10. 由于 essp 0 ,系统不是零型系统,N 1
系统的闭环传递函数为:
Φ(s)
C(s) R(s)
sN
K(s a) (Ts 1) s
a
K(s a) 1 C(s) sN (Ts 1) s a s
K (s2 5s 6) K (s 2)(s 3)
3. G(s)
s(s 1)
s(s 1)
令 s j ,应用相角条件可知:
arctan
arctan
arctan
arctan
180
2
3
1
化简上式,得:
2 ( 3)2 ( 3 )2
C(s)
G1G2G3 G1G3G5
R(s) 1 G1G2G4 G2G3G6 G1G5G3G6G2G4
R(s)到E(s) ,前向通道:P1 G1 P2 G1G5G3G6
C(s)
G1 G1G5G3G6
R(s) 1 G1G2G4 G2G3G6 G1G5G3G6G2G4
得 K 2.1,所以传递函数为
G(s)
2.1(2s 1)
s(4s 1)(0.5s 1)(0.2s 1)
() 90 arctan 2 arctan 4 arctan 0.5 arctan 0.2
(c ) 140 .43 相位裕量: 180 (c ) 39.57
7. 闭环特征方程为: s3 14s2 40s 40K 0
(1)系统稳定要满足:0 K 14
(2)令 s z 1,代入特征方程得: z3 11z2 15z 40K 27 0
系统稳定时:0.675 K 4.8
8. 分离点 d 0.41
d 2 d 0.5
2. 二阶系统结构如图所示,
(1)当r(t) t ,且不加微分反馈(即 K d 0 )时,试求系 统的阻尼系数 ,无阻尼自振频率 n 和稳态误差e() ;
(2)当加入微分反馈,且要求将系统的阻尼系数 提高到 0.8时,试求 K d 。
R(s)
2
C(s)
10
s(s 5)
40
6. 系统框图如图所示,试求传递函数 C(s) / R(s)。
R(s)
G1
G2
C(s)
H1
H2
7. 已知单位负反馈系统的开环传递函数为
G(s)
K
s(0.1s 1)(0.25s 1)
(1)试确定闭环系统稳定时开环增益 K 的取值范围;
(2)若要求系统全部闭环极点分布在s平面虚轴的平行
5.(1)系统开环传递函数为:
G(s) K s(Ts 1)
由图可知:
KT KT
1 4T
2
2a a
TK
0.5 4a
所以,系统开环传递函数为:
G(s) 4a s(0.5s 1)
(2)由于 a 1,则 3 K 4a 4
由近似对数幅频特性曲线可知:
(2)A是Ⅰ型系统,B是Ⅱ型系统,系统B对于阶跃输 入和斜坡输入的稳态误差为0,可跟随抛物线函数输入, 而系统A对于抛物线函数输入的稳态误差为∞。
2.(1)未加微分反馈时的系统闭环传递函数为:
Φ(s)
s2
20 5s
20
得: 2n2
n
20 5
即: n
20 5/4
90 2arctan
G(
j)H (
j )
K
2
2
1)
j
12)
(
2
1)
奈氏曲线顺时针包围点(1, j0) 一周,且P 0,Z 1, 闭环系统不稳定。
精品课件!
精品课件!
2
2
上式表明,部分根轨迹为圆心在 (
3
,
j0)、半径为
3 的圆。
2
2
由以上圆的方程可得根轨迹的分离
j
点为 s1 0.63 ,会合点为 s2 2.37
3 2 1 0
4. 三个回路:
L1 G1G2G4 L2 G2G3G6 L3 G1G5G3G6G2G4 R(s)到C(s) ,前向通道:P1 G1G2G3 P2 G1G3G5
20 lg 4 20 lg 2 20 lg 0.52 0
得:2 2.8
又 40 lg 2 20 lg 3
1
1
得:1 1.96
6. 两个回路: L1 G1G2H1H2 L2 G2H2
前向通道: P G1G2
C(s)
G1G2
R(s) 1 G2H 2 G1G2H1H 2
写出其传递函数。
Im
2
4
Байду номын сангаас
Re
2
5
10. 系统如左图所示,其单位阶跃响应如右图所示,系
统的位置误差essp 0 ,试确定 K 、N 与 T 的值。
R(s)
K(s a) s N (Ts 1)
cp (t)
C(s)
c() 10
1 K
初始斜率=10 t
11. 已知系统的开环传递函数为
