数学物理方法第14章
内容概要南京大学数学物理方法课件

数学物理方法复习课
第八章 分离变量法 8.1 分离变量法 主要步骤: 1. 边界条件齐次化,对非齐次边界条件首先把它化为齐次的. 2. 分离变量 u(x,t) =X(x) T(t) (1) 3. 将(1)式代入原方程得出含任意常数 λ 的常微分方程, (称为本征方程) 而 λ 为本征值. 4. 由齐次边界条件确定本征值,并求出本征方程.(得出的解为本征函数) 5. 根据迭加原理把所有满足方程的线性无关解迭加后,就能得通解. 6. 再由初始条件确定系数.
P0(x)= 1, P1(x) =x=cosθ, •P2(x)=(3x -1)/2,
2
….
•一般勒让德多项式的幂次取决 L •当 L 为偶数时都为偶次幂项,L 为奇数时都为奇次幂项. 对特殊点 x=1,0.
Pl 1 1, Pl x 1 Pl x ,
l
P2 n 1 0 0, P2 n 0 1
2u 0
(9.1.1)
1 2 u 1 u 1 2u 0. r 2 sin 2 2 2 2 r r r r sin r sin
柱坐标系下
1 u 1 2u 2 Z 2 2 0. 2 z
''
d 2R dR 今x , 4式为 : x x x 2 m 2 R 0.5 2 dx dx 5为m阶Bessel方 程 ..
2
(5)式其解为 m 阶 Bessel 函数, 解依赖于边界条件,当上下底为边界条件是齐次时, μ<0.对应的解是虚贝塞尔函数.
数学物理方法复习课
边界条件.
l Bl u r , Al r l 1 Pl cos , 2 在轴对称时(1)式退化为 r l 0
2017版新步步高高考数学大一轮复习讲义课件:第14章 系列4选讲 14.4 课时1

不等式
a>0
a=0
a<0
|x|<a
(-a,a)
∅
∅
|x|>a (-∞,-a)∪(a,+∞) (-∞,0)∪(0,+∞) R
答案 第四页,编辑于星期六:三点 十分。
(2)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法: ①|ax+b|≤c⇔ -c≤ax+b≤c ; ②|ax+b|≥c⇔ ax+b≥c或ax+b≤-c ; (3)|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法: ①利用绝对值不等式的几何意义求解,体现了数形结合的思想; ②利用“零点分段法”求解,体现了分类讨论的思想; ③通过构造函数,利用函数的图象求解,体现了函数与方程的思想.
所以 f(x)>1 的解集为x32<x<2
.
第十三页,编辑于星期六:三解点 十析分答。 案
(2)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
x-1-2a,x<-1, 解 由题设可得,f(x)=3x+1-2a,-1≤x≤a,
-x+1+2a,x>a. 所以函数 f(x)的图象与 x 轴围成的三角形的三个顶点分别为 A2a3-1,0,
第二十九页,编辑于星期六:三点 十返分。回
练出高分
第三十页,编辑于星期六:三点 十分。
1 2 3 4 5 6 7 8 9 10
1.在实数范围内,求不等式||x-2|-1|≤1的解集. 解 由||x-2|-1|≤1得-1≤|x-2|-1≤1, 解||xx--22||≤≥20, 得 0≤x≤4. ∴不等式的解集为[0,4].第十七页,Βιβλιοθήκη 辑于星期六:三解点 十析分答。 案
数学方法选讲-第十四001

第十四讲数学方法选讲算两次:在解决各种数学问题时,常要选择一个合适的量,从两个不同的方面去考察它,然后综合起来得到一个关系式(等式或不等式等),再利用这个关系解题,这称为“算两次”.它是一种重要的而且很常用的数学方法,也叫做富比尼(G.Fubini)原理.列方程解应用题是典型的“算两次”,著名的美国数学教育家波利亚(G.Polya)在他的名著《数学的发现》中指出:“为了得到一个方程,我们必须把同一个量以两种不同的方法表示出来.”用代数方法解决几何问题时,常通过“算两次”得到方程(或方程组);用反证法证题时,常是通过把一个量“算两次”导致矛盾的.特别是在利用奇偶性分析解题时,常从两个不同角度考察同一个量,而导致奇数等于偶数的矛盾等等.例1:把1,2,3,…,15,16这16个自然数,填入4×4的方格表中的16个方格内,每格内填一个数,各格内的数互不相同,求证:不论如何填,都不可能使每个横行及每个纵列的4个数的和是8个连续自然数.证明:记4行各数之和分别为S1,S2,S3,S4;4列各数之和为S'1,S'2,S'3,S'4.假设S1,S2,…,S'4是8个连续自然数n,n+1,…,n+7.一方面,由于S1+S2+S3+S4及S'1+S'2+S'3+S'4恰好都是全表中16个数的和,故S=S1+S2+S3+S4+S'1+S'2+S'3+S'4=2(1+2+3+ (16)=272.①另一方面,由假设有S=n+(n+1)+…+(n+7)=8n+28.②综合①、②得8n+28=272.解得n=30.5,不是自然数,从而结论得证.说明通过“算两次”解题.程序大体上是一个三步曲:即“一方面如何(由一部分条件而得),另一方面如何(由另一些条件而得),综合起来又如何.”例2:某次数学竞赛共有15道题,下表是对于做对n(n=0,1,2,…,15)题的人数的一个统计(其中缺少n=4至11的数据):如果已知其中做对4道题和4道题以上的学生每人平均做对6道题,做对10道题和10道题以下的学生每人平均做对4道题,问:这张表至少统计了多少人?n 0 1 2 3 ……12 13 14 15 做对n道题的人数7 8 10 21 ……15 6 3 1解法一:设这张表共统计了y人,依题设,做对不少于4道题的学生所做对的总题数为6(y -7-8-10-21).所以做对4道题至11道题的人所做对的总题数为S=6(y-7-8-10-21)-12×15-13×6-14×3-15×1=6y-591.又设做对11道题的人数为x,则由题设有S=4(y-x-15-6-3-1)+11x-0×7-1×8-2×10-3×21 =4y+7x-191.∴6y-591=4y+7x-191,即y=200+7 2 x由此可见,当x=0时,y取最小值200,即表中至少统计了200人.解法二:设表中统计了y人,这y人做错的题目总数为S1=15y-6(y-7-8-10-21)-0×7-1×8-2×10-3×21=9y+185.设做对11道题至15道题的共有x人,则又有S1=15y-4(y-x)-12×15-13×6-14×3-15×1-11(x-15-6-3-1)=11y-7x-40.∴9y+185=11y-7x-40,y=7x2252+.因x≥15+6+3+1=25,故当x=25时,y有最小值y min =7252252⨯+=200.例3:在凸n边形内任取m个点,并任意作一些线段,连结这些点及多边形的顶点,使得每两条线的内部没有公共点,并且把多边形剖分成若干个三角形,这些三角形除端点外,内部和边上都不含取定的m个点,上述过程称为多边形的三角剖分.试问:剖分出的三角形共有多少个?解:设有x个三角形,则这x个三角形的内角和为x⋅180°.又这x个三角形的全部内角可分二类:一类的顶点是原多边形的顶点,这类角的和是n 边形的内角和,等于(n-2)⋅180°;另一类的顶点是已取的m个点之一,这类角的和为m360⋅.∴x⋅180°=(n-2)⋅180°+m360⋅,∴x=2m+n-2.所以,共有2m+n-2个三角形.分类讨论:例4解方程组|1||5|15|1|x yy x-+-=⎧⎨=+-⎩解:由第二个方程,显然有y≥5,所以| y-5 |=y-5=| x-1|.代入第一个方程,得| x -1|=12,即x -1=12或x -1=-12, 分别解得x 1=32,x 2=12. 而y =5+| x -1|=112.综上,本题有两个解1132112x y ⎧=⎪⎪⎨⎪=⎪⎩,2212112x y ⎧=⎪⎪⎨⎪=⎪⎩.反证法例5 证明:满足方程{1x}+{x}=1的x 必是无理数. 证明:假设满足题设方程的x 是有理数. (1)若x 为整数,则{x}=0.于是,由方程得{1x}=1.但对任何实数都有0≤{x}<1,故 原方程无法成立.(2)若x 为非整数的有理数.令x =n +qp,这里n ,p ,q 都是整数,且1≤q <p ,(p ,q )=1,则{x}=q p .由于1p x np q=+,故可设1{}r x np q =+,这里r 是整数.因x 满足题设方程,所以1q rp np q+=+, 即 ()()q np q pr p np q ++=+, 亦即 2[(1)]q p np n q r =+--, ∴2|p q ,这与(,)p q =1矛盾. 所以,满足方程的x 必是无理数.例6:设||a b >,||d c >,求证:方程组00ax by cx dy +=⎧⎨+=⎩①②有且只有一组解x =y =0.证明:显然,x =y =0满足原方程组.设方程组另有一组解x =m ,y =n ,m ,n 不全为零.(1)若|m|>|n|,则由a >|b|,得a|m|>|b||n|=|bn|.③又由①有am +bn =0,am =-bn ,∴a|m|=|bn|,这与③式相矛盾. (2)若|m|=|n|≠0,这时③式仍成立,仍产生矛盾.(3)若|n|>|m|,由d>|c|,与第一种情形类似可导致矛盾.综上讨论,命题得证.(学生课后练习机动,1——2题即可)。
2020届高考数学(理)一轮复习课时训练:第14章选修部分72Word版含解析

【课时训练】第72节 证明不等式的基本方法解答题1. (2018广州五校联考)已知函数f(x) = |x +引+ |x — 1|,其最小值 为t.(1) 求t 的值;(2) 若正实数a , b 满足a + b = t ,求证:(1)【解】 因为 |x +3|+ |x — 1|= |x + 引+11— x|> |x +3+ 1— x| = 4, 所以 f(X )min = 4,即 t = 4.⑵【证明】由(1)得 a + b = 4,故4+ b= 1, 1+ 4= P+令;+b= 4+ 1 +4a+討5+ 2,4a xb = 4+1= 4'当且仅当 b = 2a ‘ 即 a =|,8 1 4 9 b = 3时取等号,故a + 4.2. (2018湖北八校联考)设不等式—2<|x — 1|— |x + 2|<0的解集为 M , a , b € M.1 1 1(1) 证明:3a + 6b <4;(2) 比较|1 — 4ab|与2|a — b|的大小,并说明理由.3, x < 2,(1)【证明】 记 f(x)=|x — 1|— |x + 2|= — 2x — 1,— 2<x<1,—3, x > 1.4 - b +■a12’2. 所以 1 1 3a + 6b1 11111 < 3|a| + 6|b|<3X2 + 6X 2 14.1 1由—2< —2x—1<0解得—2<x<2,则M =因为 |1 — 4abf — 4|a — b|2 = (1 - 8ab + 16a 2b 2) - 4(a 2 - 2ab + b 2)=2 2 (4a 2— 1)(4b 2— 1)>0.所以 |1 — 4ab|2>4|a — b|2,故 |1 — 4ab|>2p — b|.3. (2018广州模拟)已知定义在 R 上的函数f(x) = |x — m|+ |x|, m € N *,存在实数x 使f(x)<2成立.(1) 求实数m 的值;4 1(2) 若 a, 1, f( " + f( 0 =4,求证:一+3.a p【解】(1)因为 |x — m|+ |x|> |(x — m) — x|= |m|. 要使不等式|x — m|+凶<2有解,则|m|<2,解得—2<m<2. 因为m € N *,所以m = 1. ⑵因为 a 1, f(x) = 2x — 1(x > 1),4 1所以 f( a ) + f( p ) = 2 a- 1 + 2p — 1= 4,即卩 a+ 0= 3,所以; 小 1L 40 a L 1 a ,疋+ 2a+® =费+ a + 4 1a= 2, 0= 1时等号成立)故;+ 0,3.1 14.(2018武昌质检)已知x ,y € R ,且凶<1,|y|<1.求证:一2 +21 — x 1 — y【证明】••〒< 上3=二圧 < 匕翌L 2+2创耳=3.(当且仅当勾即a p a 0 1 — |xy|, 1— y 2 1 —|xy|21— xy ,3<二原不等式成立.5. (2018长沙一模)设a, B, 丫均为实数.(1) 证明:|cos (a+ 创w |COS a+ |sin 3,|sin (a+ 创w |COS a+ |COS3;⑵若a+ B+ 尸0,证明:|COS a+ |cos 3+ |cos 1.【证明】(1)|cos ( a+ 3|= |cos aDos 3— sin a sin 3w |cos a cos 3 +|sin osin 3w |cos o|+ |sin 3;|sin ( a+ 3| = |sin a cos 3+ cos osin 3w |sin a cos 3 + |cos osin3w |cos a+ |cos 3.(2) 由(1)知,|cos [ a+ ( 3+ Y |w |cos a+ |sin ( 3+ Y|w |cos a + |cos 3+ |cos Y,而a+ 升尸0,故|cos a+ |cos 3+ |cos Y》cos 0= 1.6. (2018贵阳模拟)已知函数f(x) = 2|x+ 1|+ |x—2|.(1)求f(x)的最小值m;b2 c2⑵若a, b, c均为正实数,且满足a+b+ c= m,求证:$ + b +(1)【解】当x< —1 时,f(x) = —2(x + 1) —(x—2)= —3x€ (3, c+=);当一1W x<2 时,f(x) = 2(x + 1) —(x—2)= x + 4€ [3,6);当x>2 时,f(x) = 2(x + 1)+ (x —2) = 3x€ [6, + =).综上,f(x)的最小值m= 3.⑵【证明】a, b, c均为,2 2 2正实数,且满足a + b+ c= 3, 因为b + 乍+ ¥ + (a + b + c)=JF 9:b层=2(a + b+ c)-曾+ b) +(当且仅当a= b= c= 1时,取等号)b 2c2a2b2c a所以皆 + C + 为a+ b+ c, 即b + C + a > 3。
数学物理方法习题答案.pdf
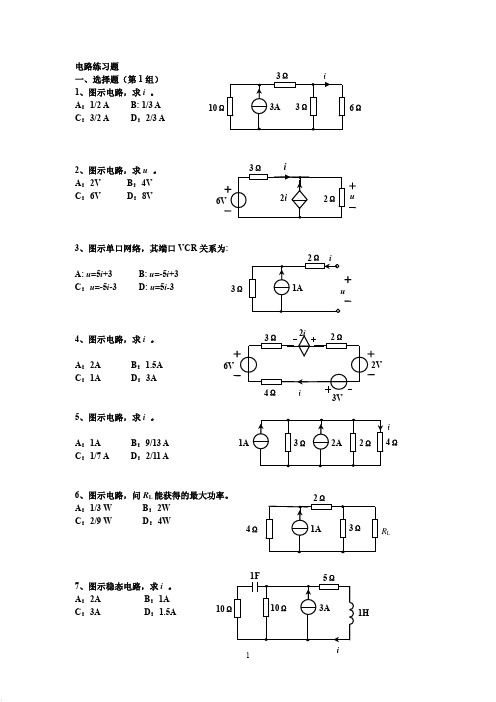
电路练习题一、选择题(第1组)1、图示电路,求i 。
A :1/2 A B: 1/3 A C :3/2 A D :2/3 A2、图示电路,求u 。
A :2VB :4VC :6VD :8V3、图示单口网络,其端口VCR 关系为:A: u =5i +3 B: u =-5i +3 C :u =-5i -3 D: u =5i-34、图示电路,求i 。
A :2AB :1.5AC :1AD :3A5、图示电路,求i 。
A :1AB :9/13 AC :1/7 AD :2/11 A6、图示电路,问R L 能获得的最大功率。
A :1/3 W B :2W C :2/9 W D :4W7、图示稳态电路,求i 。
A :2A B :1AC :3AD :1.5Ai 4ΩR L4Ω6Ω 10Ω1H108、图示稳态电路,问电容中的储能。
A :4J B :2JC :8JD :1J9、图示电路,t < 0时处于稳态, t = 0时,开关切到a , 当t = 5s 时,u c (t )是多少?A :6.3VB :5VC :2.4VD :3.16V10、图示电路,t < 0时处于稳态,t = 0时, 开关断开,求t = 1s 时u c (t )是多少? A :1.47V B :2.94V C: 5V D :4V11、图示电路原处于稳态,在t = 0时, 开关断开,求t = 0.1s 时的电流i (t )。
A :1A B :0 C :0.358A D :0.184 A12、图示正弦稳态电路,求i (t ) 。
A :)452cos(2°+t A B :)452cos(2°−t A C :)452cos(2°−t A D :)452cos(2°+t A13、图示正弦稳态电路中,有效值: I 是10A ,I R 是8A 。
问I c 是多少? A :2A B :18A C :6A D :4Ai(t)1H0.5Ω2ΩA2cos 22t u c1A c (t)2A14、图示正弦稳态电路, 求电阻上的平均功率。
数学物理方法课程总结

第一部分:一阶线性常微分方程组
● 高阶线性常微分方程化为一阶线性常微分方程组 ● 齐次线性常微分方程(组)解的结构
★基本解组 ★,eAt,A的特征值三种情况 ★通解表达式
● 非齐次线性常微分方程(组)的特解、通解。
第二部分:三类数理方程
第一章:波动方程
● 叠加原理 ● 达朗贝尔公式 ● 齐次化原理 ● 分离变量法求解波动方程的初边值混合问题 (若边界条件是非齐次的要先齐次化----通过加减,边界条 件变为齐次后再用分离变量的方法求解) ● 能量积分 ● 用能量积分证明解的唯一性
第二章:热传导方程
● 叠加原理 ● 齐次化原理 ●分离变量法求解热传导方程的初边值混合问题 (若边界条件是非齐次的要先齐次化----通过加减,边界条 件变为齐次后再用分离变量的方法求解) ● 傅里叶变换及5个性质 ● 用傅里叶变换求解热传导方程的柯西问题 ● 极值原理 ● 用极值原理证明解的唯一性
第三章:调和方程
● 变分原理 ● 分离变量法求解调和方程的边值问题 ● 格林第二公式 ● 平均值定理 ● 极值原理及其证明 ● 用极值原理证明解的唯一性 ● 格林函数法 ● 格林函数的5个性质及证明思路 ● 特殊边界情况求格林函数
复变函数的积分

f (ζk )∆zk ≤
k=1 k=1
|f (ζk )||∆zk |,
取极限即得性质 4.
§2
复积分的计算
在介绍 Cauchy 积分定理之前, 先讨论一下复积分的计算, 这样可以使我们对复积分有 更具体的了解, 通过计算还可以获得 Cauchy 积分定理的特例, 从而对该定理建立一些感性 认识. 一 *用定义计算
f (z ) dz + β
C
g (z ) dz.
2.
C1 +C2
f (z );
C2
f (z ) dz.
3.
C−
f (z ) dz = −
C
f (z ) dz. |f (z )| |dz | = |f (z )| ds.
C
4.
C
f (z ) dz ≤
C
最后一个积分中的 ds = |dz | 就是弧长的微分. 这些性质都可以直接由积分的定义来证 明.比如, 利用三角不等式, 有
ζk = ξk + iηk , 记 uk = u(ξk , ηk ),vk = v (ξk , ηk ),则 f (ζk ) = uk + ivk ,于是
n n n
f (ζk )∆zk =
k=1 k=1
(uk ∆xk − vk ∆yk ) + i
k=1
(vk ∆xk + uk ∆yk ),
由于 f (z ) 沿 C 连续, 故 u(x, y ) 和 v (x, y ) 沿 C 连续, 所以上式右边两项均有极限, 于是左边也有极限, 即 f (z ) 沿 C 可积.上式的极限正是式 (1).证毕.
本书提到的曲线一般都指光滑或逐段光滑的平面曲线. 若一段曲线的方程为 y = f (x), 则光滑指的是 f (x) 连续.若其方程为参数方程 x = x(t)、y = y (t),则光滑指的是 x (t) 和 y (t) 连续.由有限条光滑曲线衔接而成的曲线称为逐段光滑曲线.折线就是最简单的逐段 光滑曲线.曲线的方向定义如下. 1. 简单曲线:没有重点的曲线称为简单曲线.图 1 中的 a 是简单曲线,而 b 则不是. 简单曲线的方向由起点指向终点.所以规定了起点和终点就确定了它的方向. 2. 围线 (contour) : 逐段光滑的简单闭曲线称为围线. 图 1 中的 c 是简单闭曲线, 而d 则不是. 如果沿着围线走,其所包围的区域在左边,则该方向称为正方向,其实就是逆时针方 向. 二 复积分的定义 一元实变函数的积分定义在 x 轴上的有限区间内(无限区间的广义积分通过极限过程 得到), 而复变函数的积分 (简称复积分)总是定义在曲线上,参看图 2. 定义(复积分) 设函数 f (z ) 沿曲线 C :z = z (t) (α ≤ t ≤ β )有定义,在 C 上 沿参 数增加的方向 从 a = z (α) 到 b = z (β ) 取分点 a = z0 , z1 , . . . , zk−1 , zk , . . . , zn−1 , zn = b 将 C 分为 n 个弧段,在 zk−1 至 zk 的弧段上任取一点 ζk ,作和数
数学物理方法答案()刘连寿(PDF)

第七章 分离变量法7.1 直角坐标系中的分离变量法1.求解下列本证值问题的本证值和本证函数 (1)0,(0)0,()0X X X X l λ'''+=== ; (2)0,(0)0,()0X X X X l λ''''+=== ; (3)0,()0,()0X X X a X b λ''+=== ; (4)[]0,(0)0,00x l X X X X hX λ='''+==+== .2. 单簧管直径均匀的细管,一端封闭而另一端开放,试求管内空气柱的本征振动,即求解()()2u u 00,t 0,,0.a tt xx u u l x ⎧⎪-=⎨==⎪⎩t 解:(1)分离变量 .令u(,)()()x t X x T t = X ()()0x X x λ''+= 2()()0T t a T t λ''+=由 得 u(0,t)=0X(0)=0由u (l,t)=0x得X ()=0l '(2)求解本征值 由 X ()()0x X x λ''+=X(0)=0,X (l)=0' 1(n+)2X ()=sinn xx l π 得(2n+1)()=n 2x lπλ(3)求()T t 将n λ代入方程:()T t 2122()()()02n T t a T t n n l π+''+=2121()cos()sin()22n n T t A at B at n n n l lππ++=+ (4)管内本征振动为:(,)()()u x t u x T t n n =n212121[cos()sin()]sin()2220,1,2n n n A at B at x n n l l ln πππ+++=+=3. 一根均匀固定于和0x =x l =两端,假设初始时刻速度为零,而初始时刻弦的形状是一抛物线,抛物线的顶点为(,)2lh ,求弦振动的位移。
