有理数乘除法混合运算1-3
《第3课时乘、除混合运算》示范教学方案

第一章 正数和负数1.5有理数的乘除第3课时 乘、除混合运算一、教学目标1. 能熟练地运用有理数的运算法则进行有理数的加、减、乘、除混合运算.2. 能运用有理数的运算律简化运算.3. 能利用有理数的加、减、乘、除混合运算解决简单的实际问题二、教学重点及难点重点:按有理数的运算顺序,正确而合理地进行有理数混合运算及掌握有理数乘法的运算律. 难点:灵活运用运算律及符号的确定.三、教学用具多媒体课件.四、相关资料无.五、教学过程【情景引入】1. 在小学我们已经学习过加、减、乘、除四则运算,其运算顺序是先算________,再算________,如果有括号,先算__________的.那么引入负数以后的有理数加、减、乘、除四则运算呢?他们的运算先后顺序是什么?让我们带着这个疑问进入今天的学习。
设计意图:创设问题情境,激发学生的认知兴趣。
【探究新知】简便计算,并回答根据什么?1.(1)125×0.05×8×40(小学数学乘法的交换律和结合律.) (2)361276595321⨯⎪⎭⎫⎝⎛++++(小学数学的分配律)2.上题变为(1)(-0.125)×(-0.05)×8×(-40)(2)()361276595321-⨯⎪⎭⎫⎝⎛-+--能否简便计算?也就是小学数学的乘法交换律和结合律、分配律在有理数范围内能否使用? 计算下列各题:(1)(-5)×2;(2)2×(-5);(3)[2×(-3)]×(-4);(4)2×[(-3)×(-4)] (5)()⎪⎭⎫ ⎝⎛+⨯-3123;(6)()()31323⨯-+⨯- 分别比较的计算结果比较的结果.:(1)与(2);(3)与(4);(5)与(6)的计算结果一样. 计算结果一样,说明了什么?说明算式相等.即:(1)(-5)×2=2×(-5); (2)[2×(-3)]×(-4)=2×[(-3)×(-4)]; (3)()⎪⎭⎫ ⎝⎛+⨯-3123=()()31323⨯-+⨯- 由(1),我们可以得到乘法交换律;由(2),可以得到乘法结合律;由(3),可以得到分配律. 结论:乘法的运算律在有理数范围内成立. 乘法的交换律:a×b=b×a . 乘法的结合律:(a×b)×c=a×(b×c) 分配律:a×(b+c)=a×b+a×c观察式子3×(2+1)÷⎝⎛⎭⎫5-12,里面有哪几种运算,应该按什么运算顺序来计算? 结论:运算顺序规定如下(由学生归纳): 1)先算乘除,再算加减;2)同级运算,按照从左至右的顺序进行; 3)如果有括号,就先算括号里的已知海拔高度每升高1000m ,气温下降6℃.某人乘热气球旅行,在地面时测得温度是8℃,当热气球升空后,测得高空温度是-1℃,热气球的高度为________m .答案:[8-(-1)]×(1000÷6)=1500(m )设计意图:通过多个例题的设置可让学生更深刻的理解有理数的乘除法混合运算。
有理数的乘除法混合运算

有理数的乘除法混合运算有理数的乘除法混合运算是数学中的一种常见题型。
对于学习有理数的同学们来说,掌握好这种混合运算的方法和技巧是非常重要的。
在进行有理数的乘除法混合运算时,我们需要遵循一定的顺序和规则。
首先,我们要将题目中的有理数用括号括起来,以免运算时出现错误。
其次,我们要进行乘法和除法运算,按照乘除法的优先级进行计算。
最后,将所有乘法和除法的结果相加或相减,得到最终的答案。
例如,我们来看一个例子:计算表达式2+3×4÷2。
按照乘除法的优先级,先计算乘法和除法。
3×4=12,然后再将12÷2=6。
最后,将2+6=8,所以答案是8。
在进行有理数的乘除法混合运算时,我们还需要注意有理数的正负问题。
正数乘以正数或者负数乘以负数,结果都是正数;正数乘以负数或者负数乘以正数,结果都是负数。
除法运算也是类似的规则,正数除以正数或者负数除以负数,结果都是正数;正数除以负数或者负数除以正数,结果都是负数。
除此之外,我们还需要注意有理数的乘除法运算可以转化为分数的乘除法运算。
通过将有理数转化为分数形式,我们可以更方便地进行计算。
例如,计算1/3×2/5÷4/6,我们可以先进行分数的乘除法运算,然后再将结果转化为有理数的形式。
有理数的乘除法混合运算是数学中的基础知识,我们在学习数学的过程中要多加练习,掌握好这一运算方法。
通过不断的练习和巩固,我们可以提高自己的计算能力和解题能力,为数学学习打下坚实的基础。
总之,有理数的乘除法混合运算是数学中的一种常见题型,通过掌握好运算顺序和规则,以及注意有理数的正负问题,我们可以正确解答这类题目。
同时,将有理数转化为分数的形式,也可以提高我们的计算效率。
希望同学们能够重视这一知识点,努力学好数学。
第3讲 有理数的乘除及乘方 -提高班
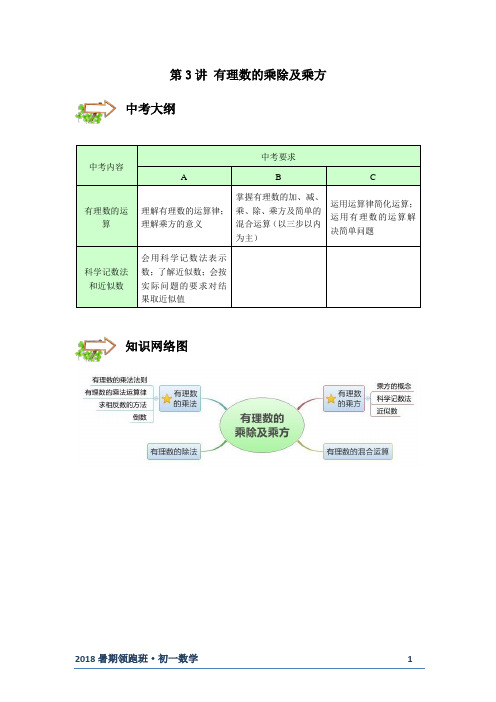
第3讲有理数的乘除及乘方中考内容中考要求A B C有理数的运算理解有理数的运算律;理解乘方的意义掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步以内为主)运用运算律简化运算;运用有理数的运算解决简单问题科学记数法和近似数会用科学记数法表示数;了解近似数;会按实际问题的要求对结果取近似值中考大纲知识网络图3.1有理数的乘法一. 有理数的乘法1. 有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.2. 有理数乘法的运算步骤:先确定积的符号,再确定积的绝对值.3. 有理数乘法的应用:要得到一个数的相反数,只要将它乘1-.4. 多个有理数相乘:(1)几个不是0的数相乘,负因数的个数是偶数时,积为正数;负因数的个数是奇数时,积为负数,即“奇负偶正”.(2)几个数相乘,如果其中有因数为0,那么积等于0. 5. 有理数乘法运算律:(1)乘法交换律:一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.ab ba =(2)乘法结合律:一般地,有理数乘法中,三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.()()ab c a bc =(3)分配律:一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.()a b c ab ac +=+二. 倒数1. 倒数的概念:乘积是1的两个数互为倒数. (1)倒数是成对出现的,单独一个数不能称为倒数.(2)互为倒数的两个数的乘积一定是1,即a ,b 互为倒数,则1a b ⨯=;反之亦然. (3)0没有倒数.2. 求一个非零有理数的倒数,把它的分子和分母颠倒位置即可. (1)非零整数可以看作分母为1的分数; (2)带分数一定要先化成假分数之后再求倒数.知识概述【例】(2017秋•顺义区期末)四个互不相等的整数的积为4,那么这四个数的和是( ) A .0 B .6C .﹣2D .2【练习】(2017秋•蓬溪县期末)如果a +b <0,并且ab >0,那么( ) A .a <0,b <0 B .a >0,b >0 C .a <0,b >0 D .a >0,b <0【例】(2016秋•芝罘区期末)已知abc >0,a >c ,ac <0,下列结论正确的是( ) A .a <0,b <0,c >0 B .a >0,b >0,c <0 C .a >0,b <0,c <0 D .a <0,b >0,c >0【例】(2017秋•滨海新区期末)对于有理数a 、b ,如果ab <0,a +b <0.则下列各式成立的是( )A .a <0,b <0B .a >0,b <0且|b |<aC .a <0,b >0且|a |<bD .a >0,b <0且|b |>a3.2有理数的除法一.有理数的除法1. 有理数除法法则:(1)除以一个不等于0的数,等于乘这个数的倒数.小试牛刀再接再厉总述思考:多个不是的数相乘,先做哪一步,再做哪一步?知识概述1a b a b÷=⋅,(0b ≠)(2)法则的另一说法:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.2. 有理数除法的运算步骤:先将除法换成乘法,然后确定积的符号,最后求出结果.3. 分数:分数可以理解为分子除以分母.二.有理数的乘除混合运算先将除法换成乘法,然后确定积的符号,最后求出结果. 注意:乘除混合运算要“从左到右”运算.【例】(2017秋•临沂月考)若x=(﹣1.125)×÷(﹣)×,则x 的倒数是( ) A .1 B .﹣1 C .±1 D .2【练习】(2017秋•郯城县月考)÷(﹣10)×(﹣)÷(﹣)【例】(2017秋•昌平区期末)计算:(﹣3)×6÷(﹣2)×.【练习】(2017秋•安图县期末)÷(﹣1)×.【例】(2017秋•怀柔区期末)计算:3×(﹣)÷(﹣1).5.(2017秋•城关区校级期中)计算: (1)﹣5÷(﹣1);(2)(﹣)÷(﹣)÷(﹣1).小试牛刀再接再厉3.3有理数的乘方一. 有理数的乘方1. 乘方的概念:求n 个相同因数的积的运算叫做乘方,乘方的结果叫做幂.(1)一般地,n 个相同的因数a 相乘,即n a a a a⋅⋅⋅⋅⋅⋅⋅个,记作,读作“a 的n 次方”;(2)在中,a 叫做底数,n 叫做指数;(3)当看作a 的n 次方的结果时,读作a 的n 次幂. 注意:()224-=,其底数为()2-,()()()22224-=-⨯-=;224-=-,其底数为2,()()222121224-=-⨯=-⨯⨯=-;239=749⎛⎫⎪⎝⎭,其底数为37,2333977749⎛⎫=⨯= ⎪⎝⎭; 239=77,其底数为3,23339777⨯==; 221391224⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,带分数的乘方运算,一定要先化成假分数后再运算.2. 一个数可以看作这个数本身的一次方,例如,5就是15,指数1通常省略不写.3. 幂的正负规律:(1)负数的奇次幂是负数,负数的偶次幂是正数,即“奇负偶正”; (2)正数的任何次幂都是正数; (3)0的任何正整数次幂都是0. 二. 科学记数法n a n a n a 总述思考:加减乘除混合运算的运算顺序是什么?知识概述1. 科学记数法:把一个大于10的数表示成10n a ⨯的形式(其中110a ≤<,n 是正整数).2. 用科学记数法表示一个n 位整数,其中10的指数是1n -,10的指数比整数的位数少1. 3. 万410=,亿810= 三.近似数1. 准确数:表示实际数量的数.2. 近似数:在一定程度上反映被考察量的大小,能说明实际问题的意义,与准确数非常地接近.3. 精确度:表示近似数与准确数的接近程度. 4. 精确度的类型: (1)纯数字类按四舍五入法对圆周率π取近似数时 3π≈(精确到个位)3.1π≈(精确到十分位,或叫精确到0.1)3.14π≈(精确到百分位,或叫精确到0.01) 3.142π≈(精确到千分位,或叫精确到0.001)(2)带单位类近似数2.6万(精确到千位) (3)科学记数法类近似数43.5110⨯(精确到百位)【例】(2018•金牛区校级模拟)下列各数|﹣2|,﹣(﹣2)2,﹣(﹣2),(﹣2)3中,负数的个数有()A .1个B .2个C .3个D .4个【练习】(2018•河北二模)下列各对数中,数值相等的是( ) A .+32与+22 B .﹣23与(﹣2)3 C .﹣32与(﹣3)2 D .3×22与(3×2)2小试牛刀再接再厉【练习】(2018•绵阳)四川省公布了2017年经济数据GDP排行榜,绵阳市排名全省第二,GDP总量为2075亿元,将2075亿用科学记数法表示为()A.0.2075×1012B.2.075×1011C.20.75×1010D.2.075×1012【例】(2018•绍兴)绿水青山就是金山银山,为了创造良好的生态生活环境,浙江省2017年清理河湖库塘淤泥约116 000 000方,数字116 000 000用科学记数法可以表示为()A.1.16×109B.1.16×108C.1.16×107D.0.116×109【例】(2016秋•吴中区期末)阅读下列各式:(a•b)2=a2b2,(a•b)3=a3b3,(a•b)4=a4b4…回答下列三个问题:(1)验证:(2×)100=____,2100×()100=_____;(2)通过上述验证,归纳得出:(a•b)n=_____;(abc)n=______.(3)请应用上述性质计算:(﹣0.125)2017×22016×42015.总述总结:“奇负偶正”你了解全了吗?3.4有理数的混合运算知识概述一.有理数混合运算顺序:1.先乘方,再乘除,最后加减;2. 同级运算,从左到右进行;3. 如有括号,先做括号内的运算,按小括号、中括号、大括号的顺序依次进行. 二. 进行有理数混合运算时的易错点:1. 乘方概念错误,如326=等.2. 底数错误,如2(2)4-=-,224-=等.3. 运算顺序发生错误,如1232123÷⨯=÷=等.4. 分配律运算错误,如112(2)22241522-⨯-=-⨯-⨯=--=-等.【例】(2017秋•招远市期末)形如的式子叫做二阶行列式,其运算法则用公式表示为=xn ﹣ym ,依此法则计算的结果为( )A .17B .﹣17C .1D .﹣1【练习】(2017秋•费县期末)现定义一种新运算“*”,规定a*b=ab +a ﹣b ,如1*3=1×3+1﹣3,则(﹣2*3)*5等于( ) A .71 B .47 C .﹣47 D .﹣71【例】(2017秋•揭西县期末)计算:(﹣2)2÷×(﹣2)﹣=______.【练习】(2017秋•河口区期末)计算8﹣23÷的值为_____.【例】(2017秋•泸县期末)计算:﹣14﹣×[2﹣(﹣3)2].小试牛刀再接再厉【例】(2018•杭州二模)计算:﹣23+6÷3×圆圆同学的计算过程如下:原式=﹣6+6÷2=0÷2=0请你判断圆圆的计算过程是否正确,若不正确,请你写出正确的计算过程.【练习】(2018•邵阳县模拟)计算:﹣14+16÷(﹣2)3×|﹣3﹣1|.【巩固】(2017秋•贵阳期末)计算:(1)1﹣43×(﹣)(2)7×2.6+7×1.5﹣4.1×8.。
专题01有理数的混合运算40道重难点题型专训(原卷版+解析)

(2) ;
(3)(﹣2)3﹣(﹣3)2;
(4) ;
(5) ;
(6) ;
(7) ;
(8) (用简便方法计算).
7.(2023春·黑龙江哈尔滨·六年级统考期中)计算:
(1)
(2)
(3)
8.(2023·全国·七年级假期作业)计算:
(1) ;
(2) ;
(3)
(4)
.
(2)解:原式
.
(3)解:原式=
=
=3.
(4)解:原式
.
【点睛】此题主要考查了有理数的混合运算,正确掌握相关运算法则是解题关键.
5.(2023秋·山东日照·七年级日照市新营中学校考阶段练习)计算:
(1)
(2)
(3)
(4)99 ×(-4)-( - - )×24
(5)计算:
【答案】(1)24
(2)-60
【详解】(1)解:
;
(2)
.
【点睛】本题考查了有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和法则.
11.(2023·上海·六年级假期作业)计算
(1)
(2)
【答案】(1)
(2)
【详解】(1)解:原式
;
(2)解:原式
;
【点睛】本题考查有理数四则混合运算的简便运算,解题的关键是熟练掌握有理数运算的各个法则.
【详解】(1)解:
;
(2)
;
(3)
;
(4)
.
【点睛】本题考查了有理数的混合运算,加法运算律,乘法运算律,熟练掌握相关运算法则是解题关键.
9.(2023·全国·七年级假期作业)简便计算
有理数混合运算(6种题型)(解析版)

有理数混合运算(6种题型)会进行有理数的混合运算,合理应用运算律,进行简便运算.一.有理数的混合运算(1)有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.【规律方法】有理数混合运算的四种运算技巧1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算.4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.二.计算器—基础知识(1)计算器的面板是由键盘和显示器组成.(2)开机键和关机键各是AC/ON,OFF,在使用计算器时要按AC/ON键,停止使用时要按OFF键.(3)显示器是用来显示计算时输入的数据和计算结果的装置.键上的功能是第一功能,直接输入,下面对应的是第二功能,需要切换成才能使用.(4)开方运算按用到乘方运算键x2的第二功能键”和的第二功能键“”.(5)对于开平方运算的按键顺序是:2ndfx2被开方数ENTE.(6)对于开立方运算的按键顺序是:32ndf∧被开方数ENTE.(7)部分标准型具备数字存储功能,它包括四个按键:MRC、M﹣、M+、MU.键入数字后,按M+将数字读入内存,此后无论进行多少步运算,只要按一次MRC即可读取先前存储的数字,按下M﹣则把该数字从内存中删除,或者按二次MRC.注意:由于计算器的类型不一样操作方式也不尽相同,可以参考说明书进行操作.三.计算器—有理数计算器包括标准型和科学型两种,其中科学型使用方法如下: (1)键入数字时,按下相应的数字键,如果按错可用(DEL )键消去一次数值,再重新输入正确的数字. (2)直接输入数字后,按下对应的功能键,进行第一功能相应的计算.(3)按下(﹣)键可输入负数,即先输入(﹣)号再输入数值.(4)开方运算按用到乘方运算键x 2的第二功能键”和的第二功能键“”.(5)对于开平方运算的按键顺序是:2ndfx 2被开方数ENTE 或直接按键,再输入数字后按“=”即可.(6)对于开立方运算的按键顺序是:32ndf ∧被开方数ENTE 或直接按x 3,再输入数字后按“=”即可 注意:由于计算器的类型不一样操作方式也不尽相同,可以参考说明书进行操作.题型一:有理数四则混合运算一、填空题1.(2022秋·江苏无锡·七年级统考期中)定义一种新运算:x y x y xy =+−★,则计算()32−=★___________.【答案】5【详解】解:∵x y x y xy =+−★,∴()()3232323265−=−+−−⨯=−++=★,故答案为:5【点睛】本题考查了新运算和有理数的混合运算,理解新运算的定义是解题的关键.二、解答题 2.(2022秋·江苏徐州·七年级校考阶段练习)计算(1)13251216−+−(2)()()()0510037÷−⨯+−÷−(3)()()()25549−⨯−÷−+【答案】(1)16− (2)37(3)47(4)1−【分析】(1)原式结合后,相加即可求出值;(2)原式先算乘除运算,再算加减运算即可求出值;(3)原式先算乘除运算,再算加法运算即可求出值;(4)原式利用减法法则变形,结合后相加即可求出值.【详解】(1)原式()1312251616=+−−=−; (2)原式33077=+=;(3)原式24947=−+=;(4)原式223331212113344=−++−=−+=−.【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.【答案】(1)24−(2)14 【分析】(1)利用乘法分配律进行计算即可;(2)先计算乘除法,再计算加减法即可.【详解】(1)解:1336124⎛⎫⨯− ⎪⎝⎭ 133636124⎛⎫=⨯+⨯− ⎪⎝⎭327=−24=−(2)()()18632−÷−⨯−()118623⎛⎫=−⨯−⨯− ⎪⎝⎭184=−14=【点睛】此题考查了有理数的混合运算,熟练掌握运算法则和运算律是解题的关键.【答案】(1)5−(2)11−(3)1179919− (4)6−(5)81(6)75=【分析】(1)根据有理数加法的运算律,同分母的相结合,能凑整的相结合,再进行计算.(2)运用乘法分配律进行计算即可.(3)将原式写成1(100)(18)19−⨯−,再根据乘法分配律进行计算即可. (4)倒用乘法分配律+ab ac ad a b c d +=++()进行计算即可.(5)先根据“除以一个数等于乘以它的倒数”,将除法运算变为乘法运算,再运用乘法分配律进行计算即可.(6)按照有理数混合运算法则:先乘方,再乘除,最后再加减,有括号的先算括号里边的,进行计算即可.【详解】(1)34(3)12.5(16)( 2.5)77−++−−−34(3)12.5(16) 2.577=−++−+34[(3)(16)](12.5 2.5)77=−+−++2015=−+=5−;(2)7537()(36)96418−+−⨯−75373636363696418=−⨯+⨯−⨯+⨯28302714=−+−+22714=−+2514=−+11=−;(3)18991819−⨯1(100)(18)19=−⨯−1100181819=−⨯+⨯ 18180019=−+ 1179919=−;(4)22218()134333⨯−+⨯−⨯ 22218134333=−⨯+⨯−⨯2(18134)3=−+−⨯2(9)3=−⨯ 6=−;(5)1571(3)()261236−+−÷−157(3)(36)2612=−+−⨯−1573633636362612=−⨯+⨯−⨯+⨯181083021=−+−+903021=−+6021=+81=;(6)211[(4)(0.4)]3(2)343÷−−⨯−÷⨯−−21[()0.1]33234=⨯−+⨯⨯+11()332610=−+⨯⨯+133215=−⨯⨯+325=−+75=【点睛】本题主要考查了有理数的四则混合运算,熟练掌握运算律和运算法则是解题的关键.【答案】(1)6(2)5 【详解】(1)解:()()745−−+−745=+−6=;(2)解:113(60)234⎛⎫−−+⨯− ⎪⎝⎭113(60)(60)(60)234=−⨯−−⨯−+⨯−302045=+−5=. 【点睛】本题考查有理数的加减混合运算,有理数的四则混合运算.掌握有理数的混合运算法则是解题关键.注意在解(2)时利用乘法分配律更简便.6.(2020秋·江苏徐州·七年级校考阶段练习)计算:(1)()()2317716−−−+−112019++−【答案】(1)3−(2)45.08−(3)19 30(4)1 3(5)7 4−(6)7(7)54−(8)17 60【详解】(1)解:()() 2317716−−−+−2317716 =−+−710=−3=−;(2)()()26.54 6.418.54 6.4−+−−+26.5418.54 6.4 6.4 =−−−+45.08=−;(3)3111253⎛⎫+−−+ ⎪⎝⎭ 3111253=−−+ 456301*********=−−+1930=;(4)531245⎛⎫⎛⎫−⨯− ⎪ ⎪⎝⎭⎝⎭58245=⨯ 13=;(5)172.5(8)516⎛⎫⎛⎫−⨯⨯−⨯− ⎪ ⎪⎝⎭⎝⎭15785216=−⨯⨯⨯74=−;(6)251(18)(3)29115⎛⎫⎛⎫−⨯−+−⨯−⨯ ⎪ ⎪⎝⎭⎝⎭ 15114115=+⨯43=+7=;(7)12(45)35⎡⎤⎛⎫⎛⎫−÷−÷− ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 15(45)32⎛⎫=−÷⨯ ⎪⎝⎭5(45)6=−÷ 6(45)5=−⨯54=−;(8)111111114354652019−+−+−++−111111113445561920=−+−+−++−11320=− 2036060=−1760=.【点睛】此题考查了有理数的四则混合运算,正确掌握有理数混合运算的法则及运算顺序是解题的关键.【答案】25【分析】根据题意的算法进行运算,即可求得结果.【详解】解:原式的倒数是129314510220⎛⎫⎛⎫−−+−÷− ⎪ ⎪⎝⎭⎝⎭()12932045102⎛⎫=−−+−⨯− ⎪⎝⎭581830=+−+25=故原式125=.【点睛】本题考查了有理数的混合运算,理解题意,正确运算是解决本题的关键.8.(2022秋·江苏扬州·七年级校联考期中)定义一种新运算:观察下列各式,并解决问题.131538=⨯+=,3135116=⨯+=,5455429=⨯+=,请你想一想:43= a b = ab b a (填入()543−. 【答案】(1)23,5a b +(2)≠(3)42−【分析】(1)根据题目所给新运算的运算顺序和运算法则进行计算即可;(2)先根据题目所给新运算的运算顺序和运算法则将a b 和b a 计算出来,再用作差法比较即可;(3)根据题目所给新运算的运算顺序和运算法则进行计算即可.【详解】(1)解:4345323=⨯+=;5a b a b =+;故答案为:23,5a b +.(2)∵5a b a b =+,5b a b a =+,∴()()()()5544a b b a a b b a a b −=+−+=−,∵a b ¹,∴440a b −≠∴a b b a ≠.故答案为:≠.(3)()543−−()5453=−−⨯+ ()517=−−()5517=−⨯+− 42=−.【点睛】本题主要考查了新定义下的有理数的混合运算,解题的关键是正确理解题意,明白题中所给新定义的运算顺序和运算法则,熟练掌握有理数的混合运算顺序和运算法则.题型二:有理数四则混合运算的应用一、填空题1.(2022秋·江苏·七年级开学考试)园林公司在林州大道旁种植了120棵树,有116棵成活,后来又补栽4棵,全部成活,这124棵树苗的成活率为_____【答案】97%【分析】根据成活率等于成活数除以总数再乘以100%计算即可.【详解】解:1164100%97% 1204+⨯≈+.答:成活率是97%.故答案为:97%.【点睛】此题属于百分率问题,明确成活率是指成活的棵数占总棵数的百分之几;要注意题中的“全部成活”,是指后来又补种的4棵全部成活,而不是种的120棵全部成活.二、解答题(1)接送完第5批客人后,该驾驶员在邗江路和文昌路十字路口什么方向,距离十字路口多少千米?(2)后来他开车回到出发地,途中没有带到客人,若该出租车每千米耗油0.09升,那么在整个过程中共耗油多少升?(3)若该出租车的计价标准为:行驶路程不超过3km收费9元,超过3km的部分按每千米加1.8元收费,在整个行驶过程中,该出租车驾驶员共收到车费多少元?【答案】(1)东3千米处(2)2.16升(3)57.6元【分析】(1)求出行驶路程的代数和,利用结果的符号和数值作出判断即可;(2)求出行驶路程的绝对值的和,利用路程和乘以每千米耗油量即可得出结论;(3)分别计算接送每批客人的收费数额再相加即可得出结论.【详解】(1)∵()()347253km ++−+−+=,∴出租车在解放路和青年路十字路口东边,距离十字路口3千米;(2)∵34725324km ++−+−++=,∴240.09 2.16⨯=(升).∴在这过程中共耗油2.16升.(3)∵接送第一批客人的收费为:9元,接送第二批客人的收费为:()9 1.84310.8+⨯−=(元),接送第三批客人的收费为:()9 1.87316.2+⨯−=(元),送第四批客人的收费为:9元,接送第五批客人的收费为:()9 1.85312.6+⨯−=(元),∴910.816.2912.657.6++++=(元).所以在这过程中该出租车驾驶员共收到车费57.6元.【点睛】本题考查了正负数的意义和有理数的运算,解题关键是明确正负数的意义,能熟练运用有理数运算法则进行计算.【答案】(1)小明家这10天轿车行驶的路程为240km(2)估计小明家一个月耗电费用为162元【分析】(1)记录数字的和再加上10个25即可得到结果;(2)用(1)的结论乘以3即可得到总路程,再根据“该轿车每行驶100km耗电15度,且轿车充电的价格为每度1.5元,”列式解答即可;【详解】(1)解:()314182623210km +−+−+−+−+=−,()251010240km ⨯−=,答:小明家这10天轿车行驶的路程为240km . (2)240310015 1.5162⨯÷⨯⨯=(元),答:估计小明家一个月(按30天算)的电动轿车耗电费用为162元.【点睛】本题考查正数与负数以及有理数的加减乘除混合运算,正确列出算式并掌握相关运算法则是解答本题的关键.4.(2022秋·江苏泰州·七年级泰州市第二中学附属初中校考期中)小刚坐公交车去参加志愿者活动,他从南站上车,上车后发现车上连自己共有12人,经过A 、B 、C 、D 4个站点时,他观察到上下车情况如下(记上车为正,下车为负):()3,2A +−,()5,3B +−,()3,4C +−,()7,4D +−. (1)经过4个站点后车上还有 人;(2)小刚发现在A 、B 、C 、D 这四站上车的人中,有一半投币付费(每人2元),还有一半刷卡付费(每人1.4元),求这四站公交公司共收入多少元? 【答案】(1)17(2)这四站公交公司共收入30.6元【分析】(1(2)先求出4个站一共上车的人数,再根据这四站上车的人中,有一半投币付费(每人2元),还有一半刷卡付费(每人1.4元),进行求解即可. 【详解】(1)解:()()()()()()()()1232533474+++−+++−+++−+++−1232533474=+−+−+−+−125=+ 17=人,∴经过4个站点后车上还有17人; (2)解:353718+++=人,11218 1.41830.622⨯⨯+⨯⨯=元,∴这四站公交公司共收入30.6元,答:这四站公交公司共收入30.6元.【点睛】本题主要考查了有理数的加法的应用,有理数混合计算的应用,正确理解题意是解题的关键.(1)这20筐苹果中,最重的一筐比最轻的一筐多重千克.(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?(3)若苹果每千克售价85元,则出售这20筐苹果可卖多少元?【答案】(1)5.5(2)超过8千克(3)43180元【分析】(1)根据正负数的意义确定最重的一筐和最轻的一筐,然后利用有理数减法计算法则求解即可;(2)把所给的记录相加,如果结果为正则超过标准重量,如果结果为负则不足;(3)先求出这20筐苹果的总重量,然后根据可卖的钱数=单价×重量进行求解即可.【详解】(1)解:由表格可知,最重的一筐比最轻的一筐重:()2.53 5.5−−=(千克).答:最重的一筐比最轻的一筐多重5.5千克.(2)解:由表格可得,()()()3124 1.520321 2.58−⨯+−⨯+−⨯+⨯+⨯+⨯()()()3830220=−+−+−+++8=(千克).答:与标准重量比较,20筐苹果总计超过8千克.(3)解:由题意可得,()202588543180⨯+⨯=(元),∴出售这20筐苹果可卖43180元.【点睛】本题主要考查了有理数减法的应用,有理数四则混合运算的应用,正确理解题意是解题的关键.6.(2022秋·江苏扬州·七年级校考阶段练习)思考下列问题并在横线上填上答案.(1)已知数轴上有M ,N 两点,点M 与原点的距离为2,M ,N 两点的距离为1.5,则满足条件的点N 所表示的数是__________;(2)在纸上画了一条数轴后,折叠纸面,使数轴上表示2的点与表示4−的点重合,若数轴上E ,F 两点之间的距离是10(E 在F 的左侧),且E 、F 两点经过上述折叠后重合,则点E 表示的数是__________,点F 表示的数是__________;(3)数轴上点A 表示数8,点B 表示数8−,点C 在点A 与点B 之间,点A 以每秒0.5个单位的速度向左运动,点B 以每秒1.5个单位的速度向右运动,点C 以每秒3个单位的速度先向右运动碰到点A 后立即返回向左运动,碰到点B 后又立即返回向右运动,碰到点A 后又立即返回向左运动…,三个点同时开始运动,当三个点聚于一个点时,这一点表示的数是多少?点C 在整个运动过程中,移动了多少单位? 【答案】(1)3.5或0.5或 3.5−或0.5− (2)6−,4 (3)8,4,24【分析】(1)先求出点M 所表示的数,进而即可求解; (2)先求出折痕对应的数为:-1,进而即可求解; (3)先求出A 、B 相遇时所花的时间,进而即可求解. 【详解】(1)解:∵点M 2, ∴点M 表示的数为:2±, ∵,M N 两点的距离为1.5,∴N 表示的数为:2 1.5 3.5±=或0.5;2 1.5 3.5−±=−或0.5−, 故答案是:3.5或0.5或 3.5−或0.5−;(2)∵折叠纸面,使数轴上表示2的点与表示4−的点重合, ∴折痕对应的数为:1−,∵数轴上,E F 两点之间的距离是10(E 在F 的左侧),且,E F 两点经过上述折叠后重合, ∴点E 表示的数是:156−−=−,点F 表示的数是:154−+=, 故答案是:6−,4;(3)当三个点聚于一个点时,则A 、B 相遇,运动的时间为:()()880.5 1.58+÷+=(秒),此时,这一点表示的数是:8 1.584−+⨯=,点C 在整个运动过程中,移动了:2483=⨯个单位.【点睛】本题主要考查数轴上的点所表示的数,两点间的距离,折叠的性质,掌握数轴上两点的距离等于对应的两数之差的绝对值,是解题的关键.【答案】(1)3(2)a 的值为8,点A 表示的数为2−,点B 表示的数为6 (3)72【分析】(1)根据数轴的性质列出运算式子,再计算有理数的加法即可得;(2)先根据3根木条的长度等于14与10−之间的距离可求出a 的值,再根据数轴的性质列出运算式子,计算有理数的加减法即可得;(3)先参照(2)的思路求出爷爷比小红大52岁,再利用124减去52即可得. 【详解】(1)解:由题意得:点B 表示的数为253−+=,故答案为:3.(2)解:由题意得:a 的值为()141038−−÷=⎡⎤⎣⎦, 则点A 表示的数为1082−+=−, 点B 表示的数为1486−=,即a 的值为8,点A 表示的数为2−,点B 表示的数为6.(3)解:由题意得:爷爷比小红大()12432352−−÷=⎡⎤⎣⎦(岁), 则爷爷现在的年龄为1245272−=(岁), 故答案为:72.【点睛】本题考查了数轴、有理数的加减法与除法的应用,熟练掌握数轴的性质是解题关键. 题型三:程序流程图与有理数计算一、单选题【答案】B【分析】分别将三组数据代入程序流程图运算求解即可. 【详解】解:①当7x =,2y =时x y >, 222()(72)525x y ∴−=−==;②当2x =−,=3y −时x y >,[]222()2(3)11x y ∴−=−−−==;③当4,1x y =−=−时x y <,[]222()4(1)(5)25x y ∴+=−+−=−=,∴能使输出的结果为25的有①③,故选:B .【点睛】本题主要考查了与程序流程图有关的有理数计算,有理数比较大小,正确读懂程序流程图是解题的关键.二、填空题2.(2022秋·江苏盐城·七年级校考阶段练习)如图所示是计算机某计算型序,若开始输入2x =−,则最后输出的结果是__________.【答案】14−【分析】直接利用运算程序,进而计算得出答案. 【详解】解:当2x =−时,()231615−⨯−−=−+=−,则5x =−时,()53115114−⨯−−=−+=−,故答案为:14−.【点睛】本题考查了有理数的混合运算,掌握有理数的运算法则,理解本题的运算程序是解决本题的关键. 3.(2020秋·江苏扬州·七年级校考期中)根据如图所示的程序计算,若输入x 的数值为2−,则输出的数值为______.【答案】 3.625−/538−/298−【分析】把x 的值代入程序中计算,再根据结果3<−输出即可. 【详解】解:把2x =−代入程序中计算得:()()2212⎡⎤⎣+⎦−÷−()()412=+÷−()52=÷−2.53=−>−,把 2.5x =−代入程序中计算得:()()22.512⎡+⎤⎣⎦−÷−()()6.2512=+÷−()7.252=÷−3.6253=−<−.故输出的数值为 3.625−. 故答案为: 3.625−.【点睛】此题考查了有理数的混合运算,代数式求值,熟练掌握运算法则是解本题的关键.【答案】4【分析】根据程序流程图的流程,列出算式,进行计算即可.【详解】解:输入的值为1时,由图可得:212420⨯−=−<;输入2−可得:()222440−⨯−=>;∴输出的值应为4; 故答案为:4.【点睛】本题考查程序流程图.按照流程图的流程准确的列出算式,是解题的关键.5.(2022秋·江苏淮安·七年级统考期中)如图所示是计算机程序计算,若开始输入1x =−,则最后输出的结果是___.【答案】-11【分析】读懂计算程序,把1x =−,代入,按计算程序计算,直到结果小于5−即可. 【详解】解:当输入x ,若()41x ⨯−−小于5−,即为输出的数,当1x =−时,()()()414113x ⨯−−=⨯−−−=−,3−不小于5−,因此,把3x =−再输入得,()()()4143111x ⨯−−=⨯−−−=−,11−小于5−,故答案为:11−.【点睛】本题考查实数的混合运算,掌握计算法则是关键.6.(2022秋·江苏无锡·七年级校考期中)如图是一个对于正整数x 的循环迭代的计算机程序.根据该程序指令,如果第一次输入x 的值是3时,那么第一次输出的值是10;把第一次输出的值再次输入,那么第二次输出的值是5;把第二次输出的值再次输入,那么第三次输出的值是16;以此类推得到一列输出的数为10,5,16,8,4,2,1,4,…若第五次输出的结果为1,则第一次输入的x 为 _____.【答案】32、5、4【详解】解:若第五次输出的结果为1, 则第5次输入为:2, 第4次输出为:2, 第4次输入为:4, 第3次输出为:4, 第3次输入为:8或1, 第2次输出为:8或1, 第2次输入为:16或2, 第1次输出为:16或2, 第1次输入为:32、5或4, 故答案为:32、5、4.【点睛】本题考查了有理数的混合运算,解题关键是读懂题意,寻找到数字变化的规律,利用规律解决问题.三、解答题 7.(2023秋·江苏扬州·七年级统考期末)如图,按图中的程序进行计算.(1)当输入的30x =时,输出的数为______;当输入的16x =−时,输出的数为______;(2)若输出的数为52-时,求输入的整数x 的值.【答案】(1)60−,64−;(2)26x =±或13±【分析】(1)根据图中的程进行列式计算,即可求解;(2)当输出的数为52-时,分两种情况进行讨论.【详解】(1)解:根据运算程序可知:当输入的30x =时,得:()3026045⨯−=−−<, ∴输入的30x =时,输出的数为60−;根据运算程序可知:当输入的16x =−时,得:()1623245−⨯−=−−>; 再输入32x =−,得:()3226445−⨯−=−−<,∴输入的32x =−时,输出的数为64−;故答案为:60−,64−;(2)解:当输出的数为52-时,分两种情况: 第一种情况:()252x ⨯−=−,解得:26x =±;第二种情况:当第一次计算结果为26−时,再循环一次输入的结果为52-,则()226x ⨯−=−,解得:13x =±,综上所述,输出的数为52-时,求输入的整数x 的值为:26x =±或13±. 【点睛】本题考查程序流程图与有理数的计算、绝对值,解题的关键是掌握有理数的运算法则和解绝对值方程.题型四:算“24”点一、填空题1.(2022秋·七年级单元测试)用一组数3,4,﹣4,﹣6算24点(每个数只能用一次):________.【答案】3×4×[﹣4﹣(﹣6)]=24(答案不唯一)【分析】此题只要符合题的要求,得数等于24即可,答案不唯一.【详解】解:3×4×[﹣4﹣(﹣6)]=12×(﹣4+6)=12×2=24,故答案为:3×4×[﹣4﹣(﹣6)]=24(答案不唯一).【点睛】本题主要考查有理数的混合运算,此题要注意要求的得数为24,而且每个数字只能用一次. 2.(2022秋·江苏镇江·七年级校联考阶段练习)“24点游戏”指的是将一副扑克牌中任意抽出四张,根据牌面上的数字进行混合运算(每张牌只能使用一次),使得运算结果是24或者是24−,现抽出的牌所对的数字是4,5−,3,1−,请你写出刚好凑成24的算式__________.【答案】[]34(5)1⨯−−−【分析】利用“24点游戏”的游戏规则写出算式即可.【详解】解:根据题意得:[]34(5)1⨯−−−38=⨯=24.故答案为:[]34(5)1⨯−−−(答案不唯一).【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.3.(2022秋·江苏南京·七年级南京钟英中学校考阶段练习)已知4个有理数:1,2,3,4−−−−,在这4个有理数之间用“,,,+−⨯÷”连接进行四则运算,每个数只用一次,使其结果等于24,你的算法是___________.【答案】(1)(2)(3)(4)24−⨯−⨯−⨯−=(答案不唯一)【分析】根据“24点”游戏规则列出算式即可.【详解】解:(1)(2)(3)(4)24−⨯−⨯−⨯−=故答案为:(1)(2)(3)(4)24−⨯−⨯−⨯−=(答案不唯一)【点睛】此题考查了有理数的混合运算,弄清“24点”游戏规则是解题的关键 4.(2022秋·江苏南京·七年级阶段练习)算“24点”是一种数学游戏:把所给的四个数字用运算符号(可以有括号)连接起来,使得运算结果为24,注意:每个数字只能用一次,请你用“5、5、5、1”这4个数字算“24点”,列出的算式是____.【答案】555124⨯−=(答案不唯一)【分析】解答此题应根据数的特点,四则混合运算的运算顺序,进行尝试凑数即可解决问题。
小升初衔接数学课堂:第5讲 有理数的乘除法

第5讲有理数的乘除法【知识衔接】————小学初中课程解读————————小学知识回顾————一、乘法(1)求几个相同加数的和的简便运算叫乘法。
(2)相乘的两个数叫因数。
(3)因数相乘所得的数叫积。
(4)两个因数相乘,交换因数的位置,它们的积不变,这叫乘法交换律。
(5)三个数相乘,先把前两个数相乘,再同第三个数相乘,或者先把后两个数相乘,再同第一个数相乘,它们的积不变,这叫乘法结合律。
(6)小数乘法的计算法则计算小数乘法,先按照乘法的法则算出积,再看因数中一共几位小数,就从积的右边起数出几位,点上小数点。
(7)一位数乘多位数乘法法则1、从个位起,用一位数依次乘多位数中的每一位数;2、哪一位上乘得的积满几十就向前进几。
(8)一个因数是两位数的乘法法则1、先用两位数个位上的数去乘另一个因数,得数的末位和两位数个位对齐;2、再用两位数的十位上的数去乘另一个因数,得数的末位和两位数十位对齐;3、然后把两次乘得的数加起来。
(9)分数的乘法则:用分子的积做分子,用分母的积做分母。
(10)分数乘整数:分子与整数相乘的积做分子,分母不变,或者整数和分母约分的积。
(11)分数乘分数:分子相乘做分子,分母相乘做分母。
特别注意,当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。
二、除法(1已知两个因数的积与其中的一个因数,求另一个因数的运算叫除法。
(2)在除法中,已知的积叫被除数。
(3)在除法中,已知的一个因数叫除数。
(4)在除法中,求出的未知因数叫商。
(5)除数是整数除法的法则除数是整数的小数除法,按照整数除法的法则去除,商的小数点要和被除数小数点对齐,如果除到被除数的末尾仍有余数,就在余数后面添0再继续除。
(6)除数是小数的除法运算法则除数是小数的除法,先移动除数小数点,使它变成整数;除数的小数点向右移几位,被除数小数点也向右移几位(位数不够在被除数末尾用0补足)然后按照除数是整数的小数除法进行计算。
(7)除数是一位数的除法法则1、从被除数高位除起,每次用除数先试除被除数的前一位数,如果它比除数小再试除前两位数;2、除数除到哪一位,就把商写在那一位上面;3、每求出一位商,余下的数必须比除数小。
有理数的运算法则
有理数的运算法则
一、有理数的加减法法则:
1. 两个有理数同号,相加后仍为同号,即正加正得正,负加负
得负;
2. 两个有理数异号,相加后正数的绝对值大于负数的绝对值,
结果的符号与绝对值较大的数相同;
3. 有理数的加法满足交换律,即 a + b = b + a。
二、有理数的乘除法法则:
1. 两个有理数同号,相乘后为正,即正乘正得正,负乘负得正;
2. 两个有理数异号,相乘后为负,即正乘负得负,负乘正得负;
3. 有理数的乘法满足交换律,即 a × b = b × a;
4. 有理数相乘,可以先化简再计算,如分子分母都可以约去公
因数;
5. 有理数相除,可以先取倒数再进行乘法运算。
三、有理数的混合运算法则:
1. 先进行括号内的运算;
2. 依次进行乘除法;
3. 依次进行加减法。
四、有理数的运算与绝对值:
1. 一个有理数的相反数和该有理数的绝对值具有相同的绝对值;
2. 任何与零相等的有理数绝对值为零。
以上是有理数的运算法则,在进行数学运算时,请按照这些规
则进行操作,以确保得到正确的结果。
七年级数学 :有理数的加减乘除混合运算
)÷×[-2-(-8)]-
1 8
0.52
。
(5 1) (3) ( 13) (3)
3
3
1.2 2 1 5 1 3.4 (1.2) 53
1 4
2
2
1 2
11
1 4
2
1 3
A1.3 434
24
B.013.23
C.6
1 2
D. 52
1 3
2
3 4
7 8
3
2 3
3
7 5
2 -1 2 -1 则2S= 2+22+23+24+...+22009 ,因此2S-S= 2009
所以1+2+22 +23+...+22008 = 2009
仿照以上推理计算出 1+5+52 +53+... 52009 的值是( )
A、 B、 52009-1
52010 -1
C、52009 -1 4
D、52010 -1 4
A、-2+4-3+5 B、-2-4+3+5 C、-2-4-3+5 D、-2+3+5+4
3. 在算式4- 35 中的△所在的位置,填入下列哪种运算符号,计算
出来的值最小( )。
A、+ B、- C、× D、÷
4.如果|x|=|y|,那么x与y的关系是________;如果-|x|=|-x|那么
x=_______. 5.某市今年财政收入达到105.5亿元,用科学记数法(保留三位有 效数字)表示105.5亿元为_______________元
为( )
第二节 有理数的加减乘除混合运算
暑假 第二节 有理数的加减乘除混合运算一 有理数的运算法则⑴加法法则:同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0。
⑵减法法则:减去一个数,等于加上这个数的相反数。
⑶乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与0相乘都得0。
⑷除法法则:除以一个数等于乘上这个数的倒数;两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不等于0的数,都得0。
二、什么叫有理数的乘方?幂?底数?指数?答:相同因数相乘积的运算叫乘方,乘方的结果叫幂,相同因数的个数叫指数,这个因数叫底数。
记作an 。
三、有理数乘方运算的法则是什么?答:负数的奇次幂是负数,负数的偶次幂是正数。
正数的任何次幂都是正数。
零的任何正整数幂都是零。
四、有理数混合运算时,对于运算顺序有什么规定?答:在有理数混合运算时,将运算分为三级,加减为一级运算,乘除为二级运算,乘方为三级运算。
同级运算时,从左到右依次进行;不是同级的混合运算,先算乘方,再算乘除,而后才算加减;运算中如有括号时,先做括号内的运算,按小括号、中括号、大括号的顺序进行。
五 什么叫科学记数法?答:将一个数用a×10n 表示,这样的记数方法叫科学记数法。
这里的a 必须是整数位只有一位的数。
n 必须是正整数。
读作a 乘10的n 次方(或a 乘10的n 次幂)。
a (1≤a <10)六 什么叫近似数?近似数是怎样获得的?什么是近似数的精确度? 答:近似数是接近准确数,但和准确数有差别的数。
在现行的教科书中近似数是通过四舍五入法获得的。
近似数与准确数的接近程度叫精确度。
七、什么叫有效数字?答:一个数从左边第一个不为零的数起,到末位数字止都叫这个数的有效数字,有效数字有几个,就叫这个数有几个有效数字。
如:0.01350叫这个数有四个有效数字。
*互为相反数的两数的和为0,互为倒数的两数的积为1;0的相反数是0,0没有倒数;相反数是本身的数只有一个0,倒数是本身的数有1和-1.交流得出平方根的性质:(展示)一个正数有正、负两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
第六讲 有理数的乘除法2021年新七年级数学暑假课程(浙教版)(解析版)
第六讲有理数的乘除法2.3-2.4 有理数的乘法有理数的除法【学习目标】1.会根据有理数的乘法法则进行乘法运算,并运用相关运算律进行简算;2.理解乘法与除法的逆运算关系,会进行有理数除法运算;3. 巩固倒数的概念,能进行简单有理数的加、减、乘、除混合运算;【基础知识】一、有理数的乘法1.有理数的乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;(2)任何数同0相乘,都得0.要点: (1) 不为0的两数相乘,先确定符号,再把绝对值相乘.(2)当因数中有负号时,必须用括号括起来,如-2与-3的乘积,应列为(-2)×(-3),不应该写成-2×-3.2. 有理数的乘法法则的推广:(1)几个不等于0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数的个数有偶数个时,积为正;(2)几个数相乘,如果有一个因数为0,那么积就等于0.要点:(1)在有理数的乘法中,每一个乘数都叫做一个因数.(2)几个不等于0的有理数相乘,先根据负因数的个数确定积的符号,然后把各因数的绝对值相乘.(3)几个数相乘,如果有一个因数为0,那么积就等于0.反之,如果积为0,那么至少有一个因数为0.3. 有理数的乘法运算律:(1)乘法交换律:两个数相乘,交换因数的位置,积相等,即:ab=ba.(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.即:abc=(ab)c =a(bc).(3)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.即:a(b+c)=ab+ac.要点:(1)在交换因数的位置时,要连同符号一起交换.(2)乘法运算律可推广为:三个以上的有理数相乘,可以任意交换因数的位置,或者把其中的几个因数相乘.如abcd=d(ac)b.一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.如a(b+c+d)=ab+ac+ad.(3)运用运算律的目的是“简化运算”,有时,根据需要可以把运算律“顺用”,也可以把运算律“逆用”.二、有理数的除法1.倒数的意义:乘积是1的两个数互为倒数.要点:(1)“互为倒数”的两个数是互相依存的.如-2的倒数是12-,-2和12-是互相依存的;(2)0和任何数相乘都不等于1,因此0没有倒数;(3)倒数的结果必须化成最简形式,使分母中不含小数和分数;(4)互为倒数的两个数必定同号(同为正数或同为负数).2. 有理数除法法则:法则一:除以一个不等于0的数,等于乘这个数的倒数,即1(0)a b a b b÷=≠. 法则二:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0. 要点:(1)一般在不能整除的情况下应用法则一,在能整除时应用法则二方便些.(2)因为0没有倒数,所以0不能当除数.(3)法则二与有理数乘法法则相似,两数相除时先确定商的符号,再确定商的绝对值.三、有理数的乘除混合运算由于乘除是同一级运算,应按从左往右的顺序计算,一般先将除法化成乘法,然后确定积的符号,最后算出结果.四、有理数的加减乘除混合运算有理数的加减乘除混合运算,如无括号,则按照“先乘除,后加减”的顺序进行,如有括号,则先算括号里面的.【考点剖析】例1.下列计算正确的有( )①(-3)(-4)-12⨯=;②(-2)5-10⨯=;③(-41)(-1)41⨯=;④0(-5)-5⨯=A .1个B .2个C .3个D .4个 【答案】B【解析】根据有理数的乘法法则进行计算,可得正确答案.①(-3)(-4)12⨯=,故此项不符合题意;②(-2)5-10⨯=,故此项符合题意;③(-41)(-1)41⨯=,故此项符合题意;④0(-5)0⨯=,故此项不符合题意;所以正确的有②,③故选:B .【点睛】此题主要考查了有理数的计算,关键是掌握乘法计算的计算法则.例2.下列运算过程中,有错误的是( )A .(3﹣412)×2=3﹣412×2 B .﹣4×(﹣7)×(﹣125)=﹣(4×125×7)C.91819×16=(10﹣119)×16=160﹣1619D.[3×(﹣25)]×(﹣2)=3×[(﹣25)×(﹣2)]【答案】A【解析】各式计算得到结果,即可作出判断.解:A、原式=3×2﹣92×2=6﹣9=﹣3,符合题意;B、原式=﹣(4×125×7),不符合题意;C、原式=(10﹣119)×16=160﹣1619,不符合题意;D、原式=3×[(﹣25)×(﹣2)],不符合题意.故选:A.【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.例3.下列说法正确的是()A.零除以任何数都得0B.几个有理数相乘,积的符号由负因数的个数决定C.绝对值相等的两个数相等D.两个数互为倒数,则它们的相同次幂仍互为倒数【答案】D【解析】A、任何数包括0,0除0无意义;B、几个不为0的有理数相乘,积的符号由负因数的个数决定;C、绝对值相等的两个数的关系应有两种情况;D、根据倒数及乘方的运算性质作答.解:A、零除以任何不等于0的数都得0,故错误;B、几个不为0的有理数相乘,积的符号由负因数的个数决定,故错误;C、绝对值相等的两个数相等或互为相反数,故错误;D、两个数互为倒数,则它们的相同次幂仍互为倒数,故正确.故选:D.【点睛】本题主要考查了绝对值、倒数的概念和性质及有理数的乘除法、乘方的运算法则.要特别注意数字0的特殊性.例4.2021-的倒数是( )A .2021-B .12021-C .12021D .2021 【答案】B【解析】根据倒数的定义即可解决.解:∵()1202112021⎛⎫-⨯-= ⎪⎝⎭, ∴-2021的倒数是12021-. ∴A 、C 、D 选项都是错误的,只有B 选项正确.故选:B【点睛】本题考查了倒数的知识点,熟知倒数的定义是解题的关键.例5.计算:32÷(﹣4)×14的结果是( )A .﹣16B .16C .﹣2D .﹣12 【答案】C【解析】根据有理数乘除法的运算法则计算可求解.【详解】解:原式=﹣8×14=﹣2.故选:C .【点睛】本题考查了有理数的乘除,解题关键是熟练掌握有理数乘除法的法则,准确运用法则进行计算.例6.在下列各题中,结论正确的是( )A .若0,0a b ><,则0b a >B .若a b >,则0a b ->C .若0,0a b <<,则0;<abD .若,0a b a >>,则0b a< 【答案】B【解析】 根据两数的符号或大小判断相应的式子是否成立即可.解:A 、两数相除,异号得负,故选项错误;B 、大数减小数,一定大于0,故选项正确;C 、两数相乘,同号得正,故选项错误;D 、若,0a b a >>,则b a 可正可负,故选项错误; 故选:B .【点睛】本题考查了有理数减法、乘除法运算,不确定符号的数在计算时的结果的符号也不确定. 例7.下列计算中正确的是( )A .()11151351353⎛⎫-⨯--=-++= ⎪⎝⎭B .()1115135152353⎛⎫-⨯--=---=- ⎪⎝⎭ C .()()()11112224622323⎛⎫⎛⎫-÷-+=-÷-+-÷=-=- ⎪ ⎪⎝⎭⎝⎭D .235532-⨯⨯-=- 【答案】D【解析】利用乘法的分配律计算,A B 选项,可判断,A B ,由于除法没有分配律,所以先计算括号内的运算,再计算除法,可判断C ,先求绝对值,再利用乘法的结合律计算D 选项,从而可判断.D解:()()()()111115115151515353⎛⎫-⨯--=-⨯--⨯--⨯ ⎪⎝⎭351517=-++=,故A ,B 错误;()11223⎛⎫-÷-+ ⎪⎝⎭()()32122666⎛⎫⎛⎫=-÷-+=-÷- ⎪ ⎪⎝⎭⎝⎭()()2612=-⨯-=,故C 错误;23235553232⎛⎫-⨯⨯-=-⨯⨯=-⎪⎝⎭,故D 正确; 故选:.D【点睛】本题考查的是乘法的结合律与分配律,有理数的除法运算,绝对值的运算,有理数的混合运算,掌握以上知识是解题的关键.例8.已知||4x =,1||2=y ,且0xy <,则x y 的值等于( ) A .8-B .2-C .8-或8D .2-或2 【答案】A【解析】根据||4x =,1||2=y ,可以求出x ,y 的值,再根据0xy <确定x y 的值即可. ||4x =,1||2=y , ∴4x =±,12y =±, 0xy <,∴x ,y 异号,∴当4x =,12y 时,4812x y ==--, 当4x =-,12y =时,4812x y -==-, 综上所述:x y的值为8-. 故选:A .【点睛】本题考查了有理数的除法,绝对值,有理数的乘法,解题的关键是明确同号得正,异号得负的意义.例9.如果四个不同的正整数m ,n ,p ,q 满足(4)(4)(4)(4)9m n p q ----=,则m n p q +++等于( )A .12B .14C .16D .18【答案】C【解析】由题意确定出m ,n ,p ,q 的值,代入原式计算即可求出值.解:∵四个互不相同的正整数m ,n ,p ,q ,满足(4-m )(4-n )(4-p )(4-q )=9,∴满足题意可能为:4-m =1,4-n =-1,4-p =3,4-q =-3,解得:m =3,n =5,p =1,q =7,则m +n +p +q =16.故选:C .【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.【过关检测】一、单选题1.计算(5164--)×(﹣12)的结果为( ) A .﹣7B .7C .﹣13D .13【答案】D【解析】根据乘法的分配律、两个负数相乘解题,注意:负负得正.【详解】 51()(12)1031364--⨯-=+= 故选:D .【点睛】本题考查有理数乘法的运算律,熟练掌握两个负数相乘得正及乘法的分配律是解题关键.2.已知两个有理数,如果两数之积小于0,两数之和大于0,那么()A.两数同时大于0 B.两数互为相反数C.两数同号D.两数异号,且正数的绝对值较大【答案】D【解析】根据两数相乘,同号得正,异号得负,可知:两数之积小于0,则两数为异号;同号两数相加为大于0,则正数的绝对值较大.【详解】由已知两数之积小于0,说明两数为异号;若两个数之和大于0,说明正数的绝对值较大;故选:D.【点睛】本题考查了有理数的加法和乘法,比较简单,熟练掌握两个法则是关键,3.-45×(10-114+0.05)=-8+1-0.04,这个运算应用了()A.加法结合律B.乘法结合律C.乘法交换律D.分配律【答案】D【解析】根据分配律特点即可求解.【详解】-45×(10-114+0.05)=-45×10-45×(-114)-45×0.05=-8+1-0.04故应用了分配律,故选D.【点睛】此题主要考查运算律的识别,解题的关键是熟知分配律的特点.4.计算﹣100÷5×15,结果正确的是()A.4 B.﹣4 C.﹣100 D.100【答案】B【解析】先确定符号,按顺序计算,注意:除法转化为乘法,所有除数都要转化为其倒数. 【详解】原式=﹣100×15×15=﹣4,故选B.【点睛】本题考查了有理数的乘除法,掌握运算法则是正确解答本题的关键.特别注意符号. 5.下列计算不正确的是()A.5×(-7)×(-8)=280B.(-18)×2 1 3⎛⎫-⎪⎝⎭×2=60 C.0×(-2)×(-3)×(-4)=0D.123235⎛⎫--⎪⎝⎭×(-60)=12×(-60)+23×(-60)+35×(-60)=-30-40-36=-106【答案】D【解析】根据有理数混合运算的法则和顺序分别计算即可判断正误.【详解】A、5×(-7)×(-8)=280,正确,不符合题意;B、(-18)×2 1 3⎛⎫-⎪⎝⎭×2=60,正确,不符合题意;C、0×(-2)×(-3)×(-4)=0,正确,不符合题意;D、123235⎛⎫--⎪⎝⎭×(-60)123(60)(60)(60)235=⨯--⨯--⨯-304036=-++46=,不正确,符合题意.故选:D.【点睛】本题主要考查了有理数的混合运算.熟练掌握有理数的运算法则是解题的关键.6.下列四个算式中,误用分配律的是()A.12×11 236⎛⎫-+⎪⎝⎭=12×2-12×13+12×16B.11236⎛⎫-+⎪⎝⎭×12=2×12-13×12+16×12C.12÷11 236⎛⎫-+⎪⎝⎭=12÷2-12÷13+12÷16D.11236⎛⎫-+⎪⎝⎭÷12=2÷12-13÷12+16÷12【答案】C【解析】根据乘法分配律的特点即可求解.【详解】当除数是一项时,可以用分配律;当除数是多项时,12÷11 236⎛⎫-+⎪⎝⎭不能用分配律.故选C.【点睛】此题主要考查有理数的运算,解题的关键是熟知乘法分配律的特点.7.王小天有若干张10元、5元的纸币,这两种纸币的张数相同,那么王小天可能有( )元钱.A.50 B.51 C.75 D.100【答案】C【解析】【解析】先求出1张10元和5元的共有多少钱,再从选项中找出这个数的倍数即可.【详解】10+5=15(元);A,50÷15=3…5,50不是15的倍数,不符合要求;B,51÷15=3…6,51不是15的倍数,不符合要求;C,75÷15=5,75是15的倍数,符合要求;D ,100÷15=6…10,100不是15的倍数,不符合要求; 故选C . 【点睛】本题先求出各一张的总钱数,只要是这个钱数的整数倍的数就符合要求. 8.互不相等的四个整数的积等于4,则这四个数的绝对值的和为( ) A .5 B .6C .7D .8【答案】B 【解析】根据题意可得出这四个数的值,继而可以确定这四个数的绝对值的的和. 【详解】∵四个互不相等的整数的积等于4, ∴这四个数分别为 1,-1,2,-2, ∴绝对值之和为1+-1+2+-2=6, 故选:B . 【点睛】本题考查有理数的乘法运算,关键在于根据题意判断四个数的值,注意审清题意,把这四个数限定在很小的范围.9.若a 、b 互为相反数,c 、d 互为倒数,m 的绝对值为2,则•a bm m cd m+-+值为( ) A .3- B .3C .5-D .3或5-【答案】B 【解析】根据题意可得,a+b=0,cd=1,m=±2,代入求解即可. 【详解】 原式=4-1+0=3 故选:B 【点睛】本题考查了代数式求值,解答本题的关键是根据题意得出a+b=0,cd=1,m=±2. 10.下列结论:①若ab >0,则a >0,b >0;②若a÷b <0,则a >0,b <0;③若a >0,b >0,则ab >0;④若a <0,b <0,则a÷b >0,其中,正确的个数是( )A .1B .2C .3D .4 【答案】B 【解析】 【解析】根据有理数的乘法法则和除法法则逐一进行判断即可. 【详解】若ab >0,则a >0,b >0或a <0,b <0,①错误; 若a÷b <0,则a >0,b <0或a <0,b >0,②错误; 若a >0,b >0,则ab >0,③正确; 若a <0,b <0,则a÷b >0,④正确, 故选B . 【点睛】本题考查了有理数的乘法、有理数的除法,掌握有理数乘法法则、有理数除法法则是解题的关键.两数相乘(除),同号得正,异号得负. 11.若1<x <2,则|2||1|||21x x x x x x---+--的值是( ) A .﹣3 B .﹣1C .2D .1【答案】D 【解析】在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号. 【详解】 解:12x <<,20x ∴-<,10x ->,0x >,∴原式1111=-++=,故选:D . 【点睛】本题主要考查了绝对值,代数式的化简求值问题.解此题的关键是在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号.12.下列等式或不等式中:①0a b +=;②0ab <;③a b a b -=+;④()00,0a b a b ab+=≠≠,表示a 、b 异号的个数有( ) A .0个 B .1个C .2个D .3个【答案】C 【解析】根据有理数的加法、乘法、绝对值运算、除法逐个判断即可得. 【详解】 ①当0ab 时,0a b +=,但,a b 同号;②0ab <,则,a b 异号; ③当0ab时,0a b a b -=+=,但,a b 同号;④因为0,0a b ≠≠, 所以分以下四种情况: 当0,0a b >>时,112a a b b ba a b++==+=, 当0,0a b ><时,1(1)0a a b b a a b b==+-++=-, 当0,0a b <>时,110b b b a a b a a -++==-+=, 当0,0a b <<时,1(1)2b b b a a b a a ==-+---+=-+, 则只有当,a b 异号时,0a ba b+=; 综上,表示,a b 异号的个数有2个, 故选:C . 【点睛】本题考查了有理数的加法、乘法、绝对值运算、除法,较难的是题④,正确分四种情况讨论是解题关键.二、填空题 13.计算:(1)(-4)×15×(-35)=_____(2)(-45)×12×47×(-358)=_____【答案】36 1 【解析】(1)原式=(-60)×(-35)=36;(2)原式=(-45×12)×(-358×47)=(-25)×(-208)=1.故答案为(1) 36,(2) 1.点睛:计算分数的乘积时,可以将分子分母相同或成倍数的两项结合起来计算,便于约分. 14.指出下列变化中所运用的运算律:(1)3×(-2)=-2×3_____;(2)3×(-2)×(-5)=3×[(-2)×(-5)]_____;(3)68×(524-216)=68×524-68×216.________.【答案】乘法交换律乘法结合律乘法分配律【解析】利用乘法运算律判断即可得到结果.【详解】解:(1)3×(-2)=-2×3,乘法交换律;(2)3×(-2)×(-5)=3×[(-2)×(-5)],乘法结合律;(3)68×(524-216)=68×524-68×216,乘法分配律.故答案为:(1)乘法交换律;(2)乘法结合律;(3)乘法分配律.【点睛】此题考查了有理数的乘法,熟练掌握运算律是解本题的关键.15.如果两个数在数轴上对应的两个点在原点同侧,则这两个数的积是________.【答案】正数【解析】根据数轴的特点即可求解.【详解】如果两个数在数轴上对应的两个点在原点同侧,则两数同号,乘积为正故答案为:正数.【点睛】此题主要考查数轴的性质,解题的关键是熟知有理数的运算法则.16.用字母表示有理数乘法的符号法则:(1)若a>0,b>0,则ab____0,若a>0,b<0,则ab____0;(2)若a<0,b>0,则ab____0,若a<0,b<0,则ab____0;(3)若a≠0,b=0,则ab____0.【答案】><<>=【解析】根据乘法法则“两个数相乘,同号得正,异号得负,任何数同0相乘得0”解答即可.【详解】(1)∵a>0,b>0,∴ab>0,∵a>0,b<0,∴ab<0;(2)∵a<0,b>0,∴ab<0,∵a<0,b<0,∴ab>0;(3)∵a≠0,b=0,∴ab=0;故答案为:>,<,<,>,=.【点睛】本题考查了有理数的乘法法则,解此题的关键是熟记法则:几个不等于零的数相乘,积的符号由负因数的个数决定:当负因数有奇数个数,积为负;当负因数的个数为偶数个时,积为正.17.填空:(1)(-2)×(-2)×2×(-2)的积的符号是____;(2)47⎛⎫-⎪⎝⎭×35⎛⎫- ⎪⎝⎭×23⎛⎫- ⎪⎝⎭×12⎛⎫-⎪⎝⎭的积的符号是___.【答案】-+【解析】(1)根据两数相乘,同号得正,异号得负即可解决;(2)根据两数相乘,同号得正,异号得负即可解决.【详解】(1)(-2)×(-2)×2×(-2)中有3个乘数为负,积的符号是-;(2)47⎛⎫-⎪⎝⎭×35⎛⎫- ⎪⎝⎭×23⎛⎫- ⎪⎝⎭×12⎛⎫-⎪⎝⎭中有4个乘数为负,积的符号是+.故答案为:-;+.【点睛】本题考查了有理数乘法及应用,熟练掌握运算法则是解题的关键.18.被除数是-312,除数比被除数小112,则商为________.【答案】0.7【解析】分析:先确定除数,再根据商=被除数÷除数,即可求解.详解:∵被除数是﹣312,除数比被除数小112,∴除数为﹣312﹣112=﹣5,∴商为﹣312÷(﹣5)=0.7.故答案为0.7.点睛:本题考查了有理数的除法,解决此题的关键是利用在除法里,商=被除数÷除数.19.若m+1与﹣2互为倒数,则m的值为_____.【答案】-3 2【解析】根据倒数的定义,互为倒数的两数乘积为1可解.【详解】解:根据题意得:(m+1)×(-2)=1,解得m=−32.故答案为:−32.【点睛】此题考查倒数,解题关键在于掌握倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.20.在-2 、-3 、4、5 中选取2个数相除,则商的最小值是________.【答案】5 2 -【解析】根据同号两数相除为正数,异号两数相除为负数,将每两个异号的数相除,选出商的最小值. 【详解】 解:∵1242,422,2255,5522, 3344,4433,3355,5533, ∴商的最小值为52-. 故答案为:52-. 【点睛】本题考查有理数的除法,掌握除法法则是解答此题的关键.21.若0a <,则aa=______ . 【答案】-1 【解析】根据绝对值的性质和有理数的除法法则判断即可. 【详解】解:当0a <时,||a a =-,所以,1aa a a -==-. 故答案为:-1. 【点睛】本题考查化简绝对值和有理数的除法.需理解负数的绝对值是它的相反数和互为相反数的两个数(这两个数不能为0)商为-1.22.若一个数的绝对值是8,另一个数的绝对值是4,且这两个数的积为负数,则在这两个数中,用大数除以小数所得的商是________. 【答案】 -2或-12【详解】试题分析:这两个数的积为负数,则这两个数一正一负,又因一个数的绝对值是8,另一个数的绝对值是4,则这两个数可能是8和-4,或4和-8.所以大数除以小数所得的商是-2或-12. 试题解析:设|a |=8,|b |=4,则a =8或a =-8,b =4或b =-4. 因为ab <0,所以当a =8时,b =-4,则8-4=-2; 当a =-8时,b =4,则4-8=-12.23.若“!”是一种数学运算符号,1!1=,2!21=⨯,3!321=⨯⨯,4!4321=⨯⨯⨯,…,则 2016!2015!的值为________. 【答案】2016 【解析】根据1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1…得出规律,就是n!=n×(n-1)×(n-2)×…×1,根据这一规律即可得出答案. 【详解】解:∵1!1=,2!21=⨯,3!321=⨯⨯,4!4321=⨯⨯⨯,…, ∴2016!201620152014120162015!201520141⨯⨯⨯⨯==⨯⨯⨯. 故答案为2016. 【点睛】此题考查了有理数的乘除法,解题的关键是根据题意,找出之间的规律,列出式子. 24.一列数a 1,a 2,a 3,…,a n ,其中a 1=﹣1,a 2=111a -,a 3=211a -,…,a n =111n a --,则a 1+a 2+a 3+…+a 2020=_____. 【答案】20172【解析】根据题意,可以写出这列数的前几个数,然后即可发现数字的变化特点,从而可以求得所求式子的值. 【详解】 解:由题意可得,11a =-,211112a a ==-, 32121a a ==-, 41a =-,…故上面的数据以1-,12,2为一个循环,依次出现, 131222-++=,202036731÷=⋅⋅⋅, 1232020a a a a ∴+++⋯+111(12)(12)(12)(1)222=-+++-+++⋯+-+++- 3673(1)2=⨯+- 20172=故答案为:20172. 【点睛】本题考查数字的变化类,解答本题的关键是明确题意,发现数字的变化特点,求出所求式子的值.三、解答题 25.计算(1)(3)(4)(11)(19)-+--+--; (2)523()(12)1234+-⨯-. 【答案】(1)1;(2)-4. 【解析】(1)利用有理数加减混合运算的计算方法计算即可; (2)利用乘法分配律进行简便运算,计算后即可得出结果. 【详解】解:(1)(3)(4)(11)(19)-+--+--(3)(4)(11)19=-+-+-+1819=-+ 1=;(2)523()(12)1234+-⨯- 523(12)(12)(12)1234=⨯-+⨯--⨯- 589=--+ 4=-.【点睛】此题考查了有理数的混合运算,掌握有理数混合运算的运算顺序及相关运算法则是解题的关键. 26.用简便方法计算.(1) (114-16-12)÷(-136); (2) (-191819)×19.【答案】(1) -21;(2)-379 【解析】(1)先将带分数转化为假分数,将除法转化为乘法,再运用乘法分配率分别计算即可; (2)先将181919⎛⎫- ⎪⎝⎭分为12019⎛⎫-+ ⎪⎝⎭,再运用乘法分配率计算即可.【详解】 解:(1)1111146236⎛⎫⎛⎫--÷- ⎪ ⎪⎝⎭⎝⎭ ()511=36462⎛⎫--⨯- ⎪⎝⎭()()()511=363636462⨯--⨯--⨯- =45618-++=21-(2)18191919⎛⎫-⨯ ⎪⎝⎭1=201919⎛⎫-+⨯ ⎪⎝⎭ 1=20191919-⨯+⨯ =3801-+=379-【点睛】本题考查了有理数乘除运算,熟练掌握乘法运算律是解题的关键.27.计算:(1)1111324⎛⎫-÷÷ ⎪⎝⎭ 110 (2)()374485212⎛⎫-+-⨯- ⎪⎝⎭ 【答案】(1)43-;(2)19. 【解析】(1)先把括号内通分,先计算括号内的减法,同时把除法转化为乘法,再利用乘法的结合律先计算后两个数的乘法,从而可得答案;(2)利用乘法的分配律把原式化为:()()()3752424244128⎛⎫-⨯-+⨯--⨯- ⎪⎝⎭,再先计算乘法,最后计算加减即可得到答案.【详解】解:(1)1111132410⎛⎫-÷÷ ⎪⎝⎭ 23410665⎛⎫=-⨯⨯ ⎪⎝⎭ 186⎛⎫=-⨯ ⎪⎝⎭4.3=- (2)()374485212⎛⎫-+-⨯- ⎪⎝⎭()()()3752424244128⎛⎫=-⨯-+⨯--⨯- ⎪⎝⎭()181415=+-+19.=【点睛】本题考查的是有理数的加减乘除的混合运算,同时考查乘法的分配律,掌握利用运算的先后顺序及乘法的分配律是解题的关键.28.某粮店进了一批大米,第一天卖出了13,第二天卖出了1.5吨,已卖的大米占这批大米的一半.这批大米有多少吨?【答案】这批大米有9吨【解析】先求出第二天占整体的部分,然后应用有理数除法法则即可.【详解】 第二天卖出大米占整体的比例:111236-= ∴11.5 1.5696÷=⨯=(吨) 故答案为9吨.【点睛】本题考查了有理数的除法和减法,先求出部分占整体的比例是本题的关键.29.已知a ,b 互为相反数,m ,n 互为倒数,x 绝对值为1,求2a b mn x m n+-+--值. 【答案】3-或1-【解析】根据相反数、倒数的定义,可知a +b =0,mn =1,将它们代入,即可求出结果.【详解】∵a 、b 互为相反数,∴a +b =0;∵m 、n 互为倒数,∴mn =1;∵x 的绝对值为1,∴x =±1.①当x =1时,原式=−2+0−1=−3;②当x =−1时,原式=−2+0+1=-1.【点睛】本题主要考查相反数、倒数及绝对值的计算,掌握互为相反数的两数的和为0、互为倒数的两数积为1是解题的关键.30.某粮库一周前存有粮食100吨,本周内粮库进出粮食的记录如下(运进为正)(1)通过计算,说明本周内哪天粮库剩下的粮食最多?(2)若运进的粮食为购进的,购买价为4000元/吨,运出的粮食为卖出的,卖出价为4600元/吨,则这一周的利润为多少?(3)若每周平均进出的粮食数量大致相同,问:再过几周粮库存粮食达到200吨?【答案】(1)本周星期一的剩下的粮食最多,为135吨;(2)14000元;(3)9周.【解析】(1)理解“+”表示进库“-”表示出库,求出每天的情况即可求解,(2)这一周的利润=卖出的钱数-购买的钱数,依此列式计算即可求解;(3)由200吨减去本周的粮食数量110吨,再根据每周的进出粮食的数量为+10吨,列式计算即可求解.【详解】解:(1)星期一:()100++35=135,星期二:()135+20115,-=星期三:()115+3085,-=星期四:()85++25=110,星期五:()110+2486,-=星期六:()8640126,++=星期天:()126+16110,-=所以本周星期一的剩下的粮食最多,为135吨.(2)由题意得:购进的粮食有:35+25+40=100(吨),卖出的粮食有:2030241690+++=(吨),所以:这一周的利润:460090400010014000⨯-⨯=(元).(3)由题意得:()()200110100909,-÷-=所以再过9周粮库存粮食达到200吨.【点睛】本题考查的是正负数的实际应用,同时考查了有理数的加减运算,有理数的乘除运算,掌握以上知识是解题的关键.31.观察下列等式112⨯=1﹣12,123⨯=12﹣13,134⨯=13﹣14,将以上三个等式两边分别相加得112⨯+123⨯+134⨯=1﹣12+12﹣13+13﹣14=1﹣14=34. (1)猜想并写出1(1)n n =+ ; (2)112⨯+123⨯+134⨯+…+120162017⨯= ; (3)探究并计算:111124466820162018++++⨯⨯⨯⨯; (4)计算:11111111141224406084112144180++++++++. 【答案】(1)111n n -+;(2)20162017;(3)2521009;(4)920. 【解析】(1)观察已知等式,进行归纳类推即可得;(2)根据(1)中的猜想进行计算即可得;(3)先根据乘法分配律提取14,再参照(2)进行计算即可得; (4)先根据乘法分配律提取12,再参照(2)进行计算即可得. 【详解】(1)111122=-⨯, 1112323=-⨯, 1113434=-⨯, 归纳类推得:111(1)1n n n n =-++, 故答案为:111n n -+; (2)111112233420162017, 111111112233420162017=-+-+-++-, 112017=-, 20162017=, 故答案为:20162017; (3)111124466820162018++++⨯⨯⨯⨯, 11111412233410081009⎛⎫=⨯+++⋯+ ⎪⨯⨯⨯⨯⎝⎭, 11111111223143410081009-+-+-+⎛⎫=⨯ ⎪⎝+-⎭, 11141009⎛⎫=⨯- ⎪⎝⎭, 1100841009=⨯, 2521009=; (4)11111111141224406084112144180++++++++, 111111111203012261245292607⎛⎫++++++++ ⎪⎝⨯⎭=,111112122334910⎛⎫=⨯++++ ⎪⨯⨯⨯⨯⎝⎭, 111111112223490131-+-+-⎛++⎫=⨯ ⎪⎝-⎭, 111210⎛⎫=⨯- ⎪⎝⎭, 19210=⨯, 920=. 【点睛】本题考查了有理数乘法与加减法的规律性问题,依据题意,正确归纳类推出一般规律是解题关键. 32.在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.(提出问题)两个有理数a 、b 满足ab >0,求a a b b+ (解答问题)解:由题意得:a ,b 两个有理数都为正数或两个有理数都为负数①a ,b 两个都是正数,即a >0,b >0,时,则 a a b b +=a b a b +=1+1=2 ②当a ,b 两个都是负数,即a <0,b <0,时a a b b +=(1)(1)2a b a b --+=-+-=-,所以a a b b + =2或-2 (探究)请根据上面的解题思路解答下面的问题:(1)两个有理数a ,b 满足ab <0,求a a b b+ (2)已知|a|=3,|b|=1,且a <b ,求a+b 的值.【答案】(1)0;(2)-2或-4【解析】(1)根据题意因为ab <0,可分两种情况,①当a >0,b <0;②当b >0,a <0,进而得出答案;(2)根据绝对值的意义,先计算出a=±3,b=±1,根据条件a <b 求解即可得出答案. 【详解】解:∵ab<0,∴ a、b异号,①当a>0,b<0时,则||||110;+=-= a ba b②当b>0,a<0,则||||-1+10;+== a ba b∴aabb+的值为0(2)∵|a|=3,|b|=1,∴a=±3,b=±1,又∵a<b,∴①a=-3,b=1,则a+b=-3+1=-2,②a=-3,b=-1,则a+b=-3+(-1)=-4,∴a+b的值为:-2或-4【点睛】本题主要考查了绝对值的意义及有理数加减乘除运算,正确分类讨论是解题关键.。
